No CrossRef data available.
Published online by Cambridge University Press: 29 June 2021
It is well known that for any integers k and g, there is a graph with chromatic number at least k and girth at least g. In 1960s, Erdös and Hajnal conjectured that for any k and g, there exists a number h(k,g), such that every graph with chromatic number at least h(k,g) contains a subgraph with chromatic number at least k and girth at least g. In 1977, Rödl proved the case when 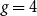 $g=4$
, for arbitrary k. We prove the fractional chromatic number version of Rödl’s result.
$g=4$
, for arbitrary k. We prove the fractional chromatic number version of Rödl’s result.
Supported in part by the NSERC Discovery Grant R611450 (Canada), by the Canada Research Chairs program, and by the Research Project J1-8130 of ARRS (Slovenia).
Part of this work was done while the author was a PIMS Postdoctoral Fellow at the Department of Mathematics, Simon Fraser University, Burnaby, B.C.