Published online by Cambridge University Press: 30 May 2022
For a subgraph 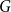 $G$
of the blow-up of a graph
$G$
of the blow-up of a graph 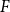 $F$
, we let
$F$
, we let 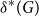 $\delta ^*(G)$
be the smallest minimum degree over all of the bipartite subgraphs of
$\delta ^*(G)$
be the smallest minimum degree over all of the bipartite subgraphs of 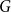 $G$
induced by pairs of parts that correspond to edges of
$G$
induced by pairs of parts that correspond to edges of 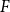 $F$
. Johansson proved that if
$F$
. Johansson proved that if 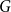 $G$
is a spanning subgraph of the blow-up of
$G$
is a spanning subgraph of the blow-up of 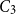 $C_3$
with parts of size
$C_3$
with parts of size  $n$
and
$n$
and 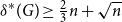 $\delta ^*(G) \ge \frac{2}{3}n + \sqrt{n}$
, then
$\delta ^*(G) \ge \frac{2}{3}n + \sqrt{n}$
, then 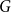 $G$
contains
$G$
contains  $n$
vertex disjoint triangles, and presented the following conjecture of Häggkvist. If
$n$
vertex disjoint triangles, and presented the following conjecture of Häggkvist. If 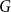 $G$
is a spanning subgraph of the blow-up of
$G$
is a spanning subgraph of the blow-up of 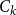 $C_k$
with parts of size
$C_k$
with parts of size  $n$
and
$n$
and 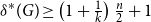 $\delta ^*(G) \ge \left(1 + \frac 1k\right)\frac n2 + 1$
, then
$\delta ^*(G) \ge \left(1 + \frac 1k\right)\frac n2 + 1$
, then 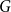 $G$
contains
$G$
contains  $n$
vertex disjoint copies of
$n$
vertex disjoint copies of 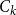 $C_k$
such that each
$C_k$
such that each 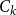 $C_k$
intersects each of the
$C_k$
intersects each of the 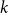 $k$
parts exactly once. A similar conjecture was also made by Fischer and the case
$k$
parts exactly once. A similar conjecture was also made by Fischer and the case 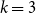 $k=3$
was proved for large
$k=3$
was proved for large  $n$
by Magyar and Martin.
$n$
by Magyar and Martin.
In this paper, we prove the conjecture of Häggkvist asymptotically. We also pose a conjecture which generalises this result by allowing the minimum degree conditions in each bipartite subgraph induced by pairs of parts of 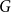 $G$
to vary. We support this new conjecture by proving the triangle case. This result generalises Johannson’s result asymptotically.
$G$
to vary. We support this new conjecture by proving the triangle case. This result generalises Johannson’s result asymptotically.
Research supported in part by NSF Grant DMS 1800761.