Published online by Cambridge University Press: 18 December 2009
We analyse a simple random process in which a token is moved in the interval A = {0, . . ., n}. Fix a probability distribution μ over D = {1, . . ., n}. Initially, the token is placed in a random position in A. In round t, a random step sized is chosen according to μ. If the token is in position x ≥ d, then it is moved to position x − d. Otherwise it stays put. Let TX be the number of rounds until the token reaches position 0. We show tight bounds for the expectation Eμ(TX) of TX for varying distributions μ. More precisely, we show that 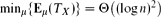 . The same bounds are proved for the analogous continuous process, where step sizes and token positions are real values in [0, n + 1), and one measures the time until the token has reached a point in [0, 1). For the proofs, a novel potential function argument is introduced. The research is motivated by the problem of approximating the minimum of a continuous function over [0, 1] with a ‘blind’ optimization strategy.
. The same bounds are proved for the analogous continuous process, where step sizes and token positions are real values in [0, n + 1), and one measures the time until the token has reached a point in [0, 1). For the proofs, a novel potential function argument is introduced. The research is motivated by the problem of approximating the minimum of a continuous function over [0, 1] with a ‘blind’ optimization strategy.