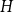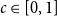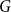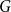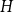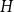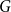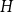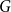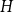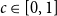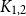1. Introduction
We asymptotically study the number of homomorphisms from a fixed graph
![]() $H$
to graphs
$H$
to graphs
![]() $G$
with a fixed edge density. Specifically, we investigate the properties of graphs
$G$
with a fixed edge density. Specifically, we investigate the properties of graphs
![]() $G$
that maximise the homomorphism density from
$G$
that maximise the homomorphism density from
![]() $H$
to
$H$
to
![]() $G$
:
$G$
:
Definition 1 (Homomorphism Density). Denote the homomorphism density of
![]() $H$
in
$H$
in
![]() $G$
by
$G$
by
where
![]() $|G|$
denotes the number of vertices in
$|G|$
denotes the number of vertices in
![]() $G$
and
$G$
and
![]() $\hom\! (H,G)$
denotes the number of homomorphisms from
$\hom\! (H,G)$
denotes the number of homomorphisms from
![]() $H$
to
$H$
to
![]() $G$
.
$G$
.
Formally, for a given graph
![]() $H$
and
$H$
and
![]() $c \in [0,1]$
, we are interested in finding a sequence of graphs that attains the value of
$c \in [0,1]$
, we are interested in finding a sequence of graphs that attains the value of
where
![]() $\mathcal{C}_c = \{G: t(K_2, G) \leq c\}$
and the
$\mathcal{C}_c = \{G: t(K_2, G) \leq c\}$
and the
![]() $\limsup$
over a class of graphs is defined as
$\limsup$
over a class of graphs is defined as
This quantity has been studied for a variety of graphs
![]() $H$
. Two families of graphs that frequently maximise
$H$
. Two families of graphs that frequently maximise
![]() $t(H, \cdot )$
are the quasi-clique and quasi-star, where a quasi-clique is an induced clique with isolated vertices and a quasi-star is the complement of a quasi-clique (see Figure 1). We remark that in some papers, the quasi-clique is defined as isolated vertices and an induced clique with one additional vertex that may only be connected to a subset of vertices in the clique [Reference Day and Sarkar4, Reference Nagy12]. This is important if one wants to determine the non-asymptotic maximiser of
$t(H, \cdot )$
are the quasi-clique and quasi-star, where a quasi-clique is an induced clique with isolated vertices and a quasi-star is the complement of a quasi-clique (see Figure 1). We remark that in some papers, the quasi-clique is defined as isolated vertices and an induced clique with one additional vertex that may only be connected to a subset of vertices in the clique [Reference Day and Sarkar4, Reference Nagy12]. This is important if one wants to determine the non-asymptotic maximiser of
![]() $t(H,G)$
for a graph
$t(H,G)$
for a graph
![]() $G$
with say
$G$
with say
![]() $n$
vertices and
$n$
vertices and
![]() $m$
edges. Since we only consider asymptotic results, we will use the simpler definition.
$m$
edges. Since we only consider asymptotic results, we will use the simpler definition.

Figure 1. An example of a quasi-star and quasi-clique.
A very general result of Alon [Reference Alon2] implies that if
![]() $H$
has a spanning subgraph that is a disjoint union of cycles and isolated edges then
$H$
has a spanning subgraph that is a disjoint union of cycles and isolated edges then
![]() $\mathcal{M}_H(c)$
is maximised on the quasi-clique for all
$\mathcal{M}_H(c)$
is maximised on the quasi-clique for all
![]() $c$
. The study of the behaviour of specific
$c$
. The study of the behaviour of specific
![]() $H$
largely began with Ahlswede and Katona [Reference Ahlswede and Katona1], who showed that for any
$H$
largely began with Ahlswede and Katona [Reference Ahlswede and Katona1], who showed that for any
![]() $c \in [0,1]$
when
$c \in [0,1]$
when
![]() $H$
is the
$H$
is the
![]() $2$
-star, a star with two edges,
$2$
-star, a star with two edges,
![]() $\mathcal{M}_H(c)$
is always achieved on either the quasi-star or quasi-clique. This result was later generalised to
$\mathcal{M}_H(c)$
is always achieved on either the quasi-star or quasi-clique. This result was later generalised to
![]() $k$
-stars, showing that for any
$k$
-stars, showing that for any
![]() $c \in [0,1]$
the number of homomorphisms from the
$c \in [0,1]$
the number of homomorphisms from the
![]() $k$
-star is maximised when
$k$
-star is maximised when
![]() $G$
is the quasi-star or quasi-clique for small
$G$
is the quasi-star or quasi-clique for small
![]() $k$
[Reference Kenyon, Radin, Ren and Sadun8], and shortly after for all
$k$
[Reference Kenyon, Radin, Ren and Sadun8], and shortly after for all
![]() $k \geq 2$
[Reference Reiher and Wagner13]. The question was also studied in the case where
$k \geq 2$
[Reference Reiher and Wagner13]. The question was also studied in the case where
![]() $H$
is the
$H$
is the
![]() $4$
-edge path, and again it was shown that the optimising graph is always either the quasi-star and quasi-clique for all densities [Reference Nagy12].
$4$
-edge path, and again it was shown that the optimising graph is always either the quasi-star and quasi-clique for all densities [Reference Nagy12].
A particularly important class of graphs for this problem is the family of threshold graphs, which contains both the quasi-clique and quasi-star.
Definition 2. (Threshold Graph) A graph
![]() $T$
is threshold if for any two vertices
$T$
is threshold if for any two vertices
![]() $u,v \in V(T)$
we have that
$u,v \in V(T)$
we have that
![]() $N(u) \subseteq \overline{N(v)}$
or
$N(u) \subseteq \overline{N(v)}$
or
![]() $N(v) \subseteq \overline{N(u)}$
, where
$N(v) \subseteq \overline{N(u)}$
, where
![]() $\overline{N(v)}\, :\!=\, \{v\} \cup N(v)$
denotes the closed neighbourhood of
$\overline{N(v)}\, :\!=\, \{v\} \cup N(v)$
denotes the closed neighbourhood of
![]() $v$
.
$v$
.
We remark that there are other characterisations of threshold graphs [Reference Mahadev and Peled11] which we will discuss in more detail in Section 2. Our main contribution is proving via a local move that the maximiser of
![]() $t(H,G)$
for any graph
$t(H,G)$
for any graph
![]() $H$
is always attained on a threshold graph.
$H$
is always attained on a threshold graph.
Theorem 3.
For any graph
![]() $H$
and
$H$
and
![]() $c \in [0,1]$
, we have that
$c \in [0,1]$
, we have that
where
![]() $\mathcal{T}$
denotes the set of all threshold graphs.
$\mathcal{T}$
denotes the set of all threshold graphs.
Such a result is of interest as threshold graphs have simpler limit objects than general graphs. Instead of considering the
![]() $\limsup$
over all graphs, we can work directly with graphons, which are graph limit objects, and find the graphon that maximises the number of homomorphisms from
$\limsup$
over all graphs, we can work directly with graphons, which are graph limit objects, and find the graphon that maximises the number of homomorphisms from
![]() $H$
[Reference Lovász10]. This approach is employed in the results of Nagy [Reference Nagy12] and Reiher and Wagner [Reference Reiher and Wagner13]. Threshold graphs may be more convenient to work with as their limits are one-dimensional, as opposed to graphons which are two dimensional [Reference Diaconis, Holmes and Janson5].
$H$
[Reference Lovász10]. This approach is employed in the results of Nagy [Reference Nagy12] and Reiher and Wagner [Reference Reiher and Wagner13]. Threshold graphs may be more convenient to work with as their limits are one-dimensional, as opposed to graphons which are two dimensional [Reference Diaconis, Holmes and Janson5].
We then extend Theorem 3 to sparse graphs and hypergraphs. To do so, we define
since homomorphism densities are zero for sparse graphs. We remark that the function
![]() $\mathcal{M}(H,n,m)$
was determined up to constant factors (depending on
$\mathcal{M}(H,n,m)$
was determined up to constant factors (depending on
![]() $H$
) by Janson, Oleszkiewicz and Ruciński [Reference Janson, Oleszkiewicz and Ruciński7] (see Theorem 22). Let us write
$H$
) by Janson, Oleszkiewicz and Ruciński [Reference Janson, Oleszkiewicz and Ruciński7] (see Theorem 22). Let us write
![]() $f(n) \sim g(n)$
if
$f(n) \sim g(n)$
if
![]() $\lim _{n \rightarrow \infty } f(n)/g(n) = 1$
. We will prove the following theorem, which extends Theorem 3 to the sparse setting.
$\lim _{n \rightarrow \infty } f(n)/g(n) = 1$
. We will prove the following theorem, which extends Theorem 3 to the sparse setting.
Theorem 4.
For any graph
![]() $H$
and function
$H$
and function
![]() $m(n) = \omega (n^{3/2})$
, we have that
$m(n) = \omega (n^{3/2})$
, we have that
where
![]() $\mathcal{T}$
denotes the set of threshold graphs. Moreover if
$\mathcal{T}$
denotes the set of threshold graphs. Moreover if
![]() $H$
has no induced
$H$
has no induced
![]() $C_4$
or
$C_4$
or
![]() $P_4$
, then
$P_4$
, then
for every
![]() $m,n \in \mathbb{N}$
.
$m,n \in \mathbb{N}$
.
We quickly remark that the bound of
![]() $\omega (n^{3/2})$
is likely not tight (cf. Question 50). Additionally, if one wants exact equality for all
$\omega (n^{3/2})$
is likely not tight (cf. Question 50). Additionally, if one wants exact equality for all
![]() $n,m \in \mathbb{N}$
, some assumptions on
$n,m \in \mathbb{N}$
, some assumptions on
![]() $H$
are necessary (cf. Remark 21).
$H$
are necessary (cf. Remark 21).
In order to state our result for hypergraphs, we first need to define the class of threshold hypergraphs. We remark that there are several non-equivalent definitions of threshold hypergraphs (see e.g. [Reference Reiterman, Rödl, Šiňajová and Tůma14]), but we will use the following definition throughout this paper.
Definition 5 (Threshold Hypergraph). Let
![]() $G$
be a
$G$
be a
![]() $k$
-uniform hypergraph with
$k$
-uniform hypergraph with
![]() $k \geq 2$
. We then say that
$k \geq 2$
. We then say that
![]() $G$
is a threshold hypergraph if for any two vertices
$G$
is a threshold hypergraph if for any two vertices
![]() $x,y$
we either have that
$x,y$
we either have that
![]() $x \ll _G y$
or
$x \ll _G y$
or
![]() $y \ll _G x$
, where we say
$y \ll _G x$
, where we say
![]() $x \ll _G y$
if for any
$x \ll _G y$
if for any
![]() $e \in E(G)$
with
$e \in E(G)$
with
![]() $x \in e$
and
$x \in e$
and
![]() $y \not \in e$
we have that
$y \not \in e$
we have that
![]() $(e \setminus \{x\}) \cup y \in E(G)$
. We omit the subscript when the underlying hypergraph
$(e \setminus \{x\}) \cup y \in E(G)$
. We omit the subscript when the underlying hypergraph
![]() $G$
is clear from context.
$G$
is clear from context.
As one might expect, taking
![]() $k = 2$
exactly coincides with the definition of threshold graphs. As such, the following theorem generalises Theorem 1.3 to the setting of
$k = 2$
exactly coincides with the definition of threshold graphs. As such, the following theorem generalises Theorem 1.3 to the setting of
![]() $k$
-uniform hypergraphs.
$k$
-uniform hypergraphs.
Theorem 6.
Let
![]() $H$
be a fixed
$H$
be a fixed
![]() $k$
-uniform hypergraph and
$k$
-uniform hypergraph and
![]() $c \in [0,1]$
then we have that
$c \in [0,1]$
then we have that
In a slight abuse of notation, we take
![]() $\mathcal{T}$
above to be the set of threshold hypergraphs and
$\mathcal{T}$
above to be the set of threshold hypergraphs and
![]() $\mathcal{C}_c$
to be the set of hypergraphs of edge density at most
$\mathcal{C}_c$
to be the set of hypergraphs of edge density at most
![]() $c$
.
$c$
.
We will prove Theorems 3, 4 and 6 in Section 3. The remainder of the paper shows a variety of applications of these ideas. We first give a simple proof in Theorem 42 of a recent result by Gerbner, Nagy, Patkós and Vizer [Reference Gerbner, Nagy, Patkós and Vizer6] that every graph is maximised on the quasi-clique for
![]() $c$
sufficiently close to
$c$
sufficiently close to
![]() $1$
. More precisely, we show that if
$1$
. More precisely, we show that if
![]() $\mathcal{M}_{K_{1,|H|-1}}(c)$
is asymptotically maximised on the quasi-clique then so is
$\mathcal{M}_{K_{1,|H|-1}}(c)$
is asymptotically maximised on the quasi-clique then so is
![]() $\mathcal{M}_{H}(c)$
.
$\mathcal{M}_{H}(c)$
.
We then contrast this with an example in Theorem 43 of a graph
![]() $H$
which for some
$H$
which for some
![]() $c\in [0,1]$
is optimised on neither the quasi-star nor the quasi-clique, disproving a conjecture of Nagy [Reference Nagy12]. To do so, we explicitly find a graph
$c\in [0,1]$
is optimised on neither the quasi-star nor the quasi-clique, disproving a conjecture of Nagy [Reference Nagy12]. To do so, we explicitly find a graph
![]() $G$
that has more homomorphisms from
$G$
that has more homomorphisms from
![]() $H$
than the quasi-star and quasi-clique when
$H$
than the quasi-star and quasi-clique when
![]() $c$
is small. This result was proved independently by Day and Sarkar [Reference Day and Sarkar4], who used a similar argument. While the arguments are fundamentally the same, the class of graphs
$c$
is small. This result was proved independently by Day and Sarkar [Reference Day and Sarkar4], who used a similar argument. While the arguments are fundamentally the same, the class of graphs
![]() $\mathcal{G}$
that we use with more homomorphisms from
$\mathcal{G}$
that we use with more homomorphisms from
![]() $H$
than the quasi-star or quasi-clique is the next simplest threshold graph, fitting well into our results.
$H$
than the quasi-star or quasi-clique is the next simplest threshold graph, fitting well into our results.
Finally, we give a new proof of the result of Ahlswede and Katona [Reference Ahlswede and Katona1] that the two-star is maximised on either the quasi-star or quasi-clique.
Theorem 7.
For any
![]() $c \in [0,1]$
, we have that
$c \in [0,1]$
, we have that
![]() $\mathcal{M}_{K_{1,2}}(c)$
is asymptotically attained on the quasi-star or quasi-clique.
$\mathcal{M}_{K_{1,2}}(c)$
is asymptotically attained on the quasi-star or quasi-clique.
For brevity, we omit the proof of Theorem 7 and refer an interested reader to the Arxiv version of the paper. The proof follows from writing an expression for the number of homomorphisms from the
![]() $2$
-star to a general threshold graph and then explicitly computing the optimum.
$2$
-star to a general threshold graph and then explicitly computing the optimum.
2. Preliminaries
2.1 Notation
We typically use
![]() $H$
as the fixed graph,
$H$
as the fixed graph,
![]() $G$
as the target graph,
$G$
as the target graph,
![]() $c$
as the edge density of
$c$
as the edge density of
![]() $G$
, and let
$G$
, and let
![]() $n$
and
$n$
and
![]() $m$
denote the number of vertices and edges in
$m$
denote the number of vertices and edges in
![]() $G$
. We let
$G$
. We let
![]() $\textrm{Hom}(H,G)$
denote the set of homomorphisms from
$\textrm{Hom}(H,G)$
denote the set of homomorphisms from
![]() $H$
to
$H$
to
![]() $G$
and
$G$
and
![]() $\hom\! (H,G)$
be the cardinality of
$\hom\! (H,G)$
be the cardinality of
![]() $\textrm{Hom}(H,G)$
. Moreover, we will be consistent with the notation described in the introduction.
$\textrm{Hom}(H,G)$
. Moreover, we will be consistent with the notation described in the introduction.
We will say a homomorphism
![]() $\varphi\; :\; V(H) \rightarrow V(G)$
uses an edge
$\varphi\; :\; V(H) \rightarrow V(G)$
uses an edge
![]() $uv \in E(G)$
if there exists an edge
$uv \in E(G)$
if there exists an edge
![]() $xy \in H$
such that
$xy \in H$
such that
![]() $u = \varphi (x)$
and
$u = \varphi (x)$
and
![]() $v = \varphi (y)$
. Similarly, it uses a vertex
$v = \varphi (y)$
. Similarly, it uses a vertex
![]() $v \in V(G)$
if
$v \in V(G)$
if
![]() $v \in \textrm{im} \varphi$
.
$v \in \textrm{im} \varphi$
.
We denote the neighbourhood of a vertex
![]() $u$
in
$u$
in
![]() $G$
by
$G$
by
![]() $N_G(u)$
, and the closed neighbourhood of a vertex
$N_G(u)$
, and the closed neighbourhood of a vertex
![]() $u$
by
$u$
by
![]() $\overline{N}_G(u) \, :\!=\, N_G(u) \cup \{u\}$
. We frequently drop the subscript
$\overline{N}_G(u) \, :\!=\, N_G(u) \cup \{u\}$
. We frequently drop the subscript
![]() $G$
when the graph is clear from context.
$G$
when the graph is clear from context.
Oftentimes when using big-Oh notation, there will be implicit constants depending on the graph
![]() $H$
or other parameters
$H$
or other parameters
![]() $k$
. In this case, we denote this using a subscript, for example,
$k$
. In this case, we denote this using a subscript, for example,
![]() $O_H(f(n))$
or
$O_H(f(n))$
or
![]() $O_k(f(n))$
.
$O_k(f(n))$
.
2.2 Threshold graphs
We begin by recalling some basic facts about threshold graphs. There are a number of equivalent definitions of threshold graphs and for a thorough treatment of the subject we refer the reader to [Reference Mahadev and Peled11]. A key second characterisation of threshold graphs will be the following:
Proposition 8. A graph is a threshold if and only if it can be built, starting from a single vertex graph, by repeatedly adding dominating or isolated vertices.
We note that this sequence is unique (up to automorphisms). In light of this, we put the set of (unlabelled)
![]() $n$
vertex threshold graphs in one-to-one correspondence with binary sequences of length
$n$
vertex threshold graphs in one-to-one correspondence with binary sequences of length
![]() $n - 1$
. In such a sequence the
$n - 1$
. In such a sequence the
![]() $i$
th element is a
$i$
th element is a
![]() $1$
if the
$1$
if the
![]() $i$
th vertex that we added is a dominating vertex and a
$i$
th vertex that we added is a dominating vertex and a
![]() $0$
if the
$0$
if the
![]() $i$
th vertex added is an isolated vertex.
$i$
th vertex added is an isolated vertex.
When using this representation we will often refer to the number of parts of a threshold graph. This refers to the number of blocks in the corresponding binary string of the given threshold graph. For instance,
![]() $1011100$
corresponds to a threshold graph with four parts. Similarly, we note that the quasi-clique and quasi-star are threshold graphs with two parts.
$1011100$
corresponds to a threshold graph with four parts. Similarly, we note that the quasi-clique and quasi-star are threshold graphs with two parts.
Finally, while we do not use this characterisation directly, we state it as it shows that threshold graphs satisfy the criteria of Corollary 16, below.
Proposition 9. A graph is threshold if and only if it contains no induced copies of a four vertex path, a four vertex cycle, or the complement of a four vertex cycle.
2.3 Basic properties of
 $\mathcal{M}_H(c)$
$\mathcal{M}_H(c)$
We note that while in the definition of
![]() $\mathcal{M}_H(c)$
we take a
$\mathcal{M}_H(c)$
we take a
![]() $\limsup$
we could have equivalently defined it as the supremum over all graphs in
$\limsup$
we could have equivalently defined it as the supremum over all graphs in
![]() $\mathcal{C}_c$
. This follows from the following useful lemma, whose proof is included in the Arxiv version of the paper.
$\mathcal{C}_c$
. This follows from the following useful lemma, whose proof is included in the Arxiv version of the paper.
Lemma 10.
Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $n$
vertices, then there exists a sequence of graphs
$n$
vertices, then there exists a sequence of graphs
![]() $G = G_1, G_2, \ldots$
such that
$G = G_1, G_2, \ldots$
such that
![]() $|G_{i+1}| \gt |G_i|$
and
$|G_{i+1}| \gt |G_i|$
and
![]() $t(H,G) = t(H,G_{i})$
for any graph
$t(H,G) = t(H,G_{i})$
for any graph
![]() $H$
.
$H$
.
Note that the sequence of graphs does not depend on
![]() $H$
. As such, by taking
$H$
. As such, by taking
![]() $H = K_2$
, we have that each graph
$H = K_2$
, we have that each graph
![]() $G_i$
in the sequence will also have the same edge density as
$G_i$
in the sequence will also have the same edge density as
![]() $G$
.
$G$
.
2.4 Fractional independence number
To prove that there exists a graph not optimised on the quasi-clique or quasi-star, we will need to define the fractional independence number, which is closely related to the number of homomorphisms by a result of Janson, Oleszkiewicz and Ruciński (cf. Theorem 22) [Reference Janson, Oleszkiewicz and Ruciński7].
Definition 11 (Fractional Independence Number). Given a graph,
![]() $G = (V, E)$
, with vertices
$G = (V, E)$
, with vertices
![]() $v_1, \ldots,v_n$
, the fractional independence number denoted
$v_1, \ldots,v_n$
, the fractional independence number denoted
![]() $\alpha ^*(G)$
is
$\alpha ^*(G)$
is
 \begin{equation*} \begin {aligned} \max _{w_1, \ldots w_n} & \sum _i w_i \\ \textrm {s.t.} \; \; & w_i + w_j \leq 1, \;\; v_i v_j \in E, \\ \qquad & w_i \in [0,1]. \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} \max _{w_1, \ldots w_n} & \sum _i w_i \\ \textrm {s.t.} \; \; & w_i + w_j \leq 1, \;\; v_i v_j \in E, \\ \qquad & w_i \in [0,1]. \end {aligned} \end{equation*}
Since we can take all the
![]() $w_i = \frac{1}{2}$
, we always have that
$w_i = \frac{1}{2}$
, we always have that
![]() $\alpha ^*(G) \geq \frac{|G|}{2}$
. It is well-known that the polytope defined by the constraints above is half-integral, that is, all its vertices are in
$\alpha ^*(G) \geq \frac{|G|}{2}$
. It is well-known that the polytope defined by the constraints above is half-integral, that is, all its vertices are in
![]() $\{0, 1/2, 1\}^n$
.
$\{0, 1/2, 1\}^n$
.
Lemma 12. The fractional independence polytope is half-integral.
We omit the proof here and refer an interested reader to the Arxiv version of the paper.
3. Threshold graph maximisation results
3.1 A local move and results for dense graphs
Given a graph
![]() $G$
there is a natural way of slowly transforming it into a threshold graph (see Figure 2): Take two vertices
$G$
there is a natural way of slowly transforming it into a threshold graph (see Figure 2): Take two vertices
![]() $u$
and
$u$
and
![]() $v$
. Remove the edges between
$v$
. Remove the edges between
![]() $u$
and
$u$
and
![]() $N(u) \setminus \overline{N(v)}$
and add edges from
$N(u) \setminus \overline{N(v)}$
and add edges from
![]() $N(u) \setminus \overline{N(v)}$
to
$N(u) \setminus \overline{N(v)}$
to
![]() $v$
. This gives us a new graph
$v$
. This gives us a new graph
![]() $G'$
in which we have
$G'$
in which we have
![]() $N_{G'}(u) \subseteq \overline{N_{G'}(v)}$
. Repeating this process takes us from
$N_{G'}(u) \subseteq \overline{N_{G'}(v)}$
. Repeating this process takes us from
![]() $G$
to a threshold graph. Notationally, we refer to this operation on a graph
$G$
to a threshold graph. Notationally, we refer to this operation on a graph
![]() $G$
as a local move on
$G$
as a local move on
![]() $(u,v)$
. We will also simply refer to it as moving the neighbours of
$(u,v)$
. We will also simply refer to it as moving the neighbours of
![]() $u$
to
$u$
to
![]() $v$
.
$v$
.

Figure 2. A neighbourhood-ordering local move.
To prove Theorem 3 we start by showing that this local move doesn’t significantly decrease the number of homomorphisms from
![]() $H$
. Towards this end, we define forbidden paths.
$H$
. Towards this end, we define forbidden paths.
Definition 13 (Forbidden Path). A forbidden path is a path
![]() $wxyz$
where
$wxyz$
where
![]() $wy$
and
$wy$
and
![]() $xz$
are not edges.
$xz$
are not edges.
We show that the homomorphisms lost after applying the local move are those that send a forbidden path in
![]() $H$
to a set containing
$H$
to a set containing
![]() $u$
,
$u$
,
![]() $v$
and a vertex in
$v$
and a vertex in
![]() $N(u) \setminus \overline{N(v)}$
.
$N(u) \setminus \overline{N(v)}$
.
Lemma 14.
Let
![]() $H$
and
$H$
and
![]() $G$
be graphs,
$G$
be graphs,
![]() $u$
and
$u$
and
![]() $v$
be vertices of
$v$
be vertices of
![]() $G$
, and let
$G$
, and let
![]() $G'$
be the resulting graph after applying a local move on
$G'$
be the resulting graph after applying a local move on
![]() $(u,v)$
. Then
$(u,v)$
. Then
![]() $\hom\! (H,G')$
is at least as large as the number of homomorphisms
$\hom\! (H,G')$
is at least as large as the number of homomorphisms
![]() $\varphi \in \textrm{Hom}(H,G)$
such that for all
$\varphi \in \textrm{Hom}(H,G)$
such that for all
![]() $w \in N(u) \setminus \overline{N(v)}$
and all forbidden paths
$w \in N(u) \setminus \overline{N(v)}$
and all forbidden paths
![]() $abcd$
in
$abcd$
in
![]() $H$
,
$H$
,
![]() $\{u,v,w\} \not \subseteq \varphi (\{a,b,c,d\})$
.
$\{u,v,w\} \not \subseteq \varphi (\{a,b,c,d\})$
.
Proof. We proceed by creating an injective function that takes a homomorphism
![]() $\varphi (x)$
from
$\varphi (x)$
from
![]() $H$
to
$H$
to
![]() $G$
satisfying the assumptions in the theorem and maps it to a homomorphism
$G$
satisfying the assumptions in the theorem and maps it to a homomorphism
![]() $\varphi '(x)$
from
$\varphi '(x)$
from
![]() $H$
to
$H$
to
![]() $G'$
. For intuition, we attempt to map
$G'$
. For intuition, we attempt to map
![]() $\varphi$
to a
$\varphi$
to a
![]() $\varphi '$
such that
$\varphi '$
such that
![]() $\varphi '(x) = \varphi (x)$
whenever possible.
$\varphi '(x) = \varphi (x)$
whenever possible.
If
![]() $\varphi (x) \not = u,v$
then we simply let
$\varphi (x) \not = u,v$
then we simply let
![]() $\varphi '(x) = \varphi (x)$
. If
$\varphi '(x) = \varphi (x)$
. If
![]() $\varphi (x) = u$
, then we again let
$\varphi (x) = u$
, then we again let
![]() $\varphi '(x) = \varphi (x)$
so long as there is not an edge
$\varphi '(x) = \varphi (x)$
so long as there is not an edge
![]() $xy \in E(H)$
with
$xy \in E(H)$
with
![]() $\varphi (y) \in N(u) \setminus \overline{N(v)}$
. If there is such an edge
$\varphi (y) \in N(u) \setminus \overline{N(v)}$
. If there is such an edge
![]() $xy \in E(H)$
, then we instead set
$xy \in E(H)$
, then we instead set
![]() $\varphi '(x) = v$
. Finally, if
$\varphi '(x) = v$
. Finally, if
![]() $\varphi (x) = v$
then we set
$\varphi (x) = v$
then we set
![]() $\varphi '(x)= \varphi (x)$
unless there is an edge
$\varphi '(x)= \varphi (x)$
unless there is an edge
![]() $xy \in E(H)$
such that
$xy \in E(H)$
such that
![]() $\varphi (y) = u$
and
$\varphi (y) = u$
and
![]() $\varphi '(y) = v$
. If such an edge exists, then we set
$\varphi '(y) = v$
. If such an edge exists, then we set
![]() $\varphi '(x) = u$
. Formally,
$\varphi '(x) = u$
. Formally,
 \begin{equation*}\varphi '(x) = \begin {cases} v & \exists y\; :\; xy \in E(H) \text { and } \varphi (x) = u \text { and } \varphi (y) \in N(u) \setminus \overline {N(v)} \\ u & \exists y, z\; :\; xy, yz \in E(H) \text { and } \varphi (x) = v \text { and } \varphi (y) = u \text { and } \varphi (z) \in N(u) \setminus \overline {N(v)} \\ \varphi (x) & \text {otherwise}. \end {cases} \end{equation*}
\begin{equation*}\varphi '(x) = \begin {cases} v & \exists y\; :\; xy \in E(H) \text { and } \varphi (x) = u \text { and } \varphi (y) \in N(u) \setminus \overline {N(v)} \\ u & \exists y, z\; :\; xy, yz \in E(H) \text { and } \varphi (x) = v \text { and } \varphi (y) = u \text { and } \varphi (z) \in N(u) \setminus \overline {N(v)} \\ \varphi (x) & \text {otherwise}. \end {cases} \end{equation*}
We start with the following claim.
Claim 15.
![]() $\varphi '$
is a homomorphism from
$\varphi '$
is a homomorphism from
![]() $H$
to
$H$
to
![]() $G'$
.
$G'$
.
Proof. It suffices to check that the edges incident to vertices mapping to
![]() $u$
or
$u$
or
![]() $v$
are preserved. Let
$v$
are preserved. Let
![]() $a,b \in V(H)$
be such that
$a,b \in V(H)$
be such that
![]() $ab \in E(H)$
and
$ab \in E(H)$
and
![]() $\varphi (a) = u$
. Since
$\varphi (a) = u$
. Since
![]() $\varphi$
is a homomorphism, we must have that
$\varphi$
is a homomorphism, we must have that
![]() $\varphi (b) \in N(u)$
. We now take cases.
$\varphi (b) \in N(u)$
. We now take cases.
-
Case I.
 $\varphi (b) \in N(u) \cap N(v)$
$\varphi (b) \in N(u) \cap N(v)$
Since
 $\varphi (b) \not = u,v$
,
$\varphi (b) \not = u,v$
,
 $\varphi '(b) = \varphi (b)$
. Moreover,
$\varphi '(b) = \varphi (b)$
. Moreover,
 $\varphi '(a)\varphi '(b) \in E(G')$
since
$\varphi '(a)\varphi '(b) \in E(G')$
since
 $a$
maps to either
$a$
maps to either
 $u$
or
$u$
or
 $v$
under
$v$
under
 $\varphi '$
and both
$\varphi '$
and both
 $u\varphi '(b)$
and
$u\varphi '(b)$
and
 $v\varphi '(b)$
are edges in
$v\varphi '(b)$
are edges in
 $G'$
.
$G'$
. -
Case II.
 $\varphi (b) \in N(u) \setminus \overline{N(v)}$
.
$\varphi (b) \in N(u) \setminus \overline{N(v)}$
.If we are in this case, then
 $\varphi '(a) = v$
as
$\varphi '(a) = v$
as
 $ab \in E(H)$
,
$ab \in E(H)$
,
 $\varphi (a) = u$
and
$\varphi (a) = u$
and
 $\varphi (b) \in N(u) \setminus \overline{N(v)}$
. Moreover,
$\varphi (b) \in N(u) \setminus \overline{N(v)}$
. Moreover,
 $\varphi '(b) = \varphi (b)$
as
$\varphi '(b) = \varphi (b)$
as
 $\varphi (b) \not = u,v$
. Since
$\varphi (b) \not = u,v$
. Since
 $v\varphi (b) \in E(G')$
, we are again done.
$v\varphi (b) \in E(G')$
, we are again done. -
Case III.
 $\varphi (b) = v$
and
$\varphi (b) = v$
and
 $\varphi '(a) = u$
(see Figure 3)
$\varphi '(a) = u$
(see Figure 3)We claim that
 $\varphi '(b) = v$
. Suppose not. Then
$\varphi '(b) = v$
. Suppose not. Then
 $\exists y, z\; :\; by, yz \in E(H), \varphi (y) = u, \text{ and } \varphi (z) \in N(u) \setminus \overline{N(v)}$
. Since
$\exists y, z\; :\; by, yz \in E(H), \varphi (y) = u, \text{ and } \varphi (z) \in N(u) \setminus \overline{N(v)}$
. Since
 $yz \in E(H)$
,
$yz \in E(H)$
,
 $\varphi '(y) = v$
and thus
$\varphi '(y) = v$
and thus
 $y \not = a$
. But now note
$y \not = a$
. But now note
 $\varphi (a) = \varphi (y) = u$
, so
$\varphi (a) = \varphi (y) = u$
, so
 $ay \not \in E(H)$
. Moreover,
$ay \not \in E(H)$
. Moreover,
 $bz \not \in E(H)$
since
$bz \not \in E(H)$
since
 $\varphi (z) \in N(u) \setminus \overline{N(v)}$
and
$\varphi (z) \in N(u) \setminus \overline{N(v)}$
and
 $\varphi (b) = v$
. It then follows that
$\varphi (b) = v$
. It then follows that
 $abyz$
is a path in
$abyz$
is a path in
 $H$
. But then
$H$
. But then
 $\varphi$
maps the forbidden path
$\varphi$
maps the forbidden path
 $abyz$
to
$abyz$
to
 $u,v,$
and a vertex in
$u,v,$
and a vertex in
 $N(u) \setminus \overline{N(v)}$
, which is a contradiction.
$N(u) \setminus \overline{N(v)}$
, which is a contradiction. -
Case IV.
 $\varphi (b) = v$
and
$\varphi (b) = v$
and
 $\varphi '(a) = v$
(see Figure 3)
$\varphi '(a) = v$
(see Figure 3)Note that since
 $\varphi '(a) = v$
we must have that there is a
$\varphi '(a) = v$
we must have that there is a
 $y$
such that
$y$
such that
 $ay \in E(H)$
and
$ay \in E(H)$
and
 $\varphi (y) \in N(u) \setminus \overline{N(v)}$
. But it then follows that
$\varphi (y) \in N(u) \setminus \overline{N(v)}$
. But it then follows that
 $\varphi '(b) = u$
since
$\varphi '(b) = u$
since
 $ba, ay \in E(H)$
.
$ba, ay \in E(H)$
.

Figure 3. Forbidden paths in proof of Claim 15.
Now let
![]() $a$
and
$a$
and
![]() $b$
be vertices such that
$b$
be vertices such that
![]() $\varphi (a) = v$
and
$\varphi (a) = v$
and
![]() $ab \in E(H)$
where
$ab \in E(H)$
where
![]() $\varphi (b) \not = u$
. Then we have one of two cases
$\varphi (b) \not = u$
. Then we have one of two cases
-
Case V.
 $\varphi '(a) = v$
$\varphi '(a) = v$
Since
 $\varphi$
is a homomorphism we have that
$\varphi$
is a homomorphism we have that
 $\varphi (b) \in N_G(v)$
. But then we have that the edge
$\varphi (b) \in N_G(v)$
. But then we have that the edge
 $ab$
is preserved by the homomorphism since
$ab$
is preserved by the homomorphism since
 $N_{G}(v) \subseteq N_{G'}(v)$
.
$N_{G}(v) \subseteq N_{G'}(v)$
. -
Case VI.
 $\varphi '(a) = u$
$\varphi '(a) = u$
In this case there exists
 $y, z$
such that
$y, z$
such that
 $ay, yz \in E(H)$
,
$ay, yz \in E(H)$
,
 $\varphi (y) = u$
and
$\varphi (y) = u$
and
 $\varphi (z) \in N(u) \setminus \overline{N(v)}$
. Now we claim
$\varphi (z) \in N(u) \setminus \overline{N(v)}$
. Now we claim
 $\varphi (b) \in N(u)$
. Suppose not, then
$\varphi (b) \in N(u)$
. Suppose not, then
 $\varphi (b) \in N(v) \setminus \overline{N(u)}$
. We now note that
$\varphi (b) \in N(v) \setminus \overline{N(u)}$
. We now note that
 $bayz$
is a forbidden path:
$bayz$
is a forbidden path:
 $by \not \in E(H)$
as
$by \not \in E(H)$
as
 $\varphi (y) = u$
and
$\varphi (y) = u$
and
 $\varphi (b) \not \in N(u)$
and
$\varphi (b) \not \in N(u)$
and
 $az \not \in E(H)$
as
$az \not \in E(H)$
as
 $\varphi (a) = v$
and
$\varphi (a) = v$
and
 $\varphi (z) \in N(u) \setminus \overline{N(v)}$
. But then
$\varphi (z) \in N(u) \setminus \overline{N(v)}$
. But then
 $bayz$
is forbidden path with
$bayz$
is forbidden path with
 $u,v$
and
$u,v$
and
 $\varphi (z) \in N(u) \setminus \overline{N(v)}$
in the image of
$\varphi (z) \in N(u) \setminus \overline{N(v)}$
in the image of
 $\varphi$
, a contradiction.
$\varphi$
, a contradiction.
Since these are all the cases we indeed have that
![]() $\varphi '$
is a valid homomorphism.
$\varphi '$
is a valid homomorphism.
To see that the map is injective, suppose that we had that
![]() $\varphi _1, \varphi _2 \mapsto \varphi '$
. Clearly
$\varphi _1, \varphi _2 \mapsto \varphi '$
. Clearly
![]() $\varphi _1(x) = \varphi _2(x)$
for all
$\varphi _1(x) = \varphi _2(x)$
for all
![]() $x$
such that
$x$
such that
![]() $\varphi '(x) \not = u,v$
. Now suppose that for some
$\varphi '(x) \not = u,v$
. Now suppose that for some
![]() $x \in V(H)$
,
$x \in V(H)$
,
![]() $\varphi _1(x) = u$
and
$\varphi _1(x) = u$
and
![]() $\varphi _2(x) = v$
. If
$\varphi _2(x) = v$
. If
![]() $\varphi '(x) = v$
, then
$\varphi '(x) = v$
, then
![]() $x$
is adjacent to some
$x$
is adjacent to some
![]() $y$
such that
$y$
such that
![]() $\varphi _1(y) \in N(u) \setminus \overline{N(v)}$
. But then
$\varphi _1(y) \in N(u) \setminus \overline{N(v)}$
. But then
![]() $\varphi _2$
also maps
$\varphi _2$
also maps
![]() $y$
to the same vertex, but
$y$
to the same vertex, but
![]() $v$
is not adjacent to
$v$
is not adjacent to
![]() $\varphi _2(y)$
in
$\varphi _2(y)$
in
![]() $G$
, which contradicts the fact that
$G$
, which contradicts the fact that
![]() $\varphi _2$
is a homomorphism.
$\varphi _2$
is a homomorphism.
So now suppose that
![]() $\varphi '(x) = u$
. Then there exist
$\varphi '(x) = u$
. Then there exist
![]() $y, z$
such that
$y, z$
such that
![]() $xy, yz \in E(H) \text{ and } \varphi _2(y) = u \text{ and } \varphi _2(z) \in N(u) \setminus \overline{N(v)}$
. But then we must have that
$xy, yz \in E(H) \text{ and } \varphi _2(y) = u \text{ and } \varphi _2(z) \in N(u) \setminus \overline{N(v)}$
. But then we must have that
![]() $\varphi _1(y) = v$
since
$\varphi _1(y) = v$
since
![]() $xy \in E(H)$
and
$xy \in E(H)$
and
![]() $\varphi _1(x) = u$
. Similarly, we have that
$\varphi _1(x) = u$
. Similarly, we have that
![]() $\varphi '(y) = v$
as
$\varphi '(y) = v$
as
![]() $xy \in E(H)$
and
$xy \in E(H)$
and
![]() $\varphi '(x) = u$
. But now
$\varphi '(x) = u$
. But now
![]() $y$
is a vertex such that
$y$
is a vertex such that
![]() $\varphi _1(y) = v$
and
$\varphi _1(y) = v$
and
![]() $\varphi _2(y) = u$
and
$\varphi _2(y) = u$
and
![]() $\varphi '(y) = v$
, which we just showed yields a contradiction.
$\varphi '(y) = v$
, which we just showed yields a contradiction.
Hence the map is injective as desired and the statement holds.
Corollary 16.
Let
![]() $H$
and
$H$
and
![]() $G$
be graphs,
$G$
be graphs,
![]() $u,v \in V(G)$
, and take
$u,v \in V(G)$
, and take
![]() $G'$
to be the resulting graph after applying a local move
$G'$
to be the resulting graph after applying a local move
![]() $(u,v)$
to
$(u,v)$
to
![]() $G$
. If
$G$
. If
![]() $H$
has no induced graphs isomorphic to
$H$
has no induced graphs isomorphic to
![]() $P_4$
or
$P_4$
or
![]() $C_4$
, then
$C_4$
, then
![]() $\hom\! (H,G') \geq \hom\! (H,G)$
.
$\hom\! (H,G') \geq \hom\! (H,G)$
.
Proof. If
![]() $H$
does not contain induced subgraphs isomorphic to
$H$
does not contain induced subgraphs isomorphic to
![]() $P_4$
and
$P_4$
and
![]() $C_4$
, then we have that
$C_4$
, then we have that
![]() $H$
has no forbidden paths. Hence
$H$
has no forbidden paths. Hence
![]() $H$
has at least as many homomorphisms to
$H$
has at least as many homomorphisms to
![]() $G'$
as it does to
$G'$
as it does to
![]() $G$
.
$G$
.
In order to use Lemma 14, we need more quantitative bounds on the number of homomorphisms lost. Towards, this end we prove the following lemma.
Lemma 17.
Let
![]() $H$
and
$H$
and
![]() $G$
be graphs, set
$G$
be graphs, set
![]() $n \, :\!=\, |V(G)|$
and let
$n \, :\!=\, |V(G)|$
and let
![]() $u,v \in V(G)$
and
$u,v \in V(G)$
and
![]() $S \subseteq V(G) \setminus \{u,v\}$
. Then there are at most
$S \subseteq V(G) \setminus \{u,v\}$
. Then there are at most
![]() $O_H(|S| n^{|H|-3})$
homomorphisms
$O_H(|S| n^{|H|-3})$
homomorphisms
![]() $\varphi \in \textrm{Hom}(H,G)$
such that there exists a forbidden path
$\varphi \in \textrm{Hom}(H,G)$
such that there exists a forbidden path
![]() $abcd$
in
$abcd$
in
![]() $H$
with
$H$
with
![]() $u,v,s \in \varphi (\{a,b,c,d\})$
for some
$u,v,s \in \varphi (\{a,b,c,d\})$
for some
![]() $s \in S$
.
$s \in S$
.
Proof. Let
![]() $abcd$
be a forbidden path in
$abcd$
be a forbidden path in
![]() $H$
. Then we must choose one of the four vertices to map to
$H$
. Then we must choose one of the four vertices to map to
![]() $u$
, one of the remaining three to map to
$u$
, one of the remaining three to map to
![]() $v$
, and one of the remaining two to map to a vertex in
$v$
, and one of the remaining two to map to a vertex in
![]() $S$
. The remaining
$S$
. The remaining
![]() $|H|-3$
vertices in the graph could go to any of
$|H|-3$
vertices in the graph could go to any of
![]() $n$
vertices. Hence, we have that there are at most
$n$
vertices. Hence, we have that there are at most
such homomorphisms. Since there are only a constant number of forbidden paths in
![]() $H$
, which we denote by
$H$
, which we denote by
![]() $k_H$
, we have that there are at most
$k_H$
, we have that there are at most
homormophism mapping a forbidden path to a set including
![]() $u$
,
$u$
,
![]() $v$
and a vertex from
$v$
and a vertex from
![]() $S$
.
$S$
.
With this lemma in hand, we note that moving the neighbours of
![]() $u$
to
$u$
to
![]() $v$
removes at most
$v$
removes at most
![]() $O_H(|N(u) \setminus \overline{N(v)}| n^{|H|-3})$
homomorphisms. Thus to argue we didn’t lose too many homomorphisms after applying multiple local moves we make the following definition.
$O_H(|N(u) \setminus \overline{N(v)}| n^{|H|-3})$
homomorphisms. Thus to argue we didn’t lose too many homomorphisms after applying multiple local moves we make the following definition.
Definition 18 (Total Movement). Let
![]() $G = G_0, G_1, \ldots, G_t$
be a sequence of graphs from applying local moves
$G = G_0, G_1, \ldots, G_t$
be a sequence of graphs from applying local moves
![]() $(u_1, v_1), \ldots, (u_t, v_t)$
, that is, each
$(u_1, v_1), \ldots, (u_t, v_t)$
, that is, each
![]() $G_i$
is obtained by applying the local move to the vertices
$G_i$
is obtained by applying the local move to the vertices
![]() $(u_i, v_i)$
in the graph
$(u_i, v_i)$
in the graph
![]() $G_{i-1}$
. Define the total movement after these
$G_{i-1}$
. Define the total movement after these
![]() $t$
moves as
$t$
moves as
 \begin{equation*}\sum _{i=1}^t \left |N_{G_{i-1}}(u_i) \setminus \overline {N_{G_{i-1}}(v_i)} \right |.\end{equation*}
\begin{equation*}\sum _{i=1}^t \left |N_{G_{i-1}}(u_i) \setminus \overline {N_{G_{i-1}}(v_i)} \right |.\end{equation*}
We now claim that we can turn
![]() $G$
into a threshold graph with small amount of total movement.
$G$
into a threshold graph with small amount of total movement.
Lemma 19.
Let
![]() $G$
be a graph. Then using local moves we can turn
$G$
be a graph. Then using local moves we can turn
![]() $G$
into a threshold graph with at most
$G$
into a threshold graph with at most
![]() $n^2$
moves and with total movement at most
$n^2$
moves and with total movement at most
![]() $|E(G)|$
.
$|E(G)|$
.
Proof. We prove this by induction on the number of vertices.
For the base case, note that a graph with a single vertex is threshold. Now assume the statement holds for graphs with at most
![]() $n$
vertices and let
$n$
vertices and let
![]() $G$
be a graph on
$G$
be a graph on
![]() $n+1$
vertices. Let
$n+1$
vertices. Let
![]() $v_{n+1}$
be the vertex of maximum degree and
$v_{n+1}$
be the vertex of maximum degree and
![]() $v_1, \ldots, v_n$
be the remaining vertices. Consider applying the following
$v_1, \ldots, v_n$
be the remaining vertices. Consider applying the following
![]() $n$
moves: Move the neighbours of
$n$
moves: Move the neighbours of
![]() $v_1$
to
$v_1$
to
![]() $v_{n+1}$
, then move the neighbours of
$v_{n+1}$
, then move the neighbours of
![]() $v_2$
to
$v_2$
to
![]() $v_{n+1}$
, continue in this way until moving the neighbours from
$v_{n+1}$
, continue in this way until moving the neighbours from
![]() $v_{n}$
to
$v_{n}$
to
![]() $v_{n+1}$
.
$v_{n+1}$
.
Let
![]() $G'$
be the graph after applying all the above moves. Clearly
$G'$
be the graph after applying all the above moves. Clearly
![]() $N_{G'}(v_1) \cup N_{G'}(v_2) \cup \ldots \cup N_{G'}(v_n) \subseteq \overline{N_{G'}(v_{n+1})}$
. Hence if
$N_{G'}(v_1) \cup N_{G'}(v_2) \cup \ldots \cup N_{G'}(v_n) \subseteq \overline{N_{G'}(v_{n+1})}$
. Hence if
![]() $v_i v_j \in E(G')$
and
$v_i v_j \in E(G')$
and
![]() $j \not = n+1$
, then we have that
$j \not = n+1$
, then we have that
![]() $v_{n+1} v_j \in E(G')$
. We then conclude that if
$v_{n+1} v_j \in E(G')$
. We then conclude that if
![]() $v_{n+1} v_j \not \in E(G')$
for
$v_{n+1} v_j \not \in E(G')$
for
![]() $j \not = n+1$
, then it must be the case that
$j \not = n+1$
, then it must be the case that
![]() $v_j$
is isolated.
$v_j$
is isolated.
Let
![]() $I$
denote the vertices in
$I$
denote the vertices in
![]() $G'$
that are isolated. Applying the inductive hypothesis to
$G'$
that are isolated. Applying the inductive hypothesis to
![]() $G'[V \setminus (I \cup \{v_{n+1}\})]$
, we have that there is a set of at most
$G'[V \setminus (I \cup \{v_{n+1}\})]$
, we have that there is a set of at most
![]() $n^2$
moves that transforms
$n^2$
moves that transforms
![]() $G'[V \setminus (I \cup \{v_{n+1}\})]$
to a threshold graph
$G'[V \setminus (I \cup \{v_{n+1}\})]$
to a threshold graph
![]() $T$
with total movement at most
$T$
with total movement at most
![]() $|E(G'[V \setminus (I \cup \{v_{n+1}\})])|$
. Applying these moves to
$|E(G'[V \setminus (I \cup \{v_{n+1}\})])|$
. Applying these moves to
![]() $G'$
gives us a graph
$G'$
gives us a graph
![]() $G''$
. But now note that
$G''$
. But now note that
![]() $G''$
can be described as adding a dominating vertex to
$G''$
can be described as adding a dominating vertex to
![]() $T$
followed by
$T$
followed by
![]() $|I|$
isolated vertices. So
$|I|$
isolated vertices. So
![]() $G''$
is a threshold graph. Note that we made at most
$G''$
is a threshold graph. Note that we made at most
![]() $n^2 + n \leq (n+1)^2$
moves.
$n^2 + n \leq (n+1)^2$
moves.
To bound the total movement cost, note that any edge incident to
![]() $v_{n+1}$
was moved at most once by the initial set of
$v_{n+1}$
was moved at most once by the initial set of
![]() $n$
moves. So by the inductive hypothesis, the total movement cost is at most
$n$
moves. So by the inductive hypothesis, the total movement cost is at most
![]() $E(G'[V \setminus (I \cup \{v_{n+1}\})]) + \deg _{G'}(v_{n+1}) = |E(G)|$
, as desired.
$E(G'[V \setminus (I \cup \{v_{n+1}\})]) + \deg _{G'}(v_{n+1}) = |E(G)|$
, as desired.
We can now prove a strengthening of Theorem 3.
Theorem 20.
For any graph
![]() $G$
with
$G$
with
![]() $n$
vertices and any graph
$n$
vertices and any graph
![]() $H$
, there exists a threshold graph
$H$
, there exists a threshold graph
![]() $T$
on
$T$
on
![]() $n$
vertices with
$n$
vertices with
![]() $|E(T)| \leq |E(G)|$
such that
$|E(T)| \leq |E(G)|$
such that
Proof. We use the local moves to transform the true maximum graph into a threshold graph and argue that we haven’t lost too many homomorphisms. By Lemma 19, there exists a sequence of local moves on pairs
![]() $(u_1, v_1)$
, …,
$(u_1, v_1)$
, …,
![]() $(u_k, v_k)$
with total movement at most
$(u_k, v_k)$
with total movement at most
![]() $|E(G)|$
that transforms
$|E(G)|$
that transforms
![]() $G$
into a threshold graph
$G$
into a threshold graph
![]() $T$
. Let
$T$
. Let
![]() $G_i$
be the graph defined by applying
$G_i$
be the graph defined by applying
![]() $(u_i, v_i)$
to
$(u_i, v_i)$
to
![]() $G_{i-1}$
. By Lemmas 14 and 17, we have that
$G_{i-1}$
. By Lemmas 14 and 17, we have that
We thus conclude that
 \begin{equation*}\hom\! (H,T)\geq \hom\! (H,G) - \sum _{i=1}^k O_H(|N_{G_{i-1}}(u_i) \setminus \overline {N_{G_{i-1}}(v_i)}| n^{|H|-3} ) \geq \hom\! (H,G) - O_H( n^{|H|-1} ) \end{equation*}
\begin{equation*}\hom\! (H,T)\geq \hom\! (H,G) - \sum _{i=1}^k O_H(|N_{G_{i-1}}(u_i) \setminus \overline {N_{G_{i-1}}(v_i)}| n^{|H|-3} ) \geq \hom\! (H,G) - O_H( n^{|H|-1} ) \end{equation*}
where the final inequality uses that the total movement of our sequence of local moves is at most
![]() $|E(G)| \leq n^2$
.
$|E(G)| \leq n^2$
.
Remark 21.
Note that such a result will not hold non-asymptotically for
![]() $\mathcal{M}(H,n,m)$
. Specifically, we note that no threshold graph achieves
$\mathcal{M}(H,n,m)$
. Specifically, we note that no threshold graph achieves
![]() $\mathcal{M}(C_4, 4, 4)$
.
$\mathcal{M}(C_4, 4, 4)$
.
3.2 Extension to sparse graphs
We now extend this result to sparse graphs by strengthening Lemma 17. To do this, we will find it convenient to use the following result.
Theorem 22 (Janson, Oleszkiewicz and Ruciński [Reference Janson, Oleszkiewicz and Ruciński7]). Let
![]() $H$
be a graph and
$H$
be a graph and
![]() $m \geq |E(H)|$
and
$m \geq |E(H)|$
and
![]() $n \geq |H|$
with
$n \geq |H|$
with
![]() $n \leq m \leq \binom{n}{2}$
. Then
$n \leq m \leq \binom{n}{2}$
. Then
where
![]() $\alpha ^*(H)$
denotes the fractional independence number of the graph.
$\alpha ^*(H)$
denotes the fractional independence number of the graph.
From this, we easily obtain the following lemma:
Lemma 23.
Let
![]() $H$
be a graph,
$H$
be a graph,
![]() $k$
be a non-negative integer, and
$k$
be a non-negative integer, and
![]() $H'$
be an induced subgraph of
$H'$
be an induced subgraph of
![]() $H$
on
$H$
on
![]() $|V(H)|-k$
vertices. Then for every
$|V(H)|-k$
vertices. Then for every
![]() $n \geq |H|$
and
$n \geq |H|$
and
![]() $n \leq m \leq \binom{n}{2}$
with
$n \leq m \leq \binom{n}{2}$
with
![]() $m \geq |E(H)|$
$m \geq |E(H)|$
Proof. Let
![]() $\Delta = \alpha ^*(H) - \alpha ^*(H') \geq 0$
. By Theorem 22 and some algebraic manipulation we see that
$\Delta = \alpha ^*(H) - \alpha ^*(H') \geq 0$
. By Theorem 22 and some algebraic manipulation we see that
 \begin{align*} \mathcal{M}(H',n,m) & = O_H \left ( \left (\frac{m}{n} \right )^{|H'| - \alpha ^*(H')} n^{\alpha ^*(H')} \right ) \\ & = O_H \left ( \left (\frac{m}{n} \right )^{|H| - k - \alpha ^*(H) + \Delta } n^{\alpha ^*(H) - \Delta } \right ) \\ & = O_H \left ( \left (\frac{m}{n}\right )^{-k} \left ( \frac{m}{n^2} \right )^\Delta m^{{|H| - \alpha ^*(H)}} n^{2 \alpha ^*(H) - |H|} \right ) \\ & = O_H(\mathcal{M}(H,n,m)/\left (\frac{m}{n} \right )^k). \end{align*}
\begin{align*} \mathcal{M}(H',n,m) & = O_H \left ( \left (\frac{m}{n} \right )^{|H'| - \alpha ^*(H')} n^{\alpha ^*(H')} \right ) \\ & = O_H \left ( \left (\frac{m}{n} \right )^{|H| - k - \alpha ^*(H) + \Delta } n^{\alpha ^*(H) - \Delta } \right ) \\ & = O_H \left ( \left (\frac{m}{n}\right )^{-k} \left ( \frac{m}{n^2} \right )^\Delta m^{{|H| - \alpha ^*(H)}} n^{2 \alpha ^*(H) - |H|} \right ) \\ & = O_H(\mathcal{M}(H,n,m)/\left (\frac{m}{n} \right )^k). \end{align*}
where the last equality used that
![]() $\mathcal{M}(H,n,m) = \Omega _H(m^{|H|-\alpha ^*(H)} n^{2 \alpha ^*(H) - |H|})$
and
$\mathcal{M}(H,n,m) = \Omega _H(m^{|H|-\alpha ^*(H)} n^{2 \alpha ^*(H) - |H|})$
and
![]() $m \leq n^2$
.
$m \leq n^2$
.
We remark that the above lemma can be proved without the result of Theorem 22 by taking a graph that approximately achieves
![]() $\mathcal{M}(H',n/2,m/4)$
and adding
$\mathcal{M}(H',n/2,m/4)$
and adding
![]() $\Omega (m/n)$
dominating vertices to it to get a graph with many copies of
$\Omega (m/n)$
dominating vertices to it to get a graph with many copies of
![]() $H$
.
$H$
.
Lemma 24.
Let
![]() $H$
and
$H$
and
![]() $G$
be graphs, where
$G$
be graphs, where
![]() $G$
has
$G$
has
![]() $n \geq |H|$
vertices and
$n \geq |H|$
vertices and
![]() $m \geq \max (|E(H)|, n)$
edges, and let
$m \geq \max (|E(H)|, n)$
edges, and let
![]() $u,v \in V(G)$
and
$u,v \in V(G)$
and
![]() $S \subseteq V(G) \setminus \{u,v\}$
. Then there are at most
$S \subseteq V(G) \setminus \{u,v\}$
. Then there are at most
![]() $O_H(|S| \mathcal{M}(H,n,m)/\left (\frac{m}{n} \right )^3)$
homomorphisms
$O_H(|S| \mathcal{M}(H,n,m)/\left (\frac{m}{n} \right )^3)$
homomorphisms
![]() $\varphi \in \textrm{Hom}(H,G)$
such there exists a forbidden path
$\varphi \in \textrm{Hom}(H,G)$
such there exists a forbidden path
![]() $abcd \in H$
in which
$abcd \in H$
in which
![]() $\{u,v,s\} \subseteq \varphi (\{a,b,c,d\})$
for some
$\{u,v,s\} \subseteq \varphi (\{a,b,c,d\})$
for some
![]() $s \in S$
.
$s \in S$
.
Proof. Let
![]() $abcd$
be a forbidden path. Then there are clearly
$abcd$
be a forbidden path. Then there are clearly
![]() $O(|S|)$
ways to map
$O(|S|)$
ways to map
![]() $3$
vertices from
$3$
vertices from
![]() $a,b,c,d$
into
$a,b,c,d$
into
![]() $u,v$
and some vertex from
$u,v$
and some vertex from
![]() $|S|$
. For ease of notation, assume these three vertices are
$|S|$
. For ease of notation, assume these three vertices are
![]() $a,b,c$
. Now consider
$a,b,c$
. Now consider
![]() $H' = H[V(H) \setminus \{a,b,c\}]$
. We note that the number of homomorphisms is at most
$H' = H[V(H) \setminus \{a,b,c\}]$
. We note that the number of homomorphisms is at most
![]() $O_H(|S| \mathcal{M}(H',n,m))$
. So it suffices to show that
$O_H(|S| \mathcal{M}(H',n,m))$
. So it suffices to show that
![]() $\mathcal{M}(H',n,m) = O_H \left (\mathcal{M}(H,n,m)/\left (\frac{m}{n} \right )^3 \right )$
. But this follows from Lemma 23.
$\mathcal{M}(H',n,m) = O_H \left (\mathcal{M}(H,n,m)/\left (\frac{m}{n} \right )^3 \right )$
. But this follows from Lemma 23.
We can now prove our strengthening of Theorem 20.
Theorem 25.
For any graph
![]() $H$
and integers
$H$
and integers
![]() $n$
and
$n$
and
![]() $m \leq \binom{n}{2}$
, there exists a threshold graph
$m \leq \binom{n}{2}$
, there exists a threshold graph
![]() $T$
on
$T$
on
![]() $n$
vertices and at most
$n$
vertices and at most
![]() $m$
edges such that
$m$
edges such that
Proof. The proof follows almost identically to Theorem 3. Let
![]() $G^\star$
be the graph on
$G^\star$
be the graph on
![]() $n$
vertices and
$n$
vertices and
![]() $m$
edges with
$m$
edges with
By Lemma 19, there exists a sequence of local moves on pairs
![]() $(u_1, v_1)$
,
$(u_1, v_1)$
,
![]() $\ldots$
,
$\ldots$
,
![]() $(u_k, v_k)$
with total movement at most
$(u_k, v_k)$
with total movement at most
![]() $|E(G^\star )|$
that transforms
$|E(G^\star )|$
that transforms
![]() $G^\star$
into a threshold graph
$G^\star$
into a threshold graph
![]() $T$
. Let
$T$
. Let
![]() $G_i^\star$
be the graph defined by applying
$G_i^\star$
be the graph defined by applying
![]() $(u_i, v_i)$
to
$(u_i, v_i)$
to
![]() $G_{i-1}^\star$
. By Lemmas 14 and 24, we have that
$G_{i-1}^\star$
. By Lemmas 14 and 24, we have that
We thus conclude that
 \begin{align*} \hom\! (H,T) &\geq \hom\! (H,G^\star ) - \sum _{i=1}^k O_H\left(|N_{G_{i-1}^\star }(u_i) \setminus \overline{N_{G_{i-1}^\star }(v_i)} | \cdot \mathcal{M}(H,n,m)/ \left (\frac{m}{n} \right )^3 \right) \\ &\geq \mathcal{M}(H,n,m) - O_H \left ( \frac{n^3}{m^2} \cdot \mathcal{M}(H,n,m) \right ) \end{align*}
\begin{align*} \hom\! (H,T) &\geq \hom\! (H,G^\star ) - \sum _{i=1}^k O_H\left(|N_{G_{i-1}^\star }(u_i) \setminus \overline{N_{G_{i-1}^\star }(v_i)} | \cdot \mathcal{M}(H,n,m)/ \left (\frac{m}{n} \right )^3 \right) \\ &\geq \mathcal{M}(H,n,m) - O_H \left ( \frac{n^3}{m^2} \cdot \mathcal{M}(H,n,m) \right ) \end{align*}
where the final inequality uses the total movement of our moves is
![]() $|E(G)|$
.
$|E(G)|$
.
3.3 Extension to hypergraphs
For hypergraphs, we only prove results for asymptotic maximisation in the dense case. As before, we use a sequence of moves to transform our hypergraph. We can view this as a shifting or compression argument, which are common in extremal set theory.
Definition 26 (Hypergraph Move). Let
![]() $G = (V,E)$
be a
$G = (V,E)$
be a
![]() $k$
-uniform hypergraph and
$k$
-uniform hypergraph and
![]() $u,v$
be two vertices in
$u,v$
be two vertices in
![]() $G$
. We say a hypergraph move from
$G$
. We say a hypergraph move from
![]() $u$
to
$u$
to
![]() $v$
in
$v$
in
![]() $G$
is as follows: For each hyperedge
$G$
is as follows: For each hyperedge
![]() $e \in E(G)$
containing
$e \in E(G)$
containing
![]() $u$
and not
$u$
and not
![]() $v$
such that
$v$
such that
![]() $(e \setminus \{u\}) \cup \{v\} \not \in E(G)$
, remove
$(e \setminus \{u\}) \cup \{v\} \not \in E(G)$
, remove
![]() $e$
and add
$e$
and add
![]() $(e \setminus \{u\}) \cup \{v\}$
.
$(e \setminus \{u\}) \cup \{v\}$
.
Note that this move generalises our local move for graphs. That said, we will be able to get by with a worse bound on the number of homomorphisms lost from such a hypergraph move:
Lemma 27.
Let
![]() $H$
and
$H$
and
![]() $G$
be
$G$
be
![]() $k$
-uniform hypergraphs and let
$k$
-uniform hypergraphs and let
![]() $G'$
be the resulting hypergraph after applying a hypergraph move from
$G'$
be the resulting hypergraph after applying a hypergraph move from
![]() $u$
to
$u$
to
![]() $v$
in
$v$
in
![]() $G$
. Then the number of homomorphisms from
$G$
. Then the number of homomorphisms from
![]() $H$
to
$H$
to
![]() $G'$
is at least the number of homomorphisms
$G'$
is at least the number of homomorphisms
![]() $\varphi$
from
$\varphi$
from
![]() $H$
to
$H$
to
![]() $G$
that use at most one of
$G$
that use at most one of
![]() $u$
and
$u$
and
![]() $v$
.
$v$
.
Proof. We again construct an injective map from a subset of
![]() $\hom\! (H,G)$
to
$\hom\! (H,G)$
to
![]() $\hom\! (H,G')$
. Specifically, given
$\hom\! (H,G')$
. Specifically, given
![]() $\varphi \in \hom\! (H,G)$
, we map it to
$\varphi \in \hom\! (H,G)$
, we map it to
 \begin{equation*}\varphi '(x) = \begin {cases} v & \varphi (x) = u \text { and }\exists e \in E(H)\; :\; x \in e \text { and } (\varphi (e) \setminus \{u\}) \cup \{v\} \not \in E(G) \\ \varphi (x) & \text {otherwise}. \end {cases}\end{equation*}
\begin{equation*}\varphi '(x) = \begin {cases} v & \varphi (x) = u \text { and }\exists e \in E(H)\; :\; x \in e \text { and } (\varphi (e) \setminus \{u\}) \cup \{v\} \not \in E(G) \\ \varphi (x) & \text {otherwise}. \end {cases}\end{equation*}
We can easily verify that
![]() $\varphi '$
is a homomorphism if
$\varphi '$
is a homomorphism if
![]() $\varphi$
uses at most one of
$\varphi$
uses at most one of
![]() $u$
and
$u$
and
![]() $v$
. To see that the map is injective, suppose
$v$
. To see that the map is injective, suppose
![]() $\varphi _1, \varphi _2 \in \hom\! (H,G)$
both map to a homomorphism
$\varphi _1, \varphi _2 \in \hom\! (H,G)$
both map to a homomorphism
![]() $\varphi ' \in \hom\! (H,G')$
. Towards a contradiction, assume
$\varphi ' \in \hom\! (H,G')$
. Towards a contradiction, assume
![]() $\varphi _1 \not = \varphi _2$
. By definition,
$\varphi _1 \not = \varphi _2$
. By definition,
![]() $\varphi '(x) = \varphi _1(x)$
whenever
$\varphi '(x) = \varphi _1(x)$
whenever
![]() $\varphi _1(x) \not = u$
. As an analogous statement holds for
$\varphi _1(x) \not = u$
. As an analogous statement holds for
![]() $\varphi _2$
, we have that
$\varphi _2$
, we have that
![]() $\varphi _1(x) = \varphi _2(x) = \varphi '(x)$
for all
$\varphi _1(x) = \varphi _2(x) = \varphi '(x)$
for all
![]() $x$
such that
$x$
such that
![]() $\varphi _1(x) \not = u$
and
$\varphi _1(x) \not = u$
and
![]() $\varphi _2(x) \not = u$
. So without loss of generality there exists an
$\varphi _2(x) \not = u$
. So without loss of generality there exists an
![]() $x$
such that
$x$
such that
![]() $\varphi _1(x) = u$
and
$\varphi _1(x) = u$
and
![]() $\varphi _2(x) = v$
. Then
$\varphi _2(x) = v$
. Then
![]() $\varphi '(x) = v$
and there exists an
$\varphi '(x) = v$
and there exists an
![]() $e \in E(H)$
containing
$e \in E(H)$
containing
![]() $x$
such that
$x$
such that
![]() $(\varphi _1(e) \setminus \{u\}) \cup \{v\} \not \in E(G)$
. But now note that
$(\varphi _1(e) \setminus \{u\}) \cup \{v\} \not \in E(G)$
. But now note that
![]() $\varphi _2(e) = (\varphi _1(e) \setminus \{u\}) \cup \{v\} \not \in E(G)$
, so we have reached a contradiction.
$\varphi _2(e) = (\varphi _1(e) \setminus \{u\}) \cup \{v\} \not \in E(G)$
, so we have reached a contradiction.
The key lemma of this section will be the following result to transform hypergraphs into threshold hypergraphs:
Lemma 28.
Let
![]() $G$
be a
$G$
be a
![]() $k$
-uniform hypergraphs with
$k$
-uniform hypergraphs with
![]() $n$
vertices, then
$n$
vertices, then
![]() $G$
can be transformed into a threshold hypergraph
$G$
can be transformed into a threshold hypergraph
![]() $T$
by removing
$T$
by removing
![]() $o_k(n^k)$
edges and using
$o_k(n^k)$
edges and using
![]() $o_k(n^2)$
hypergraph moves.
$o_k(n^2)$
hypergraph moves.
This quickly gives Theorem 6.
Proof of Lemma
6, assuming Lemma 28
. Let
![]() $G$
be a hypergraph with
$G$
be a hypergraph with
![]() $n$
vertices. By Lemma 28 we can use
$n$
vertices. By Lemma 28 we can use
![]() $o_k(n^2)$
hypergraph moves
$o_k(n^2)$
hypergraph moves
![]() $(u_1, v_1), \ldots, (u_\ell, v_\ell )$
and remove at most
$(u_1, v_1), \ldots, (u_\ell, v_\ell )$
and remove at most
![]() $o_k(n^k)$
edges to turn it into a threshold hypergraph
$o_k(n^k)$
edges to turn it into a threshold hypergraph
![]() $T$
. Now note the number of homormorphisms
$T$
. Now note the number of homormorphisms
![]() $H$
to any hypergraph
$H$
to any hypergraph
![]() $G'$
that use any two specific vertices
$G'$
that use any two specific vertices
![]() $u,v \in V(G')$
is at most
$u,v \in V(G')$
is at most
![]() $O_H(n^{|H|-2})$
. Similarly, there are at most
$O_H(n^{|H|-2})$
. Similarly, there are at most
![]() $O_{H,k}(n^{|H|-k})$
homomorphisms that use every vertex in a hyperedge
$O_{H,k}(n^{|H|-k})$
homomorphisms that use every vertex in a hyperedge
![]() $e \in E(G')$
. Thus by Lemma 27 each hypergraph move
$e \in E(G')$
. Thus by Lemma 27 each hypergraph move
![]() $(u_i, v_i)$
removes at most
$(u_i, v_i)$
removes at most
![]() $O_H(n^{|H|-2})$
homomorphisms. Moreover, removing a hyperedge
$O_H(n^{|H|-2})$
homomorphisms. Moreover, removing a hyperedge
![]() $e$
removes at most
$e$
removes at most
![]() $O_{H,k}(n^{|H|-k})$
homomorphisms. We conclude that
$O_{H,k}(n^{|H|-k})$
homomorphisms. We conclude that
We now proceed to prove Lemma 28. Like in the case of graphs, we will apply a set of local moves to
![]() $G$
, yielding a hypergraph
$G$
, yielding a hypergraph
![]() $G'$
, in such a way that there exists a vertex
$G'$
, in such a way that there exists a vertex
![]() $v \in G'$
with
$v \in G'$
with
![]() $u \ll _{G'} v$
for all
$u \ll _{G'} v$
for all
![]() $u \in V(G')$
. We then repeat the process on
$u \in V(G')$
. We then repeat the process on
![]() $G'$
to slowly transform it into a threshold hypergraph. One way to do this would of course be to apply a local move from every vertex
$G'$
to slowly transform it into a threshold hypergraph. One way to do this would of course be to apply a local move from every vertex
![]() $u \in V(G)$
to
$u \in V(G)$
to
![]() $v$
, however, this would result in a total of
$v$
, however, this would result in a total of
![]() $\Omega (n^2)$
moves. To improve on this, we show that we only need to apply moves from a neighbourhood-dominating set to
$\Omega (n^2)$
moves. To improve on this, we show that we only need to apply moves from a neighbourhood-dominating set to
![]() $v$
.
$v$
.
Definition 29 (Neighbourhood-Dominating Set). Given a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G=(V,E)$
, a vertex
$G=(V,E)$
, a vertex
![]() $v \in V$
and a subset
$v \in V$
and a subset
![]() $S \subseteq V$
, a neighbourhood-dominating set
$S \subseteq V$
, a neighbourhood-dominating set
![]() $D \subseteq V$
of
$D \subseteq V$
of
![]() $S$
with respect to
$S$
with respect to
![]() $v$
is a set of vertices such that for every vertex
$v$
is a set of vertices such that for every vertex
![]() $s \in S$
and hyperedge
$s \in S$
and hyperedge
![]() $e$
containing
$e$
containing
![]() $s$
either
$s$
either
![]() $v \in e$
or there exists a
$v \in e$
or there exists a
![]() $d \in D$
such that
$d \in D$
such that
![]() $(e \setminus \{s\}) \cup \{d\} \in E(G)$
.
$(e \setminus \{s\}) \cup \{d\} \in E(G)$
.
Of course, this is only useful if there are neighbourhood-dominating sets of size
![]() $o(n)$
. To prove that small neighbourhood-dominating sets exist, we will apply the following lemma to a suitably defined graph corresponding to our hypergraph
$o(n)$
. To prove that small neighbourhood-dominating sets exist, we will apply the following lemma to a suitably defined graph corresponding to our hypergraph
![]() $G$
.
$G$
.
Lemma 30.
Let
![]() $G = (A \cup B, E)$
be a bipartite graph with
$G = (A \cup B, E)$
be a bipartite graph with
![]() $|A| = n$
and
$|A| = n$
and
![]() $|B| \leq n^k$
for a positive integer
$|B| \leq n^k$
for a positive integer
![]() $k$
. Moreover, assume that the minimum degree of a vertex in
$k$
. Moreover, assume that the minimum degree of a vertex in
![]() $B$
is
$B$
is
![]() $\delta$
, then there exists a set
$\delta$
, then there exists a set
![]() $D \subseteq A$
such that
$D \subseteq A$
such that
![]() $N_G(D) = B$
and
$N_G(D) = B$
and
![]() $|D| = O_k (n\log (n)/\delta )$
.
$|D| = O_k (n\log (n)/\delta )$
.
Proof. Assume that
![]() $\delta \gt k \log (n)$
as otherwise we can simply take
$\delta \gt k \log (n)$
as otherwise we can simply take
![]() $D = A$
. We will follow the classical proof for dominating sets given in [Reference Alon and Spencer3]. Take a random set
$D = A$
. We will follow the classical proof for dominating sets given in [Reference Alon and Spencer3]. Take a random set
![]() $S$
such that every vertex of
$S$
such that every vertex of
![]() $A$
is in
$A$
is in
![]() $S$
independently with probability
$S$
independently with probability
![]() $p$
and let
$p$
and let
![]() $N$
denote the set of vertices in
$N$
denote the set of vertices in
![]() $B$
without a neighbour in
$B$
without a neighbour in
![]() $S$
. Build a set
$S$
. Build a set
![]() $D$
by adding a neighbour of each vertex in
$D$
by adding a neighbour of each vertex in
![]() $N$
to
$N$
to
![]() $S$
. Then observe that
$S$
. Then observe that
![]() $N_G(D) = B$
and in expectation we have
$N_G(D) = B$
and in expectation we have
Taking
![]() $p = \frac{1}{\delta } \log (\delta n^{k-1})$
then gives
$p = \frac{1}{\delta } \log (\delta n^{k-1})$
then gives
We now associate some graphs to our hypergraphs:
Definition 31 (Incidence Graph). Given a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G = (V,E)$
, we associate a bipartite incidence graph
$G = (V,E)$
, we associate a bipartite incidence graph
![]() $I = (A \cup B, E(I))$
. Each vertex in
$I = (A \cup B, E(I))$
. Each vertex in
![]() $A$
will correspond to a vertex in
$A$
will correspond to a vertex in
![]() $G$
and each vertex in
$G$
and each vertex in
![]() $B$
corresponds to a subset
$B$
corresponds to a subset
![]() $S \in \binom{[n]}{k-1}$
such that
$S \in \binom{[n]}{k-1}$
such that
![]() $S \subset e \in E(G)$
. There is an edge between a vertex
$S \subset e \in E(G)$
. There is an edge between a vertex
![]() $v \in A$
and a subset
$v \in A$
and a subset
![]() $S \in B$
if
$S \in B$
if
![]() $\{v\} \cup S \in E(G)$
.
$\{v\} \cup S \in E(G)$
.
In particular, we will often be interested in induced subgraphs of the incidence graph with respect to a vertex
![]() $v$
.
$v$
.
Definition 32 (Induced Incidence Graphs). Given a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G = (V,E)$
, a set of vertices
$G = (V,E)$
, a set of vertices
![]() $S \subseteq V$
and a
$S \subseteq V$
and a
![]() $v \in V$
, we say the the incidence graph induced by
$v \in V$
, we say the the incidence graph induced by
![]() $S$
with respect to
$S$
with respect to
![]() $v$
is
$v$
is
![]() $I[S \cup N_I(S) \setminus \{b \in \{\binom{[n]}{k-1}\; :\; v \in b \text{ or } b \cup v \in E\}]$
, where
$I[S \cup N_I(S) \setminus \{b \in \{\binom{[n]}{k-1}\; :\; v \in b \text{ or } b \cup v \in E\}]$
, where
![]() $I = (A \cup B, E(I))$
is the incidence graph of
$I = (A \cup B, E(I))$
is the incidence graph of
![]() $G$
.
$G$
.
With these definitions in hand, we get the following corollary.
Corollary 33.
Let
![]() $G = (V,E)$
be a
$G = (V,E)$
be a
![]() $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
![]() $n$
vertices,
$n$
vertices,
![]() $S \subseteq V$
,
$S \subseteq V$
,
![]() $v \in V$
and
$v \in V$
and
![]() $I= (A \cup B, E(I))$
be the incidence graph of
$I= (A \cup B, E(I))$
be the incidence graph of
![]() $G$
induced by
$G$
induced by
![]() $S$
with respect to
$S$
with respect to
![]() $v$
. If every vertex
$v$
. If every vertex
![]() $b \in B$
has degree at least
$b \in B$
has degree at least
![]() $n^{2/3}$
, then there exists a neighbourhood-dominating set
$n^{2/3}$
, then there exists a neighbourhood-dominating set
![]() $D \subseteq S$
of
$D \subseteq S$
of
![]() $S$
with respect to
$S$
with respect to
![]() $v$
of size at most
$v$
of size at most
![]() $O_k(\sqrt{n})$
.
$O_k(\sqrt{n})$
.
Proof. First note that if
![]() $|S| \lt \sqrt{n} + 1$
we can take
$|S| \lt \sqrt{n} + 1$
we can take
![]() $D = S$
. So we assume
$D = S$
. So we assume
![]() $|S| \geq \sqrt{n} + 1$
. We then have that
$|S| \geq \sqrt{n} + 1$
. We then have that
![]() $|B| \leq n^{k-1} \leq |A|^{2k-2}$
. By Lemma 30, it follows that there exists a set
$|B| \leq n^{k-1} \leq |A|^{2k-2}$
. By Lemma 30, it follows that there exists a set
![]() $D \subseteq S$
of size at most
$D \subseteq S$
of size at most
![]() $O_k(n \log (n)/ n^{2/3}) = O_k(\sqrt{n})$
such that
$O_k(n \log (n)/ n^{2/3}) = O_k(\sqrt{n})$
such that
![]() $N_I(D) = B$
.
$N_I(D) = B$
.
We claim that
![]() $D \cup \{v\}$
is a dominating set of
$D \cup \{v\}$
is a dominating set of
![]() $S$
with respect to
$S$
with respect to
![]() $v$
. Indeed, let
$v$
. Indeed, let
![]() $s \in S$
and
$s \in S$
and
![]() $e$
be an edge containing
$e$
be an edge containing
![]() $s$
with
$s$
with
![]() $v \not \in e$
. If
$v \not \in e$
. If
![]() $e \setminus \{s\} \cup \{v\} \in E$
then we are done, so suppose this is not the case. It then follows that
$e \setminus \{s\} \cup \{v\} \in E$
then we are done, so suppose this is not the case. It then follows that
![]() $e \setminus \{s\} \in B$
, so there exists a vertex
$e \setminus \{s\} \in B$
, so there exists a vertex
![]() $d \in D$
that is a neighbour of
$d \in D$
that is a neighbour of
![]() $e \setminus \{s\}$
in
$e \setminus \{s\}$
in
![]() $I$
, which implies
$I$
, which implies
![]() $(e \setminus \{s\}) \cup \{d\} \in E(G)$
, as desired.
$(e \setminus \{s\}) \cup \{d\} \in E(G)$
, as desired.
Our general scheme to transform our hypergraph will now be to remove edges of low degree so the induced incidence graph has high minimum degree and then apply local moves from our dominating sets to
![]() $v$
. We will then repeat this process to find a dominating vertex
$v$
. We will then repeat this process to find a dominating vertex
![]() $u$
of
$u$
of
![]() $V \setminus \{v\}$
.
$V \setminus \{v\}$
.
Formally, we define the following domination procedure from
![]() $S$
to
$S$
to
![]() $v$
: Let
$v$
: Let
![]() $G_0$
be a hypergraph,
$G_0$
be a hypergraph,
![]() $S \subset V(G_0)$
and
$S \subset V(G_0)$
and
![]() $v \in V(G_0)$
. Define a sequence of hypergraphs
$v \in V(G_0)$
. Define a sequence of hypergraphs
![]() $G_0, G_1, \ldots, G_k$
as follows: Let
$G_0, G_1, \ldots, G_k$
as follows: Let
![]() $I_i = (A_i \cup B_i, E(I_i))$
be the incidence graph of
$I_i = (A_i \cup B_i, E(I_i))$
be the incidence graph of
![]() $G_i$
induced by
$G_i$
induced by
![]() $S$
and with respect to
$S$
and with respect to
![]() $v$
. While there exists a
$v$
. While there exists a
![]() $b \in B_i$
with
$b \in B_i$
with
![]() $\deg (b) \leq n^{2/3}$
remove all edges of the form
$\deg (b) \leq n^{2/3}$
remove all edges of the form
![]() $b \cup \{s\}$
for some
$b \cup \{s\}$
for some
![]() $s \in S$
from
$s \in S$
from
![]() $G_i$
to get a hypergraph
$G_i$
to get a hypergraph
![]() $H_i$
. Let
$H_i$
. Let
![]() $D_i$
be the smallest dominating set of
$D_i$
be the smallest dominating set of
![]() $S$
with respect to
$S$
with respect to
![]() $v$
in
$v$
in
![]() $H_i$
. Apply local moves from each vertex
$H_i$
. Apply local moves from each vertex
![]() $d \in D_i$
to
$d \in D_i$
to
![]() $v$
, yielding
$v$
, yielding
![]() $G_{i+1}$
.
$G_{i+1}$
.
Lemma 34.
After running the domination procedure from
![]() $S$
to
$S$
to
![]() $v$
we have that
$v$
we have that
![]() $s \ll _{G_k} v$
for all
$s \ll _{G_k} v$
for all
![]() $s \in S$
.
$s \in S$
.
Proof. Fix
![]() $s \in S$
and an edge
$s \in S$
and an edge
![]() $e \in E(G_k)$
containing
$e \in E(G_k)$
containing
![]() $s$
such that
$s$
such that
![]() $v \not \in e$
. We will show that
$v \not \in e$
. We will show that
![]() $e \setminus \{s\} \cup \{v\} \in E(G_k)$
. First, observe that we never remove hyperedges containing
$e \setminus \{s\} \cup \{v\} \in E(G_k)$
. First, observe that we never remove hyperedges containing
![]() $v$
as no subsets
$v$
as no subsets
![]() $b$
in the induced incidence graph contain
$b$
in the induced incidence graph contain
![]() $v$
or are neighbours of
$v$
or are neighbours of
![]() $v$
. Since we only add edges incident to
$v$
. Since we only add edges incident to
![]() $v$
,
$v$
,
![]() $e \in E(G_i)$
for all
$e \in E(G_i)$
for all
![]() $i$
. It then follows that there exists
$i$
. It then follows that there exists
![]() $d_1, \ldots, d_k$
such that
$d_1, \ldots, d_k$
such that
![]() $e \setminus \{s\} \cup \{d_i\} \in E(H_i)$
. Note that if
$e \setminus \{s\} \cup \{d_i\} \in E(H_i)$
. Note that if
![]() $e \setminus \{s\} \cup \{d_i\}$
exists when we apply the local move from
$e \setminus \{s\} \cup \{d_i\}$
exists when we apply the local move from
![]() $d_i$
to
$d_i$
to
![]() $v$
, then clearly
$v$
, then clearly
![]() $e \setminus \{s\} \cup \{v\} \in G_{i+1}$
. As we never remove edges containing
$e \setminus \{s\} \cup \{v\} \in G_{i+1}$
. As we never remove edges containing
![]() $v$
,
$v$
,
![]() $e \setminus \{s\} \cup \{v\} \in G_{k}$
.
$e \setminus \{s\} \cup \{v\} \in G_{k}$
.
Now towards a contradiction, suppose that for each
![]() $i$
we applied a local move from
$i$
we applied a local move from
![]() $d_i' \in D_i$
to
$d_i' \in D_i$
to
![]() $v$
before the move from
$v$
before the move from
![]() $d_i$
to
$d_i$
to
![]() $v$
, and the move from
$v$
, and the move from
![]() $d_i'$
causes the removal of
$d_i'$
causes the removal of
![]() $e \setminus \{s\} \cup \{d_i\}$
. Observe that
$e \setminus \{s\} \cup \{d_i\}$
. Observe that
![]() $d_i' \not = d_j'$
for
$d_i' \not = d_j'$
for
![]() $i \lt j$
. Indeed suppose
$i \lt j$
. Indeed suppose
![]() $d_i' = d_j'$
. Note
$d_i' = d_j'$
. Note
![]() $d_i' \ll _{G_{i+1}} v$
. Since we only add edges incident to
$d_i' \ll _{G_{i+1}} v$
. Since we only add edges incident to
![]() $v$
and never remove edges containing
$v$
and never remove edges containing
![]() $v$
, we have that
$v$
, we have that
![]() $d_i' \ll _{H_{\ell }} v$
for all
$d_i' \ll _{H_{\ell }} v$
for all
![]() $\ell \gt i$
. In particular, at the time of making the move from
$\ell \gt i$
. In particular, at the time of making the move from
![]() $d_j'$
to
$d_j'$
to
![]() $v$
we have that
$v$
we have that
![]() $d_j' \ll v$
, so the local move from
$d_j' \ll v$
, so the local move from
![]() $d_j'$
to
$d_j'$
to
![]() $v$
would remove no edges, a contradiction.
$v$
would remove no edges, a contradiction.
But we now observe that
![]() $\{d_1', \ldots, d_k'\} \subseteq e \setminus \{s\}$
, a contradiction as
$\{d_1', \ldots, d_k'\} \subseteq e \setminus \{s\}$
, a contradiction as
![]() $|e \setminus \{s\}| = k - 1$
.
$|e \setminus \{s\}| = k - 1$
.
It now remains to show that removing edges of low degree and applying local moves does not ruin the order we have built.
Lemma 35.
Let
![]() $G$
be a
$G$
be a
![]() $k$
-uniform hypergraph and let
$k$
-uniform hypergraph and let
![]() $u,v,w,x \in V(G)$
. Moreover, assume
$u,v,w,x \in V(G)$
. Moreover, assume
![]() $x \not = u,v$
,
$x \not = u,v$
,
![]() $u \ll _G x$
,
$u \ll _G x$
,
![]() $v \ll _G x$
and
$v \ll _G x$
and
![]() $w \ll _G x$
. Let
$w \ll _G x$
. Let
![]() $G'$
be the resulting hypergraph after applying a hypergraph move from
$G'$
be the resulting hypergraph after applying a hypergraph move from
![]() $u$
to
$u$
to
![]() $v$
in
$v$
in
![]() $G$
. Then
$G$
. Then
![]() $w \ll _{G'} x$
.
$w \ll _{G'} x$
.
Proof. We start with the case that
![]() $w = v$
.
$w = v$
.
Claim 36.
![]() $v \ll _{G'} x$
$v \ll _{G'} x$
Proof. Let
![]() $e \in E(G')$
be a hyperedge containing
$e \in E(G')$
be a hyperedge containing
![]() $v$
and not containing
$v$
and not containing
![]() $x$
. We will show that
$x$
. We will show that
![]() $f = (e \setminus \{v\}) \cup \{x\} \in E(G')$
. We consider two cases.
$f = (e \setminus \{v\}) \cup \{x\} \in E(G')$
. We consider two cases.
-
Case I.
 $e \in E(G)$
$e \in E(G)$
Since
 $v \ll _G x$
, we must have that
$v \ll _G x$
, we must have that
 $f \in E(G)$
. Note that the move from
$f \in E(G)$
. Note that the move from
 $u$
to
$u$
to
 $v$
only removes edges containing
$v$
only removes edges containing
 $u$
, so if
$u$
, so if
 $u \not \in f$
, then
$u \not \in f$
, then
 $f \in E(G')$
. On the other hand, if
$f \in E(G')$
. On the other hand, if
 $u \in f$
, we will show that
$u \in f$
, we will show that
 $(f \setminus \{u\}) \cup \{v\} \in E(G)$
, which again implies that
$(f \setminus \{u\}) \cup \{v\} \in E(G)$
, which again implies that
 $f$
is not removed by the local move. Indeed, if
$f$
is not removed by the local move. Indeed, if
 $u \in f$
, then
$u \in f$
, then
 $u \in e$
. Using
$u \in e$
. Using
 $u \ll _G x$
then yields
$u \ll _G x$
then yields
 $g = (e \setminus \{u\}) \cup \{x\} \in E(G)$
. But
$g = (e \setminus \{u\}) \cup \{x\} \in E(G)$
. But
 $g = (f \setminus \{u\}) \cup \{v\}$
, so we have
$g = (f \setminus \{u\}) \cup \{v\}$
, so we have
 $f \in E(G')$
as desired.
$f \in E(G')$
as desired. -
Case II.
 $e \not \in E(G)$
$e \not \in E(G)$
Since
 $e \not \in E(G)$
, it must have been added during the hypergraph move. In this case, we will show that
$e \not \in E(G)$
, it must have been added during the hypergraph move. In this case, we will show that
 $f \in E(G)$
. Note that this implies that
$f \in E(G)$
. Note that this implies that
 $f \in E(G')$
: Since the local move only adds edges not containing
$f \in E(G')$
: Since the local move only adds edges not containing
 $u$
, it follows that
$u$
, it follows that
 $u \not \in e$
and thus
$u \not \in e$
and thus
 $u \not \in f$
. So if
$u \not \in f$
. So if
 $f \in E(G)$
, it cannot be removed by the local move, as it only removes edges containing
$f \in E(G)$
, it cannot be removed by the local move, as it only removes edges containing
 $u$
. To see that
$u$
. To see that
 $f \in E(G)$
, note that in order for the local move to add
$f \in E(G)$
, note that in order for the local move to add
 $e$
, we must have
$e$
, we must have
 $(e \setminus \{v\}) \cup \{u\} \in E(G)$
. Since
$(e \setminus \{v\}) \cup \{u\} \in E(G)$
. Since
 $u \ll _G x$
,
$u \ll _G x$
,
 $(e \setminus \{v\}) \cup \{x\} = f \in E(G)$
, completing the proof.
$(e \setminus \{v\}) \cup \{x\} = f \in E(G)$
, completing the proof.
Since after applying the hypergraph move we have that
![]() $u \ll _{G'} v$
, we have also shown that
$u \ll _{G'} v$
, we have also shown that
![]() $u \ll _{G'} x$
. So it only remains to handle the case of
$u \ll _{G'} x$
. So it only remains to handle the case of
![]() $w \not = u,v$
.
$w \not = u,v$
.
Claim 37.
![]() $w \ll _{G'} x$
for
$w \ll _{G'} x$
for
![]() $w \not = u,v$
$w \not = u,v$
Proof. Let
![]() $e \in E(G')$
be an edge containing
$e \in E(G')$
be an edge containing
![]() $w$
and not containing
$w$
and not containing
![]() $x$
. We will again show
$x$
. We will again show
![]() $f = (e \setminus \{w\}) \cup \{x\} \in E(G')$
via cases on whether or not
$f = (e \setminus \{w\}) \cup \{x\} \in E(G')$
via cases on whether or not
![]() $e$
is in
$e$
is in
![]() $E(G)$
.
$E(G)$
.
-
Case I.
 $e \in E(G)$
$e \in E(G)$
As
 $w \ll _G x$
,
$w \ll _G x$
,
 $f \in E(G)$
. Now, since
$f \in E(G)$
. Now, since
 $e$
wasn’t removed it either doesn’t contain
$e$
wasn’t removed it either doesn’t contain
 $u$
, contains both
$u$
, contains both
 $u$
and
$u$
and
 $v$
, or
$v$
, or
 $(e \setminus \{u\}) \cup \{v\} \in E(G)$
. If
$(e \setminus \{u\}) \cup \{v\} \in E(G)$
. If
 $u \not \in e$
, then
$u \not \in e$
, then
 $u \not \in f$
and
$u \not \in f$
and
 $f \in E(G')$
, since we only remove edges containing
$f \in E(G')$
, since we only remove edges containing
 $u$
in the hypergraph move. Similarly, if
$u$
in the hypergraph move. Similarly, if
 $e$
contains
$e$
contains
 $u$
and
$u$
and
 $v$
, then so does
$v$
, then so does
 $f$
and we again have
$f$
and we again have
 $f \in E(G')$
as we don’t remove edges with both
$f \in E(G')$
as we don’t remove edges with both
 $u$
and
$u$
and
 $v$
in the hypergraph move. In now remains to handle the case where
$v$
in the hypergraph move. In now remains to handle the case where
 $(e \setminus \{u\}) \cup \{v\} \in E(G)$
. As
$(e \setminus \{u\}) \cup \{v\} \in E(G)$
. As
 $w \ll _G x$
, we see
$w \ll _G x$
, we see
 $(e \setminus \{u, w\}) \cup \{v, x\} = (f \setminus \{u\}) \cup \{v\} \in E(G)$
. But this again implies
$(e \setminus \{u, w\}) \cup \{v, x\} = (f \setminus \{u\}) \cup \{v\} \in E(G)$
. But this again implies
 $f \in E(G')$
.
$f \in E(G')$
. -
Case II.
 $e \not \in E(G)$
$e \not \in E(G)$
In this case,
 $e$
must be added during the hypergraph move. Since we only add hyperedges containing
$e$
must be added during the hypergraph move. Since we only add hyperedges containing
 $v$
,
$v$
,
 $v \in e$
. Moreover since
$v \in e$
. Moreover since
 $e$
was added,
$e$
was added,
 $(e \setminus \{v\}) \cup \{u\} \in E(G)$
. As
$(e \setminus \{v\}) \cup \{u\} \in E(G)$
. As
 $w \ll _G x$
,
$w \ll _G x$
,
 $g = (e \setminus \{v, w\}) \cup \{u, x\} \in E(G)$
. Now note that after the hypergraph move we must have that
$g = (e \setminus \{v, w\}) \cup \{u, x\} \in E(G)$
. Now note that after the hypergraph move we must have that
 $(g \setminus \{u\}) \cup \{v\} = f \in E(G')$
.
$(g \setminus \{u\}) \cup \{v\} = f \in E(G')$
.
Since we have handled all the cases, that is,
![]() $w = v$
,
$w = v$
,
![]() $w = u$
and
$w = u$
and
![]() $w \not = u,v$
, the proof now follows.
$w \not = u,v$
, the proof now follows.
Lemma 38.
Let
![]() $G = (V,E)$
be a
$G = (V,E)$
be a
![]() $k$
-uniform hypergraph,
$k$
-uniform hypergraph,
![]() $S \subseteq V$
,
$S \subseteq V$
,
![]() $v \in S$
and
$v \in S$
and
![]() $I = (A \cup B, E(I))$
be the incidence graph induced by
$I = (A \cup B, E(I))$
be the incidence graph induced by
![]() $S$
with respect to
$S$
with respect to
![]() $v$
. Let
$v$
. Let
![]() $x \in V(G)$
and
$x \in V(G)$
and
![]() $y \in V(G) \setminus S$
be such that
$y \in V(G) \setminus S$
be such that
![]() $x \ll _G y$
and
$x \ll _G y$
and
![]() $s \ll _G y$
for all
$s \ll _G y$
for all
![]() $s \in S$
. Suppose that for every subset
$s \in S$
. Suppose that for every subset
![]() $b \in B$
with
$b \in B$
with
![]() $\deg _I(b) \leq n^{2/3}$
, we remove the edges
$\deg _I(b) \leq n^{2/3}$
, we remove the edges
![]() $b \cup \{s\}$
for
$b \cup \{s\}$
for
![]() $s \in S$
from
$s \in S$
from
![]() $E(G)$
, resulting in a hypergraph
$E(G)$
, resulting in a hypergraph
![]() $G'$
. Then
$G'$
. Then
![]() $x \ll _{G'} y$
.
$x \ll _{G'} y$
.
Proof. Let
![]() $e \in E(G')$
be an edge containing
$e \in E(G')$
be an edge containing
![]() $x$
and not
$x$
and not
![]() $y$
. We will show that
$y$
. We will show that
![]() $f = e \setminus \{x\} \cup \{y\} \in E(G')$
. Since
$f = e \setminus \{x\} \cup \{y\} \in E(G')$
. Since
![]() $E(G') \subseteq E(G)$
,
$E(G') \subseteq E(G)$
,
![]() $e \in E(G)$
. Combining this with the fact that
$e \in E(G)$
. Combining this with the fact that
![]() $x \ll _G y$
implies
$x \ll _G y$
implies
![]() $f \in E(G)$
. Now fix some
$f \in E(G)$
. Now fix some
![]() $s \in f \cap S \subseteq e \cap S$
. We will show that
$s \in f \cap S \subseteq e \cap S$
. We will show that
![]() $f \setminus \{s\}$
does not lead to the removal of
$f \setminus \{s\}$
does not lead to the removal of
![]() $f$
. To do so, we take cases on why
$f$
. To do so, we take cases on why
![]() $e \setminus \{s\}$
didn’t lead to the removal of
$e \setminus \{s\}$
didn’t lead to the removal of
![]() $e$
.
$e$
.
-
Case I.
 $\deg _I(e \setminus \{s\}) \gt n^{2/3}$
$\deg _I(e \setminus \{s\}) \gt n^{2/3}$
Note that
 $s \not = x$
as
$s \not = x$
as
 $x \not \in f$
. Combining this with the fact that
$x \not \in f$
. Combining this with the fact that
 $x \ll _G y$
, we observe that for any
$x \ll _G y$
, we observe that for any
 $t \not = y$
, if
$t \not = y$
, if
 $e \setminus \{s\} \cup \{t\} \in E(G)$
then
$e \setminus \{s\} \cup \{t\} \in E(G)$
then
 $e \setminus \{s, x\} \cup \{t,y\} = (f \setminus \{s\}) \cup \{t\} \in E(G)$
. So,
$e \setminus \{s, x\} \cup \{t,y\} = (f \setminus \{s\}) \cup \{t\} \in E(G)$
. So,
 $\deg _I(f \setminus \{s\}) \geq \deg _I(e \setminus \{s\}) \gt n^{2/3}$
and
$\deg _I(f \setminus \{s\}) \geq \deg _I(e \setminus \{s\}) \gt n^{2/3}$
and
 $f \setminus \{s\}$
doesn’t lead to the removal of
$f \setminus \{s\}$
doesn’t lead to the removal of
 $f$
.
$f$
. -
Case II.
 $v \in e$
$v \in e$
If
 $x \not = v$
, then
$x \not = v$
, then
 $v \in f$
. Observe that by construction, the incidence graph has no edges corresponding to hyperedges in
$v \in f$
. Observe that by construction, the incidence graph has no edges corresponding to hyperedges in
 $G$
containing
$G$
containing
 $v$
. So we never remove edges containing
$v$
. So we never remove edges containing
 $v$
, and
$v$
, and
 $f \in E(G')$
. Now assume that
$f \in E(G')$
. Now assume that
 $x = v$
. Since
$x = v$
. Since
 $s \ll _G y$
, we have that
$s \ll _G y$
, we have that
 $e \setminus \{s\} \cup \{y\} \in E(G)$
. But now note
$e \setminus \{s\} \cup \{y\} \in E(G)$
. But now note
 $f \setminus \{s\} \cup \{v\} = e \setminus \{s\} \cup \{y\}$
. It then follows that
$f \setminus \{s\} \cup \{v\} = e \setminus \{s\} \cup \{y\}$
. It then follows that
 $f \setminus \{s\} \not \in B$
. Thus, we conclude
$f \setminus \{s\} \not \in B$
. Thus, we conclude
 $f \setminus \{s\}$
doesn’t lead to the removal of
$f \setminus \{s\}$
doesn’t lead to the removal of
 $f$
.
$f$
. -
Case III.
 $e \setminus \{s\} \cup \{v\} \in E(G)$
$e \setminus \{s\} \cup \{v\} \in E(G)$
Since
 $x \ll _G y$
,
$x \ll _G y$
,
 $e \setminus \{s,x\} \cup \{v,y\} \in E(G)$
. But
$e \setminus \{s,x\} \cup \{v,y\} \in E(G)$
. But
 $e \setminus \{s,x\} \cup \{v,y\} = f \setminus \{s\} \cup \{v\}$
. Thus
$e \setminus \{s,x\} \cup \{v,y\} = f \setminus \{s\} \cup \{v\}$
. Thus
 $f \setminus \{s\} \not \in B$
and again doesn’t cause the removal of
$f \setminus \{s\} \not \in B$
and again doesn’t cause the removal of
 $f$
.
$f$
.
Since we chose
![]() $s$
arbitrarily,
$s$
arbitrarily,
![]() $f \in E(G')$
, as desired.
$f \in E(G')$
, as desired.
With this, we can now prove Lemma 28.
Proof of Lemma
28
. We apply the following algorithm to transform
![]() $G$
into a threshold hypergraph:
$G$
into a threshold hypergraph:
Initially, let
![]() $T = \emptyset$
. Repeat
$T = \emptyset$
. Repeat
![]() $n$
times: Choose a vertex
$n$
times: Choose a vertex
![]() $v \in V \setminus T$
. Apply the domination procedure with
$v \in V \setminus T$
. Apply the domination procedure with
![]() $G_0 = G$
from
$G_0 = G$
from
![]() $V \setminus T$
to
$V \setminus T$
to
![]() $v$
, resulting in a hypergraphs
$v$
, resulting in a hypergraphs
![]() $G_1, G_2, \ldots, G_k$
, intermediate hypergraphs
$G_1, G_2, \ldots, G_k$
, intermediate hypergraphs
![]() $H_0, \ldots, H_{k-1}$
, and dominating sets
$H_0, \ldots, H_{k-1}$
, and dominating sets
![]() $D_0, \ldots, D_{k-1}$
. Set
$D_0, \ldots, D_{k-1}$
. Set
![]() $T = T \cup \{v\}$
and
$T = T \cup \{v\}$
and
![]() $G = G_k$
.
$G = G_k$
.
Claim 39.
When the algorithm terminates,
![]() $G$
is a threshold hypergraph.
$G$
is a threshold hypergraph.
Proof. Suppose that at time
![]() $r$
we have that
$r$
we have that
![]() $T = \{t_1, \ldots, t_r\}$
, where
$T = \{t_1, \ldots, t_r\}$
, where
![]() $t_i$
is the
$t_i$
is the
![]() $i$
th vertex added to
$i$
th vertex added to
![]() $T$
. We prove by induction on
$T$
. We prove by induction on
![]() $r$
that
$r$
that
![]() $t_1 \gg _{G} t_2 \gg _G \ldots \gg _G t_r \gg s$
for all
$t_1 \gg _{G} t_2 \gg _G \ldots \gg _G t_r \gg s$
for all
![]() $s \in V(G) \setminus T$
. The base case of
$s \in V(G) \setminus T$
. The base case of
![]() $r = 0$
is vacuously true. So now suppose the statement is true for some
$r = 0$
is vacuously true. So now suppose the statement is true for some
![]() $r$
.
$r$
.
Note that
![]() $H_0$
is the result of repeatedly deleting edges
$H_0$
is the result of repeatedly deleting edges
![]() $b \cup \{s\}$
with
$b \cup \{s\}$
with
![]() $\deg (b) \leq n^{2/3}$
in the incidence graph of
$\deg (b) \leq n^{2/3}$
in the incidence graph of
![]() $G$
induced by
$G$
induced by
![]() $V \setminus T$
with respect to
$V \setminus T$
with respect to
![]() $v$
. So by Lemma 38, we have that
$v$
. So by Lemma 38, we have that
![]() $t_1 \gg _{H_0} t_2 \gg _{H_0} \ldots \gg _{H_0} t_r \gg _{H_0} s$
for all
$t_1 \gg _{H_0} t_2 \gg _{H_0} \ldots \gg _{H_0} t_r \gg _{H_0} s$
for all
![]() $s \in V(G) \setminus T$
.
$s \in V(G) \setminus T$
.
After deleting low degree vertices, the domination procedure applies hypergraph moves from vertices in
![]() $V \setminus T$
to
$V \setminus T$
to
![]() $v$
. By Lemma 35, each of these moves preserves the ordering. Thus,
$v$
. By Lemma 35, each of these moves preserves the ordering. Thus,
![]() $t_1 \gg _{G_1} t_2 \gg _{G_1} \ldots \gg _{G_1} t_r \gg _{G_1} s$
for all
$t_1 \gg _{G_1} t_2 \gg _{G_1} \ldots \gg _{G_1} t_r \gg _{G_1} s$
for all
![]() $s \in V(G) \setminus T$
.
$s \in V(G) \setminus T$
.
We can now repeat this argument
![]() $k$
times to get that
$k$
times to get that
![]() $t_1 \gg _{G_k} t_2 \gg _{G_k} \ldots \gg _{G_k} t_r \gg _{G_k} s$
for all
$t_1 \gg _{G_k} t_2 \gg _{G_k} \ldots \gg _{G_k} t_r \gg _{G_k} s$
for all
![]() $s \in V(G) \setminus T$
. Finally, we are promised by Lemma 34 that
$s \in V(G) \setminus T$
. Finally, we are promised by Lemma 34 that
![]() $v \gg _{G_k} s$
for all
$v \gg _{G_k} s$
for all
![]() $s \in V(G) \setminus (T \cup v)$
. As
$s \in V(G) \setminus (T \cup v)$
. As
![]() $t_{r+1} = v$
, the inductive hypothesis holds and the proof is complete.
$t_{r+1} = v$
, the inductive hypothesis holds and the proof is complete.
Claim 40.
Each iteration applies at most
![]() $O_k(\sqrt{n})$
local moves.
$O_k(\sqrt{n})$
local moves.
Proof. Note that by Corollary 33, every dominating set
![]() $D_i$
has size at most
$D_i$
has size at most
![]() $O_k(\sqrt{n})$
. It then follows that each iteration uses at most
$O_k(\sqrt{n})$
. It then follows that each iteration uses at most
![]() $O_k(k\sqrt{n}) = O_k(\sqrt{n})$
local moves.
$O_k(k\sqrt{n}) = O_k(\sqrt{n})$
local moves.
Note that the above claim implies that we make
![]() $O_k(n^{3/2})$
hypergraph moves in total.
$O_k(n^{3/2})$
hypergraph moves in total.
Claim 41.
The algorithm removes
![]() $o_k(n^k)$
hyperedges in total.
$o_k(n^k)$
hyperedges in total.
Proof. Fix some
![]() $b \in \binom{[n]}{k-1}$
. We claim that
$b \in \binom{[n]}{k-1}$
. We claim that
![]() $b$
only causes the removal of edges at most
$b$
only causes the removal of edges at most
![]() $k$
times. Indeed, after removing all edges of the form
$k$
times. Indeed, after removing all edges of the form
![]() $b \cup \{s\}$
, we must add some hyperedge containing
$b \cup \{s\}$
, we must add some hyperedge containing
![]() $b$
for
$b$
for
![]() $b$
to cause the removal of more hyperedges. Let
$b$
to cause the removal of more hyperedges. Let
![]() $e$
be the first hyperedge containing
$e$
be the first hyperedge containing
![]() $b$
added after
$b$
added after
![]() $b$
’s
$b$
’s
![]() $\ell$
th removal.
$\ell$
th removal.
![]() $e$
must have been added by some local move, say from
$e$
must have been added by some local move, say from
![]() $s$
to
$s$
to
![]() $v$
. Now since
$v$
. Now since
![]() $e$
is the first such edge we have that
$e$
is the first such edge we have that
![]() $b \not \subset e \setminus \{v\} \cup \{s\}$
. So
$b \not \subset e \setminus \{v\} \cup \{s\}$
. So
![]() $v \in b$
. Since we make local moves to any vertex at most once and there are
$v \in b$
. Since we make local moves to any vertex at most once and there are
![]() $k-1$
elements in
$k-1$
elements in
![]() $b$
, it follows that
$b$
, it follows that
![]() $b$
’s low degree only causes the remove of hyperedges at most
$b$
’s low degree only causes the remove of hyperedges at most
![]() $k$
times. (Note that we are crucially using that
$k$
times. (Note that we are crucially using that
![]() $b$
cannot be added and removed multiple times when running the domination procedure with a vertex
$b$
cannot be added and removed multiple times when running the domination procedure with a vertex
![]() $v \in b$
. Indeed, if
$v \in b$
. Indeed, if
![]() $b$
is added due to a local move to
$b$
is added due to a local move to
![]() $v$
, it cannot be removed until the next iteration as local moves to
$v$
, it cannot be removed until the next iteration as local moves to
![]() $v$
never remove hyperedges containing
$v$
never remove hyperedges containing
![]() $v$
, and after the addition of an edge
$v$
, and after the addition of an edge
![]() $e$
containing
$e$
containing
![]() $b$
,
$b$
,
![]() $b$
will no longer appear in the incidence graph induced by
$b$
will no longer appear in the incidence graph induced by
![]() $V \setminus T$
with respect to
$V \setminus T$
with respect to
![]() $v$
.)
$v$
.)
We now conclude that each
![]() $b \in \binom{[n]}{k-1}$
causes the removal of at most
$b \in \binom{[n]}{k-1}$
causes the removal of at most
![]() $kn^{2/3}$
edges. So in total we remove at most
$kn^{2/3}$
edges. So in total we remove at most
hyperedges in total.
With these three claims the proof is now complete as we have shown that the algorithm presented transforms the graph into a threshold hypergraph by using
![]() $O_k(n^{3/2})$
local moves and removing
$O_k(n^{3/2})$
local moves and removing
![]() $o_k(n^k)$
hyperedges.
$o_k(n^k)$
hyperedges.
We end this section by remarking that the ideas in this proof simplify considerably in the case of graphs giving an alternative proof of Theorem 3. That said this argument loses slightly more homomorphisms than Theorem 20 and yields a weaker version of Theorem 4.
4. Applications of threshold maximisation
4.1 Maximisation on the clique
Before we begin with the applications, we start by reproving a result of [Reference Gerbner, Nagy, Patkós and Vizer6] that shows for any graph
![]() $H$
the quasi-clique maximises the number of homomorphisms from
$H$
the quasi-clique maximises the number of homomorphisms from
![]() $H$
for
$H$
for
![]() $c$
sufficiently large. This will contrast with the results of Section 4.2, where we show that for small edge density
$c$
sufficiently large. This will contrast with the results of Section 4.2, where we show that for small edge density
![]() $c$
there are graphs
$c$
there are graphs
![]() $H$
whose optimisers are threshold graphs that must have strictly more than two parts.
$H$
whose optimisers are threshold graphs that must have strictly more than two parts.
Theorem 42.
For every fixed graph
![]() $H$
, there exists
$H$
, there exists
![]() $k_H \lt 1$
such that for all
$k_H \lt 1$
such that for all
![]() $c \gt k_H$
,
$c \gt k_H$
,
![]() $\mathcal{M}_H(c)$
is achieved on the quasi-clique.
$\mathcal{M}_H(c)$
is achieved on the quasi-clique.
Proof. We will prove the result for a connected graph
![]() $H$
. If the graph is not connected, we can apply the result to each of the components and take the maximum of the
$H$
. If the graph is not connected, we can apply the result to each of the components and take the maximum of the
![]() $k_H$
’s over all the components.
$k_H$
’s over all the components.
Let
![]() $T$
be a spanning tree of
$T$
be a spanning tree of
![]() $H$
. We note that clearly for any graph
$H$
. We note that clearly for any graph
![]() $G$
,
$G$
,
![]() $t(H,G) \leq t(T,G)$
since
$t(H,G) \leq t(T,G)$
since
![]() $T$
was obtained by removing edges from
$T$
was obtained by removing edges from
![]() $H$
. Now using a result from Sidorenko [Reference Sidorenko15] we have that
$H$
. Now using a result from Sidorenko [Reference Sidorenko15] we have that
![]() $t(T,G) \leq t(K_{1, |H|-1}, G)$
for all
$t(T,G) \leq t(K_{1, |H|-1}, G)$
for all
![]() $G$
. By a result of Reiher and Wagner [Reference Reiher and Wagner13], we have that there exists a
$G$
. By a result of Reiher and Wagner [Reference Reiher and Wagner13], we have that there exists a
![]() $k_H$
such that for
$k_H$
such that for
![]() $c \gt k_H$
,
$c \gt k_H$
,
![]() $\mathcal{M}_{K_{1, |H|-1}}(c)$
is achieved on the quasi-clique. But now note that for any quasi-clique
$\mathcal{M}_{K_{1, |H|-1}}(c)$
is achieved on the quasi-clique. But now note that for any quasi-clique
![]() $\mathcal{K}$
have that
$\mathcal{K}$
have that
![]() $t(H, \mathcal{K}) = t(K_{1, |H|-1}, \mathcal{K})$
, so
$t(H, \mathcal{K}) = t(K_{1, |H|-1}, \mathcal{K})$
, so
![]() $\mathcal{M}_H(c)$
is also attained on the quasi-clique.
$\mathcal{M}_H(c)$
is also attained on the quasi-clique.
4.2 Graphs requiring three parts
In this section, we show that Theorem 22 implies that some graphs require at least
![]() $3$
parts to optimise, which disproves a conjecture of Nagy that all graphs require only two parts [Reference Nagy12].
$3$
parts to optimise, which disproves a conjecture of Nagy that all graphs require only two parts [Reference Nagy12].
Theorem 43.
Let
![]() $H$
be a graph with
$H$
be a graph with
![]() $\alpha ^*(H) \gt \alpha (H)$
and
$\alpha ^*(H) \gt \alpha (H)$
and
![]() $\alpha ^*(H) \gt \frac{|H|}{2}$
, then for
$\alpha ^*(H) \gt \frac{|H|}{2}$
, then for
![]() $c$
sufficiently small,
$c$
sufficiently small,
![]() $H$
is not optimised on the quasi-star or quasi-clique.
$H$
is not optimised on the quasi-star or quasi-clique.
To begin, we show that for all graphs
![]() $H$
there exists a threshold graph
$H$
there exists a threshold graph
![]() $T$
on three parts such that
$T$
on three parts such that
![]() $t(H,T)$
matches the upper bound from Theorem 22 up to constant factors depending on
$t(H,T)$
matches the upper bound from Theorem 22 up to constant factors depending on
![]() $H$
. We will then prove Theorem 44 by showing that threshold graphs with at most two parts have significantly fewer homomorphisms.
$H$
. We will then prove Theorem 44 by showing that threshold graphs with at most two parts have significantly fewer homomorphisms.
Lemma 44.
Let
![]() $H$
be a fixed graph and
$H$
be a fixed graph and
![]() $n$
and
$n$
and
![]() $m$
be positive integers such that
$m$
be positive integers such that
![]() $2n \leq m \leq \binom{n}{2}$
, then there exists a threshold graph
$2n \leq m \leq \binom{n}{2}$
, then there exists a threshold graph
![]() $T$
with at most 3 parts, with
$T$
with at most 3 parts, with
![]() $n$
vertices and at most
$n$
vertices and at most
![]() $m$
edges, such that
$m$
edges, such that
Proof. We will let
![]() $G$
be a threshold graph with three parts:
$G$
be a threshold graph with three parts:
where we let
![]() $\alpha = \lfloor \sqrt{m} \rfloor$
,
$\alpha = \lfloor \sqrt{m} \rfloor$
,
![]() $\gamma = \lfloor m/(2n) \rfloor$
,
$\gamma = \lfloor m/(2n) \rfloor$
,
![]() $\beta = n - \alpha - \gamma$
. Then we have that there are at most
$\beta = n - \alpha - \gamma$
. Then we have that there are at most
edges as desired.
To analyse the number of homomorphisms, we note that we lost at most a factor of two from the floors. That is
![]() $\alpha \geq \sqrt{m}/2$
and
$\alpha \geq \sqrt{m}/2$
and
![]() $\gamma \geq (m/4n)$
. Clearly, we also have that
$\gamma \geq (m/4n)$
. Clearly, we also have that
![]() $\beta \geq n - \sqrt{m} - m/(2n) \geq n/25$
.
$\beta \geq n - \sqrt{m} - m/(2n) \geq n/25$
.
Now let
![]() $f\; :\; V(H) \rightarrow \{0,1/2,1\}$
be an optimal fractional independence function, that is,
$f\; :\; V(H) \rightarrow \{0,1/2,1\}$
be an optimal fractional independence function, that is,
![]() $f(v_1), \ldots, f(v_n)$
is an optimal solution to the linear program used to define to the fractional independence number (see Definition 11). Note that such a function exists since the feasibility polytope for fractional independence is half-integral. Now, we claim that any injective function
$f(v_1), \ldots, f(v_n)$
is an optimal solution to the linear program used to define to the fractional independence number (see Definition 11). Note that such a function exists since the feasibility polytope for fractional independence is half-integral. Now, we claim that any injective function
![]() $\varphi$
that sends
$\varphi$
that sends
![]() $f^{-1}(1/2)$
to the first block of
$f^{-1}(1/2)$
to the first block of
![]() $1$
’s,
$1$
’s,
![]() $f^{-1}(0)$
to the second block of
$f^{-1}(0)$
to the second block of
![]() $1$
’s and
$1$
’s and
![]() $f^{-1}(1)$
to the block of
$f^{-1}(1)$
to the block of
![]() $0's$
is a homomorphism. This claim will complete the proof since there are at least
$0's$
is a homomorphism. This claim will complete the proof since there are at least
 \begin{equation*}\left ( \frac {\sqrt {m}}{2} \right )^{|f^{-1}(1/2)|} \left (\frac {n}{25} \right )^{|f^{-1}(1)|} \left (\frac {m}{4n} \right )^{|f^{-1}(0)|} = \Omega _H(m^{|H| - \alpha ^*(H)} n^{2\alpha ^*(H) - |H|})\end{equation*}
\begin{equation*}\left ( \frac {\sqrt {m}}{2} \right )^{|f^{-1}(1/2)|} \left (\frac {n}{25} \right )^{|f^{-1}(1)|} \left (\frac {m}{4n} \right )^{|f^{-1}(0)|} = \Omega _H(m^{|H| - \alpha ^*(H)} n^{2\alpha ^*(H) - |H|})\end{equation*}
such functions. To see that these are homomorphisms, suppose
![]() $uv \in E(H)$
. Without loss of generality assume
$uv \in E(H)$
. Without loss of generality assume
![]() $f(u) \leq f(v)$
. Now if
$f(u) \leq f(v)$
. Now if
![]() $u \in f^{-1}(0)$
, then since every vertex in the final block of
$u \in f^{-1}(0)$
, then since every vertex in the final block of
![]() $1$
’s is domininating we have that
$1$
’s is domininating we have that
![]() $\varphi (u) \varphi (v) \in E(G)$
. Otherwise if
$\varphi (u) \varphi (v) \in E(G)$
. Otherwise if
![]() $f(u) = f(v) = \frac{1}{2}$
, then we have that both
$f(u) = f(v) = \frac{1}{2}$
, then we have that both
![]() $\varphi (u)$
and
$\varphi (u)$
and
![]() $\varphi (v)$
are mapped to vertices in the first block of ones. Since any two vertices in this block are connected, we have
$\varphi (v)$
are mapped to vertices in the first block of ones. Since any two vertices in this block are connected, we have
![]() $\varphi (u) \varphi (v) \in E(G)$
and this is indeed a homomorphism.
$\varphi (u) \varphi (v) \in E(G)$
and this is indeed a homomorphism.
Corollary 45.
Let
![]() $H$
be a fixed graph and
$H$
be a fixed graph and
![]() $c \in [0,1]$
, then
$c \in [0,1]$
, then
![]() $\mathcal{M}_H(c) = \Omega _H(c^{|H| - \alpha ^*(H)})$
.
$\mathcal{M}_H(c) = \Omega _H(c^{|H| - \alpha ^*(H)})$
.
We will now show that if
![]() $H$
satisfies the conditions of Theorem 43, then with only two parts we get far fewer homomorphisms from
$H$
satisfies the conditions of Theorem 43, then with only two parts we get far fewer homomorphisms from
![]() $H$
as
$H$
as
![]() $c \rightarrow 0$
than the optimum.
$c \rightarrow 0$
than the optimum.
Proof of Theorem
43
. Since isolated vertices do not affect the optimising graph, we assume without loss of generality that
![]() $H$
has no isolated vertices.
$H$
has no isolated vertices.
By Corollary 45, we have that there exists a graph
![]() $G$
and constant
$G$
and constant
![]() $C_1$
such that
$C_1$
such that
This implies that
![]() $\mathcal{M}_H(c) \geq C_1 c^{|H|-\alpha ^*(H)}$
by Lemma 10. For the sake of contradiction, assume that
$\mathcal{M}_H(c) \geq C_1 c^{|H|-\alpha ^*(H)}$
by Lemma 10. For the sake of contradiction, assume that
![]() $H$
is optimised on the quasi-star or quasi-clique. Note that if it’s optimised on the quasi-clique then we have that for all graphs
$H$
is optimised on the quasi-star or quasi-clique. Note that if it’s optimised on the quasi-clique then we have that for all graphs
![]() $G$
$G$
Since
![]() $\alpha ^*(H) \gt |H|/2$
, we have that for
$\alpha ^*(H) \gt |H|/2$
, we have that for
![]() $c$
sufficiently small
$c$
sufficiently small
![]() $C_1 c^{|H|-\alpha ^*(H)} \gt c^{|H|/2}$
, a contradiction.
$C_1 c^{|H|-\alpha ^*(H)} \gt c^{|H|/2}$
, a contradiction.
So we must have that the homomorphism density of
![]() $H$
is maximised on the quasi-star. Recall now that every vertex in the quasi-star either has degree
$H$
is maximised on the quasi-star. Recall now that every vertex in the quasi-star either has degree
![]() $d_0$
or
$d_0$
or
![]() $d_1$
for some integers
$d_1$
for some integers
![]() $d_0$
and
$d_0$
and
![]() $d_1$
with
$d_1$
with
![]() $d_0 \lt d_1$
. Note that in any homomorphism from
$d_0 \lt d_1$
. Note that in any homomorphism from
![]() $H$
to the quasi-star, the vertices in
$H$
to the quasi-star, the vertices in
![]() $H$
mapping to the vertices in the quasi-star of degree
$H$
mapping to the vertices in the quasi-star of degree
![]() $d_0$
must form an independent set. Hence we have at least
$d_0$
must form an independent set. Hence we have at least
![]() $|H| - \alpha (H)$
vertices are mapped to one of the at most
$|H| - \alpha (H)$
vertices are mapped to one of the at most
![]() $cn$
dominating vertices in the quasi-star of edge density
$cn$
dominating vertices in the quasi-star of edge density
![]() $c$
. By a union bound argument, this implies that there are at most
$c$
. By a union bound argument, this implies that there are at most
![]() $O_H(c^{n-\alpha (H)} n^{|H|})$
homomorphisms. But now note again that for
$O_H(c^{n-\alpha (H)} n^{|H|})$
homomorphisms. But now note again that for
![]() $c$
sufficiently small we have that
$c$
sufficiently small we have that
![]() $C_2 c^{|H|-\alpha (H)} \lt C_1 c^{|H|-\alpha ^*(H)}$
, which is a contradiction.
$C_2 c^{|H|-\alpha (H)} \lt C_1 c^{|H|-\alpha ^*(H)}$
, which is a contradiction.
Thus such a graph
![]() $H$
is optimised on neither the quasi-star nor the quasi-clique.
$H$
is optimised on neither the quasi-star nor the quasi-clique.
Corollary 46. There exist graphs that are optimised on neither the quasi-star nor the quasi-clique. Moreover these graphs can be taken to be connected and threshold.
Proof. Take
![]() $H = K_3 \sqcup K_{1,2}$
. Then
$H = K_3 \sqcup K_{1,2}$
. Then
![]() $\alpha (H) = 3$
and
$\alpha (H) = 3$
and
![]() $\alpha ^*(H) = 3.5$
. The result then follows by Theorem 43.
$\alpha ^*(H) = 3.5$
. The result then follows by Theorem 43.
If we wish to take the graph to be connected, adding edges from each vertex in the clique to the vertex of degree
![]() $2$
in the star gives a graph
$2$
in the star gives a graph
![]() $H$
where we still have
$H$
where we still have
![]() $\alpha (H) = 3$
and
$\alpha (H) = 3$
and
![]() $\alpha ^*(H) = 3.5$
. Moreover, such a graph is a threshold graph. We can also take
$\alpha ^*(H) = 3.5$
. Moreover, such a graph is a threshold graph. We can also take
![]() $H = K_\ell \sqcup K_{1,2}$
for any
$H = K_\ell \sqcup K_{1,2}$
for any
![]() $\ell \geq 3$
if we want arbitrarily large examples.
$\ell \geq 3$
if we want arbitrarily large examples.
Remark 47.
We note that a graph has
![]() $\alpha ^*(H) = |H|/2$
if and only if
$\alpha ^*(H) = |H|/2$
if and only if
![]() $H$
has a spanning subgraph that is the disjoint union of cycles and edges [2]. (Equivalently,
$H$
has a spanning subgraph that is the disjoint union of cycles and edges [2]. (Equivalently,
![]() $\alpha ^*(H) = |H|/2$
if and only if
$\alpha ^*(H) = |H|/2$
if and only if
![]() $t(H,\cdot )$
is optimised on the quasi-clique for all edge densities
$t(H,\cdot )$
is optimised on the quasi-clique for all edge densities
![]() $c \in [0,1]$
.) For the reverse direction, one simply checks that
$c \in [0,1]$
.) For the reverse direction, one simply checks that
![]() $\alpha ^*(C_\ell ) = \ell/2$
for all integers
$\alpha ^*(C_\ell ) = \ell/2$
for all integers
![]() $\ell$
. The forward direction follows by noting that if
$\ell$
. The forward direction follows by noting that if
![]() $|S| \gt |N_H(S)|$
for some
$|S| \gt |N_H(S)|$
for some
![]() $S \subseteq V(H)$
, then taking
$S \subseteq V(H)$
, then taking
 \begin{equation*}w_v \, :\!=\, \begin {cases} 1 & v \in S \setminus N(S) \\ 0 & v \in N(S) \setminus S \\ \frac {1}{2} & \text { otherwise} \end {cases}\end{equation*}
\begin{equation*}w_v \, :\!=\, \begin {cases} 1 & v \in S \setminus N(S) \\ 0 & v \in N(S) \setminus S \\ \frac {1}{2} & \text { otherwise} \end {cases}\end{equation*}
gives a feasible solution to the fractional independence program of value strictly greater than
![]() $|H|/2$
. The result now follows from a result of Alon [2], which states that
$|H|/2$
. The result now follows from a result of Alon [2], which states that
![]() $\max _{S \subseteq V(H)} |S| - |N_H(S)| = 0$
if and only if
$\max _{S \subseteq V(H)} |S| - |N_H(S)| = 0$
if and only if
![]() $H$
has a spanning subgraph that is a dijoint union of cycles and edges.
$H$
has a spanning subgraph that is a dijoint union of cycles and edges.
5. Conclusion
We end with a few open questions. First, perhaps the most natural question to ask
Question 48.
For any
![]() $c \in [0,1]$
and graph
$c \in [0,1]$
and graph
![]() $H$
is it true that
$H$
is it true that
![]() $t(H, \cdot )$
asymptotically maximised on a threshold graph with a bounded number of parts? Is there a bound on the number of parts that is independent of
$t(H, \cdot )$
asymptotically maximised on a threshold graph with a bounded number of parts? Is there a bound on the number of parts that is independent of
![]() $H$
?
$H$
?
An intermediate question, easier to resolve than the above, is whether the simpler, one-dimensional limit objects of threshold graphs can help find the optimisers of
![]() $t(H, \cdot )$
for particular graphs
$t(H, \cdot )$
for particular graphs
![]() $H$
. (Recall that much of our current understanding of the optimisers for particular
$H$
. (Recall that much of our current understanding of the optimisers for particular
![]() $H$
’s of interest is the result of working with graphons, which are two-dimensional limit objects of graphs [Reference Nagy12, Reference Reiher and Wagner13].)
$H$
’s of interest is the result of working with graphons, which are two-dimensional limit objects of graphs [Reference Nagy12, Reference Reiher and Wagner13].)
Question 49.
Can the one-dimensional graphons for threshold graphs help us find the maximiser of
![]() $t(H, \cdot )$
with edge density at most
$t(H, \cdot )$
with edge density at most
![]() $c$
for various
$c$
for various
![]() $H$
? In particular, can they be used to solve the problem when
$H$
? In particular, can they be used to solve the problem when
![]() $H$
is a
$H$
is a
![]() $k$
-star?
$k$
-star?
We also remark that our result in Theorem 4 is likely not tight and can probably be extended to sparser graphs, leading us to the next question
Question 50.
Does Theorem
4
hold for sparser graphs, that is, for
![]() $m = o(n^{3/2})$
?
$m = o(n^{3/2})$
?
Finally, we note that there are several more restrictive definitions of threshold hypergraphs [Reference Reiterman, Rödl, Šiňajová and Tůma14]. For instance, one can consider the following notion.
Definition 51 (
![]() $T_2$
-Threshold Hypergraph). Let
$T_2$
-Threshold Hypergraph). Let
![]() $G = (V,E)$
be a
$G = (V,E)$
be a
![]() $k$
-uniform hypergraph and
$k$
-uniform hypergraph and
![]() $n$
denote
$n$
denote
![]() $|V(G)|$
. We say
$|V(G)|$
. We say
![]() $G$
is a
$G$
is a
![]() $T_2$
-threshold hypergraph if there exists a set of positive weights
$T_2$
-threshold hypergraph if there exists a set of positive weights
![]() $w_1, \ldots, w_n$
and a real number
$w_1, \ldots, w_n$
and a real number
![]() $t$
such that
$t$
such that
![]() $e \in E(G)$
if and only if
$e \in E(G)$
if and only if
We note that
![]() $T_2$
-threshold hypergraphs are a strict subset of threshold hypergraphs [Reference Reiterman, Rödl, Šiňajová and Tůma14] and ask whether our theorems can be extended to this more restrictive class.
$T_2$
-threshold hypergraphs are a strict subset of threshold hypergraphs [Reference Reiterman, Rödl, Šiňajová and Tůma14] and ask whether our theorems can be extended to this more restrictive class.
Question 52.
Does Theorem
6
hold for other definitions of threshold hypergraphs, such as
![]() $T_2$
-threshold hypergraphs?
$T_2$
-threshold hypergraphs?
Acknowledgements
We thank Annie Raymond, Mohit Singh and Rekha Thomas for useful conversations. Grigoriy Blekherman was partially supported by NSF grant DMS-1901950. We thank the anonymous referee for their comments which helped to greatly improve the paper.