Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wolfovitz, Guy
2012.
A concentration result with application to subgraph count.
Random Structures & Algorithms,
Vol. 40,
Issue. 2,
p.
254.
Warnke, Lutz
2020.
On the missing log in upper tail estimates.
Journal of Combinatorial Theory, Series B,
Vol. 140,
Issue. ,
p.
98.


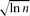 ) and λ ≤ (
) and λ ≤ (