Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-05T21:44:09.953Z Has data issue: false hasContentIssue false
  • English
  • Français

A Stability Result for Families with Fixed Diameter

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  06 March 2017

PETER FRANKL
PETER FRANKL*
Affiliation:
Alfred Rényi Institute of Mathematics, Hungarian Academy of Sciences, Reáltanoda utca 13--15, H-1053, Budapest, Hungary (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 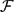$\mathcal F$ ⊂ 2[n] be a family of subsets. The diameter of 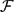$\mathcal F$ is the maximum of the size of symmetric differences among pairs of members of 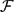$\mathcal F$. In 1966 Kleitman determined the maximum of |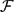$\mathcal F$| for fixed diameter. However, this important classical result lacked a characterization of the families meeting the bound. This is remedied in the present paper, where a best possible stability result is established as well.

In Section 4 we introduce a ‘parity trick’ that provides an easy way of deducing the odd case from the even case in both Kleitman's original theorem and its stability version.

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05C65: Hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 4 , July 2017 , pp. 506 - 516
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Frankl, P. A stability result for the Katona Theorem. J. Combin. Theory Ser. B, submitted.Google Scholar
[2] Frankl, P. and Tokushige, N. (1992) Some best possible inequalities concerning cross-intersecting families. J. Combin. Theory Ser. A 61 87–97.CrossRefGoogle Scholar
[3] Hilton, A. J. W. and Milner, E. C. (1967) Some intersection theorems for systems of finite sets. Quart. J. Math. Oxford 18 369–384.CrossRefGoogle Scholar
[4] Katona, G. O. H. (1964) Intersection theorems for systems of finite sets. Acta Math. Hungar. 15 329–337.Google Scholar
[5] Kleitman, D. J. (1966) On a combinatorial conjecture of Erdős. J. Combin. Theory 1 209–214.CrossRefGoogle Scholar
[6] Wang, J. and Zhang, H. (2013) Nontrivial independent sets of bipartite graphs and cross-intersecting families, J. Combin. Theory Ser. A 120 129–141.Google Scholar