Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alon, Noga
Frankl, Peter
Huang, Hao
Rödl, Vojtech
Ruciński, Andrzej
and
Sudakov, Benny
2012.
Large matchings in uniform hypergraphs and the conjectures of Erdős and Samuels.
Journal of Combinatorial Theory, Series A,
Vol. 119,
Issue. 6,
p.
1200.
Bourgain, J.
2013.
Möbius-Walsh correlation bounds and an estimate of Mauduit and Rivat.
Journal d'Analyse Mathématique,
Vol. 119,
Issue. 1,
p.
147.
Frankl, Peter
2013.
Improved bounds for Erdősʼ Matching Conjecture.
Journal of Combinatorial Theory, Series A,
Vol. 120,
Issue. 5,
p.
1068.
Kao, Yi-Hsuan
Dimakis, Alexandros G.
Leong, Derek
and
Ho, Tracey
2013.
Distributed storage allocations and a hypergraph conjecture of Erdős.
p.
902.
Bushaw, Neal
and
Kettle, Nathan
2014.
Turán Numbers for Forests of Paths in Hypergraphs.
SIAM Journal on Discrete Mathematics,
Vol. 28,
Issue. 2,
p.
711.
Füredi, Zoltán
and
Jiang, Tao
2014.
Hypergraph Turán numbers of linear cycles.
Journal of Combinatorial Theory, Series A,
Vol. 123,
Issue. 1,
p.
252.
Łuczak, Tomasz
and
Mieczkowska, Katarzyna
2014.
On Erdős' extremal problem on matchings in hypergraphs.
Journal of Combinatorial Theory, Series A,
Vol. 124,
Issue. ,
p.
178.
Füredi, Zoltán
2014.
Linear trees in uniform hypergraphs.
European Journal of Combinatorics,
Vol. 35,
Issue. ,
p.
264.
Do, Loc
Lauw, Hady W.
and
Wang, Ke
2015.
Mining revenue-maximizing bundling configuration.
Proceedings of the VLDB Endowment,
Vol. 8,
Issue. 5,
p.
593.
Zhao, Yi
2016.
Recent Trends in Combinatorics.
Vol. 159,
Issue. ,
p.
145.
Frankl, Peter
and
Tokushige, Norihide
2016.
Invitation to intersection problems for finite sets.
Journal of Combinatorial Theory, Series A,
Vol. 144,
Issue. ,
p.
157.
Araujo-Pardo, Gabriela
Díaz-Patiño, Juan Carlos
Montejano, Luis
and
Oliveros, Deborah
2016.
The (p,q)-extremal problem and the fractional chromatic number of Kneser hypergraphs.
Discrete Mathematics,
Vol. 339,
Issue. 11,
p.
2819.
Han, Jie
2016.
Perfect Matchings in Hypergraphs and the Erdös Matching Conjecture.
SIAM Journal on Discrete Mathematics,
Vol. 30,
Issue. 3,
p.
1351.
Mubayi, Dhruv
and
Verstraëte, Jacques
2016.
Recent Trends in Combinatorics.
Vol. 159,
Issue. ,
p.
117.
Das, Shagnik
Gan, Wenying
and
Sudakov, Benny
2016.
The minimum number of disjoint pairs in set systems and related problems.
Combinatorica,
Vol. 36,
Issue. 6,
p.
623.
Meagher, Karen
and
Purdy, Alison
2016.
Intersection theorems for multisets.
European Journal of Combinatorics,
Vol. 52,
Issue. ,
p.
120.
Frankl, Peter
and
Kupavskii, Andrey
2017.
Families with no s pairwise disjoint sets.
Journal of the London Mathematical Society,
Vol. 95,
Issue. 3,
p.
875.
Jiang, Tao
Miller, Zevi
and
Yager, Derrek
2017.
On the bandwidth of the Kneser graph.
Discrete Applied Mathematics,
Vol. 227,
Issue. ,
p.
84.
Huang, Hao
and
Zhao, Yi
2017.
Degree versions of the Erdős–Ko–Rado theorem and Erdős hypergraph matching conjecture.
Journal of Combinatorial Theory, Series A,
Vol. 150,
Issue. ,
p.
233.
Frankl, Peter
2017.
On the maximum number of edges in a hypergraph with given matching number.
Discrete Applied Mathematics,
Vol. 216,
Issue. ,
p.
562.


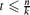 , every
, every 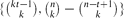 edges. Although this appears to be a basic instance of the hypergraph Turán problem (with a
edges. Although this appears to be a basic instance of the hypergraph Turán problem (with a 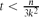 . This improves upon the best previously known range
. This improves upon the best previously known range 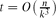 , which dates back to the 1970s.
, which dates back to the 1970s.