Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T00:18:30.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp bounds for decomposing graphs into edges and triangles

Part of: Graph theory

Published online by Cambridge University Press:  12 October 2020

Adam Blumenthal ,
Bernard Lidický ,
Yanitsa Pehova ,
Florian Pfender ,
Oleg Pikhurko  and
Jan Volec
Adam Blumenthal
Affiliation:
Department of Mathematics and Computer Science, Westminster College, New Wilmington, PA, USA
Bernard Lidický*
Affiliation:
Department of Mathematics, Iowa State University, Ames, IA 50011, USA
Yanitsa Pehova
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK
Florian Pfender
Affiliation:
Department of Mathematical and Statistical Sciences, University of Colorado Denver, CO 80217, USA
Oleg Pikhurko
Affiliation:
Mathematics Institute and DIMAP, University of Warwick, Coventry CV4 7AL, UK
Jan Volec
Affiliation:
Department of Mathematics, Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague, Trojanova 13, 120 00 Prague, Czech Republic
*
*Corresponding author. Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a real constant α, let 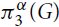$\pi _3^\alpha (G)$ be the minimum of twice the number of K2’s plus α times the number of K3’s over all edge decompositions of G into copies of K2 and K3, where Kr denotes the complete graph on r vertices. Let 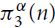$\pi _3^\alpha (n)$ be the maximum of $\pi _3^\alpha (G)$ over all graphs G with n vertices.

The extremal function 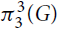$\pi _3^3(n)$ was first studied by Győri and Tuza (Studia Sci. Math. Hungar.22 (1987) 315–320). In recent progress on this problem, Král’, Lidický, Martins and Pehova (Combin. Probab. Comput.28 (2019) 465–472) proved via flag algebras that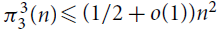$\pi _3^3(n) \le (1/2 + o(1)){n^2}$. We extend their result by determining the exact value of 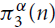$\pi _3^\alpha (n)$ and the set of extremal graphs for all α and sufficiently large n. In particular, we show for α = 3 that Kn and the complete bipartite graph 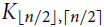${K_{\lfloor n/2 \rfloor,\lceil n/2 \rceil }}$ are the only possible extremal examples for large n.

MSC classification

Primary: 05C70: Factorization, matching, partitioning, covering and packing
Secondary: 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 2 , March 2021 , pp. 271 - 287
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) (2020)

Footnotes

†

Research supported in part by NSF grants DMS-1600390 and DMS-1855653.

‡

Supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 648509). This publication reflects only its authors’ view; the European Research Council Executive Agency is not responsible for any use that may be made of the information it contains.

§

Research supported in part by NSF grants DMS-1600483 and DMS-1855622.

Supported by ERC grant 306493 and EPSRC grant EP/K012045/1 and by Leverhulme research project grant RPG-2018-424.

ǁ

Previous affiliation: Faculty of Informatics, Masaryk University, Botanická 68A, 602 00 Brno, Czech Republic. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement 800607. This publication reflects only its authors’ view; the European Research Council Executive Agency is not responsible for any use that may be made of the information it contains.

References

Alon, N.,Fischer, E.,Krivelevich, M. andSzegedy, M. (2000) Efficient testing of large graphs. Combinatorica 20 451–476.CrossRefGoogle Scholar
Barber, B.,Kühn, D.,Lo, A. andOsthus, D. (2016) Edge-decompositions of graphs with high minimum degree. Adv. Math. 288 337–385.Google Scholar
Bollobás, B. (1998) Modern Graph Theory. Springer.CrossRefGoogle Scholar
Chung, F. R. K. (1981) On the decomposition of graphs. SIAM J. Algebraic Discrete Methods 2 1–12.CrossRefGoogle Scholar
Delcourt, M. andPostle, L. (2019) Progress towards Nash-Williams’ conjecture on triangle decompositions. arXiv:1909.00514Google Scholar
Dross, F. (2016) Fractional triangle decompositions in graphs with large minimum degree. SIAM J. Discrete Math. 30 36–42.Google Scholar
Dukes, P. andHorsley, D. (2020) On the minimum degree required for a triangle decomposition. SIAM J. Discrete Math. 34 597–610.Google Scholar
Erdős, P. (1967) Some recent results on extremal problems in graph theory: results. In Theory of Graphs (Internat. Sympos., Rome, 1966), pp. 117–123 (English), pp. 124–130 (French). Gordon & Breach.Google Scholar
Erdős, P. (1971) Some unsolved problems in graph theory and combinatorial analysis. In Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), pp. 97–109. Academic Press.Google Scholar
Erdős, P.,Goodman, A.W. and Pósa, L. (1966) The representation of a graph by set intersections. Canad. J. Math. 18 106–112.Google Scholar
Győri, E. (1988) On the number of edge-disjoint triangles in graphs of given size. In Combinatorics (Eger, 1987), Vol. 52 of Colloquia Mathematica Societatis János Bolyai, pp. 267–276. North-Holland.Google Scholar
Győri, E. (1991) On the number of edge disjoint cliques in graphs of given size. Combinatorica 11 231–243.CrossRefGoogle Scholar
Győri, E. (1992) Edge disjoint cliques in graphs. In Sets, Graphs and Numbers (Budapest, 1991), Vol. 60 of Colloquia Mathematica Societatis János Bolyai, pp. 357–363. North-Holland.Google Scholar
Győri, E. andKeszegh, B. (2017) On the number of edge-disjoint triangles in K 4-free graphs. Combinatorica 37 1113–1124.CrossRefGoogle Scholar
Győri, E. andKostochka, A. V. (1979) On a problem of G. O. H. Katona and T. Tarján. Acta Math. Acad. Sci. Hungar. 34 321–327.Google Scholar
Győri, E. andTuza, Z. (1987) Decompositions of graphs into complete subgraphs of given order. Studia Sci. Math. Hungar. 22 315–320.Google Scholar
Haxell, P.E. and Rödl, V. (2001) Integer and fractional packings in dense graphs. Combinatorica 21 13–38.CrossRefGoogle Scholar
Kahn, J. (1981) Proof of a conjecture of Katona and Tarján. Period. Math. Hungar. 12 81–82.Google Scholar
Král’, D.,Lidický, B.,Martins, T.L. and Pehova, Y. (2019) Decomposing graphs into edges and triangles. Combin. Probab. Comput. 28 465–472.Google Scholar
Liu, H.,Pikhurko, O. andStaden, K. (2020) The exact minimum number of triangles in graphs of given order and size. Forum Math. Pi 8 e8.CrossRefGoogle Scholar
Nash-Williams, C. (1970) An unsolved problem concerning decomposition of graphs into triangles. In Combinatorial Theory and Its Applications III, pp. 1179–1183. North-Holland.Google Scholar
Pikhurko, O. andRazborov, A. (2017) Asymptotic structure of graphs with the minimum number of triangles. Combin. Probab. Comput. 26 138–160.Google Scholar
Pyber, L. (1992) Covering the edges of a graph by …. In Sets, Graphs and Numbers (Budapest, 1991), Vol. 60 of Colloquia Mathematica Societatis János Bolyai, pp. 583–610. North-Holland.Google Scholar
Razborov, A. (2007) Flag algebras. J. Symb. Logic 72 1239–1282.Google Scholar
Razborov, A. (2008) On the minimal density of triangles in graphs. Combin. Probab. Comput. 17 603–618.Google Scholar
Simonovits, M. (1968) A method for solving extremal problems in graph theory, stability problems. In Theory of Graphs (Proc. Colloq., Tihany, 1966), pp. 279–319. Academic Press.Google Scholar
Tuza, Z. (2001) Unsolved combinatorial problems, Part I. BRICS Lecture Series LS-01-1.Google Scholar
Yuster, R. (2005) Integer and fractional packing of families of graphs. Random Struct. Algorithms 26 110–118.Google Scholar