Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T21:44:09.524Z Has data issue: false hasContentIssue false
  • English
  • Français

Saturated Subgraphs of the Hypercube

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  19 September 2016

J. ROBERT JOHNSON  and
TREVOR PINTO
J. ROBERT JOHNSON
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, London E1 4NS, UK (e-mail: [email protected])
TREVOR PINTO
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, London E1 4NS, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We say a graph is (Qn,Qm)-saturated if it is a maximal Qm-free subgraph of the n-dimensional hypercube Qn. A graph is said to be (Qn,Qm)-semi-saturated if it is a subgraph of Qn and adding any edge forms a new copy of Qm. The minimum number of edges a (Qn,Qm)-saturated graph (respectively (Qn,Qm)-semi-saturated graph) can have is denoted by sat(Qn,Qm) (respectively s-sat(Qn,Qm)). We prove that

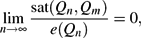$$ \begin{linenomath} \lim_{n\to\infty}\ffrac{\sat(Q_n,Q_m)}{e(Q_n)}=0, \end{linenomath}$$
for fixed m, disproving a conjecture of Santolupo that, when m=2, this limit is 1/4. Further, we show by a different method that sat(Qn, Q2)=O(2n), and that s-sat(Qn, Qm)=O(2n), for fixed m. We also prove the lower bound
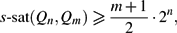$$ \begin{linenomath} \ssat(Q_n,Q_m)\geq \ffrac{m+1}{2}\cdot 2^n, \end{linenomath}$$
thus determining sat(Qn,Q2) to within a constant factor, and discuss some further questions.

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05D05: Extremal set theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 1 , January 2017 , pp. 52 - 67
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Alon, N., Krech, A. and Szabó, T. (2007) Turán's theorem in the hypercube. SIAM J. Discrete Math. 21 66–72.Google Scholar
[2] Balogh, J., Hu, P., Lidický, B. and Liu, H. (2014) Upper bounds on the size of 4- and 6-cycle-free subgraphs of the hypercube. European J. Combin. 35 75–85.CrossRefGoogle Scholar
[3] Brass, P., Harborth, H. and Nienborg, H. (1995) On the maximum number of edges in a C 4-free subgraph of Q n . J. Graph Theory 19 17–23.Google Scholar
[4] Choi, S. and Guan, P. (2008) Minimum critical squarefree subgraph of a hypercube. Congressus Numerantium 189 57–64.Google Scholar
[5] Erdős, P. (1984) Some problems in graph theory, combinatorial analysis and combinatorial number theory. In Graph Theory and Combinatorics (Bollobás, B., ed.), Academic Press, pp. 1–17.Google Scholar
[6] Erdős, P., Hajnal, A. and Moon, J. W. (1964) A problem in graph theory. Amer. Math. Monthly 71 1107–1110.Google Scholar
[7] Faudree, J. R., Faudree, R. J. and Schmitt, R. (2011) A survey of minimum saturated graphs. Electron. J. Combin. 18.Google Scholar
[8] Katona, G. O. H. and Tarján, T. G. (1983) Extremal problems with excluded subgraphs in the n-cube. In Graph Theory: Łagów, Poland, Vol. 1018 of Lecture Notes in Mathematics, Springer, pp. 84–93.Google Scholar
[9] van Lint, J. H. (1999) Introduction to Coding Theory, Springer.Google Scholar
[10] Morrison, N., Noel, J. A. and Scott, A. (2014) On saturated k-Sperner systems. Electron. J. Combin. 21, Paper #P3.22.CrossRefGoogle Scholar
[11] Pikhurko, O. (2004) Results and open problems on minimum saturated hypergraphs. Ars Combinatorica 72 435–451.Google Scholar