Hostname: page-component-55f67697df-xq6d9 Total loading time: 0 Render date: 2025-05-08T20:16:36.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Sampling from the random cluster model on random regular graphs at all temperatures via Glauber dynamics

Part of: Theory of computing Markov processes

Published online by Cambridge University Press:  09 December 2024

Andreas Galanis Open the ORCID record for Andreas Galanis [Opens in a new window] ,
Leslie Ann Goldberg Open the ORCID record for Leslie Ann Goldberg [Opens in a new window]  and
Paulina Smolarova Open the ORCID record for Paulina Smolarova [Opens in a new window]
Andreas Galanis
Affiliation:
University of Oxford, Oxford, UK
Leslie Ann Goldberg
Affiliation:
University of Oxford, Oxford, UK
Paulina Smolarova*
Affiliation:
University of Oxford, Oxford, UK
*
Corresponding author: Paulina Smolarova; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the performance of Glauber dynamics for the random cluster model with real parameter 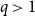$q\gt 1$ and temperature 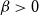$\beta \gt 0$. Recent work by Helmuth, Jenssen, and Perkins detailed the ordered/disordered transition of the model on random 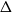$\Delta$-regular graphs for all sufficiently large 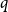$q$ and obtained an efficient sampling algorithm for all temperatures 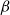$\beta$ using cluster expansion methods. Despite this major progress, the performance of natural Markov chains, including Glauber dynamics, is not yet well understood on the random regular graph, partly because of the non-local nature of the model (especially at low temperatures) and partly because of severe bottleneck phenomena that emerge in a window around the ordered/disordered transition. Nevertheless, it is widely conjectured that the bottleneck phenomena that impede mixing from worst-case starting configurations can be avoided by initialising the chain more judiciously. Our main result establishes this conjecture for all sufficiently large 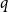$q$ (with respect to 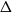$\Delta$). Specifically, we consider the mixing time of Glauber dynamics initialised from the two extreme configurations, the all-in and all-out, and obtain a pair of fast mixing bounds which cover all temperatures 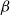$\beta$, including in particular the bottleneck window. Our result is inspired by the recent approach of Gheissari and Sinclair for the Ising model who obtained a similar flavoured mixing-time bound on the random regular graph for sufficiently low temperatures. To cover all temperatures in the RC model, we refine appropriately the structural results of Helmuth, Jenssen and Perkins about the ordered/disordered transition and show spatial mixing properties ‘within the phase’, which are then related to the evolution of the chain.

Keywords

Approximate countingGlauber dynamicsrandom cluster modelapproximate samplingrandom regular graphs

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 68Q87: Probability in computer science (algorithm analysis, random structures, phase transitions, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 34 , Issue 3 , May 2025 , pp. 359 - 391
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bencs, F., Borbényi, M. and Csikvári, P. (2022) Random cluster model on regular graphs. Commun. Math. Phys. 1–46.Google Scholar
Blanca, A., Chen, Z., Štefankovič, D. and Vigoda, E. (2021) The Swendsen-Wang dynamics on trees, In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques (APPROX/RANDOM 2021), vol. 207, pp. 1–15.Google Scholar
Blanca, A., Galanis, A., Goldberg, L. A., Štefankovič, D., Vigoda, E. and Yang, K. (2020) Sampling in uniqueness from the Potts and random-cluster models on random regular graphs. Siam. J. Discrete. Math. 34(1) 742–793.CrossRefGoogle Scholar
Blanca, A. and Gheissari, R. (2021) Random-cluster dynamics on random regular graphs in tree uniqueness. Commun. Math. Phys. 386(2) 1243–1287.CrossRefGoogle Scholar
Blanca, A. and Gheissari, R. (2024) On the tractability of sampling from the Potts model at low temperatures via random-cluster dynamics. Probab. Theory Relat. Fields. https://doi.org/10.1007/s00440-024-01289-xCrossRefGoogle Scholar
Borgs, C., Chayes, J., Helmuth, T., Perkins, W. and Tetali, P. (2020) Efficient sampling and counting algorithms for the Potts model on ℤ $\mathbb{Z}$ d at all temperatures. In Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing, (STOC ’20), pp. 738–751.CrossRefGoogle Scholar
Carlson, C., Davies, E., Fraiman, N., Kolla, A., Potukuchi, A. and Yap, C. (2022) Algorithms for the ferromagnetic Potts model on expanders. In 63rd Annual Symposium on Foundations of Computer Science (FOCS 2022), pp. 344–355.CrossRefGoogle Scholar
Chen, Z., Galanis, A., Goldberg, L. A., Perkins, W., Stewart, J. and Vigoda, E. (2021) Fast algorithms at low temperatures via markov chains†. Random Struct. Algor. 58(2) 294–321.CrossRefGoogle Scholar
Chen, Zongchen, Galanis, Andreas, Štefankovič, Daniel and Vigoda, Eric (2022) Sampling colorings and independent sets of random regular bipartite graphs in the non-uniqueness region. In Proceedings of the 2022 Annual ACM-SIAM Symposium on Discrete Algorithms, (SODA ’22), pp. 2198–2207.CrossRefGoogle Scholar
Coja-Oghlan, A., Galanis, A., Goldberg, L. A., Ravelomanana, J. B., Štefankovič, D. and Vigoda, E. (2023) Metastability of the Potts ferromagnet on random regular graphs. Commun. Math. Phys. 401 185–225.CrossRefGoogle Scholar
Coulson, M., Davies, E., Kolla, A., Patel, V. and Regts, G. (2020) Statistical physics approaches to unique games. In 35th Computational Complexity Conference, (CCC 2020), volume 169 of LIPIcs, 1–27.Google Scholar
Efthymiou, C. (2022) On sampling symmetric Gibbs distributions on sparse random graphs and hypergraphs, 49th International Colloquium on Automata, Languages, and Programming (ICALP 2022), pp. 1–16.Google Scholar
Feng, W., Guo, H. and Wang, J. (2022) Sampling from the ferromagnetic Ising model with external fields. CoRR, abs/2205.01985, 2022. arXiv:2205.01985 Google Scholar
Galanis, A., Štefankovic, D., Vigoda, E. and Yang, L. (2016) Ferromagnetic Potts model: Refined #bis-hardness and related results. Siam. J. Comput. 45(6) 2004–2065.CrossRefGoogle Scholar
Gheissari, R. and Sinclair, A. (2022) Low-temperature Ising dynamics with random initializations. In 54th Annual ACM SIGACT Symposium on Theory of Computing, (STOC ’22), 1445–1458.CrossRefGoogle Scholar
Gheissari, R. and Sinclair, A. (2023) Spatial mixing and the random-cluster dynamics on lattices. In Proceedings of the 2023 Annual ACM-SIAM Symposium on Discrete Algorithms, (SODA ’23), 4606–4621.CrossRefGoogle Scholar
Goldberg, L. A. and Jerrum, M. (2012) Approximating the partition function of the ferromagnetic Potts model. J. ACM 59(5) 1–31.CrossRefGoogle Scholar
Grimmett, G. (2006) The random-cluster model. Springer, 333 CrossRefGoogle Scholar
Guo, H. and Jerrum, M. (2017) Random cluster dynamics for the Ising model is rapidly mixing. In Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms. (SODA 2017), pp. 1818–1827.CrossRefGoogle Scholar
Häggström, O. (1996) The random-cluster model on a homogeneous tree. Probab. Theory Rel. 104 231–253.CrossRefGoogle Scholar
Helmuth, T., Jenssen, M. and Perkins, W. (2023) Finite-size scaling, phase coexistence, and algorithms for the random cluster model on random graphs. Annales de l’Institut Henri Poincare (B) Probabilites et statistiques 59(2) 817–848.Google Scholar
Helmuth, T., Perkins, W. and Regts, G. (2019) Algorithmic Pirogov-Sinai theory. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, (STOC ’19), pp. 1009–1020.CrossRefGoogle Scholar
Jerrum, M. (2003) Counting, sampling and integrating: algorithms and complexity. Basel: Springer Basel AG.CrossRefGoogle Scholar
Jonasson, J. (1999) The random cluster model on a general graph and a phase transition characterization of nonamenability. Stoch. Proc. Appl. 79(2) 335–354.CrossRefGoogle Scholar
Mossel, E. and Sly, A. (2013) Exact thresholds for Ising Gibbs samplers on general graphs. Ann. Probab. 41(1) 294–328.CrossRefGoogle Scholar
Peres, Y. and Winkler, P. (2013) Can extra updates delay mixing? Commun. Math. Phys. 323(3) 1007–1016.CrossRefGoogle Scholar
Trevisan, L. (2016) Lecture notes on graph partitioning, expanders and spectral methods. URL: https://lucatrevisan.github.io/books/expanders-2016.pdf.Google Scholar