Published online by Cambridge University Press: 22 September 2015
In my recent paper [1] there is a mistake in the proof of Corollary 3. The first line of the displayed equation in that proof asserts that
However, since the paper uses complex-valued representations, the integrand on the right here may not retain the absolute value of that on the left. Without this equality, the proof of Corollary 3 can no longer be reduced to an application of Lemma 2. However, it can be proved directly from Schur Orthogonality along very similar lines to the proof of Lemma 2.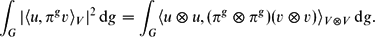 \[\int_G|\langle u,\pi^g v\rangle_V|^2\,\rm{d} g = \int_G\langle u\otimes u,(\pi^g\otimes \pi^g)(v\otimes v)\rangle_{V\otimes V}\, \rm{d} g.\]
\[\int_G|\langle u,\pi^g v\rangle_V|^2\,\rm{d} g = \int_G\langle u\otimes u,(\pi^g\otimes \pi^g)(v\otimes v)\rangle_{V\otimes V}\, \rm{d} g.\]