Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-11T09:03:19.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Projecting Difference Sets on the Positive Orthant

Published online by Cambridge University Press:  01 September 2008

RON HOLZMAN ,
VSEVOLOD F. LEV  and
ROM PINCHASI
RON HOLZMAN
Affiliation:
Department of Mathematics, Technion-Israel Institute of Technology, Haifa 32000, Israel (e-mail: [email protected], [email protected])
VSEVOLOD F. LEV
Affiliation:
Department of Mathematics, The University of Haifa at Oranim, Tivon 36006, Israel (e-mail: [email protected])
ROM PINCHASI
Affiliation:
Department of Mathematics, Technion-Israel Institute of Technology, Haifa 32000, Israel (e-mail: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let n ≥ 1 be an integer. Given a vector a=(a1,. . ,an)∈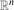, write 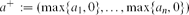(the ‘projection of a onto the positive orthant’). For a set A⊆ 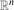put A+:={a+: a ∈ A} and A−A:={a−b: a, b ∈ A}. Improving previously known bounds, we show that |(A−A)+| ≥ |A|3/5/6 for any finite set A⊆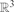, and that |(A−A)+| ≥ c|A|6/11/(log |A|)2/11 with an absolute constant c>0 for any finite set A⊆ 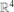such that |A| ≥ 2.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 5 , September 2008 , pp. 681 - 688
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Balasubramanian, R. and Soundararajan, K. (1996) On a conjecture of R. L. Graham. Acta Arith. 75 1–38.CrossRefGoogle Scholar
[2]Granville, A. and Roesler, F. (1999) The set of differences of a given set. Amer. Math. Monthly 106 338–344.CrossRefGoogle Scholar
[3]Marica, J. and Schönheim, J. (1969) Differences of sets and a problem of Graham. Canad. Math. Bull. 12 635–637.CrossRefGoogle Scholar