Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T13:06:49.787Z Has data issue: false hasContentIssue false
  • English
  • Français

The power of two choices for random walks

Part of: Graph theory Markov processes Discrete mathematics in relation to computer science Theory of computing

Published online by Cambridge University Press:  28 May 2021

Agelos Georgakopoulos ,
John Haslegrave ,
Thomas Sauerwald  and
John Sylvester
Agelos Georgakopoulos
Affiliation:
Mathematics Institute, University of Warwick, Coventry, UK
John Haslegrave
Affiliation:
Mathematics Institute, University of Warwick, Coventry, UK
Thomas Sauerwald*
Affiliation:
Department of Computer Science & Technology, University of Cambridge, Cambridge, UK
John Sylvester
Affiliation:
Department of Computer Science & Technology, University of Cambridge, Cambridge, UK
*
*Corresponding author. Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We apply the power-of-two-choices paradigm to a random walk on a graph: rather than moving to a uniform random neighbour at each step, a controller is allowed to choose from two independent uniform random neighbours. We prove that this allows the controller to significantly accelerate the hitting and cover times in several natural graph classes. In particular, we show that the cover time becomes linear in the number n of vertices on discrete tori and bounded degree trees, of order 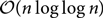$${\mathcal O}(n\log \log n)$$ on bounded degree expanders, and of order 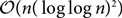$${\mathcal O}(n{(\log \log n)^2})$$ on the Erdős–Rényi random graph in a certain sparsely connected regime. We also consider the algorithmic question of computing an optimal strategy and prove a dichotomy in efficiency between computing strategies for hitting and cover times.

MSC classification

Primary: 05C81: Random walks on graphs 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 68R10: Graph theory (including graph drawing) 68Q17: Computational difficulty of problems (lower bounds, completeness, difficulty of approximation, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 73 - 100
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Footnotes

A preliminary version of this paper appeared at The 11th Innovations in Theoretical Computer Science Conference (ITCS 2020), volume 151 of LIPIcs, pages 76:1–76:19 [22]

References

Achlioptas, D., D’Souza, R. M. and Spencer, J. (2009) Explosive percolation in random networks. Science 323 1453–1455.CrossRefGoogle ScholarPubMed
Aldous, D. and Fill, J. A. (2002) Reversible Markov Chains and Random Walks on Graphs. Unfinished monograph, recompiled 2014.Google Scholar
Avin, C. and Krishnamachari, B. (2008) The power of choice in random walks: An empirical study. Comput. Netw. 52 44–60. (1) Performance of Wireless Networks (2) Synergy of Telecommunication and Broadcasting Networks.Google Scholar
Azar, Y., Broder, A. Z., Karlin, A. R., Linial, N. and Phillips, S. (1996) Biased random walks. Combinatorica 16 1–18.Google Scholar
Azar, Y., Broder, A. Z., Karlin, A. R. and Upfal, E. (1999) Balanced allocations. SIAM J. Comput. 29 180–200.CrossRefGoogle Scholar
Azimzadeh, P. and Forsyth, P. A. (2016) Weakly chained matrices, policy iteration, and impulse control. SIAM J. Numer. Anal. 54 1341–1364.CrossRefGoogle Scholar
Beeler, K. E., Berenhaut, K. S., Cooper, J. N., Hunter, M. N. and Barr, P. S. (2014) Deterministic walks with choice. Discrete Appl. Math. 162 100–107.CrossRefGoogle Scholar
Berenbrink, P., Cooper, C. and Friedetzky, T. (2015) Random walks which prefer unvisited edges: Exploring high girth even degree expanders in linear time. Random Struct. Algor. 46 36–54.CrossRefGoogle Scholar
Berenbrink, P., Czumaj, A., Steger, A. and Vöcking, B. (2000) Balanced allocations: The heavily loaded case. In Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing, ACM, pp. 745–754.CrossRefGoogle Scholar
Bohman, T. and Frieze, A. (2002) Addendum to ‘Avoiding a giant component’ [Random Struct. Algor. 19 75–85, 2001]. Random Struct. Algor. 20 126–130.Google Scholar
Bohman, T. and Kravitz, D. (2006) Creating a giant component. Combin. Probab. Comput. 15 489–511.CrossRefGoogle Scholar
Bollobás, B. (2001) Random Graphs, 2nd edition, vol. 73 of Cambridge Studies in Advanced Mathematics. Cambridge University Press.Google Scholar
Chandra, A. K., Raghavan, P., Ruzzo, W. L., Smolensky, R. and Tiwari, P. (1996/1997) The electrical resistance of a graph captures its commute and cover times. Comput. Complexity 6 312–340.CrossRefGoogle Scholar
Chung, F. R. K. and Lu, L. (2006) Survey: Concentration inequalities and martingale inequalities: A survey. Internet Math. 3 79–127.CrossRefGoogle Scholar
Coja-Oghlan, A. (2007) On the Laplacian eigenvalues of G n,p. Combin. Probab. Comput., 16 923–946.Google Scholar
Cooper, C. and Frieze, A. (2007) The cover time of sparse random graphs. Random Struct. Algor. 30(1–2) 1–16.CrossRefGoogle Scholar
Cooper, C., Frieze, A. M. and Johansson, T. (2018) The cover time of a biased random walk on a random cubic graph. In 29th International Conference on Probabilistic, Combinatorial and Asymptotic Methods for the Analysis of Algorithms, AofA 2018, June 25–29, 2018, Uppsala, Sweden, Vol. 110 of LIPIcs (J. A. Fill and M. D. Ward, eds), Schloss Dagstuhl - Leibniz-Zentrum für Informatik, pp. 16:1–16:12.Google Scholar
Cooper, C., Ilcinkas, D., Klasing, R. and Kosowski, A. (2009) Derandomizing random walks in undirected graphs using locally fair exploration strategies. In Automata, Languages and Programming (Albers, S., Marchetti-Spaccamela, A., Matias, Y., Nikoletseas, S. and Thomas, W., eds), Springer Berlin Heidelberg, pp. 411–422.CrossRefGoogle Scholar
Derman, C. (1970) Finite State Markovian Decision Processes. Academic Press, Inc.Google Scholar
Ding, J., Lee, J. R. and Peres, Y. (2012) Cover times, blanket times, and majorizing measures. Ann. Math. (2) 175 1409–1471.CrossRefGoogle Scholar
Garey, M. R., Johnson, D. S. and Stockmeyer, L. (1976) Some simplified NP-complete graph problems. Theoret. Comput. Sci. 1 237–267.CrossRefGoogle Scholar
Georgakopoulos, A., Haslegrave, J., Sauerwald, T. and Sylvester, J. (2020) Choice and bias in random walks. In 11th Innovations in Theoretical Computer Science Conference, ITCS 2020, January 12–14, 2020, Seattle, Washington, USA, Vol. 151 of LIPIcs (T. Vidick, ed), Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, pp. 76:1–76:19.Google Scholar
Grötschel, M., Lovász, L. and Schrijver, A. (1993) Geometric Algorithms and Combinatorial Optimization, 2nd edition, Vol. 2 of Algorithms and Combinatorics. Springer-Verlag.CrossRefGoogle Scholar
Haslegrave, J. and Jordan, J. (2016) Preferential attachment with choice. Random Struct. Algor. 48 751–766.CrossRefGoogle Scholar
Haslegrave, J., Sauerwald, T. and Sylvester, J. (2020) Time Dependent Biased Random Walks. Preprint, arXiv:2006.02475.Google Scholar
Horn, R. A. and Johnson, C. R. (2013) Matrix Analysis. 2nd edition, Cambridge University Press.Google Scholar
Karmarkar, N. (1984) A new polynomial-time algorithm for linear programming. Combinatorica 4 373–395.CrossRefGoogle Scholar
Levin, D. A., Peres, Y. and Wilmer, E. L. (2009) Markov Chains and Mixing Times. American Mathematical Society. With a chapter by James G. Propp and David B. Wilson.CrossRefGoogle Scholar
Lyons, R. and Peres, Y. (2016) Probability on Trees and Networks, Vol. 42 of Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press.CrossRefGoogle Scholar
Malyshkin, Y. and Paquette, E. (2015) The power of choice over preferential attachment. ALEA Lat. Am. J. Probab. Math. Stat. 12 903–915.Google Scholar
Mitzenmacher, M. (2001) The power of two choices in randomized load balancing. IEEE Trans. Parallel Distrib. Syst. 12 1094–1104.CrossRefGoogle Scholar
Orenshtein, T. and Shinkar, I. (2014) Greedy random walk. Combin. Probab. Comput., 23 269–289.CrossRefGoogle Scholar
Riordan, O. and Warnke, L. (2012) Achlioptas process phase transitions are continuous. Ann. Appl. Probab. 22 1450–1464.CrossRefGoogle Scholar
Spencer, J. and Wormald, N. (2007) Birth control for giants. Combinatorica 27 587–628.CrossRefGoogle Scholar