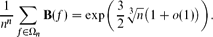Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T23:42:59.051Z Has data issue: false hasContentIssue false
  • English
  • Français

Period Lengths for Iterated Functions

Published online by Cambridge University Press:  16 September 2010

ERIC SCHMUTZ
ERIC SCHMUTZ*
Affiliation:
Mathematics Department, Drexel University, 3401 Market Street, Philadelphia, Pa., 19104, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Ωn be the nn-element set consisting of all functions that have {1, 2, 3, . . ., n} as both domain and codomain. Let T(f) be the order of f, i.e., the period of the sequence f, f(2), f(3), f(4) . . . of compositional iterates. A closely related number, B(f) = the product of the lengths of the cycles of f, has previously been used as an approximation for T. This paper proves that the average values of these two quantities are quite different. The expected value of T is 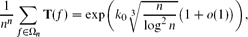where k0 is a complicated but explicitly defined constant that is approximately 3.36. The expected value of B is much larger:

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 2 , March 2011 , pp. 289 - 298
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abramowitz, M. and Stegun, I. A. (1964) Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, Dover.Google Scholar
[2]Arratia, R. and Tavaré, S. (1992) Limit theorems for combinatorial structures via discrete process approximations. Random Struct. Alg. 3 321–345.CrossRefGoogle Scholar
[3]Barbour, A. D. and Tavaré, S. (1994) A rate for the Erdös–Turán law. Combin. Probab. Comput. 3 167–176.CrossRefGoogle Scholar
[4]Deńes, J. (1970) Some combinatorial properties of transformations and their connections with the theory of graphs. J. Combin. Theory 9 108–116.CrossRefGoogle Scholar
[5]Erdös, P. and Turán, P. (1967) On some problems of a statistical group theory III. Acta Math. Acad. Sci. Hungar. 18 309–320.CrossRefGoogle Scholar
[6]Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics, Cambridge University Press.CrossRefGoogle Scholar
[7]Goh, W. and Schmutz, E. (1991) The expected order of a random permutation. Bull. London Math. Soc. 23 34–42.CrossRefGoogle Scholar
[8]Hansen, J. C. (1989) A functional central limit theorem for random mappings. Ann. Probab. 17 317–332.CrossRefGoogle Scholar
[9]Harris, B. (1960) Probability distributions related to random mappings. Ann. Math. Statist. 31 1045–1062.CrossRefGoogle Scholar
[10]Harris, B. (1973) The asymptotic distribution of the order of elements in symmetric semigroups. J. Combin. Theory Ser. A 15 66–74.CrossRefGoogle Scholar
[11]Landau, E. (1953) Handbuch der Lehre von der Verteilung der Primzahlen, Vol. 2, Chelsea Publishing, pp. 222–229.Google Scholar
[12]Massias, J. P., Nicolas, J. L. and Robin, G. (1988) Évaluation asymptotique de l'ordre maximum d'un élément du groupe symétrique. Acta Arith. 50 221–242.CrossRefGoogle Scholar
[13]Odlyzko, A. M. (1992) Explicit Tauberian estimates for functions with positive coefficients. J. Comput. Appl. Math. 41 187–197.CrossRefGoogle Scholar
[14]Schmutz, E. (1988) Statistical group theory. Doctoral Dissertation, Mathematics Department, University of Pennsylvania, Philadelphia, USA.Google Scholar
[15]Sloane, N. J. A.The On-Line Encyclopedia of Integer Sequences, published electronically at: www.research.att.com/~njas/sequences/, sequence A000792, accessed March 2010.Google Scholar
[16]Stong, R. (1998) The average order of a permutation. Electron. J. Combin. 5 #41.CrossRefGoogle Scholar
[17]Szalay, M. (1980) On the maximal order in Sn and S*n. Acta Arith. 37 321–331.CrossRefGoogle Scholar