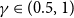1. Introduction
Clustering is one of the central problems in network analysis and machine learning [Reference Newman, Watts and Strogatz59, Reference Ng, Jordan and Weiss60, Reference Shi and Malik65]. Many clustering algorithms make use of graph models, which represent pairwise relationships among data. A well-studied probabilistic model is the stochastic block model (SBM), which was first introduced in [Reference Holland, Laskey and Leinhardt39] as a random graph model that generates community structure with given ground truth for clusters so that one can study algorithm accuracy. The past decades have brought many notable results in the analysis of different algorithms and fundamental limits for community detection in SBMs in different settings [Reference Coja-Oghlan20, Reference Guédon and Vershynin37, Reference Montanari and Sen54, Reference Van70]. A major breakthrough was the proof of phase transition behaviours of community detection algorithms in various connectivity regimes [Reference Abbe, Bandeira and Hall2, Reference Abbe and Sandon5, Reference Bordenave, Lelarge and Massoulié12, Reference Massoulié52, Reference Mossel, Neeman and Sly55, Reference Mossel, Neeman and Sly57, Reference Mossel, Neeman and Sly58]. See the survey [Reference Abbe1] for more references.
Hypergraphs can represent more complex relationships among data [Reference Battiston, Cencetti, Iacopini, Latora, Lucas, Patania, Young and Petri10, Reference Benson, Gleich and Leskovec11], including recommendation systems [Reference Bu, Tan, Chen, Wang, Wu, Zhang and He13, Reference Li and Li49], computer vision [Reference Govindu34, Reference Wen, Du, Li, Bian and Lyu73], and biological networks [Reference Michoel and Nachtergaele53, Reference Tian, Hwang and Kuang68], and they have been shown empirically to have advantages over graphs [Reference Zhou, Huang and Schölkopf79]. Besides community detection problems, sparse hypergraphs and their spectral theory have also found applications in data science [Reference Harris and Zhu38, Reference Jain and Oh40, Reference Zhou and Zhu80], combinatorics [Reference Dumitriu and Zhu26, Reference Friedman and Wigderson29, Reference Soma and Yoshida66], and statistical physics [Reference Cáceres, Misobuchi and Pimentel14, Reference Sen64].
With the motivation from a broad set of applications, many efforts have been made in recent years to study community detection on random hypergraphs. The hypergraph stochastic block model (HSBM), as a generalisation of graph SBM, was first introduced and studied in [Reference Ghoshdastidar and Dukkipati31]. In this model, we observe a random uniform hypergraph where each hyperedge appears independently with some given probability depending on the community structure of the vertices in the hyperedge.
Succinctly put, the HSBM recovery problem is to find the ground truth clusters either approximately or exactly, given a sample hypergraph and estimates of model parameters. We may ask the following questions about the quality of the solutions (see [Reference Abbe1] for further details in the graph case).
1. Exact recovery (strong consistency): With high probability, find all clusters exactly (up to permutation).
2. Almost exact recovery (weak consistency): With high probability, find a partition of the vertex set such that at most
 $o(n)$ vertices are misclassified.
$o(n)$ vertices are misclassified.3. Partial recovery: Given a fixed
 $\gamma \in (0.5,1)$, with high probability, find a partition of the vertex set such that at least a fraction
$\gamma \in (0.5,1)$, with high probability, find a partition of the vertex set such that at least a fraction  $\gamma$ of the vertices are clustered correctly.
$\gamma$ of the vertices are clustered correctly.4. Weak recovery (detection): With high probability, find a partition correlated with the true partition.
For exact recovery of uniform HSBMs, it was shown that the phase transition occurs in the regime of logarithmic expected degrees in [16, Reference Eli Chien, Lin and Wang17, Reference Lin, Eli Chien and Wang50]. The thresholds are given for binary [Reference Gaudio and Joshi30, Reference Kim, Bandeira and Goemans43] and multiple [Reference Zhang and Tan77] community cases, by generalising the techniques in [Reference Abbe, Bandeira and Hall2–Reference Abbe and Sandon4]. After our work appeared on arXiv, thresholds for exact recovery on non-uniform HSBMs were given by [Reference Dumitriu and Wang25, Reference Wang71]. Strong consistency on the degree-corrected non-uniform HSBM was studied in [Reference Deng, Xu and Ying24]. Spectral methods were considered in [6, 16, Reference Cole and Zhu21, Reference Gaudio and Joshi30, Reference Yuan, Zhao and Zhao75, Reference Zhang and Tan77], while semidefinite programming methods were analysed in [Reference Alaluusua, Avrachenkov, Vinay Kumar and Leskelä8, Reference Kim, Bandeira and Goemans43, Reference Lee, Kim and Chung46]. Weak consistency for HSBMs was studied in [16, Reference Eli Chien, Lin and Wang17, Reference Ghoshdastidar and Dukkipati32, Reference Ghoshdastidar and Dukkipati33, Reference Ke, Shi and Xia42].
For detection of the HSBM, the authors of [Reference Angelini, Caltagirone, Krzakala and Zdeborová9] proposed a conjecture that the phase transition occurs in the regime of constant expected degrees. The positive part of the conjecture for the binary and multi-block case was solved in [Reference Pal and Zhu62] and [Reference Stephan and Zhu67], respectively. Their algorithms can output a partition better than a random guess when above the Kesten-Stigum threshold, but can not guarantee the correctness ratio. [Reference Gu and Pandey35, Reference Gu and Polyanskiy36] proved that detection is impossible and the Kesten-Stigum threshold is tight for ![]() $m$-uniform hypergraphs with binary communities when
$m$-uniform hypergraphs with binary communities when ![]() $m =3, 4$, while KS threshold is not tight when
$m =3, 4$, while KS threshold is not tight when ![]() $m\geq 7$, and some regimes remain unknown.
$m\geq 7$, and some regimes remain unknown.
1.1. Non-uniform hypergraph stochastic block model
The non-uniform HSBM was first studied in [Reference Ghoshdastidar and Dukkipati32], which removed the uniform hypergraph assumption in previous works, and it is a more realistic model to study higher-order interaction on networks [Reference Lung, Gaskó and Suciu51, Reference Wen, Du, Li, Bian and Lyu73]. It can be seen as a superposition of several uniform HSBMs with different model parameters. We first define the uniform HSBM in our setting and extend it to non-uniform hypergraphs.
Definition 1.1 (Uniform HSBM). Let ![]() $V=\{V_1,\dots V_k\}$ be a partition of the set
$V=\{V_1,\dots V_k\}$ be a partition of the set ![]() $[n]$ into
$[n]$ into ![]() $k$ blocks of size
$k$ blocks of size ![]() $\frac{n}{k}$ (assuming
$\frac{n}{k}$ (assuming ![]() $n$ is divisible by
$n$ is divisible by ![]() $k$). Let
$k$). Let ![]() $m \in \mathbb{N}$ be some fixed integer. For any set of
$m \in \mathbb{N}$ be some fixed integer. For any set of ![]() $m$ distinct vertices
$m$ distinct vertices ![]() $i_1,\dots i_m$, a hyperedge
$i_1,\dots i_m$, a hyperedge ![]() $\{i_1,\dots i_m\}$ is generated with probability
$\{i_1,\dots i_m\}$ is generated with probability ![]() $a_m/\binom{n}{m-1}$ if vertices
$a_m/\binom{n}{m-1}$ if vertices ![]() $i_1,\dots i_m$ are in the same block; otherwise with probability
$i_1,\dots i_m$ are in the same block; otherwise with probability ![]() $b_m/ \binom{n}{m-1}$. We denote this distribution on the set of
$b_m/ \binom{n}{m-1}$. We denote this distribution on the set of ![]() $m$-uniform hypergraphs as
$m$-uniform hypergraphs as
Definition 1.2 (Non-uniform HSBM). Let ![]() $H = (V, E)$ be a non-uniform random hypergraph, which can be considered as a collection of
$H = (V, E)$ be a non-uniform random hypergraph, which can be considered as a collection of ![]() $m$-uniform hypergraphs, i.e.,
$m$-uniform hypergraphs, i.e., ![]() $H = \bigcup _{m = 2}^{M} H_m$ with each
$H = \bigcup _{m = 2}^{M} H_m$ with each ![]() $H_m$ sampled from (1).
$H_m$ sampled from (1).
Examples of ![]() $2$-uniform and
$2$-uniform and ![]() $3$-uniform HSBM, and an example of non-uniform HSBM with
$3$-uniform HSBM, and an example of non-uniform HSBM with ![]() ${\mathcal M} = \{2, 3\}$ and
${\mathcal M} = \{2, 3\}$ and ![]() $k=3$ is displayed in Fig. 1a, b, c respectively.
$k=3$ is displayed in Fig. 1a, b, c respectively.

Figure 1. An example of non-uniform HSBM sampled from model 1.2.
1.2. Main results
To illustrate our main results, we first introduce the concepts ![]() $\gamma$-correctness and sigal-to-noise ratio to measure the accuracy of the obtained partitions.
$\gamma$-correctness and sigal-to-noise ratio to measure the accuracy of the obtained partitions.
Definition 1.3 (![]() $\gamma$-correctness). Suppose we have
$\gamma$-correctness). Suppose we have ![]() $k$ disjoint blocks
$k$ disjoint blocks ![]() $V_1,\dots, V_k$. A collection of subsets
$V_1,\dots, V_k$. A collection of subsets ![]() $\widehat{V}_1,\dots, \widehat{V}_k$ of
$\widehat{V}_1,\dots, \widehat{V}_k$ of ![]() $V$ is
$V$ is ![]() $\gamma$-correct if
$\gamma$-correct if ![]() $|V_i\cap \widehat{V}_i|\geq \gamma |V_i|$ for all
$|V_i\cap \widehat{V}_i|\geq \gamma |V_i|$ for all ![]() $i\in [k]$.
$i\in [k]$.
Definition 1.4. For model 1.2 under Assumption 1.5, we define the signal-to-noise ratio (![]() $\mathrm{SNR}$) as
$\mathrm{SNR}$) as
 \begin{align} \mathrm{SNR}_{{\mathcal M}}(k) \,:\!=\,\frac{ \left [\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )} \,. \end{align}
\begin{align} \mathrm{SNR}_{{\mathcal M}}(k) \,:\!=\,\frac{ \left [\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )} \,. \end{align}
Let ![]() ${\mathcal M}_{\max }$ denote the maximum element in the set
${\mathcal M}_{\max }$ denote the maximum element in the set ![]() $\mathcal M$. The following constant
$\mathcal M$. The following constant ![]() $C_{{\mathcal M}}(k)$ is used to characterise the accuracy of the clustering result,
$C_{{\mathcal M}}(k)$ is used to characterise the accuracy of the clustering result,
Note that a non-uniform HSBM can be seen as a collection of noisy observations for the same underlying community structure through several uniform HSBMs of different orders. A possible issue is that some uniform hypergraphs with small SNR might not be informative (if we observe an ![]() $m$-uniform hypergraph with parameters
$m$-uniform hypergraph with parameters ![]() $a_m=b_m$, including hyperedge information from it ultimately increases the noise). To improve our error rate guarantees, we start by adding a pre-processing step (Algorithm 3) for hyperedge selection according to SNR and then apply the algorithm on the sub-hypergraph with maximal SNR.
$a_m=b_m$, including hyperedge information from it ultimately increases the noise). To improve our error rate guarantees, we start by adding a pre-processing step (Algorithm 3) for hyperedge selection according to SNR and then apply the algorithm on the sub-hypergraph with maximal SNR.
We state the following assumption that will be used in our analysis of Algorithms 1 (![]() $k=2$) and 2 (
$k=2$) and 2 (![]() $k\geq 3$).
$k\geq 3$).
Assumption 1.5. For each ![]() $m\in{\mathcal M}$, assume
$m\in{\mathcal M}$, assume ![]() $a_m, b_m$ are constants independent of
$a_m, b_m$ are constants independent of ![]() $n$, and
$n$, and ![]() $a_m \geq b_m$. Let
$a_m \geq b_m$. Let ![]() ${\mathcal M}_{\max }$ denote the maximum element in the set
${\mathcal M}_{\max }$ denote the maximum element in the set ![]() $\mathcal M$. Given
$\mathcal M$. Given ![]() $\nu \in (1/k, 1)$, assume that there exists a universal constant
$\nu \in (1/k, 1)$, assume that there exists a universal constant ![]() $C$ and some
$C$ and some ![]() $\nu$-dependent constant
$\nu$-dependent constant ![]() $C_{\nu } \gt 0$, such that
$C_{\nu } \gt 0$, such that
 \begin{align} \sum _{m\in{\mathcal{M}}} (m-1)(a_m-b_m) &\geq C_{\nu } \sqrt{d}\cdot k^{{\mathcal{M}}_{\max }-1} \cdot \bigg ( 2^{3} \cdot \unicode{x1D7D9}_{\{ k = 2\}} + \sqrt{\log \Big (\frac{k}{1-\nu }\Big )} \cdot \unicode{x1D7D9}_{\{ k\geq 3\}} \bigg ) . \end{align}
\begin{align} \sum _{m\in{\mathcal{M}}} (m-1)(a_m-b_m) &\geq C_{\nu } \sqrt{d}\cdot k^{{\mathcal{M}}_{\max }-1} \cdot \bigg ( 2^{3} \cdot \unicode{x1D7D9}_{\{ k = 2\}} + \sqrt{\log \Big (\frac{k}{1-\nu }\Big )} \cdot \unicode{x1D7D9}_{\{ k\geq 3\}} \bigg ) . \end{align}
One does not have to take too large a ![]() $C$ for (4a); for example,
$C$ for (4a); for example, ![]() $C = (2^{1/{\mathcal M}_{\max }} - 1)^{-1/3}$ should suffice, but even smaller
$C = (2^{1/{\mathcal M}_{\max }} - 1)^{-1/3}$ should suffice, but even smaller ![]() $C$ may work. Both of the two inequalities above constant prevent the hypergraph from being too sparse, while (4b) also requires that the difference between in-block and across-blocks densities is large enough. The choices of
$C$ may work. Both of the two inequalities above constant prevent the hypergraph from being too sparse, while (4b) also requires that the difference between in-block and across-blocks densities is large enough. The choices of ![]() $C, C_{\nu }$ and their relationship will be discussed in Remark 5.15.
$C, C_{\nu }$ and their relationship will be discussed in Remark 5.15.
1.2.1. The 2-block case
We start with Algorithm 1, which outputs a ![]() $\gamma$-correct partition when the non-uniform HSBM
$\gamma$-correct partition when the non-uniform HSBM ![]() $H$ is sampled from model 1.2 with only
$H$ is sampled from model 1.2 with only ![]() $2$ communities. Inspired by the innovative graph algorithm in [Reference Chin, Rao and Van19], we generalise it to non-uniform hypergraphs while we provide a complete and detailed analysis at the same time.
$2$ communities. Inspired by the innovative graph algorithm in [Reference Chin, Rao and Van19], we generalise it to non-uniform hypergraphs while we provide a complete and detailed analysis at the same time.
Algorithm 1. Binary Partition

Theorem 1.6 (![]() $k=2$). Let
$k=2$). Let ![]() $\nu \in (0.5, 1)$ and
$\nu \in (0.5, 1)$ and ![]() $\rho = 2\exp ({-}C_{{\mathcal M}}(2) \cdot \mathrm{SNR}_{{\mathcal M}}(2))$ with
$\rho = 2\exp ({-}C_{{\mathcal M}}(2) \cdot \mathrm{SNR}_{{\mathcal M}}(2))$ with ![]() $\mathrm{SNR}_{{\mathcal M}}(k)$,
$\mathrm{SNR}_{{\mathcal M}}(k)$, ![]() $C_{{\mathcal M}}(k)$ defined in (2), (3), and let
$C_{{\mathcal M}}(k)$ defined in (2), (3), and let ![]() $\gamma = \max \{\nu,\, 1 - 2\rho \}$. Then under Assumption 1.5, Algorithm 1 outputs a
$\gamma = \max \{\nu,\, 1 - 2\rho \}$. Then under Assumption 1.5, Algorithm 1 outputs a ![]() $\gamma$-correct partition for sufficiently large
$\gamma$-correct partition for sufficiently large ![]() $n$ with probability at least
$n$ with probability at least ![]() $1 - O(n^{-2})$.
$1 - O(n^{-2})$.
1.2.2. The  $k$-block case
$k$-block case
For the multi-community case (![]() $k \geq 3$), another algorithm with more subroutines is developed in Algorithm 2, which outputs a
$k \geq 3$), another algorithm with more subroutines is developed in Algorithm 2, which outputs a ![]() $\gamma$-correct partition with high probability. We state the result as follows.
$\gamma$-correct partition with high probability. We state the result as follows.
Algorithm 2. General Partition

Theorem 1.7 (![]() $k\geq 3$). Let
$k\geq 3$). Let ![]() $\nu \in (1/k, 1)$ and
$\nu \in (1/k, 1)$ and ![]() $\rho = \exp ({-}C_{{\mathcal M}}(k) \cdot \mathrm{SNR}_{{\mathcal M}}(k))$ with
$\rho = \exp ({-}C_{{\mathcal M}}(k) \cdot \mathrm{SNR}_{{\mathcal M}}(k))$ with ![]() $\mathrm{SNR}_{{\mathcal M}}(k), C_{{\mathcal M}}(k)$ defined in (2), (3), and let
$\mathrm{SNR}_{{\mathcal M}}(k), C_{{\mathcal M}}(k)$ defined in (2), (3), and let ![]() $\gamma = \max \{\nu,\, 1 - k\rho \}$. Then under Assumption 1.5, Algorithm 2 outputs a
$\gamma = \max \{\nu,\, 1 - k\rho \}$. Then under Assumption 1.5, Algorithm 2 outputs a ![]() $\gamma$-correct partition for sufficiently large
$\gamma$-correct partition for sufficiently large ![]() $n$ with probability at least
$n$ with probability at least ![]() $1 - O(n^{-2})$.
$1 - O(n^{-2})$.
The time complexities of Algorithms 1 and 2 are ![]() $O(n^{3})$, with the bulk of time spent in Stage 1 by the spectral method.
$O(n^{3})$, with the bulk of time spent in Stage 1 by the spectral method.
To the best of our knowledge, Theorems 1.6 and 1.7 are the first results for partial recovery of non-uniform HSBMs. When the number of blocks is ![]() $2$, Algorithm 1 guarantees a better error rate for partial recovery as in Theorem 1.6. This happens because Algorithm 1 does not need the merging routine in Algorithm 2: if one of the communities is obtained, then the other one is also obtained via the complement.
$2$, Algorithm 1 guarantees a better error rate for partial recovery as in Theorem 1.6. This happens because Algorithm 1 does not need the merging routine in Algorithm 2: if one of the communities is obtained, then the other one is also obtained via the complement.
Remark 1.8. Taking ![]() ${\mathcal M} = \{2 \}$, Theorem 1.7 can be reduced to [Reference Chin, Rao and Van19, Lemma 9] for the graph case. The failure probability
${\mathcal M} = \{2 \}$, Theorem 1.7 can be reduced to [Reference Chin, Rao and Van19, Lemma 9] for the graph case. The failure probability ![]() $O(n^{-2})$ can be decreased to
$O(n^{-2})$ can be decreased to ![]() $O(n^{-p})$ for any
$O(n^{-p})$ for any ![]() $p\gt 0$, as long as one is willing to pay the price by increasing the constants
$p\gt 0$, as long as one is willing to pay the price by increasing the constants ![]() $C$,
$C$, ![]() $C_v$ in (4a), (4b).
$C_v$ in (4a), (4b).
Our Algorithms 1 and 2 can be summarised in 3 steps:
1. Hyperedge selection: select hyperedges of certain sizes to provide the maximal signal-to-noise ratio (SNR) for the induced sub-hypergraph.
2. Spectral partition: construct a regularised adjacency matrix and obtain an approximate partition based on singular vectors (first approximation).
3. Correction and merging: incorporate the hyperedge information from adjacency tensors to upgrade the error rate guarantee (second, better approximation).
The algorithm requires the input of model parameters ![]() $a_m,b_m$, which can be estimated by counting cycles in hypergraphs as shown in [Reference Mossel, Neeman and Sly55, Reference Yuan, Liu, Feng and Shang74]. Estimation of the number of blocks can be done by counting the outliers in the spectrum of the non-backtracking operator, e.g., as shown (for different regimes and different parameters) in [Reference Angelini, Caltagirone, Krzakala and Zdeborová9, Reference Le and Levina44, Reference Saade, Krzakala and Zdeborová63, Reference Stephan and Zhu67].
$a_m,b_m$, which can be estimated by counting cycles in hypergraphs as shown in [Reference Mossel, Neeman and Sly55, Reference Yuan, Liu, Feng and Shang74]. Estimation of the number of blocks can be done by counting the outliers in the spectrum of the non-backtracking operator, e.g., as shown (for different regimes and different parameters) in [Reference Angelini, Caltagirone, Krzakala and Zdeborová9, Reference Le and Levina44, Reference Saade, Krzakala and Zdeborová63, Reference Stephan and Zhu67].
1.2.3. Weak consistency
Throughout the proofs for Theorems 1.6 and 1.7, we make only one assumption on the growth or finiteness of ![]() $d$ and
$d$ and ![]() $\mathrm{SNR}_{{\mathcal M}}(k)$, and it happens in estimating the failure probability as noted in Remark 1.10. Consequently, the corollary below follows, which covers the case when
$\mathrm{SNR}_{{\mathcal M}}(k)$, and it happens in estimating the failure probability as noted in Remark 1.10. Consequently, the corollary below follows, which covers the case when ![]() $d$ and
$d$ and ![]() $\mathrm{SNR}_{{\mathcal M}}(k)$ grow with
$\mathrm{SNR}_{{\mathcal M}}(k)$ grow with ![]() $n$.
$n$.
Corollary 1.9 (Weak consistency). For fixed ![]() $M$ and
$M$ and ![]() $k$, if
$k$, if ![]() $\mathrm{SNR}_{{\mathcal M}}(k)$ defined in (2) goes to infinity as
$\mathrm{SNR}_{{\mathcal M}}(k)$ defined in (2) goes to infinity as ![]() $n\to \infty$ and
$n\to \infty$ and ![]() $\mathrm{SNR}_{{\mathcal M}}(k) = o(\log n)$, then with probability
$\mathrm{SNR}_{{\mathcal M}}(k) = o(\log n)$, then with probability ![]() $1- O(n^{-2})$, Algorithms 1 and 2 output a partition with only
$1- O(n^{-2})$, Algorithms 1 and 2 output a partition with only ![]() $o(n)$ misclassified vertices.
$o(n)$ misclassified vertices.
The paper [Reference Ghoshdastidar and Dukkipati32] also proves weak consistency for non-uniform HSBMs, but in a much denser regime than we do here (![]() $d = \Omega (\log ^2(n))$, instead of
$d = \Omega (\log ^2(n))$, instead of ![]() $d=\omega (1)$, as in Corollary 1.9). In fact, we now know that strong consistency should be achievable in this denser regime, as [Reference Dumitriu and Wang25] shows. When restricting to the uniform HSBM case, Corollary 1.9 achieves weak consistency under the same sparsity condition as in [Reference Ahn, Lee and Suh7].
$d=\omega (1)$, as in Corollary 1.9). In fact, we now know that strong consistency should be achievable in this denser regime, as [Reference Dumitriu and Wang25] shows. When restricting to the uniform HSBM case, Corollary 1.9 achieves weak consistency under the same sparsity condition as in [Reference Ahn, Lee and Suh7].
Remark 1.10. To be precise, Algorithms 1 and 2 work optimally in the ![]() $\mathrm{SNR}_{{\mathcal M}} = o (\log n)$ regime. When
$\mathrm{SNR}_{{\mathcal M}} = o (\log n)$ regime. When ![]() $\mathrm{SNR}_{{\mathcal M}}(k) = \Omega (\log n)$, it implies that
$\mathrm{SNR}_{{\mathcal M}}(k) = \Omega (\log n)$, it implies that ![]() $\rho = n^{-\Omega (1)}$, and one may have
$\rho = n^{-\Omega (1)}$, and one may have ![]() $e^{-n\rho } = \Omega (1)$ in (31), which may not decrease to
$e^{-n\rho } = \Omega (1)$ in (31), which may not decrease to ![]() $0$ as
$0$ as ![]() $n\to \infty$. Therefore the theoretical guarantees of Algorithms 5 and 6 may not remain valid. This, however, should not matter: in the regime when
$n\to \infty$. Therefore the theoretical guarantees of Algorithms 5 and 6 may not remain valid. This, however, should not matter: in the regime when ![]() $\mathrm{SNR}_{{\mathcal M}}(k) = \Omega (\log n)$, strong (rather than weak) consistency is expected, as per [Reference Dumitriu and Wang25]. Therefore, the regime of interest for weak consistency is
$\mathrm{SNR}_{{\mathcal M}}(k) = \Omega (\log n)$, strong (rather than weak) consistency is expected, as per [Reference Dumitriu and Wang25]. Therefore, the regime of interest for weak consistency is ![]() $\mathrm{SNR}_{{\mathcal M}} = o(\log n)$.
$\mathrm{SNR}_{{\mathcal M}} = o(\log n)$.
1.3. Comparison with existing results
Although many algorithms and theoretical results have been developed for hypergraph community detection, most of them are restricted to uniform hypergraphs, and few results are known for non-uniform ones. We will discuss the most relevant results.
In [Reference Ke, Shi and Xia42], the authors studied the degree-corrected HSBM with general connection probability parameters by using a tensor power iteration algorithm and Tucker decomposition. Their algorithm achieves weak consistency for uniform hypergraphs when the average degree is ![]() $\omega (\log ^2 n)$, which is the regime complementary to the regime we studied here. They discussed a way to generalise the algorithm to non-uniform hypergraphs, but the theoretical analysis remains open. The recent paper [Reference Zhen and Wang78] analysed non-uniform hypergraph community detection by using hypergraph embedding and optimisation algorithms and obtained weak consistency when the expected degrees are of
$\omega (\log ^2 n)$, which is the regime complementary to the regime we studied here. They discussed a way to generalise the algorithm to non-uniform hypergraphs, but the theoretical analysis remains open. The recent paper [Reference Zhen and Wang78] analysed non-uniform hypergraph community detection by using hypergraph embedding and optimisation algorithms and obtained weak consistency when the expected degrees are of ![]() $\omega (\log n)$, again a complementary regime to ours. Results on spectral norm concentration of sparse random tensors were obtained in [Reference Cooper23, Reference Jain and Oh40, Reference Lei, Chen and Lynch47, Reference Nguyen, Drineas and Tran61, Reference Zhou and Zhu80], but no provable tensor algorithm in the bounded expected degree case is known. Testing for the community structure for non-uniform hypergraphs was studied in [Reference Jin, Ke and Liang41, Reference Yuan, Liu, Feng and Shang74], which is a problem different from community detection.
$\omega (\log n)$, again a complementary regime to ours. Results on spectral norm concentration of sparse random tensors were obtained in [Reference Cooper23, Reference Jain and Oh40, Reference Lei, Chen and Lynch47, Reference Nguyen, Drineas and Tran61, Reference Zhou and Zhu80], but no provable tensor algorithm in the bounded expected degree case is known. Testing for the community structure for non-uniform hypergraphs was studied in [Reference Jin, Ke and Liang41, Reference Yuan, Liu, Feng and Shang74], which is a problem different from community detection.
In our approach, we relied on knowing the tensors for each uniform hypergraph. However, in computations, we only ran the spectral algorithm on the adjacency matrix of the entire hypergraph since the stability of tensor algorithms does not yet come with guarantees due to the lack of concentration, and for non-uniform hypergraphs, ![]() $M-1$ adjacency tensors would be needed. This approach presented the challenge that, unlike for graphs, the adjacency matrix of a random non-uniform hypergraph has dependent entries, and the concentration properties of such a random matrix were previously unknown. We overcame this issue and proved concentration bounds from scratch down to the bounded degree regime. Similar to [Reference Feige and Ofek28, Reference Le, Levina and Vershynin45], we provided here a regularisation analysis by removing rows in the adjacency matrix with large row sums (suggestive of large degree vertices) and proving a concentration result for the regularised matrix down to the bounded expected degree regime (see Theorem 3.3).
$M-1$ adjacency tensors would be needed. This approach presented the challenge that, unlike for graphs, the adjacency matrix of a random non-uniform hypergraph has dependent entries, and the concentration properties of such a random matrix were previously unknown. We overcame this issue and proved concentration bounds from scratch down to the bounded degree regime. Similar to [Reference Feige and Ofek28, Reference Le, Levina and Vershynin45], we provided here a regularisation analysis by removing rows in the adjacency matrix with large row sums (suggestive of large degree vertices) and proving a concentration result for the regularised matrix down to the bounded expected degree regime (see Theorem 3.3).
In terms of partial recovery for hypergraphs, our results are new, even in the uniform case. In [Reference Ahn, Lee and Suh7, Theorem 1], for uniform hypergraphs, the authors showed detection (not partial recovery) is possible when the average degree is ![]() $\Omega (1)$; in addition, the error rate is not exponential in the model parameters, but only polynomial. Here, we mention two more results for the graph case. In the arbitrarily slowly growing degrees regime, it was shown in [Reference Fei and Chen27, Reference Zhang and Zhou76] that the error rate in (2) is optimal up to a constant in the exponent. In the bounded expected degrees regime, the authors in [Reference Chin and Sly18, Reference Mossel, Neeman and Sly56] provided algorithms that can asymptotically recover the optimal fraction of vertices, when the signal-to-noise ratio is large enough. It’s an open problem to extend their analysis to obtain a minimax error rate for hypergraphs.
$\Omega (1)$; in addition, the error rate is not exponential in the model parameters, but only polynomial. Here, we mention two more results for the graph case. In the arbitrarily slowly growing degrees regime, it was shown in [Reference Fei and Chen27, Reference Zhang and Zhou76] that the error rate in (2) is optimal up to a constant in the exponent. In the bounded expected degrees regime, the authors in [Reference Chin and Sly18, Reference Mossel, Neeman and Sly56] provided algorithms that can asymptotically recover the optimal fraction of vertices, when the signal-to-noise ratio is large enough. It’s an open problem to extend their analysis to obtain a minimax error rate for hypergraphs.
In [Reference Ghoshdastidar and Dukkipati32], the authors considered weak consistency in a non-uniform HSBM model with a spectral algorithm based on the hypergraph Laplacian matrix, and showed that weak consistency is achievable if the expected degree is of ![]() $\Omega (\log ^2 n)$ with high probability [Reference Ghoshdastidar and Dukkipati31, Theorem 4.2]. Their algorithm can’t be applied to sparse regimes straightforwardly since the normalised Laplacian is not well-defined due to the existence of isolated vertices in the bounded degree case. In addition, our weak consistency results obtained here are valid as long as the expected degree is
$\Omega (\log ^2 n)$ with high probability [Reference Ghoshdastidar and Dukkipati31, Theorem 4.2]. Their algorithm can’t be applied to sparse regimes straightforwardly since the normalised Laplacian is not well-defined due to the existence of isolated vertices in the bounded degree case. In addition, our weak consistency results obtained here are valid as long as the expected degree is ![]() $\omega (1)$ and
$\omega (1)$ and ![]() $o(\log n)$, which is the entire set of problems on which weak consistency is expected. By contrast, in [Reference Ghoshdastidar and Dukkipati32], weak consistency is shown only when the minimum expected degree is
$o(\log n)$, which is the entire set of problems on which weak consistency is expected. By contrast, in [Reference Ghoshdastidar and Dukkipati32], weak consistency is shown only when the minimum expected degree is ![]() $\Omega (\log ^2(n))$, which is a regime complementary to ours and where exact recovery should (in principle) be possible: for example, this is known to be an exact recovery regime in the uniform case [Reference Eli Chien, Lin and Wang17, Reference Kim, Bandeira and Goemans43, Reference Lee, Kim and Chung46, Reference Zhang and Tan77].
$\Omega (\log ^2(n))$, which is a regime complementary to ours and where exact recovery should (in principle) be possible: for example, this is known to be an exact recovery regime in the uniform case [Reference Eli Chien, Lin and Wang17, Reference Kim, Bandeira and Goemans43, Reference Lee, Kim and Chung46, Reference Zhang and Tan77].
In subsequent works [Reference Dumitriu and Wang25, Reference Wang71] we proposed algorithms to achieve weak consistency. However, their methods can not cover the regime when the expected degree is ![]() $\Omega (1)$ due to the lack of concentration. Additionally, [Reference Wang, Pun, Wang, Wang and So72] proposed Projected Tensor Power Method as the refinement stage to achieve strong consistency, as long as the first stage partition is partially correct, as ours.
$\Omega (1)$ due to the lack of concentration. Additionally, [Reference Wang, Pun, Wang, Wang and So72] proposed Projected Tensor Power Method as the refinement stage to achieve strong consistency, as long as the first stage partition is partially correct, as ours.
1.4. Organization of the paper
In Section 2, we include the definitions of adjacency matrices of hypergraphs. The concentration results for the adjacency matrices are provided in Section 3. The algorithms for partial recovery are presented in Section 4. The proof for the correctness of our algorithms for Theorem 1.7 and Corollary 1.9 are given in Section 5. The proof of Theorem 1.6, as well as the proofs of many auxiliary lemmas and useful lemmas in the literature, are provided in the supplemental materials.
2. Preliminaries
Definition 2.1 (Adjacency tensor). Given an ![]() $m$-uniform hypergraph
$m$-uniform hypergraph ![]() $H_m=([n], E_m)$, we can associate to it an order-
$H_m=([n], E_m)$, we can associate to it an order- ![]() $m$ adjacency tensor
$m$ adjacency tensor ![]() $\boldsymbol{\mathcal{A}}^{(m)}$. For any
$\boldsymbol{\mathcal{A}}^{(m)}$. For any ![]() $m$-hyperedge
$m$-hyperedge ![]() $e = \{ i_1, \dots, i_m \}$, let
$e = \{ i_1, \dots, i_m \}$, let ![]() $\boldsymbol{\mathcal{A}}^{(m)}_e$ denote the corresponding entry
$\boldsymbol{\mathcal{A}}^{(m)}_e$ denote the corresponding entry ![]() $\boldsymbol{\mathcal{A}}_{[i_{1},\dots,i_{m}]}^{(m)}$, such that
$\boldsymbol{\mathcal{A}}_{[i_{1},\dots,i_{m}]}^{(m)}$, such that
Definition 2.2 (Adjacency matrix). For the non-uniform hypergraph ![]() $H$ sampled from model 1.2, let
$H$ sampled from model 1.2, let ![]() $\boldsymbol{\mathcal{A}}^{(m)}$ be the order-
$\boldsymbol{\mathcal{A}}^{(m)}$ be the order- ![]() $m$ adjacency tensor corresponding to the underlying
$m$ adjacency tensor corresponding to the underlying ![]() $m$-uniform hypergraph for each
$m$-uniform hypergraph for each ![]() $m\in{\mathcal M}$. The adjacency matrix
$m\in{\mathcal M}$. The adjacency matrix ![]() ${\mathbf{A}} \,:\!=\, [{\mathbf{A}}_{ij}]_{n \times n}$ of the non-uniform hypergraph
${\mathbf{A}} \,:\!=\, [{\mathbf{A}}_{ij}]_{n \times n}$ of the non-uniform hypergraph ![]() $H$ is defined by
$H$ is defined by
 \begin{equation} {\mathbf{A}}_{ij} = \unicode{x1D7D9}_{\{ i \neq j\} } \cdot \sum _{m\in{\mathcal M}}\,\,\sum _{\substack{e\in E_m\\
\{i,j\}\subset e} }\boldsymbol{\mathcal{A}}^{(m)}_{e}\,. \end{equation}
\begin{equation} {\mathbf{A}}_{ij} = \unicode{x1D7D9}_{\{ i \neq j\} } \cdot \sum _{m\in{\mathcal M}}\,\,\sum _{\substack{e\in E_m\\
\{i,j\}\subset e} }\boldsymbol{\mathcal{A}}^{(m)}_{e}\,. \end{equation}
We compute the expectation of ![]() ${\mathbf{A}}$ first. In each
${\mathbf{A}}$ first. In each ![]() $m$-uniform hypergraph
$m$-uniform hypergraph ![]() $H_m$, two distinct vertices
$H_m$, two distinct vertices ![]() $i, j\in V$ with
$i, j\in V$ with ![]() $i \neq j$ are picked arbitrarily since our model does not allow for loops. Assume for a moment
$i \neq j$ are picked arbitrarily since our model does not allow for loops. Assume for a moment ![]() $\frac{n}{k} \in \mathbb{N}$, then the expected number of
$\frac{n}{k} \in \mathbb{N}$, then the expected number of ![]() $m$-hyperedge containing
$m$-hyperedge containing ![]() $i$ and
$i$ and ![]() $j$ can be computed as follows.
$j$ can be computed as follows.
• If
 $i$ and
$i$ and  $j$ are from the same block, the
$j$ are from the same block, the  $m$-hyperedge is sampled with probability
$m$-hyperedge is sampled with probability  $a_m/\binom{n}{m-1}$ when the other
$a_m/\binom{n}{m-1}$ when the other  $m-2$ vertices are from the same block as
$m-2$ vertices are from the same block as  $i$,
$i$,  $j$, otherwise with probability
$j$, otherwise with probability  $b_m/\binom{n}{m-1}$. Then
$b_m/\binom{n}{m-1}$. Then
 \begin{align*} \alpha _m\,:\!=\,{\mathbb{E}}{\mathbf{A}}_{ij} = \binom{\frac{n}{k} -2}{m-2} \frac{a_m}{\binom{n}{m-1}} + \left [ \binom{n-2}{m-2} - \binom{\frac{n}{k} - 2}{m-2} \right ]\frac{b_m}{\binom{n}{m-1}} \,. \end{align*}
\begin{align*} \alpha _m\,:\!=\,{\mathbb{E}}{\mathbf{A}}_{ij} = \binom{\frac{n}{k} -2}{m-2} \frac{a_m}{\binom{n}{m-1}} + \left [ \binom{n-2}{m-2} - \binom{\frac{n}{k} - 2}{m-2} \right ]\frac{b_m}{\binom{n}{m-1}} \,. \end{align*}
• If
 $i$ and
$i$ and  $j$ are not from the same block, we sample the
$j$ are not from the same block, we sample the  $m$-hyperedge with probability
$m$-hyperedge with probability  $b_m/\binom{n}{m-1}$, and
$b_m/\binom{n}{m-1}$, and
 \begin{align*} \beta _m \,:\!=\,{\mathbb{E}}{\mathbf{A}}_{ij} = \binom{n-2}{m-2} \frac{b_m}{\binom{n}{m-1}}\,. \end{align*}
\begin{align*} \beta _m \,:\!=\,{\mathbb{E}}{\mathbf{A}}_{ij} = \binom{n-2}{m-2} \frac{b_m}{\binom{n}{m-1}}\,. \end{align*}
By assumption ![]() $a_m \geq b_m$, then
$a_m \geq b_m$, then ![]() $\alpha _m \geq \beta _m$ for each
$\alpha _m \geq \beta _m$ for each ![]() $m\in{\mathcal M}$. Summing over
$m\in{\mathcal M}$. Summing over ![]() $m$, the expected adjacency matrix under the
$m$, the expected adjacency matrix under the ![]() $k$-block non-uniform
$k$-block non-uniform ![]() $\mathrm{HSBM}$ can be written as
$\mathrm{HSBM}$ can be written as
 \begin{align} {\mathbb{E}}{\mathbf{A}} = \begin{bmatrix} \alpha{\mathbf{J}}_{\frac{n}{k}} & \quad \beta{\mathbf{J}}_{\frac{n}{k}} & \quad \cdots & \quad \beta{\mathbf{J}}_{\frac{n}{k}} \\[4pt]
\beta{\mathbf{J}}_{\frac{n}{k}} & \quad \alpha{\mathbf{J}}_{\frac{n}{k}} & \quad \cdots & \quad \beta{\mathbf{J}}_{\frac{n}{k}} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\beta{\mathbf{J}}_{\frac{n}{k}} & \quad \beta{\mathbf{J}}_{\frac{n}{k}} & \quad \cdots & \quad \alpha{\mathbf{J}}_{\frac{n}{k}} \end{bmatrix} - \alpha{\mathbf{I}}_{n}\,, \end{align}
\begin{align} {\mathbb{E}}{\mathbf{A}} = \begin{bmatrix} \alpha{\mathbf{J}}_{\frac{n}{k}} & \quad \beta{\mathbf{J}}_{\frac{n}{k}} & \quad \cdots & \quad \beta{\mathbf{J}}_{\frac{n}{k}} \\[4pt]
\beta{\mathbf{J}}_{\frac{n}{k}} & \quad \alpha{\mathbf{J}}_{\frac{n}{k}} & \quad \cdots & \quad \beta{\mathbf{J}}_{\frac{n}{k}} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\beta{\mathbf{J}}_{\frac{n}{k}} & \quad \beta{\mathbf{J}}_{\frac{n}{k}} & \quad \cdots & \quad \alpha{\mathbf{J}}_{\frac{n}{k}} \end{bmatrix} - \alpha{\mathbf{I}}_{n}\,, \end{align}
where ![]() ${\mathbf{J}}_{\frac{n}{k}}\in{\mathbb{R}}^{\frac{n}{k} \times \frac{n}{k}}$ denotes the all-one matrix and
${\mathbf{J}}_{\frac{n}{k}}\in{\mathbb{R}}^{\frac{n}{k} \times \frac{n}{k}}$ denotes the all-one matrix and
Lemma 2.3. The eigenvalues of ![]() ${\mathbb{E}}{\mathbf{A}}$ are given below:
${\mathbb{E}}{\mathbf{A}}$ are given below:
 \begin{align*} \lambda _1({\mathbb{E}}{\mathbf{A}}) =&\, \frac{n}{k}(\alpha + (k-1)\beta ) - \alpha \,,\\[4pt]
\lambda _i({\mathbb{E}}{\mathbf{A}}) =&\, \frac{n}{k}(\alpha - \beta ) -\alpha \,, \quad 2\leq i \leq k\,,\\[4pt]
\lambda _i({\mathbb{E}}{\mathbf{A}}) =&\, - \alpha \,, \,\quad \quad \quad k+1\leq i \leq n\,. \end{align*}
\begin{align*} \lambda _1({\mathbb{E}}{\mathbf{A}}) =&\, \frac{n}{k}(\alpha + (k-1)\beta ) - \alpha \,,\\[4pt]
\lambda _i({\mathbb{E}}{\mathbf{A}}) =&\, \frac{n}{k}(\alpha - \beta ) -\alpha \,, \quad 2\leq i \leq k\,,\\[4pt]
\lambda _i({\mathbb{E}}{\mathbf{A}}) =&\, - \alpha \,, \,\quad \quad \quad k+1\leq i \leq n\,. \end{align*}
Lemma 2.3 can be verified via direct computation. Lemma 2.4 is used for approximately equi-partitions, meaning that eigenvalues of ![]() $\widetilde{{\mathbb{E}}{\mathbf{A}}}$ can be approximated by eigenvalues of
$\widetilde{{\mathbb{E}}{\mathbf{A}}}$ can be approximated by eigenvalues of ![]() ${\mathbb{E}}{\mathbf{A}}$ when
${\mathbb{E}}{\mathbf{A}}$ when ![]() $n$ is sufficiently large.
$n$ is sufficiently large.
Lemma 2.4. For any partition ![]() $(V_1, \dots, V_k)$ of
$(V_1, \dots, V_k)$ of ![]() $V$ where
$V$ where ![]() $n_i \,:\!=\, |V_i|$, consider the following matrix
$n_i \,:\!=\, |V_i|$, consider the following matrix
 \begin{align*} \widetilde{{\mathbb{E}}{\mathbf{A}}} = \begin{bmatrix} \alpha{\mathbf{J}}_{n_1} & \quad \beta{\mathbf{J}}_{n_1 \times n_2} & \quad \cdots & \quad \beta{\mathbf{J}}_{n_1 \times n_{k-1}} & \quad \beta{\mathbf{J}}_{n_1 \times n_k} \\[4pt]
\beta{\mathbf{J}}_{n_2 \times n_1} & \quad \alpha{\mathbf{J}}_{n_2} & \quad \cdots & \quad \beta{\mathbf{J}}_{n_2 \times n_{k-1}} & \quad \beta{\mathbf{J}}_{n_2 \times n_k} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots & \quad \vdots \\[4pt]
\beta{\mathbf{J}}_{n_{k-1} \times n_1} & \quad \beta{\mathbf{J}}_{n_{k-1} \times n_2} & \quad \cdots & \quad \alpha{\mathbf{J}}_{n_{k-1}} & \quad \beta{\mathbf{J}}_{n_{k-1} \times n_k} \\[4pt]
\beta{\mathbf{J}}_{n_k \times n_1} & \quad \beta{\mathbf{J}}_{n_k \times n_2} & \quad \cdots & \quad \beta{\mathbf{J}}_{n_k \times n_{k-1}} & \quad \alpha{\mathbf{J}}_{n_k} \end{bmatrix} - \alpha{\mathbf{I}}_{n}\,. \end{align*}
\begin{align*} \widetilde{{\mathbb{E}}{\mathbf{A}}} = \begin{bmatrix} \alpha{\mathbf{J}}_{n_1} & \quad \beta{\mathbf{J}}_{n_1 \times n_2} & \quad \cdots & \quad \beta{\mathbf{J}}_{n_1 \times n_{k-1}} & \quad \beta{\mathbf{J}}_{n_1 \times n_k} \\[4pt]
\beta{\mathbf{J}}_{n_2 \times n_1} & \quad \alpha{\mathbf{J}}_{n_2} & \quad \cdots & \quad \beta{\mathbf{J}}_{n_2 \times n_{k-1}} & \quad \beta{\mathbf{J}}_{n_2 \times n_k} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots & \quad \vdots \\[4pt]
\beta{\mathbf{J}}_{n_{k-1} \times n_1} & \quad \beta{\mathbf{J}}_{n_{k-1} \times n_2} & \quad \cdots & \quad \alpha{\mathbf{J}}_{n_{k-1}} & \quad \beta{\mathbf{J}}_{n_{k-1} \times n_k} \\[4pt]
\beta{\mathbf{J}}_{n_k \times n_1} & \quad \beta{\mathbf{J}}_{n_k \times n_2} & \quad \cdots & \quad \beta{\mathbf{J}}_{n_k \times n_{k-1}} & \quad \alpha{\mathbf{J}}_{n_k} \end{bmatrix} - \alpha{\mathbf{I}}_{n}\,. \end{align*}
Assume that ![]() $n_i = \frac{n}{k} + O(\sqrt{n} \log n)$ for all
$n_i = \frac{n}{k} + O(\sqrt{n} \log n)$ for all ![]() $i\in [k]$. Then, for all
$i\in [k]$. Then, for all ![]() $1\leq i \leq k$,
$1\leq i \leq k$,
Note that both ![]() $(\,\widetilde{{\mathbb{E}}{\mathbf{A}}} + \alpha{\mathbf{I}}_{n})$ and
$(\,\widetilde{{\mathbb{E}}{\mathbf{A}}} + \alpha{\mathbf{I}}_{n})$ and ![]() $(\,{\mathbb{E}}{\mathbf{A}} + \alpha{\mathbf{I}}_{n})$ are rank
$(\,{\mathbb{E}}{\mathbf{A}} + \alpha{\mathbf{I}}_{n})$ are rank ![]() $k$ matrices, then
$k$ matrices, then ![]() $\lambda _i(\widetilde{{\mathbb{E}}{\mathbf{A}}}) = \lambda _i({\mathbb{E}}{\mathbf{A}}) = -\alpha$ for all
$\lambda _i(\widetilde{{\mathbb{E}}{\mathbf{A}}}) = \lambda _i({\mathbb{E}}{\mathbf{A}}) = -\alpha$ for all ![]() $(k+1) \leq i \leq n$. At the same time,
$(k+1) \leq i \leq n$. At the same time, ![]() $\mathrm{SNR}$ in (2) is related to the following quantity
$\mathrm{SNR}$ in (2) is related to the following quantity
 \begin{equation*} \begin{aligned} &\, \frac{[\lambda _2({\mathbb{E}}{\mathbf{A}})]^{2}}{\lambda _1({\mathbb{E}}{\mathbf{A}})} = \frac{[(n-k)\alpha - n \beta ]^2}{k[(n - k)\alpha + n(k-1)\beta ]} = \frac{ \left [\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )}(1+o(1)). \end{aligned} \end{equation*}
\begin{equation*} \begin{aligned} &\, \frac{[\lambda _2({\mathbb{E}}{\mathbf{A}})]^{2}}{\lambda _1({\mathbb{E}}{\mathbf{A}})} = \frac{[(n-k)\alpha - n \beta ]^2}{k[(n - k)\alpha + n(k-1)\beta ]} = \frac{ \left [\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )}(1+o(1)). \end{aligned} \end{equation*}
When ![]() ${\mathcal M} = \{2\}$ and
${\mathcal M} = \{2\}$ and ![]() $k$ is fixed,
$k$ is fixed, ![]() $\mathrm{SNR}$ in (2) is equal to
$\mathrm{SNR}$ in (2) is equal to ![]() $\frac{(a - b)^2}{k[a + (k-1)b]}$, which corresponds to the
$\frac{(a - b)^2}{k[a + (k-1)b]}$, which corresponds to the ![]() $\mathrm{SNR}$ for the undirected graph in [Reference Chin, Rao and Van19], see also [Reference Abbe1, Section 6].
$\mathrm{SNR}$ for the undirected graph in [Reference Chin, Rao and Van19], see also [Reference Abbe1, Section 6].
3. Spectral norm concentration
The correctness of Algorithms 2 and 1 relies on the concentration of the adjacency matrix of ![]() $H$. The following two concentration results for general random hypergraphs are included, which are independent of HSBM model. The proofs are deferred to Section A.
$H$. The following two concentration results for general random hypergraphs are included, which are independent of HSBM model. The proofs are deferred to Section A.
Theorem 3.1. Let ![]() $H=\bigcup _{m =2}^{M} H_m$, where
$H=\bigcup _{m =2}^{M} H_m$, where ![]() $H_m = ([n], E_m)$ is an Erdős-Rényi inhomogeneous hypergraph of order
$H_m = ([n], E_m)$ is an Erdős-Rényi inhomogeneous hypergraph of order ![]() $m$ for each
$m$ for each ![]() $m\in \{2, \cdots, M\}$. Let
$m\in \{2, \cdots, M\}$. Let ![]() $\boldsymbol{\mathcal{T}}^{\,(m)}$ denote the probability tensor such that
$\boldsymbol{\mathcal{T}}^{\,(m)}$ denote the probability tensor such that ![]() $\boldsymbol{\mathcal{T}}^{(m)} ={\mathbb{E}} \boldsymbol{\mathcal{A}}^{(m)}$ and
$\boldsymbol{\mathcal{T}}^{(m)} ={\mathbb{E}} \boldsymbol{\mathcal{A}}^{(m)}$ and ![]() $\boldsymbol{\mathcal{T}}^{(m)}_{[i_1,\dots, i_m]} = d_{[i_1,\dots,i_m]}/ \binom{n}{m-1}$, denoting
$\boldsymbol{\mathcal{T}}^{(m)}_{[i_1,\dots, i_m]} = d_{[i_1,\dots,i_m]}/ \binom{n}{m-1}$, denoting ![]() $d_m=\max d_{[i_1,\dots, i_m]}$. Suppose for some constant
$d_m=\max d_{[i_1,\dots, i_m]}$. Suppose for some constant ![]() $c\gt 0$,
$c\gt 0$,
 \begin{align} d\,:\!=\,\sum _{m =2}^{M} (m-1)\cdot d_m \geq c\log n\,. \end{align}
\begin{align} d\,:\!=\,\sum _{m =2}^{M} (m-1)\cdot d_m \geq c\log n\,. \end{align}
Then for any ![]() $K\gt 0$, there exists a constant
$K\gt 0$, there exists a constant ![]() $ C= 512M(M-1)(K+6)\left [ 2 + (M-1)(1+K)/c \right ]$ such that with probability at least
$ C= 512M(M-1)(K+6)\left [ 2 + (M-1)(1+K)/c \right ]$ such that with probability at least ![]() $1-2n^{-K}-2e^{-n}$, the adjacency matrix
$1-2n^{-K}-2e^{-n}$, the adjacency matrix ![]() ${\mathbf{A}}$ of
${\mathbf{A}}$ of ![]() $H$ satisfies
$H$ satisfies
The inequality (10) can be reduced to the result for graph case obtained in [Reference Feige and Ofek28, Reference Lei and Rinaldo48] by taking ![]() ${\mathcal M} = \{2\}$. The result for a uniform hypergraph is obtained in [Reference Lee, Kim and Chung46]. Note that
${\mathcal M} = \{2\}$. The result for a uniform hypergraph is obtained in [Reference Lee, Kim and Chung46]. Note that ![]() $d$ is a fixed constant in our community detection problem, thus the Assumption 3.1 does not hold and the inequality (9) cannot be directly applied. However, we can still prove a concentration bound for a regularised version of
$d$ is a fixed constant in our community detection problem, thus the Assumption 3.1 does not hold and the inequality (9) cannot be directly applied. However, we can still prove a concentration bound for a regularised version of ![]() ${\mathbf{A}}$, following the same strategy of the proof for Theorem 3.1.
${\mathbf{A}}$, following the same strategy of the proof for Theorem 3.1.
Definition 3.2 (Regularized matrix). Given any ![]() $n\times n$ matrix
$n\times n$ matrix ![]() ${\mathbf{A}}$ and an index set
${\mathbf{A}}$ and an index set ![]() $\mathcal{I}$, let
$\mathcal{I}$, let ![]() ${\mathbf{A}}_{\mathcal{I}}$ be the
${\mathbf{A}}_{\mathcal{I}}$ be the ![]() $n\times n$ matrix obtained from
$n\times n$ matrix obtained from ![]() ${\mathbf{A}}$ by zeroing out the rows and columns not indexed by
${\mathbf{A}}$ by zeroing out the rows and columns not indexed by ![]() $\mathcal{I}$. Namely,
$\mathcal{I}$. Namely,
Since every hyperedge of size ![]() $m$ containing
$m$ containing ![]() $i$ is counted
$i$ is counted ![]() $(m-1)$ times in the
$(m-1)$ times in the ![]() $i$-th row sum of
$i$-th row sum of ![]() ${\mathbf{A}}$, the
${\mathbf{A}}$, the ![]() $i$-th row sum of
$i$-th row sum of ![]() ${\mathbf{A}}$ is given by
${\mathbf{A}}$ is given by
 \begin{align*} \mathrm{row}(i) \,:\!=\,\sum _{j}{\mathbf{A}}_{ij} \,:\!=\, \sum _{j} \unicode{x1D7D9}_{\{ i \neq j\} } \sum _{m\in{\mathcal M}}\,\,\sum _{\substack{e\in E_m\\
\{i,j\}\subset e} }\boldsymbol{\mathcal{A}}^{(m)}_{e} = \sum _{m\in{\mathcal M}}\,(m-1) \sum _{e\in E_m:\, i\in e} \boldsymbol{\mathcal{A}}_e^{(m)}. \end{align*}
\begin{align*} \mathrm{row}(i) \,:\!=\,\sum _{j}{\mathbf{A}}_{ij} \,:\!=\, \sum _{j} \unicode{x1D7D9}_{\{ i \neq j\} } \sum _{m\in{\mathcal M}}\,\,\sum _{\substack{e\in E_m\\
\{i,j\}\subset e} }\boldsymbol{\mathcal{A}}^{(m)}_{e} = \sum _{m\in{\mathcal M}}\,(m-1) \sum _{e\in E_m:\, i\in e} \boldsymbol{\mathcal{A}}_e^{(m)}. \end{align*}
Theorem 3.3 is the concentration result for the regularised ![]() ${\mathbf{A}}_{\mathcal{I}}$, by zeroing out rows and columns corresponding to vertices with high row sums.
${\mathbf{A}}_{\mathcal{I}}$, by zeroing out rows and columns corresponding to vertices with high row sums.
Theorem 3.3. Following all the notations in Theorem 3.1, for any constant ![]() $\tau \gt 1$, define
$\tau \gt 1$, define
Let ![]() ${\mathbf{A}}_{\mathcal{I}}$ be the regularised version of
${\mathbf{A}}_{\mathcal{I}}$ be the regularised version of ![]() ${\mathbf{A}}$, as in Definition 3.2. Then for any
${\mathbf{A}}$, as in Definition 3.2. Then for any ![]() $K\gt 0$, there exists a constant
$K\gt 0$, there exists a constant ![]() $C_{\tau }=2( (5M+1)(M-1)+\alpha _0\sqrt{\tau })$ with
$C_{\tau }=2( (5M+1)(M-1)+\alpha _0\sqrt{\tau })$ with ![]() $\alpha _0=16+\frac{32}{\tau }(1+e^2)+128M(M-1)(K+4)\left (1+\frac{1}{e^2}\right )$, such that
$\alpha _0=16+\frac{32}{\tau }(1+e^2)+128M(M-1)(K+4)\left (1+\frac{1}{e^2}\right )$, such that ![]() $ \| ({\mathbf{A}}-{\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}\|\leq C_{\tau }\sqrt{d}$ with probability at least
$ \| ({\mathbf{A}}-{\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}\|\leq C_{\tau }\sqrt{d}$ with probability at least ![]() $1-2(e/2)^{-n} -n^{-K}$.
$1-2(e/2)^{-n} -n^{-K}$.
Algorithm 3. Pre-processing

Algorithm 4. Spectral Partition

4. Algorithms blocks
In this section, we are going to present the algorithmic blocks constructing our main partition method (Algorithm 2): pre-processing (Algorithm 3), initial result by spectral method (Algorithm 4), correction of blemishes via majority rule (Algorithm 5), and merging (Algorithm 6).
Algorithm 5. Correction

Algorithm 6. Merging

4.1. Three or more blocks ( $k\geq 3$)
$k\geq 3$)
The proof of Theorem 1.7 is structured as follows.
Lemma 4.1. Under the assumptions of Theorem 1.7, Algorithm 4 outputs a ![]() $\nu$-correct partition
$\nu$-correct partition ![]() $U_1^{\prime }, \cdots, U_k^{\prime }$ of
$U_1^{\prime }, \cdots, U_k^{\prime }$ of ![]() $Z = (Z\cap V_{1}) \cup \cdots \cup (Z\cap V_{k})$ with probability at least
$Z = (Z\cap V_{1}) \cup \cdots \cup (Z\cap V_{k})$ with probability at least ![]() $1 - O(n^{-2})$.
$1 - O(n^{-2})$.
Lines ![]() $4$ and
$4$ and ![]() $6$ contribute most complexity in Algorithm 4, requiring
$6$ contribute most complexity in Algorithm 4, requiring ![]() $O(n^{3})$ and
$O(n^{3})$ and ![]() $O(n^{2}\log ^2(n))$ each (technically, one should be able to get away with
$O(n^{2}\log ^2(n))$ each (technically, one should be able to get away with ![]() $O(n^2 \log (1/\varepsilon ))$ in line 4, for some desired accuracy
$O(n^2 \log (1/\varepsilon ))$ in line 4, for some desired accuracy ![]() $\varepsilon$ to get the singular vectors). We will conservatively estimate the time complexity of Algorithm 4 as
$\varepsilon$ to get the singular vectors). We will conservatively estimate the time complexity of Algorithm 4 as ![]() $O(n^3)$.
$O(n^3)$.
Lemma 4.2. Under the assumptions of Theorem 1.7, for any ![]() $\nu$-correct partition
$\nu$-correct partition ![]() $U_1^{\prime }, \cdots, U_k^{\prime }$ of
$U_1^{\prime }, \cdots, U_k^{\prime }$ of ![]() $Z = (Z\cap V_{1}) \cup \cdots \cup (Z\cap V_{k})$ and the red hypergraph over
$Z = (Z\cap V_{1}) \cup \cdots \cup (Z\cap V_{k})$ and the red hypergraph over ![]() $Z$, Algorithm 5 computes a
$Z$, Algorithm 5 computes a ![]() $\gamma _{\mathrm{C}}$-correct partition
$\gamma _{\mathrm{C}}$-correct partition ![]() $\widehat{U}_1, \cdots, \widehat{U}_k$ with probability
$\widehat{U}_1, \cdots, \widehat{U}_k$ with probability ![]() $1 -O(e^{-n\rho })$, while
$1 -O(e^{-n\rho })$, while ![]() $\gamma _{\mathrm{C}} = \max \{\nu,\, 1 - k\rho \}$ with
$\gamma _{\mathrm{C}} = \max \{\nu,\, 1 - k\rho \}$ with ![]() $ \rho \,:\!=\, k\exp\!\left ({-}C_{{\mathcal M}}(k) \cdot \mathrm{SNR}_{{\mathcal M}}(k) \right )$ where
$ \rho \,:\!=\, k\exp\!\left ({-}C_{{\mathcal M}}(k) \cdot \mathrm{SNR}_{{\mathcal M}}(k) \right )$ where ![]() $\mathcal M$ is obtained from Algorithm 3, and
$\mathcal M$ is obtained from Algorithm 3, and ![]() $\mathrm{SNR}_{{\mathcal M}}(k)$ and
$\mathrm{SNR}_{{\mathcal M}}(k)$ and ![]() $C_{{\mathcal M}}(k)$ are defined in (2), (3).
$C_{{\mathcal M}}(k)$ are defined in (2), (3).
Lemma 4.3. Given any ![]() $\nu$-correct partition
$\nu$-correct partition ![]() $\widehat{U}_1, \cdots, \widehat{U}_k$ of
$\widehat{U}_1, \cdots, \widehat{U}_k$ of ![]() $Z = (Z\cap V_{1}) \cup \cdots \cup (Z\cap V_{k})$ and the blue hypergraph between
$Z = (Z\cap V_{1}) \cup \cdots \cup (Z\cap V_{k})$ and the blue hypergraph between ![]() $Y$ and
$Y$ and ![]() $Z$, with probability
$Z$, with probability ![]() $1 -O(e^{-n\rho })$, Algorithm 6 outputs a
$1 -O(e^{-n\rho })$, Algorithm 6 outputs a ![]() $\gamma$-correct partition
$\gamma$-correct partition ![]() $\widehat{V}_1, \cdots, \widehat{V}_{k}$ of
$\widehat{V}_1, \cdots, \widehat{V}_{k}$ of ![]() $V_1 \cup V_2 \cup \cdots \cup V_k$, while
$V_1 \cup V_2 \cup \cdots \cup V_k$, while ![]() $\gamma =\max \{\nu,\, 1 - k\rho \}$.
$\gamma =\max \{\nu,\, 1 - k\rho \}$.
The time complexities of Algorithms 5 and 6 are ![]() $O(n)$, since each vertex is adjacent to only constant many hyperedges.
$O(n)$, since each vertex is adjacent to only constant many hyperedges.
Algorithm 7. Spectral Partition

Algorithm 8. Correction

4.2. The binary case ( $k = 2$)
$k = 2$)
The spectral partition step is given in Algorithm 7, and the correction step is given in Algorithm 8.
Lemma 4.4. Under the conditions of Theorem 1.6, the Algorithm 7 outputs a ![]() $\nu$-correct partition
$\nu$-correct partition ![]() $V_1^{\prime }, V_2^{\prime }$ of
$V_1^{\prime }, V_2^{\prime }$ of ![]() $V = V_1 \cup V_2$ with probability at least
$V = V_1 \cup V_2$ with probability at least ![]() $1 - O(n^{-2})$.
$1 - O(n^{-2})$.
Lemma 4.5. Given any ![]() $\nu$-correct partition
$\nu$-correct partition ![]() $V_1^{\prime }, V_2^{\prime }$ of
$V_1^{\prime }, V_2^{\prime }$ of ![]() $V = V_1 \cup V_2$, with probability at least
$V = V_1 \cup V_2$, with probability at least ![]() $1 -O(e^{-n\rho })$, the Algorithm 8 computes a
$1 -O(e^{-n\rho })$, the Algorithm 8 computes a ![]() $\gamma$-correct partition
$\gamma$-correct partition ![]() $\widehat{V}_1, \widehat{V}_2$ with
$\widehat{V}_1, \widehat{V}_2$ with ![]() $\gamma = \{\nu,\, 1 - 2\rho \}$ and
$\gamma = \{\nu,\, 1 - 2\rho \}$ and ![]() $\rho = 2\exp ({-}C_{{\mathcal M}}(2) \cdot \mathrm{SNR}_{{\mathcal M}}(2))$, where
$\rho = 2\exp ({-}C_{{\mathcal M}}(2) \cdot \mathrm{SNR}_{{\mathcal M}}(2))$, where ![]() $\mathrm{SNR}_{{\mathcal M}}(2)$ and
$\mathrm{SNR}_{{\mathcal M}}(2)$ and ![]() $C_{{\mathcal M}}(2)$ are defined in (2), (3).
$C_{{\mathcal M}}(2)$ are defined in (2), (3).
5. Algorithm’s correctness
We are going to present the correctness of Algorithm 2 in this section. The correctness of Algorithm 1 is deferred to Section C. We first introduce some definitions.
Vertex set splitting and adjacency matrix
In Algorithm 2, we first randomly partition the vertex set ![]() $V$ into two disjoint subsets
$V$ into two disjoint subsets ![]() $Z$ and
$Z$ and ![]() $Y$ by assigning
$Y$ by assigning ![]() $+1$ and
$+1$ and ![]() $-1$ to each vertex independently with equal probability. Let
$-1$ to each vertex independently with equal probability. Let ![]() ${\mathbf{B}} \in{\mathbb{R}}^{|Z|\times |Y|}$ denote the submatrix of
${\mathbf{B}} \in{\mathbb{R}}^{|Z|\times |Y|}$ denote the submatrix of ![]() ${\mathbf{A}}$, while
${\mathbf{A}}$, while ![]() ${\mathbf{A}}$ was defined in (6), where rows and columns of
${\mathbf{A}}$ was defined in (6), where rows and columns of ![]() ${\mathbf{B}}$ correspond to vertices in
${\mathbf{B}}$ correspond to vertices in ![]() $Z$ and
$Z$ and ![]() $Y$ respectively. Let
$Y$ respectively. Let ![]() $n_i$ denote the number of vertices in
$n_i$ denote the number of vertices in ![]() $Z\cap V_i$, where
$Z\cap V_i$, where ![]() $V_i$ denotes the true partition with
$V_i$ denotes the true partition with ![]() $|V_i| = \frac{n}{k}$ for all
$|V_i| = \frac{n}{k}$ for all ![]() $i\in [k]$, then
$i\in [k]$, then ![]() $n_i$ can be written as a sum of independent Bernoulli random variables, i.e.,
$n_i$ can be written as a sum of independent Bernoulli random variables, i.e.,
and ![]() $|Y\cap V_i| = |V_i| - |Z\cap V_i| = \frac{n}{k} - n_i$ for each
$|Y\cap V_i| = |V_i| - |Z\cap V_i| = \frac{n}{k} - n_i$ for each ![]() $i \in [k]$.
$i \in [k]$.
Definition 5.1. The splitting ![]() $V = Z \cup Y$ is perfect if
$V = Z \cup Y$ is perfect if ![]() $|Z\cap V_i| = |Y\cap V_i| = n/(2k)$ for all
$|Z\cap V_i| = |Y\cap V_i| = n/(2k)$ for all ![]() $i\in [k]$. And the splitting
$i\in [k]$. And the splitting ![]() $Y = Y_1 \cup Y_2$ is perfect if
$Y = Y_1 \cup Y_2$ is perfect if ![]() $|Y_1\cap V_i| = |Y_2\cap V_i| = n/(4k)$ for all
$|Y_1\cap V_i| = |Y_2\cap V_i| = n/(4k)$ for all ![]() $i\in [k]$.
$i\in [k]$.
However, the splitting is imperfect in most cases since the size of ![]() $Z$ and
$Z$ and ![]() $Y$ would not be exactly the same under the independence assumption. The random matrix
$Y$ would not be exactly the same under the independence assumption. The random matrix ![]() ${\mathbf{B}}$ is parameterised by
${\mathbf{B}}$ is parameterised by ![]() $\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$ and
$\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$ and ![]() $\{n_i\}_{i=1}^{k}$. If we take expectation over
$\{n_i\}_{i=1}^{k}$. If we take expectation over ![]() $\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$ given the block size information
$\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$ given the block size information ![]() $\{n_i\}_{i=1}^{k}$, then it gives rise to the expectation of the imperfect splitting, denoted by
$\{n_i\}_{i=1}^{k}$, then it gives rise to the expectation of the imperfect splitting, denoted by ![]() $\widetilde{{\mathbf{B}}}$,
$\widetilde{{\mathbf{B}}}$,
 \begin{equation*} \widetilde {{\mathbf{B}}} \,:\!=\, \begin {bmatrix} \alpha {\mathbf{J}}_{n_1 \times ( \frac {n}{k} - n_1)} & \quad \beta {\mathbf{J}}_{n_1 \times (\frac {n}{k} - n_2)} & \quad \dots & \quad \beta {\mathbf{J}}_{n_1 \times (\frac {n}{k}- n_k)} \\[4pt]
\beta {\mathbf{J}}_{n_2 \times (\frac {n}{k}- n_1)} & \quad \alpha {\mathbf{J}}_{n_2 \times (\frac {n}{k}- n_2)} & \quad\dots & \quad \beta {\mathbf{J}}_{n_2 \times (\frac {n}{k}- n_k)} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\beta {\mathbf{J}}_{n_k \times (\frac {n}{k}- n_1)} & \quad \beta {\mathbf{J}}_{n_k \times (\frac {n}{k}- n_2)} & \quad \dots & \quad \alpha {\mathbf{J}}_{n_k \times (\frac {n}{k}- n_k)} \end {bmatrix}\,, \end{equation*}
\begin{equation*} \widetilde {{\mathbf{B}}} \,:\!=\, \begin {bmatrix} \alpha {\mathbf{J}}_{n_1 \times ( \frac {n}{k} - n_1)} & \quad \beta {\mathbf{J}}_{n_1 \times (\frac {n}{k} - n_2)} & \quad \dots & \quad \beta {\mathbf{J}}_{n_1 \times (\frac {n}{k}- n_k)} \\[4pt]
\beta {\mathbf{J}}_{n_2 \times (\frac {n}{k}- n_1)} & \quad \alpha {\mathbf{J}}_{n_2 \times (\frac {n}{k}- n_2)} & \quad\dots & \quad \beta {\mathbf{J}}_{n_2 \times (\frac {n}{k}- n_k)} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\beta {\mathbf{J}}_{n_k \times (\frac {n}{k}- n_1)} & \quad \beta {\mathbf{J}}_{n_k \times (\frac {n}{k}- n_2)} & \quad \dots & \quad \alpha {\mathbf{J}}_{n_k \times (\frac {n}{k}- n_k)} \end {bmatrix}\,, \end{equation*}
where ![]() $\alpha$,
$\alpha$, ![]() $\beta$ are defined in (8). In the perfect splitting case, the dimension of each block is
$\beta$ are defined in (8). In the perfect splitting case, the dimension of each block is ![]() $n/(2k)\times n/(2k)$ since
$n/(2k)\times n/(2k)$ since ![]() ${\mathbb{E}} n_i = n/(2k)$ for all
${\mathbb{E}} n_i = n/(2k)$ for all ![]() $i \in [k]$, and the expectation matrix
$i \in [k]$, and the expectation matrix ![]() $\overline{{\mathbf{B}}}$ can be written as
$\overline{{\mathbf{B}}}$ can be written as
 \begin{equation*} \overline {{\mathbf{B}}} \,:\!=\, \begin {bmatrix} \alpha {\mathbf{J}}_{\frac {n}{2k}} & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} & \quad \dots & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} \\[4pt]
\beta {\mathbf{J}}_{\frac {n}{2k}} & \quad \alpha {\mathbf{J}}_{\frac {n}{2k}} & \quad \dots & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\beta {\mathbf{J}}_{\frac {n}{2k}} & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} & \quad\dots & \quad \alpha {\mathbf{J}}_{\frac {n}{2k}} \end {bmatrix}\,. \end{equation*}
\begin{equation*} \overline {{\mathbf{B}}} \,:\!=\, \begin {bmatrix} \alpha {\mathbf{J}}_{\frac {n}{2k}} & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} & \quad \dots & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} \\[4pt]
\beta {\mathbf{J}}_{\frac {n}{2k}} & \quad \alpha {\mathbf{J}}_{\frac {n}{2k}} & \quad \dots & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\beta {\mathbf{J}}_{\frac {n}{2k}} & \quad \beta {\mathbf{J}}_{\frac {n}{2k}} & \quad\dots & \quad \alpha {\mathbf{J}}_{\frac {n}{2k}} \end {bmatrix}\,. \end{equation*}
In Algorithm 4, ![]() $Y_1$ is a random subset of
$Y_1$ is a random subset of ![]() $Y$ obtained by selecting each element with probability
$Y$ obtained by selecting each element with probability ![]() $1/2$ independently, and
$1/2$ independently, and ![]() $Y_2 = Y\setminus Y_1$. Let
$Y_2 = Y\setminus Y_1$. Let ![]() $n^{\prime }_{i}$ denote the number of vertices in
$n^{\prime }_{i}$ denote the number of vertices in ![]() $Y_1\cap V_i$, then
$Y_1\cap V_i$, then ![]() $n^{\prime }_{i}$ can be written as a sum of independent Bernoulli random variables,
$n^{\prime }_{i}$ can be written as a sum of independent Bernoulli random variables,
and ![]() $|Y_2\cap V_i| = |V_i| - |Z\cap V_i| - |Y_1\cap V_i| = n/k - n_i - n^{\prime }_{i}$ for all
$|Y_2\cap V_i| = |V_i| - |Z\cap V_i| - |Y_1\cap V_i| = n/k - n_i - n^{\prime }_{i}$ for all ![]() $i \in [k]$.
$i \in [k]$.
Induced sub-hypergraph
Definition 5.2 (Induced Sub-hypergraph). Let ![]() $H = (V, E)$ be a non-uniform random hypergraph and
$H = (V, E)$ be a non-uniform random hypergraph and ![]() $S\subset V$ be any subset of the vertices of
$S\subset V$ be any subset of the vertices of ![]() $H$. Then the induced sub-hypergraph
$H$. Then the induced sub-hypergraph ![]() $H[S]$ is the hypergraph whose vertex set is
$H[S]$ is the hypergraph whose vertex set is ![]() $S$ and whose hyperedge set
$S$ and whose hyperedge set ![]() $E[S]$ consists of all of the edges in
$E[S]$ consists of all of the edges in ![]() $E$ that have all endpoints located in
$E$ that have all endpoints located in ![]() $S$.
$S$.
Let ![]() $H[Y_1 \cup Z]$(resp.
$H[Y_1 \cup Z]$(resp. ![]() $H[Y_2 \cup Z]$) denote the induced sub-hypergraph on vertex set
$H[Y_2 \cup Z]$) denote the induced sub-hypergraph on vertex set ![]() $Y_1\cup Z$ (resp.
$Y_1\cup Z$ (resp. ![]() $Y_2 \cup Z$), and
$Y_2 \cup Z$), and ![]() ${\mathbf{B}}_1 \in{\mathbb{R}}^{|Z|\times |Y_1|}$ (resp.
${\mathbf{B}}_1 \in{\mathbb{R}}^{|Z|\times |Y_1|}$ (resp. ![]() ${\mathbf{B}}_2 \in{\mathbb{R}}^{|Z|\times |Y_2|}$) denote the adjacency matrices corresponding to the sub-hypergraphs, where rows and columns of
${\mathbf{B}}_2 \in{\mathbb{R}}^{|Z|\times |Y_2|}$) denote the adjacency matrices corresponding to the sub-hypergraphs, where rows and columns of ![]() ${\mathbf{B}}_1$ (resp.
${\mathbf{B}}_1$ (resp. ![]() ${\mathbf{B}}_2$) are corresponding to elements in
${\mathbf{B}}_2$) are corresponding to elements in ![]() $Z$ and
$Z$ and ![]() $Y_1$ (resp.,
$Y_1$ (resp., ![]() $Z$ and
$Z$ and ![]() $Y_2$). Therefore,
$Y_2$). Therefore, ![]() ${\mathbf{B}}_1$ and
${\mathbf{B}}_1$ and ![]() ${\mathbf{B}}_2$ are parameterised by
${\mathbf{B}}_2$ are parameterised by ![]() $\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$,
$\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$, ![]() $\{n_i\}_{i=1}^{k}$ and
$\{n_i\}_{i=1}^{k}$ and ![]() $\{n^{\prime }_{i}\}_{i=1}^{k}$, and the entries in
$\{n^{\prime }_{i}\}_{i=1}^{k}$, and the entries in ![]() ${\mathbf{B}}_1$ are independent of the entries in
${\mathbf{B}}_1$ are independent of the entries in ![]() ${\mathbf{B}}_2$, due to the independence of hyperedges. If we take expectation over
${\mathbf{B}}_2$, due to the independence of hyperedges. If we take expectation over ![]() $\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$ conditioning on
$\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in{\mathcal M}}$ conditioning on ![]() $\{n_i\}_{i=1}^{k}$ and
$\{n_i\}_{i=1}^{k}$ and ![]() $\{n^{\prime }_{i}\}_{i=1}^{k}$, then it gives rise to the expectation of the imperfect splitting, denoted by
$\{n^{\prime }_{i}\}_{i=1}^{k}$, then it gives rise to the expectation of the imperfect splitting, denoted by ![]() $\widetilde{{\mathbf{B}}}_1$,
$\widetilde{{\mathbf{B}}}_1$,
 \begin{equation} \widetilde{{\mathbf{B}}}_1 \,:\!=\, \begin{bmatrix} \widetilde{\alpha }_{11}{\mathbf{J}}_{n_1 \times n^{\prime }_{1}} & \quad \dots & \quad \widetilde{\beta }_{1k}{\mathbf{J}}_{n_1 \times n^{\prime }_{k}} \\[4pt]
\vdots & \quad \ddots & \quad \vdots \\[4pt]
\widetilde{\beta }_{k1}{\mathbf{J}}_{n_k \times n^{\prime }_{1}} & \quad \dots & \quad \widetilde{\alpha }_{kk}{\mathbf{J}}_{n_k \times n^{\prime }_{k}} \end{bmatrix}\,, \end{equation}
\begin{equation} \widetilde{{\mathbf{B}}}_1 \,:\!=\, \begin{bmatrix} \widetilde{\alpha }_{11}{\mathbf{J}}_{n_1 \times n^{\prime }_{1}} & \quad \dots & \quad \widetilde{\beta }_{1k}{\mathbf{J}}_{n_1 \times n^{\prime }_{k}} \\[4pt]
\vdots & \quad \ddots & \quad \vdots \\[4pt]
\widetilde{\beta }_{k1}{\mathbf{J}}_{n_k \times n^{\prime }_{1}} & \quad \dots & \quad \widetilde{\alpha }_{kk}{\mathbf{J}}_{n_k \times n^{\prime }_{k}} \end{bmatrix}\,, \end{equation}
where
 \begin{align} \widetilde{\alpha }_{ii} \,:\!=\,&\, \sum _{m \in{\mathcal{M}}}\left \{ \binom{n_i + n_i^{\prime } - 2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} + \binom{\sum _{l=1}^{k}(n_l + n_l^{\prime }) - 2}{m-2} \frac{b_m}{\binom{n}{m-1}} \right \}\,, \end{align}
\begin{align} \widetilde{\alpha }_{ii} \,:\!=\,&\, \sum _{m \in{\mathcal{M}}}\left \{ \binom{n_i + n_i^{\prime } - 2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} + \binom{\sum _{l=1}^{k}(n_l + n_l^{\prime }) - 2}{m-2} \frac{b_m}{\binom{n}{m-1}} \right \}\,, \end{align}
 \begin{align} \widetilde{\beta }_{ij} \,:\!=\,&\, \sum _{m \in{\mathcal{M}}} \binom{\sum _{l=1}^{k}(n_l + n_l^{\prime }) - 2}{m-2}\frac{b_m}{\binom{n}{m-1}}\,,\quad i\neq j, \, i, j\in [k]\,. \end{align}
\begin{align} \widetilde{\beta }_{ij} \,:\!=\,&\, \sum _{m \in{\mathcal{M}}} \binom{\sum _{l=1}^{k}(n_l + n_l^{\prime }) - 2}{m-2}\frac{b_m}{\binom{n}{m-1}}\,,\quad i\neq j, \, i, j\in [k]\,. \end{align}
The expectation of the perfect splitting, denoted by ![]() $\overline{{\mathbf{B}}}_1$, can be written as
$\overline{{\mathbf{B}}}_1$, can be written as
 \begin{equation} \overline{{\mathbf{B}}}_1 \,:\!=\, \begin{bmatrix} \overline{\alpha }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \dots & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} \\[4pt]
\overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \overline{\alpha }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \dots & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad\dots & \quad \overline{\alpha }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} \end{bmatrix}\,, \end{equation}
\begin{equation} \overline{{\mathbf{B}}}_1 \,:\!=\, \begin{bmatrix} \overline{\alpha }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \dots & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} \\[4pt]
\overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \overline{\alpha }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \dots & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} \\[4pt]
\vdots & \quad \vdots & \quad \ddots & \quad \vdots \\[4pt]
\overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad \overline{\beta }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} & \quad\dots & \quad \overline{\alpha }{\mathbf{J}}_{\frac{n}{2k} \times \frac{n}{4k}} \end{bmatrix}\,, \end{equation}
where
 \begin{align} \overline{\alpha } \,:\!=\, \sum _{m \in{\mathcal M}}\left \{ \binom{ \frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} + \binom{\frac{3n}{4} - 2}{m-2}\frac{b_m}{\binom{n}{m-1}} \right \}\,,\quad \overline{\beta } \,:\!=\, \sum _{m \in{\mathcal M}} \binom{\frac{3n}{4} - 2}{m-2}\frac{b_m}{\binom{n}{m-1}}\,. \end{align}
\begin{align} \overline{\alpha } \,:\!=\, \sum _{m \in{\mathcal M}}\left \{ \binom{ \frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} + \binom{\frac{3n}{4} - 2}{m-2}\frac{b_m}{\binom{n}{m-1}} \right \}\,,\quad \overline{\beta } \,:\!=\, \sum _{m \in{\mathcal M}} \binom{\frac{3n}{4} - 2}{m-2}\frac{b_m}{\binom{n}{m-1}}\,. \end{align}
The matrices ![]() $\widetilde{{\mathbf{B}}}_2, \overline{{\mathbf{B}}}_2$ can be defined similarly, since dimensions of
$\widetilde{{\mathbf{B}}}_2, \overline{{\mathbf{B}}}_2$ can be defined similarly, since dimensions of ![]() $|Y_2\cap V_i|$ are also determined by
$|Y_2\cap V_i|$ are also determined by ![]() $n_i$ and
$n_i$ and ![]() $n^{\prime }_{i}$. Obviously,
$n^{\prime }_{i}$. Obviously, ![]() $\overline{{\mathbf{B}}}_2 = \overline{{\mathbf{B}}}_1$ since
$\overline{{\mathbf{B}}}_2 = \overline{{\mathbf{B}}}_1$ since ![]() ${\mathbb{E}} n^{\prime }_{i} ={\mathbb{E}} (n/k- n_{i} - n_i^{\prime }) = n/(4k)$ for all
${\mathbb{E}} n^{\prime }_{i} ={\mathbb{E}} (n/k- n_{i} - n_i^{\prime }) = n/(4k)$ for all ![]() $i\in [k]$.
$i\in [k]$.
Fixing Dimensions
The dimensions of ![]() $\widetilde{{\mathbf{B}}}_1$ and
$\widetilde{{\mathbf{B}}}_1$ and ![]() $\widetilde{{\mathbf{B}}}_2$, as well as blocks they consist of, are not deterministic – since
$\widetilde{{\mathbf{B}}}_2$, as well as blocks they consist of, are not deterministic – since ![]() $n_i$ and
$n_i$ and ![]() $n^{\prime }_i$, defined in (12) and (13) respectively, are sums of independent random variables. As such, we cannot directly compare them. In order to overcome this difficulty, we embed
$n^{\prime }_i$, defined in (12) and (13) respectively, are sums of independent random variables. As such, we cannot directly compare them. In order to overcome this difficulty, we embed ![]() ${\mathbf{B}}_1$ and
${\mathbf{B}}_1$ and ![]() ${\mathbf{B}}_2$ into the following
${\mathbf{B}}_2$ into the following ![]() $n\times n$ matrices:
$n\times n$ matrices:
 \begin{equation} {\mathbf{A}}_1\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad{\mathbf{B}}_1 & \quad \mathbf{0}_{|Z|\times |Y_2|} \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,,\quad{\mathbf{A}}_2\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad \mathbf{0}_{|Z|\times |Y_1|} & \quad{\mathbf{B}}_2 \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,. \end{equation}
\begin{equation} {\mathbf{A}}_1\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad{\mathbf{B}}_1 & \quad \mathbf{0}_{|Z|\times |Y_2|} \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,,\quad{\mathbf{A}}_2\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad \mathbf{0}_{|Z|\times |Y_1|} & \quad{\mathbf{B}}_2 \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,. \end{equation}
Note that ![]() ${\mathbf{A}}_1$ and
${\mathbf{A}}_1$ and ![]() ${\mathbf{A}}_2$ have the same size. Also by definition, the entries in
${\mathbf{A}}_2$ have the same size. Also by definition, the entries in ![]() ${\mathbf{A}}_1$ are independent of the entries in
${\mathbf{A}}_1$ are independent of the entries in ![]() ${\mathbf{A}}_2$. If we take expectation over
${\mathbf{A}}_2$. If we take expectation over ![]() $\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m\in{\mathcal M}}$ conditioning on
$\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m\in{\mathcal M}}$ conditioning on ![]() $\{n_i\}_{i=1}^{k}$ and
$\{n_i\}_{i=1}^{k}$ and ![]() $\{n^{\prime }_{i}\}_{i=1}^{k}$, then we obtain the expectation matrices of the imperfect splitting, denoted by
$\{n^{\prime }_{i}\}_{i=1}^{k}$, then we obtain the expectation matrices of the imperfect splitting, denoted by ![]() $\widetilde{{\mathbf{A}}}_1$(resp.
$\widetilde{{\mathbf{A}}}_1$(resp. ![]() $\widetilde{{\mathbf{A}}}_2$), written as
$\widetilde{{\mathbf{A}}}_2$), written as
 \begin{equation} \widetilde{{\mathbf{A}}}_1\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad \widetilde{{\mathbf{B}}}_1 & \quad \mathbf{0}_{|Z|\times |Y_2|} \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,,\quad \widetilde{{\mathbf{A}}}_2\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad \mathbf{0}_{|Z|\times |Y_1|} & \quad \widetilde{{\mathbf{B}}}_2 \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,. \end{equation}
\begin{equation} \widetilde{{\mathbf{A}}}_1\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad \widetilde{{\mathbf{B}}}_1 & \quad \mathbf{0}_{|Z|\times |Y_2|} \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,,\quad \widetilde{{\mathbf{A}}}_2\,:\!=\, \begin{bmatrix} \mathbf{0}_{|Z|\times |Z|} & \quad \mathbf{0}_{|Z|\times |Y_1|} & \quad \widetilde{{\mathbf{B}}}_2 \\[4pt]
\mathbf{0}_{|Y|\times |Z|} & \quad \mathbf{0}_{|Y|\times |Y_1|} & \quad \mathbf{0}_{|Y|\times |Y_2|} \end{bmatrix}\,. \end{equation}
The expectation matrix of the perfect splitting, denoted by ![]() $\overline{{\mathbf{A}}}_1$(resp.
$\overline{{\mathbf{A}}}_1$(resp. ![]() $\overline{{\mathbf{A}}}_2$), can be written as
$\overline{{\mathbf{A}}}_2$), can be written as
 \begin{equation} \overline{{\mathbf{A}}}_1\,:\!=\, \begin{bmatrix} \mathbf{0}_{ \frac{n}{2} \times \frac{n}{2}} & \quad \overline{{\mathbf{B}}}_1 & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} \\[4pt]
\mathbf{0}_{\frac{n}{2}\times \frac{n}{2}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} \end{bmatrix}\,,\quad \overline{{\mathbf{A}}}_2\,:\!=\, \begin{bmatrix} \mathbf{0}_{ \frac{n}{2} \times \frac{n}{2}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} & \quad \overline{{\mathbf{B}}}_2\\[4pt]
\mathbf{0}_{\frac{n}{2}\times \frac{n}{2}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} \end{bmatrix}\,. \end{equation}
\begin{equation} \overline{{\mathbf{A}}}_1\,:\!=\, \begin{bmatrix} \mathbf{0}_{ \frac{n}{2} \times \frac{n}{2}} & \quad \overline{{\mathbf{B}}}_1 & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} \\[4pt]
\mathbf{0}_{\frac{n}{2}\times \frac{n}{2}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} \end{bmatrix}\,,\quad \overline{{\mathbf{A}}}_2\,:\!=\, \begin{bmatrix} \mathbf{0}_{ \frac{n}{2} \times \frac{n}{2}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} & \quad \overline{{\mathbf{B}}}_2\\[4pt]
\mathbf{0}_{\frac{n}{2}\times \frac{n}{2}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} & \quad \mathbf{0}_{\frac{n}{2}\times \frac{n}{4}} \end{bmatrix}\,. \end{equation}
Obviously, ![]() $\widetilde{{\mathbf{A}}}_i$ and
$\widetilde{{\mathbf{A}}}_i$ and ![]() $\widetilde{{\mathbf{B}}}_i$(resp.
$\widetilde{{\mathbf{B}}}_i$(resp. ![]() $\overline{{\mathbf{A}}}_i$ and
$\overline{{\mathbf{A}}}_i$ and ![]() $\overline{{\mathbf{B}}}_i$) have the same non-zero singular values for
$\overline{{\mathbf{B}}}_i$) have the same non-zero singular values for ![]() $i = 1, 2$. In the remaining of this section, we will deal with
$i = 1, 2$. In the remaining of this section, we will deal with ![]() $\widetilde{{\mathbf{A}}}_i$ and
$\widetilde{{\mathbf{A}}}_i$ and ![]() $\overline{{\mathbf{A}}}_i$ instead of
$\overline{{\mathbf{A}}}_i$ instead of ![]() $\widetilde{{\mathbf{B}}}_i$ and
$\widetilde{{\mathbf{B}}}_i$ and ![]() $\overline{{\mathbf{B}}}_i$ for
$\overline{{\mathbf{B}}}_i$ for ![]() $i = 1, 2$.
$i = 1, 2$.
5.1. Spectral partition: Proof of Lemma 4.1
5.1.1. Proof outline
Recall that ![]() ${\mathbf{A}}_1$ is defined as the adjacency matrix of the induced sub-hypergraph
${\mathbf{A}}_1$ is defined as the adjacency matrix of the induced sub-hypergraph ![]() $H[Y_1\cup Z]$ in equation (5.2). Consequently, the index set should contain information only from
$H[Y_1\cup Z]$ in equation (5.2). Consequently, the index set should contain information only from ![]() $H[Y_1\cup Z]$. Define the index sets
$H[Y_1\cup Z]$. Define the index sets
where ![]() $d = \sum _{m \in{\mathcal M}}(m-1)a_m$, and
$d = \sum _{m \in{\mathcal M}}(m-1)a_m$, and ![]() $\mathrm{row}(i)\big |_{Y_1 \cup Z}$ is the row sum of
$\mathrm{row}(i)\big |_{Y_1 \cup Z}$ is the row sum of ![]() $i$ on
$i$ on ![]() $H[Y_1\cup Z]$. We say
$H[Y_1\cup Z]$. We say ![]() $\mathrm{row}(i)\big |_{Y_1 \cup Z}=0$ if
$\mathrm{row}(i)\big |_{Y_1 \cup Z}=0$ if ![]() $i\not \in Y_1\cup Z$, and for vertex
$i\not \in Y_1\cup Z$, and for vertex ![]() $i\in Y_1\cup Z$,
$i\in Y_1\cup Z$,
 \begin{align*} \mathrm{row}(i)\Big |_{Y_1 \cup Z} \,:\!=\, \sum _{j=1}^{n} \sum _{m\in{\mathcal M}}\,\,\sum _{ \substack{e\in E_m[Y_1\cup Z]\\
\{i, j\}\subset e} } \,\, \boldsymbol{\mathcal{A}}_e^{(m)} = \sum _{m\in{\mathcal M}}(m-1)\sum _{ \substack{e\in E_m[Y_1\cup Z]\\
\{i, j\}\subset e} } \,\, \boldsymbol{\mathcal{A}}_e^{(m)}\,. \end{align*}
\begin{align*} \mathrm{row}(i)\Big |_{Y_1 \cup Z} \,:\!=\, \sum _{j=1}^{n} \sum _{m\in{\mathcal M}}\,\,\sum _{ \substack{e\in E_m[Y_1\cup Z]\\
\{i, j\}\subset e} } \,\, \boldsymbol{\mathcal{A}}_e^{(m)} = \sum _{m\in{\mathcal M}}(m-1)\sum _{ \substack{e\in E_m[Y_1\cup Z]\\
\{i, j\}\subset e} } \,\, \boldsymbol{\mathcal{A}}_e^{(m)}\,. \end{align*}
As a result, the matrix ![]() $({\mathbf{A}}_1)_{\mathcal{I}_1}$ is obtained by restricting
$({\mathbf{A}}_1)_{\mathcal{I}_1}$ is obtained by restricting ![]() ${\mathbf{A}}_1$ on index set
${\mathbf{A}}_1$ on index set ![]() $\mathcal{I}_1$. The next
$\mathcal{I}_1$. The next ![]() $4$ steps guarantee that Algorithm 4 outputs a
$4$ steps guarantee that Algorithm 4 outputs a ![]() $\nu$-correct partition.
$\nu$-correct partition.
(i) Find the singular subspace
 ${\mathbf{U}}$ spanned by the first
${\mathbf{U}}$ spanned by the first  $k$ left singular vectors of
$k$ left singular vectors of  $({\mathbf{A}}_1)_{\mathcal{I}_1}$.
$({\mathbf{A}}_1)_{\mathcal{I}_1}$.(ii) Randomly pick
 $s = 2k \log ^2 n$ vertices from
$s = 2k \log ^2 n$ vertices from  $Y_2$ and denote the corresponding columns in
$Y_2$ and denote the corresponding columns in  ${\mathbf{A}}_2$ by
${\mathbf{A}}_2$ by  $\boldsymbol{a}_{i_1},\dots,\boldsymbol{a}_{i_s}$. Project each vector
$\boldsymbol{a}_{i_1},\dots,\boldsymbol{a}_{i_s}$. Project each vector  $\boldsymbol{a}_i - \overline{\boldsymbol{a}}$ onto the singular subspace
$\boldsymbol{a}_i - \overline{\boldsymbol{a}}$ onto the singular subspace  ${\mathbf{U}}$, with
${\mathbf{U}}$, with  $\overline{\boldsymbol{a}}\in{\mathbb{R}}^{n}$ defined by
$\overline{\boldsymbol{a}}\in{\mathbb{R}}^{n}$ defined by  $\overline{\boldsymbol{a}}(j) = \unicode{x1D7D9}_{j\in Z} \cdot (\overline{\alpha } + \overline{\beta })/2$, where
$\overline{\boldsymbol{a}}(j) = \unicode{x1D7D9}_{j\in Z} \cdot (\overline{\alpha } + \overline{\beta })/2$, where  $\overline{\alpha }$,
$\overline{\alpha }$,  $\overline{\beta }$ were defined in (17).
$\overline{\beta }$ were defined in (17).(iii) For each projected vector
 $P_{{\mathbf{U}}}(\boldsymbol{a}_i - \overline{\boldsymbol{a}})$, identify the top
$P_{{\mathbf{U}}}(\boldsymbol{a}_i - \overline{\boldsymbol{a}})$, identify the top  $n/(2k)$ coordinates in value and place the corresponding vertices into a set
$n/(2k)$ coordinates in value and place the corresponding vertices into a set  $U^{\prime }_i$. Discard half of the obtained
$U^{\prime }_i$. Discard half of the obtained  $s$ subsets, those with the lowest blue edge densities.
$s$ subsets, those with the lowest blue edge densities.(iv) Sort the remaining sets according to blue hyperedge density and identify
 $k$ distinct subsets
$k$ distinct subsets  $U^{\prime }_1, \cdots, U^{\prime }_k$ such that
$U^{\prime }_1, \cdots, U^{\prime }_k$ such that  $|U^{\prime }_i \cap U^{\prime }_j| \lt \lceil (1 - \nu )n/k\rceil$ if
$|U^{\prime }_i \cap U^{\prime }_j| \lt \lceil (1 - \nu )n/k\rceil$ if  $i\neq j$.
$i\neq j$.
Based on the ![]() $4$ steps above in Algorithm 4, the proof of Lemma 4.1 is structured in
$4$ steps above in Algorithm 4, the proof of Lemma 4.1 is structured in ![]() $4$ parts.
$4$ parts.
(i) Let
 $\widetilde{{\mathbf{U}}}$ denote the subspace spanned by first
$\widetilde{{\mathbf{U}}}$ denote the subspace spanned by first  $k$ left singular vectors of
$k$ left singular vectors of  $\widetilde{{\mathbf{A}}}_1$ defined in (19). Subsection 5.1.2 shows that the subspace angle between
$\widetilde{{\mathbf{A}}}_1$ defined in (19). Subsection 5.1.2 shows that the subspace angle between  ${\mathbf{U}}$ and
${\mathbf{U}}$ and  $\widetilde{{\mathbf{U}}}$ is smaller than any
$\widetilde{{\mathbf{U}}}$ is smaller than any  $c\in (0, 1)$ as long as
$c\in (0, 1)$ as long as  $a_m, b_m$ satisfy certain conditions depending on
$a_m, b_m$ satisfy certain conditions depending on  $c$.
$c$.(ii) The vector
 $\widetilde{{\boldsymbol \delta }}_i$, defined in (22), reflects the underlying true partition
$\widetilde{{\boldsymbol \delta }}_i$, defined in (22), reflects the underlying true partition  $Z\cap V_{k(i)}$ for each
$Z\cap V_{k(i)}$ for each  $i\in [s]$, where
$i\in [s]$, where  $k(i)$ denotes the membership of vertex
$k(i)$ denotes the membership of vertex  $i$. Subsection 5.1.3 shows that
$i$. Subsection 5.1.3 shows that  $\overline{{\boldsymbol \delta }}_i$, an approximation of
$\overline{{\boldsymbol \delta }}_i$, an approximation of  $\widetilde{{\boldsymbol \delta }}_i$ defined in (23), can be recovered by the projected vector
$\widetilde{{\boldsymbol \delta }}_i$ defined in (23), can be recovered by the projected vector  $P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}})$, since projection error
$P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}})$, since projection error  $\|P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}}) - \overline{{\boldsymbol \delta }}_{i}\|_2 \lt c\|\overline{{\boldsymbol \delta }}_{i}\|_2$ for any
$\|P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}}) - \overline{{\boldsymbol \delta }}_{i}\|_2 \lt c\|\overline{{\boldsymbol \delta }}_{i}\|_2$ for any  $c\in (0, 1)$ if
$c\in (0, 1)$ if  $a_m, b_m$ satisfy the desired property in part (i).
$a_m, b_m$ satisfy the desired property in part (i).(iii) Subsection 5.1.4 indicates that the coincidence ratio between the remaining sets and the true partition is at least
 $\nu$, after discarding half of the sets with the lowest blue edge densities.
$\nu$, after discarding half of the sets with the lowest blue edge densities.(iv) Lemma 5.13 proves that we can find
 $k$ distinct subsets
$k$ distinct subsets  $U^{\prime }_i$ within
$U^{\prime }_i$ within  $k\log ^2 n$ trials with high probability.
$k\log ^2 n$ trials with high probability.
5.1.2. Bounding the angle between  ${\mathbf{U}}$ and
${\mathbf{U}}$ and  $\widetilde{{\mathbf{U}}}$
$\widetilde{{\mathbf{U}}}$
The angle between subspaces ![]() ${\mathbf{U}}$ and
${\mathbf{U}}$ and ![]() $\widetilde{{\mathbf{U}}}$ is defined as
$\widetilde{{\mathbf{U}}}$ is defined as
A natural idea is to apply Wedin’s ![]() $\sin \Theta$ Theorem (Lemma D.7). Lemma 5.3 indicates that the difference of
$\sin \Theta$ Theorem (Lemma D.7). Lemma 5.3 indicates that the difference of ![]() $\sigma _i(\widetilde{{\mathbf{A}}}_1)$ and
$\sigma _i(\widetilde{{\mathbf{A}}}_1)$ and ![]() $\sigma _i(\overline{{\mathbf{A}}}_1)$ is relatively small, compared to
$\sigma _i(\overline{{\mathbf{A}}}_1)$ is relatively small, compared to ![]() $\sigma _i(\overline{{\mathbf{A}}}_1)$.
$\sigma _i(\overline{{\mathbf{A}}}_1)$.
Lemma 5.3. Let ![]() $\sigma _i(\overline{{\mathbf{A}}}_1)$(resp.
$\sigma _i(\overline{{\mathbf{A}}}_1)$(resp. ![]() $\sigma _i(\widetilde{{\mathbf{A}}}_1)$) denote the singular values of
$\sigma _i(\widetilde{{\mathbf{A}}}_1)$) denote the singular values of ![]() $\overline{{\mathbf{A}}}_1$ (resp.
$\overline{{\mathbf{A}}}_1$ (resp. ![]() $\widetilde{{\mathbf{A}}}_1$) for all
$\widetilde{{\mathbf{A}}}_1$) for all ![]() $i\in [k]$, where the matrices
$i\in [k]$, where the matrices ![]() $\overline{{\mathbf{A}}}_1$ and
$\overline{{\mathbf{A}}}_1$ and ![]() $\widetilde{{\mathbf{A}}}_1$ are defined in (20) and (19) respectively. Then
$\widetilde{{\mathbf{A}}}_1$ are defined in (20) and (19) respectively. Then
 \begin{align*} \sigma _1(\overline{{\mathbf{A}}}_1) =&\,\frac{n\left [ \overline{\alpha } + (k-1)\overline{\beta } \right ] }{2\sqrt{2}k}= \frac{n}{2\sqrt{2}k}\sum _{m\in{\mathcal M}} \left [ \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}} + k\binom{\frac{3n}{4} - 2}{m-2}\frac{b_m}{\binom{n}{m-1}} \right ] \,,&\\[5pt]
\sigma _i(\overline{{\mathbf{A}}}_1) =&\, \frac{n( \overline{\alpha } - \overline{\beta })}{2\sqrt{2}k} = \frac{n}{2\sqrt{2}k}\sum _{m\in{\mathcal M}} \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}}\,, 2 \leq i \leq k\,,&\\[5pt]
\sigma _i(\overline{{\mathbf{A}}}_1) =&\, 0\,, k+1 \leq i \leq n\,.& \end{align*}
\begin{align*} \sigma _1(\overline{{\mathbf{A}}}_1) =&\,\frac{n\left [ \overline{\alpha } + (k-1)\overline{\beta } \right ] }{2\sqrt{2}k}= \frac{n}{2\sqrt{2}k}\sum _{m\in{\mathcal M}} \left [ \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}} + k\binom{\frac{3n}{4} - 2}{m-2}\frac{b_m}{\binom{n}{m-1}} \right ] \,,&\\[5pt]
\sigma _i(\overline{{\mathbf{A}}}_1) =&\, \frac{n( \overline{\alpha } - \overline{\beta })}{2\sqrt{2}k} = \frac{n}{2\sqrt{2}k}\sum _{m\in{\mathcal M}} \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}}\,, 2 \leq i \leq k\,,&\\[5pt]
\sigma _i(\overline{{\mathbf{A}}}_1) =&\, 0\,, k+1 \leq i \leq n\,.& \end{align*}
with ![]() $\overline{\alpha }$,
$\overline{\alpha }$, ![]() $\overline{\beta }$ defined in (17). Moreover, with probability at least
$\overline{\beta }$ defined in (17). Moreover, with probability at least ![]() $1 - 2k\exp ({-}k\log ^2(n))$,
$1 - 2k\exp ({-}k\log ^2(n))$,
Therefore, with Lemma 5.3, we can write ![]() $ \sigma _i(\widetilde{{\mathbf{A}}}_1) = \sigma _i(\overline{{\mathbf{A}}}_1)(1 + o(1)).$ Define
$ \sigma _i(\widetilde{{\mathbf{A}}}_1) = \sigma _i(\overline{{\mathbf{A}}}_1)(1 + o(1)).$ Define ![]() ${\mathbf{E}}_1 \,:\!=\,{\mathbf{A}}_1 - \widetilde{{\mathbf{A}}}_1$ and its restriction on
${\mathbf{E}}_1 \,:\!=\,{\mathbf{A}}_1 - \widetilde{{\mathbf{A}}}_1$ and its restriction on ![]() $\mathcal{I}_1$ as
$\mathcal{I}_1$ as
as well as ![]() ${\boldsymbol \Delta }_{1}\,:\!=\, (\widetilde{{\mathbf{A}}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1$. Then
${\boldsymbol \Delta }_{1}\,:\!=\, (\widetilde{{\mathbf{A}}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1$. Then ![]() $({\mathbf{A}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1$ is decomposed as
$({\mathbf{A}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1$ is decomposed as
Lemma 5.4. Let ![]() $d = \sum _{m\in{\mathcal M}} (m-1)a_m$, where
$d = \sum _{m\in{\mathcal M}} (m-1)a_m$, where ![]() $\mathcal M$ is obtained from Algorithm 3. There exists a constant
$\mathcal M$ is obtained from Algorithm 3. There exists a constant ![]() $C_1\geq (2^{1/{\mathcal M}_{\max }} - 1)^{-1/3}$ such that if
$C_1\geq (2^{1/{\mathcal M}_{\max }} - 1)^{-1/3}$ such that if ![]() $d \geq C_1$, then with probability at least
$d \geq C_1$, then with probability at least ![]() $1 - \exp\!\left ({-} d^{-2}n/{\mathcal M}_{\max } \right )$, no more than
$1 - \exp\!\left ({-} d^{-2}n/{\mathcal M}_{\max } \right )$, no more than ![]() $d^{-3}n$ vertices have row sums greater than
$d^{-3}n$ vertices have row sums greater than ![]() $20{\mathcal M}_{\max }d$.
$20{\mathcal M}_{\max }d$.
Lemma 5.4 shows that the number of high-degree vertices is relatively small. Consequently, Corollary 5.5 indicates ![]() $\|{\boldsymbol \Delta }_1\| \leq \sqrt{d}$ with high probability.
$\|{\boldsymbol \Delta }_1\| \leq \sqrt{d}$ with high probability.
Corollary 5.5. Assume ![]() $d \geq \max \{C_1, \sqrt{2}\}$, where
$d \geq \max \{C_1, \sqrt{2}\}$, where ![]() $C_1$ is the constant in Lemma 5.4, then
$C_1$ is the constant in Lemma 5.4, then ![]() $\|{\boldsymbol \Delta }_1\| \leq \sqrt{d}$ with probability at least
$\|{\boldsymbol \Delta }_1\| \leq \sqrt{d}$ with probability at least ![]() $1 - \exp\!\left ({-} d^{-2}n/{\mathcal M}_{\max } \right )$.
$1 - \exp\!\left ({-} d^{-2}n/{\mathcal M}_{\max } \right )$.
Proof of Corollary 5.5. Note that ![]() $n - |\mathcal{I}| \leq d^{-3}n$ and
$n - |\mathcal{I}| \leq d^{-3}n$ and ![]() $\mathcal{I} \subset \mathcal{I}_1$, then
$\mathcal{I} \subset \mathcal{I}_1$, then ![]() $n - |\mathcal{I}_1| \leq d^{-3}n$. From Lemma 5.4, there are at most
$n - |\mathcal{I}_1| \leq d^{-3}n$. From Lemma 5.4, there are at most ![]() $d^{-3} n$ vertices with row sum greater than
$d^{-3} n$ vertices with row sum greater than ![]() $20{\mathcal M}_{\max }d$ in the adjacency matrix
$20{\mathcal M}_{\max }d$ in the adjacency matrix ![]() ${\mathbf{A}}_1$, then the matrix
${\mathbf{A}}_1$, then the matrix ![]() ${\boldsymbol \Delta }_1 = (\widetilde{{\mathbf{A}}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1$ has at most
${\boldsymbol \Delta }_1 = (\widetilde{{\mathbf{A}}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1$ has at most ![]() $2d^{-3} n^{2}$ non-zero entries. Every entry of
$2d^{-3} n^{2}$ non-zero entries. Every entry of ![]() $\widetilde{{\mathbf{A}}}_1$ in (19) is bounded by
$\widetilde{{\mathbf{A}}}_1$ in (19) is bounded by ![]() $\alpha$, then,
$\alpha$, then,
 \begin{align*} \|{\boldsymbol \Delta }_1\| \leq &\, \|{\boldsymbol \Delta }_1 \|_{{\mathrm{F}}} = \|(\widetilde{{\mathbf{A}}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1\|_{{\mathrm{F}}} \\
\leq &\, \sqrt{2 d^{-3}n^{2}} \, \alpha = \sqrt{2 d^{-3}} n \sum _{m\in{\mathcal M}} \left [ \binom{ \frac{n}{k}-2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} +\left({n - 2 \atop m-2}\right) \frac{b_m}{\binom{n}{m-1}} \right ]\\
\leq &\, \sqrt{2d^{-3} } \sum _{m\in{\mathcal M}} (m-1)a_m \leq \sqrt{2d^{-1}} \leq \sqrt{d}\,. \end{align*}
\begin{align*} \|{\boldsymbol \Delta }_1\| \leq &\, \|{\boldsymbol \Delta }_1 \|_{{\mathrm{F}}} = \|(\widetilde{{\mathbf{A}}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1\|_{{\mathrm{F}}} \\
\leq &\, \sqrt{2 d^{-3}n^{2}} \, \alpha = \sqrt{2 d^{-3}} n \sum _{m\in{\mathcal M}} \left [ \binom{ \frac{n}{k}-2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} +\left({n - 2 \atop m-2}\right) \frac{b_m}{\binom{n}{m-1}} \right ]\\
\leq &\, \sqrt{2d^{-3} } \sum _{m\in{\mathcal M}} (m-1)a_m \leq \sqrt{2d^{-1}} \leq \sqrt{d}\,. \end{align*}
Moreover, taking ![]() $\tau =20{\mathcal M}_{\max }, K=3$ in Theorem 3.3, with probability at least
$\tau =20{\mathcal M}_{\max }, K=3$ in Theorem 3.3, with probability at least ![]() $1 - n^{-2}$
$1 - n^{-2}$
where constant ![]() $C_3$ depends on
$C_3$ depends on ![]() ${\mathcal M}_{\max }$. Together with upper bounds for
${\mathcal M}_{\max }$. Together with upper bounds for ![]() $\|({\mathbf{E}}_1)_{\mathcal{I}_1}\|$ and
$\|({\mathbf{E}}_1)_{\mathcal{I}_1}\|$ and ![]() $\|{\boldsymbol \Delta }_1\|$, Lemma 5.6 shows that the angle between
$\|{\boldsymbol \Delta }_1\|$, Lemma 5.6 shows that the angle between ![]() ${\mathbf{U}}$ and
${\mathbf{U}}$ and ![]() $\widetilde{{\mathbf{U}}}$ is relatively small with high probability.
$\widetilde{{\mathbf{U}}}$ is relatively small with high probability.
Lemma 5.6. For any ![]() $c\in (0,1)$, there exists some constant
$c\in (0,1)$, there exists some constant ![]() $C_2$ such that, if
$C_2$ such that, if
then ![]() $\sin \angle ({\mathbf{U}}, \widetilde{{\mathbf{U}}}) \leq c$ with probability
$\sin \angle ({\mathbf{U}}, \widetilde{{\mathbf{U}}}) \leq c$ with probability ![]() $1 - n^{-2}$. Here
$1 - n^{-2}$. Here ![]() $\angle ({\mathbf{U}}, \widetilde{{\mathbf{U}}})$ is the angle between
$\angle ({\mathbf{U}}, \widetilde{{\mathbf{U}}})$ is the angle between ![]() ${\mathbf{U}}$ and
${\mathbf{U}}$ and ![]() $\widetilde{{\mathbf{U}}}$.
$\widetilde{{\mathbf{U}}}$.
Proof of Lemma 5.6. From (22) and Corollary 5.5, with probability at least ![]() $1 - n^{-2}$,
$1 - n^{-2}$,
Since ![]() $\sigma _{k+1}(\widetilde{{\mathbf{A}}}_1)=0$, using Lemma 5.3 to approximate
$\sigma _{k+1}(\widetilde{{\mathbf{A}}}_1)=0$, using Lemma 5.3 to approximate ![]() $\sigma _k(\widetilde{{\mathbf{A}}}_1)$, we obtain
$\sigma _k(\widetilde{{\mathbf{A}}}_1)$, we obtain
 \begin{align*} &\,\sigma _k(\widetilde{{\mathbf{A}}}_1) - \sigma _{k+1}(\widetilde{{\mathbf{A}}}_1) =\sigma _k(\widetilde{{\mathbf{A}}}_1)=(1+o(1))\sigma _k(\overline{{\mathbf{A}}}_1) \geq \frac{1}{2}\sigma _k(\overline{{\mathbf{A}}}_1)\\[6pt]
\geq &\, \frac{n}{4\sqrt{2}k }\sum _{m \in{\mathcal M}}\left({ \frac{3n}{4k} -2 \atop m-2}\right) \frac{a_m - b_m}{\left({n \atop m-1}\right)} \geq \frac{1}{8k}\sum _{m\in{\mathcal M}} \bigg (\frac{3}{4k} \bigg )^{m-2}(m-1)(a_m-b_m)\\[6pt]
\geq &\, \frac{1}{8k}\left (\frac{1}{2k}\right )^{{\mathcal M}_{\max } - 2}\sum _{m\in{\mathcal M}} (m-1)(a_m-b_m)\geq \frac{C_2 \sqrt{d}}{2^{{\mathcal M}_{\max } + 1}}\,. \end{align*}
\begin{align*} &\,\sigma _k(\widetilde{{\mathbf{A}}}_1) - \sigma _{k+1}(\widetilde{{\mathbf{A}}}_1) =\sigma _k(\widetilde{{\mathbf{A}}}_1)=(1+o(1))\sigma _k(\overline{{\mathbf{A}}}_1) \geq \frac{1}{2}\sigma _k(\overline{{\mathbf{A}}}_1)\\[6pt]
\geq &\, \frac{n}{4\sqrt{2}k }\sum _{m \in{\mathcal M}}\left({ \frac{3n}{4k} -2 \atop m-2}\right) \frac{a_m - b_m}{\left({n \atop m-1}\right)} \geq \frac{1}{8k}\sum _{m\in{\mathcal M}} \bigg (\frac{3}{4k} \bigg )^{m-2}(m-1)(a_m-b_m)\\[6pt]
\geq &\, \frac{1}{8k}\left (\frac{1}{2k}\right )^{{\mathcal M}_{\max } - 2}\sum _{m\in{\mathcal M}} (m-1)(a_m-b_m)\geq \frac{C_2 \sqrt{d}}{2^{{\mathcal M}_{\max } + 1}}\,. \end{align*}
Then for any ![]() $c\in (0, 1)$, we can find
$c\in (0, 1)$, we can find ![]() $C_2 = [2^{{\mathcal M}_{\max } + 2}(C_3 + 1)/c]$ such that
$C_2 = [2^{{\mathcal M}_{\max } + 2}(C_3 + 1)/c]$ such that ![]() $\|({\mathbf{A}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1\|\leq (1-1/\sqrt{2}) \sigma _k(\widetilde{{\mathbf{A}}}_1)$. By Wedin’s Theorem (Lemma D.7), the angle
$\|({\mathbf{A}}_1)_{\mathcal{I}_1} - \widetilde{{\mathbf{A}}}_1\|\leq (1-1/\sqrt{2}) \sigma _k(\widetilde{{\mathbf{A}}}_1)$. By Wedin’s Theorem (Lemma D.7), the angle ![]() $\angle ({\mathbf{U}}, \widetilde{{\mathbf{U}}})$ is bounded by
$\angle ({\mathbf{U}}, \widetilde{{\mathbf{U}}})$ is bounded by
5.1.3. Bound the projection error
Randomly pick ![]() $s=2k\log ^2 n$ vertices from
$s=2k\log ^2 n$ vertices from ![]() $Y_2$. Let
$Y_2$. Let ![]() $\boldsymbol{a}_{i_1},\dots,\boldsymbol{a}_{i_s}$,
$\boldsymbol{a}_{i_1},\dots,\boldsymbol{a}_{i_s}$, ![]() $\widetilde{\boldsymbol{a}}_{i_1}$,
$\widetilde{\boldsymbol{a}}_{i_1}$,![]() $\dots$,
$\dots$, ![]() $\widetilde{\boldsymbol{a}}_{i_s}$,
$\widetilde{\boldsymbol{a}}_{i_s}$, ![]() $\overline{\boldsymbol{a}}_{i_1},\dots, \overline{\boldsymbol{a}}_{i_s}$ and
$\overline{\boldsymbol{a}}_{i_1},\dots, \overline{\boldsymbol{a}}_{i_s}$ and ![]() $\boldsymbol{e}_{i_1}, \dots,\boldsymbol{e}_{i_s}$ be the corresponding columns of
$\boldsymbol{e}_{i_1}, \dots,\boldsymbol{e}_{i_s}$ be the corresponding columns of ![]() ${\mathbf{A}}_2$,
${\mathbf{A}}_2$, ![]() $\widetilde{{\mathbf{A}}}_2$,
$\widetilde{{\mathbf{A}}}_2$, ![]() $\overline{{\mathbf{A}}}_2$ and
$\overline{{\mathbf{A}}}_2$ and ![]() ${\mathbf{E}}_2\,:\!=\,{\mathbf{A}}_2 - \widetilde{{\mathbf{A}}}_2$ respectively, where
${\mathbf{E}}_2\,:\!=\,{\mathbf{A}}_2 - \widetilde{{\mathbf{A}}}_2$ respectively, where ![]() ${\mathbf{A}}_2$,
${\mathbf{A}}_2$, ![]() $\widetilde{{\mathbf{A}}}_2$ and
$\widetilde{{\mathbf{A}}}_2$ and ![]() $\overline{{\mathbf{A}}}_2$ were defined in (18), (19) and (20). Let
$\overline{{\mathbf{A}}}_2$ were defined in (18), (19) and (20). Let ![]() $k(i)$ denote the membership of vertex
$k(i)$ denote the membership of vertex ![]() $i$. Note that entries of vector
$i$. Note that entries of vector ![]() $\widetilde{\boldsymbol{a}}_{i}$ are
$\widetilde{\boldsymbol{a}}_{i}$ are ![]() $\widetilde{\alpha }_{ii}$,
$\widetilde{\alpha }_{ii}$, ![]() $\widetilde{\beta }_{ij}$ or
$\widetilde{\beta }_{ij}$ or ![]() $0$, according to the membership of vertices in
$0$, according to the membership of vertices in ![]() $Z$, where
$Z$, where ![]() $\widetilde{\alpha }_{ii}$,
$\widetilde{\alpha }_{ii}$, ![]() $\widetilde{\beta }_{ij}$ were defined in (15a), (15b). Then the corresponding vector
$\widetilde{\beta }_{ij}$ were defined in (15a), (15b). Then the corresponding vector ![]() $\widetilde{{\boldsymbol \delta }}_i \in{\mathbb{R}}^{n}$ with the entries given by
$\widetilde{{\boldsymbol \delta }}_i \in{\mathbb{R}}^{n}$ with the entries given by
 \begin{equation} \widetilde{\boldsymbol{a}}_{i}(j) = \begin{cases} \widetilde{\alpha }_{ii}, & \mathrm{if } j\in Z\cap V_{k(i)}\\[6pt]
\widetilde{\beta }_{ij}, & \mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0\,, & \mathrm{if } j\in Y \end{cases}\,,\quad \widetilde{{\boldsymbol \delta }}_i(j) = \begin{cases} (\widetilde{\alpha }_{ii} - \widetilde{\beta }_{ij})/2 \gt 0, & \mathrm{if } j\in Z\cap V_{k(i)} \\[6pt]
(\widetilde{\beta }_{ij} - \widetilde{\alpha }_{ii})/2 \lt 0, & \mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0, & \mathrm{if } j\in Y \end{cases}, \end{equation}
\begin{equation} \widetilde{\boldsymbol{a}}_{i}(j) = \begin{cases} \widetilde{\alpha }_{ii}, & \mathrm{if } j\in Z\cap V_{k(i)}\\[6pt]
\widetilde{\beta }_{ij}, & \mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0\,, & \mathrm{if } j\in Y \end{cases}\,,\quad \widetilde{{\boldsymbol \delta }}_i(j) = \begin{cases} (\widetilde{\alpha }_{ii} - \widetilde{\beta }_{ij})/2 \gt 0, & \mathrm{if } j\in Z\cap V_{k(i)} \\[6pt]
(\widetilde{\beta }_{ij} - \widetilde{\alpha }_{ii})/2 \lt 0, & \mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0, & \mathrm{if } j\in Y \end{cases}, \end{equation}
can be used to recover the vertex set ![]() $Z\cap V_{k(i)}$ based on the sign of elements in
$Z\cap V_{k(i)}$ based on the sign of elements in ![]() $\widetilde{{\boldsymbol \delta }}_i$. However, it is hard to handle with
$\widetilde{{\boldsymbol \delta }}_i$. However, it is hard to handle with ![]() $\widetilde{{\boldsymbol \delta }}_i$ due to the randomness of
$\widetilde{{\boldsymbol \delta }}_i$ due to the randomness of ![]() $\widetilde{\alpha }_{ii}$,
$\widetilde{\alpha }_{ii}$, ![]() $\widetilde{\beta }_{ij}$ originated from
$\widetilde{\beta }_{ij}$ originated from ![]() $n_i$ and
$n_i$ and ![]() $n^{\prime }_i$. Note that
$n^{\prime }_i$. Note that ![]() $n_i$ and
$n_i$ and ![]() $n^{\prime }_i$ concentrate around
$n^{\prime }_i$ concentrate around ![]() $n/(2k)$ and
$n/(2k)$ and ![]() $n/(4k)$ respectively as shown in Lemma 5.3. Thus a good approximation of
$n/(4k)$ respectively as shown in Lemma 5.3. Thus a good approximation of ![]() $\widetilde{{\boldsymbol \delta }}_i$, which rules out randomness of
$\widetilde{{\boldsymbol \delta }}_i$, which rules out randomness of ![]() $n_i$ and
$n_i$ and ![]() $n^{\prime }_i$, was given by
$n^{\prime }_i$, was given by ![]() $\overline{{\boldsymbol \delta }}_i \,:\!=\, \overline{\boldsymbol{a}}_{i} - \overline{\boldsymbol{a}}$, with entries given by
$\overline{{\boldsymbol \delta }}_i \,:\!=\, \overline{\boldsymbol{a}}_{i} - \overline{\boldsymbol{a}}$, with entries given by ![]() $\overline{\boldsymbol{a}}(j)\,:\!=\, \unicode{x1D7D9}_{j\in Z}\cdot (\overline{\alpha } + \overline{\beta })/2$, where
$\overline{\boldsymbol{a}}(j)\,:\!=\, \unicode{x1D7D9}_{j\in Z}\cdot (\overline{\alpha } + \overline{\beta })/2$, where ![]() $\overline{\alpha }$ and
$\overline{\alpha }$ and ![]() $\overline{\beta }$ were defined in (17), and
$\overline{\beta }$ were defined in (17), and
 \begin{equation} \overline{\boldsymbol{a}}_i (j) = \begin{cases} \overline{\alpha }, \quad &\mathrm{if } j\in Z\cap V_{k(i)} \\[6pt]
\overline{\beta }, \quad &\mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0, \quad &\mathrm{if } j\in Y \end{cases} \,,\quad \overline{{\boldsymbol \delta }}_i(j) = \begin{cases} (\overline{\alpha } - \overline{\beta })/2 \gt 0, \quad & \mathrm{if } j\in Z\cap V_{k(i)} \\[6pt]
(\overline{\beta } - \overline{\alpha })/2 \lt 0, \quad &\mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0, \quad &\mathrm{if } j\in Y \end{cases} \,. \end{equation}
\begin{equation} \overline{\boldsymbol{a}}_i (j) = \begin{cases} \overline{\alpha }, \quad &\mathrm{if } j\in Z\cap V_{k(i)} \\[6pt]
\overline{\beta }, \quad &\mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0, \quad &\mathrm{if } j\in Y \end{cases} \,,\quad \overline{{\boldsymbol \delta }}_i(j) = \begin{cases} (\overline{\alpha } - \overline{\beta })/2 \gt 0, \quad & \mathrm{if } j\in Z\cap V_{k(i)} \\[6pt]
(\overline{\beta } - \overline{\alpha })/2 \lt 0, \quad &\mathrm{if } j\in Z\setminus V_{k(i)} \\[6pt]
0, \quad &\mathrm{if } j\in Y \end{cases} \,. \end{equation}
By construction, ![]() $\overline{{\boldsymbol \delta }}_i$ identifies vertex set
$\overline{{\boldsymbol \delta }}_i$ identifies vertex set ![]() $Z \cap V_{k(i)}$ in the case of perfect splitting for any
$Z \cap V_{k(i)}$ in the case of perfect splitting for any ![]() $i\in \{i_1, \cdots, i_s\}\cap Y_2\cap V_{k(i)}$. However, the access to
$i\in \{i_1, \cdots, i_s\}\cap Y_2\cap V_{k(i)}$. However, the access to ![]() $\overline{{\boldsymbol \delta }}_i$ is limited in practice, thus the projection
$\overline{{\boldsymbol \delta }}_i$ is limited in practice, thus the projection ![]() $P_{{\mathbf{U}}}(\boldsymbol{a}_i - \overline{\boldsymbol{a}})$ is used instead as an approximation of
$P_{{\mathbf{U}}}(\boldsymbol{a}_i - \overline{\boldsymbol{a}})$ is used instead as an approximation of ![]() $\overline{{\boldsymbol \delta }}_i$. Lemma 5.7 proves that at least half of the projected vectors have small projection errors.
$\overline{{\boldsymbol \delta }}_i$. Lemma 5.7 proves that at least half of the projected vectors have small projection errors.
Lemma 5.7. For any ![]() $c\in (0, 1)$, there exist constants
$c\in (0, 1)$, there exist constants ![]() $C_1$ and
$C_1$ and ![]() $C_2$ such that if
$C_2$ such that if ![]() $d\gt C_1$ and
$d\gt C_1$ and
then among all projected vectors ![]() $P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}})$ for
$P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}})$ for ![]() $i\in \{i_1, \cdots, i_s\}\cap Y_2$, with probability
$i\in \{i_1, \cdots, i_s\}\cap Y_2$, with probability ![]() $1 - O(n^{-k})$, at least half of them satisfy
$1 - O(n^{-k})$, at least half of them satisfy
Proof Lemma 5.7. Note that ![]() $\overline{{\boldsymbol \delta }}_i = P_{\overline{{\mathbf{U}}}}\overline{{\boldsymbol \delta }}_i$, where
$\overline{{\boldsymbol \delta }}_i = P_{\overline{{\mathbf{U}}}}\overline{{\boldsymbol \delta }}_i$, where ![]() $\overline{{\mathbf{U}}}$ is spanned by the first
$\overline{{\mathbf{U}}}$ is spanned by the first ![]() $k$ left singular vectors of
$k$ left singular vectors of ![]() $\overline{{\mathbf{A}}}_1$ with
$\overline{{\mathbf{A}}}_1$ with ![]() $\mathrm{rank}(\overline{{\mathbf{A}}}_1) = k$, and
$\mathrm{rank}(\overline{{\mathbf{A}}}_1) = k$, and ![]() $\overline{{\mathbf{A}}}_1$,
$\overline{{\mathbf{A}}}_1$, ![]() $\overline{{\mathbf{A}}}_2$ preserve the same eigen-subspace. The approximation error between
$\overline{{\mathbf{A}}}_2$ preserve the same eigen-subspace. The approximation error between ![]() $ P_{{\mathbf{U}}}(\boldsymbol{a}_i - \overline{\boldsymbol{a}})$ and
$ P_{{\mathbf{U}}}(\boldsymbol{a}_i - \overline{\boldsymbol{a}})$ and ![]() $\overline{{\boldsymbol \delta }}_i$ can be decomposed as
$\overline{{\boldsymbol \delta }}_i$ can be decomposed as
Then by triangle inequality,
Note that ![]() $\|\overline{{\boldsymbol \delta }}_i\| = O(n^{-\frac{1}{2} })$ and
$\|\overline{{\boldsymbol \delta }}_i\| = O(n^{-\frac{1}{2} })$ and ![]() $n^{\prime }_{i}$ concentrates around
$n^{\prime }_{i}$ concentrates around ![]() $n/(4k)$ for each
$n/(4k)$ for each ![]() $i\in [k]$ with deviation at most
$i\in [k]$ with deviation at most ![]() $\sqrt{n}\log (n)$, then by definitions of
$\sqrt{n}\log (n)$, then by definitions of ![]() $\overline{\alpha }$ and
$\overline{\alpha }$ and ![]() $\overline{\beta }$ in (17),
$\overline{\beta }$ in (17),
Meanwhile, by an argument similar to Lemma 5.6, it can be proved that ![]() $\sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \lt c/2$ for any
$\sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \lt c/2$ for any ![]() $c\in (0, 1)$, if constants
$c\in (0, 1)$, if constants ![]() $C_1, C_2$ are chosen properly, hence
$C_1, C_2$ are chosen properly, hence ![]() $\|P_{{\mathbf{U}}} - P_{\overline{{\mathbf{U}}}}\|\cdot \|\overline{{\boldsymbol \delta }}_i\|_{2}\lt \frac{c}{2} \|\overline{{\boldsymbol \delta }}_i\|_{2}$. Lemma 5.8 shows that at least half of the indices from
$\|P_{{\mathbf{U}}} - P_{\overline{{\mathbf{U}}}}\|\cdot \|\overline{{\boldsymbol \delta }}_i\|_{2}\lt \frac{c}{2} \|\overline{{\boldsymbol \delta }}_i\|_{2}$. Lemma 5.8 shows that at least half of the indices from ![]() $\{i_1, \cdots, i_s\}\cap Y_2$ satisfy
$\{i_1, \cdots, i_s\}\cap Y_2$ satisfy ![]() $\|P_{{\mathbf{U}}}\boldsymbol{e}_i \|_2 \lt \frac{c}{2}\|\overline{{\boldsymbol \delta }}_{i}\|_2$, which completes the proof.
$\|P_{{\mathbf{U}}}\boldsymbol{e}_i \|_2 \lt \frac{c}{2}\|\overline{{\boldsymbol \delta }}_{i}\|_2$, which completes the proof.
Lemma 5.8. Let ![]() $d = \sum _{m\in{\mathcal M}_{\max }} (m-1)a_m$. For any
$d = \sum _{m\in{\mathcal M}_{\max }} (m-1)a_m$. For any ![]() $c\in (0, 1)$, with probability
$c\in (0, 1)$, with probability ![]() $1 - O(n^{-k\log n})$, at least
$1 - O(n^{-k\log n})$, at least ![]() $\frac{s}{2}$ of the vectors
$\frac{s}{2}$ of the vectors ![]() $\boldsymbol{e}_{i_1}, \dots,\boldsymbol{e}_{i_s}$ satisfy
$\boldsymbol{e}_{i_1}, \dots,\boldsymbol{e}_{i_s}$ satisfy
Definition 5.9. The vector ![]() $\boldsymbol{a}_i$ satisfying (25) is referred as good vector. The index of the good vector is hence referred to as a good vertex.
$\boldsymbol{a}_i$ satisfying (25) is referred as good vector. The index of the good vector is hence referred to as a good vertex.
To avoid introducing extra notations, let ![]() $\boldsymbol{a}_{i_1}, \dots,\boldsymbol{a}_{i_{s_1}}$ denote good vectors with
$\boldsymbol{a}_{i_1}, \dots,\boldsymbol{a}_{i_{s_1}}$ denote good vectors with ![]() $i_1, \cdots, i_{s_1}$ denoting good indices. Lemma 5.8 indicates that the number of good vectors is at least
$i_1, \cdots, i_{s_1}$ denoting good indices. Lemma 5.8 indicates that the number of good vectors is at least ![]() $s_1\geq \frac{s}{2} = k\log ^2 n$.
$s_1\geq \frac{s}{2} = k\log ^2 n$.
5.1.4. Accuracy
We are going to prove the accuracy of the initial partition obtained from Algorithm 4. Lemmas 5.10, 5.11 and 5.13 are crucial in proving our results. We present the proof logic first and defer the Lemma statements later.
For each projected vector ![]() $P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}})$, let
$P_{{\mathbf{U}}}(\boldsymbol{a}_{i} - \overline{\boldsymbol{a}})$, let ![]() $U^{\prime }_{i}$ denote the set of its largest
$U^{\prime }_{i}$ denote the set of its largest ![]() $\frac{n}{2k}$ coordinates, where
$\frac{n}{2k}$ coordinates, where ![]() $i\in \{i_1, \cdots, i_s\}$ and
$i\in \{i_1, \cdots, i_s\}$ and ![]() $s = 2k \log ^2 n$. Note that vector
$s = 2k \log ^2 n$. Note that vector ![]() $\overline{{\boldsymbol \delta }}_{i_j}$ in (23) only identifies blocks
$\overline{{\boldsymbol \delta }}_{i_j}$ in (23) only identifies blocks ![]() $V_{k(i_j)}$ and
$V_{k(i_j)}$ and ![]() $V\setminus V_{k(i_j)}$, which can be regarded as clustering two blocks with different sizes. By Lemma 5.7, good vectors satisfy
$V\setminus V_{k(i_j)}$, which can be regarded as clustering two blocks with different sizes. By Lemma 5.7, good vectors satisfy ![]() $\|P_{{\mathbf{U}}}(\boldsymbol{a}_{i_j} - \overline{\boldsymbol{a}}) - \overline{{\boldsymbol \delta }}_{i_j}\|_2 \lt c \, \|\overline{{\boldsymbol \delta }}_{i_j}\|_2$ for any
$\|P_{{\mathbf{U}}}(\boldsymbol{a}_{i_j} - \overline{\boldsymbol{a}}) - \overline{{\boldsymbol \delta }}_{i_j}\|_2 \lt c \, \|\overline{{\boldsymbol \delta }}_{i_j}\|_2$ for any ![]() $c\in (0, 1)$. Then by Lemma 5.10 (after proper normalisation), for a good index
$c\in (0, 1)$. Then by Lemma 5.10 (after proper normalisation), for a good index ![]() $i_j$, the number of vertices in
$i_j$, the number of vertices in ![]() $U^{\prime }_{i_j}$ clustered correctly is at least
$U^{\prime }_{i_j}$ clustered correctly is at least ![]() $(1 - \frac{4}{3}kc^{2})\frac{n}{k}$. By choosing
$(1 - \frac{4}{3}kc^{2})\frac{n}{k}$. By choosing ![]() $c = \sqrt{3(1-\nu )/(8k)}$, the condition
$c = \sqrt{3(1-\nu )/(8k)}$, the condition ![]() $|U^{\prime }_{i_j} \cap V_i| \gt (1+\nu )/2 |U^{\prime }_{i_j}|$ in part (ii) of Lemma 5.11 is satisfied. In Lemma 5.6, we choose
$|U^{\prime }_{i_j} \cap V_i| \gt (1+\nu )/2 |U^{\prime }_{i_j}|$ in part (ii) of Lemma 5.11 is satisfied. In Lemma 5.6, we choose
where ![]() $C_3$ defined in (22). Hence, with high probability, all good vectors have at least
$C_3$ defined in (22). Hence, with high probability, all good vectors have at least ![]() $\mu _{\mathrm{T}}$ blue hyperedges (we call this “high blue hyperedge density”). From Lemma 5.8, at least half of the selected vectors are good. Then, in Algorithm 4, throwing out half of the obtained sets
$\mu _{\mathrm{T}}$ blue hyperedges (we call this “high blue hyperedge density”). From Lemma 5.8, at least half of the selected vectors are good. Then, in Algorithm 4, throwing out half of the obtained sets ![]() $U^{\prime }_{i}$ (those with the lowest blue hyperedge density) guarantees that the remaining sets are good.
$U^{\prime }_{i}$ (those with the lowest blue hyperedge density) guarantees that the remaining sets are good.
Recall that, by choosing constant appropriately, we can make the subspace angle ![]() $\sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \lt c$ for any
$\sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \lt c$ for any ![]() $c\in (0, 1)$ (
$c\in (0, 1)$ (![]() $\overline{{\mathbf{U}}}$ is spanned by the first
$\overline{{\mathbf{U}}}$ is spanned by the first ![]() $k$ left singular vectors of
$k$ left singular vectors of ![]() $\overline{{\mathbf{A}}}_1$). Then for each vector
$\overline{{\mathbf{A}}}_1$). Then for each vector ![]() $\overline{{\boldsymbol \delta }}_{i_1}, \cdots, \overline{{\boldsymbol \delta }}_{i_k}$ with each
$\overline{{\boldsymbol \delta }}_{i_1}, \cdots, \overline{{\boldsymbol \delta }}_{i_k}$ with each ![]() $i_j$ selected from different vertex set
$i_j$ selected from different vertex set ![]() $V_j$, there is a vector
$V_j$, there is a vector ![]() $P_{{\mathbf{U}}}(\boldsymbol{a}_{i_j} - \overline{\boldsymbol{a}})$ in
$P_{{\mathbf{U}}}(\boldsymbol{a}_{i_j} - \overline{\boldsymbol{a}})$ in ![]() ${\mathbf{U}}$ arbitrarily close to
${\mathbf{U}}$ arbitrarily close to ![]() $\overline{{\boldsymbol \delta }}_{i_j}$, which was proved by Lemma 5.7. From (i) of Lemma 5.11, so obtained
$\overline{{\boldsymbol \delta }}_{i_j}$, which was proved by Lemma 5.7. From (i) of Lemma 5.11, so obtained ![]() $U_{i_j}^{\prime }$ must satisfy
$U_{i_j}^{\prime }$ must satisfy ![]() $|U_{i_j}^{\prime }\cap V_j|\geq \nu |U_{i_j}^{\prime }|$ for each
$|U_{i_j}^{\prime }\cap V_j|\geq \nu |U_{i_j}^{\prime }|$ for each ![]() $j\in [k]$. The remaining thing is to select
$j\in [k]$. The remaining thing is to select ![]() $k$ different
$k$ different ![]() $U_{i_j}^{\prime }$ with each of them concentrating around distinct
$U_{i_j}^{\prime }$ with each of them concentrating around distinct ![]() $V_j$ for each
$V_j$ for each ![]() $j\in [k]$. This problem is equivalent to finding
$j\in [k]$. This problem is equivalent to finding ![]() $k$ vertices in
$k$ vertices in ![]() $Y_2$, each from a different partition class, which can be done with
$Y_2$, each from a different partition class, which can be done with ![]() $k\log ^2(n)$ samplings as shown in Lemma 5.13.
$k\log ^2(n)$ samplings as shown in Lemma 5.13.
To summarise, this section is a more precise and quantitative version of the following argument: with high probability,
 \begin{align*}
\left \{ i_j \,:\, \exists i\,\mbox{s.t.}\,|U^{\prime}_{i_j} \cap V_i| \geq \frac{1+\nu }{2} \frac{n}{k}\right \} & \subset \left \{ i_j \,:\, U^{\prime}_{i_j} \text{ has $\geq \mu _T$ blue hyperedges}\right \}\\
& \subset \left \{ i_j\,:\, \exists i\,\mbox{s.t.}\,|U^{\prime}_{i_j} \cap V_i| \geq \nu \frac{n}{k}\right \} \,. \end{align*}
\begin{align*}
\left \{ i_j \,:\, \exists i\,\mbox{s.t.}\,|U^{\prime}_{i_j} \cap V_i| \geq \frac{1+\nu }{2} \frac{n}{k}\right \} & \subset \left \{ i_j \,:\, U^{\prime}_{i_j} \text{ has $\geq \mu _T$ blue hyperedges}\right \}\\
& \subset \left \{ i_j\,:\, \exists i\,\mbox{s.t.}\,|U^{\prime}_{i_j} \cap V_i| \geq \nu \frac{n}{k}\right \} \,. \end{align*}
Lemma 5.10 (Adapted from Lemma 23 in [Reference Chin, Rao and Van19]). Suppose ![]() $n, k$ are such that
$n, k$ are such that ![]() $\frac{n}{k} \in \mathbb{N}$. Let
$\frac{n}{k} \in \mathbb{N}$. Let ![]() $\boldsymbol{v},\bar{\boldsymbol{v}} \in{\mathbb{R}}^n$ be two unit vectors, and let
$\boldsymbol{v},\bar{\boldsymbol{v}} \in{\mathbb{R}}^n$ be two unit vectors, and let ![]() $\bar{\boldsymbol{v}}$ be such that
$\bar{\boldsymbol{v}}$ be such that ![]() $\frac{n}{k}$ of its entries are equal to
$\frac{n}{k}$ of its entries are equal to ![]() $\frac{1}{\sqrt{n}}$ and the rest are equal to
$\frac{1}{\sqrt{n}}$ and the rest are equal to ![]() $-\frac{1}{\sqrt{n}}$. If
$-\frac{1}{\sqrt{n}}$. If ![]() $\sin \angle (\bar{\boldsymbol{v}},\boldsymbol{v}) \lt c \leq 0.5$, then
$\sin \angle (\bar{\boldsymbol{v}},\boldsymbol{v}) \lt c \leq 0.5$, then ![]() $\boldsymbol{v}$ contains at least
$\boldsymbol{v}$ contains at least ![]() $(1 - \frac{4}{3}kc^{2}) \frac{n}{k}$ positive entries
$(1 - \frac{4}{3}kc^{2}) \frac{n}{k}$ positive entries ![]() $\boldsymbol{v}_i$ such that
$\boldsymbol{v}_i$ such that ![]() $\bar{\boldsymbol{v}}_i$ is also positive.
$\bar{\boldsymbol{v}}_i$ is also positive.
Lemma 5.11. Suppose that we are given a set ![]() $X \subset Z$ with size
$X \subset Z$ with size ![]() $|X| = n/(2k)$. Define
$|X| = n/(2k)$. Define
 \begin{align*} \mu _1\,:\!=\,&\,\frac{1}{2} \sum _{m\in{\mathcal M}}m(m-1) \left \{ \left [ \binom{\frac{\nu n}{2k}}{m} + \binom{\frac{(1 - \nu )n}{2k}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \}\,,\\
\mu _{2} \,:\!=\,&\, \frac{1}{2} \sum _{m\in{\mathcal M}} m(m-1)\left \{ \left [ \binom{\frac{(1 + \nu ) n}{4k} }{m} + (k-1)\binom{ \frac{(1 - \nu )n}{4k(k-1)}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \}\,, \end{align*}
\begin{align*} \mu _1\,:\!=\,&\,\frac{1}{2} \sum _{m\in{\mathcal M}}m(m-1) \left \{ \left [ \binom{\frac{\nu n}{2k}}{m} + \binom{\frac{(1 - \nu )n}{2k}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \}\,,\\
\mu _{2} \,:\!=\,&\, \frac{1}{2} \sum _{m\in{\mathcal M}} m(m-1)\left \{ \left [ \binom{\frac{(1 + \nu ) n}{4k} }{m} + (k-1)\binom{ \frac{(1 - \nu )n}{4k(k-1)}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \}\,, \end{align*}
and ![]() $\mu _{\mathrm{T}} \,:\!=\, (\mu _1 + \mu _2)/2 \in [\mu _1, \mu _2]$. There is a constant
$\mu _{\mathrm{T}} \,:\!=\, (\mu _1 + \mu _2)/2 \in [\mu _1, \mu _2]$. There is a constant ![]() $c\gt 0$ depending on
$c\gt 0$ depending on ![]() $k, a_m, \nu$ such that for sufficiently large
$k, a_m, \nu$ such that for sufficiently large ![]() $n$,
$n$,
(i) If
 $|X\cap V_i| \leq \nu |X|$ for each
$|X\cap V_i| \leq \nu |X|$ for each  $i\in [k]$, then with probability
$i\in [k]$, then with probability  $1 - e^{-cn}$, the number of blue hyperedges in the hypergraph induced by
$1 - e^{-cn}$, the number of blue hyperedges in the hypergraph induced by  $X$ is at most
$X$ is at most  $\mu _{\mathrm{T}}$.
$\mu _{\mathrm{T}}$.(ii) Conversely, if
 $|X\cap V_i| \geq \frac{1+ \nu }{2}|X|$ for some
$|X\cap V_i| \geq \frac{1+ \nu }{2}|X|$ for some  $i\in \{1, \dots, k\}$, then with probability
$i\in \{1, \dots, k\}$, then with probability  $1 - e^{-cn}$, the number of blue hyperedges in the hypergraph induced by
$1 - e^{-cn}$, the number of blue hyperedges in the hypergraph induced by  $X$ is at least
$X$ is at least  $\mu _{\mathrm{T}}$.
$\mu _{\mathrm{T}}$.
Remark 5.12. Lemma 5.11 is reduced to [Reference Chin, Rao and Van19, Lemma 31] when ![]() ${\mathcal M} = \{2\}$.
${\mathcal M} = \{2\}$.
Lemma 5.13. Through random sampling without replacement in Step ![]() $6$ of Algorithm 4, we can find at least
$6$ of Algorithm 4, we can find at least ![]() $k$ indices
$k$ indices ![]() $i_1,\dots, i_k$ in
$i_1,\dots, i_k$ in ![]() $Y_2$ among
$Y_2$ among ![]() $k\log ^2 n$ samples such that with probability
$k\log ^2 n$ samples such that with probability ![]() $1 -n^{-\Omega (\log n)}$,
$1 -n^{-\Omega (\log n)}$,
5.2. Local correction: Proof of Lemma 4.2
For notation convenience, let ![]() $U_i\,:\!=\, Z \cap V_i$ denote the intersection of
$U_i\,:\!=\, Z \cap V_i$ denote the intersection of ![]() $Z$ and true partition
$Z$ and true partition ![]() $V_i$ for all
$V_i$ for all ![]() $i\in [k]$. In Algorithm 2, we first colour the hyperedges with red and blue with equal probability. By running Algorithm 4 on the red hypergraph, we obtain a
$i\in [k]$. In Algorithm 2, we first colour the hyperedges with red and blue with equal probability. By running Algorithm 4 on the red hypergraph, we obtain a ![]() $\nu$-correct partition
$\nu$-correct partition ![]() $U_1^{\prime }, \dots, U_k^{\prime }$, i.e.,
$U_1^{\prime }, \dots, U_k^{\prime }$, i.e.,
In the rest of this subsection, we condition on the event that (27) holds true.
Consider a hyperedge ![]() $e = \{i_{1}, \cdots, i_{m}\}$ in the underlying
$e = \{i_{1}, \cdots, i_{m}\}$ in the underlying ![]() $m$-uniform hypergraph. If vertices
$m$-uniform hypergraph. If vertices ![]() $i_{1}, \cdots, i_{m}$ are from the same block, then
$i_{1}, \cdots, i_{m}$ are from the same block, then ![]() $e$ is a red hyperedge with probability
$e$ is a red hyperedge with probability ![]() $a_{m}/2\binom{n}{m-1}$; if vertices
$a_{m}/2\binom{n}{m-1}$; if vertices ![]() $i_{1}, \cdots, i_{m}$ are not from the same block, then
$i_{1}, \cdots, i_{m}$ are not from the same block, then ![]() $e$ is a red hyperedge with probability
$e$ is a red hyperedge with probability ![]() $b_{m}/2\binom{n}{m-1}$. The presence of those two types of hyperedges can be denoted by
$b_{m}/2\binom{n}{m-1}$. The presence of those two types of hyperedges can be denoted by
 \begin{equation*} T_{e}^{(a_m)}\sim \mathrm {Bernoulli}\left ( \frac {a_{m}}{ 2\left({n \atop m-1}\right) }\right )\,, \quad T_{e}^{(b_m)}\sim \mathrm {Bernoulli}\left ( \frac {b_{m}}{ 2\left({n \atop m-1}\right) }\right )\,, \end{equation*}
\begin{equation*} T_{e}^{(a_m)}\sim \mathrm {Bernoulli}\left ( \frac {a_{m}}{ 2\left({n \atop m-1}\right) }\right )\,, \quad T_{e}^{(b_m)}\sim \mathrm {Bernoulli}\left ( \frac {b_{m}}{ 2\left({n \atop m-1}\right) }\right )\,, \end{equation*}
respectively. For any finite set ![]() $S$, let
$S$, let ![]() $[S]^{l}$ denote the family of
$[S]^{l}$ denote the family of ![]() $l$-subsets of
$l$-subsets of ![]() $S$, i.e.,
$S$, i.e., ![]() $[S]^{l} = \{Z| Z\subseteq S, |Z| = l \}$. Consider a vertex
$[S]^{l} = \{Z| Z\subseteq S, |Z| = l \}$. Consider a vertex ![]() $u\in U_1\,:\!=\, Z \cap V_1$. The weighted number of red hyperedges, which contains
$u\in U_1\,:\!=\, Z \cap V_1$. The weighted number of red hyperedges, which contains ![]() $u\in U_1$ with the remaining vertices in
$u\in U_1$ with the remaining vertices in ![]() $U_j^{\prime }$, can be written as
$U_j^{\prime }$, can be written as
 \begin{align} S_{1j}^{\prime }(u)\,:\!=\, \sum _{m\in{\mathcal M}}(m-1)\cdot \left \{ \sum _{e\in \, \mathcal{E}^{(a_m)}_{1, j}} T_e^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{1, j} } T_e^{(b_m)}\right \}\,,\quad u\in U_1\,, \end{align}
\begin{align} S_{1j}^{\prime }(u)\,:\!=\, \sum _{m\in{\mathcal M}}(m-1)\cdot \left \{ \sum _{e\in \, \mathcal{E}^{(a_m)}_{1, j}} T_e^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{1, j} } T_e^{(b_m)}\right \}\,,\quad u\in U_1\,, \end{align}
where ![]() $\mathcal{E}^{(a_m)}_{1, j}\,:\!=\, E_m([U_1]^{1}, [ U_1 \cap U_j^{\prime }]^{m-1} )$ denotes the set of
$\mathcal{E}^{(a_m)}_{1, j}\,:\!=\, E_m([U_1]^{1}, [ U_1 \cap U_j^{\prime }]^{m-1} )$ denotes the set of ![]() $m$-hyperedges with one vertex from
$m$-hyperedges with one vertex from ![]() $[U_1]^{1}$ and the other
$[U_1]^{1}$ and the other ![]() $m-1$ from
$m-1$ from ![]() $[U_1 \cap U^{\prime }_{j}]^{m-1}$, while
$[U_1 \cap U^{\prime }_{j}]^{m-1}$, while ![]() $ \mathcal{E}^{(b_m)}_{1, j} \,:\!=\, E_m \Big ([U_1]^{1}, \,\, [U_j^{\prime }]^{m-1} \setminus [U_1\cap U_j^{\prime }]^{m-1} \Big )$ denotes the set of
$ \mathcal{E}^{(b_m)}_{1, j} \,:\!=\, E_m \Big ([U_1]^{1}, \,\, [U_j^{\prime }]^{m-1} \setminus [U_1\cap U_j^{\prime }]^{m-1} \Big )$ denotes the set of ![]() $m$-hyperedges with one vertex in
$m$-hyperedges with one vertex in ![]() $[U_1]^{1}$ while the remaining
$[U_1]^{1}$ while the remaining ![]() $m-1$ vertices in
$m-1$ vertices in ![]() $[U_j^{\prime }]^{m-1}\setminus [U_1 \cap U_j^{\prime }]^{m-1}$(not all
$[U_j^{\prime }]^{m-1}\setminus [U_1 \cap U_j^{\prime }]^{m-1}$(not all ![]() $m$ vertices are from
$m$ vertices are from ![]() $V_1$) with their cardinalities
$V_1$) with their cardinalities
We multiply ![]() $(m-1)$ in (28) as weight since the rest
$(m-1)$ in (28) as weight since the rest ![]() $m-1$ vertices are all located in
$m-1$ vertices are all located in ![]() $U^{\prime }_{j}$, which can be regarded as
$U^{\prime }_{j}$, which can be regarded as ![]() $u$’s neighbours in
$u$’s neighbours in ![]() $U^{\prime }_{j}$. According to the fact
$U^{\prime }_{j}$. According to the fact ![]() $|U^{\prime }_j \cap U_j| \geq (\nu n/2k)$ in (27) and
$|U^{\prime }_j \cap U_j| \geq (\nu n/2k)$ in (27) and ![]() $|U_{j}^{\prime }| = n/(2k)$ for
$|U_{j}^{\prime }| = n/(2k)$ for ![]() $j\in [k]$,
$j\in [k]$,
To simplify the calculation, we take the lower and upper bound of ![]() $\big|\mathcal{E}^{(a_m)}_{1, 1}\big|$ and
$\big|\mathcal{E}^{(a_m)}_{1, 1}\big|$ and ![]() $\big|\mathcal{E}^{(a_m)}_{1, j}\big|\,(j\neq 1)$ respectively. By taking expectation with respect to
$\big|\mathcal{E}^{(a_m)}_{1, j}\big|\,(j\neq 1)$ respectively. By taking expectation with respect to ![]() $T_{e}^{(a_m)}$ and
$T_{e}^{(a_m)}$ and ![]() $T_{e}^{(b_m)}$, then for any
$T_{e}^{(b_m)}$, then for any ![]() $u \in U_1$, we have
$u \in U_1$, we have
 \begin{align*}{\mathbb{E}} S_{11}^{\prime }(u) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} \frac{a_m - b_m}{2\binom{n}{m-1}} + \binom{\frac{n}{2k}}{m-1} \frac{b_m}{2\binom{n}{m-1}}\right ]\,,\\
{\mathbb{E}} S_{1j}^{\prime }(u) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{(1-\nu )n}{2k}}{m-1} \frac{a_m - b_m}{2\binom{n}{m-1}} + \binom{\frac{n}{2k}}{m-1} \frac{b_m}{2\binom{n}{m-1}}\right ]\,, \quad j\neq 1\,. \end{align*}
\begin{align*}{\mathbb{E}} S_{11}^{\prime }(u) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} \frac{a_m - b_m}{2\binom{n}{m-1}} + \binom{\frac{n}{2k}}{m-1} \frac{b_m}{2\binom{n}{m-1}}\right ]\,,\\
{\mathbb{E}} S_{1j}^{\prime }(u) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{(1-\nu )n}{2k}}{m-1} \frac{a_m - b_m}{2\binom{n}{m-1}} + \binom{\frac{n}{2k}}{m-1} \frac{b_m}{2\binom{n}{m-1}}\right ]\,, \quad j\neq 1\,. \end{align*}
By assumptions in Theorem 1.7, ![]() ${\mathbb{E}} S_{11}^{\prime }(u) -{\mathbb{E}} S_{1j}^{\prime }(u) = \Omega (1)$. Define
${\mathbb{E}} S_{11}^{\prime }(u) -{\mathbb{E}} S_{1j}^{\prime }(u) = \Omega (1)$. Define
 \begin{align} \mu _{\mathrm{C}} \,:\!=\, \frac{1}{2}\sum _{m\in{\mathcal M}} (m-1)\cdot \left \{ \left [ \binom{\frac{\nu n}{2k}}{m-1} + \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ] \frac{a_m - b_m}{2\binom{n}{m-1}} + 2\cdot \binom{\frac{n}{2k}}{m-1}\frac{b_m}{2\binom{n}{m-1}}\right \}\,. \end{align}
\begin{align} \mu _{\mathrm{C}} \,:\!=\, \frac{1}{2}\sum _{m\in{\mathcal M}} (m-1)\cdot \left \{ \left [ \binom{\frac{\nu n}{2k}}{m-1} + \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ] \frac{a_m - b_m}{2\binom{n}{m-1}} + 2\cdot \binom{\frac{n}{2k}}{m-1}\frac{b_m}{2\binom{n}{m-1}}\right \}\,. \end{align}
In Algorithm 5, vertex ![]() $u$ is assigned to
$u$ is assigned to ![]() $\widehat{U}_{i}$ if it has the maximal number of neighbours in
$\widehat{U}_{i}$ if it has the maximal number of neighbours in ![]() $U_i^{\prime }$. If
$U_i^{\prime }$. If ![]() $u\in U_1$ is mislabelled, then one of the following events must happen:
$u\in U_1$ is mislabelled, then one of the following events must happen:
•
 $S_{11}^{\prime }(u) \leq \mu _{\mathrm{C}}$, meaning that
$S_{11}^{\prime }(u) \leq \mu _{\mathrm{C}}$, meaning that  $u$ was mislabelled by Algorithm 5.
$u$ was mislabelled by Algorithm 5.•
 $S_{1j}^{\prime }(u) \geq \mu _{\mathrm{C}}$ for some
$S_{1j}^{\prime }(u) \geq \mu _{\mathrm{C}}$ for some  $j\neq 1$, meaning that
$j\neq 1$, meaning that  $u$ survived Algorithm 5 without being corrected.
$u$ survived Algorithm 5 without being corrected.
Lemma 5.14 shows that the probabilities of those two events can be bounded in terms of the SNR.
Lemma 5.14. For sufficiently large ![]() $n$ and any
$n$ and any ![]() $u\in U_1 = Z \cap V_1$, we have
$u\in U_1 = Z \cap V_1$, we have
where ![]() $\rho \,:\!=\, \exp\!\left ({-}C_{{\mathcal M}}\cdot \mathrm{SNR}_{{\mathcal M}} \right )$ with
$\rho \,:\!=\, \exp\!\left ({-}C_{{\mathcal M}}\cdot \mathrm{SNR}_{{\mathcal M}} \right )$ with ![]() $\mathrm{SNR}_{{\mathcal M}}$ and
$\mathrm{SNR}_{{\mathcal M}}$ and ![]() $C_{{\mathcal M}}$ defined in (2).
$C_{{\mathcal M}}$ defined in (2).
As a result, the probability that either of those events happened is bounded by ![]() $\rho$. The number of mislabelled vertices in
$\rho$. The number of mislabelled vertices in ![]() $U_1$ after Algorithm 5 is at most
$U_1$ after Algorithm 5 is at most
 \begin{align*} R_1 = \sum _{t=1}^{|U_1|}\Gamma _{t}\, + \sum _{j=2}^{k}\sum _{t=1}^{|U_1\cap U_j^{\prime }|}\Lambda _{t}\,, \end{align*}
\begin{align*} R_1 = \sum _{t=1}^{|U_1|}\Gamma _{t}\, + \sum _{j=2}^{k}\sum _{t=1}^{|U_1\cap U_j^{\prime }|}\Lambda _{t}\,, \end{align*}
where ![]() $\Gamma _{t}$ (resp.
$\Gamma _{t}$ (resp. ![]() $\Lambda _{t}$) are i.i.d indicator random variables with mean
$\Lambda _{t}$) are i.i.d indicator random variables with mean ![]() $\rho _1^{\prime }$ (resp.
$\rho _1^{\prime }$ (resp. ![]() $\rho _j^{\prime }$,
$\rho _j^{\prime }$, ![]() $j\neq 1$). Then
$j\neq 1$). Then
 \begin{align*}{\mathbb{E}} R_1 \leq \frac{n}{2k} \rho _1^{\prime } + \sum _{j=2}^{k}\frac{(1 - \nu )n}{2k} \rho _j^{\prime } \leq \frac{n}{2k} \cdot k\rho = \frac{n\rho }{2}\,. \end{align*}
\begin{align*}{\mathbb{E}} R_1 \leq \frac{n}{2k} \rho _1^{\prime } + \sum _{j=2}^{k}\frac{(1 - \nu )n}{2k} \rho _j^{\prime } \leq \frac{n}{2k} \cdot k\rho = \frac{n\rho }{2}\,. \end{align*}
Let ![]() $t_1\,:\!=\, n \rho/2$, where
$t_1\,:\!=\, n \rho/2$, where ![]() $\nu$ denotes the correctness after Algorithm 4, then by Chernoff bound (Lemma D.1),
$\nu$ denotes the correctness after Algorithm 4, then by Chernoff bound (Lemma D.1),
Then with probability ![]() $1 - O(e^{-n\rho })$, the fraction of mislabelled vertices in
$1 - O(e^{-n\rho })$, the fraction of mislabelled vertices in ![]() $U_1$ is smaller than
$U_1$ is smaller than ![]() $k\rho$, i.e., the correctness of
$k\rho$, i.e., the correctness of ![]() $U_1$ is at least
$U_1$ is at least ![]() $\gamma _{\mathrm{C}} \,:\!=\, \max \{\nu \,, 1 - k\rho \}$. Therefore, Algorithm 5 outputs a
$\gamma _{\mathrm{C}} \,:\!=\, \max \{\nu \,, 1 - k\rho \}$. Therefore, Algorithm 5 outputs a ![]() $\gamma _{\mathrm{C}}$-correct partition
$\gamma _{\mathrm{C}}$-correct partition ![]() $\widehat{U}_1, \cdots, \widehat{U}_{k}$ with probability
$\widehat{U}_1, \cdots, \widehat{U}_{k}$ with probability ![]() $1- O(e^{-n\rho })$.
$1- O(e^{-n\rho })$.
5.3. Merging: Proof of Lemma 4.3
By running Algorithm 5 on the red hypergraph, we obtain a ![]() $\gamma _{\mathrm{C}}$-correct partition
$\gamma _{\mathrm{C}}$-correct partition ![]() $\widehat{U}_1, \cdots, \widehat{U}_{k}$ where
$\widehat{U}_1, \cdots, \widehat{U}_{k}$ where ![]() $\gamma _{\mathrm{C}}\,:\!=\,\max \{\nu \,, 1 - k\rho \} \geq \nu$, i.e.,
$\gamma _{\mathrm{C}}\,:\!=\,\max \{\nu \,, 1 - k\rho \} \geq \nu$, i.e.,
In the rest of this subsection, we shall condition on this event and abbreviate ![]() $Y\cap V_l$ by
$Y\cap V_l$ by ![]() $W_l\,:\!=\, Y\cap V_l$. The failure probability of Algorithm 6 is estimated by the presence of hyperedges between vertex sets
$W_l\,:\!=\, Y\cap V_l$. The failure probability of Algorithm 6 is estimated by the presence of hyperedges between vertex sets ![]() $Y$ and
$Y$ and ![]() $Z$.
$Z$.
Consider a hyperedge ![]() $e = \{i_{1}, \cdots, i_{m}\}$ in the underlying
$e = \{i_{1}, \cdots, i_{m}\}$ in the underlying ![]() $m$-uniform hypergraph. If vertices
$m$-uniform hypergraph. If vertices ![]() $i_{1}, \cdots, i_{m}$ are all from the same cluster
$i_{1}, \cdots, i_{m}$ are all from the same cluster ![]() $V_{l}$, then the probability that
$V_{l}$, then the probability that ![]() $e$ is an existing blue edge conditioning on the event that
$e$ is an existing blue edge conditioning on the event that ![]() $e$ is not a red edge is
$e$ is not a red edge is
 \begin{align} \psi _m\,:\!=\,{\mathbb{P}}\left [e \text{ is a blue edge } \Big | e \text{ is not a red edge } \right ] = \frac{\frac{a_{m}}{2\left({n \atop m-1}\right)}}{1 - \frac{a_{m}}{2\left({n \atop m-1}\right)}} = \frac{a_{m}}{2\left({n \atop m-1}\right)}(1+o(1))\,, \end{align}
\begin{align} \psi _m\,:\!=\,{\mathbb{P}}\left [e \text{ is a blue edge } \Big | e \text{ is not a red edge } \right ] = \frac{\frac{a_{m}}{2\left({n \atop m-1}\right)}}{1 - \frac{a_{m}}{2\left({n \atop m-1}\right)}} = \frac{a_{m}}{2\left({n \atop m-1}\right)}(1+o(1))\,, \end{align}
and the presence of ![]() $e$ can be represented by an indicator random variable
$e$ can be represented by an indicator random variable ![]() $\zeta _e^{(a_m)} \sim \mathrm{Bernoulli}\left (\psi _m\right )$. Similarly, if vertices
$\zeta _e^{(a_m)} \sim \mathrm{Bernoulli}\left (\psi _m\right )$. Similarly, if vertices ![]() $i_{1}, \cdots, i_{m}$ are not all from the same cluster
$i_{1}, \cdots, i_{m}$ are not all from the same cluster ![]() $V_l$, the probability that
$V_l$, the probability that ![]() $e$ is an existing blue edge conditioning on the event that
$e$ is an existing blue edge conditioning on the event that ![]() $e$ is not red
$e$ is not red
 \begin{align} \phi _m\,:\!=\,{\mathbb{P}}\left [e \text{ is a blue edge } \Big | e \text{ is not a red edge } \right ] = \frac{\frac{b_{m}}{2\left({n \atop m-1}\right)}}{1 - \frac{b_{m}}{2\left({n \atop m-1}\right)}} =\frac{b_{m}}{2\left({n \atop m-1}\right)}(1+o(1))\,, \end{align}
\begin{align} \phi _m\,:\!=\,{\mathbb{P}}\left [e \text{ is a blue edge } \Big | e \text{ is not a red edge } \right ] = \frac{\frac{b_{m}}{2\left({n \atop m-1}\right)}}{1 - \frac{b_{m}}{2\left({n \atop m-1}\right)}} =\frac{b_{m}}{2\left({n \atop m-1}\right)}(1+o(1))\,, \end{align}
and the presence of ![]() $e$ can be represented by an indicator variable
$e$ can be represented by an indicator variable ![]() $\xi _e^{(b_m)} \sim \mathrm{Bernoulli}\left (\phi _m\right )$.
$\xi _e^{(b_m)} \sim \mathrm{Bernoulli}\left (\phi _m\right )$.
For any vertex ![]() $w\in W_l \,:\!=\, Y\cap V_l$ with fixed
$w\in W_l \,:\!=\, Y\cap V_l$ with fixed ![]() $l \in [k]$, we want to compute the number of hyperedges containing
$l \in [k]$, we want to compute the number of hyperedges containing ![]() $w$ with all remaining vertices located in vertex set
$w$ with all remaining vertices located in vertex set ![]() $\widehat{U}_{j}$ for some fixed
$\widehat{U}_{j}$ for some fixed ![]() $j\in [k]$. Following a similar argument given in Subsection 5.2, this number can be written as
$j\in [k]$. Following a similar argument given in Subsection 5.2, this number can be written as
 \begin{align} \widehat{S}_{lj}(w)\,:\!=\, \sum _{m\in{\mathcal M}}(m-1)\cdot \left \{ \sum _{e\in \, \widehat{\mathcal{E}}^{(a_m)}_{l, j}} \zeta _e^{(a_m)} + \sum _{e\in \widehat{\mathcal{E}}^{(b_m)}_{l, j} } \xi _e^{(b_m)}\right \}\,,\quad w\in W_l\,, \end{align}
\begin{align} \widehat{S}_{lj}(w)\,:\!=\, \sum _{m\in{\mathcal M}}(m-1)\cdot \left \{ \sum _{e\in \, \widehat{\mathcal{E}}^{(a_m)}_{l, j}} \zeta _e^{(a_m)} + \sum _{e\in \widehat{\mathcal{E}}^{(b_m)}_{l, j} } \xi _e^{(b_m)}\right \}\,,\quad w\in W_l\,, \end{align}
where ![]() $\widehat{\mathcal{E}}^{(a_m)}_{l, j}\,:\!=\, E_m([W_l]^{1}, [U_l\cap \widehat{U}_j]^{m-1})$ denotes the set of
$\widehat{\mathcal{E}}^{(a_m)}_{l, j}\,:\!=\, E_m([W_l]^{1}, [U_l\cap \widehat{U}_j]^{m-1})$ denotes the set of ![]() $m$-hyperedges with
$m$-hyperedges with ![]() $1$ vertex from
$1$ vertex from ![]() $[W_l]^{1}$ and the other
$[W_l]^{1}$ and the other ![]() $m-1$ vertices from
$m-1$ vertices from ![]() $[U_l\cap \widehat{U}_j]^{m-1}$, while
$[U_l\cap \widehat{U}_j]^{m-1}$, while ![]() $ \widehat{\mathcal{E}}^{(b_m)}_{l, j} \,:\!=\, E_m ([W_l]^{1}, \,\, [\widehat{U}_j]^{m-1} \setminus [U_l\cap \widehat{U}_j]^{m-1})$ denotes the set of
$ \widehat{\mathcal{E}}^{(b_m)}_{l, j} \,:\!=\, E_m ([W_l]^{1}, \,\, [\widehat{U}_j]^{m-1} \setminus [U_l\cap \widehat{U}_j]^{m-1})$ denotes the set of ![]() $m$-hyperedges with
$m$-hyperedges with ![]() $1$ vertex in
$1$ vertex in ![]() $[W_l]^{1}$ while the remaining
$[W_l]^{1}$ while the remaining ![]() $m-1$ vertices are in
$m-1$ vertices are in ![]() $[\widehat{U}_j]^{m-1}\setminus [U_l\cap \widehat{U}_j]^{m-1}$, with their cardinalities
$[\widehat{U}_j]^{m-1}\setminus [U_l\cap \widehat{U}_j]^{m-1}$, with their cardinalities
Similarly, we multiply ![]() $(m-1)$ in (35) as weight since the rest
$(m-1)$ in (35) as weight since the rest ![]() $m-1$ vertices can be regarded as
$m-1$ vertices can be regarded as ![]() $u$’s neighbours in
$u$’s neighbours in ![]() $\widehat{U}_{j}$. By accuracy of Algorithm 5 in (32),
$\widehat{U}_{j}$. By accuracy of Algorithm 5 in (32), ![]() $|\widehat{U}_{j} \cap U_j| \geq \nu n/(2k)$, then
$|\widehat{U}_{j} \cap U_j| \geq \nu n/(2k)$, then
Taking expectation with respect to ![]() $\zeta _e^{(a_m)}$ and
$\zeta _e^{(a_m)}$ and ![]() $\xi _e^{(b_m)}$, for any
$\xi _e^{(b_m)}$, for any ![]() $w \in W_l$, we have
$w \in W_l$, we have
 \begin{align*}{\mathbb{E}} \widehat{S}_{ll}(w) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2k}}{m-1} \phi _{m}\right ],\\[7pt]
{\mathbb{E}} \widehat{S}_{lj}(w) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{(1 - \nu ) n}{2k}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2k}}{m-1} \phi _{m} \right ],\,\, j\neq l\,. \end{align*}
\begin{align*}{\mathbb{E}} \widehat{S}_{ll}(w) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2k}}{m-1} \phi _{m}\right ],\\[7pt]
{\mathbb{E}} \widehat{S}_{lj}(w) &= \sum _{m\in{\mathcal M}} (m-1)\cdot \left [ \binom{\frac{(1 - \nu ) n}{2k}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2k}}{m-1} \phi _{m} \right ],\,\, j\neq l\,. \end{align*}
By assumptions in Theorem 1.7, ![]() ${\mathbb{E}} \widehat{S}_{ll}(w) -{\mathbb{E}} \widehat{S}_{lj}(w) = \Omega (1)$. We define
${\mathbb{E}} \widehat{S}_{ll}(w) -{\mathbb{E}} \widehat{S}_{lj}(w) = \Omega (1)$. We define
 \begin{align} \mu _{\mathrm{M}} \,:\!=\, \frac{1}{2}\sum _{m\in{\mathcal M}} (m-1)\cdot \left \{ \left [ \binom{\frac{\nu n}{2k}}{m-1} + \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ](\psi _{m} - \phi _{m}) + 2\binom{\frac{n}{2k}}{m-1} \phi _{m}\right \}\,. \end{align}
\begin{align} \mu _{\mathrm{M}} \,:\!=\, \frac{1}{2}\sum _{m\in{\mathcal M}} (m-1)\cdot \left \{ \left [ \binom{\frac{\nu n}{2k}}{m-1} + \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ](\psi _{m} - \phi _{m}) + 2\binom{\frac{n}{2k}}{m-1} \phi _{m}\right \}\,. \end{align}
After Algorithm 6, if a vertex ![]() $w\in W_l$ is mislabelled, one of the following events must happen
$w\in W_l$ is mislabelled, one of the following events must happen
•
 $\widehat{S}_{ll}(w) \leq \mu _{\mathrm{M}}$, which implies that
$\widehat{S}_{ll}(w) \leq \mu _{\mathrm{M}}$, which implies that  $u$ was mislabelled by Algorithm 6.
$u$ was mislabelled by Algorithm 6.•
 $\widehat{S}_{lj}(w) \geq \mu _{\mathrm{M}}$ for some
$\widehat{S}_{lj}(w) \geq \mu _{\mathrm{M}}$ for some  $j\neq l$, which implies that
$j\neq l$, which implies that  $u$ survived Algorithm 6 without being corrected.
$u$ survived Algorithm 6 without being corrected.
By an argument similar to Lemma 5.14, we can prove that for any ![]() $w\in W_l$,
$w\in W_l$,
where ![]() $\rho \,:\!=\, \exp\!\left ({-}C_{{\mathcal M}}\cdot \mathrm{SNR}_{{\mathcal M}} \right )$. The misclassified probability for
$\rho \,:\!=\, \exp\!\left ({-}C_{{\mathcal M}}\cdot \mathrm{SNR}_{{\mathcal M}} \right )$. The misclassified probability for ![]() $w\in W_l$ is upper bounded by
$w\in W_l$ is upper bounded by ![]() $\sum _{j=1}^{k}\hat{\rho }_{j} \leq k\rho$. The number of mislabelled vertices in
$\sum _{j=1}^{k}\hat{\rho }_{j} \leq k\rho$. The number of mislabelled vertices in ![]() $W_l$ is at most
$W_l$ is at most ![]() $ R_l = \sum _{t=1}^{|W_l|}\Gamma _{t} \,,$ where
$ R_l = \sum _{t=1}^{|W_l|}\Gamma _{t} \,,$ where ![]() $\Gamma _{t}$ are i.i.d indicator random variables with mean
$\Gamma _{t}$ are i.i.d indicator random variables with mean ![]() $k \rho$ and
$k \rho$ and ![]() ${\mathbb{E}} R_l \leq n/(2k)\cdot k\rho = n\rho/2$. Let
${\mathbb{E}} R_l \leq n/(2k)\cdot k\rho = n\rho/2$. Let ![]() $t_l\,:\!=\, n \rho/2$, by Chernoff bound (Lemma D.1),
$t_l\,:\!=\, n \rho/2$, by Chernoff bound (Lemma D.1),
Hence with probability ![]() $1 - O(e^{-n\rho })$, the fraction of mislabelled vertices in
$1 - O(e^{-n\rho })$, the fraction of mislabelled vertices in ![]() $W_l$ is smaller than
$W_l$ is smaller than ![]() $k\rho$, i.e., the correctness in
$k\rho$, i.e., the correctness in ![]() $W_l$ is at least
$W_l$ is at least ![]() $\gamma _{\mathrm{M}} \,:\!=\,\max \{ \nu,\, 1 - k\rho \}$.
$\gamma _{\mathrm{M}} \,:\!=\,\max \{ \nu,\, 1 - k\rho \}$.
5.4. Proof of Theorem 1.7
Now we are ready to prove Theorem 1.7. The correctness of Algorithms 5 and 6 are denoted by ![]() $\gamma _{\mathrm{C}}$ and
$\gamma _{\mathrm{C}}$ and ![]() $\gamma _{\mathrm{M}}$ respectively, then with probability at least
$\gamma _{\mathrm{M}}$ respectively, then with probability at least ![]() $1 - O(e^{-n\rho })$, the correctness
$1 - O(e^{-n\rho })$, the correctness ![]() $\gamma$ of Algorithm 2 is
$\gamma$ of Algorithm 2 is ![]() $ \gamma \,:\!=\, \min \{\gamma _{\mathrm{C}}, \gamma _{\mathrm{M}}\} = \max \{\nu,\, 1 - k\rho \}.$ We will have
$ \gamma \,:\!=\, \min \{\gamma _{\mathrm{C}}, \gamma _{\mathrm{M}}\} = \max \{\nu,\, 1 - k\rho \}.$ We will have ![]() $\gamma = 1 - k\rho$ if
$\gamma = 1 - k\rho$ if ![]() $\nu \leq 1 - k\rho$, equivalently,
$\nu \leq 1 - k\rho$, equivalently,
otherwise ![]() $\gamma = \nu$. The inequality (37) holds since
$\gamma = \nu$. The inequality (37) holds since
 \begin{align*} \text{SNR}_{{\mathcal M}}(k) =& \frac{ \left [\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )}\\[7pt]
\geq & \frac{[\sum _{m\in{\mathcal M}} (a_m-b_m)]^2}{k^{2{\mathcal M}_{\max }-2}({\mathcal M}_{\max }-1)d}\geq \frac{(C_{\nu })^2}{{\mathcal M}_{\max }-1} \log \Big (\frac{k}{1 - \nu } \Big ) \geq \frac{1}{C_{{\mathcal M}}}\log \Big (\frac{k}{1-\nu } \Big )\,. \end{align*}
\begin{align*} \text{SNR}_{{\mathcal M}}(k) =& \frac{ \left [\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in{\mathcal M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )}\\[7pt]
\geq & \frac{[\sum _{m\in{\mathcal M}} (a_m-b_m)]^2}{k^{2{\mathcal M}_{\max }-2}({\mathcal M}_{\max }-1)d}\geq \frac{(C_{\nu })^2}{{\mathcal M}_{\max }-1} \log \Big (\frac{k}{1 - \nu } \Big ) \geq \frac{1}{C_{{\mathcal M}}}\log \Big (\frac{k}{1-\nu } \Big )\,. \end{align*}
where the first two inequalities hold since ![]() $d \,:\!=\, \sum _{m\in{\mathcal M}}(m-1)a_m$ and Condition (4b), while the last inequality holds by taking
$d \,:\!=\, \sum _{m\in{\mathcal M}}(m-1)a_m$ and Condition (4b), while the last inequality holds by taking ![]() $C_{\nu }\geq \max \{ \sqrt{({\mathcal M}_{\max }-1)/C_{{\mathcal M}} }, C_2 \}$ with
$C_{\nu }\geq \max \{ \sqrt{({\mathcal M}_{\max }-1)/C_{{\mathcal M}} }, C_2 \}$ with ![]() $C_2$ defined in (26).
$C_2$ defined in (26).
Remark 5.15. The lower bound ![]() $C$ in (4a) comes from the requirement in Lemma 5.4 that only a few high-degree vertices be deleted. The constant
$C$ in (4a) comes from the requirement in Lemma 5.4 that only a few high-degree vertices be deleted. The constant ![]() $C_{\nu }$ in (4b) comes from the requirement in Lemma 5.6 that the subspace angle is small. When
$C_{\nu }$ in (4b) comes from the requirement in Lemma 5.6 that the subspace angle is small. When ![]() $C$ is not so large (or the hypergraph is too sparse), one could still achieve good accuracy
$C$ is not so large (or the hypergraph is too sparse), one could still achieve good accuracy ![]() $\gamma$ if
$\gamma$ if ![]() $C_{\nu }$ is large enough (the difference between
$C_{\nu }$ is large enough (the difference between ![]() $a_m$ and
$a_m$ and ![]() $b_m$ is large enough).
$b_m$ is large enough).
Remark 5.16. Condition (37) indicates that the improvement of accuracy from local refinement (Algorithms 5 and 6) will be guaranteed when ![]() $\text{SNR}_{{\mathcal M}}(k)$ is large enough. If
$\text{SNR}_{{\mathcal M}}(k)$ is large enough. If ![]() $\text{SNR}_{{\mathcal M}}(k)$ is small, we use correctness of Algorithm 4 instead, i.e.,
$\text{SNR}_{{\mathcal M}}(k)$ is small, we use correctness of Algorithm 4 instead, i.e., ![]() $\gamma = \nu$, to represent the correctness of Algorithm 2.
$\gamma = \nu$, to represent the correctness of Algorithm 2.
5.5. Proof of Corollary 1.9
For any fixed ![]() $\nu \in (1/k, 1)$,
$\nu \in (1/k, 1)$, ![]() $\mathrm{SNR}_{{\mathcal M}}(k) \to \infty$ implies
$\mathrm{SNR}_{{\mathcal M}}(k) \to \infty$ implies ![]() $\rho \to 0$ and
$\rho \to 0$ and
Since
Condition (4b) is satisfied. Applying Theorem 1.7, we find ![]() $\gamma = 1 - o(1)$, which implies weak consistency. The constraint of
$\gamma = 1 - o(1)$, which implies weak consistency. The constraint of ![]() $\mathrm{SNR}_{{\mathcal M}}(k) = o(\log n)$ is used in the proof of Lemma 4.2, see Remark 1.10.
$\mathrm{SNR}_{{\mathcal M}}(k) = o(\log n)$ is used in the proof of Lemma 4.2, see Remark 1.10.
Acknowledgements
I.D. and H.W. are partially supported by NSF DMS-2154099. I.D. and Y.Z. acknowledge support from NSF DMS-1928930 during their participation in the programme Universality and Integrability in Random Matrix Theory and Interacting Particle Systems hosted by the Mathematical Sciences Research Institute in Berkeley, California during the Fall semester of 2021. Y.Z. is partially supported by NSF-Simons Research Collaborations on the Mathematical and Scientific Foundations of Deep Learning. Y.Z. thanks Zhixin Zhou for his helpful comments. The authors thank the anonymous reviewers for detailed comments and suggestions which greatly improve the presentation of this work.
Appendix A. Proof of Theorems 3.1 and 3.3
A.1. Discretization
To prove Theorem 3.1, we start with a standard ![]() $\varepsilon$-net argument.
$\varepsilon$-net argument.
Lemma A.1 (Lemma 4.4.1 in [Reference Vershynin69]). Let ![]() ${\mathbf{W}}$ be any Hermitian
${\mathbf{W}}$ be any Hermitian ![]() $n\times n$ matrix and let
$n\times n$ matrix and let ![]() $\mathcal{N}_{\varepsilon }$ be an
$\mathcal{N}_{\varepsilon }$ be an ![]() $\varepsilon$-net on the unit sphere
$\varepsilon$-net on the unit sphere ![]() $\mathbb{S}^{n-1}$ with
$\mathbb{S}^{n-1}$ with ![]() $\varepsilon \in (0,1)$, then
$\varepsilon \in (0,1)$, then ![]() $ \|{\mathbf{W}}\| \leq \frac{1}{1-\varepsilon }\sup _{\boldsymbol{x}\in \mathcal{N}_{\varepsilon }} |\langle{\mathbf{W}} \boldsymbol{x}, \boldsymbol{x}\rangle |.$
$ \|{\mathbf{W}}\| \leq \frac{1}{1-\varepsilon }\sup _{\boldsymbol{x}\in \mathcal{N}_{\varepsilon }} |\langle{\mathbf{W}} \boldsymbol{x}, \boldsymbol{x}\rangle |.$
By [Reference Vershynin69, Corollary 4.2.13], the size of ![]() $\mathcal{N}_{\varepsilon }$ is bounded by
$\mathcal{N}_{\varepsilon }$ is bounded by ![]() $|\mathcal{N}_{\varepsilon }|\leq (1+2/\varepsilon )^n$. We would have
$|\mathcal{N}_{\varepsilon }|\leq (1+2/\varepsilon )^n$. We would have ![]() $\log |\mathcal{N}| \leq n \log (5)$ when
$\log |\mathcal{N}| \leq n \log (5)$ when ![]() $\mathcal{N}$ is taken as an
$\mathcal{N}$ is taken as an ![]() $(1/2)$-net of
$(1/2)$-net of ![]() $\mathbb S^n$. Define
$\mathbb S^n$. Define ![]() ${\mathbf{W}} \,:\!=\,{\mathbf{A}} -{\mathbb{E}}{\mathbf{A}}$, then
${\mathbf{W}} \,:\!=\,{\mathbf{A}} -{\mathbb{E}}{\mathbf{A}}$, then ![]() ${\mathbf{W}}_{ii}=0$ for each
${\mathbf{W}}_{ii}=0$ for each ![]() $i\in [n]$ by the definition of adjacency matrix in equation (7), and we obtain
$i\in [n]$ by the definition of adjacency matrix in equation (7), and we obtain
For any fixed ![]() $\boldsymbol{x}\in \mathbb{S}^{n-1}$, consider the light and heavy pairs as follows.
$\boldsymbol{x}\in \mathbb{S}^{n-1}$, consider the light and heavy pairs as follows.
where ![]() $d = \sum _{m=2}^{M}(m-1)d_m$. Thus by the triangle inequality,
$d = \sum _{m=2}^{M}(m-1)d_m$. Thus by the triangle inequality,
 \begin{equation*} | \langle \boldsymbol{x}, {\mathbf{W}} \boldsymbol{x}\rangle | \leq \left |\sum _{(i,j)\in \mathcal {L}(\boldsymbol{x})} {\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j \right | + \left |\sum _{(i,j)\in \mathcal {H}(\boldsymbol{x})} {\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j \right |,\end{equation*}
\begin{equation*} | \langle \boldsymbol{x}, {\mathbf{W}} \boldsymbol{x}\rangle | \leq \left |\sum _{(i,j)\in \mathcal {L}(\boldsymbol{x})} {\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j \right | + \left |\sum _{(i,j)\in \mathcal {H}(\boldsymbol{x})} {\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j \right |,\end{equation*}
and by equation (A.1),
 \begin{align} \|{\mathbf{A}} -{\mathbb{E}}{\mathbf{A}}\| \leq 2\sup _{\boldsymbol{x} \in \mathcal{N} }\Bigg |\sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg | + 2\sup _{\boldsymbol{x}\in \mathcal{N} }\Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\,. \end{align}
\begin{align} \|{\mathbf{A}} -{\mathbb{E}}{\mathbf{A}}\| \leq 2\sup _{\boldsymbol{x} \in \mathcal{N} }\Bigg |\sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg | + 2\sup _{\boldsymbol{x}\in \mathcal{N} }\Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\,. \end{align}
A.2. Contribution from light pairs
For each ![]() $m$-hyperedge
$m$-hyperedge ![]() $e\in E_m$, we define
$e\in E_m$, we define ![]() $\boldsymbol{\mathcal{W}}^{(m)}_e \,:\!=\, \boldsymbol{\mathcal{A}}^{(m)}_e -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_e.$ Then for any fixed
$\boldsymbol{\mathcal{W}}^{(m)}_e \,:\!=\, \boldsymbol{\mathcal{A}}^{(m)}_e -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_e.$ Then for any fixed ![]() $\boldsymbol{x}\in \mathbb{S}^{n-1}$, the contribution from light couples can be written as
$\boldsymbol{x}\in \mathbb{S}^{n-1}$, the contribution from light couples can be written as
 \begin{align} &\,\sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j = \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})} \left ( \sum _{m=2}^{M}\,\, \sum _{\substack{e\in E_m\\
\{i,j\}\subset e} } \boldsymbol{\mathcal{W}}^{(m)}_e \right ) \boldsymbol{x}_i\boldsymbol{x}_j \notag \\
=&\, \sum _{m=2}^M \sum _{e\in E_m} \boldsymbol{\mathcal{W}}^{(m)}_e \left ( \sum _{\substack{(i,j)\in \mathcal{L}(\boldsymbol{x})\\
i\neq j,\, \{i,j\}\subset e} }\boldsymbol{x}_i \boldsymbol{x}_j \right ) = \sum _{m=2}^M \sum _{e\in E_m} \boldsymbol{\mathcal{Y}}_e^{(m)} \,, \end{align}
\begin{align} &\,\sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j = \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})} \left ( \sum _{m=2}^{M}\,\, \sum _{\substack{e\in E_m\\
\{i,j\}\subset e} } \boldsymbol{\mathcal{W}}^{(m)}_e \right ) \boldsymbol{x}_i\boldsymbol{x}_j \notag \\
=&\, \sum _{m=2}^M \sum _{e\in E_m} \boldsymbol{\mathcal{W}}^{(m)}_e \left ( \sum _{\substack{(i,j)\in \mathcal{L}(\boldsymbol{x})\\
i\neq j,\, \{i,j\}\subset e} }\boldsymbol{x}_i \boldsymbol{x}_j \right ) = \sum _{m=2}^M \sum _{e\in E_m} \boldsymbol{\mathcal{Y}}_e^{(m)} \,, \end{align}
where the constraint ![]() $i\neq j$ comes from the fact
$i\neq j$ comes from the fact ![]() ${\mathbf{W}}_{ii} =0$ and we denote
${\mathbf{W}}_{ii} =0$ and we denote
 \begin{align*} \boldsymbol{\mathcal{Y}}_e^{(m)}\,:\!=\, \boldsymbol{\mathcal{W}}^{(m)}_e \left ( \sum _{\substack{(i,j)\in \mathcal{L}(\boldsymbol{x})\\
i\neq j, \, \{i,j\}\subset e}}\,\, \boldsymbol{x}_i \boldsymbol{x}_j\right )\,. \end{align*}
\begin{align*} \boldsymbol{\mathcal{Y}}_e^{(m)}\,:\!=\, \boldsymbol{\mathcal{W}}^{(m)}_e \left ( \sum _{\substack{(i,j)\in \mathcal{L}(\boldsymbol{x})\\
i\neq j, \, \{i,j\}\subset e}}\,\, \boldsymbol{x}_i \boldsymbol{x}_j\right )\,. \end{align*}
Note that ![]() ${\mathbb{E}} \boldsymbol{\mathcal{Y}}_e^{(m)} = 0$, and by the definition of light pair equation (A.2),
${\mathbb{E}} \boldsymbol{\mathcal{Y}}_e^{(m)} = 0$, and by the definition of light pair equation (A.2),
Moreover, equation (A.4) is a sum of independent, mean-zero random variables, and
 \begin{align*} \sum _{m=2}^M \sum _{e\in E_m}{\mathbb{E}} [(\boldsymbol{\mathcal{Y}}_e^{(m)})^2] \,:\!=\, &\,\sum _{m=2}^M \sum _{e\in E_m} \Bigg [{\mathbb{E}}[(\boldsymbol{\mathcal{W}}_{e}^{(m)})^2] \Bigg ( \sum _{\substack{(i,j)\in \mathcal{L}(\boldsymbol{x})\\
i\neq j, \{i,j\}\subset e}}\boldsymbol{x}_i \boldsymbol{x}_j \Bigg )^2 \Bigg ] \\
\leq &\, \sum _{m=2}^M \sum _{e\in E_m} \Bigg [{\mathbb{E}}[ \boldsymbol{\mathcal{A}}^{(m)}_e ] \cdot m(m-1) \Bigg (\sum _{\substack{(i,j)\in \mathcal{L}(x)\\
i\neq j, \{i,j\}\subset e}} \boldsymbol{x}_i^2 \boldsymbol{x}_j^2 \Bigg ) \Bigg ]\\
\leq &\, \sum _{m=2}^M \frac{d_m \cdot m(m-1)}{\binom{n}{m-1}}\binom{n}{m-2} \sum _{(i,j)\in [n]^2}\boldsymbol{x}_i^2 \boldsymbol{x}_j^2 \\
\leq &\, \sum _{m=2}^M \frac{d_m m(m-1)^2}{n-m+2} \leq \frac{2}{n}\sum _{m=2}^M d_m (m-1)^3\leq \frac{2d(M-1)^2}{n}\,, \end{align*}
\begin{align*} \sum _{m=2}^M \sum _{e\in E_m}{\mathbb{E}} [(\boldsymbol{\mathcal{Y}}_e^{(m)})^2] \,:\!=\, &\,\sum _{m=2}^M \sum _{e\in E_m} \Bigg [{\mathbb{E}}[(\boldsymbol{\mathcal{W}}_{e}^{(m)})^2] \Bigg ( \sum _{\substack{(i,j)\in \mathcal{L}(\boldsymbol{x})\\
i\neq j, \{i,j\}\subset e}}\boldsymbol{x}_i \boldsymbol{x}_j \Bigg )^2 \Bigg ] \\
\leq &\, \sum _{m=2}^M \sum _{e\in E_m} \Bigg [{\mathbb{E}}[ \boldsymbol{\mathcal{A}}^{(m)}_e ] \cdot m(m-1) \Bigg (\sum _{\substack{(i,j)\in \mathcal{L}(x)\\
i\neq j, \{i,j\}\subset e}} \boldsymbol{x}_i^2 \boldsymbol{x}_j^2 \Bigg ) \Bigg ]\\
\leq &\, \sum _{m=2}^M \frac{d_m \cdot m(m-1)}{\binom{n}{m-1}}\binom{n}{m-2} \sum _{(i,j)\in [n]^2}\boldsymbol{x}_i^2 \boldsymbol{x}_j^2 \\
\leq &\, \sum _{m=2}^M \frac{d_m m(m-1)^2}{n-m+2} \leq \frac{2}{n}\sum _{m=2}^M d_m (m-1)^3\leq \frac{2d(M-1)^2}{n}\,, \end{align*}
when ![]() $n\geq 2m-2$, where
$n\geq 2m-2$, where ![]() $d_m=\max d_{[i_1,\dots, i_m]}$ and
$d_m=\max d_{[i_1,\dots, i_m]}$ and ![]() $d = \sum _{m=2}^{M}(m-1)d_m$. Then Bernstein’s inequality (Lemma D.3) implies that for any
$d = \sum _{m=2}^{M}(m-1)d_m$. Then Bernstein’s inequality (Lemma D.3) implies that for any ![]() $\alpha \gt 0$,
$\alpha \gt 0$,
 \begin{align*} &{\mathbb{P}} \Bigg ( \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg | \geq \alpha \sqrt{d}\Bigg ) ={\mathbb{P}} \Bigg ( \Bigg | \sum _{m=2}^M \sum _{e\in E_m} \boldsymbol{\mathcal{Y}}_e^{(m)} \Bigg | \geq \alpha \sqrt{d}\Bigg ) \\
\leq & 2\exp \Bigg ({-}\frac{\frac{1}{2}\alpha ^2d}{\frac{2d}{n}(M-1)^2+ \frac{1}{3} (M-1)M \frac{\sqrt{d}}{n} \alpha \sqrt{d}}\Bigg ) \leq 2\exp \Bigg ({-}\frac{\alpha ^2 n}{4(M-1)^2+\frac{2\alpha (M-1)M}{3}}\Bigg ). \end{align*}
\begin{align*} &{\mathbb{P}} \Bigg ( \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg | \geq \alpha \sqrt{d}\Bigg ) ={\mathbb{P}} \Bigg ( \Bigg | \sum _{m=2}^M \sum _{e\in E_m} \boldsymbol{\mathcal{Y}}_e^{(m)} \Bigg | \geq \alpha \sqrt{d}\Bigg ) \\
\leq & 2\exp \Bigg ({-}\frac{\frac{1}{2}\alpha ^2d}{\frac{2d}{n}(M-1)^2+ \frac{1}{3} (M-1)M \frac{\sqrt{d}}{n} \alpha \sqrt{d}}\Bigg ) \leq 2\exp \Bigg ({-}\frac{\alpha ^2 n}{4(M-1)^2+\frac{2\alpha (M-1)M}{3}}\Bigg ). \end{align*}
Therefore by taking a union bound,
 \begin{align} &\,{\mathbb{P}} \Bigg ( \sup _{\boldsymbol{x}\in \mathcal{N} }\Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\geq \alpha \sqrt{d}\Bigg )\leq |\mathcal{N}| \cdot{\mathbb{P}} \Bigg ( \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg | \geq \alpha \sqrt{d}\Bigg ) \notag \\
\leq &\, 2\exp \Bigg ( \log (5) \cdot n-\frac{\alpha ^2 n}{4(M-1)^2+\frac{2\alpha (M-1)M}{3}}\Bigg )\leq 2e^{-n}\,, \end{align}
\begin{align} &\,{\mathbb{P}} \Bigg ( \sup _{\boldsymbol{x}\in \mathcal{N} }\Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\geq \alpha \sqrt{d}\Bigg )\leq |\mathcal{N}| \cdot{\mathbb{P}} \Bigg ( \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\mathbf{W}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg | \geq \alpha \sqrt{d}\Bigg ) \notag \\
\leq &\, 2\exp \Bigg ( \log (5) \cdot n-\frac{\alpha ^2 n}{4(M-1)^2+\frac{2\alpha (M-1)M}{3}}\Bigg )\leq 2e^{-n}\,, \end{align}
where we choose ![]() $\alpha =5M(M-1)$ in the last line.
$\alpha =5M(M-1)$ in the last line.
A.3. Contribution from heavy pairs
Note that for any ![]() $i\not =j$,
$i\not =j$,
 \begin{align} {\mathbb{E}}{\mathbf{A}}_{ij}\leq \sum _{m=2}^M \binom{n-2}{m-2}\frac{d_m}{\binom{n}{m-1}} \leq \sum _{m=2}^M\frac{(m-1)d_m}{n}=\frac{d}{n}. \end{align}
\begin{align} {\mathbb{E}}{\mathbf{A}}_{ij}\leq \sum _{m=2}^M \binom{n-2}{m-2}\frac{d_m}{\binom{n}{m-1}} \leq \sum _{m=2}^M\frac{(m-1)d_m}{n}=\frac{d}{n}. \end{align}
and
 \begin{align} &\Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})}{\mathbb{E}}{\mathbf{A}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg | = \Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})}{\mathbb{E}}{\mathbf{A}}_{ij} \frac{\boldsymbol{x}_i^2 \boldsymbol{x}_j^2}{\boldsymbol{x}_i \boldsymbol{x}_j}\Bigg | \\
\leq \,& \sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} \frac{d}{n}\frac{\boldsymbol{x}_i^2 \boldsymbol{x}_j^2}{|\boldsymbol{x}_i\boldsymbol{x}_j|}\leq \sqrt{d}\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} \boldsymbol{x}_i^2 \boldsymbol{x}_j^2\leq \sqrt{d}. \notag \end{align}
\begin{align} &\Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})}{\mathbb{E}}{\mathbf{A}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg | = \Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})}{\mathbb{E}}{\mathbf{A}}_{ij} \frac{\boldsymbol{x}_i^2 \boldsymbol{x}_j^2}{\boldsymbol{x}_i \boldsymbol{x}_j}\Bigg | \\
\leq \,& \sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} \frac{d}{n}\frac{\boldsymbol{x}_i^2 \boldsymbol{x}_j^2}{|\boldsymbol{x}_i\boldsymbol{x}_j|}\leq \sqrt{d}\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} \boldsymbol{x}_i^2 \boldsymbol{x}_j^2\leq \sqrt{d}. \notag \end{align}
Therefore it suffices to show that, with high probability,
Here we use the discrepancy analysis from [Reference Cook, Goldstein and Johnson22, Reference Feige and Ofek28]. We consider the weighted graph associated with the adjacency matrix ![]() ${\mathbf{A}}$.
${\mathbf{A}}$.
Definition A.2 (Uniform upper tail property, UUTP). Let ![]() ${\mathbf{M}}$ be an
${\mathbf{M}}$ be an ![]() $n\times n$ random symmetric matrix with non-negative entries and
$n\times n$ random symmetric matrix with non-negative entries and ![]() ${\mathbf{Q}}$ be an
${\mathbf{Q}}$ be an ![]() $n\times n$ symmetric matrix with entries
$n\times n$ symmetric matrix with entries ![]() ${\mathbf{Q}}_{ij}\in [0,a]$ for all
${\mathbf{Q}}_{ij}\in [0,a]$ for all ![]() $i,j\in [n]$. Define
$i,j\in [n]$. Define
 \begin{align*} \mu \,:\!=\, \sum _{i,j=1}^n{\mathbf{Q}}_{ij}{\mathbb{E}}{\mathbf{M}}_{ij}, \quad \tilde{\sigma }^2 \,:\!=\,\sum _{i,j=1}^n{\mathbf{Q}}_{ij}^2{\mathbb{E}}{\mathbf{M}}_{ij}. \end{align*}
\begin{align*} \mu \,:\!=\, \sum _{i,j=1}^n{\mathbf{Q}}_{ij}{\mathbb{E}}{\mathbf{M}}_{ij}, \quad \tilde{\sigma }^2 \,:\!=\,\sum _{i,j=1}^n{\mathbf{Q}}_{ij}^2{\mathbb{E}}{\mathbf{M}}_{ij}. \end{align*}
We say that ![]() ${\mathbf{M}}$ satisfies the uniform upper tail property
${\mathbf{M}}$ satisfies the uniform upper tail property ![]() $\mathbf{UUTP}(c_0,\gamma _0)$ with
$\mathbf{UUTP}(c_0,\gamma _0)$ with ![]() $c_0\gt 0,\gamma _0\geq 0$, if for any
$c_0\gt 0,\gamma _0\geq 0$, if for any ![]() $a,t\gt 0$,
$a,t\gt 0$,
 \begin{align*}{\mathbb{P}} \Bigg ( f_{{\mathbf{Q}}}({\mathbf{M}})\geq (1 + \gamma _0)\mu +t\Bigg )\leq \exp \Bigg ({-}c_0 \frac{\tilde{\sigma }^2}{a^2} h\Bigg ( \frac{at}{\tilde{\sigma }^2}\Bigg )\Bigg ). \end{align*}
\begin{align*}{\mathbb{P}} \Bigg ( f_{{\mathbf{Q}}}({\mathbf{M}})\geq (1 + \gamma _0)\mu +t\Bigg )\leq \exp \Bigg ({-}c_0 \frac{\tilde{\sigma }^2}{a^2} h\Bigg ( \frac{at}{\tilde{\sigma }^2}\Bigg )\Bigg ). \end{align*}
where function ![]() $f_{{\mathbf{Q}}}({\mathbf{M}})\,:\,{\mathbb{R}}^{n \times n} \mapsto{\mathbb{R}}$ is defined by
$f_{{\mathbf{Q}}}({\mathbf{M}})\,:\,{\mathbb{R}}^{n \times n} \mapsto{\mathbb{R}}$ is defined by ![]() $f_{{\mathbf{Q}}}({\mathbf{M}})\,:\!=\, \sum _{i,j=1}^n{\mathbf{Q}}_{ij}{\mathbf{M}}_{ij}$ for
$f_{{\mathbf{Q}}}({\mathbf{M}})\,:\!=\, \sum _{i,j=1}^n{\mathbf{Q}}_{ij}{\mathbf{M}}_{ij}$ for ![]() ${\mathbf{M}} \in {\mathbb{R}}^{n \times n}$, and function
${\mathbf{M}} \in {\mathbb{R}}^{n \times n}$, and function ![]() $h(x) \,:\!=\, (1 + x) \mathrm{log}(1 + x) - x$ for all
$h(x) \,:\!=\, (1 + x) \mathrm{log}(1 + x) - x$ for all ![]() $x\gt -1$.
$x\gt -1$.
Lemma A.3. Let ![]() ${\mathbf{A}}$ be the adjacency matrix of non-uniform hypergraph
${\mathbf{A}}$ be the adjacency matrix of non-uniform hypergraph ![]() $H = \bigcup _{m=2}^{M}H_m$, then
$H = \bigcup _{m=2}^{M}H_m$, then ![]() ${\mathbf{A}}$ satisfies
${\mathbf{A}}$ satisfies ![]() $\mathbf{UUTP}(c_0,\gamma _0)$ with
$\mathbf{UUTP}(c_0,\gamma _0)$ with ![]() $c_0 = [M(M-1)]^{-1}, \gamma _0 = 0$.
$c_0 = [M(M-1)]^{-1}, \gamma _0 = 0$.
Proof of Lemma A.3. Note that
 \begin{align*} &\,f_{{\mathbf{Q}}}({\mathbf{A}}) - \mu = \sum _{i,j=1}^n{\mathbf{Q}}_{ij}({\mathbf{A}}_{ij} -{\mathbb{E}}{\mathbf{A}}_{ij}) = \sum _{i,j=1}^n{\mathbf{Q}}_{ij}{\mathbf{W}}_{ij}\\
= &\, \sum _{i,j=1}^n{\mathbf{Q}}_{ij} \Bigg ( \sum _{m=2}^{M}\,\, \sum _{\substack{e\in E_m\\
i\neq j,\, \{i,j\}\subset e} } \boldsymbol{\mathcal{W}}^{(m)}_e \Bigg ) =\sum _{m=2}^M \,\, \sum _{e\in E_m} \boldsymbol{\mathcal{W}}^{(m)}_e \Bigg ( \sum _{\{i,j\}\subset e, \, i\neq j}{\mathbf{Q}}_{ij}\Bigg ) =\sum _{m=2}^{M} \,\,\sum _{e\in E_m}\boldsymbol{\mathcal{Z}}^{(m)}_e\,, \end{align*}
\begin{align*} &\,f_{{\mathbf{Q}}}({\mathbf{A}}) - \mu = \sum _{i,j=1}^n{\mathbf{Q}}_{ij}({\mathbf{A}}_{ij} -{\mathbb{E}}{\mathbf{A}}_{ij}) = \sum _{i,j=1}^n{\mathbf{Q}}_{ij}{\mathbf{W}}_{ij}\\
= &\, \sum _{i,j=1}^n{\mathbf{Q}}_{ij} \Bigg ( \sum _{m=2}^{M}\,\, \sum _{\substack{e\in E_m\\
i\neq j,\, \{i,j\}\subset e} } \boldsymbol{\mathcal{W}}^{(m)}_e \Bigg ) =\sum _{m=2}^M \,\, \sum _{e\in E_m} \boldsymbol{\mathcal{W}}^{(m)}_e \Bigg ( \sum _{\{i,j\}\subset e, \, i\neq j}{\mathbf{Q}}_{ij}\Bigg ) =\sum _{m=2}^{M} \,\,\sum _{e\in E_m}\boldsymbol{\mathcal{Z}}^{(m)}_e\,, \end{align*}
where ![]() $\boldsymbol{\mathcal{Z}}^{(m)}_e = \boldsymbol{\mathcal{W}}^{(m)}_e \big ( \sum _{\{i,j\}\subset e, i\neq j}{\mathbf{Q}}_{ij}\big )$ are independent centred random variables upper bounded by
$\boldsymbol{\mathcal{Z}}^{(m)}_e = \boldsymbol{\mathcal{W}}^{(m)}_e \big ( \sum _{\{i,j\}\subset e, i\neq j}{\mathbf{Q}}_{ij}\big )$ are independent centred random variables upper bounded by ![]() $ |\boldsymbol{\mathcal{Z}}^{(m)}_e| \leq \sum _{ \{i,j\} \subset e,\, i\neq j}{\mathbf{Q}}_{ij}\leq M(M-1)a$ for each
$ |\boldsymbol{\mathcal{Z}}^{(m)}_e| \leq \sum _{ \{i,j\} \subset e,\, i\neq j}{\mathbf{Q}}_{ij}\leq M(M-1)a$ for each ![]() $ m\in \{2, \dots, M\}$ since
$ m\in \{2, \dots, M\}$ since ![]() ${\mathbf{Q}}_{ij} \in [0, a]$. Moreover, the variance of the sum can be written as
${\mathbf{Q}}_{ij} \in [0, a]$. Moreover, the variance of the sum can be written as
 \begin{align*} &\, \sum _{m=2}^M \sum _{e\in E_m}{\mathbb{E}}(\boldsymbol{\mathcal{Z}}^{(m)}_e)^2 = \sum _{m=2}^M \,\, \sum _{e\in E_m}{\mathbb{E}}(\boldsymbol{\mathcal{W}}^{(m)}_e)^2 \Bigg ( \sum _{\{i,j\}\subset e, \, i\neq j}{\mathbf{Q}}_{ij}\Bigg )^2\\
\leq &\,\sum _{m=2}^M \,\,\sum _{e\in E_m}{\mathbb{E}} [\boldsymbol{\mathcal{A}}^{(m)}_{e}] \cdot m(m-1) \sum _{ \{i,j \}\subset e, i\neq j }{\mathbf{Q}}_{ij}^2 \leq M(M-1)\sum _{i,j=1}^n{\mathbf{Q}}_{ij}^2{\mathbb{E}}{\mathbf{A}}_{ij} = M(M-1)\tilde{\sigma }^2. \end{align*}
\begin{align*} &\, \sum _{m=2}^M \sum _{e\in E_m}{\mathbb{E}}(\boldsymbol{\mathcal{Z}}^{(m)}_e)^2 = \sum _{m=2}^M \,\, \sum _{e\in E_m}{\mathbb{E}}(\boldsymbol{\mathcal{W}}^{(m)}_e)^2 \Bigg ( \sum _{\{i,j\}\subset e, \, i\neq j}{\mathbf{Q}}_{ij}\Bigg )^2\\
\leq &\,\sum _{m=2}^M \,\,\sum _{e\in E_m}{\mathbb{E}} [\boldsymbol{\mathcal{A}}^{(m)}_{e}] \cdot m(m-1) \sum _{ \{i,j \}\subset e, i\neq j }{\mathbf{Q}}_{ij}^2 \leq M(M-1)\sum _{i,j=1}^n{\mathbf{Q}}_{ij}^2{\mathbb{E}}{\mathbf{A}}_{ij} = M(M-1)\tilde{\sigma }^2. \end{align*}
where the last inequality holds since by definition ![]() ${\mathbb{E}}{\mathbf{A}}_{ij} = \sum _{m=2}^M \,\,\sum _{\substack{e\in E_m\\
\{i,j\}\subset e}}{\mathbb{E}} [\boldsymbol{\mathcal{A}}^{(m)}_{e}]$. Then by Bennett’s inequality Lemma D.4, we obtain
${\mathbb{E}}{\mathbf{A}}_{ij} = \sum _{m=2}^M \,\,\sum _{\substack{e\in E_m\\
\{i,j\}\subset e}}{\mathbb{E}} [\boldsymbol{\mathcal{A}}^{(m)}_{e}]$. Then by Bennett’s inequality Lemma D.4, we obtain
 \begin{align*}{\mathbb{P}} (f_{{\mathbf{Q}}}({\mathbf{A}})- \mu \geq t) \leq \exp \Bigg ({-}\frac{\tilde{\sigma }^2}{M(M-1)a^2} h \Bigg ( \frac{at}{\tilde{\sigma }^2}\Bigg ) \Bigg )\, \end{align*}
\begin{align*}{\mathbb{P}} (f_{{\mathbf{Q}}}({\mathbf{A}})- \mu \geq t) \leq \exp \Bigg ({-}\frac{\tilde{\sigma }^2}{M(M-1)a^2} h \Bigg ( \frac{at}{\tilde{\sigma }^2}\Bigg ) \Bigg )\, \end{align*}
where the inequality holds since the function ![]() $x\cdot h(1/x) = (1+x)\log (1 + 1/x) - 1$ is decreasing with respect to
$x\cdot h(1/x) = (1+x)\log (1 + 1/x) - 1$ is decreasing with respect to ![]() $x$.
$x$.
Definition A.4 (Discrepancy property, DP). Let ![]() ${\mathbf{M}}$ be an
${\mathbf{M}}$ be an ![]() $n\times n$ matrix with non-negative entries. For
$n\times n$ matrix with non-negative entries. For ![]() $S,T\subset [n]$, define
$S,T\subset [n]$, define ![]() $ e_{{\mathbf{M}}}(S,T)=\sum _{i\in S, j\in T}{\mathbf{M}}_{ij}.$ We say
$ e_{{\mathbf{M}}}(S,T)=\sum _{i\in S, j\in T}{\mathbf{M}}_{ij}.$ We say ![]() ${\mathbf{M}}$ has the discrepancy property with parameter
${\mathbf{M}}$ has the discrepancy property with parameter ![]() $\delta \gt 0$,
$\delta \gt 0$, ![]() $\kappa _1\gt 1, \kappa _2\geq 0$, denoted by
$\kappa _1\gt 1, \kappa _2\geq 0$, denoted by ![]() $\mathbf{DP}(\delta,\kappa _1,\kappa _2)$, if for all non-empty
$\mathbf{DP}(\delta,\kappa _1,\kappa _2)$, if for all non-empty ![]() $S,T\subset [n]$, at least one of the following hold:
$S,T\subset [n]$, at least one of the following hold:
(1)
 $e_{{\mathbf{M}}}(S,T)\leq \kappa _1 \delta |S| |T|$;
$e_{{\mathbf{M}}}(S,T)\leq \kappa _1 \delta |S| |T|$;(2)
 $e_{{\mathbf{M}}}(S,T) \cdot \log \left(\frac{e_{{\mathbf{M}}}(S,T)}{\delta |S|\cdot |T|}\right)\leq \kappa _2 (|S|\vee |T|)\cdot \log \left(\frac{en}{|S|\vee |T|}\right)$.
$e_{{\mathbf{M}}}(S,T) \cdot \log \left(\frac{e_{{\mathbf{M}}}(S,T)}{\delta |S|\cdot |T|}\right)\leq \kappa _2 (|S|\vee |T|)\cdot \log \left(\frac{en}{|S|\vee |T|}\right)$.
Lemma A.5 shows that if a symmetric random matrix ![]() ${\mathbf{A}}$ satisfies the upper tail property
${\mathbf{A}}$ satisfies the upper tail property ![]() $\mathbf{UUTP}(c_0,\gamma _0)$ with parameter
$\mathbf{UUTP}(c_0,\gamma _0)$ with parameter ![]() $c_0\gt 0,\gamma _0\geq 0$, then the discrepancy property holds with high probability.
$c_0\gt 0,\gamma _0\geq 0$, then the discrepancy property holds with high probability.
Lemma A.5 (Lemma 6.4 in [Reference Cook, Goldstein and Johnson22]). Let ![]() ${\mathbf{M}}$ be an
${\mathbf{M}}$ be an ![]() $n\times n$ symmetric random matrix with non-negative entries. Assume that for some
$n\times n$ symmetric random matrix with non-negative entries. Assume that for some ![]() $\delta \gt 0$,
$\delta \gt 0$, ![]() $\delta \gt 0$,
$\delta \gt 0$, ![]() ${\mathbb{E}}{\mathbf{M}}_{ij}\leq \delta$ for all
${\mathbb{E}}{\mathbf{M}}_{ij}\leq \delta$ for all ![]() $i,j\in [n]$ and
$i,j\in [n]$ and ![]() ${\mathbf{M}}$ has
${\mathbf{M}}$ has ![]() $\mathbf{UUTP}(c_0,\gamma _0)$ with parameter
$\mathbf{UUTP}(c_0,\gamma _0)$ with parameter ![]() $c_0,\gamma _0 \gt 0$. Then for any
$c_0,\gamma _0 \gt 0$. Then for any ![]() $K\gt 0$, the discrepancy property
$K\gt 0$, the discrepancy property ![]() $\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ holds for
$\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ holds for ![]() ${\mathbf{M}}$ with probability at least
${\mathbf{M}}$ with probability at least ![]() $1 - n^{-K}$
$1 - n^{-K}$ ![]() $ \kappa _1 = e^2(1+\gamma _0)^2, \kappa _2 = \frac{2}{c_0}(1+\gamma _0)(K+4).$
$ \kappa _1 = e^2(1+\gamma _0)^2, \kappa _2 = \frac{2}{c_0}(1+\gamma _0)(K+4).$
When the discrepancy property holds, then deterministically the contribution from heavy pairs is ![]() $O(\sqrt{d})$, as shown in the following lemma.
$O(\sqrt{d})$, as shown in the following lemma.
Lemma A.6 (Lemma 6.6 in [Reference Cook, Goldstein and Johnson22]). Let ![]() ${\mathbf{M}}$ be a non-negative symmetric
${\mathbf{M}}$ be a non-negative symmetric ![]() $n\times n$ matrix with all row sums bounded by
$n\times n$ matrix with all row sums bounded by ![]() $d$. Suppose
$d$. Suppose ![]() ${\mathbf{M}}$ has
${\mathbf{M}}$ has ![]() ${\mathbf{M}}$ has
${\mathbf{M}}$ has ![]() $\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ with
$\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ with ![]() $\delta =Cd/n$ for some
$\delta =Cd/n$ for some ![]() $C\gt 0,\kappa _1\gt 1$,
$C\gt 0,\kappa _1\gt 1$, ![]() $\kappa _2\geq 0$. Then for any
$\kappa _2\geq 0$. Then for any ![]() $x\in \mathbb{S}^{n-1}$,
$x\in \mathbb{S}^{n-1}$,
 \begin{align*} \Bigg | \sum _{(i,j)\in \mathcal{H}(x)}{\mathbf{M}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\leq \alpha _0\sqrt{d}, \end{align*}
\begin{align*} \Bigg | \sum _{(i,j)\in \mathcal{H}(x)}{\mathbf{M}}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\leq \alpha _0\sqrt{d}, \end{align*}
where ![]() $ \alpha _0=16+32C(1+\kappa _1)+64\kappa _2 (1+\frac{2}{\kappa _1\log \kappa _1}).$
$ \alpha _0=16+32C(1+\kappa _1)+64\kappa _2 (1+\frac{2}{\kappa _1\log \kappa _1}).$
Lemma A.7 proves that ![]() ${\mathbf{A}}$ has bounded row and column sums with high probability.
${\mathbf{A}}$ has bounded row and column sums with high probability.
Lemma A.7. For any ![]() $K\gt 0$, there is a constant
$K\gt 0$, there is a constant ![]() $\alpha _1\gt 0$ such that with probability at least
$\alpha _1\gt 0$ such that with probability at least ![]() $1-n^{-K}$,
$1-n^{-K}$,
 \begin{align} \max _{1\leq i\leq n} \,\sum _{j=1}^n{\mathbf{A}}_{ij} \leq \alpha _1 d \end{align}
\begin{align} \max _{1\leq i\leq n} \,\sum _{j=1}^n{\mathbf{A}}_{ij} \leq \alpha _1 d \end{align}
with ![]() $\alpha _1= 4 + \frac{2(M-1)(1+K)}{3c}$ and
$\alpha _1= 4 + \frac{2(M-1)(1+K)}{3c}$ and ![]() $d\geq c\log n$.
$d\geq c\log n$.
Proof. For a fixed ![]() $i\in [n]$,
$i\in [n]$,
 \begin{align*} &\sum _{j=1}^n{\mathbf{A}}_{ij} =\sum _{m=2}^M\sum _{e\in E_m: i\in e} (m-1)\boldsymbol{\mathcal{A}}^{(m)}_e\,, \quad \, \sum _{j=1}^n ({\mathbf{A}}_{ij} -{\mathbb{E}}{\mathbf{A}}_{ij}) =\sum _{m=2}^M\sum _{e\in E_m: i\in e} (m-1)\boldsymbol{\mathcal{W}}^{(m)}_e\,, \\
&\sum _{j=1}^n{\mathbb{E}}{\mathbf{A}}_{ij} \leq \sum _{m=2}^M \binom{n}{m-1} \frac{(m-1)d_m}{\binom{n}{m-1}}=d,\\
& \sum _{m=2}^M(m-1)^2\sum _{e\in E_m: i\in e}{\mathbb{E}}[(\boldsymbol{\mathcal{W}}^{(m)}_e)^2] \leq \sum _{m=2}^M (m-1)^2\sum _{e\in E_m: i\in e}{\mathbb{E}}[\boldsymbol{\mathcal{A}}^{(m)}_e]\leq (M-1)d\,. \end{align*}
\begin{align*} &\sum _{j=1}^n{\mathbf{A}}_{ij} =\sum _{m=2}^M\sum _{e\in E_m: i\in e} (m-1)\boldsymbol{\mathcal{A}}^{(m)}_e\,, \quad \, \sum _{j=1}^n ({\mathbf{A}}_{ij} -{\mathbb{E}}{\mathbf{A}}_{ij}) =\sum _{m=2}^M\sum _{e\in E_m: i\in e} (m-1)\boldsymbol{\mathcal{W}}^{(m)}_e\,, \\
&\sum _{j=1}^n{\mathbb{E}}{\mathbf{A}}_{ij} \leq \sum _{m=2}^M \binom{n}{m-1} \frac{(m-1)d_m}{\binom{n}{m-1}}=d,\\
& \sum _{m=2}^M(m-1)^2\sum _{e\in E_m: i\in e}{\mathbb{E}}[(\boldsymbol{\mathcal{W}}^{(m)}_e)^2] \leq \sum _{m=2}^M (m-1)^2\sum _{e\in E_m: i\in e}{\mathbb{E}}[\boldsymbol{\mathcal{A}}^{(m)}_e]\leq (M-1)d\,. \end{align*}
Then for ![]() $\alpha _1= 4 + \frac{2(M-1)(1+K)}{3c}$, by Bernstein’s inequality, with the assumption that
$\alpha _1= 4 + \frac{2(M-1)(1+K)}{3c}$, by Bernstein’s inequality, with the assumption that ![]() $d\geq c\log n$,
$d\geq c\log n$,
 \begin{align}{\mathbb{P}}\Bigg (\sum _{j=1}^n{\mathbf{A}}_{ij}\geq \alpha _1 d \Bigg ) &\leq{\mathbb{P}} \Bigg (\sum _{j=1}^n{\mathbf{A}}_{ij} -{\mathbb{E}}{\mathbf{A}}_{ij}\geq (\alpha _1-1) d\Bigg ) \notag \\
&\leq \exp \Bigg ({-}\frac{\frac{1}{2}(\alpha _1-1)^2 d^2}{(M-1)d+\frac{1}{3}(M-1)(\alpha _1-1)d}\Bigg ) \leq n^{-\frac{3c(\alpha _1-1)^2}{(M-1)(2\alpha _1+4)}}\leq n^{-1-K.} \end{align}
\begin{align}{\mathbb{P}}\Bigg (\sum _{j=1}^n{\mathbf{A}}_{ij}\geq \alpha _1 d \Bigg ) &\leq{\mathbb{P}} \Bigg (\sum _{j=1}^n{\mathbf{A}}_{ij} -{\mathbb{E}}{\mathbf{A}}_{ij}\geq (\alpha _1-1) d\Bigg ) \notag \\
&\leq \exp \Bigg ({-}\frac{\frac{1}{2}(\alpha _1-1)^2 d^2}{(M-1)d+\frac{1}{3}(M-1)(\alpha _1-1)d}\Bigg ) \leq n^{-\frac{3c(\alpha _1-1)^2}{(M-1)(2\alpha _1+4)}}\leq n^{-1-K.} \end{align}
Taking a union bound over ![]() $i\in [n]$, then equation (A.9) holds with probability
$i\in [n]$, then equation (A.9) holds with probability ![]() $1-n^{-K}$.
$1-n^{-K}$.
Now we are ready to obtain equation (A.8).
Lemma A.8. For any ![]() $K\gt 0$, there is a constant
$K\gt 0$, there is a constant ![]() $\beta$ depending on
$\beta$ depending on ![]() $K, c, M$ such that with probability at least
$K, c, M$ such that with probability at least ![]() $1-2n^{-K}$,
$1-2n^{-K}$,
 \begin{align} \Bigg |\sum _{(i,j)\in \mathcal H(x)}{\mathbf{A}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq \beta \sqrt{d}. \end{align}
\begin{align} \Bigg |\sum _{(i,j)\in \mathcal H(x)}{\mathbf{A}}_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq \beta \sqrt{d}. \end{align}
Proof. By Lemma A.3, ![]() ${\mathbf{A}}$ satisfies
${\mathbf{A}}$ satisfies ![]() $\mathbf{UUTP}(\frac{1}{M(M-1)},0)$. From equation (A.6) and Lemma A.5, the property
$\mathbf{UUTP}(\frac{1}{M(M-1)},0)$. From equation (A.6) and Lemma A.5, the property ![]() $\mathbf{DP}(\delta, \kappa _1,\kappa _2)$ holds for
$\mathbf{DP}(\delta, \kappa _1,\kappa _2)$ holds for ![]() ${\mathbf{A}}$ with probability at least
${\mathbf{A}}$ with probability at least ![]() $1-n^{-K}$ with
$1-n^{-K}$ with
Let ![]() $\mathcal{E}_1$ be the event that
$\mathcal{E}_1$ be the event that ![]() $\mathbf{DP}(\delta, \kappa _1,\kappa _2)$ holds for
$\mathbf{DP}(\delta, \kappa _1,\kappa _2)$ holds for ![]() ${\mathbf{A}}$. Let
${\mathbf{A}}$. Let ![]() $\mathcal{E}_2$ be the event that all row sums of
$\mathcal{E}_2$ be the event that all row sums of ![]() ${\mathbf{A}}$ are bounded by
${\mathbf{A}}$ are bounded by ![]() $\alpha _1 d$. Then
$\alpha _1 d$. Then ![]() ${\mathbb{P}} (\mathcal{E}_1 \cap \mathcal{E}_2)\geq 1-2n^{-K}.$ On the event
${\mathbb{P}} (\mathcal{E}_1 \cap \mathcal{E}_2)\geq 1-2n^{-K}.$ On the event ![]() $\mathcal{E}_1 \cap \mathcal{E}_2$, by Lemma A.6, equation (A.11) holds with
$\mathcal{E}_1 \cap \mathcal{E}_2$, by Lemma A.6, equation (A.11) holds with ![]() $ \beta = \alpha _0\alpha _1,$ where
$ \beta = \alpha _0\alpha _1,$ where
A.4. Proof of Theorem 3.1
Proof. From equation (A.5), with probability at least ![]() $1-2e^{-n}$, the contribution from light pairs in equation (A.3) is bounded by
$1-2e^{-n}$, the contribution from light pairs in equation (A.3) is bounded by ![]() $2\alpha \sqrt{d}$ with
$2\alpha \sqrt{d}$ with ![]() $\alpha =5M(M-1)$. From equations (A.7) and (A.11), with probability at least
$\alpha =5M(M-1)$. From equations (A.7) and (A.11), with probability at least ![]() $1-2n^{-K}$, the contribution from heavy pairs in equation (A.3) is bounded by
$1-2n^{-K}$, the contribution from heavy pairs in equation (A.3) is bounded by ![]() $2\sqrt{d}+2\beta \sqrt{d}$. Therefore with probability at least
$2\sqrt{d}+2\beta \sqrt{d}$. Therefore with probability at least ![]() $1-2e^{-n}-2n^{-K}$,
$1-2e^{-n}-2n^{-K}$,
where ![]() $C_M$ is a constant depending only on
$C_M$ is a constant depending only on ![]() $c, K, M$ such that
$c, K, M$ such that ![]() $ C_M= 2(\alpha +1+\beta ).$ In particular, we can take
$ C_M= 2(\alpha +1+\beta ).$ In particular, we can take ![]() $\alpha =5M(M-1),$
$\alpha =5M(M-1),$ ![]() $\beta =512M(M-1)(K+5)\left ( 2+\frac{(M-1)(1+K)}{c}\right )$, and
$\beta =512M(M-1)(K+5)\left ( 2+\frac{(M-1)(1+K)}{c}\right )$, and ![]() $ C_M=512M(M-1)(K+6)\left ( 2+\frac{(M-1)(1+K)}{c}\right ).$ This finishes the proof of Theorem 3.1.
$ C_M=512M(M-1)(K+6)\left ( 2+\frac{(M-1)(1+K)}{c}\right ).$ This finishes the proof of Theorem 3.1.
A.5. Proof of Theorem 3.3
Let ![]() ${\mathcal{S}}\subset [n]$ be any given subset. From equation (A.5), with probability at least
${\mathcal{S}}\subset [n]$ be any given subset. From equation (A.5), with probability at least ![]() $1-2e^{-n}$,
$1-2e^{-n}$,
 \begin{align} \sup _{\boldsymbol{x}\in \mathcal{N} } \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\Bigg ({\mathbf{A}}_{{\mathcal{S}}} -{\mathbb{E}}{\mathbf{A}}_{{\mathcal{S}}}\Bigg )}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq 5M(M-1)\sqrt{d}. \end{align}
\begin{align} \sup _{\boldsymbol{x}\in \mathcal{N} } \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}{\Bigg ({\mathbf{A}}_{{\mathcal{S}}} -{\mathbb{E}}{\mathbf{A}}_{{\mathcal{S}}}\Bigg )}_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq 5M(M-1)\sqrt{d}. \end{align}
Since there are at most ![]() $2^n$ many choices for
$2^n$ many choices for ![]() $\mathcal{S}$, by taking a union bound, with probability at least
$\mathcal{S}$, by taking a union bound, with probability at least ![]() $1-2(e/2)^{-n}$, we have for all
$1-2(e/2)^{-n}$, we have for all ![]() ${\mathcal{S}}\subset [n]$, equation (A.12) holds. In particular, by taking
${\mathcal{S}}\subset [n]$, equation (A.12) holds. In particular, by taking ![]() ${\mathcal{S}} = \mathcal{I} = \{i\in [n]\,:\, \mathrm{row}(i)\leq \tau d\}$, with probability at least
${\mathcal{S}} = \mathcal{I} = \{i\in [n]\,:\, \mathrm{row}(i)\leq \tau d\}$, with probability at least ![]() $1-2(e/2)^{-n}$, we have
$1-2(e/2)^{-n}$, we have
 \begin{align} \sup _{\boldsymbol{x}\in \mathcal{N}} \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}[({\mathbf{A}} -{\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}]_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq 5M(M-1)\sqrt{d}. \end{align}
\begin{align} \sup _{\boldsymbol{x}\in \mathcal{N}} \Bigg | \sum _{(i,j)\in \mathcal{L}(\boldsymbol{x})}[({\mathbf{A}} -{\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}]_{ij} \boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq 5M(M-1)\sqrt{d}. \end{align}
Similar to equation (A.7), deterministically,
 \begin{align} \Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} [({\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}]_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq (M-1)\sqrt{d}. \end{align}
\begin{align} \Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} [({\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}]_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq (M-1)\sqrt{d}. \end{align}
Next we show the contribution from heavy pairs for ![]() ${\mathbf{A}}_{\mathcal{I}}$ is bounded.
${\mathbf{A}}_{\mathcal{I}}$ is bounded.
Lemma A.9. For any ![]() $K\gt 0$, there is a constant
$K\gt 0$, there is a constant ![]() $\beta _{\tau }$ depending on
$\beta _{\tau }$ depending on ![]() $K, c, M,\tau$ such that with probability at least
$K, c, M,\tau$ such that with probability at least ![]() $1-n^{-K}$,
$1-n^{-K}$,
 \begin{align} \Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} [({\mathbf{A}})_{\mathcal{I}}]_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq \beta _{\tau } \sqrt{d}. \end{align}
\begin{align} \Bigg |\sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} [({\mathbf{A}})_{\mathcal{I}}]_{ij}\boldsymbol{x}_i \boldsymbol{x}_j\Bigg |\leq \beta _{\tau } \sqrt{d}. \end{align}
Proof. Note that ![]() ${\mathbf{A}}$ satisfies
${\mathbf{A}}$ satisfies ![]() $\mathbf{UUTP}\left (\frac{1}{M(M-1)},0 \right )$ from Lemma A.3. According to Lemma A.5, with probability at least
$\mathbf{UUTP}\left (\frac{1}{M(M-1)},0 \right )$ from Lemma A.3. According to Lemma A.5, with probability at least ![]() $1-n^{-K}$,
$1-n^{-K}$, ![]() $\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ holds for
$\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ holds for ![]() ${\mathbf{A}}$ with
${\mathbf{A}}$ with
The ![]() $\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ property holds for
$\mathbf{DP}(\delta,\kappa _1,\kappa _2)$ property holds for ![]() ${\mathbf{A}}_{\mathcal{I}}$ as well, since
${\mathbf{A}}_{\mathcal{I}}$ as well, since ![]() ${\mathbf{A}}_{\mathcal{I}}$ is obtained from
${\mathbf{A}}_{\mathcal{I}}$ is obtained from ![]() ${\mathbf{A}}$ by restricting to
${\mathbf{A}}$ by restricting to ![]() $\mathcal{I}$. Note that all row sums in
$\mathcal{I}$. Note that all row sums in ![]() ${\mathbf{A}}_{\mathcal{I}}$ are bounded by
${\mathbf{A}}_{\mathcal{I}}$ are bounded by ![]() $\tau d$. By Lemma A.6,
$\tau d$. By Lemma A.6,
 \begin{align} \Bigg | \sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} [{\mathbf{A}}_{\mathcal{I}}]_{ij}\boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\leq \alpha _0\sqrt{\tau d}, \end{align}
\begin{align} \Bigg | \sum _{(i,j)\in \mathcal{H}(\boldsymbol{x})} [{\mathbf{A}}_{\mathcal{I}}]_{ij}\boldsymbol{x}_i \boldsymbol{x}_j \Bigg |\leq \alpha _0\sqrt{\tau d}, \end{align}
where we can take ![]() $ \alpha _0=16+\frac{32}{\tau }(1+e^2)+128M(M-1)(K+4)\left (1+\frac{1}{e^2}\right ).$
$ \alpha _0=16+\frac{32}{\tau }(1+e^2)+128M(M-1)(K+4)\left (1+\frac{1}{e^2}\right ).$
We can then take ![]() $\beta _{\tau }=\alpha _0\sqrt{\tau }$ in equation (A.15). Therefore, combining equations (A.13), (A.14), (A.16), with probability at least
$\beta _{\tau }=\alpha _0\sqrt{\tau }$ in equation (A.15). Therefore, combining equations (A.13), (A.14), (A.16), with probability at least ![]() $1-2(e/2)^{-n}-n^{-K}$, there exists a constant
$1-2(e/2)^{-n}-n^{-K}$, there exists a constant ![]() $C_{\tau }$ depending only on
$C_{\tau }$ depending only on ![]() $\tau, M, K$ such that
$\tau, M, K$ such that ![]() $ \|({\mathbf{A}}-{\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}\|\leq C_{\tau } \sqrt{d},$ where
$ \|({\mathbf{A}}-{\mathbb{E}}{\mathbf{A}})_{\mathcal{I}}\|\leq C_{\tau } \sqrt{d},$ where ![]() $C_{\tau }=2( (5M+1)(M-1)+\alpha _0\sqrt{\tau })$. This finishes the proof of Theorem 3.3.
$C_{\tau }=2( (5M+1)(M-1)+\alpha _0\sqrt{\tau })$. This finishes the proof of Theorem 3.3.
Appendix B. Technical Lemmas
B.1. Proof of Lemma 2.4
Proof. By Weyl’s inequality (Lemma D.5), the difference between eigenvalues of ![]() $\widetilde{{\mathbb{E}}{\mathbf{A}}}$ and
$\widetilde{{\mathbb{E}}{\mathbf{A}}}$ and ![]() ${\mathbb{E}}{\mathbf{A}}$ can be upper bounded by
${\mathbb{E}}{\mathbf{A}}$ can be upper bounded by
 \begin{align*} |\lambda _i( \widetilde{{\mathbb{E}}{\mathbf{A}}} ) - \lambda _i({\mathbb{E}}{\mathbf{A}})| & \leq \|\widetilde{{\mathbb{E}}{\mathbf{A}}} -{\mathbb{E}}{\mathbf{A}} \|_2 \leq \|\widetilde{{\mathbb{E}}{\mathbf{A}}} -{\mathbb{E}}{\mathbf{A}} \|_{{\mathrm{F}}}\\
&\leq \left [2k \cdot \frac{n}{k} \cdot \sqrt{n}\log (n) \cdot (\alpha - \beta )^2 \right ]^{1/2}= O \Big (n^{3/4}\log ^{1/2}(n)(\alpha - \beta )\Big ). \end{align*}
\begin{align*} |\lambda _i( \widetilde{{\mathbb{E}}{\mathbf{A}}} ) - \lambda _i({\mathbb{E}}{\mathbf{A}})| & \leq \|\widetilde{{\mathbb{E}}{\mathbf{A}}} -{\mathbb{E}}{\mathbf{A}} \|_2 \leq \|\widetilde{{\mathbb{E}}{\mathbf{A}}} -{\mathbb{E}}{\mathbf{A}} \|_{{\mathrm{F}}}\\
&\leq \left [2k \cdot \frac{n}{k} \cdot \sqrt{n}\log (n) \cdot (\alpha - \beta )^2 \right ]^{1/2}= O \Big (n^{3/4}\log ^{1/2}(n)(\alpha - \beta )\Big ). \end{align*}
The lemma follows, as ![]() $\lambda _i({\mathbb{E}}{\mathbf{A}}) = \Omega \left ( n (\alpha - \beta ) \right )$ for all
$\lambda _i({\mathbb{E}}{\mathbf{A}}) = \Omega \left ( n (\alpha - \beta ) \right )$ for all ![]() $1 \leq i \leq k$.
$1 \leq i \leq k$.
B.2. Proof of Lemma 5.3
Proof. We first compute the singular values of ![]() $\overline{{\mathbf{B}}}_1$. From equation (16), the rank of matrix
$\overline{{\mathbf{B}}}_1$. From equation (16), the rank of matrix ![]() $\overline{{\mathbf{B}}}_1$ is
$\overline{{\mathbf{B}}}_1$ is ![]() $k$, and the least non-trivial singular value of
$k$, and the least non-trivial singular value of ![]() $\overline{{\mathbf{B}}}_1$ is
$\overline{{\mathbf{B}}}_1$ is
 \begin{align*} \sigma _k (\overline{{\mathbf{B}}}_1) = \frac{n}{2\sqrt{2}k}(\overline{\alpha } - \overline{\beta }) = \frac{n}{2\sqrt{2}k}\sum _{m\in \mathcal{M}} \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}}\,, \end{align*}
\begin{align*} \sigma _k (\overline{{\mathbf{B}}}_1) = \frac{n}{2\sqrt{2}k}(\overline{\alpha } - \overline{\beta }) = \frac{n}{2\sqrt{2}k}\sum _{m\in \mathcal{M}} \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}}\,, \end{align*}
where ![]() $\mathcal{M}$ is obtained from Algorithm 3. By the definition of
$\mathcal{M}$ is obtained from Algorithm 3. By the definition of ![]() $\overline{{\mathbf{A}}}_1$ in equation (20), the least non-trivial singular value of
$\overline{{\mathbf{A}}}_1$ in equation (20), the least non-trivial singular value of ![]() $\overline{{\mathbf{A}}}_1$ is
$\overline{{\mathbf{A}}}_1$ is
 \begin{align*} \sigma _k (\overline{{\mathbf{A}}}_1) = \sigma _k (\overline{{\mathbf{B}}}_1) = \frac{n}{2\sqrt{2}k}(\overline{\alpha } - \overline{\beta }) = \frac{n}{2\sqrt{2}k}\sum _{m\in \mathcal{M}} \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}}\,. \end{align*}
\begin{align*} \sigma _k (\overline{{\mathbf{A}}}_1) = \sigma _k (\overline{{\mathbf{B}}}_1) = \frac{n}{2\sqrt{2}k}(\overline{\alpha } - \overline{\beta }) = \frac{n}{2\sqrt{2}k}\sum _{m\in \mathcal{M}} \binom{\frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{ \binom{n}{m-1}}\,. \end{align*}
Recall that ![]() $n_i$, defined in equation (12), denotes the number of vertices in
$n_i$, defined in equation (12), denotes the number of vertices in ![]() $Z\cap V_i$, which can be written as
$Z\cap V_i$, which can be written as ![]() $n_i = \sum _{v\in V_i} \mathbf{1}_{\{ v \in Z\} }.$ By Hoeffding’s Lemma D.2,
$n_i = \sum _{v\in V_i} \mathbf{1}_{\{ v \in Z\} }.$ By Hoeffding’s Lemma D.2,
Similarly, ![]() $n^{\prime }_{i}$, defined in equation (13), satisfies
$n^{\prime }_{i}$, defined in equation (13), satisfies
As defined in equations (14) and (16), both ![]() $\widetilde{{\mathbf{B}}}_1$ and
$\widetilde{{\mathbf{B}}}_1$ and ![]() $\overline{{\mathbf{B}}}_1$ are deterministic block matrices. Then with probability at least
$\overline{{\mathbf{B}}}_1$ are deterministic block matrices. Then with probability at least ![]() $1 - 2k\exp\!\left ({-} k\log ^2 (n)\right )$, the dimensions of each block inside
$1 - 2k\exp\!\left ({-} k\log ^2 (n)\right )$, the dimensions of each block inside ![]() $\widetilde{{\mathbf{B}}}_1$ and
$\widetilde{{\mathbf{B}}}_1$ and ![]() $\overline{{\mathbf{B}}}_1$ are approximately the same, with deviations up to
$\overline{{\mathbf{B}}}_1$ are approximately the same, with deviations up to ![]() $\sqrt{n}\log (n)$. Consequently, the matrix
$\sqrt{n}\log (n)$. Consequently, the matrix ![]() $\widetilde{{\mathbf{A}}}_1$, which was defined in equation (19), can be treated as a perturbed version of
$\widetilde{{\mathbf{A}}}_1$, which was defined in equation (19), can be treated as a perturbed version of ![]() $\overline{{\mathbf{A}}}_1$. By Weyl’s inequality (Lemma D.5), for any
$\overline{{\mathbf{A}}}_1$. By Weyl’s inequality (Lemma D.5), for any ![]() $i\in [k]$,
$i\in [k]$,
 \begin{align*} |\sigma _i(\overline{{\mathbf{B}}}_1) - \sigma _i(\widetilde{{\mathbf{B}}}_1)| &= |\sigma _i(\overline{{\mathbf{A}}}_1) - \sigma _i(\widetilde{{\mathbf{A}}}_1)|\leq \|\overline{{\mathbf{A}}}_1 - \widetilde{{\mathbf{A}}}_1\|_2 \leq \|\overline{{\mathbf{A}}}_1 - \widetilde{{\mathbf{A}}}_1\|_{{\mathrm{F}}}\\
&\leq \left [2k \cdot \frac{n}{k} \cdot \sqrt{n}\log (n) \cdot (\overline{\alpha } - \overline{\beta })^2 \right ]^{1/2}= O \left (n^{3/4}\log ^{1/2}(n) \cdot (\overline{\alpha } - \overline{\beta })\right ). \end{align*}
\begin{align*} |\sigma _i(\overline{{\mathbf{B}}}_1) - \sigma _i(\widetilde{{\mathbf{B}}}_1)| &= |\sigma _i(\overline{{\mathbf{A}}}_1) - \sigma _i(\widetilde{{\mathbf{A}}}_1)|\leq \|\overline{{\mathbf{A}}}_1 - \widetilde{{\mathbf{A}}}_1\|_2 \leq \|\overline{{\mathbf{A}}}_1 - \widetilde{{\mathbf{A}}}_1\|_{{\mathrm{F}}}\\
&\leq \left [2k \cdot \frac{n}{k} \cdot \sqrt{n}\log (n) \cdot (\overline{\alpha } - \overline{\beta })^2 \right ]^{1/2}= O \left (n^{3/4}\log ^{1/2}(n) \cdot (\overline{\alpha } - \overline{\beta })\right ). \end{align*}
As a result, with probability at least ![]() $1 - 2k\exp ({-}k \log ^2(n))$, we have
$1 - 2k\exp ({-}k \log ^2(n))$, we have
B.3. Proof of Lemma 5.4
Proof. Without loss of generality, we can assume ![]() $\mathcal M=\{2,\dots, M\}$. If
$\mathcal M=\{2,\dots, M\}$. If ![]() $\mathcal M$ is a subset of
$\mathcal M$ is a subset of ![]() $\{2,\dots, M\}$, we can take
$\{2,\dots, M\}$, we can take ![]() $a_m=b_m=0$ for
$a_m=b_m=0$ for ![]() $m\not \in \mathcal M$. Note that in fact, if the best SNR is obtained when
$m\not \in \mathcal M$. Note that in fact, if the best SNR is obtained when ![]() $\mathcal{M}$ is a strict subset, we can substitute
$\mathcal{M}$ is a strict subset, we can substitute ![]() $\mathcal{M}_{\max }$ for
$\mathcal{M}_{\max }$ for ![]() $M$.
$M$.
Let ![]() $X\subset V$ be a subset of vertices in hypergraph
$X\subset V$ be a subset of vertices in hypergraph ![]() $H = (V, E)$ with size
$H = (V, E)$ with size ![]() $|X| = cn$ for some
$|X| = cn$ for some ![]() $c\in (0,1)$ to be decided later. Suppose
$c\in (0,1)$ to be decided later. Suppose ![]() $X$ is a set of vertices with high degrees that we want to zero out. We first count the
$X$ is a set of vertices with high degrees that we want to zero out. We first count the ![]() $m$-uniform hyperedges on
$m$-uniform hyperedges on ![]() $X$ separately, then weight them by
$X$ separately, then weight them by ![]() $(m-1)$, and finally sum over
$(m-1)$, and finally sum over ![]() $m$ to compute the row sums in
$m$ to compute the row sums in ![]() ${\mathbf{A}}$ corresponding to each vertex in
${\mathbf{A}}$ corresponding to each vertex in ![]() $X$. Let
$X$. Let ![]() $E_m(X)$ denote the set of
$E_m(X)$ denote the set of ![]() $m$-uniform hyperedges with all vertices located in
$m$-uniform hyperedges with all vertices located in ![]() $X$, and
$X$, and ![]() $E_m (X^{c})$ denote the set of
$E_m (X^{c})$ denote the set of ![]() $m$-uniform hyperedges with all vertices in
$m$-uniform hyperedges with all vertices in ![]() $X^{c}=V\setminus X$, respectively. Let
$X^{c}=V\setminus X$, respectively. Let ![]() $E_m(X, X^{c})$ denote the set of
$E_m(X, X^{c})$ denote the set of ![]() $m$-uniform hyperedges with at least
$m$-uniform hyperedges with at least ![]() $1$ endpoint in
$1$ endpoint in ![]() $X$ and
$X$ and ![]() $1$ endpoint in
$1$ endpoint in ![]() $X^{c}$. The relationship between total row sums and the number of non-uniform hyperedges in the vertex set
$X^{c}$. The relationship between total row sums and the number of non-uniform hyperedges in the vertex set ![]() $X$ can be expressed as
$X$ can be expressed as
 \begin{align} \sum _{v \in X} \mathrm{row}(v) \leq &\, \sum _{m = 2}^{M} (m-1)\Big ( m|E_m(X)| + (m-1)|E_m(X, X^{c})| \Big ) \end{align}
\begin{align} \sum _{v \in X} \mathrm{row}(v) \leq &\, \sum _{m = 2}^{M} (m-1)\Big ( m|E_m(X)| + (m-1)|E_m(X, X^{c})| \Big ) \end{align}
If the row sum of each vertex ![]() $v \in X$ is at least
$v \in X$ is at least ![]() $20Md$, where
$20Md$, where ![]() $d = \sum _{m=2}^{M} (m-1)a_m$, it follows
$d = \sum _{m=2}^{M} (m-1)a_m$, it follows
 \begin{equation} \sum _{m = 2}^{M} (m-1)\Big (m |E_m(X)| + (m-1)|E_m(X, X^{c})| \Big ) \geq cn\cdot (20Md)\,. \end{equation}
\begin{equation} \sum _{m = 2}^{M} (m-1)\Big (m |E_m(X)| + (m-1)|E_m(X, X^{c})| \Big ) \geq cn\cdot (20Md)\,. \end{equation}
Then either
 \begin{align*} \sum _{m = 2}^{M} m(m-1) |E_m(X)| \geq 4Mcnd, \quad \text{or} \quad \sum _{m = 2}^{M} (m-1)^2|E_m(X, X^{c})| \geq 16Mcnd. \end{align*}
\begin{align*} \sum _{m = 2}^{M} m(m-1) |E_m(X)| \geq 4Mcnd, \quad \text{or} \quad \sum _{m = 2}^{M} (m-1)^2|E_m(X, X^{c})| \geq 16Mcnd. \end{align*}
B.3.1. Concentration of  $\sum _{m=2}^{M} m(m-1)|E_m(X)|$
$\sum _{m=2}^{M} m(m-1)|E_m(X)|$
Recall that ![]() $\big |E_m(X)\big |$ denotes the number of
$\big |E_m(X)\big |$ denotes the number of ![]() $m$-uniform hyperedges with all vertices located in
$m$-uniform hyperedges with all vertices located in ![]() $X$, which can be viewed as the sum of independent Bernoulli random variables
$X$, which can be viewed as the sum of independent Bernoulli random variables ![]() $T_{e}^{(a_m)}$ and
$T_{e}^{(a_m)}$ and ![]() $T_{e}^{(b_m)}$ given by
$T_{e}^{(b_m)}$ given by
 \begin{equation} T_{e}^{(a_m)}\sim \mathrm{Bernoulli}\left ( \frac{a_{m}}{\left({n \atop m-1}\right) }\right ), \quad T_{e}^{(b_m)}\sim \mathrm{Bernoulli}\left ( \frac{b_{m}}{\left({n \atop m-1}\right) }\right )\,. \end{equation}
\begin{equation} T_{e}^{(a_m)}\sim \mathrm{Bernoulli}\left ( \frac{a_{m}}{\left({n \atop m-1}\right) }\right ), \quad T_{e}^{(b_m)}\sim \mathrm{Bernoulli}\left ( \frac{b_{m}}{\left({n \atop m-1}\right) }\right )\,. \end{equation}
Let {![]() $V_{1}, \dots, V_{k}$} be the true partition of
$V_{1}, \dots, V_{k}$} be the true partition of ![]() $V$. Suppose that there are
$V$. Suppose that there are ![]() $\eta _{i}cn$ vertices in block
$\eta _{i}cn$ vertices in block ![]() $V_{i}\cap X$ for each
$V_{i}\cap X$ for each ![]() $i\in [k]$ with restriction
$i\in [k]$ with restriction ![]() $\sum _{i=1}^{k}\eta _{i} = 1$, then
$\sum _{i=1}^{k}\eta _{i} = 1$, then ![]() $\big |E_m(X)\big |$ can be written as
$\big |E_m(X)\big |$ can be written as
where ![]() $E_{m}(X, a_m) \,:\!=\, \cup _{i=1}^{k}E_{m}(V_i\cap X)$ denotes the union for sets of hyperedges with all vertices in the same block
$E_{m}(X, a_m) \,:\!=\, \cup _{i=1}^{k}E_{m}(V_i\cap X)$ denotes the union for sets of hyperedges with all vertices in the same block ![]() $V_i\cap X$ for some
$V_i\cap X$ for some ![]() $i\in [k]$, and
$i\in [k]$, and
denotes the set of hyperedges with vertices crossing different ![]() $V_i\cap X$. We can compute the expectation of
$V_i\cap X$. We can compute the expectation of ![]() $\big |E_m(X)\big |$ as
$\big |E_m(X)\big |$ as
 \begin{equation} {\mathbb{E}} |E_m(X)| = \sum _{i=1}^{k}\left({\eta _{i}cn \atop m}\right) \frac{a_m - b_m }{\left({n \atop m-1}\right) } +\left({ cn \atop m}\right) \frac{b_{m}}{\left({n \atop m-1}\right) }. \end{equation}
\begin{equation} {\mathbb{E}} |E_m(X)| = \sum _{i=1}^{k}\left({\eta _{i}cn \atop m}\right) \frac{a_m - b_m }{\left({n \atop m-1}\right) } +\left({ cn \atop m}\right) \frac{b_{m}}{\left({n \atop m-1}\right) }. \end{equation}
Then
 \begin{align} \sum _{m=2}^{M} m(m-1) \cdot{\mathbb{E}} |E_m(X)| & = \sum _{m=2}^{M} m(m-1) \Bigg [ \sum _{i=1}^{k}\left({\eta _{i}cn \atop m}\right) \frac{a_m - b_m }{\left({n \atop m-1}\right) } +\left({ cn \atop m}\right) \frac{b_{m}}{\left({n \atop m-1}\right) } \Bigg ]. \end{align}
\begin{align} \sum _{m=2}^{M} m(m-1) \cdot{\mathbb{E}} |E_m(X)| & = \sum _{m=2}^{M} m(m-1) \Bigg [ \sum _{i=1}^{k}\left({\eta _{i}cn \atop m}\right) \frac{a_m - b_m }{\left({n \atop m-1}\right) } +\left({ cn \atop m}\right) \frac{b_{m}}{\left({n \atop m-1}\right) } \Bigg ]. \end{align}
As ![]() $\sum \limits _{i=1}^k \eta _i=1$, it follows that
$\sum \limits _{i=1}^k \eta _i=1$, it follows that ![]() $ \sum _{i=1}^k \binom{\eta _i c n}{m} \leq \binom{cn}{m}$ by induction, thus
$ \sum _{i=1}^k \binom{\eta _i c n}{m} \leq \binom{cn}{m}$ by induction, thus
 \begin{equation*} \frac {a_m - b_m }{ \left({n \atop m-1}\right) } \sum _{i=1}^{k} \left({\eta _{i}cn \atop m}\right) + \frac {b_{m}}{ \left({n \atop m-1}\right) } \left({ cn \atop m}\right) = \frac {a_m}{ \left({n \atop m-1}\right) } \sum _{i=1}^{k} \left({\eta _{i}cn \atop m}\right) + \frac {b_{m}}{ \left({n \atop m-1}\right) } \left ( \left({ cn \atop m}\right) - \sum _{i=1}^k \left({\eta _{i}cn \atop m}\right) \right ) \end{equation*}
\begin{equation*} \frac {a_m - b_m }{ \left({n \atop m-1}\right) } \sum _{i=1}^{k} \left({\eta _{i}cn \atop m}\right) + \frac {b_{m}}{ \left({n \atop m-1}\right) } \left({ cn \atop m}\right) = \frac {a_m}{ \left({n \atop m-1}\right) } \sum _{i=1}^{k} \left({\eta _{i}cn \atop m}\right) + \frac {b_{m}}{ \left({n \atop m-1}\right) } \left ( \left({ cn \atop m}\right) - \sum _{i=1}^k \left({\eta _{i}cn \atop m}\right) \right ) \end{equation*}
where both terms on the right are positive numbers. Using this and taking ![]() $b_m = a_m$, we obtain the following upper bound for all
$b_m = a_m$, we obtain the following upper bound for all ![]() $n$,
$n$,
 \begin{align*} \sum _{m=2}^{M} m(m-1){\mathbb{E}} |E_m(X)|\leq \sum _{m=2}^M m(m-1)\binom{cn}{m} \frac{a_m}{\binom{n}{m-1}} \leq cn\sum _{m=2}^M (m-1)a_m =cnd \,. \end{align*}
\begin{align*} \sum _{m=2}^{M} m(m-1){\mathbb{E}} |E_m(X)|\leq \sum _{m=2}^M m(m-1)\binom{cn}{m} \frac{a_m}{\binom{n}{m-1}} \leq cn\sum _{m=2}^M (m-1)a_m =cnd \,. \end{align*}
Note that ![]() $\sum _{m = 2}^{M} m(m-1) |E_m(X)|$ is a weighted sum of independent Bernoulli random variables (corresponding to hyperedges), each upper bounded by
$\sum _{m = 2}^{M} m(m-1) |E_m(X)|$ is a weighted sum of independent Bernoulli random variables (corresponding to hyperedges), each upper bounded by ![]() $M^2$. Also, its variance is bounded by
$M^2$. Also, its variance is bounded by
 \begin{align*} \sigma ^2\,:\!=\, \,&{\mathbb{V}\mathrm{ar}}\left (\sum _{m = 2}^{M} m(m-1) |E_m(X)|\right )=\sum _{m=2}^M m^2(m-1)^2{\mathbb{V}\mathrm{ar}}\left ( |E_m(X)|\right ) \\
\leq \,& \sum _{m=2}^M m^2(m-1)^2{\mathbb{E}} |E_m(X)|\leq M^2cnd. \end{align*}
\begin{align*} \sigma ^2\,:\!=\, \,&{\mathbb{V}\mathrm{ar}}\left (\sum _{m = 2}^{M} m(m-1) |E_m(X)|\right )=\sum _{m=2}^M m^2(m-1)^2{\mathbb{V}\mathrm{ar}}\left ( |E_m(X)|\right ) \\
\leq \,& \sum _{m=2}^M m^2(m-1)^2{\mathbb{E}} |E_m(X)|\leq M^2cnd. \end{align*}
We can apply Bernstein’s Lemma D.3 and obtain
 \begin{align} \,& \mathbb P\left ( \sum _{m = 2}^{M} m(m-1) |E_m(X)| \geq 4Mcnd \right )\notag \\
\leq \,& \mathbb P\left ( \sum _{m = 2}^{M} m(m-1)( |E_m(X)| -{\mathbb{E}}|E_m(X)| )\geq 3Mcnd \right )\notag \\
\leq \,& \exp\!\left ({-}\frac{(3Mcnd)^2}{M^2cnd + M^2cnd/3} \right ) \leq \exp ({-}6cnd)\,. \end{align}
\begin{align} \,& \mathbb P\left ( \sum _{m = 2}^{M} m(m-1) |E_m(X)| \geq 4Mcnd \right )\notag \\
\leq \,& \mathbb P\left ( \sum _{m = 2}^{M} m(m-1)( |E_m(X)| -{\mathbb{E}}|E_m(X)| )\geq 3Mcnd \right )\notag \\
\leq \,& \exp\!\left ({-}\frac{(3Mcnd)^2}{M^2cnd + M^2cnd/3} \right ) \leq \exp ({-}6cnd)\,. \end{align}
B.3.2. Concentration of  $\sum _{m=2}^{M} (m-1)^2|E_m(X, X^{c})|$
$\sum _{m=2}^{M} (m-1)^2|E_m(X, X^{c})|$
For any finite set ![]() $S$, let
$S$, let ![]() $[S]^{j}$ denote the family of
$[S]^{j}$ denote the family of ![]() $j$-subsets of
$j$-subsets of ![]() $S$, i.e.,
$S$, i.e., ![]() $[S]^{j} = \{Z| Z\subseteq S, |Z| = j \}$. Let
$[S]^{j} = \{Z| Z\subseteq S, |Z| = j \}$. Let ![]() $E_m([Y]^{j}, [Z]^{m-j})$ denote the set of
$E_m([Y]^{j}, [Z]^{m-j})$ denote the set of ![]() $m$-hyperedges, where
$m$-hyperedges, where ![]() $j$ vertices are from
$j$ vertices are from ![]() $Y$ and
$Y$ and ![]() $m-j$ vertices are from
$m-j$ vertices are from ![]() $Z$ within each
$Z$ within each ![]() $m$-hyperedge. We want to count the number of
$m$-hyperedge. We want to count the number of ![]() $m$-hyperedges between
$m$-hyperedges between ![]() $X$ and
$X$ and ![]() $X^c$, according to the number of vertices located in
$X^c$, according to the number of vertices located in ![]() $X^c$ within each
$X^c$ within each ![]() $m$-hyperedge. Suppose that there are
$m$-hyperedge. Suppose that there are ![]() $j$ vertices from
$j$ vertices from ![]() $X^c$ within each
$X^c$ within each ![]() $m$-hyperedge for some
$m$-hyperedge for some ![]() $1\leq j \leq m-1$.
$1\leq j \leq m-1$.
(i) Assume that all those
 $j$ vertices are in the same
$j$ vertices are in the same  $[V_{i}\setminus X]^{j}$. If the remaining
$[V_{i}\setminus X]^{j}$. If the remaining  $m-j$ vertices are from
$m-j$ vertices are from  $[V_{i}\cap X]^{m-j}$, then this
$[V_{i}\cap X]^{m-j}$, then this  $m$-hyperedge is connected with probability
$m$-hyperedge is connected with probability  $a_m/ \binom{n}{m-1}$, otherwise
$a_m/ \binom{n}{m-1}$, otherwise  $b_m/ \binom{n}{m-1}$. The number of this type
$b_m/ \binom{n}{m-1}$. The number of this type  $m$-hyperedges can be written as
where
$m$-hyperedges can be written as
where \begin{align*} \sum _{i=1}^{k} \left [ \sum _{e\in \mathcal{E}^{(a_m)}_{j, i}} T_{e}^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{j, i}} T_{e}^{(b_m)} \right ]\,, \end{align*}
\begin{align*} \sum _{i=1}^{k} \left [ \sum _{e\in \mathcal{E}^{(a_m)}_{j, i}} T_{e}^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{j, i}} T_{e}^{(b_m)} \right ]\,, \end{align*}
 $\mathcal{E}^{(a_m)}_{j, i}\,:\!=\, E_m([V_i \cap X^c]^{j}, [V_i\cap X]^{m-j})$, and
denotes the set
$\mathcal{E}^{(a_m)}_{j, i}\,:\!=\, E_m([V_i \cap X^c]^{j}, [V_i\cap X]^{m-j})$, and
denotes the set \begin{align*} \mathcal{E}^{(b_m)}_{j, i} \,:\!=\, E_m \Big ([V_i\cap X^c]^{j}, \,\, [X]^{m-j} \setminus [V_i\cap X]^{m-j} \Big ) \end{align*}
\begin{align*} \mathcal{E}^{(b_m)}_{j, i} \,:\!=\, E_m \Big ([V_i\cap X^c]^{j}, \,\, [X]^{m-j} \setminus [V_i\cap X]^{m-j} \Big ) \end{align*}
 $m$-hyperedges with
$m$-hyperedges with  $j$ vertices in
$j$ vertices in  $[V_i\cap X^c]^{j}$ and the remaining
$[V_i\cap X^c]^{j}$ and the remaining  $m-j$ vertices in
$m-j$ vertices in  $[X]^{j}\setminus [V_i\cap X]^{j}$. We compute all possible choices and upper bound the cardinality of
$[X]^{j}\setminus [V_i\cap X]^{j}$. We compute all possible choices and upper bound the cardinality of  $\mathcal{E}^{(a_m)}_{j, i}$ and
$\mathcal{E}^{(a_m)}_{j, i}$ and  $\mathcal{E}^{(b_m)}_{j, i}$ by
$\mathcal{E}^{(b_m)}_{j, i}$ by
 \begin{align*} \big |\mathcal{E}^{(a_m)}_{j, i} \big | \leq &\, \binom{ (\frac{1}{k} - \eta _{i}c)n}{j} \binom{\eta _{i}cn}{m - j}\,,\quad \big |\mathcal{E}^{(b_m)}_{j, i} \big | \leq \binom{ (\frac{1}{k} - \eta _{i}c)n}{j} \left [ \binom{cn}{m - j} - \binom{\eta _{i}cn}{m - j} \right ]\,. \end{align*}
\begin{align*} \big |\mathcal{E}^{(a_m)}_{j, i} \big | \leq &\, \binom{ (\frac{1}{k} - \eta _{i}c)n}{j} \binom{\eta _{i}cn}{m - j}\,,\quad \big |\mathcal{E}^{(b_m)}_{j, i} \big | \leq \binom{ (\frac{1}{k} - \eta _{i}c)n}{j} \left [ \binom{cn}{m - j} - \binom{\eta _{i}cn}{m - j} \right ]\,. \end{align*}
(ii) If those
 $j$ vertices in
$j$ vertices in  $[V\setminus X]^{j}$ are not in the same
$[V\setminus X]^{j}$ are not in the same  $[V_i \cap X]^{j}$ (which only happens
$[V_i \cap X]^{j}$ (which only happens  $j \geq 2$), then the number of this type hyperedges can be written as
$j \geq 2$), then the number of this type hyperedges can be written as  $\sum _{e\in \mathcal{E}^{(b_m)}_{j}} T_{e}^{(b_m)}$, where
$\sum _{e\in \mathcal{E}^{(b_m)}_{j}} T_{e}^{(b_m)}$, where
 \begin{align*} \mathcal{E}^{(b_m)}_{j} \,:\!=\,&\, E_m \Big ([V\setminus X]^{j}\setminus \big ( \cup _{i=1}^{k}[V_i\setminus X]^{j} \big ), \,\,\, [X]^{m-j}\Big )\,,\\
\big | \mathcal{E}^{(b_m)}_{j} \big | \leq &\, \left [ \binom{(1-c)n}{j} -\sum _{i=1}^{k} \binom{( \frac{1}{k} - \eta _{i}c) n}{j} \right ] \binom{cn}{m-j}\,. \end{align*}
\begin{align*} \mathcal{E}^{(b_m)}_{j} \,:\!=\,&\, E_m \Big ([V\setminus X]^{j}\setminus \big ( \cup _{i=1}^{k}[V_i\setminus X]^{j} \big ), \,\,\, [X]^{m-j}\Big )\,,\\
\big | \mathcal{E}^{(b_m)}_{j} \big | \leq &\, \left [ \binom{(1-c)n}{j} -\sum _{i=1}^{k} \binom{( \frac{1}{k} - \eta _{i}c) n}{j} \right ] \binom{cn}{m-j}\,. \end{align*}
Therefore, ![]() $|E_m(X, X^c)|$ can be written as a sum of independent Bernoulli random variables,
$|E_m(X, X^c)|$ can be written as a sum of independent Bernoulli random variables,
 \begin{align} |E_m(X, X^c)| = \sum _{j=1}^{m-1}\sum _{i=1}^{k} \left [ \sum _{e\in \mathcal{E}^{(a_m)}_{j, i}} T_{e}^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{j, i}} T_{e}^{(b_m)} \right ] + \sum _{j=2}^{m-1}\sum _{e\in \mathcal{E}^{(b_m)}_{j}} T_{e}^{(b_m)}\,. \end{align}
\begin{align} |E_m(X, X^c)| = \sum _{j=1}^{m-1}\sum _{i=1}^{k} \left [ \sum _{e\in \mathcal{E}^{(a_m)}_{j, i}} T_{e}^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{j, i}} T_{e}^{(b_m)} \right ] + \sum _{j=2}^{m-1}\sum _{e\in \mathcal{E}^{(b_m)}_{j}} T_{e}^{(b_m)}\,. \end{align}
Then the expectation can be rewritten as
 \begin{align} &\,{\mathbb{E}} \left (|E_m(X, X^c)| \right ) \nonumber\\
=&\, \sum _{j=1}^{m-1} \sum _{i=1}^{k} \binom{( \frac{1}{k} - \eta _{i}c) n}{j} \Bigg \{ \binom{\eta _{i}cn}{m-j} \frac{a_m}{ \binom{n}{m-1} } + \bigg [ \binom{cn}{m-j} - \binom{\eta _{i}cn}{m-j} \bigg ] \frac{b_m}{ \binom{n}{m-1} } \Bigg \} \notag \\
\,& + \sum _{j=1}^{m-1} \Bigg [\left({(1 - c) n \atop j}\right) - \sum _{i=1}^{k}\left({( \frac{1}{k} - \eta _{i}c) n \atop j}\right) \Bigg ]\left({cn \atop m - j}\right) \frac{b_m}{ \binom{n}{m-1} } \\
=\,& \sum _{j=1}^{m-1} \sum _{i=1}^{k}\binom{( \frac{1}{k} - \eta _{i}c) n}{j} \binom{\eta _{i}cn}{m-j} \frac{a_m - b_m}{ \binom{n}{m-1} } + \sum _{j=1}^{m-1} \binom{(1-c)n}{j} \binom{cn}{m-j} \frac{b_m}{ \binom{n}{m-1} }\notag \\
=&\, \sum _{i=1}^{k} \Bigg [\left({ \frac{n}{k} \atop m}\right) -\left({\eta _{i}cn \atop m}\right) -\left({(\frac{1}{k} - \eta _{i}c) n \atop m}\right) \Bigg ]\frac{a_m - b_m}{\left({n \atop m-1}\right) } + \Bigg [\left({n \atop m}\right) -\left({cn \atop m}\right) -\left({(1 - c) n \atop m}\right) \Bigg ] \frac{b_m}{\left({n \atop m-1}\right) }\notag \,, \end{align}
\begin{align} &\,{\mathbb{E}} \left (|E_m(X, X^c)| \right ) \nonumber\\
=&\, \sum _{j=1}^{m-1} \sum _{i=1}^{k} \binom{( \frac{1}{k} - \eta _{i}c) n}{j} \Bigg \{ \binom{\eta _{i}cn}{m-j} \frac{a_m}{ \binom{n}{m-1} } + \bigg [ \binom{cn}{m-j} - \binom{\eta _{i}cn}{m-j} \bigg ] \frac{b_m}{ \binom{n}{m-1} } \Bigg \} \notag \\
\,& + \sum _{j=1}^{m-1} \Bigg [\left({(1 - c) n \atop j}\right) - \sum _{i=1}^{k}\left({( \frac{1}{k} - \eta _{i}c) n \atop j}\right) \Bigg ]\left({cn \atop m - j}\right) \frac{b_m}{ \binom{n}{m-1} } \\
=\,& \sum _{j=1}^{m-1} \sum _{i=1}^{k}\binom{( \frac{1}{k} - \eta _{i}c) n}{j} \binom{\eta _{i}cn}{m-j} \frac{a_m - b_m}{ \binom{n}{m-1} } + \sum _{j=1}^{m-1} \binom{(1-c)n}{j} \binom{cn}{m-j} \frac{b_m}{ \binom{n}{m-1} }\notag \\
=&\, \sum _{i=1}^{k} \Bigg [\left({ \frac{n}{k} \atop m}\right) -\left({\eta _{i}cn \atop m}\right) -\left({(\frac{1}{k} - \eta _{i}c) n \atop m}\right) \Bigg ]\frac{a_m - b_m}{\left({n \atop m-1}\right) } + \Bigg [\left({n \atop m}\right) -\left({cn \atop m}\right) -\left({(1 - c) n \atop m}\right) \Bigg ] \frac{b_m}{\left({n \atop m-1}\right) }\notag \,, \end{align}
where we used the fact ![]() $\binom{(1-c)n}{1} = \sum _{i=1}^{k}\binom{(1/k - \eta _i c)n}{1}$ in the first equality and Vandermonde’s identity
$\binom{(1-c)n}{1} = \sum _{i=1}^{k}\binom{(1/k - \eta _i c)n}{1}$ in the first equality and Vandermonde’s identity ![]() $\left({n_{1} + n_{2} \atop m}\right) = \sum _{j=0}^{m}\left({n_{1} \atop j}\right)\left({n_{2} \atop m-j}\right)$ in last equality. Note that
$\left({n_{1} + n_{2} \atop m}\right) = \sum _{j=0}^{m}\left({n_{1} \atop j}\right)\left({n_{2} \atop m-j}\right)$ in last equality. Note that
counts the number of subsets of ![]() $V$ with
$V$ with ![]() $m$ elements such that at least one element belongs to
$m$ elements such that at least one element belongs to ![]() $X$ and at least one element belongs to
$X$ and at least one element belongs to ![]() $X^c$. On the other hand,
$X^c$. On the other hand,
 \begin{equation*} g_c = \sum _{i=1}^{k} \left [ \left({ \frac {n}{k} \atop m}\right) - \left({\eta _{i}cn \atop m}\right) - \left({(\frac {1}{k} - \eta _{i}c) n \atop m}\right) \right ]\,. \end{equation*}
\begin{equation*} g_c = \sum _{i=1}^{k} \left [ \left({ \frac {n}{k} \atop m}\right) - \left({\eta _{i}cn \atop m}\right) - \left({(\frac {1}{k} - \eta _{i}c) n \atop m}\right) \right ]\,. \end{equation*}
counts the number of subsets of ![]() $V$ with
$V$ with ![]() $m$ elements such that all elements belong to a single
$m$ elements such that all elements belong to a single ![]() $V_i$, and given such an
$V_i$, and given such an ![]() $i$, that at least one element belongs to
$i$, that at least one element belongs to ![]() $X \cap V_i$ and at least one belongs to
$X \cap V_i$ and at least one belongs to ![]() $X^c \cap V_i$.
$X^c \cap V_i$.
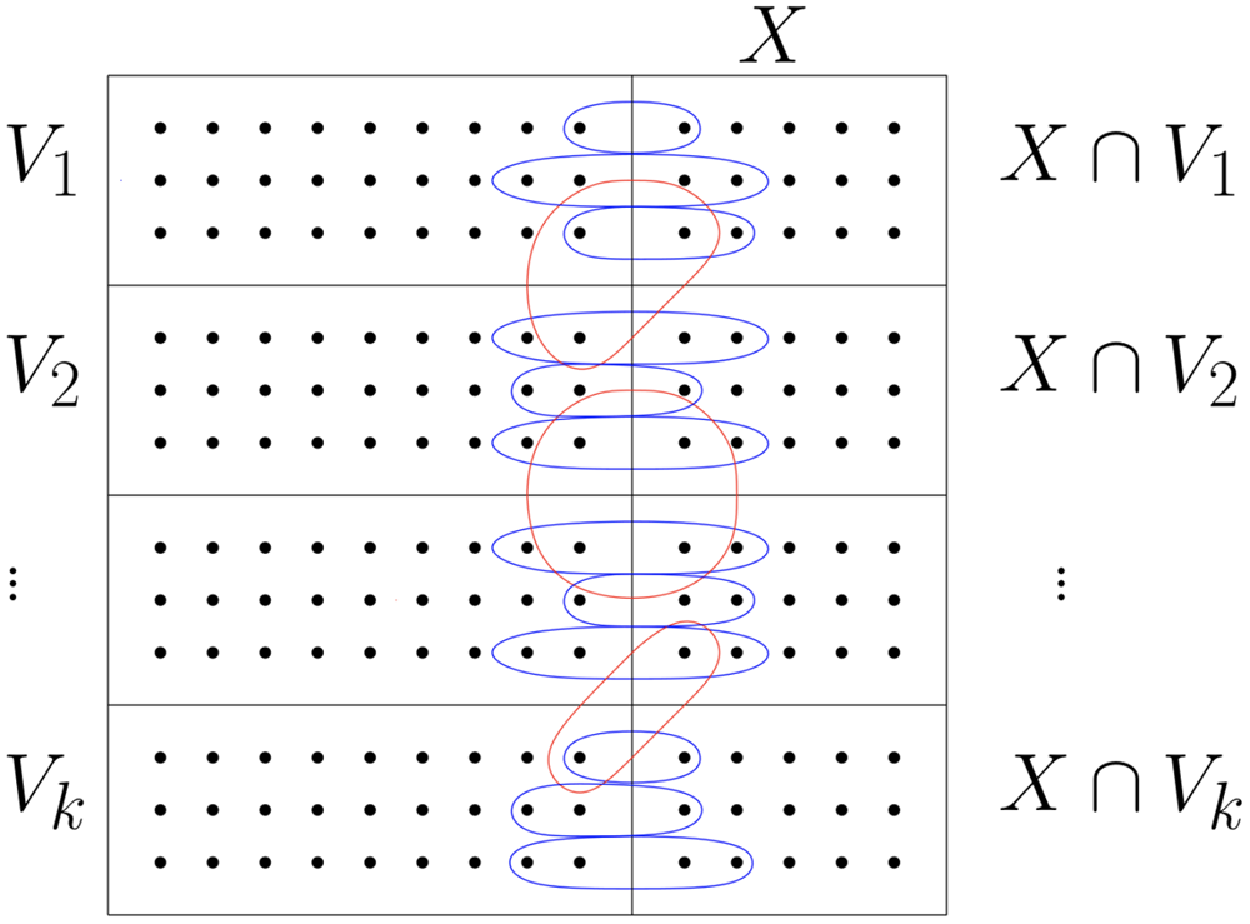
Figure B.1. Comparison of ![]() $f_c$ and
$f_c$ and ![]() $g_c$.
$g_c$.
As Fig. B.1 shows, ![]() $g_{c}$ only counts the blue pairs while
$g_{c}$ only counts the blue pairs while ![]() $f_c$ counts red pairs in addition. By virtue of the fact that there are fewer conditions imposed on the sets included in the count for
$f_c$ counts red pairs in addition. By virtue of the fact that there are fewer conditions imposed on the sets included in the count for ![]() $f_c$, we must have
$f_c$, we must have ![]() $f_c \geq g_c$. Thus, rewriting equation (B.8), we obtain
$f_c \geq g_c$. Thus, rewriting equation (B.8), we obtain
 \begin{align*}{\mathbb{E}} (|E_m(X, X^c)|) &\,= g_c \frac{a_m}{\left({n \atop m-1}\right) } + (f_c-g_c) \frac{b_m}{\left({n \atop m-1}\right) }\,\,. \end{align*}
\begin{align*}{\mathbb{E}} (|E_m(X, X^c)|) &\,= g_c \frac{a_m}{\left({n \atop m-1}\right) } + (f_c-g_c) \frac{b_m}{\left({n \atop m-1}\right) }\,\,. \end{align*}
Since both terms in the above sum are positive, we can upper bound by taking ![]() $a_m=b_m$ to obtain
$a_m=b_m$ to obtain
 \begin{align*}{\mathbb{E}} \left ( |E_m(X, X^c)| \right ) \leq f_c \frac{a_m}{\left({n \atop m-1}\right) } = \Bigg [\left({n \atop m}\right) -\left({cn \atop m}\right) -\left({(1 - c) n \atop m}\right) \Bigg ] \frac{a_m}{\left({n \atop m-1}\right) } \,. \end{align*}
\begin{align*}{\mathbb{E}} \left ( |E_m(X, X^c)| \right ) \leq f_c \frac{a_m}{\left({n \atop m-1}\right) } = \Bigg [\left({n \atop m}\right) -\left({cn \atop m}\right) -\left({(1 - c) n \atop m}\right) \Bigg ] \frac{a_m}{\left({n \atop m-1}\right) } \,. \end{align*}
By summing over ![]() $m$, the expectation of
$m$, the expectation of ![]() $\sum _{m=2}^{M}(m-1)^2|E_m(X, X^{c})|$ satisfies
$\sum _{m=2}^{M}(m-1)^2|E_m(X, X^{c})|$ satisfies
 \begin{align*} \sum _{m=2}^M (m-1)^2\cdot{\mathbb{E}} \left (|E_m(X, X^c)| \right )&\leq \sum _{m=2}^M (m-1)^2\Bigg [\left({n \atop m}\right) -\left({cn \atop m}\right) -\left({(1 - c) n \atop m}\right) \Bigg ] \frac{a_m}{\left({n \atop m-1}\right) }\,, \\
&\leq 2n \sum _{m=2}^M(1-c^m-(1-c)^m)(m-1)a_m\leq 8Mcnd\,, \end{align*}
\begin{align*} \sum _{m=2}^M (m-1)^2\cdot{\mathbb{E}} \left (|E_m(X, X^c)| \right )&\leq \sum _{m=2}^M (m-1)^2\Bigg [\left({n \atop m}\right) -\left({cn \atop m}\right) -\left({(1 - c) n \atop m}\right) \Bigg ] \frac{a_m}{\left({n \atop m-1}\right) }\,, \\
&\leq 2n \sum _{m=2}^M(1-c^m-(1-c)^m)(m-1)a_m\leq 8Mcnd\,, \end{align*}
where the last upper inequality holds when ![]() $c\in (0, 2^{1/M} - 1]$, since
$c\in (0, 2^{1/M} - 1]$, since
 \begin{align} &\, [(1 - c) + c]^m - c^m -(1-c)^m \notag \\
= &\, \binom{m}{1}(1 - c)^{m-1}c + \binom{m}{2}(1 - c)^{m-2}c^2 + \cdots + \binom{m}{m-1}(1 - c)^{1}c^{m-1}\notag \\
\leq &\, \binom{m}{1}c + \binom{m}{2}c^2 + \cdots + \binom{m}{m-1}c^{m-1}\leq (1 + c)^{m} - 1 \leq 2mc\,, \end{align}
\begin{align} &\, [(1 - c) + c]^m - c^m -(1-c)^m \notag \\
= &\, \binom{m}{1}(1 - c)^{m-1}c + \binom{m}{2}(1 - c)^{m-2}c^2 + \cdots + \binom{m}{m-1}(1 - c)^{1}c^{m-1}\notag \\
\leq &\, \binom{m}{1}c + \binom{m}{2}c^2 + \cdots + \binom{m}{m-1}c^{m-1}\leq (1 + c)^{m} - 1 \leq 2mc\,, \end{align}
where the last inequality holds by the following Claim.
Claim B.1. Let ![]() $m \geq 2$ be some finite integer. Then for
$m \geq 2$ be some finite integer. Then for ![]() $0 \lt c \lt = 2^{1/m} - 1$, it follows that
$0 \lt c \lt = 2^{1/m} - 1$, it follows that ![]() $(1 + c)^{m} - 1 \leq 2mc$.
$(1 + c)^{m} - 1 \leq 2mc$.
Proof of the Claim We finish the proof by induction. First, the argument ![]() $(1 + c)^{j} - 1 \leq 2jc$ holds true for the base cases
$(1 + c)^{j} - 1 \leq 2jc$ holds true for the base cases ![]() $j = 1, 2$. Suppose that the argument holds for the case
$j = 1, 2$. Suppose that the argument holds for the case ![]() $j \geq 2$. For the case
$j \geq 2$. For the case ![]() $j + 1 \leq m$, it follows that
$j + 1 \leq m$, it follows that
where the last inequality holds true if ![]() $c(1 + c)^{j} \leq 2c$, and it holds since
$c(1 + c)^{j} \leq 2c$, and it holds since ![]() $c \leq 2^{1/m} - 1 \leq 2^{1/j} - 1$ for all
$c \leq 2^{1/m} - 1 \leq 2^{1/j} - 1$ for all ![]() $j\leq m$.
$j\leq m$.
Similarly, we apply Bernstein Lemma D.3 again with ![]() $K=M^2$,
$K=M^2$, ![]() $\sigma ^2\leq 8M^3cnd$ and obtain
$\sigma ^2\leq 8M^3cnd$ and obtain
 \begin{align} & \, \mathbb P\left ( \sum _{m = 2}^{M} (m-1)^2 |E_m(X,X^c)| \geq 16Mcnd \right ) \notag \\
\leq \,&\, \mathbb P\left ( \sum _{m = 2}^{M} (m-1)^2( |E_m(X,X^c)| -{\mathbb{E}}|E_m(X,X^c)|)\geq 8Mcnd \right ) \leq \exp ({-}6cnd/M)\,. \end{align}
\begin{align} & \, \mathbb P\left ( \sum _{m = 2}^{M} (m-1)^2 |E_m(X,X^c)| \geq 16Mcnd \right ) \notag \\
\leq \,&\, \mathbb P\left ( \sum _{m = 2}^{M} (m-1)^2( |E_m(X,X^c)| -{\mathbb{E}}|E_m(X,X^c)|)\geq 8Mcnd \right ) \leq \exp ({-}6cnd/M)\,. \end{align}
By the binomial coefficient upper bound ![]() $\binom{n}{k}\leq (\frac{en}{k})^k$ for
$\binom{n}{k}\leq (\frac{en}{k})^k$ for ![]() $1\leq k\leq n$, there are at most
$1\leq k\leq n$, there are at most
many subsets ![]() $X$ of size
$X$ of size ![]() $|X| = cn$. Let
$|X| = cn$. Let ![]() $d$ be sufficiently large so that
$d$ be sufficiently large so that ![]() $d^{-3} \leq c_0$. Substituting
$d^{-3} \leq c_0$. Substituting ![]() $c = d^{-3}$ in equation (B.11), we have
$c = d^{-3}$ in equation (B.11), we have
Taking ![]() $c=d^{-3}$ in equations (B.6) and (B.10), we obtain
$c=d^{-3}$ in equations (B.6) and (B.10), we obtain
 \begin{align*} & \mathbb P\left ( \sum _{m = 2}^{M} (m-1) (m|E_m(X)| + (m-1)|E_m(X,X^c)|)\geq 20Md^{-2}n \right )\leq 2\exp ({-}2d^{-2}n/M)\,. \end{align*}
\begin{align*} & \mathbb P\left ( \sum _{m = 2}^{M} (m-1) (m|E_m(X)| + (m-1)|E_m(X,X^c)|)\geq 20Md^{-2}n \right )\leq 2\exp ({-}2d^{-2}n/M)\,. \end{align*}
Taking a union bound over all possible ![]() $X$ with
$X$ with ![]() $|X|=d^{-3}n$, we obtain with probability at least
$|X|=d^{-3}n$, we obtain with probability at least ![]() $1-2\exp (3d^{-3}\log d n-2d^{-2}n/M)\leq 1-2\exp ({-}d^{-2}n/M)$, no more than
$1-2\exp (3d^{-3}\log d n-2d^{-2}n/M)\leq 1-2\exp ({-}d^{-2}n/M)$, no more than ![]() $d^{-3}n$ many vertices have total row sum greater than
$d^{-3}n$ many vertices have total row sum greater than ![]() $20Md$. Note that we have imposed the condition that
$20Md$. Note that we have imposed the condition that ![]() $c = d^{-3} \in (0, 2^{1/M} - 1]$ in (B.9), thus
$c = d^{-3} \in (0, 2^{1/M} - 1]$ in (B.9), thus ![]() $d\geq (2^{1/M} - 1)^{-1/3}$, producing the lower bound in Assumption 1.5.
$d\geq (2^{1/M} - 1)^{-1/3}$, producing the lower bound in Assumption 1.5.
B.4. Proof of Lemma 5.8
Proof. Note that ![]() ${\mathbf{U}}$ is spanned by first
${\mathbf{U}}$ is spanned by first ![]() $k$ singular vectors of
$k$ singular vectors of ![]() $({\mathbf{A}}_1)_{\mathcal{I}_1}$. Let
$({\mathbf{A}}_1)_{\mathcal{I}_1}$. Let ![]() $\{\boldsymbol{u}_i\}_{i=1}^{k}$ be an orthonormal basis of the
$\{\boldsymbol{u}_i\}_{i=1}^{k}$ be an orthonormal basis of the ![]() ${\mathbf{U}}$, then the projection
${\mathbf{U}}$, then the projection ![]() $P_{{\mathbf{U}}} \,:\!=\, \sum _{l=1}^{k}\langle\boldsymbol{u}_{l},\cdot \, \rangle\boldsymbol{u}_{l}$. Let
$P_{{\mathbf{U}}} \,:\!=\, \sum _{l=1}^{k}\langle\boldsymbol{u}_{l},\cdot \, \rangle\boldsymbol{u}_{l}$. Let ![]() $k(i)$ index the membership of vertex
$k(i)$ index the membership of vertex ![]() $i$. For each fixed
$i$. For each fixed ![]() $i\in V_{k(i)} \cap Y_2\cap \{i_1, \cdots, i_s\}$,
$i\in V_{k(i)} \cap Y_2\cap \{i_1, \cdots, i_s\}$,
 \begin{align*} P_{{\mathbf{U}}}\boldsymbol{e}_i =&\, \sum _{l=1}^{k}\langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle\boldsymbol{u}_{l}, \quad \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 =\, \sum _{l=1}^k \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2. \end{align*}
\begin{align*} P_{{\mathbf{U}}}\boldsymbol{e}_i =&\, \sum _{l=1}^{k}\langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle\boldsymbol{u}_{l}, \quad \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 =\, \sum _{l=1}^k \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2. \end{align*}
As a consequence of independence between entries in ![]() ${\mathbf{A}}_1$ and entries in
${\mathbf{A}}_1$ and entries in ![]() ${\mathbf{A}}_2$, defined in equation (18), it is known that
${\mathbf{A}}_2$, defined in equation (18), it is known that ![]() $\{\boldsymbol{u}_l\}_{l=1}^{k}$ and
$\{\boldsymbol{u}_l\}_{l=1}^{k}$ and ![]() $\boldsymbol{e}_i$ are independent of each other, since
$\boldsymbol{e}_i$ are independent of each other, since ![]() $\boldsymbol{e}_i$ are columns of
$\boldsymbol{e}_i$ are columns of ![]() ${\mathbf{E}}_2 \,:\!=\,{\mathbf{A}}_2 - \widetilde{{\mathbf{A}}}_2$. If the expectation is taken over
${\mathbf{E}}_2 \,:\!=\,{\mathbf{A}}_2 - \widetilde{{\mathbf{A}}}_2$. If the expectation is taken over ![]() $\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}$ conditioning on
$\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}$ conditioning on ![]() $\{\boldsymbol{u}_l\}_{l=1}^{k}$, then
$\{\boldsymbol{u}_l\}_{l=1}^{k}$, then
 \begin{align*}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]=&\, \sum _{j=1}^{n}\boldsymbol{u}_{l}(j) \cdot{\mathbb{E}} \left ( \Big [ ({\mathbf{A}}_2)_{ji} - ({\mathbb{E}}{\mathbf{A}}_2)_{ji} \Big ] \right ) = 0\,,\\
{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] =&\, \sum _{l=1}^{k}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]\,, \end{align*}
\begin{align*}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]=&\, \sum _{j=1}^{n}\boldsymbol{u}_{l}(j) \cdot{\mathbb{E}} \left ( \Big [ ({\mathbf{A}}_2)_{ji} - ({\mathbb{E}}{\mathbf{A}}_2)_{ji} \Big ] \right ) = 0\,,\\
{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] =&\, \sum _{l=1}^{k}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]\,, \end{align*}
where ![]() $\mathcal{M}$ is obtained from Algorithm 3. Expand each
$\mathcal{M}$ is obtained from Algorithm 3. Expand each ![]() $\langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2$ and rewrite it into
$\langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2$ and rewrite it into ![]() $2$ parts,
$2$ parts,
 \begin{align} \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2 =&\, \sum _{j_1 = 1}^{k} \sum _{j_2 = 1}^{k}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2) \notag \\
=&\, \underbrace{\sum _{j = 1}^{k}[\boldsymbol{u}_{l}(j)]^2[\boldsymbol{e}_i(j)]^2}_{(a)} + \underbrace{\sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2)}_{(b)}\,,\quad \forall l\in [k]\,. \end{align}
\begin{align} \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2 =&\, \sum _{j_1 = 1}^{k} \sum _{j_2 = 1}^{k}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2) \notag \\
=&\, \underbrace{\sum _{j = 1}^{k}[\boldsymbol{u}_{l}(j)]^2[\boldsymbol{e}_i(j)]^2}_{(a)} + \underbrace{\sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2)}_{(b)}\,,\quad \forall l\in [k]\,. \end{align}
Part ![]() $(a)$ is the contribution from graph, i.e.,
$(a)$ is the contribution from graph, i.e., ![]() $2$-uniform hypergraph, while part
$2$-uniform hypergraph, while part ![]() $(b)$ is the contribution from
$(b)$ is the contribution from ![]() $m$-uniform hypergraph with
$m$-uniform hypergraph with ![]() $m\geq 3$, which only occurs in hypergraph clustering. The expectation of part
$m\geq 3$, which only occurs in hypergraph clustering. The expectation of part ![]() $(a)$ in is upper bounded by
$(a)$ in is upper bounded by ![]() $\alpha$ as defined in equation (8), since
$\alpha$ as defined in equation (8), since
 \begin{align*} &{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \sum _{j = 1}^{k}[\boldsymbol{u}_{l}(j)]^2[\boldsymbol{e}_i(j)]^2 \Bigg \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] = \sum _{j=1}^{n}[\boldsymbol{u}_{l}(j)]^2 \cdot{\mathbb{V}\mathrm{ar}}\Big (({\mathbf{A}}_{2})_{ji} \Big ) \\
\leq \,& \sum _{j=1}^{n}[\boldsymbol{u}_{l}(j)]^2 \cdot ({\mathbb{E}}{\mathbf{A}}_{2})_{ji} \leq \alpha = \sum _{m\in \mathcal{M}}\Bigg [ \binom{\frac{n}{k} -2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1} } + \binom{n}{m-2} \frac{b_m}{\binom{n}{m-1} }\Bigg ]\\
\leq \,& \sum _{m\in \mathcal{M}} \binom{n}{m-2} \frac{a_m}{\binom{n}{m-1} } \leq \frac{2}{n}\sum _{m\in \mathcal{M}} (m-1)a_m = \frac{2d}{n}, \quad \forall l \in [k] \end{align*}
\begin{align*} &{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \sum _{j = 1}^{k}[\boldsymbol{u}_{l}(j)]^2[\boldsymbol{e}_i(j)]^2 \Bigg \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] = \sum _{j=1}^{n}[\boldsymbol{u}_{l}(j)]^2 \cdot{\mathbb{V}\mathrm{ar}}\Big (({\mathbf{A}}_{2})_{ji} \Big ) \\
\leq \,& \sum _{j=1}^{n}[\boldsymbol{u}_{l}(j)]^2 \cdot ({\mathbb{E}}{\mathbf{A}}_{2})_{ji} \leq \alpha = \sum _{m\in \mathcal{M}}\Bigg [ \binom{\frac{n}{k} -2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1} } + \binom{n}{m-2} \frac{b_m}{\binom{n}{m-1} }\Bigg ]\\
\leq \,& \sum _{m\in \mathcal{M}} \binom{n}{m-2} \frac{a_m}{\binom{n}{m-1} } \leq \frac{2}{n}\sum _{m\in \mathcal{M}} (m-1)a_m = \frac{2d}{n}, \quad \forall l \in [k] \end{align*}
where ![]() $\|\boldsymbol{u}_l\|_2^2 = \sum _{j=1}^{n}[\boldsymbol{u}_{l}(j)]^2 = 1$. For part
$\|\boldsymbol{u}_l\|_2^2 = \sum _{j=1}^{n}[\boldsymbol{u}_{l}(j)]^2 = 1$. For part ![]() $(b)$,
$(b)$,
 \begin{align*} &\,{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2) \Bigg \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]\\
=&\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2){\mathbb{E}} \left [ \Big ( ({\mathbf{A}}_2)_{j_{1}i} - ({\mathbb{E}}{\mathbf{A}}_2)_{j_{1}i} \Big ) \Big ( ({\mathbf{A}}_2)_{j_{2}i} - ({\mathbb{E}}{\mathbf{A}}_2)_{j_{2}i} \Big ) \right ]\\
=&\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2){\mathbb{E}} \Bigg (\sum _{m\in \mathcal{M}}\,\,\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1\}\subset e} }\, (\boldsymbol{\mathcal{A}}^{(m)}_{e} -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e} ) \Bigg ) \Bigg (\sum _{m\in \mathcal{M}}\,\,\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_2\}\subset e} }\, (\boldsymbol{\mathcal{A}}^{(m)}_{e} -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e} ) \Bigg ). \end{align*}
\begin{align*} &\,{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2) \Bigg \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]\\
=&\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2){\mathbb{E}} \left [ \Big ( ({\mathbf{A}}_2)_{j_{1}i} - ({\mathbb{E}}{\mathbf{A}}_2)_{j_{1}i} \Big ) \Big ( ({\mathbf{A}}_2)_{j_{2}i} - ({\mathbb{E}}{\mathbf{A}}_2)_{j_{2}i} \Big ) \right ]\\
=&\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2){\mathbb{E}} \Bigg (\sum _{m\in \mathcal{M}}\,\,\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1\}\subset e} }\, (\boldsymbol{\mathcal{A}}^{(m)}_{e} -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e} ) \Bigg ) \Bigg (\sum _{m\in \mathcal{M}}\,\,\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_2\}\subset e} }\, (\boldsymbol{\mathcal{A}}^{(m)}_{e} -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e} ) \Bigg ). \end{align*}
According to Definition 2.1 of the adjacency tensor, ![]() $\boldsymbol{\mathcal{A}}^{(m)}_{e_1}$ and
$\boldsymbol{\mathcal{A}}^{(m)}_{e_1}$ and ![]() $\boldsymbol{\mathcal{A}}^{(m)}_{e_2}$ are independent if hyperedge
$\boldsymbol{\mathcal{A}}^{(m)}_{e_2}$ are independent if hyperedge ![]() $e_1 \neq e_2$, then only the terms with hyperedge
$e_1 \neq e_2$, then only the terms with hyperedge ![]() $e\supset \{i, j_1, j_2\}$ have non-zero contribution. Then the expectation of part
$e\supset \{i, j_1, j_2\}$ have non-zero contribution. Then the expectation of part ![]() $(b)$ can be rewritten as
$(b)$ can be rewritten as
 \begin{align} &\,{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2) \Bigg \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]\notag \\
= &\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}}\,\, \sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1, j_2\}\subset e} }{\mathbb{E}} \big (\boldsymbol{\mathcal{A}}^{(m)}_{e} -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e} \big )^2 \notag \\
\leq &\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}} \,\,\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1, j_2\}\subset e} }{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e}\notag \\
= &\sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}}\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1, j_2\}\subset e} } \frac{a_m}{\binom{n}{m-1}}\,. \end{align}
\begin{align} &\,{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{e}_i(j_1)\boldsymbol{u}_{l}(j_2)\boldsymbol{e}_i(j_2) \Bigg \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ]\notag \\
= &\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}}\,\, \sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1, j_2\}\subset e} }{\mathbb{E}} \big (\boldsymbol{\mathcal{A}}^{(m)}_{e} -{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e} \big )^2 \notag \\
\leq &\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}} \,\,\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1, j_2\}\subset e} }{\mathbb{E}}\boldsymbol{\mathcal{A}}^{(m)}_{e}\notag \\
= &\sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}}\sum _{\substack{e\in E_m[Y_2\cup Z]\\
\{i,j_1, j_2\}\subset e} } \frac{a_m}{\binom{n}{m-1}}\,. \end{align}
Note that ![]() $|Y_2 \cup Z| \leq n$, then the number of possible hyperedges
$|Y_2 \cup Z| \leq n$, then the number of possible hyperedges ![]() $e$, while
$e$, while ![]() $e\in E_m[Y_2\cup Z]$ and
$e\in E_m[Y_2\cup Z]$ and ![]() $e \supset \{i,j_1, j_2\}$, is at most
$e \supset \{i,j_1, j_2\}$, is at most ![]() $\binom{n}{m-3}$. Thus equation (B.13) is upper bounded by
$\binom{n}{m-3}$. Thus equation (B.13) is upper bounded by
 \begin{align*} &\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}} \binom{n}{m-3} \frac{a_m}{\binom{n}{m-1}} \\
\leq &\,\sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}} \frac{(m-1)(m-2)}{(n-m)^2}a_m \leq \frac{d \mathcal{M}_{\max } }{n^2} \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2)\end{align*}
\begin{align*} &\, \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}} \binom{n}{m-3} \frac{a_m}{\binom{n}{m-1}} \\
\leq &\,\sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2) \sum _{m\in \mathcal{M}} \frac{(m-1)(m-2)}{(n-m)^2}a_m \leq \frac{d \mathcal{M}_{\max } }{n^2} \sum _{j_1 \neq j_2}\boldsymbol{u}_{l}(j_1)\boldsymbol{u}_{l}(j_2)\end{align*}
 \begin{align*}
\leq &\, \frac{d \mathcal{M}_{\max } }{2n^2} \sum _{j_1 \neq j_2}\Big ( [\boldsymbol{u}_{l}(j_1)]^2 + [\boldsymbol{u}_{l}(j_2)]^2 \Big ) \leq \frac{d \mathcal{M}_{\max }(n-1) }{2n^2}\Bigg ( \sum _{j_1 = 1}^{n} [\boldsymbol{u}_{l}(j_1)]^2 + \sum _{j_2 = 1}^{n}[\boldsymbol{u}_{l}(j_2)]^2 \Bigg )\\
\leq & \frac{d \mathcal{M}_{\max } }{n}\,, \end{align*}
\begin{align*}
\leq &\, \frac{d \mathcal{M}_{\max } }{2n^2} \sum _{j_1 \neq j_2}\Big ( [\boldsymbol{u}_{l}(j_1)]^2 + [\boldsymbol{u}_{l}(j_2)]^2 \Big ) \leq \frac{d \mathcal{M}_{\max }(n-1) }{2n^2}\Bigg ( \sum _{j_1 = 1}^{n} [\boldsymbol{u}_{l}(j_1)]^2 + \sum _{j_2 = 1}^{n}[\boldsymbol{u}_{l}(j_2)]^2 \Bigg )\\
\leq & \frac{d \mathcal{M}_{\max } }{n}\,, \end{align*}
where ![]() $\|\boldsymbol{u}_l\|_2 = 1$,
$\|\boldsymbol{u}_l\|_2 = 1$, ![]() $d = \sum _{m\in \mathcal{M}}(m-1)a_m$. With the upper bounds for part
$d = \sum _{m\in \mathcal{M}}(m-1)a_m$. With the upper bounds for part ![]() $(a)$ and
$(a)$ and ![]() $(b)$ in equation (B.12), the conditional expectation of
$(b)$ in equation (B.12), the conditional expectation of ![]() $\|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2$ is bounded by
$\|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2$ is bounded by
 \begin{align*}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] =&\, \sum _{l=1}^{k}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] \leq \frac{kd}{n}(\mathcal{M}_{\max } + 2)\,, \end{align*}
\begin{align*}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] =&\, \sum _{l=1}^{k}{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \langle\boldsymbol{u}_{l},\boldsymbol{e}_i\rangle ^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] \leq \frac{kd}{n}(\mathcal{M}_{\max } + 2)\,, \end{align*}
Let ![]() $X_i$ be the Bernoulli random variable defined by
$X_i$ be the Bernoulli random variable defined by
By Markov’s inequality,
 \begin{align*}{\mathbb{E}} X_i ={\mathbb{P}}\left ( \|P_{{\mathbf{U}}}\boldsymbol{e}_i \|_2 \gt 2 \sqrt{ kd(\mathcal{M}_{\max } + 2)/n } \right ) \leq \frac{{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] }{4kd(\mathcal{M}_{\max } + 2)/n} \leq \frac{1}{4}\,. \end{align*}
\begin{align*}{\mathbb{E}} X_i ={\mathbb{P}}\left ( \|P_{{\mathbf{U}}}\boldsymbol{e}_i \|_2 \gt 2 \sqrt{ kd(\mathcal{M}_{\max } + 2)/n } \right ) \leq \frac{{\mathbb{E}}_{\{\boldsymbol{\mathcal{A}}^{(m)}\}_{m \in \mathcal{M}}} \left [ \|P_{{\mathbf{U}}}\boldsymbol{e}_i\|_2^2 \Big \vert \{\boldsymbol{u}_l\}_{l=1}^{k} \right ] }{4kd(\mathcal{M}_{\max } + 2)/n} \leq \frac{1}{4}\,. \end{align*}
Let ![]() $\delta \,:\!=\, \frac{s}{2 \sum _{j=1}^{s}{\mathbb{E}} X_{i_j}} - 1$ where
$\delta \,:\!=\, \frac{s}{2 \sum _{j=1}^{s}{\mathbb{E}} X_{i_j}} - 1$ where ![]() $s = 2k\log ^2(n)$. By Hoeffding Lemma D.2,
$s = 2k\log ^2(n)$. By Hoeffding Lemma D.2,
 \begin{align*} &\,{\mathbb{P}} \Bigg ( \sum _{j=1}^{s}X_{i_j} \geq \frac{s}{2}\Bigg ) ={\mathbb{P}} \Bigg ( \sum _{j=1}^{s}(X_{i_j} -{\mathbb{E}} X_{i_j}) \geq \delta \sum _{j=1}^{s}{\mathbb{E}} X_{i_j}\Bigg ) \\
\leq &\, \exp \Bigg ({-} \frac{2\delta ^2 \big (\sum _{j=1}^{s}{\mathbb{E}} X_{i_j} \big )^2}{s} \Bigg ) = O \Bigg ( \frac{1}{n^{k\log (n)}} \Bigg )\,. \end{align*}
\begin{align*} &\,{\mathbb{P}} \Bigg ( \sum _{j=1}^{s}X_{i_j} \geq \frac{s}{2}\Bigg ) ={\mathbb{P}} \Bigg ( \sum _{j=1}^{s}(X_{i_j} -{\mathbb{E}} X_{i_j}) \geq \delta \sum _{j=1}^{s}{\mathbb{E}} X_{i_j}\Bigg ) \\
\leq &\, \exp \Bigg ({-} \frac{2\delta ^2 \big (\sum _{j=1}^{s}{\mathbb{E}} X_{i_j} \big )^2}{s} \Bigg ) = O \Bigg ( \frac{1}{n^{k\log (n)}} \Bigg )\,. \end{align*}
Therefore, with probability ![]() $1 - O(n^{-k\log (n)})$, at least
$1 - O(n^{-k\log (n)})$, at least ![]() $s/2$ of the vectors
$s/2$ of the vectors ![]() $\boldsymbol{e}_{i_1}, \dots,\boldsymbol{e}_{i_s}$ satisfy
$\boldsymbol{e}_{i_1}, \dots,\boldsymbol{e}_{i_s}$ satisfy
Meanwhile, for any ![]() $c\in (0, 2)$, there exists some large enough constant
$c\in (0, 2)$, there exists some large enough constant ![]() $C_2 \geq 2^{\mathcal{M}_{\max } + 1}\sqrt{(\mathcal{M}_{\max } + 2)/k}/c$ such that if
$C_2 \geq 2^{\mathcal{M}_{\max } + 1}\sqrt{(\mathcal{M}_{\max } + 2)/k}/c$ such that if ![]() $\sum _{m \in \mathcal{M}}(m-1)(a_m -b_m) \gt C_2 k^{\mathcal{M}_{\max }-1}\sqrt{d}$, then
$\sum _{m \in \mathcal{M}}(m-1)(a_m -b_m) \gt C_2 k^{\mathcal{M}_{\max }-1}\sqrt{d}$, then
 \begin{align*} &\|\overline{{\boldsymbol \delta }}_i\|_2 =\frac{\sqrt{n}(\bar{\alpha} -\bar{\beta })}{2} = \frac{\sqrt{n}}{2}\sum _{m \in \mathcal{M}} \binom{ \frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} \\[5pt]
=\,& \frac{(1 + o(1))}{2\sqrt{n}} \sum _{m \in \mathcal{M}} \Big ( \frac{3}{4k} \Big )^{m-2} (m-1)(a_m - b_m) \geq \frac{k}{(2k)^{\mathcal{M}_{\max }-1} \sqrt{n}} \sum _{m \in \mathcal{M}} (m-1)(a_m - b_m),\\[5pt]
\gt \,& \frac{ C_2 k^{\mathcal{M}_{\max }}\sqrt{d} }{(2k)^{\mathcal{M}_{\max }-1} \sqrt{n} }\geq \frac{ 2^{\mathcal{M}_{\max } + 1 }\sqrt{(\mathcal{M}_{\max } + 2)} k^{\mathcal{M}_{\max }}\sqrt{d} }{c(2k)^{\mathcal{M}_{\max }-1} \sqrt{kn}} \\[5pt]
\gt &\frac{2}{c}\, 2\sqrt{ \frac{kd(\mathcal{M}_{\max } + 2)}{n}} \gt \frac{2}{c} \|P_{{\mathbf{U}}}\boldsymbol{e}_i \|_2 . \end{align*}
\begin{align*} &\|\overline{{\boldsymbol \delta }}_i\|_2 =\frac{\sqrt{n}(\bar{\alpha} -\bar{\beta })}{2} = \frac{\sqrt{n}}{2}\sum _{m \in \mathcal{M}} \binom{ \frac{3n}{4k} - 2}{m-2} \frac{a_m - b_m}{\binom{n}{m-1}} \\[5pt]
=\,& \frac{(1 + o(1))}{2\sqrt{n}} \sum _{m \in \mathcal{M}} \Big ( \frac{3}{4k} \Big )^{m-2} (m-1)(a_m - b_m) \geq \frac{k}{(2k)^{\mathcal{M}_{\max }-1} \sqrt{n}} \sum _{m \in \mathcal{M}} (m-1)(a_m - b_m),\\[5pt]
\gt \,& \frac{ C_2 k^{\mathcal{M}_{\max }}\sqrt{d} }{(2k)^{\mathcal{M}_{\max }-1} \sqrt{n} }\geq \frac{ 2^{\mathcal{M}_{\max } + 1 }\sqrt{(\mathcal{M}_{\max } + 2)} k^{\mathcal{M}_{\max }}\sqrt{d} }{c(2k)^{\mathcal{M}_{\max }-1} \sqrt{kn}} \\[5pt]
\gt &\frac{2}{c}\, 2\sqrt{ \frac{kd(\mathcal{M}_{\max } + 2)}{n}} \gt \frac{2}{c} \|P_{{\mathbf{U}}}\boldsymbol{e}_i \|_2 . \end{align*}
B.5. Proof of Lemma 5.10
Proof. Split ![]() $[n]$ into
$[n]$ into ![]() $V^{\prime}_1$ and
$V^{\prime}_1$ and ![]() $V^{\prime}_2$ such that
$V^{\prime}_2$ such that ![]() $V^{\prime}_{1} = \{i|\boldsymbol{v}(i) \gt 0\}$ and
$V^{\prime}_{1} = \{i|\boldsymbol{v}(i) \gt 0\}$ and ![]() $V^{\prime}_{2} = \{i|\boldsymbol{v}(i) \leq 0\}$. Without loss of generality, assume that the first
$V^{\prime}_{2} = \{i|\boldsymbol{v}(i) \leq 0\}$. Without loss of generality, assume that the first ![]() $\frac{n}{k}$ entries of
$\frac{n}{k}$ entries of ![]() $\bar{\boldsymbol{v}}$ are positive. We can write
$\bar{\boldsymbol{v}}$ are positive. We can write ![]() $\boldsymbol{v}$ in terms of its orthogonal projection onto
$\boldsymbol{v}$ in terms of its orthogonal projection onto ![]() $\bar{\boldsymbol{v}}$ as
$\bar{\boldsymbol{v}}$ as
where ![]() $\bar{\boldsymbol{v}} \perp{\boldsymbol \varepsilon }$ with
$\bar{\boldsymbol{v}} \perp{\boldsymbol \varepsilon }$ with ![]() $\|{\boldsymbol \varepsilon }\|_2 \lt c$ and
$\|{\boldsymbol \varepsilon }\|_2 \lt c$ and ![]() $c_{1} \geq \sqrt{1 - c^{2}}$. The number of entries of
$c_{1} \geq \sqrt{1 - c^{2}}$. The number of entries of ![]() $\boldsymbol \varepsilon$ smaller than
$\boldsymbol \varepsilon$ smaller than ![]() $-\frac{\sqrt{1 - c^{2}}}{\sqrt{n}}$ is at most
$-\frac{\sqrt{1 - c^{2}}}{\sqrt{n}}$ is at most ![]() $\frac{c^{2}}{1 - c^{2}}n$. Note that
$\frac{c^{2}}{1 - c^{2}}n$. Note that ![]() $c_{1} \geq \sqrt{1 - c^{2}}$, so at least
$c_{1} \geq \sqrt{1 - c^{2}}$, so at least ![]() $\frac{n}{k} - \frac{c^{2}}{1 - c^{2}}n$ indices
$\frac{n}{k} - \frac{c^{2}}{1 - c^{2}}n$ indices ![]() $i$ with
$i$ with ![]() $\bar{\boldsymbol{v}}_i = \frac{1}{\sqrt{n}}$ will have
$\bar{\boldsymbol{v}}_i = \frac{1}{\sqrt{n}}$ will have ![]() $\boldsymbol{v}_i \gt 0$, thus the ratio we are seeking is at least
$\boldsymbol{v}_i \gt 0$, thus the ratio we are seeking is at least
 \begin{align*} \frac{ \frac{n}{k} - \frac{c^{2}}{1 - c^{2}}n }{ \frac{n}{k}} = 1 - \frac{kc^2}{1 - c^2} \gt 1 - \frac{4k}{3}c^2. \end{align*}
\begin{align*} \frac{ \frac{n}{k} - \frac{c^{2}}{1 - c^{2}}n }{ \frac{n}{k}} = 1 - \frac{kc^2}{1 - c^2} \gt 1 - \frac{4k}{3}c^2. \end{align*}
B.6. Proof of Lemma 5.11
Proof. We start with the following simple claim: for any ![]() $m \geq 2$ and any
$m \geq 2$ and any ![]() $\nu \in [1/2, 1)$,
$\nu \in [1/2, 1)$,
Indeed, one quick way to see this is by induction on ![]() $m$; we will induct from
$m$; we will induct from ![]() $m$ to
$m$ to ![]() $m+2$. Assume the inequality is true for
$m+2$. Assume the inequality is true for ![]() $m$; then
$m$; then
 \begin{eqnarray*} \nu ^{m+2} +(1-\nu )^{m+2} & = & \nu ^2 \nu ^{m} + (1-\nu )^2 (1-\nu )^m \\
& = & \nu ^2 \nu ^{m} + (1-2\nu +\nu ^2)(1-\nu )^m \,\leq \,\nu ^2 \nu ^{m} + \nu ^2 (1-\nu )^m \\
& = & \nu ^2 (\nu ^m + (1-\nu )^m ) \,\lt \, (\nu ^2 + (1-\nu )^2) (\nu ^m + (1-\nu )^m ) \\[5pt]
& \lt & \left (\frac{1+\nu }{2} \right )^2 \left ( \frac{1+\nu }{2} \right )^m = \left ( \frac{1+\nu }{2} \right )^{m+2}\,, \end{eqnarray*}
\begin{eqnarray*} \nu ^{m+2} +(1-\nu )^{m+2} & = & \nu ^2 \nu ^{m} + (1-\nu )^2 (1-\nu )^m \\
& = & \nu ^2 \nu ^{m} + (1-2\nu +\nu ^2)(1-\nu )^m \,\leq \,\nu ^2 \nu ^{m} + \nu ^2 (1-\nu )^m \\
& = & \nu ^2 (\nu ^m + (1-\nu )^m ) \,\lt \, (\nu ^2 + (1-\nu )^2) (\nu ^m + (1-\nu )^m ) \\[5pt]
& \lt & \left (\frac{1+\nu }{2} \right )^2 \left ( \frac{1+\nu }{2} \right )^m = \left ( \frac{1+\nu }{2} \right )^{m+2}\,, \end{eqnarray*}
where we have used the induction hypothesis together with ![]() $1-2\nu \leq 0$ and
$1-2\nu \leq 0$ and ![]() $(1-\nu )^2\gt 0$. After easily checking that the inequality works for
$(1-\nu )^2\gt 0$. After easily checking that the inequality works for ![]() $m=2,3$, the induction is complete. We shall now check that the quantities defined in Lemma 5.11 obey the relationship
$m=2,3$, the induction is complete. We shall now check that the quantities defined in Lemma 5.11 obey the relationship ![]() $\mu _2 \geq \mu _1$ and
$\mu _2 \geq \mu _1$ and ![]() $\mu _2 - \mu _1 = \Omega (n)$, for
$\mu _2 - \mu _1 = \Omega (n)$, for ![]() $n$ large enough. First, note that the only thing we need to check is that, for sufficiently large
$n$ large enough. First, note that the only thing we need to check is that, for sufficiently large ![]() $n$,
$n$,
in fact, we will show the stronger statement that for any ![]() $m \geq 2$ and
$m \geq 2$ and ![]() $n$ large enough,
$n$ large enough,
and this will suffice to see that the second part of the assertion, ![]() $\mu _2-\mu _1 = \Omega (n)$, is also true. Asymptotically,
$\mu _2-\mu _1 = \Omega (n)$, is also true. Asymptotically, ![]() $\binom{\frac{\nu n}{2k}}{m} \sim \frac{\nu ^m}{m!} \left ( \frac{n}{2k} \right )^m$,
$\binom{\frac{\nu n}{2k}}{m} \sim \frac{\nu ^m}{m!} \left ( \frac{n}{2k} \right )^m$, ![]() $\binom{\frac{(1-\nu )n}{2k}}{m} \sim \frac{(1-\nu )^m}{m!} \left ( \frac{n}{2k} \right )^m$, and
$\binom{\frac{(1-\nu )n}{2k}}{m} \sim \frac{(1-\nu )^m}{m!} \left ( \frac{n}{2k} \right )^m$, and ![]() $\binom{\frac{(1+\nu )n}{4k}}{m} \sim \frac{\left ( \frac{1+\nu }{2} \right )^m}{m!} \left ( \frac{n}{2k} \right )^m$. Note then that equation (B.16) follows from equation (B.15).
$\binom{\frac{(1+\nu )n}{4k}}{m} \sim \frac{\left ( \frac{1+\nu }{2} \right )^m}{m!} \left ( \frac{n}{2k} \right )^m$. Note then that equation (B.16) follows from equation (B.15).
Let {![]() $V_{1}, \dots, V_{k}$} be the true partition of
$V_{1}, \dots, V_{k}$} be the true partition of ![]() $V$. Recall that hyperedges in
$V$. Recall that hyperedges in ![]() $H = \cup _{m\in \mathcal{M}}H_m$ are coloured red and blue with equal probability in Algorithm 2. Let
$H = \cup _{m\in \mathcal{M}}H_m$ are coloured red and blue with equal probability in Algorithm 2. Let ![]() $E_m(X)$ denote the set of blue
$E_m(X)$ denote the set of blue ![]() $m$-uniform hyperedges with all vertices located in the vertex set
$m$-uniform hyperedges with all vertices located in the vertex set ![]() $X$. Assume
$X$. Assume ![]() $|X \cap V_i| = \eta _i |X|$ with
$|X \cap V_i| = \eta _i |X|$ with ![]() $\sum _{i=1}^{k}\eta _{i} = 1$. For each
$\sum _{i=1}^{k}\eta _{i} = 1$. For each ![]() $m\in \mathcal{M}$, the presence of hyperedge
$m\in \mathcal{M}$, the presence of hyperedge ![]() $e\in E_{m}(X)$ can be represented by independent Bernoulli random variables
$e\in E_{m}(X)$ can be represented by independent Bernoulli random variables
 \begin{equation*} T_{e}^{(a_m)}\sim \mathrm {Bernoulli}\left ( \frac {a_{m}}{ 2 \binom {n}{m-1} }\right ), \quad T_{e}^{(b_m)} \sim \mathrm {Bernoulli}\left ( \frac {b_{m}}{ 2\binom {n}{m-1} }\right )\,, \end{equation*}
\begin{equation*} T_{e}^{(a_m)}\sim \mathrm {Bernoulli}\left ( \frac {a_{m}}{ 2 \binom {n}{m-1} }\right ), \quad T_{e}^{(b_m)} \sim \mathrm {Bernoulli}\left ( \frac {b_{m}}{ 2\binom {n}{m-1} }\right )\,, \end{equation*}
depending on whether ![]() $e$ is a hyperedge with all vertices in the same block. Denote by
$e$ is a hyperedge with all vertices in the same block. Denote by
the union of all ![]() $m$-uniform sets of hyperedges with all vertices in the same
$m$-uniform sets of hyperedges with all vertices in the same ![]() $V_i\cap X$ for some
$V_i\cap X$ for some ![]() $i\in [k]$, and by
$i\in [k]$, and by
the set of ![]() $m$-uniform hyperedges with vertices across different blocks
$m$-uniform hyperedges with vertices across different blocks ![]() $V_i\cap X$. Then the cardinality
$V_i\cap X$. Then the cardinality ![]() $|E_m(X)|$ can be written as the
$|E_m(X)|$ can be written as the
and by summing over ![]() $m$, the weighted cardinality
$m$, the weighted cardinality ![]() $|E(X)|$ is written as
$|E(X)|$ is written as
 \begin{align*} |E(X)| \,:\!=\, \sum _{m\in \mathcal{M}}m(m-1)|E_m(X)| = \sum _{m\in \mathcal{M}}m(m-1)\left \{ \sum _{e\in E_{m}(X, a_m)} T_e^{(a_m)} \, + \sum _{e\in E_m(X, b_m)} T_e^{(b_m)} \right \}\,, \end{align*}
\begin{align*} |E(X)| \,:\!=\, \sum _{m\in \mathcal{M}}m(m-1)|E_m(X)| = \sum _{m\in \mathcal{M}}m(m-1)\left \{ \sum _{e\in E_{m}(X, a_m)} T_e^{(a_m)} \, + \sum _{e\in E_m(X, b_m)} T_e^{(b_m)} \right \}\,, \end{align*}
with its expectation
 \begin{align} {\mathbb{E}} |E(X)| = \sum _{m\in \mathcal{M}}m(m-1)\left \{ \sum _{i=1}^{k} \binom{ \eta _{i} \frac{n}{2k}}{m} \frac{a_m - b_m }{ 2\binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ 2 \binom{n}{m-1} } \right \}\,, \end{align}
\begin{align} {\mathbb{E}} |E(X)| = \sum _{m\in \mathcal{M}}m(m-1)\left \{ \sum _{i=1}^{k} \binom{ \eta _{i} \frac{n}{2k}}{m} \frac{a_m - b_m }{ 2\binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ 2 \binom{n}{m-1} } \right \}\,, \end{align}
since
 \begin{align*} |E_m(X, a_m)| = \sum _{i=1}^{k} |E_{m}(V_i\cap X)|= \sum _{i=1}^{k} \binom{\eta _{i} \frac{n}{2k}}{m}\,, \quad |E_m(X, b_m)|= \binom{ \frac{n}{2k}}{m} - \sum _{i=1}^{k} \binom{\eta _{i} \frac{n}{2k}}{m}\,, \end{align*}
\begin{align*} |E_m(X, a_m)| = \sum _{i=1}^{k} |E_{m}(V_i\cap X)|= \sum _{i=1}^{k} \binom{\eta _{i} \frac{n}{2k}}{m}\,, \quad |E_m(X, b_m)|= \binom{ \frac{n}{2k}}{m} - \sum _{i=1}^{k} \binom{\eta _{i} \frac{n}{2k}}{m}\,, \end{align*}
Next, we prove the two Statements in Lemma 5.11 separately. First, assume that ![]() $|X\cap V_i| \leq \nu |X|$ ( i.e.,
$|X\cap V_i| \leq \nu |X|$ ( i.e., ![]() $\eta _i \leq \nu$) for each
$\eta _i \leq \nu$) for each ![]() $i\in [k]$. Then
$i\in [k]$. Then
 \begin{align*}{\mathbb{E}} |E(X)| \leq &\, \frac{1}{2} \sum _{m\in \mathcal{M}}m(m-1) \left \{ \left [ \binom{\frac{\nu n}{2k}}{m} + \binom{\frac{(1 - \nu )n}{2k}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \} \,=\!:\,\mu _1\,. \end{align*}
\begin{align*}{\mathbb{E}} |E(X)| \leq &\, \frac{1}{2} \sum _{m\in \mathcal{M}}m(m-1) \left \{ \left [ \binom{\frac{\nu n}{2k}}{m} + \binom{\frac{(1 - \nu )n}{2k}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \} \,=\!:\,\mu _1\,. \end{align*}
To justify the above inequality, note that since ![]() $\sum \limits _{i=1}^k \eta _i = 1$, the sum
$\sum \limits _{i=1}^k \eta _i = 1$, the sum ![]() $\sum _{i=1}^k \binom{\eta _i \frac{n}{2k}}{m}$ is maximised when all but
$\sum _{i=1}^k \binom{\eta _i \frac{n}{2k}}{m}$ is maximised when all but ![]() $2$ of the
$2$ of the ![]() $\eta _i$ are
$\eta _i$ are ![]() $0$, and since all
$0$, and since all ![]() $\eta _i \leq \nu$, this means that
$\eta _i \leq \nu$, this means that
 \begin{equation*} \sum _{i=1}^k \binom {\eta _i \frac {n}{2k}}{m} \leq \binom {\frac {\nu n}{2k}}{m} + \binom {\frac {(1-\nu ) n}{2k}}{m}\,. \end{equation*}
\begin{equation*} \sum _{i=1}^k \binom {\eta _i \frac {n}{2k}}{m} \leq \binom {\frac {\nu n}{2k}}{m} + \binom {\frac {(1-\nu ) n}{2k}}{m}\,. \end{equation*}
Note that ![]() $m(m-1)(T_{e}^{(a_m)} -{\mathbb{E}} T_{e}^{(a_m)})$ and
$m(m-1)(T_{e}^{(a_m)} -{\mathbb{E}} T_{e}^{(a_m)})$ and ![]() $m(m-1)(T_{e}^{(b_m)} -{\mathbb{E}} T_{e}^{(b_m)})$ are independent mean-zero random variables bounded by
$m(m-1)(T_{e}^{(b_m)} -{\mathbb{E}} T_{e}^{(b_m)})$ are independent mean-zero random variables bounded by ![]() $M(M-1)$ for all
$M(M-1)$ for all ![]() $m\in \mathcal{M}$, and
$m\in \mathcal{M}$, and ![]() ${\mathbb{V}\mathrm{ar}}(|E(X)|) \leq M^2(M - 1)^2{\mathbb{E}} |E(X)| = \Omega (n)$. Recall that
${\mathbb{V}\mathrm{ar}}(|E(X)|) \leq M^2(M - 1)^2{\mathbb{E}} |E(X)| = \Omega (n)$. Recall that ![]() $\mu _{\mathrm{T}}\,:\!=\, (\mu _1 + \mu _2)/2$. Define
$\mu _{\mathrm{T}}\,:\!=\, (\mu _1 + \mu _2)/2$. Define ![]() $t = \mu _{\mathrm{T}} -{\mathbb{E}}|E(X)|$, then
$t = \mu _{\mathrm{T}} -{\mathbb{E}}|E(X)|$, then ![]() $ 0 \lt (\mu _2 - \mu _1)/2 \leq t \leq \mu _{\mathrm{T}}$, hence
$ 0 \lt (\mu _2 - \mu _1)/2 \leq t \leq \mu _{\mathrm{T}}$, hence ![]() $t = \Omega (n)$. By Bernstein’s Lemma D.3, we have
$t = \Omega (n)$. By Bernstein’s Lemma D.3, we have
where ![]() $c\gt 0$ is some constant. On the other hand, if
$c\gt 0$ is some constant. On the other hand, if ![]() $|X\cap V_i| \geq \frac{1+\nu }{2}|X|$ for some
$|X\cap V_i| \geq \frac{1+\nu }{2}|X|$ for some ![]() $i\in [k]$, then
$i\in [k]$, then
 \begin{align*} &\,{\mathbb{E}}|E(X)|\geq \frac{1}{2} \sum _{m\in \mathcal{M}}m(m-1) \left \{ \left [ \binom{\frac{(1 + \nu )n}{4k} }{m} + (k-1)\binom{ \frac{(1 - \nu )n}{4k(k-1)}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \} \,=\!:\,\mu _2\,. \end{align*}
\begin{align*} &\,{\mathbb{E}}|E(X)|\geq \frac{1}{2} \sum _{m\in \mathcal{M}}m(m-1) \left \{ \left [ \binom{\frac{(1 + \nu )n}{4k} }{m} + (k-1)\binom{ \frac{(1 - \nu )n}{4k(k-1)}}{m} \right ] \frac{a_m - b_m }{ \binom{n}{m-1} } + \binom{\frac{n}{2k}}{m} \frac{b_{m}}{ \binom{n}{m-1} } \right \} \,=\!:\,\mu _2\,. \end{align*}
The above can be justified by noting that at least one ![]() $|X\cap V_i| \geq \frac{1+\nu }{2} |X|$, and that the rest of the vertices will yield a minimal binomial sum when they are evenly split between the remaining
$|X\cap V_i| \geq \frac{1+\nu }{2} |X|$, and that the rest of the vertices will yield a minimal binomial sum when they are evenly split between the remaining ![]() $V_j$. Similarly, define
$V_j$. Similarly, define ![]() $t = \mu _{\mathrm{T}} -{\mathbb{E}}|E(X)|$, then
$t = \mu _{\mathrm{T}} -{\mathbb{E}}|E(X)|$, then ![]() $0 \lt (\mu _2 - \mu _1)/2 \leq -t = \Omega (n)$, and Bernstein’s Lemma D.3 gives
$0 \lt (\mu _2 - \mu _1)/2 \leq -t = \Omega (n)$, and Bernstein’s Lemma D.3 gives
 \begin{align*}{\mathbb{P}} \Big ( |E(X)| \leq \mu _{\mathrm{T}} \Big ) = &\,{\mathbb{P}} \Big ( |E(X)| -{\mathbb{E}}|E(X)| \leq -t \Big )\\
\leq &\, \exp\!\left ({-}\frac{t^2/2}{{\mathbb{V}\mathrm{ar}}(|E(X)|) + M(M-1)({-}t)/3} \right ) = O(e^{-c^{\prime } n})\,, \end{align*}
\begin{align*}{\mathbb{P}} \Big ( |E(X)| \leq \mu _{\mathrm{T}} \Big ) = &\,{\mathbb{P}} \Big ( |E(X)| -{\mathbb{E}}|E(X)| \leq -t \Big )\\
\leq &\, \exp\!\left ({-}\frac{t^2/2}{{\mathbb{V}\mathrm{ar}}(|E(X)|) + M(M-1)({-}t)/3} \right ) = O(e^{-c^{\prime } n})\,, \end{align*}
where ![]() $c^{\prime }\gt 0$ is some other constant.
$c^{\prime }\gt 0$ is some other constant.
B.7. Proof of Lemma 5.13
Proof. If vertex ![]() $i$ is uniformly chosen from
$i$ is uniformly chosen from ![]() $Y_2$, the probability that
$Y_2$, the probability that ![]() $i \notin V_{l}$ for some
$i \notin V_{l}$ for some ![]() $l \in [k]$ is
$l \in [k]$ is
where ![]() $n_t$ and
$n_t$ and ![]() $n_t^{\prime }$, defined in equations (12) and (13), denote the cardinality of
$n_t^{\prime }$, defined in equations (12) and (13), denote the cardinality of ![]() $Z\cap V_t$ and
$Z\cap V_t$ and ![]() $Y_1\cap V_t$ respectively. As proved in Appendix B.2, with probability at least
$Y_1\cap V_t$ respectively. As proved in Appendix B.2, with probability at least ![]() $1 - 2\exp ({-}k \log ^2(n))$, we have
$1 - 2\exp ({-}k \log ^2(n))$, we have
then ![]() ${\mathbb{P}}(i\notin V_{l} | i\in Y_2) = 1-\frac{1}{k} \Big (1 + o(1) \Big )\,.$ After
${\mathbb{P}}(i\notin V_{l} | i\in Y_2) = 1-\frac{1}{k} \Big (1 + o(1) \Big )\,.$ After ![]() $k\log ^2 n$ samples from
$k\log ^2 n$ samples from ![]() $Y_2$, the probability that there exists at least one node which belongs to
$Y_2$, the probability that there exists at least one node which belongs to ![]() $V_l$ is at least
$V_l$ is at least
The proof is completed by a union bound over ![]() $l\in [k]$.
$l\in [k]$.
B.8. Proof of Lemma 5.14
Proof. We calculate ![]() ${\mathbb{P}}(S_{11}^{\prime }(u) \leq \mu _{\mathrm{C}})$ first. Define
${\mathbb{P}}(S_{11}^{\prime }(u) \leq \mu _{\mathrm{C}})$ first. Define ![]() $t_{\mathrm{1C}} \,:\!=\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{11}^{\prime }(u)$, then by Bernstein’s inequality (Lemma D.3) and taking
$t_{\mathrm{1C}} \,:\!=\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{11}^{\prime }(u)$, then by Bernstein’s inequality (Lemma D.3) and taking ![]() $K = \mathcal{M}_{\max } - 1$,
$K = \mathcal{M}_{\max } - 1$,
 \begin{align*} &\,{\mathbb{P}} \left ( S_{11}^{\prime }(u) \leq \mu _{\mathrm{C}}\right ) ={\mathbb{P}} \left ( S^{\prime }_{11}(u) -{\mathbb{E}} S^{\prime }_{11}(u) \leq t_{\mathrm{1C}}\right )\\[4pt]
\leq &\, \exp\!\left ({-} \frac{t_{\mathrm{1C}}^2/2}{{\mathbb{V}\mathrm{ar}}[S_{11}^{\prime }(u)] +(\mathcal{M}_{\max } - 1)\cdot t_{\mathrm{1C}}/3} \right ) \leq \exp\!\left ({-}\frac{3t_{\mathrm{1C}}^2/(\mathcal{M}_{\max } - 1)}{6(\mathcal{M}_{\max } - 1)\cdot{\mathbb{E}} S_{11}^{\prime }(u) + 2 t_{\mathrm{1C}}} \right )\\[4pt]
\leq &\, \exp\!\left ({-}\frac{[(\nu )^{\mathcal{M}_{\max }-1} - (1 - \nu )^{\mathcal{M}_{\max }-1}]^2 }{(\mathcal{M}_{\max } - 1)^2\cdot 2^{2\mathcal{M}_{\max } + 3}} \cdot \frac{ \left [\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )}\right )\,, \end{align*}
\begin{align*} &\,{\mathbb{P}} \left ( S_{11}^{\prime }(u) \leq \mu _{\mathrm{C}}\right ) ={\mathbb{P}} \left ( S^{\prime }_{11}(u) -{\mathbb{E}} S^{\prime }_{11}(u) \leq t_{\mathrm{1C}}\right )\\[4pt]
\leq &\, \exp\!\left ({-} \frac{t_{\mathrm{1C}}^2/2}{{\mathbb{V}\mathrm{ar}}[S_{11}^{\prime }(u)] +(\mathcal{M}_{\max } - 1)\cdot t_{\mathrm{1C}}/3} \right ) \leq \exp\!\left ({-}\frac{3t_{\mathrm{1C}}^2/(\mathcal{M}_{\max } - 1)}{6(\mathcal{M}_{\max } - 1)\cdot{\mathbb{E}} S_{11}^{\prime }(u) + 2 t_{\mathrm{1C}}} \right )\\[4pt]
\leq &\, \exp\!\left ({-}\frac{[(\nu )^{\mathcal{M}_{\max }-1} - (1 - \nu )^{\mathcal{M}_{\max }-1}]^2 }{(\mathcal{M}_{\max } - 1)^2\cdot 2^{2\mathcal{M}_{\max } + 3}} \cdot \frac{ \left [\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )}\right )\,, \end{align*}
where ![]() $\mathcal{M}$ is obtained from Algorithm 3 with
$\mathcal{M}$ is obtained from Algorithm 3 with ![]() $\mathcal{M}_{\max }$ denoting the maximum value in
$\mathcal{M}_{\max }$ denoting the maximum value in ![]() $\mathcal{M}$, and the last two inequalities hold since
$\mathcal{M}$, and the last two inequalities hold since ![]() ${\mathbb{V}\mathrm{ar}}[S_{11}^{\prime }(u)] \leq (\mathcal{M}_{\max } - 1)^2{\mathbb{E}} S_{11}^{\prime }(u)$, and for sufficiently large
${\mathbb{V}\mathrm{ar}}[S_{11}^{\prime }(u)] \leq (\mathcal{M}_{\max } - 1)^2{\mathbb{E}} S_{11}^{\prime }(u)$, and for sufficiently large ![]() $n$,
$n$,
 \begin{align*} t_{\mathrm{1C}} \,:\!=\,&\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{11}^{\prime }(u) = -\frac{1}{2} \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} - \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ]\frac{a_m - b_m}{2\binom{n}{m-1}}\\[4pt]
\leq &\, - \frac{1}{2}\sum _{m\in \mathcal{M}} \frac{(\nu )^{m-1} - (1 - \nu )^{m-1}}{2^{m}}\cdot (m-1) \frac{a_m - b_m}{k^{m-1}}(1 + o(1))\\[4pt]
\leq &\, -\frac{(\nu )^{\mathcal{M}_{\max } - 1} - (1 - \nu )^{\mathcal{M}_{\max } - 1} }{2^{\mathcal{M}_{\max } + 2}} \sum _{m\in \mathcal{M}}(m-1) \cdot \frac{a_m - b_m}{k^{m-1}} \,, \end{align*}
\begin{align*} t_{\mathrm{1C}} \,:\!=\,&\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{11}^{\prime }(u) = -\frac{1}{2} \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} - \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ]\frac{a_m - b_m}{2\binom{n}{m-1}}\\[4pt]
\leq &\, - \frac{1}{2}\sum _{m\in \mathcal{M}} \frac{(\nu )^{m-1} - (1 - \nu )^{m-1}}{2^{m}}\cdot (m-1) \frac{a_m - b_m}{k^{m-1}}(1 + o(1))\\[4pt]
\leq &\, -\frac{(\nu )^{\mathcal{M}_{\max } - 1} - (1 - \nu )^{\mathcal{M}_{\max } - 1} }{2^{\mathcal{M}_{\max } + 2}} \sum _{m\in \mathcal{M}}(m-1) \cdot \frac{a_m - b_m}{k^{m-1}} \,, \end{align*}
 \begin{align*} &\, 6(\mathcal{M}_{\max } - 1){\mathbb{E}} S_{11}^{\prime }(u) + 2t_{\mathrm{1C}} = 2\mu _{\mathrm{C}} + (6\mathcal{M}_{\max } - 8){\mathbb{E}} S^{\prime }_{11}(u)\\[4pt]
= &\, \sum _{m\in \mathcal{M}} (m-1)\left \{ \left [ (6\mathcal{M}_{\max } - 7)\binom{\frac{\nu n}{2k}}{m-1} + \binom{\frac{(1 - \nu ) n}{2k}}{m-1} \right ] \frac{a_m - b_m}{2\binom{n}{m-1}}\right.\\[4pt]
&\qquad\qquad \left. + 6(\mathcal{M}_{\max } - 1)\binom{\frac{n}{2k}}{m-1}\frac{b_m}{2\binom{n}{m-1}}\right \}\\[4pt]
= &\, \sum _{m\in \mathcal{M}} (m-1)\left [ \frac{(6\mathcal{M}_{\max } - 7)\cdot (\nu )^{m-1} + (1 - \nu )^{m-1} }{2^{m}}\cdot \frac{a_m - b_m}{k^{m-1}} + \frac{(6\mathcal{M}_{\max } - 6)b_m}{2^{m}k^{m-1}} \right ](1+o(1))\\[4pt]
\leq &\, \sum _{m\in \mathcal{M}} \frac{(6\mathcal{M}_{\max } - 7)\cdot (\nu )^{m-1} + (1 - \nu )^{m-1} }{2^{m}}\cdot (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m\right )(1+o(1))\\[4pt]
\leq &\, \frac{3(\mathcal{M}_{\max } - 1)}{2}\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m\right )\,. \end{align*}
\begin{align*} &\, 6(\mathcal{M}_{\max } - 1){\mathbb{E}} S_{11}^{\prime }(u) + 2t_{\mathrm{1C}} = 2\mu _{\mathrm{C}} + (6\mathcal{M}_{\max } - 8){\mathbb{E}} S^{\prime }_{11}(u)\\[4pt]
= &\, \sum _{m\in \mathcal{M}} (m-1)\left \{ \left [ (6\mathcal{M}_{\max } - 7)\binom{\frac{\nu n}{2k}}{m-1} + \binom{\frac{(1 - \nu ) n}{2k}}{m-1} \right ] \frac{a_m - b_m}{2\binom{n}{m-1}}\right.\\[4pt]
&\qquad\qquad \left. + 6(\mathcal{M}_{\max } - 1)\binom{\frac{n}{2k}}{m-1}\frac{b_m}{2\binom{n}{m-1}}\right \}\\[4pt]
= &\, \sum _{m\in \mathcal{M}} (m-1)\left [ \frac{(6\mathcal{M}_{\max } - 7)\cdot (\nu )^{m-1} + (1 - \nu )^{m-1} }{2^{m}}\cdot \frac{a_m - b_m}{k^{m-1}} + \frac{(6\mathcal{M}_{\max } - 6)b_m}{2^{m}k^{m-1}} \right ](1+o(1))\\[4pt]
\leq &\, \sum _{m\in \mathcal{M}} \frac{(6\mathcal{M}_{\max } - 7)\cdot (\nu )^{m-1} + (1 - \nu )^{m-1} }{2^{m}}\cdot (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m\right )(1+o(1))\\[4pt]
\leq &\, \frac{3(\mathcal{M}_{\max } - 1)}{2}\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m\right )\,. \end{align*}
Similarly, for ![]() ${\mathbb{P}}(S_{1j}^{\prime }(u) \geq \mu _{\mathrm{C}})$, define
${\mathbb{P}}(S_{1j}^{\prime }(u) \geq \mu _{\mathrm{C}})$, define ![]() $t_{\mathrm{jC}} \,:\!=\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{1j}^{\prime }(u)$ for
$t_{\mathrm{jC}} \,:\!=\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{1j}^{\prime }(u)$ for ![]() $j\neq 1$, by Bernstein’s Lemma D.3,
$j\neq 1$, by Bernstein’s Lemma D.3,
 \begin{align*} &\,{\mathbb{P}} \left ( S_{1j}^{\prime }(u) \geq \mu _{\mathrm{C}}\right ) ={\mathbb{P}} \left ( S^{\prime }_{1j}(u) -{\mathbb{E}} S^{\prime }_{1j}(u) \geq t_{\mathrm{jC}}\right )\\
\leq &\, \exp\!\left ({-} \frac{t_{\mathrm{jC}}^2/2}{{\mathbb{V}\mathrm{ar}}[S_{1j}^{\prime }(u)] + (\mathcal{M}_{\max } - 1)\cdot t_{\mathrm{jC}}/3} \right ) \leq \exp\!\left ({-}\frac{3t_{\mathrm{jC}}^2/(\mathcal{M}_{\max } - 1)}{6(\mathcal{M}_{\max } - 1)\cdot{\mathbb{E}} S_{1j}^{\prime }(u) + 2 t_{\mathrm{jC}}} \right )\\
\leq &\, \exp\!\left ({-}\frac{[(\nu )^{\mathcal{M}_{\max }-1} - (1 - \nu )^{\mathcal{M}_{\max }-1}]^2 }{(\mathcal{M}_{\max } - 1)^2\cdot 2^{2\mathcal{M}_{\max } + 3}} \cdot \frac{ \left [\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )} \right )\,. \end{align*}
\begin{align*} &\,{\mathbb{P}} \left ( S_{1j}^{\prime }(u) \geq \mu _{\mathrm{C}}\right ) ={\mathbb{P}} \left ( S^{\prime }_{1j}(u) -{\mathbb{E}} S^{\prime }_{1j}(u) \geq t_{\mathrm{jC}}\right )\\
\leq &\, \exp\!\left ({-} \frac{t_{\mathrm{jC}}^2/2}{{\mathbb{V}\mathrm{ar}}[S_{1j}^{\prime }(u)] + (\mathcal{M}_{\max } - 1)\cdot t_{\mathrm{jC}}/3} \right ) \leq \exp\!\left ({-}\frac{3t_{\mathrm{jC}}^2/(\mathcal{M}_{\max } - 1)}{6(\mathcal{M}_{\max } - 1)\cdot{\mathbb{E}} S_{1j}^{\prime }(u) + 2 t_{\mathrm{jC}}} \right )\\
\leq &\, \exp\!\left ({-}\frac{[(\nu )^{\mathcal{M}_{\max }-1} - (1 - \nu )^{\mathcal{M}_{\max }-1}]^2 }{(\mathcal{M}_{\max } - 1)^2\cdot 2^{2\mathcal{M}_{\max } + 3}} \cdot \frac{ \left [\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} \right ) \right ]^2 }{\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{k^{m-1}} + b_m \right )} \right )\,. \end{align*}
The last two inequalities holds since ![]() ${\mathbb{V}\mathrm{ar}}[S_{1j}^{\prime }(u)] \leq (\mathcal{M}_{\max } - 1)^2{\mathbb{E}} S_{1j}^{\prime }(u)$, and for sufficiently large
${\mathbb{V}\mathrm{ar}}[S_{1j}^{\prime }(u)] \leq (\mathcal{M}_{\max } - 1)^2{\mathbb{E}} S_{1j}^{\prime }(u)$, and for sufficiently large ![]() $n$,
$n$,
 \begin{align*} t_{\mathrm{jC}} \,:\!=\,&\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{1j}^{\prime }(u) = \frac{1}{2} \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} - \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ]\frac{a_m - b_m}{2\binom{n}{m-1}}\\
\geq &\, \frac{(\nu )^{\mathcal{M}_{\max } - 1} - (1 - \nu )^{\mathcal{M}_{\max } - 1} }{2^{\mathcal{M}_{\max } + 2}} \sum _{m\in \mathcal{M}}(m-1) \cdot \frac{a_m - b_m}{k^{m-1}} \,\,, \end{align*}
\begin{align*} t_{\mathrm{jC}} \,:\!=\,&\, \mu _{\mathrm{C}} -{\mathbb{E}} S_{1j}^{\prime }(u) = \frac{1}{2} \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2k}}{m-1} - \binom{\frac{(1 - \nu )n}{2k}}{m-1} \right ]\frac{a_m - b_m}{2\binom{n}{m-1}}\\
\geq &\, \frac{(\nu )^{\mathcal{M}_{\max } - 1} - (1 - \nu )^{\mathcal{M}_{\max } - 1} }{2^{\mathcal{M}_{\max } + 2}} \sum _{m\in \mathcal{M}}(m-1) \cdot \frac{a_m - b_m}{k^{m-1}} \,\,, \end{align*}
Appendix C. Algorithm correctness for the binary case
We will show the correctness of Algorithm 1 and prove Theorem 1.6 in this section. The analysis will mainly follow from the analysis in Section 5. We only detail the differences.
Without loss of generality, we assume ![]() $n$ is even to guarantee the existence of a binary partition of size
$n$ is even to guarantee the existence of a binary partition of size ![]() $n/2$. The method to deal with the odd
$n/2$. The method to deal with the odd ![]() $n$ case was discussed in Lemma 2.4. Then, let the index set be
$n$ case was discussed in Lemma 2.4. Then, let the index set be ![]() $\mathcal{I} = \{i\in [n]\,:\, \mathrm{row}(i) \leq 20\mathcal{M}_{\max } d\}$, as shown in equation (11). Let
$\mathcal{I} = \{i\in [n]\,:\, \mathrm{row}(i) \leq 20\mathcal{M}_{\max } d\}$, as shown in equation (11). Let ![]() $\boldsymbol{u}_i$ (resp.
$\boldsymbol{u}_i$ (resp. ![]() $\bar{\boldsymbol{u}}_i$) denote the eigenvector associated to
$\bar{\boldsymbol{u}}_i$) denote the eigenvector associated to ![]() $\lambda _i({\mathbf{A}}_{\mathcal{I}})$ (resp.
$\lambda _i({\mathbf{A}}_{\mathcal{I}})$ (resp. ![]() $\lambda _i(\overline{{\mathbf{A}}})$) for
$\lambda _i(\overline{{\mathbf{A}}})$) for ![]() $i =1, 2$. Define two linear subspaces
$i =1, 2$. Define two linear subspaces ![]() ${\mathbf{U}}\,:\!=\, \mathrm{Span}\{\boldsymbol{u}_{1},\boldsymbol{u}_{2}\}$ and
${\mathbf{U}}\,:\!=\, \mathrm{Span}\{\boldsymbol{u}_{1},\boldsymbol{u}_{2}\}$ and ![]() $\overline{{\mathbf{U}}}\,:\!=\, \mathrm{Span}\{\bar{\boldsymbol{u}}_{1},\bar{\boldsymbol{u}}_{2}\}$, then the angle between
$\overline{{\mathbf{U}}}\,:\!=\, \mathrm{Span}\{\bar{\boldsymbol{u}}_{1},\bar{\boldsymbol{u}}_{2}\}$, then the angle between ![]() ${\mathbf{U}}$ and
${\mathbf{U}}$ and ![]() $\overline{{\mathbf{U}}}$ is defined as
$\overline{{\mathbf{U}}}$ is defined as ![]() $ \sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \,:\!=\, \|P_{{\mathbf{U}}} - P_{\overline{{\mathbf{U}}}}\|$, where
$ \sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \,:\!=\, \|P_{{\mathbf{U}}} - P_{\overline{{\mathbf{U}}}}\|$, where ![]() $P_{{\mathbf{U}}}$ and
$P_{{\mathbf{U}}}$ and ![]() $P_{\overline{{\mathbf{U}}}}$ are the orthogonal projections onto
$P_{\overline{{\mathbf{U}}}}$ are the orthogonal projections onto ![]() ${\mathbf{U}}$ and
${\mathbf{U}}$ and ![]() $\overline{{\mathbf{U}}}$, respectively.
$\overline{{\mathbf{U}}}$, respectively.
C.1. Proof of Lemma 4.4
The strategy to bound the angle is similar to Subsection 5.1.2, except that we apply Davis-Kahan Theorem (Lemma D.6) here.
Define ![]() ${\mathbf{E}} \,:\!=\,{\mathbf{A}} - \overline{{\mathbf{A}}}$ and its restriction on
${\mathbf{E}} \,:\!=\,{\mathbf{A}} - \overline{{\mathbf{A}}}$ and its restriction on ![]() $\mathcal{I}$, namely
$\mathcal{I}$, namely ![]() ${\mathbf{E}}_{\mathcal{I}} \,:\!=\, ({\mathbf{A}} - \overline{{\mathbf{A}}})_{\mathcal{I}} ={\mathbf{A}}_{\mathcal{I}} - \overline{{\mathbf{A}}}_{\mathcal{I}}$, as well as
${\mathbf{E}}_{\mathcal{I}} \,:\!=\, ({\mathbf{A}} - \overline{{\mathbf{A}}})_{\mathcal{I}} ={\mathbf{A}}_{\mathcal{I}} - \overline{{\mathbf{A}}}_{\mathcal{I}}$, as well as ![]() ${\boldsymbol \Delta }\,:\!=\, \overline{{\mathbf{A}}}_{\mathcal{I}} - \overline{{\mathbf{A}}}$. Then the deviation
${\boldsymbol \Delta }\,:\!=\, \overline{{\mathbf{A}}}_{\mathcal{I}} - \overline{{\mathbf{A}}}$. Then the deviation ![]() ${\mathbf{A}}_{\mathcal{I}} - \overline{{\mathbf{A}}}$ is decomposed as
${\mathbf{A}}_{\mathcal{I}} - \overline{{\mathbf{A}}}$ is decomposed as
Theorem 3.3 indicates ![]() $\|{\mathbf{E}}_{\mathcal{I}}\|\leq C_3\sqrt{d}$ with probability at least
$\|{\mathbf{E}}_{\mathcal{I}}\|\leq C_3\sqrt{d}$ with probability at least ![]() $1 - n^{-2}$ when taking
$1 - n^{-2}$ when taking ![]() $\tau =20\mathcal{M}_{\max }, K=3$, where
$\tau =20\mathcal{M}_{\max }, K=3$, where ![]() $C_3$ is a constant depending only on
$C_3$ is a constant depending only on ![]() $\mathcal{M}_{\max }$. Moreover, Lemma 5.4 shows that the number of vertices with high degrees is relatively small. Consequently, an argument similar to Corollary 5.5 leads to the conclusion
$\mathcal{M}_{\max }$. Moreover, Lemma 5.4 shows that the number of vertices with high degrees is relatively small. Consequently, an argument similar to Corollary 5.5 leads to the conclusion ![]() $\|{\boldsymbol \Delta }\| \leq \sqrt{d}$ w.h.p. Together with upper bounds for
$\|{\boldsymbol \Delta }\| \leq \sqrt{d}$ w.h.p. Together with upper bounds for ![]() $\|{\mathbf{E}}_{\mathcal{I}}\|$ and
$\|{\mathbf{E}}_{\mathcal{I}}\|$ and ![]() $\|{\boldsymbol \Delta }\|$, Lemma C.1 shows that the angle between
$\|{\boldsymbol \Delta }\|$, Lemma C.1 shows that the angle between ![]() ${\mathbf{U}}$ and
${\mathbf{U}}$ and ![]() $\overline{{\mathbf{U}}}$ is relatively small with high probability.
$\overline{{\mathbf{U}}}$ is relatively small with high probability.
Lemma C.1. For any ![]() $c\in (0,1)$, there exists a constant
$c\in (0,1)$, there exists a constant ![]() $C_2$ depending on
$C_2$ depending on ![]() $\mathcal M_{\max }$ and
$\mathcal M_{\max }$ and ![]() $c$ such that if
$c$ such that if
then ![]() $\sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \leq c$ with probability
$\sin \angle ({\mathbf{U}}, \overline{{\mathbf{U}}}) \leq c$ with probability ![]() $1 - n^{-2}$.
$1 - n^{-2}$.
Proof. First, with probability ![]() $1 - n^{-2}$, we have
$1 - n^{-2}$, we have
According to the definitions in equation (8), ![]() $\alpha \geq \beta$ and
$\alpha \geq \beta$ and ![]() $\alpha = O(1/n)$,
$\alpha = O(1/n)$, ![]() $\beta = O(1/n)$. Meanwhile, Lemma 2.3 shows that
$\beta = O(1/n)$. Meanwhile, Lemma 2.3 shows that ![]() $|\lambda _2(\overline{{\mathbf{A}}})| = [{-} \alpha + (\alpha - \beta )n/2]$ and
$|\lambda _2(\overline{{\mathbf{A}}})| = [{-} \alpha + (\alpha - \beta )n/2]$ and ![]() $|\lambda _{3}(\overline{{\mathbf{A}}})| = \alpha$. The
$|\lambda _{3}(\overline{{\mathbf{A}}})| = \alpha$. The
 \begin{align*} &\,|\lambda _2(\overline{{\mathbf{A}}})| - |\lambda _{3}(\overline{{\mathbf{A}}})| = \frac{n}{2}(\alpha - \beta ) - 2\alpha \geq \frac{3}{4}\cdot \frac{n}{2}(\alpha - \beta ) = \frac{3n}{8} \sum _{m\in \mathcal{M}} \binom{\frac{n}{2} - 2}{m-2} \frac{(a_m - b_m)}{\binom{n}{m-1}}\\
\geq &\, \frac{1}{4}\sum _{m\in \mathcal{M}} \frac{(m-1)(a_m - b_m)}{2^{m-2}} \geq \frac{1}{2^{\mathcal{M}_{\max }}}\sum _{m\in \mathcal{M}}(m-1)(a_m - b_m) \geq 4C_2\sqrt{d}\,. \end{align*}
\begin{align*} &\,|\lambda _2(\overline{{\mathbf{A}}})| - |\lambda _{3}(\overline{{\mathbf{A}}})| = \frac{n}{2}(\alpha - \beta ) - 2\alpha \geq \frac{3}{4}\cdot \frac{n}{2}(\alpha - \beta ) = \frac{3n}{8} \sum _{m\in \mathcal{M}} \binom{\frac{n}{2} - 2}{m-2} \frac{(a_m - b_m)}{\binom{n}{m-1}}\\
\geq &\, \frac{1}{4}\sum _{m\in \mathcal{M}} \frac{(m-1)(a_m - b_m)}{2^{m-2}} \geq \frac{1}{2^{\mathcal{M}_{\max }}}\sum _{m\in \mathcal{M}}(m-1)(a_m - b_m) \geq 4C_2\sqrt{d}\,. \end{align*}
Then for some large enough ![]() $C_2$, the following condition for Davis-Kahan Theorem (Lemma D.6) is satisfied
$C_2$, the following condition for Davis-Kahan Theorem (Lemma D.6) is satisfied
Then for any ![]() $c\in (0, 1)$, we can choose
$c\in (0, 1)$, we can choose ![]() $C_2 = (C_3 + 1)/c$ such that
$C_2 = (C_3 + 1)/c$ such that
Now, we focus on the accuracy of Algorithm 7, once the conditions in Lemma C.1 are satisfied.
Lemma C.2 (Lemma 23 in [Reference Chin, Rao and Van19]). If ![]() $\sin \angle (\overline{{\mathbf{U}}},{\mathbf{U}}) \leq c \leq \frac{1}{4}$, there exists a unit vector
$\sin \angle (\overline{{\mathbf{U}}},{\mathbf{U}}) \leq c \leq \frac{1}{4}$, there exists a unit vector ![]() $\boldsymbol{v}\in{\mathbf{U}}$ such that the angle between
$\boldsymbol{v}\in{\mathbf{U}}$ such that the angle between ![]() $\bar{\boldsymbol{u}}_{2}$ and
$\bar{\boldsymbol{u}}_{2}$ and ![]() $\boldsymbol{v}$ satisfies
$\boldsymbol{v}$ satisfies ![]() $\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \leq 2 \sqrt{c}$.
$\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \leq 2 \sqrt{c}$.
The desired vector ![]() $\boldsymbol{v}$, as constructed in Algorithm 7, is the unit vector perpendicular to
$\boldsymbol{v}$, as constructed in Algorithm 7, is the unit vector perpendicular to ![]() $P_{{\mathbf{U}}}\mathbf{1}_n$, where
$P_{{\mathbf{U}}}\mathbf{1}_n$, where ![]() $P_{{\mathbf{U}}}\mathbf{1}_n$ is the projection of all-ones vector onto
$P_{{\mathbf{U}}}\mathbf{1}_n$ is the projection of all-ones vector onto ![]() ${\mathbf{U}}$. Lemmas C.1 and C.2 together give the following corollary.
${\mathbf{U}}$. Lemmas C.1 and C.2 together give the following corollary.
Corollary C.3. For any ![]() $c \in (0, 1)$, there exists a unit vector
$c \in (0, 1)$, there exists a unit vector ![]() $\boldsymbol{v}\in{\mathbf{U}}$ such that the angle between
$\boldsymbol{v}\in{\mathbf{U}}$ such that the angle between ![]() $\bar{\boldsymbol{u}}_{2}$ and
$\bar{\boldsymbol{u}}_{2}$ and ![]() $\boldsymbol{v}$ satisfies
$\boldsymbol{v}$ satisfies ![]() $\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \leq c \lt 1$ with probability
$\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \leq c \lt 1$ with probability ![]() $1 - O(e^{-n})$.
$1 - O(e^{-n})$.
Proof. For any ![]() $c \in (0, 1)$, we could choose constants
$c \in (0, 1)$, we could choose constants ![]() $C_2$,
$C_2$, ![]() $C_3$ in Lemma C.1 such that
$C_3$ in Lemma C.1 such that ![]() $\sin \angle (\overline{{\mathbf{U}}},{\mathbf{U}}) \leq \frac{c^{2}}{4} \lt 1$. Then by Lemma C.2, we construct
$\sin \angle (\overline{{\mathbf{U}}},{\mathbf{U}}) \leq \frac{c^{2}}{4} \lt 1$. Then by Lemma C.2, we construct ![]() $\boldsymbol{v}$ such that
$\boldsymbol{v}$ such that ![]() $\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \leq c$.
$\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \leq c$.
Lemma C.4 (Lemma 23 in [Reference Chin, Rao and Van19]). If ![]() $\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \lt c \leq 0.5$, then we can identify at least
$\sin \angle (\bar{\boldsymbol{u}}_{2},\boldsymbol{v}) \lt c \leq 0.5$, then we can identify at least ![]() $(1 - 8c^{2}/3)n$ vertices from each block correctly.
$(1 - 8c^{2}/3)n$ vertices from each block correctly.
The proof of Lemma 4.4 is completed when choosing ![]() $C_2$,
$C_2$, ![]() $C_3$ in Lemma C.1 s.t.
$C_3$ in Lemma C.1 s.t. ![]() $c \leq \frac{1}{4}$.
$c \leq \frac{1}{4}$.
C.2 Proof of Lemma 4.5
The proof strategy is similar to Subsections 5.2 and 5.3. In Algorithm 1, we first colour the hyperedges with red and blue with equal probability. By running Algorithm 8 on the red graph, we obtain a ![]() $\nu$-correct partition
$\nu$-correct partition ![]() $V_1^{\prime }, V_2^{\prime }$ of
$V_1^{\prime }, V_2^{\prime }$ of ![]() $V = V_1 \cup V_2$, i.e.,
$V = V_1 \cup V_2$, i.e., ![]() $|V_{l}\cap V_{l}^{\prime }| \geq \nu n/2$ for
$|V_{l}\cap V_{l}^{\prime }| \geq \nu n/2$ for ![]() $l = 1, 2$. In the rest of the proof, we condition on this event and the event that the maximum red degree of a vertex is at most
$l = 1, 2$. In the rest of the proof, we condition on this event and the event that the maximum red degree of a vertex is at most ![]() $\log ^{2}(n)$ with probability at least
$\log ^{2}(n)$ with probability at least ![]() $1 - o(1)$. This can be proved by Bernstein’s inequality (Lemma D.3).
$1 - o(1)$. This can be proved by Bernstein’s inequality (Lemma D.3).
Similarly, we consider the probability of a hyperedge ![]() $e = \{i_{1}, \cdots, i_{m}\}$ being blue conditioning on the event that
$e = \{i_{1}, \cdots, i_{m}\}$ being blue conditioning on the event that ![]() $e$ is not a red hyperedge in each underlying
$e$ is not a red hyperedge in each underlying ![]() $m$-uniform hypergraph separately. If vertices
$m$-uniform hypergraph separately. If vertices ![]() $i_{1}, \cdots, i_{m}$ are all from the same true cluster, then the probability is
$i_{1}, \cdots, i_{m}$ are all from the same true cluster, then the probability is ![]() $\psi _m$, otherwise
$\psi _m$, otherwise ![]() $\phi _m$, where
$\phi _m$, where ![]() $\psi _m$ and
$\psi _m$ and ![]() $\phi _m$ are defined in equations (29) and (30), and the presence of those hyperedges are represented by random variables
$\phi _m$ are defined in equations (29) and (30), and the presence of those hyperedges are represented by random variables ![]() $\zeta _e^{(a_m)} \sim \mathrm{Bernoulli}\left (\psi _m\right )$,
$\zeta _e^{(a_m)} \sim \mathrm{Bernoulli}\left (\psi _m\right )$, ![]() $\xi _e^{(b_m)} \sim \mathrm{Bernoulli}\left (\phi _m\right )$, respectively.
$\xi _e^{(b_m)} \sim \mathrm{Bernoulli}\left (\phi _m\right )$, respectively.
Following a similar argument in Subsection 5.2, the row sum of ![]() $u$ can be written as
$u$ can be written as
 \begin{align*} S^{\prime }_{lj}(u)\,:\!=\, \sum _{m\in \mathcal{M}}(m-1)\cdot \left \{ \sum _{e\in \, \mathcal{E}^{(a_m)}_{l, j}} \zeta _e^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{l, j}} \xi _e^{(b_m)}\right \}\,,\quad u\in V_l\,, \end{align*}
\begin{align*} S^{\prime }_{lj}(u)\,:\!=\, \sum _{m\in \mathcal{M}}(m-1)\cdot \left \{ \sum _{e\in \, \mathcal{E}^{(a_m)}_{l, j}} \zeta _e^{(a_m)} + \sum _{e\in \mathcal{E}^{(b_m)}_{l, j}} \xi _e^{(b_m)}\right \}\,,\quad u\in V_l\,, \end{align*}
where ![]() $\mathcal{E}^{(a_m)}_{l, j}\,:\!=\, E_m([V_l]^{1}, [V_l\cap V^{\prime }_j]^{m-1})$ denotes the set of
$\mathcal{E}^{(a_m)}_{l, j}\,:\!=\, E_m([V_l]^{1}, [V_l\cap V^{\prime }_j]^{m-1})$ denotes the set of ![]() $m$-hyperedges with
$m$-hyperedges with ![]() $1$ vertex from
$1$ vertex from ![]() $[V_l]^{1}$ and the other
$[V_l]^{1}$ and the other ![]() $m-1$ vertices from
$m-1$ vertices from ![]() $[V_l\cap V^{\prime }_j]^{m-1}$, while
$[V_l\cap V^{\prime }_j]^{m-1}$, while ![]() $ \mathcal{E}^{(b_m)}_{l, j} \,:\!=\, E_m \Big ([V_l]^{1}, \,\, [V^{\prime }_j]^{m-1} \setminus [V_l\cap V^{\prime }_j]^{m-1} \Big )$ denotes the set of
$ \mathcal{E}^{(b_m)}_{l, j} \,:\!=\, E_m \Big ([V_l]^{1}, \,\, [V^{\prime }_j]^{m-1} \setminus [V_l\cap V^{\prime }_j]^{m-1} \Big )$ denotes the set of ![]() $m$-hyperedges with
$m$-hyperedges with ![]() $1$ vertex in
$1$ vertex in ![]() $[V_l]^{1}$ while the remaining
$[V_l]^{1}$ while the remaining ![]() $m-1$ vertices in
$m-1$ vertices in ![]() $[V^{\prime }_j]^{m-1}\setminus [V_l\cap V^{\prime }_j]^{m-1}$, with their cardinalities
$[V^{\prime }_j]^{m-1}\setminus [V_l\cap V^{\prime }_j]^{m-1}$, with their cardinalities
According to the fact ![]() $|V_{l}\cap V_{l}^{\prime }| \geq \nu n/2$,
$|V_{l}\cap V_{l}^{\prime }| \geq \nu n/2$, ![]() $|V_l| = n/2$,
$|V_l| = n/2$, ![]() $|V^{\prime }_l| = n/2$ for
$|V^{\prime }_l| = n/2$ for ![]() $l = 1, 2$, we have
$l = 1, 2$, we have
To simplify the calculation, we take the lower and upper bound of ![]() $|\mathcal{E}^{(a_m)}_{l, l}|$ and
$|\mathcal{E}^{(a_m)}_{l, l}|$ and ![]() $|\mathcal{E}^{(a_m)}_{l, j}|(j\neq l)$ respectively. Taking expectation with respect to
$|\mathcal{E}^{(a_m)}_{l, j}|(j\neq l)$ respectively. Taking expectation with respect to ![]() $\zeta _e^{(a_m)}$ and
$\zeta _e^{(a_m)}$ and ![]() $\xi _e^{(b_m)}$, for any
$\xi _e^{(b_m)}$, for any ![]() $u \in V_l$, we have
$u \in V_l$, we have
 \begin{align*}{\mathbb{E}} S^{\prime }_{ll}(u) &= \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2}}{m-1} \phi _{m}\right ], \\
{\mathbb{E}} S^{\prime }_{lj}(u) &= \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{(1 - \nu ) n}{2}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2}}{m-1} \phi _{m} \right ],\,\, j\neq l\,. \end{align*}
\begin{align*}{\mathbb{E}} S^{\prime }_{ll}(u) &= \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{\nu n}{2}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2}}{m-1} \phi _{m}\right ], \\
{\mathbb{E}} S^{\prime }_{lj}(u) &= \sum _{m\in \mathcal{M}} (m-1)\cdot \left [ \binom{\frac{(1 - \nu ) n}{2}}{m-1} (\psi _{m} - \phi _{m}) + \binom{\frac{n}{2}}{m-1} \phi _{m} \right ],\,\, j\neq l\,. \end{align*}
By assumptions in Theorem 1.7, ![]() ${\mathbb{E}} S^{\prime }_{ll}(u) -{\mathbb{E}} S^{\prime }_{lj}(u) = \Omega (1)$. We define
${\mathbb{E}} S^{\prime }_{ll}(u) -{\mathbb{E}} S^{\prime }_{lj}(u) = \Omega (1)$. We define
 \begin{align*} \mu _{\mathrm{C}} \,:\!=\, \frac{1}{2}\sum _{m\in \mathcal{M}} (m-1)\cdot \left \{ \left [ \binom{\frac{\nu n}{2}}{m-1} + \binom{ \frac{(1 - \nu )n}{2} }{m-1} \right ](\psi _{m} - \phi _{m}) + 2\binom{ \frac{n}{2} }{m-1} \phi _{m}\right \}\,. \end{align*}
\begin{align*} \mu _{\mathrm{C}} \,:\!=\, \frac{1}{2}\sum _{m\in \mathcal{M}} (m-1)\cdot \left \{ \left [ \binom{\frac{\nu n}{2}}{m-1} + \binom{ \frac{(1 - \nu )n}{2} }{m-1} \right ](\psi _{m} - \phi _{m}) + 2\binom{ \frac{n}{2} }{m-1} \phi _{m}\right \}\,. \end{align*}
After Algorithm 6, if a vertex ![]() $u\in V_l$ is mislabelled, one of the following events must happen
$u\in V_l$ is mislabelled, one of the following events must happen
•
 $S^{\prime }_{ll}(u) \leq \mu _{\mathrm{C}}$,
$S^{\prime }_{ll}(u) \leq \mu _{\mathrm{C}}$,•
 $S^{\prime }_{lj}(u) \geq \mu _{\mathrm{C}}$, for some
$S^{\prime }_{lj}(u) \geq \mu _{\mathrm{C}}$, for some  $j\neq l$.
$j\neq l$.
By an argument similar to Lemma 5.14, we can prove that
where ![]() $\rho = \exp\!\left ({-}C_{\mathcal M}(2)\cdot \mathrm{SNR}_{\mathcal{M}}(2) \right )$ and
$\rho = \exp\!\left ({-}C_{\mathcal M}(2)\cdot \mathrm{SNR}_{\mathcal{M}}(2) \right )$ and
 \begin{align*} C_{\mathcal M}(2)\,:\!=\,\frac{[(\nu )^{\mathcal{M}_{\max }-1} - (1 - \nu )^{\mathcal{M}_{\max }-1}]^2 }{8(\mathcal{M}_{\max } - 1)^2}, \quad \mathrm{SNR}_{\mathcal{M}}(2)\,:\!=\, \frac{ \left [\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{2^{m-1}} \right ) \right ]^2 }{\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{2^{m-1}} + b_m \right )}\,. \end{align*}
\begin{align*} C_{\mathcal M}(2)\,:\!=\,\frac{[(\nu )^{\mathcal{M}_{\max }-1} - (1 - \nu )^{\mathcal{M}_{\max }-1}]^2 }{8(\mathcal{M}_{\max } - 1)^2}, \quad \mathrm{SNR}_{\mathcal{M}}(2)\,:\!=\, \frac{ \left [\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{2^{m-1}} \right ) \right ]^2 }{\sum _{m\in \mathcal{M}} (m-1)\left (\frac{a_m - b_m}{2^{m-1}} + b_m \right )}\,. \end{align*}
As a result, the probability that either of those events happened is bounded by ![]() $\rho$. The number of mislabelled vertices in
$\rho$. The number of mislabelled vertices in ![]() $V_1$ after Algorithm 5 is at most
$V_1$ after Algorithm 5 is at most
 \begin{align*} R_l = \sum _{i=1}^{|V_l\setminus V_l^{\prime }|}\Gamma _{i}\, + \sum _{i=1}^{|V_l \cap V_l^{\prime } |}\Lambda _{i}\,, \end{align*}
\begin{align*} R_l = \sum _{i=1}^{|V_l\setminus V_l^{\prime }|}\Gamma _{i}\, + \sum _{i=1}^{|V_l \cap V_l^{\prime } |}\Lambda _{i}\,, \end{align*}
where ![]() $\Gamma _{i}$ (resp.
$\Gamma _{i}$ (resp. ![]() $\Lambda _{i}$) are i.i.d indicator random variables with mean
$\Lambda _{i}$) are i.i.d indicator random variables with mean ![]() $\rho _1^{\prime }$ (resp.
$\rho _1^{\prime }$ (resp. ![]() $\rho _2^{\prime }$). Then
$\rho _2^{\prime }$). Then
where ![]() $\nu$ is the correctness after Algorithm 4. Let
$\nu$ is the correctness after Algorithm 4. Let ![]() $t_l\,:\!=\, (1 + \nu/2)n\rho$, then by Chernoff Lemma D.1,
$t_l\,:\!=\, (1 + \nu/2)n\rho$, then by Chernoff Lemma D.1,
which means that with probability ![]() $1- O(e^{- n\rho })$, the fraction of mislabelled vertices in
$1- O(e^{- n\rho })$, the fraction of mislabelled vertices in ![]() $V_l$ is smaller than
$V_l$ is smaller than ![]() $2\rho$, i.e., the correctness of
$2\rho$, i.e., the correctness of ![]() $V_l$ is at least
$V_l$ is at least ![]() $\gamma \,:\!=\, \max \{\nu, 1 - 2\rho \}$.
$\gamma \,:\!=\, \max \{\nu, 1 - 2\rho \}$.
Appendix D. Useful Lemmas
Lemma D.1 (Chernoff’s inequality, Theorem 2.3.6 in [Reference Vershynin69]). Let ![]() $X_i$ be independent Bernoulli random variables with parameters
$X_i$ be independent Bernoulli random variables with parameters ![]() $p_i$. Consider their sum
$p_i$. Consider their sum ![]() $S_N = \sum _{i=1}^{N}X_i$ and denote its mean by
$S_N = \sum _{i=1}^{N}X_i$ and denote its mean by ![]() $\mu ={\mathbb{E}} S_N$. Then for any
$\mu ={\mathbb{E}} S_N$. Then for any ![]() $\delta \in (0, 1]$,
$\delta \in (0, 1]$,
Lemma D.2 (Hoeffding’s inequality, Theorem 2.2.6 in [Reference Vershynin69]). Let ![]() $X_1,\dots, X_N$ be independent random variables with
$X_1,\dots, X_N$ be independent random variables with ![]() $X_i \in [a_i, b_i]$ for each
$X_i \in [a_i, b_i]$ for each ![]() $i\in \{1, \dots, N\}$. Then for any,
$i\in \{1, \dots, N\}$. Then for any, ![]() $t \geq 0$, we have
$t \geq 0$, we have
 \begin{align*}{\mathbb{P}}\Bigg ( \bigg |\sum _{i=1}^{N}(X_i -{\mathbb{E}} X_i ) \bigg | \geq t \Bigg ) \leq 2\exp \Bigg ({-}\frac{2t^{2} }{ \sum _{i=1}^{N}(b_i - a_i )^{2} } \Bigg )\,. \end{align*}
\begin{align*}{\mathbb{P}}\Bigg ( \bigg |\sum _{i=1}^{N}(X_i -{\mathbb{E}} X_i ) \bigg | \geq t \Bigg ) \leq 2\exp \Bigg ({-}\frac{2t^{2} }{ \sum _{i=1}^{N}(b_i - a_i )^{2} } \Bigg )\,. \end{align*}
Lemma D.3 (Bernstein’s inequality, Theorem 2.8.4 in [Reference Vershynin69]). Let ![]() $X_1,\dots,X_N$ be independent mean-zero random variables such that
$X_1,\dots,X_N$ be independent mean-zero random variables such that ![]() $|X_i|\leq K$ for all
$|X_i|\leq K$ for all ![]() $i$. Let
$i$. Let ![]() $\sigma ^2 = \sum _{i=1}^{N}{\mathbb{E}} X_i^2$. Then for every
$\sigma ^2 = \sum _{i=1}^{N}{\mathbb{E}} X_i^2$. Then for every ![]() $t \geq 0$, we have
$t \geq 0$, we have
 \begin{align*}{\mathbb{P}} \Bigg ( \Big |\sum _{i=1}^{N} X_i \Big | \geq t \Bigg ) \leq 2 \exp \Bigg ({-} \frac{t^2/2}{\sigma ^2 + Kt/3} \Bigg )\,. \end{align*}
\begin{align*}{\mathbb{P}} \Bigg ( \Big |\sum _{i=1}^{N} X_i \Big | \geq t \Bigg ) \leq 2 \exp \Bigg ({-} \frac{t^2/2}{\sigma ^2 + Kt/3} \Bigg )\,. \end{align*}
Lemma D.4 (Bennett’s inequality, Theorem 2.9.2 in [Reference Vershynin69]). Let ![]() $X_1,\dots, X_N$ be independent random variables. Assume that
$X_1,\dots, X_N$ be independent random variables. Assume that ![]() $|X_i -{\mathbb{E}} X_i| \leq K$ almost surely for every
$|X_i -{\mathbb{E}} X_i| \leq K$ almost surely for every ![]() $i$. Then for any
$i$. Then for any ![]() $t\gt 0$, we have
$t\gt 0$, we have
 \begin{align*}{\mathbb{P}} \Bigg ( \sum _{i=1}^{N} (X_i -{\mathbb{E}} X_i) \geq t \Bigg ) \leq \exp \Bigg ({-} \frac{\sigma ^2}{K^2} \cdot h \bigg ( \frac{Kt}{\sigma ^2} \bigg )\Bigg )\,, \end{align*}
\begin{align*}{\mathbb{P}} \Bigg ( \sum _{i=1}^{N} (X_i -{\mathbb{E}} X_i) \geq t \Bigg ) \leq \exp \Bigg ({-} \frac{\sigma ^2}{K^2} \cdot h \bigg ( \frac{Kt}{\sigma ^2} \bigg )\Bigg )\,, \end{align*}
where ![]() $\sigma ^2 = \sum _{i=1}^{N}\mathrm{Var}(X_i)$, and
$\sigma ^2 = \sum _{i=1}^{N}\mathrm{Var}(X_i)$, and ![]() $h(u) \,:\!=\, (1 + u)\log (1 + u) - u$.
$h(u) \,:\!=\, (1 + u)\log (1 + u) - u$.
Lemma D.5 (Weyl’s inequality). Let ![]() ${\mathbf{A}},{\mathbf{E}} \in{\mathbb{R}}^{m \times n}$ be two real
${\mathbf{A}},{\mathbf{E}} \in{\mathbb{R}}^{m \times n}$ be two real ![]() $m\times n$ matrices, then
$m\times n$ matrices, then ![]() $|\sigma _i({\mathbf{A}} +{\mathbf{E}}) - \sigma _i({\mathbf{A}})| \leq \|{\mathbf{E}}\|$ for every
$|\sigma _i({\mathbf{A}} +{\mathbf{E}}) - \sigma _i({\mathbf{A}})| \leq \|{\mathbf{E}}\|$ for every ![]() $1 \leq i \leq \min \{ m, n\}$. Furthermore, if
$1 \leq i \leq \min \{ m, n\}$. Furthermore, if ![]() $m = n$ and
$m = n$ and ![]() ${\mathbf{A}},{\mathbf{E}} \in{\mathbb{R}}^{n \times n}$ are real symmetric, then
${\mathbf{A}},{\mathbf{E}} \in{\mathbb{R}}^{n \times n}$ are real symmetric, then ![]() $|\lambda _i({\mathbf{A}} +{\mathbf{E}}) - \lambda _i({\mathbf{A}})| \leq \|{\mathbf{E}}\|$ for all
$|\lambda _i({\mathbf{A}} +{\mathbf{E}}) - \lambda _i({\mathbf{A}})| \leq \|{\mathbf{E}}\|$ for all ![]() $1 \leq i \leq n$.
$1 \leq i \leq n$.
Lemma D.6 (Davis-Kahan’s ![]() $\sin{\boldsymbol \Theta }$ Theorem, Theorem 2.2.1 in [Reference Chen, Chi, Fan and Ma15]). Let
$\sin{\boldsymbol \Theta }$ Theorem, Theorem 2.2.1 in [Reference Chen, Chi, Fan and Ma15]). Let ![]() $\overline{{\mathbf{M}}}$ and
$\overline{{\mathbf{M}}}$ and ![]() ${\mathbf{M}} = \overline{{\mathbf{M}}} +{\mathbf{E}}$ be two real symmetric
${\mathbf{M}} = \overline{{\mathbf{M}}} +{\mathbf{E}}$ be two real symmetric ![]() $n \times n$ matrices,
$n \times n$ matrices, ![]() $n \times n$ matrices, with eigenvalue decompositions given respectively by
$n \times n$ matrices, with eigenvalue decompositions given respectively by
 \begin{align*} \overline{{\mathbf{M}}} =& \, \sum \limits _{i=1}^{n}\overline{\lambda }_i \overline{\boldsymbol{u}}_{i}{\overline{\boldsymbol{u}}_{i}}^{{\mathsf T}} = \begin{bmatrix} \overline{{\mathbf{U}}} & \quad \overline{{\mathbf{U}}}_{\perp } \end{bmatrix} \begin{bmatrix} \overline{{\boldsymbol \Lambda }} & \quad {\mathbf{0}}\\[4pt]
{\mathbf{0}} & \quad \overline{{\boldsymbol \Lambda }}_{\perp } \end{bmatrix} \begin{bmatrix}{\overline{{\mathbf{U}}}}^{{\mathsf T}}\\[4pt]
{\overline{{\mathbf{U}}}}^{{\mathsf T}}_{\perp } \end{bmatrix}\,,\\[4pt]
{\mathbf{M}} =& \, \sum \limits _{i=1}^{n}\lambda _i\boldsymbol{u}_i\boldsymbol{u}_i^{\mathsf T} = \begin{bmatrix}{\mathbf{U}} & \quad {\mathbf{U}}_{\perp } \end{bmatrix} \begin{bmatrix}{\boldsymbol \Lambda } & \quad {\mathbf{0}}\\[4pt]
{\mathbf{0}} & \quad {\boldsymbol \Lambda }_{\perp } \end{bmatrix} \begin{bmatrix}{\mathbf{U}}^{{\mathsf T}}\\[4pt]
{\mathbf{U}}_{\perp }^{{\mathsf T}} \end{bmatrix}\,. \end{align*}
\begin{align*} \overline{{\mathbf{M}}} =& \, \sum \limits _{i=1}^{n}\overline{\lambda }_i \overline{\boldsymbol{u}}_{i}{\overline{\boldsymbol{u}}_{i}}^{{\mathsf T}} = \begin{bmatrix} \overline{{\mathbf{U}}} & \quad \overline{{\mathbf{U}}}_{\perp } \end{bmatrix} \begin{bmatrix} \overline{{\boldsymbol \Lambda }} & \quad {\mathbf{0}}\\[4pt]
{\mathbf{0}} & \quad \overline{{\boldsymbol \Lambda }}_{\perp } \end{bmatrix} \begin{bmatrix}{\overline{{\mathbf{U}}}}^{{\mathsf T}}\\[4pt]
{\overline{{\mathbf{U}}}}^{{\mathsf T}}_{\perp } \end{bmatrix}\,,\\[4pt]
{\mathbf{M}} =& \, \sum \limits _{i=1}^{n}\lambda _i\boldsymbol{u}_i\boldsymbol{u}_i^{\mathsf T} = \begin{bmatrix}{\mathbf{U}} & \quad {\mathbf{U}}_{\perp } \end{bmatrix} \begin{bmatrix}{\boldsymbol \Lambda } & \quad {\mathbf{0}}\\[4pt]
{\mathbf{0}} & \quad {\boldsymbol \Lambda }_{\perp } \end{bmatrix} \begin{bmatrix}{\mathbf{U}}^{{\mathsf T}}\\[4pt]
{\mathbf{U}}_{\perp }^{{\mathsf T}} \end{bmatrix}\,. \end{align*}
Here, ![]() $\{ \overline{\lambda }_{i}\}_{i=1}^{n}$(resp.
$\{ \overline{\lambda }_{i}\}_{i=1}^{n}$(resp. ![]() $\{\lambda _{i}\}_{i=1}^{n}$) stand for the eigenvalues of
$\{\lambda _{i}\}_{i=1}^{n}$) stand for the eigenvalues of ![]() $\overline{{\mathbf{M}}}$(resp.
$\overline{{\mathbf{M}}}$(resp. ![]() ${\mathbf{M}}$), and
${\mathbf{M}}$), and ![]() $\overline{\boldsymbol{u}}_i$(resp.
$\overline{\boldsymbol{u}}_i$(resp. ![]() $\boldsymbol{u}_i$) denotes the eigenvector associated
$\boldsymbol{u}_i$) denotes the eigenvector associated ![]() $\overline{\lambda }_{i}$(resp.
$\overline{\lambda }_{i}$(resp. ![]() $\lambda _i$). Additionally, for some fixed integer
$\lambda _i$). Additionally, for some fixed integer ![]() $r\in [n]$, we denote
$r\in [n]$, we denote
The matrices ![]() $\boldsymbol \Lambda$,
$\boldsymbol \Lambda$, ![]() ${\boldsymbol \Lambda }_{\perp }$,
${\boldsymbol \Lambda }_{\perp }$, ![]() ${\mathbf{U}}$,
${\mathbf{U}}$, ![]() ${\mathbf{U}}_{\perp }$ are defined analogously. Assume that
${\mathbf{U}}_{\perp }$ are defined analogously. Assume that
and the projection matrices are given by ![]() $P_{\mathbf{U}} \,:\!=\,{\mathbf{U}}{\mathbf{U}}^{{\mathsf T}}$,
$P_{\mathbf{U}} \,:\!=\,{\mathbf{U}}{\mathbf{U}}^{{\mathsf T}}$, ![]() $P_{\overline{{\mathbf{U}}}} \,:\!=\, \overline{{\mathbf{U}}} \,\overline{{\mathbf{U}}}^{{\mathsf T}}$, then one has
$P_{\overline{{\mathbf{U}}}} \,:\!=\, \overline{{\mathbf{U}}} \,\overline{{\mathbf{U}}}^{{\mathsf T}}$, then one has ![]() $\|P_{\mathbf{U}} - P_{\overline{{\mathbf{U}}}}\| \leq (2\|{\mathbf{E}}\|/\Delta )$. In particular, suppose that
$\|P_{\mathbf{U}} - P_{\overline{{\mathbf{U}}}}\| \leq (2\|{\mathbf{E}}\|/\Delta )$. In particular, suppose that ![]() $|\overline{\lambda }_1| \geq |\overline{\lambda }_2| \geq \cdots \geq |\overline{\lambda }_r| \geq |\overline{\lambda }_{r+1}| \geq \cdots |\overline{\lambda }_{n}|$ (resp.
$|\overline{\lambda }_1| \geq |\overline{\lambda }_2| \geq \cdots \geq |\overline{\lambda }_r| \geq |\overline{\lambda }_{r+1}| \geq \cdots |\overline{\lambda }_{n}|$ (resp. ![]() $|\lambda _1| \geq \cdots \geq |\lambda _{n}|$). If
$|\lambda _1| \geq \cdots \geq |\lambda _{n}|$). If ![]() $\|{\mathbf{E}}\|\leq (1 - 1/\sqrt{2})(|\overline{\lambda }|_{r} - |\overline{\lambda }|_{r+1})$, then one has
$\|{\mathbf{E}}\|\leq (1 - 1/\sqrt{2})(|\overline{\lambda }|_{r} - |\overline{\lambda }|_{r+1})$, then one has
Lemma D.7 (Wedin’s ![]() $\sin{\boldsymbol \Theta }$ Theorem, Theorem 2.3.1 in [Reference Chen, Chi, Fan and Ma15]). Let
$\sin{\boldsymbol \Theta }$ Theorem, Theorem 2.3.1 in [Reference Chen, Chi, Fan and Ma15]). Let ![]() $\overline{{\mathbf{M}}}$ and
$\overline{{\mathbf{M}}}$ and ![]() ${\mathbf{M}} = \overline{{\mathbf{M}}} +{\mathbf{E}}$ be two
${\mathbf{M}} = \overline{{\mathbf{M}}} +{\mathbf{E}}$ be two ![]() $n_1 \times n_2$ real matrices and
$n_1 \times n_2$ real matrices and ![]() $n_2$ real matrices and
$n_2$ real matrices and ![]() $n_1\geq n_2$, with SVDs given respectively by
$n_1\geq n_2$, with SVDs given respectively by

Here, ![]() $\overline{\sigma }_1 \geq \dots \geq \overline{\sigma }_{n_1}$ (resp.
$\overline{\sigma }_1 \geq \dots \geq \overline{\sigma }_{n_1}$ (resp. ![]() $\sigma _1 \geq \dots \geq \sigma _{n_1}$) stand for the singular values of
$\sigma _1 \geq \dots \geq \sigma _{n_1}$) stand for the singular values of ![]() $\overline{{\mathbf{M}}}$(resp.
$\overline{{\mathbf{M}}}$(resp. ![]() ${\mathbf{M}}$),
${\mathbf{M}}$), ![]() $\overline{\boldsymbol{u}}_i$(resp.
$\overline{\boldsymbol{u}}_i$(resp. ![]() $\boldsymbol{u}_i$) denotes the left singular vector associated with the singular value
$\boldsymbol{u}_i$) denotes the left singular vector associated with the singular value ![]() $\overline{\sigma }_i$(resp.
$\overline{\sigma }_i$(resp. ![]() $\sigma _i$), and
$\sigma _i$), and ![]() $\overline{\boldsymbol{v}}_i$(resp.
$\overline{\boldsymbol{v}}_i$(resp. ![]() $\boldsymbol{v}_i$) denotes the right singular vector associated with the singular value
$\boldsymbol{v}_i$) denotes the right singular vector associated with the singular value ![]() $\overline{\sigma }_i$(resp.
$\overline{\sigma }_i$(resp. ![]() $\sigma _i$). In addition, for any fixed integer
$\sigma _i$). In addition, for any fixed integer ![]() $r\in [n]$, we denote
$r\in [n]$, we denote
 \begin{align*}{\boldsymbol \Sigma }\,:\!=\, \mathrm{diag}\{\sigma _1, \dots, \sigma _r\}, \quad{\boldsymbol \Sigma }_{\perp }\,:\!=\,&\, \mathrm{diag}\{\sigma _{r+1}, \dots, \sigma _{n_1}\},\\
{\mathbf{U}}\,:\!=\, [\boldsymbol{u}_1, \dots,\boldsymbol{u}_r] \in{\mathbb{R}}^{n_1 \times r}, \quad{\mathbf{U}}_{\perp }\,:\!=\,&\, [\boldsymbol{u}_{r+1}, \dots,\boldsymbol{u}_{n_1}] \in{\mathbb{R}}^{n_1 \times (n_1 - r)},\\
{\mathbf{V}}\,:\!=\, [\boldsymbol{v}_1, \dots,\boldsymbol{v}_r] \in{\mathbb{R}}^{n_2 \times r}, \quad{\mathbf{V}}_{\perp }\,:\!=\,&\, [\boldsymbol{v}_{r+1}, \dots,\boldsymbol{v}_{n_2}] \in{\mathbb{R}}^{n_2 \times (n_2 - r)}. \end{align*}
\begin{align*}{\boldsymbol \Sigma }\,:\!=\, \mathrm{diag}\{\sigma _1, \dots, \sigma _r\}, \quad{\boldsymbol \Sigma }_{\perp }\,:\!=\,&\, \mathrm{diag}\{\sigma _{r+1}, \dots, \sigma _{n_1}\},\\
{\mathbf{U}}\,:\!=\, [\boldsymbol{u}_1, \dots,\boldsymbol{u}_r] \in{\mathbb{R}}^{n_1 \times r}, \quad{\mathbf{U}}_{\perp }\,:\!=\,&\, [\boldsymbol{u}_{r+1}, \dots,\boldsymbol{u}_{n_1}] \in{\mathbb{R}}^{n_1 \times (n_1 - r)},\\
{\mathbf{V}}\,:\!=\, [\boldsymbol{v}_1, \dots,\boldsymbol{v}_r] \in{\mathbb{R}}^{n_2 \times r}, \quad{\mathbf{V}}_{\perp }\,:\!=\,&\, [\boldsymbol{v}_{r+1}, \dots,\boldsymbol{v}_{n_2}] \in{\mathbb{R}}^{n_2 \times (n_2 - r)}. \end{align*}
The matrices ![]() $\overline{{\boldsymbol \Sigma }}$,
$\overline{{\boldsymbol \Sigma }}$, ![]() $\overline{{\boldsymbol \Sigma }}_{\perp }$,
$\overline{{\boldsymbol \Sigma }}_{\perp }$, ![]() $\overline{{\mathbf{V}}}$,
$\overline{{\mathbf{V}}}$, ![]() $\overline{{\mathbf{V}}}_{\perp }$ are defined analogously. If
$\overline{{\mathbf{V}}}_{\perp }$ are defined analogously. If ![]() ${\mathbf{E}} ={\mathbf{M}} -{\mathbf{M}} - \overline{{\mathbf{M}}}$ satisfies
${\mathbf{E}} ={\mathbf{M}} -{\mathbf{M}} - \overline{{\mathbf{M}}}$ satisfies ![]() $\|{\mathbf{E}}\|\leq \overline{\sigma }_r$ - with the projection matrices
$\|{\mathbf{E}}\|\leq \overline{\sigma }_r$ - with the projection matrices ![]() $P_{\mathbf{U}} \,:\!=\,{\mathbf{U}}{\mathbf{U}}^{{\mathsf T}}$, one has
$P_{\mathbf{U}} \,:\!=\,{\mathbf{U}}{\mathbf{U}}^{{\mathsf T}}$, one has
In particular, if ![]() $\|{\mathbf{E}}\|\leq (1 - 1/\sqrt{2})(\overline{\sigma }_{r} - \overline{\sigma }_{r+1})$, then one has
$\|{\mathbf{E}}\|\leq (1 - 1/\sqrt{2})(\overline{\sigma }_{r} - \overline{\sigma }_{r+1})$, then one has