No CrossRef data available.
Published online by Cambridge University Press: 01 August 2017
A subset C of edges in a k-uniform hypergraph H is a loose Hamilton cycle if C covers all the vertices of H and there exists a cyclic ordering of these vertices such that the edges in C are segments of that order and such that every two consecutive edges share exactly one vertex. The binomial random k-uniform hypergraph Hkn,p has vertex set [n] and an edge set E obtained by adding each k-tuple e ∈ (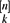 $\binom{[n]}{k}$) to E with probability p, independently at random.
$\binom{[n]}{k}$) to E with probability p, independently at random.
Here we consider the problem of finding edge-disjoint loose Hamilton cycles covering all but o(|E|) edges, referred to as the packing problem. While it is known that the threshold probability of the appearance of a loose Hamilton cycle in Hkn,p is
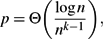 $p=\Theta\biggl(\frac{\log n}{n^{k-1}}\biggr),$
$p=\Theta\biggl(\frac{\log n}{n^{k-1}}\biggr),$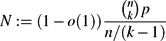 $N:=(1-o(1))\frac{\binom{n}{k}p}{n/(k-1)}$
$N:=(1-o(1))\frac{\binom{n}{k}p}{n/(k-1)}$
Our proof utilizes and modifies the idea of ‘online sprinkling’ recently introduced by Vu and the first author.