No CrossRef data available.
Published online by Cambridge University Press: 26 November 2024
We study the mixing time of the single-site update Markov chain, known as the Glauber dynamics, for generating a random independent set of a tree. Our focus is obtaining optimal convergence results for arbitrary trees. We consider the more general problem of sampling from the Gibbs distribution in the hard-core model where independent sets are weighted by a parameter 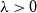 $\lambda \gt 0$; the special case
$\lambda \gt 0$; the special case 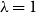 $\lambda =1$ corresponds to the uniform distribution over all independent sets. Previous work of Martinelli, Sinclair and Weitz (2004) obtained optimal mixing time bounds for the complete
$\lambda =1$ corresponds to the uniform distribution over all independent sets. Previous work of Martinelli, Sinclair and Weitz (2004) obtained optimal mixing time bounds for the complete 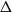 $\Delta$-regular tree for all
$\Delta$-regular tree for all 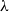 $\lambda$. However, Restrepo, Stefankovic, Vera, Vigoda, and Yang (2014) showed that for sufficiently large
$\lambda$. However, Restrepo, Stefankovic, Vera, Vigoda, and Yang (2014) showed that for sufficiently large 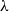 $\lambda$ there are bounded-degree trees where optimal mixing does not hold. Recent work of Eppstein and Frishberg (2022) proved a polynomial mixing time bound for the Glauber dynamics for arbitrary trees, and more generally for graphs of bounded tree-width.
$\lambda$ there are bounded-degree trees where optimal mixing does not hold. Recent work of Eppstein and Frishberg (2022) proved a polynomial mixing time bound for the Glauber dynamics for arbitrary trees, and more generally for graphs of bounded tree-width.
We establish an optimal bound on the relaxation time (i.e., inverse spectral gap) of 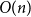 $O(n)$ for the Glauber dynamics for unweighted independent sets on arbitrary trees. We stress that our results hold for arbitrary trees and there is no dependence on the maximum degree
$O(n)$ for the Glauber dynamics for unweighted independent sets on arbitrary trees. We stress that our results hold for arbitrary trees and there is no dependence on the maximum degree 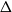 $\Delta$. Interestingly, our results extend (far) beyond the uniqueness threshold which is on the order
$\Delta$. Interestingly, our results extend (far) beyond the uniqueness threshold which is on the order 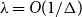 $\lambda =O(1/\Delta )$. Our proof approach is inspired by recent work on spectral independence. In fact, we prove that spectral independence holds with a constant independent of the maximum degree for any tree, but this does not imply mixing for general trees as the optimal mixing results of Chen, Liu, and Vigoda (2021) only apply for bounded-degree graphs. We instead utilize the combinatorial nature of independent sets to directly prove approximate tensorization of variance via a non-trivial inductive proof.
$\lambda =O(1/\Delta )$. Our proof approach is inspired by recent work on spectral independence. In fact, we prove that spectral independence holds with a constant independent of the maximum degree for any tree, but this does not imply mixing for general trees as the optimal mixing results of Chen, Liu, and Vigoda (2021) only apply for bounded-degree graphs. We instead utilize the combinatorial nature of independent sets to directly prove approximate tensorization of variance via a non-trivial inductive proof.
Charilaos Efthymiou: Research supported in part by EPSRC NIA, grant EP/V050842/1, and Centre of Discrete Mathematics and Applications (DIMAP). Daniel Stefankovic: Research supported in part by NSF grant CCF-1563757. Eric Vigoda: Research supported in part by NSF grant CCF-2147094.