Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T12:47:04.452Z Has data issue: false hasContentIssue false
  • English
  • Français

On the smallest singular value of symmetric random matrices

Part of: Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  05 November 2021

Vishesh Jain ,
Ashwin Sah  and
Mehtaab Sawhney
Vishesh Jain*
Affiliation:
Department of Statistics, Stanford University, Stanford, CA 94305, USA
Ashwin Sah
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Mehtaab Sawhney
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for an 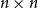$n\times n$ random symmetric matrix 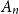$A_n$ , whose entries on and above the diagonal are independent copies of a sub-Gaussian random variable 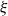$\xi$ with mean 0 and variance 1,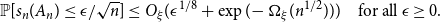

\begin{equation*}\mathbb{P}[s_n(A_n) \le \epsilon/\sqrt{n}] \le O_{\xi}(\epsilon^{1/8} + \exp(\!-\Omega_{\xi}(n^{1/2}))) \quad \text{for all } \epsilon \ge 0.\end{equation*}
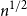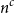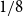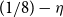This improves a result of Vershynin, who obtained such a bound with $n^{1/2}$ replaced by $n^{c}$ for a small constant c, and $1/8$ replaced by $(1/8) - \eta$ (with implicit constants also depending on 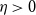$\eta > 0$ ). Furthermore, when 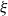$\xi$ is a Rademacher random variable, we prove that
\begin{equation*}\mathbb{P}[s_n(A_n) \le \epsilon/\sqrt{n}] \le O(\epsilon^{1/8} + \exp(\!-\Omega((\!\log{n})^{1/4}n^{1/2}))) \quad \text{for all } \epsilon \ge 0.\end{equation*}
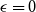The special case $\epsilon = 0$ improves a recent result of Campos, Mattos, Morris, and Morrison, which showed that 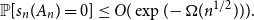$\mathbb{P}[s_n(A_n) = 0] \le O(\exp(\!-\Omega(n^{1/2}))).$ Notably, in a departure from the previous two best bounds on the probability of singularity of symmetric matrices, which had relied on somewhat specialized and involved combinatorial techniques, our methods fall squarely within the broad geometric framework pioneered by Rudelson and Vershynin, and suggest the possibility of a principled geometric approach to the study of the singular spectrum of symmetric random matrices. The main innovations in our work are new notions of arithmetic structure – the Median Regularized Least Common Denominator (MRLCD) and the Median Threshold, which are natural refinements of the Regularized Least Common Denominator (RLCD)introduced by Vershynin, and should be more generally useful in contexts where one needs to combine anticoncentration information of different parts of a vector.

Keywords

random matrix theoryleast singular valuerandom symmetric matrices

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 4 , July 2022 , pp. 662 - 683
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balogh, J., Morris, R. and Samotij, W. (2018) The method of hypergraph containers. In Proceedings of the International Congress of Mathematicians—Rio de Janeiro 2018, Vol. IV of Invited Lectures, World Scientific Publishing, Hackensack, NJ, pp. 3059–3092.Google Scholar
Bourgain, J., Vu, V. H. and Wood, P. M. (2010) On the singularity probability of discrete random matrices. J. Funct. Anal. 258 559–603.CrossRefGoogle Scholar
Campos, M., Jenssen, M., Michelen, M. and Sahasrabudhe, J. Singularity of random symmetric matrices revisited. arXiv:2011.03013.Google Scholar
Campos, M., Jenssen, M., Michelen, M. and Sahasrabudhe, J. The singularity probability of a random symmetric matrix is exponentially small. arXiv:2105.11384.Google Scholar
Campos, M., Mattos, L., Morris, R. and Morrison, N. (2021) On the singularity of random symmetric matrices. Duke Math. J. 170(5) 881–907.CrossRefGoogle Scholar
Costello, K. P., Tao, T. and Vu, V. (2006) Random symmetric matrices are almost surely nonsingular. Duke Math. J. 135 395–413.CrossRefGoogle Scholar
Erdös, P. (1945) On a lemma of Littlewood and Offord. Bull. Am. Math. Soc. 51 898–902.CrossRefGoogle Scholar
Ferber, A. Singularity of random symmetric matrices–simple proof. arXiv:2006.07439.Google Scholar
Ferber, A. and Jain, V. (2019) Singularity of random symmetric matrices–a combinatorial approach to improved bounds. In Forum of Mathematics, Sigma, Vol. 7, Cambridge University Press.CrossRefGoogle Scholar
Ferber, A., Jain, V., Luh, K. and Samotij, W. On the counting problem in inverse Littlewood–Offord theory. arXiv:1904.10425.Google Scholar
Jain, V., Sah, A. and Sawhney, M. Singularity of discrete random matrices II. arXiv:2010.06554.Google Scholar
Jain, V., Sah, A. and Sawhney, M. The smallest singular value of dense random regular digraphs. arXiv:2008.04755.Google Scholar
Kahn, J., Komlós, J. and Szemerédi, E. (1995) On the probability that a random $\pm$ 1-matrix is singular. J. Am. Math. Soc. 8 223–240.Google Scholar
Komlós, J. (1967) On determinant of (0, 1) matrices. Studia Science Mathematics Hungarica 27–21.Google Scholar
Livshyts, G. V. The smallest singular value of heavy-tailed not necessarily iid random matrices via random rounding. arXiv:1811.07038.Google Scholar
Livshyts, G. V., Tikhomirov, K. and Vershynin, R. The smallest singular value of inhomogeneous square random matrices. arXiv:1909.04219.Google Scholar
Lopatto, P. and Luh, K. Tail bounds for gaps between eigenvalues of sparse random matrices. arXiv:1901.05948.Google Scholar
Luh, K. and Vu, V. Sparse random matrices have simple spectrum. arXiv:1802.03662.Google Scholar
Mirošnikov, A. L. and Rogozin, B. A. (1980) Inequalities for concentration functions. Teor. Veroyatnost. i Primenen. 25 178–183.Google Scholar
Nguyen, H., Tao, T. and Vu, V. (2017) Random matrices: tail bounds for gaps between eigenvalues. Prob. Theory Related Fields 167 777–816.CrossRefGoogle Scholar
Nguyen, H. H. (2012) Inverse Littlewood-Offord problems and the singularity of random symmetric matrices. Duke Math. J. 161 545–586.CrossRefGoogle Scholar
Nguyen, H. H. (2012) On the least singular value of random symmetric matrices. Electron. J. Probab. 17(53) 19.CrossRefGoogle Scholar
O’Rourke, S. and Touri, B. (2016) On a conjecture of Godsil concerning controllable random graphs. SIAM J. Control Opt. 54 3347–3378.CrossRefGoogle Scholar
Rogozin, B. A. (1961) On the increase of dispersion of sums of independent random variables. Teor. Verojatnost. i Primenen 6 106–108.Google Scholar
Rudelson, M. Recent developments in non-asymptotic theory of random matrices. In Modern Aspects of Random Matrix Theory, Proceedings of Symposia in Applied Mathematics, Vol. 72 of American Mathematical Society, Providence, RI, 2014, pp. 83–120.CrossRefGoogle Scholar
Rudelson, M. and Vershynin, R. (2008) The Littlewood–Offord problem and invertibility of random matrices. Adv. Math. 218 600–633.CrossRefGoogle Scholar
Tao, T. and Vu, V. (2006) On random $\pm$ 1 matrices: singularity and determinant. Random Struct. Algorithms 28 1–23.CrossRefGoogle Scholar
Tao, T. and Vu, V. H. (2007) On the singularity probability of random Bernoulli matrices. J. Am. Math. Soc. 20 603–628.CrossRefGoogle Scholar
Tikhomirov, K. (2020) Singularity of random Bernoulli matrices. Ann. Math. (2) 191 593–634.CrossRefGoogle Scholar
Vershynin, R. (2014) Invertibility of symmetric random matrices, Random Struct. Algorithms 44 135–182.CrossRefGoogle Scholar
Wei, F. Investigate invertibility of sparse symmetric matrix. arXiv:1712.04341.Google Scholar