Article contents
On the peel number and the leaf-height of Galton–Watson trees
Published online by Cambridge University Press: 09 June 2022
Abstract
We study several parameters of a random Bienaymé–Galton–Watson tree
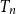 $T_n$
of size
$T_n$
of size
 $n$
defined in terms of an offspring distribution
$n$
defined in terms of an offspring distribution
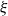 $\xi$
with mean
$\xi$
with mean
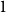 $1$
and nonzero finite variance
$1$
and nonzero finite variance
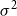 $\sigma ^2$
. Let
$\sigma ^2$
. Let
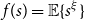 $f(s)=\mathbb{E}\{s^\xi \}$
be the generating function of the random variable
$f(s)=\mathbb{E}\{s^\xi \}$
be the generating function of the random variable
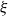 $\xi$
. We show that the independence number is in probability asymptotic to
$\xi$
. We show that the independence number is in probability asymptotic to
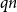 $qn$
, where
$qn$
, where
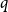 $q$
is the unique solution to
$q$
is the unique solution to
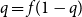 $q = f(1-q)$
. One of the many algorithms for finding the largest independent set of nodes uses a notion of repeated peeling away of all leaves and their parents. The number of rounds of peeling is shown to be in probability asymptotic to
$q = f(1-q)$
. One of the many algorithms for finding the largest independent set of nodes uses a notion of repeated peeling away of all leaves and their parents. The number of rounds of peeling is shown to be in probability asymptotic to
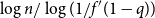 $\log n/\log (1/f'(1-q))$
. Finally, we study a related parameter which we call the leaf-height. Also sometimes called the protection number, this is the maximal shortest path length between any node and a leaf in its subtree. If
$\log n/\log (1/f'(1-q))$
. Finally, we study a related parameter which we call the leaf-height. Also sometimes called the protection number, this is the maximal shortest path length between any node and a leaf in its subtree. If
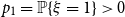 $p_1 = \mathbb{P}\{\xi =1\}\gt 0$
, then we show that the maximum leaf-height over all nodes in
$p_1 = \mathbb{P}\{\xi =1\}\gt 0$
, then we show that the maximum leaf-height over all nodes in
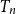 $T_n$
is in probability asymptotic to
$T_n$
is in probability asymptotic to
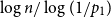 $\log n/\log (1/p_1)$
. If
$\log n/\log (1/p_1)$
. If
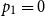 $p_1 = 0$
and
$p_1 = 0$
and
 $\kappa$
is the first integer
$\kappa$
is the first integer
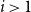 $i\gt 1$
with
$i\gt 1$
with
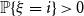 $\mathbb{P}\{\xi =i\}\gt 0$
, then the leaf-height is in probability asymptotic to
$\mathbb{P}\{\xi =i\}\gt 0$
, then the leaf-height is in probability asymptotic to
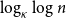 $\log _\kappa \log n$
.
$\log _\kappa \log n$
.
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 1
- Cited by



