Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T07:57:06.988Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Tetrahedra with Minimum, Unit, and Distinct Volumes in Three-Space

Published online by Cambridge University Press:  01 March 2008

ADRIAN DUMITRESCU  and
CSABA D. TÓTH
ADRIAN DUMITRESCU
Affiliation:
Department of Computer Science, University of Wisconsin–Milwaukee, WI 53201-0784, USA (e-mail: [email protected])
CSABA D. TÓTH
Affiliation:
Department of Mathematics, University of Calgary, AB, CanadaT2N 1N4 (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We formulate and give partial answers to several combinatorial problems on volumes of simplices determined by n points in 3-space, and in general in d dimensions.

  1. (i) The number of tetrahedra of minimum (non-zero) volume spanned by n points in 3 is at most 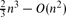, and there are point sets for which this number is 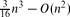. We also present an O(n3) time algorithm for reporting all tetrahedra of minimum non-zero volume, and thereby extend an algorithm of Edelsbrunner, O'Rourke and Seidel. In general, for every 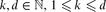, the maximum number of k-dimensional simplices of minimum (non-zero) volume spanned by n points in d is Θ(nk).

  2. (ii) The number of unit volume tetrahedra determined by n points in 3 is O(n7/2), and there are point sets for which this number is Ω(n3 log logn).

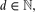  3. (iii) For every , the minimum number of distinct volumes of all full-dimensional simplices determined by n points in d, not all on a hyperplane, is Θ(n).

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 2 , March 2008 , pp. 203 - 224
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Agarwal, P. K. and Sharir, M. (2000) Arrangements and their applications. In Handbook of Computational Geometry (Sack, J.-R. and Urrutia, J., eds.), Chapter 2, Elsevier, pp. 49–119.CrossRefGoogle Scholar
[2]Anagnostou, E., Guibas, L. J. and Polimenis, V. G. (1990) Topological sweeping in three dimensions. In Proc. SIGAL Internat. Sympos. on Algorithms, Vol. 450 of Lecture Notes in Computer Science, Springer, pp. 310–317.CrossRefGoogle Scholar
[3]Apfelbaum, R. and Sharir, M. (2005) Repeated angles in three and four dimensions. SIAM J. Discrete Math. 19 294–300.CrossRefGoogle Scholar
[4]Aronov, B., Koltun, V. and Sharir, M. (2005) Incidences between points and circles in three and higher dimensions. Discrete Comput. Geom. 33 185–206.CrossRefGoogle Scholar
[5]Aronov, B., Pach, J., Sharir, M. and Tardos, G. (2004) Distinct distances in three and higher dimensions. Combin. Probab. Comput. 13 283–293.CrossRefGoogle Scholar
[6]Beck, J. (1983) On the lattice property of the plane and some problems of Dirac, Motzkin and Erdős in combinatorial geometry. Combinatorica 3 281–297.CrossRefGoogle Scholar
[7]Braß, P. and Knauer, C. (2003) On counting point–hyperplane incidences. Comput. Geom. 25 13–20.CrossRefGoogle Scholar
[8]Braß, P., Moser, W. and Pach, J. (2005) Research Problems in Discrete Geometry, Springer, New York.Google Scholar
[9]Braß, P., Rote, G. and Swanepoel, K. J. (2001) Triangles of extremal area or perimeter in a finite planar point set. Discrete Comput. Geom. 26 51–58.CrossRefGoogle Scholar
[10]Burton, G. R. and Purdy, G. (1979) The directions determined by n points in the plane. J. London Math. Soc. 20 109–114.CrossRefGoogle Scholar
[11]Chazelle, B., Guibas, L. and Lee, D. T. (1985) The power of geometric duality. BIT 25 76–90.CrossRefGoogle Scholar
[12]Clarkson, K. L., Edelsbrunner, H., Guibas, L. G., Sharir, M. and Welzl, E. (1990) Combinatorial complexity bounds for arrangements of curves and spheres. Discrete Comput. Geom. 5 99–160.CrossRefGoogle Scholar
[13]Croft, H. T., Falconer, K. J. and Guy, R. K. (1991) Unsolved Problems in Geometry, Springer, New York.CrossRefGoogle Scholar
[14]Dumitrescu, A. and Tóth, C. D. (2007) Distinct triangle areas in a planar point set. In Proc. 12th Conf. on Integer Programming and Optimization, Vol. 4513 of Lecture Notes in Computer Science, Springer, pp. 119–129.CrossRefGoogle Scholar
[15]Dumitrescu, A., Sharir, M. and Tóth, C. D. (2007) Extremal problems on triangle areas in two and three dimensions. Manuscript.CrossRefGoogle Scholar
[16]Edelsbrunner, H. (1987) Algorithms in Combinatorial Geometry, Springer, Heidelberg.CrossRefGoogle Scholar
[17]Edelsbrunner, H. and Guibas, L. J. (1989) Topologically sweeping an arrangement. J. Comput. Syst. Sci. 38 165–194. Corrigendum: Topologically sweeping an arrangement, J. Comput. Syst. Sci. 42 249–251 (1991).CrossRefGoogle Scholar
[18]Edelsbrunner, H., O'Rourke, J. and Seidel, R. (1986) Constructing arrangements of lines and hyperplanes with applications. SIAM J. Comput. 15 341–363.CrossRefGoogle Scholar
[19]Edelsbrunner, H., Seidel, R. and Sharir, M. (1993) On the zone theorem for hyperplane arrangements. SIAM J. Comput. 22 418–429.CrossRefGoogle Scholar
[20]Elekes, G. and Tóth, C. D. (2005) Incidences of not-too-degenerate hyperplanes. In Proc. 21st ACM Sympos. Comput. Geom., ACM Press, pp. 16–21.CrossRefGoogle Scholar
[21]Erdős, P. (1946) On sets of distances of n points. Amer. Math. Monthly 53 248–250.CrossRefGoogle Scholar
[22]Erdős, P. and Purdy, G. (1995) Extremal problems in combinatorial geometry. In Handbook of Combinatorics, Vol. 1, Elsevier, Amsterdam, pp. 809–874.Google Scholar
[23]Erdős, P. and Purdy, G. (1971) Some extremal problems in geometry. J. Combin. Theory 10 246–252.CrossRefGoogle Scholar
[24]Erdős, P. and Purdy, G. (1976) Some extremal problems in geometry IV. Congressus Numerantium 17 (Proc. 7th South-Eastern Conf. on Combinatorics, Graph Theory, and Computing) 307–322.Google Scholar
[25]Erdős, P., Purdy, G. and Straus, E. G. (1982) On a problem in combinatorial geometry. Discrete Math. 40 45–52.CrossRefGoogle Scholar
[26]Feldman, S. and Sharir, M. (2005) An improved bound for joints in arrangements of lines in space. Discrete Comput. Geom. 33 307–320.CrossRefGoogle Scholar
[27]Iosevich, A., Konyagin, S., Rudnev, M. and Ten, V. (2006) Combinatorial complexity of convex sequences. Discrete Comput. Geom. 35 143–158.CrossRefGoogle Scholar
[28]Katz, N. H. and Tardos, G. (2004) A new entropy inequality for the Erdős distance problem. In Towards a Theory of Geometric Graphs, Vol. 342 of Contemp. Math., AMS, Providence, RI, pp. 119–126.CrossRefGoogle Scholar
[29]Pach, J., Pinchasi, R. and Sharir, M. (2004) On the number of directions determined by a three-dimensional points set. J. Combin. Theory Ser. A 108 1–16.CrossRefGoogle Scholar
[30]Pach, J., Radoičić, R., Tardos, G. and Tóth, G. (2006) Improving the Crossing Lemma by finding more crossings in sparse graphs. Discrete Comput. Geom. 36 527–552.CrossRefGoogle Scholar
[31]Pach, J. and Sharir, M. (1992) Repeated angles in the plane and related problems. J. Combin. Theory Ser. A 59 12–22.CrossRefGoogle Scholar
[32]Pach, J. and Sharir, M. (2004) Geometric incidences. In Towards a Theory of Geometric Graphs, Vol. 342 of Contemp. Math., AMS, Providence, RI, pp. 185–223.CrossRefGoogle Scholar
[33]Pinchasi, R. The minimum number of distinct areas of triangles determined by a set of n points in the plane. SIAM J. Discrete Math., to appear.Google Scholar
[34]Sharir, M. and Welzl, E. (2004) Point–line incidences in space. Combin. Probab. Comput. 13 203–220.CrossRefGoogle Scholar
[35]Straus, E. G. (1978) Some extremal problems in combinatorial geometry. In Proc. Conf. Combinatorial Theory, Vol. 686 of Lecture Notes in Mathematics, Springer, pp. 308–312.CrossRefGoogle Scholar
[36]Szemerédi, E. and Trotter, W. T. (1983) Extremal problems in discrete geometry. Combinatorica 3 381–392.CrossRefGoogle Scholar