Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T23:44:23.369Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Lower Tail Variational Problem for Random Graphs

Part of: Graph theory Limit theorems

Published online by Cambridge University Press:  16 August 2016

YUFEI ZHAO
YUFEI ZHAO*
Affiliation:
Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

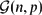We study the lower tail large deviation problem for subgraph counts in a random graph. Let XH denote the number of copies of H in an Erdős–Rényi random graph $\mathcal{G}(n,p)$. We are interested in estimating the lower tail probability 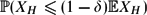$\mathbb{P}(X_H \le (1-\delta) \mathbb{E} X_H)$ for fixed 0 < δ < 1.

Thanks to the results of Chatterjee, Dembo and Varadhan, this large deviation problem has been reduced to a natural variational problem over graphons, at least for p ≥ n−αH (and conjecturally for a larger range of p). We study this variational problem and provide a partial characterization of the so-called ‘replica symmetric’ phase. Informally, our main result says that for every H, and 0 < δ < δH for some δH > 0, as p → 0 slowly, the main contribution to the lower tail probability comes from Erdős–Rényi random graphs with a uniformly tilted edge density. On the other hand, this is false for non-bipartite H and δ close to 1.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C35: Extremal problems 60F10: Large deviations
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 2 , March 2017 , pp. 301 - 320
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Aristoff, D. and Radin, C. (2013) Emergent structures in large networks. J. Appl. Probab. 50 883–888.Google Scholar
[2] Aristoff, D. and Zhu, L. (2015) Asymptotic structure and singularities in constrained directed graphs. Stochastic Process. Appl. 125 4154–4177.Google Scholar
[3] Aristoff, D. and Zhu, L. On the phase transition curve in a directed exponential random graph model. arXiv:1404.6514 Google Scholar
[4] Borgs, C., Chayes, J. and Lovász, L. (2010) Moments of two-variable functions and the uniqueness of graph limits. Geom. Funct. Anal. 19 1597–1619.Google Scholar
[5] Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T. and Vesztergombi, K. (2008) Convergent sequences of dense graphs I: Subgraph frequencies, metric properties and testing. Adv. Math. 219 1801–1851.Google Scholar
[6] Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T. and Vesztergombi, K. (2012) Convergent sequences of dense graphs II: Multiway cuts and statistical physics. Ann. of Math. (2) 176 151–219.CrossRefGoogle Scholar
[7] Chatterjee, S. (2012) The missing log in large deviations for triangle counts. Random Struct. Alg. 40 437–451.Google Scholar
[8] Chatterjee, S. and Dembo, A. (2016) Nonlinear large deviations. Adv. Math. 299 396–450.Google Scholar
[9] Chatterjee, S. and Diaconis, P. (2013) Estimating and understanding exponential random graph models. Ann. Statist. 41 2428–2461.Google Scholar
[10] Chatterjee, S. and Varadhan, S. R. S. (2011) The large deviation principle for the Erdős–Rényi random graph. European J. Combin. 32 1000–1017.Google Scholar
[11] Conlon, D., Fox, J. and Sudakov, B. (2010) An approximate version of Sidorenko's conjecture. Geom. Funct. Anal. 20 1354–1366.Google Scholar
[12] Conlon, D., Fox, J. and Sudakov, B. (2015) Recent developments in graph Ramsey theory. In Surveys in Combinatorics, pp. 49–118.Google Scholar
[13] DeMarco, B. and Kahn, J. (2012) Upper tails for triangles. Random Struct. Alg. 40 452–459.Google Scholar
[14] Goodman, A. W. (1959 On sets of acquaintances and strangers at any party. Amer. Math. Monthly 66 778–783.Google Scholar
[15] Hatami, H. (2010) Graph norms and Sidorenko's conjecture. Israel J. Math. 175 125–150.Google Scholar
[16] Janson, S. (1990) Poisson approximation for large deviations. Random Struct. Alg. 1 221–229.Google Scholar
[17] Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley-Interscience.CrossRefGoogle Scholar
[18] Janson, S. and Warnke, L. (2016) The lower tail: Poisson approximation revisited. Random Struct. Alg. 48 219–246.Google Scholar
[19] Katona, G. (1968) A theorem of finite sets. In Theory of Graphs: Proc. Colloq. Tihany 1966, Academic Press, pp. 187–207.Google Scholar
[20] Kenyon, R., Radin, C., Ren, K. and Sadun, L. Multipodal structure and phase transitions in large constrained graphs. arXiv:1405.0599 Google Scholar
[21] Kenyon, R. and Yin, M. On the asymptotics of constrained exponential random graphs. arXiv:1406.3662 Google Scholar
[22] Kim, J., Lee, C. and Lee, J. (2016) Two approaches to Sidorenko's conjecture. Trans. Amer. Math. Soc. 368 5057–5074.CrossRefGoogle Scholar
[23] Kruskal, J. B. (1963) The number of simplices in a complex. In Mathematical Optimization Techniques (Bellman, R., ed.), University of California Press, pp. 251–278.Google Scholar
[24] Li, J. L. X. and Szegedy, B. On the logarithmic calculus and Sidorenko's conjecture. Combinatorica, to appear.Google Scholar
[25] Lovász, L. (2012) Large Networks and Graph Limits, Vol. 60 of American Mathematical Society Colloquium Publications, AMS.Google Scholar
[26] Lovász, L. and Szegedy, B. (2006) Limits of dense graph sequences. J. Combin. Theory Ser. B 96 933–957.Google Scholar
[27] Lovász, L. and Szegedy, B. (2007) Szemerédi's lemma for the analyst. Geom. Funct. Anal. 17 252–270.Google Scholar
[28] Lubetzky, E. and Zhao, Y. (2015) On replica symmetry of large deviations in random graphs. Random Struct. Alg. 47 109–146.Google Scholar
[29] Lubetzky, E. and Zhao, Y. On the variational problem for upper tails in sparse random graphs. Random Struct. Alg., to appearGoogle Scholar
[30] Nikiforov, V. (2011) The number of cliques in graphs of given order and size. Trans. Amer. Math. Soc. 363 1599–1618.Google Scholar
[31] Radin, C., Ren, K. and Sadun, L. (2014) The asymptotics of large constrained graphs. J. Phys. A 47 175001.Google Scholar
[32] Radin, C. and Sadun, L. (2013) Phase transitions in a complex network. J. Phys. A 46 305002.Google Scholar
[33] Radin, C. and Sadun, L. (2015) Singularities in the entropy of asymptotically large simple graphs. J. Statist. Phys. 158 853–865.Google Scholar
[34] Radin, C. and Yin, M. (2013) Phase transitions in exponential random graphs. Ann. Appl. Probab. 23 2458–2471.CrossRefGoogle Scholar
[35] Razborov, A. A. (2008) On the minimal density of triangles in graphs. Combin. Probab. Comput. 17 603–618.Google Scholar
[36] Reiher, C. The clique density theorem. Ann. Math., to appearGoogle Scholar
[37] Sidorenko, A. (1993) A correlation inequality for bipartite graphs. Graphs Combin. 9 201–204.Google Scholar
[38] Szegedy, B. An information theoretic approach to Sidorenko's conjecture. arXiv:1406.6738 Google Scholar
[39] Thomason, A. (1989) A disproof of a conjecture of Erdős in Ramsey theory. J. London Math. Soc. (2) 39 246–255.Google Scholar
[40] Yin, M. (2013) Critical phenomena in exponential random graphs. J. Statist. Phys. 153 1008–1021.Google Scholar
[41] Yin, M. (2015) Large deviations and exact asymptotics for constrained exponential random graphs. Electron. Commun. Probab. 20, 14 pp.Google Scholar
[42] Yin, M., Rinaldo, A. and Fadnavis, S. Asymptotic quantization of exponential random graphs. Ann. Appl. Probab., to appearGoogle Scholar
[43] Yin, M. and Zhu, L. Asymptotics for sparse exponential random graph models. Braz. J. Prob. Stat., to appearGoogle Scholar
[44] Yin, M. and Zhu, L. (2016) Reciprocity in directed networks. Phys. A 447 71–84.Google Scholar
[45] Zhu, L. Asymptotic structure of constrained exponential random graph models. arXiv:1408.1536 Google Scholar