Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tokushige, Norihide
2013.
The eigenvalue method for cross t-intersecting families.
Journal of Algebraic Combinatorics,
Vol. 38,
Issue. 3,
p.
653.
Liu, Jiuqiang
and
Yang, Wenbo
2014.
Set systems with restrictedk-wiseL-intersections modulo a prime number.
European Journal of Combinatorics,
Vol. 36,
Issue. ,
p.
707.
Ku, Cheng Yeaw
and
Wong, Kok Bin
2015.
Onr-crosst-intersecting families for weak compositions.
Discrete Mathematics,
Vol. 338,
Issue. 7,
p.
1090.
Ku, Cheng Yeaw
and
Wong, Kok Bin
2015.
AN ANALOGUE OF THE HILTON-MILNER THEOREM FOR WEAK COMPOSITIONS.
Bulletin of the Korean Mathematical Society,
Vol. 52,
Issue. 3,
p.
1007.
Frankl, Peter
and
Tokushige, Norihide
2016.
Invitation to intersection problems for finite sets.
Journal of Combinatorial Theory, Series A,
Vol. 144,
Issue. ,
p.
157.
Ku, Cheng Yeaw
and
Wong, Kok Bin
2016.
A non-trivial intersection theorem for permutations with fixed number of cycles.
Discrete Mathematics,
Vol. 339,
Issue. 2,
p.
646.
Frankl, Peter
Shinohara, Masashi
and
Tokushige, Norihide
2016.
Multiply union families in Nn.
European Journal of Combinatorics,
Vol. 58,
Issue. ,
p.
66.
MUBAYI, DHRUV
and
WANG, LUJIA
2018.
Multicolour Sunflowers.
Combinatorics, Probability and Computing,
Vol. 27,
Issue. 6,
p.
974.
Ku, Cheng Yeaw
and
Wong, Kok Bin
2020.
Erdős-Ko-Rado theorems for set partitions with certain block size.
Journal of Combinatorial Theory, Series A,
Vol. 172,
Issue. ,
p.
105180.
Keller, Nathan
and
Lifshitz, Noam
2021.
The junta method for hypergraphs and the Erdős-Chvátal simplex conjecture.
Advances in Mathematics,
Vol. 392,
Issue. ,
p.
107991.
Frankl, P.
2021.
On the arithmetic mean of the size of cross-union families.
Acta Mathematica Hungarica,
Vol. 164,
Issue. 1,
p.
312.
Frankl, Peter
2021.
Old and new applications of Katona’s circle.
European Journal of Combinatorics,
Vol. 95,
Issue. ,
p.
103339.
Frankl, Péter
2022.
On the size of the product of overlapping families.
Moscow Journal of Combinatorics and Number Theory,
Vol. 11,
Issue. 3,
p.
237.
Wu, Biao
2023.
A refined result on cross-intersecting families.
Discrete Applied Mathematics,
Vol. 339,
Issue. ,
p.
149.
Gupta, Pranshu
Mogge, Yannick
Piga, Simón
and
Schülke, Bjarne
2023.
r$r$‐Cross t$t$‐intersecting families via necessary intersection points.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 3,
p.
1447.
Cao, Mengyu
Lu, Mei
Lv, Benjian
and
Wang, Kaishun
2024.
Nearly extremal non-trivial crosst-intersecting families andr-wiset-intersecting families.
European Journal of Combinatorics,
Vol. 120,
Issue. ,
p.
103958.
Ku, Cheng Yeaw
and
Wong, Kok Bin
2025.
Diversity and intersecting theorems for weak compositions.
Discrete Mathematics,
Vol. 348,
Issue. 2,
p.
114250.


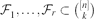 . Suppose that
. Suppose that 
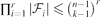 .
.