Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-18T01:55:03.097Z Has data issue: false hasContentIssue false
  • English
  • Français

On random walks and switched random walks on homogeneous spaces

Part of: Markov processes Algebraic combinatorics

Published online by Cambridge University Press:  28 November 2022

Elvira Moreno Open the ORCID record for Elvira Moreno [Opens in a new window]  and
Mauricio Velasco Open the ORCID record for Mauricio Velasco [Opens in a new window]
Elvira Moreno
Affiliation:
Computing and Mathematical Sciences, California Institute of Technology, Department of Computing and Mathematical Sciences, 1200 E. California Blvd., MC 305-16, Pasadena, CA 91125-2100, USA
Mauricio Velasco*
Affiliation:
Departamento DE Matemáticas, Universidad de los Andes, Carrera 1 No. 18a 10, Edificio H, Primer Piso, 111711 Bogotá, Colombia
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove new mixing rate estimates for the random walks on homogeneous spaces determined by a probability distribution on a finite group 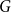$G$ . We introduce the switched random walk determined by a finite set of probability distributions on 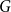$G$ , prove that its long-term behaviour is determined by the Fourier joint spectral radius of the distributions, and give Hermitian sum-of-squares algorithms for the effective estimation of this quantity.

Keywords

Mixing ratesRandom walksSwitched random walksJoint spectral radiusHermitian polynomial norms

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 05E10: Combinatorial aspects of representation theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 3 , May 2023 , pp. 398 - 421
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmadi, A. A. and Jungers, R. M. (2016) Lower bounds on complexity of Lyapunov functions for switched linear systems. Nonlinear Anal. Hybrid Syst. 21 118–129. DOI 10.1016/j.nahs.2016.01.003.CrossRefGoogle Scholar
Jungers, R. M., Ahmadi, A. A., Parrilo, P. A. and Roozbehani, M. (2017) A characterization of Lyapunov inequalities for stability of switched systems. IEEE Trans. Automat. Control 62(6) 3062–3067. DOI 10.1109/TAC.2017.2671345.Google Scholar
Diaconis, P. (1988) Group Representations in Probability and Statistics. Institute of Mathematical Statistics, Hayward, CA, Institute of Mathematical Statistics Lecture Notes—Monograph Series, 11,Google Scholar
Boyd, S., Diaconis, P., Parrilo, P. and Xiao, L. (2009) Fastest mixing Markov chain on graphs with symmetries. SIAM J. Optim. 20(2) 792–819. DOI 10.1137/070689413.CrossRefGoogle Scholar
Boyd, S., Diaconis, P. and Xiao, L. (2004) Fastest mixing Markov chain on a graph. SIAM Rev. 46(4) 667–689. DOI 10.1137/S0036144503423264.CrossRefGoogle Scholar
Blekherman, G., Parrilo, P. A. and Thomas, R. R. (2013) Semidefinite Optimization and Convex Algebraic Geometry. Society for Industrial and Applied Mathematics (SIAM), Mathematical Optimization Society, Philadelphia, PA, MOS-SIAM Series on Optimization, 13,Google Scholar
Blondel, V. D. and Tsitsiklis, J. N. (2000) The boundedness of all products of a pair of matrices is undecidable. Syst. Control Lett. 41(2) 135–140. DOI 10.1016/S0167-6911(00)00049-9.CrossRefGoogle Scholar
Ahmadi, A. A., de Klerk, E. and Hall, G. (2019) Polynomial norms. SIAM J. Optim. 29(1) 399–422. DOI 10.1137/18M1172843.CrossRefGoogle Scholar
Curto, R. E. and Fialkow, L. A. (2002) A duality proof of Tchakaloff’s theorem. J. Math. Anal. Appl. 269(2) 519–532. DOI 10.1016/S0022-247X(02)00034-3.CrossRefGoogle Scholar
Diaconis, P. and Shahshahani, M. (1981) Generating a random permutation with random transpositions. Z Wahrsch. Verw. Gebiete 57(2) 159–179. DOI 10.1007/BF00535487.CrossRefGoogle Scholar
Fulton, W. and Harris, J. (1991) Representation Theory, Graduate Texts in Mathematics. Springer-Verlag, New York, A first course; Readings in Mathematics, 129,Google Scholar
Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Am. Statist. Assoc. 58 13–30.CrossRefGoogle Scholar
Parrilo, P. A. and Jadbabaie, A. (2008) Approximation of the joint spectral radius using sum of squares. Linear Algebra Appl. 428(10) 2385–2402. DOI 10.1016/j.laa.2007.12.027.CrossRefGoogle Scholar
Breuillard, E. On the joint spectral radius, ArXiv preprint, posted on March 2021, https://arxiv.org/abs/2103.09089 Google Scholar
Madras, N. (2002). Lectures on Monte Carlo Methods. American Mathematical Society, Providence, RI, Fields Institute Monographs, 16,Google Scholar
Bernstein, M. (2018) A random walk on the symmetric group generated by random involutions. Electron. J. Probab. 23 PaperNo. 26, 28. DOI 10.1214/18-EJP140.CrossRefGoogle Scholar
Bernstein, M. and Nestoridi, E. (2019) Cutoff for random to random card shuffle. Ann. Probab. 47(5) 3303–3320. DOI 10.1214/19-AOP1340.CrossRefGoogle Scholar
Goldberg, M. and Zwas, G. (1974) On matrices having equal spectral radius and spectral norm. Linear Algebra Appl. 8(5) 427–434. DOI 10.1016/0024-3795(74)90076-7.CrossRefGoogle Scholar
Rota, G.-C. and Strang, G. (1960) A note on the joint spectral radius. Nederl. Akad. Wetensch. Proc. Ser. A 63 = Indag. Math. 22 379–381, 1960.CrossRefGoogle Scholar
Boyd, S., Diaconis, P. and Xiao, L. (2004) Fastest mixing Markov chain on a graph. SIAM Rev. 46(4) 667–689. DOI 10.1137/S0036144503423264.CrossRefGoogle Scholar
Sagan, B. E. (2001) . The Symmetric Group: Representations, Combinatorial Algorithms, and Symmetric Functions. Springer-Verlag, New York, Graduate Texts in Mathematics, 203, 2nd,CrossRefGoogle Scholar