Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-23T09:13:57.520Z Has data issue: false hasContentIssue false
  • English
  • Français

On minimum spanning trees for random Euclidean bipartite graphs

Part of: Graph theory Geometric probability and stochastic geometry Limit theorems Stochastic processes

Published online by Cambridge University Press:  30 November 2023

Mario Correddu  and
Dario Trevisan
Mario Correddu*
Affiliation:
Dipartimento di Matematica, Università di Pisa, Pisa, Italy
Dario Trevisan
Affiliation:
Dipartimento di Matematica, Università di Pisa, Pisa, Italy
*
Corresponding author: Mario Correddu; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the minimum spanning tree problem on a weighted complete bipartite graph 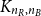$K_{n_R, n_B}$ whose 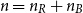$n=n_R+n_B$ vertices are random, i.i.d. uniformly distributed points in the unit cube in 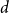$d$ dimensions and edge weights are the 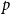$p$-th power of their Euclidean distance, with 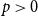$p\gt 0$. In the large $n$ limit with 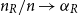$n_R/n \to \alpha _R$ and 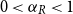$0\lt \alpha _R\lt 1$, we show that the maximum vertex degree of the tree grows logarithmically, in contrast with the classical, non-bipartite, case, where a uniform bound holds depending on 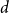$d$ only. Despite this difference, for 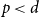$p\lt d$, we are able to prove that the total edge costs normalized by the rate 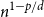$n^{1-p/d}$ converge to a limiting constant that can be represented as a series of integrals, thus extending a classical result of Avram and Bertsimas to the bipartite case and confirming a conjecture of Riva, Caracciolo and Malatesta.

Keywords

Euclidean functionalsminimum spanning treegeometric probability

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry 05C05: Trees
Secondary: 60G55: Point processes 60F25: $L^p$-limit theorems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 3 , May 2024 , pp. 319 - 350
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avram, F. and Bertsimas, D. ( 1992) The minimum spanning tree constant in geometrical probability and under the independent model: a unified approach. Ann. Appl. Probab. 2(1) 113–130. DOI: 10.1214/aoap/1177005773.CrossRefGoogle Scholar
Ajtai, M., Komlós, J. and Tusnády, c. (1984) On optimal matchings. Combinatorica 4(4) 259–264. DOI: 10.1007/BF02579135.CrossRefGoogle Scholar
Aldous, D. and Steele, J. M. (1992) Asymptotics for Euclidean minimal spanning trees on random points. Probab. Theory Relat. Fields 92(2) 247–258. DOI: 10.1007/BF01194923.CrossRefGoogle Scholar
Asano, T., Bhattacharya, B., Keil, M. and Yao, F. (1988) Clustering algorithms based on minimum and maximum spanning trees. In: Proceedings of the Fourth Annual Symposium on Computational Geometry. SCG ’88, Association for Computing Machinery, pp. 252–257. DOI: 10.1145/73393.73419.CrossRefGoogle Scholar
Ambrosio, L., Stra, F. andTrevisan, D. (2019) A PDE approach to a 2-dimensional matching problem. Probab. Theory Relat. Fields 173(1-2) 433–477. DOI: 10.1007/s00440-018-0837-x.CrossRefGoogle Scholar
Barthe, F. and Bordenave, C. (2013) Combinatorial optimization over two random point sets. In Séminaire de Probabilités XLV (Donati-Martin, C., Lejay, A. and Rouault, A., eds.), Springer International Publishing, pp. 483–535. DOI: 10.1007/978-3-319-00321-4_19.CrossRefGoogle Scholar
Burkholder, D. L. and Gundy, R. F. (1970) Extrapolation and interpolation of quasilinear operators on martingales. Acta Math. 124 249–304. DOI: 10.1007/BF02394573.CrossRefGoogle Scholar
Beardwood, J., Halton, J. H. and Hammersley, J. M. (1959) The shortest path through many points. Math. Proc. Camb. Philos. Soc. 55(4) 299–327. DOI: 10.1017/S0305004100034095.CrossRefGoogle Scholar
Capelli, R., Caracciolo, S., Di Gioacchino, A. and Malatesta, E. M. (2018) Exact value for the average optimal cost of the bipartite traveling salesman and two-factor problems in two dimensions. Phys. Rev. E 98(3) 030101. DOI: 10.1103/PhysRevE.98.030101.CrossRefGoogle Scholar
Caracciolo, S., Lucibello, C., Parisi, G. and Sicuro, G. (2014) Scaling hypothesis for the Euclidean bipartite matching problem. Phys. Rev. E 90(1) 012118. DOI: 10.1103/PhysRevE.90.012118.CrossRefGoogle ScholarPubMed
Caracciolo, S., Di Gioacchino, A., Gherardi, M. and Malatesta, E. M. (2018) Solution for a bipartite Euclidean traveling-salesman problem in one dimensio. Phys. Rev. E 97(5) 052109. DOI: 10.1103/PhysRevE.97.052109.CrossRefGoogle Scholar
Chazelle, B. (2000) A minimum spanning tree algorithm with inverse-Ackermann type complexity. J. ACM 47(6) 1028–1047.CrossRefGoogle Scholar
Christofides, N. (1976) Worst-case analysis of a new heuristic for the travelling salesman problem. Tech. rep. Carnegie-Mellon Univ Pittsburgh Pa Management Sciences Research Group.Google Scholar
Chatterjee, S. and Sen, S. (2017) Minimal spanning trees and Stein’s method. Ann. Appl. Probab. 27(3) 1588–1645. DOI: 10.1214/16-AAP1239.CrossRefGoogle Scholar
Frieze, A. M. and McDiarmid, C. J. H. (1989) On random minimum length spanning trees. Combinatorica 9(4) 363–374. DOI: 10.1007/BF02125348.CrossRefGoogle Scholar
Frieze, A. M. (1985) On the value of a random minimum spanning tree problem. Discrete Appl. Math. 10(1) 47–56. DOI: 10.1016/0166-218X(85)90058-7.CrossRefGoogle Scholar
Graham, R. L. and Hell, P. (1985) On the history of the minimum spanning tree problem. IEEE Ann. Hist. Comput. 7(1) 43–57. DOI: 10.1109/MAHC.1985.10011.CrossRefGoogle Scholar
Karger, D. R., Klein, P. N. and Tarjan, R. E. (1995) A randomized lineartime algorithm to find minimum spanning trees. J. ACM 42(2) 321–328. DOI: 10.1145/201019.201022.CrossRefGoogle Scholar
Kesten, H. and Lee, S. (1996) The central limit theorem for weighted minimal spanning trees on random points. Ann. Appl. Probab. 6(2) 495–527. DOI: 10.1214/aoap/1034968141.CrossRefGoogle Scholar
Kou, L., Markowsky, G. and Berman, L. (1981) A fast algorithm for Steiner trees. Acta Inform. 15(2) 141–145. DOI: 10.1007/BF00288961.CrossRefGoogle Scholar
Ledoux, M. (2001) The Concentration of Measure Phenomenon, Vol. 89, American Mathematical Society.Google Scholar
McDiarmid, C. (1989) On the method of bounded differences. In Surveys in Combinatorics, 1989 (Norwich, 1989), Vol. 141 of London Math. Soc. Lecture Note Ser., Cambridge Univ. Press, pp. 148–188.Google Scholar
Milne, S. C. (1980) Peano curves and smoothness of functions. Adv. Math. 35(2) 129–157.CrossRefGoogle Scholar
Penrose, M. D. (1996) The random minimal spanning tree in high dimensions. Ann. Probab. 24(4) 1903–1925. DOI: 10.1214/aop/1041903210.CrossRefGoogle Scholar
Riva, A., Caracciolo, S. and Malatesta, E. (2018-2019) The random Minimum Spanning Tree problem. https://pcteserver.mi.infn.it/~caraccio/Lauree/Riva.pdf.Google Scholar
Steele, J. M. (2002) Minimal spanning trees for graphs with random edge lengths. In Mathematics and Computer Science II, Trends in Mathematics (Chauvin, B., Flajolet, P., Gardy, D. and Mokkadem, A., eds.), Birkhäuser, pp. 223–245. DOI: 10.1007/978-3-0348-8211-8_14.Google Scholar
Steele, J. M. (1981) Subadditive Euclidean functionals and nonlinear growth in geometric probability. Ann. Probab. 9(3) 365–376. DOI: 10.1214/aop/1176994411.CrossRefGoogle Scholar
Steele, J. M. (1988) Growth rates of Euclidean minimal spanning trees with power weighted edges. Ann. Probab. 16(4), 1767–1787.CrossRefGoogle Scholar
Talagrand, M. (2014) Upper and Lower Bounds for Stochastic Processes: Modern Methods and Classical Problems, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge/ A Series of Modern Surveys in Mathematics, Springer-Verlag. DOI: 10.1007/978-3-642-54075-2.CrossRefGoogle Scholar
Talagrand, M. (1992) The Ajtai-Komlos-Tusnady matching theorem for general measures. In Probability in Banach Spaces, 8: Proceedings of the Eighth International Conference, Progress in Probability (R. M. Dudley, M. G. Hahn and J. Kuelbs, eds.), Birkhäuser, pp. 39–54. DOI: 10.1007/978-1-4612-0367-4_2.CrossRefGoogle Scholar
Yukich, J. E. (2000) Asymptotics for weighted minimal spanning trees on random points. Stochast. Process. Appl. 85(1) 123–138. DOI: 10.1016/S0304-4149(99)00068-X.CrossRefGoogle Scholar
Yukich, J. E. (1998) Probability Theory of Classical Euclidean Optimization Problems, Lecture Notes in Mathematics, Springer-Verlag. DOI: 10.1007/BFb0093472.CrossRefGoogle Scholar