No CrossRef data available.
Article contents
On mappings on the hypercube with small average stretch
Published online by Cambridge University Press: 18 October 2022
Abstract
Let
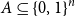 $A \subseteq \{0,1\}^n$
be a set of size
$A \subseteq \{0,1\}^n$
be a set of size
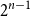 $2^{n-1}$
, and let
$2^{n-1}$
, and let
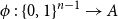 $\phi \,:\, \{0,1\}^{n-1} \to A$
be a bijection. We define the average stretch of
$\phi \,:\, \{0,1\}^{n-1} \to A$
be a bijection. We define the average stretch of
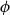 $\phi$
as
$\phi$
as
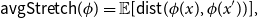 \begin{equation*} {\sf avgStretch}(\phi ) = {\mathbb E}[{{\sf dist}}(\phi (x),\phi (x'))], \end{equation*}
\begin{equation*} {\sf avgStretch}(\phi ) = {\mathbb E}[{{\sf dist}}(\phi (x),\phi (x'))], \end{equation*}
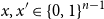 $x,x' \in \{0,1\}^{n-1}$
that differ in exactly one coordinate.
$x,x' \in \{0,1\}^{n-1}$
that differ in exactly one coordinate.
In this paper, we continue the line of research studying mappings on the discrete hypercube with small average stretch. We prove the following results.
For any set
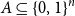 $A \subseteq \{0,1\}^n$
of density
$A \subseteq \{0,1\}^n$
of density
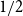 $1/2$
there exists a bijection
$1/2$
there exists a bijection
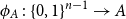 $\phi _A \,:\, \{0,1\}^{n-1} \to A$
such that
$\phi _A \,:\, \{0,1\}^{n-1} \to A$
such that
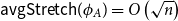 ${\sf avgStretch}(\phi _A) = O\left(\sqrt{n}\right)$
.
${\sf avgStretch}(\phi _A) = O\left(\sqrt{n}\right)$
.For
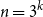 $n = 3^k$
let
$n = 3^k$
let
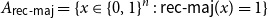 ${A_{\textsf{rec-maj}}} = \{x \in \{0,1\}^n \,:\,{\textsf{rec-maj}}(x) = 1\}$
, where
${A_{\textsf{rec-maj}}} = \{x \in \{0,1\}^n \,:\,{\textsf{rec-maj}}(x) = 1\}$
, where
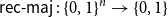 ${\textsf{rec-maj}} \,:\, \{0,1\}^n \to \{0,1\}$
is the function recursive majority of 3’s. There exists a bijection
${\textsf{rec-maj}} \,:\, \{0,1\}^n \to \{0,1\}$
is the function recursive majority of 3’s. There exists a bijection
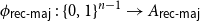 $\phi _{{\textsf{rec-maj}}} \,:\, \{0,1\}^{n-1} \to{A_{\textsf{rec-maj}}}$
such that
$\phi _{{\textsf{rec-maj}}} \,:\, \{0,1\}^{n-1} \to{A_{\textsf{rec-maj}}}$
such that
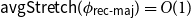 ${\sf avgStretch}(\phi _{{\textsf{rec-maj}}}) = O(1)$
.
${\sf avgStretch}(\phi _{{\textsf{rec-maj}}}) = O(1)$
.Let
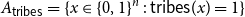 ${A_{{\sf tribes}}} = \{x \in \{0,1\}^n \,:\,{\sf tribes}(x) = 1\}$
. There exists a bijection
${A_{{\sf tribes}}} = \{x \in \{0,1\}^n \,:\,{\sf tribes}(x) = 1\}$
. There exists a bijection
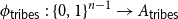 $\phi _{{\sf tribes}} \,:\, \{0,1\}^{n-1} \to{A_{{\sf tribes}}}$
such that
$\phi _{{\sf tribes}} \,:\, \{0,1\}^{n-1} \to{A_{{\sf tribes}}}$
such that
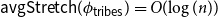 ${\sf avgStretch}(\phi _{{\sf tribes}}) = O(\!\log (n))$
.
${\sf avgStretch}(\phi _{{\sf tribes}}) = O(\!\log (n))$
.
These results answer the questions raised by Benjamini, Cohen, and Shinkar (Isr. J. Math 2016).
Keywords
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press



