Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T07:13:41.507Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Form of Coordinate Percolation

Published online by Cambridge University Press:  01 November 2008

ELIZABETH R. MOSEMAN  and
PETER WINKLER
ELIZABETH R. MOSEMAN
Affiliation:
Department of Mathematical Sciences, USMA, West Point NY 10996, USA (e-mail: [email protected])
PETER WINKLER
Affiliation:
Department of Mathematics, Dartmouth College, Hanover NH 03755-3551, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ai,bi, i = 0, 1, 2, . . . be drawn uniformly and independently from the unit interval, and let t be a fixed real number. Let a site (i, j) ∈ 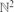be open if ai + bj ≤ t, and closed otherwise. We obtain a simple, exact expression for the probability Θ(t) that there is an infinite path (oriented or not) of open sites, containing the origin. Θ(t) is continuous and has continuous first derivative except at the critical point (t=1), near which it has critical exponent (3 − 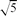)/2.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 6 , November 2008 , pp. 837 - 845
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Balister, P. N., Bollobás, B. and Stacey, A. M. (2000) Dependent percolation in two dimensions. Probab. Theory Rel. Fields 117 495–513.CrossRefGoogle Scholar
[2]Bollobás, B. and Riordan, O. (2006) Percolation, Cambridge University Press.Google Scholar
[3]Brightwell, G. R. and Winkler, P. (2007) Submodular percolation. Preprint.Google Scholar
[4]Broadbent, S. R. and Hammersley, J. M. (1957) Percolation processes I: Crystals and mazes. Proc. Cambridge Philos. Soc. 53 629–641.Google Scholar
[5]Coppersmith, D., Tetali, P. and Winkler, P. (1993) Collisions among random walks on a graph. SIAM J. Discrete Math. 6 363–374.CrossRefGoogle Scholar
[6]Diaconis, P. and Freedman, D. (1981) On the statistics of vision: The Julesz conjecture. J. Math. Psych. 24 112–138.Google Scholar
[7]Gács, P. (2000) The clairvoyant demon has a hard task. Combin. Probab. Comput. 9 421–424.CrossRefGoogle Scholar
[8]Gács, P. (2004) Compatible sequences and a slow Winkler percolation. Combin. Probab. Comput. 13 815–856.Google Scholar
[9]Grimmett, G. (1999) Percolation, 2nd edn, Springer.Google Scholar
[10]Moseman, E. (2007) The combinatorics of coordinate percolation. PhD thesis, Dartmouth College.Google Scholar
[11]Pete, G. (2008) Corner percolation on Z2 and the square root of 17 Ann. Prob. 36 51715–1747.Google Scholar
[12]Winkler, P. (2000) Dependent percolation and colliding random walks. Random Struct. Alg. 16 58–84.Google Scholar