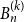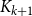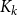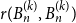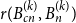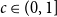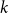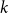1. Introduction
Given two graphs
![]() $H_1$
and
$H_1$
and
![]() $H_2$
, their Ramsey number
$H_2$
, their Ramsey number
![]() $r(H_1,H_2)$
is the smallest positive integer
$r(H_1,H_2)$
is the smallest positive integer
![]() $N$
such that every red/blue colouring of the edges of
$N$
such that every red/blue colouring of the edges of
![]() $K_N$
is guaranteed to contain a red copy of
$K_N$
is guaranteed to contain a red copy of
![]() $H_1$
or a blue copy of
$H_1$
or a blue copy of
![]() $H_2$
. One of the main open problems in Ramsey theory is to determine the asymptotic order of
$H_2$
. One of the main open problems in Ramsey theory is to determine the asymptotic order of
![]() $r(K_n,K_n)$
. However, despite intense and longstanding interest, the lower and upper bounds
$r(K_n,K_n)$
. However, despite intense and longstanding interest, the lower and upper bounds
![]() $\sqrt 2^n \leq r(K_n,K_n) \leq 4^n$
for this problem have remained largely unchanged since 1947 and 1935, respectively [Reference Erdős11, Reference Erdős and Szekeres13].
$\sqrt 2^n \leq r(K_n,K_n) \leq 4^n$
for this problem have remained largely unchanged since 1947 and 1935, respectively [Reference Erdős11, Reference Erdős and Szekeres13].
Another major question in graph Ramsey theory, which has seen more progress, is to determine the growth rate of the off-diagonal Ramsey number
![]() $r(K_s,K_n)$
, where we think of
$r(K_s,K_n)$
, where we think of
![]() $s$
as fixed and let
$s$
as fixed and let
![]() $n$
tend to infinity. The first non-trivial case is when
$n$
tend to infinity. The first non-trivial case is when
![]() $s=3$
, where it is known that
$s=3$
, where it is known that
with the upper bound due to Ajtai, Komlós, and Szemerédi [Reference Ajtai, Komlós and Szemerédi1] and the lower bound to Kim [Reference Kim15]. Subsequent work of Shearer [Reference Shearer23], Bohman–Keevash [Reference Bohman and Keevash3], and Fiz Pontiveros–Griffiths–Morris [Reference Pontiveros, Griffiths and Morris20] has led to a better understanding of the implicit constant, which is now known up to a factor of
![]() $4+o(1)$
. However, the successes in estimating
$4+o(1)$
. However, the successes in estimating
![]() $r(K_3, K_n)$
have not carried over to
$r(K_3, K_n)$
have not carried over to
![]() $r(K_s, K_n)$
for any other fixed
$r(K_s, K_n)$
for any other fixed
![]() $s$
and a polynomial gap persists between the upper and lower bounds for all
$s$
and a polynomial gap persists between the upper and lower bounds for all
![]() $s \geq 4$
(though see [Reference Mubayi and Verstraëte17] for a promising approach to improving the lower bound).
$s \geq 4$
(though see [Reference Mubayi and Verstraëte17] for a promising approach to improving the lower bound).
The book graph
![]() $B_n ^{(k)}$
is the graph obtained by gluing
$B_n ^{(k)}$
is the graph obtained by gluing
![]() $n$
copies of the clique
$n$
copies of the clique
![]() $K_{k+1}$
along a common
$K_{k+1}$
along a common
![]() $K_k$
. The ‘book’ terminology comes from the case
$K_k$
. The ‘book’ terminology comes from the case
![]() $k=2$
, where
$k=2$
, where
![]() $B_n ^{(2)}$
consists of
$B_n ^{(2)}$
consists of
![]() $n$
triangles glued along a common edge. Continuing the analogy, each
$n$
triangles glued along a common edge. Continuing the analogy, each
![]() $K_{k+1}$
is called a page of the book and the common
$K_{k+1}$
is called a page of the book and the common
![]() $K_k$
is called the spine. Ramsey numbers of books arise naturally in the study of
$K_k$
is called the spine. Ramsey numbers of books arise naturally in the study of
![]() $r(K_n, K_n)$
; indeed, Ramsey’s original proof [Reference Ramsey21] of the finiteness of
$r(K_n, K_n)$
; indeed, Ramsey’s original proof [Reference Ramsey21] of the finiteness of
![]() $r(K_n,K_n)$
proceeds inductively by establishing the finiteness of certain book Ramsey numbers, while the Erdős–Szekeres bound [Reference Erdős and Szekeres13] and its improvements [Reference Conlon8, Reference Sah22] are also best interpreted through the language of books. Because of this, Ramsey numbers of books have attracted a great deal of attention over the years, starting with papers of Erdős, Faudree, Rousseau, and Schelp [Reference Erdős, Faudree, Rousseau and Schelp12] and of Thomason [Reference Thomason25]. Both of these papers prove bounds of the form
$r(K_n,K_n)$
proceeds inductively by establishing the finiteness of certain book Ramsey numbers, while the Erdős–Szekeres bound [Reference Erdős and Szekeres13] and its improvements [Reference Conlon8, Reference Sah22] are also best interpreted through the language of books. Because of this, Ramsey numbers of books have attracted a great deal of attention over the years, starting with papers of Erdős, Faudree, Rousseau, and Schelp [Reference Erdős, Faudree, Rousseau and Schelp12] and of Thomason [Reference Thomason25]. Both of these papers prove bounds of the form
![]() $2^k n-o_k(n) \leq r\big(B_n^{(k)}, B_n ^{(k)}\big) \leq 4^k n$
, where we think of
$2^k n-o_k(n) \leq r\big(B_n^{(k)}, B_n ^{(k)}\big) \leq 4^k n$
, where we think of
![]() $k$
as fixed and
$k$
as fixed and
![]() $n \to \infty$
, with Thomason conjecturing that the lower bound is closer to the truth. This was confirmed in a recent breakthrough result of the first author [Reference Conlon9], who proved that, for every fixed
$n \to \infty$
, with Thomason conjecturing that the lower bound is closer to the truth. This was confirmed in a recent breakthrough result of the first author [Reference Conlon9], who proved that, for every fixed
![]() $k$
,
$k$
,
The original proof of this result relied heavily on an application of Szemerédi’s celebrated regularity lemma, leading to rather poor control on the error term. In the prequel to this paper [Reference Conlon, Fox and Wigderson10], we gave two alternative proofs of this result, one a simplified version of the first author’s original proof and the other a proof which avoids the use of the full regularity lemma, allowing us to gain significantly better control over the error term (for a discussion of how further improvements might ultimately impinge on the estimation of
![]() $r(K_n, K_n)$
, we refer the reader to [Reference Conlon, Fox and Wigderson10]). We also proved a stability result, saying that extremal colourings for this Ramsey problem are quasirandom.
$r(K_n, K_n)$
, we refer the reader to [Reference Conlon, Fox and Wigderson10]). We also proved a stability result, saying that extremal colourings for this Ramsey problem are quasirandom.
In this paper, we study a natural off-diagonal generalization of this problem. Specifically, we fix some
![]() $k \in \mathbb{N}$
and some
$k \in \mathbb{N}$
and some
![]() $c \in (0,1]$
and we wish to understand the asymptotics of the Ramsey number
$c \in (0,1]$
and we wish to understand the asymptotics of the Ramsey number
![]() $r(B_{\lfloor cn \rfloor } ^{(k)}, B_{n} ^{(k)})$
as
$r(B_{\lfloor cn \rfloor } ^{(k)}, B_{n} ^{(k)})$
as
![]() $n \to \infty$
. Note that for
$n \to \infty$
. Note that for
![]() $c=1$
this is precisely the question considered above. Henceforth, we omit the floor signs and write
$c=1$
this is precisely the question considered above. Henceforth, we omit the floor signs and write
![]() $B_{cn}^{(k)}$
instead of
$B_{cn}^{(k)}$
instead of
![]() $B_{\lfloor cn \rfloor }^{(k)}$
.
$B_{\lfloor cn \rfloor }^{(k)}$
.
Our results reveal that the behaviour of the function
![]() $r(B_{cn} ^{(k)},B_n ^{(k)})$
varies greatly as
$r(B_{cn} ^{(k)},B_n ^{(k)})$
varies greatly as
![]() $c$
moves from
$c$
moves from
![]() $0$
to
$0$
to
![]() $1$
. As we shall see, for
$1$
. As we shall see, for
![]() $c$
sufficiently small, the behaviour of this Ramsey number is determined by a simple block construction, while, for
$c$
sufficiently small, the behaviour of this Ramsey number is determined by a simple block construction, while, for
![]() $c$
sufficiently far from
$c$
sufficiently far from
![]() $0$
, its behaviour is determined by a random colouring. There is also an intermediate range of
$0$
, its behaviour is determined by a random colouring. There is also an intermediate range of
![]() $c$
where our results say nothing, but where several interesting questions arise. We will say more about this in the concluding remarks.
$c$
where our results say nothing, but where several interesting questions arise. We will say more about this in the concluding remarks.
To describe our results in detail, we begin by observing that for any positive integers
![]() $k$
,
$k$
,
![]() $m$
, and
$m$
, and
![]() $n$
with
$n$
with
![]() $m \leq n$
, we have
$m \leq n$
, we have
Indeed, let
![]() $N=k(n+k-1)$
. We partition the vertices of
$N=k(n+k-1)$
. We partition the vertices of
![]() $K_N$
into
$K_N$
into
![]() $k$
blocks, each of size
$k$
blocks, each of size
![]() $n+k-1$
. We colour all edges inside a block blue and all edges between blocks red. Then any blue
$n+k-1$
. We colour all edges inside a block blue and all edges between blocks red. Then any blue
![]() $B_n ^{(k)}$
must appear inside a block, which it cannot, since
$B_n ^{(k)}$
must appear inside a block, which it cannot, since
![]() $B_n ^{(k)}$
has
$B_n ^{(k)}$
has
![]() $n+k$
vertices. On the other hand, since the red graph is
$n+k$
vertices. On the other hand, since the red graph is
![]() $k$
-partite, it does not contain any red
$k$
-partite, it does not contain any red
![]() $K_{k+1}$
and so cannot contain a red
$K_{k+1}$
and so cannot contain a red
![]() $B_m ^{(k)}$
.
$B_m ^{(k)}$
.
This simple inequality is a special case of a more general lower bound, usually attributed to Chvátal and Harary [Reference Chvátal and Harary7], that
![]() $r(H_1,H_2) \geq (\chi (H_1)-1)(|V(H_2)|-1)+1$
provided
$r(H_1,H_2) \geq (\chi (H_1)-1)(|V(H_2)|-1)+1$
provided
![]() $H_2$
is connected. In general, this lower bound is far from optimal,Footnote 1 but it is tight for certain sparse graphs. The study of when it is tight goes under the name of Ramsey goodness, a term introduced by Burr and Erdős [Reference Burr and Erdős5] in their first systematic investigation of the concept. One of the central results in the field of Ramsey goodness is due to Nikiforov and Rousseau [Reference Nikiforov and Rousseau18], who proved an extremely general theorem about when this lower bound is tight. As a very special case of their theorem, one has the following result; see also [Reference Fox, He and Wigderson14] for a new proof with better quantitative bounds.
$H_2$
is connected. In general, this lower bound is far from optimal,Footnote 1 but it is tight for certain sparse graphs. The study of when it is tight goes under the name of Ramsey goodness, a term introduced by Burr and Erdős [Reference Burr and Erdős5] in their first systematic investigation of the concept. One of the central results in the field of Ramsey goodness is due to Nikiforov and Rousseau [Reference Nikiforov and Rousseau18], who proved an extremely general theorem about when this lower bound is tight. As a very special case of their theorem, one has the following result; see also [Reference Fox, He and Wigderson14] for a new proof with better quantitative bounds.
Theorem 1.1 (Nikiforov–Rousseau [Reference Nikiforov and Rousseau19, Theorem 2.12]). For every
![]() $k \geq 2$
, there exists some
$k \geq 2$
, there exists some
![]() $c_0 \in (0,1)$
such that, for any
$c_0 \in (0,1)$
such that, for any
![]() $0\lt c \leq c_0$
and
$0\lt c \leq c_0$
and
![]() $n$
sufficiently large,
$n$
sufficiently large,
Moreover, Nikiforov and Rousseau’s proof shows that the unique colouring on
![]() $k(n+k-1)$
vertices with no red
$k(n+k-1)$
vertices with no red
![]() $B_{cn}^{(k)}$
and no blue
$B_{cn}^{(k)}$
and no blue
![]() $B_n ^{(k)}$
is the colouring we described, where the red graph is a balanced complete
$B_n ^{(k)}$
is the colouring we described, where the red graph is a balanced complete
![]() $k$
-partite graph (meaning that all the parts have orders as equal as possible). By adapting their proof, we are able to prove a corresponding structural stability result, which says that any colouring on
$k$
-partite graph (meaning that all the parts have orders as equal as possible). By adapting their proof, we are able to prove a corresponding structural stability result, which says that any colouring on
![]() $N=(k+o(1))n$
vertices is either ‘close’ to being balanced complete
$N=(k+o(1))n$
vertices is either ‘close’ to being balanced complete
![]() $k$
-partite in red or contains monochromatic books with substantially more pages than what is guaranteed by Theorem 1.1. Note that if
$k$
-partite in red or contains monochromatic books with substantially more pages than what is guaranteed by Theorem 1.1. Note that if
![]() $N$
is sufficiently large and congruent to
$N$
is sufficiently large and congruent to
![]() $1$
modulo
$1$
modulo
![]() $k$
, then Theorem 1.1 says that any red/blue colouring of
$k$
, then Theorem 1.1 says that any red/blue colouring of
![]() $E(K_N)$
contains a red
$E(K_N)$
contains a red
![]() $K_k$
with at least
$K_k$
with at least
![]() $\frac ck(N-1)-c(k-1)$
extensions to a red
$\frac ck(N-1)-c(k-1)$
extensions to a red
![]() $K_{k+1}$
or a blue
$K_{k+1}$
or a blue
![]() $K_k$
with at least
$K_k$
with at least
![]() $\frac 1k(N-1)-(k-1)$
extensions to a blue
$\frac 1k(N-1)-(k-1)$
extensions to a blue
![]() $K_{k+1}$
.
$K_{k+1}$
.
Theorem 1.2.
For every
![]() $k \geq 2$
and every
$k \geq 2$
and every
![]() $\theta \gt 0$
, there exist
$\theta \gt 0$
, there exist
![]() $c,\gamma \in (0,1)$
such that the following holds for any sufficiently large
$c,\gamma \in (0,1)$
such that the following holds for any sufficiently large
![]() $N$
and any red/blue colouring of
$N$
and any red/blue colouring of
![]() $E(K_N)$
. Either one can recolour at most
$E(K_N)$
. Either one can recolour at most
![]() $\theta N^2$
edges to turn the red graph into a balanced complete
$\theta N^2$
edges to turn the red graph into a balanced complete
![]() $k$
-partite graph or else the colouring contains one of the following:
$k$
-partite graph or else the colouring contains one of the following:
-
at least
 $\gamma N^k$
red
$\gamma N^k$
red
 $K_k$
, each with at least
$K_k$
, each with at least
 $(\frac ck+\gamma )N$
extensions to a red
$(\frac ck+\gamma )N$
extensions to a red
 $K_{k+1}$
, or
$K_{k+1}$
, or
-
at least
 $\gamma N^k$
blue
$\gamma N^k$
blue
 $K_k$
, each with at least
$K_k$
, each with at least
 $(\frac 1k+\gamma )N$
extensions to a blue
$(\frac 1k+\gamma )N$
extensions to a blue
 $K_{k+1}$
.
$K_{k+1}$
.
Informally, this theorem says that either the colouring is close to complete
![]() $k$
-partite in red or else a constant fraction of the
$k$
-partite in red or else a constant fraction of the
![]() $k$
-tuples induce a clique that forms the spine of a monochromatic book with at least
$k$
-tuples induce a clique that forms the spine of a monochromatic book with at least
![]() $\gamma N$
more pages than what is guaranteed by the Ramsey bound alone.
$\gamma N$
more pages than what is guaranteed by the Ramsey bound alone.
However, once
![]() $c$
is sufficiently far from
$c$
is sufficiently far from
![]() $0$
, the deterministic construction that yields (1) stops being optimal. Indeed, as in the diagonal case, we can get another lower bound on
$0$
, the deterministic construction that yields (1) stops being optimal. Indeed, as in the diagonal case, we can get another lower bound on
![]() $r\big(B_{cn}^{(k)},B_n ^{(k)}\big)$
by considering random colourings. More precisely, let us fix
$r\big(B_{cn}^{(k)},B_n ^{(k)}\big)$
by considering random colourings. More precisely, let us fix
![]() $k \in \mathbb{N}$
and
$k \in \mathbb{N}$
and
![]() $c \in (0,1]$
and define
$c \in (0,1]$
and define
We set
![]() $N=(p^{-k}-o(1))n$
and independently colour every edge of
$N=(p^{-k}-o(1))n$
and independently colour every edge of
![]() $K_N$
blue with probability
$K_N$
blue with probability
![]() $p$
and red with probability
$p$
and red with probability
![]() $1-p$
. Given a blue
$1-p$
. Given a blue
![]() $K_k$
in this colouring, the expected number of extensions to a blue
$K_k$
in this colouring, the expected number of extensions to a blue
![]() $K_{k+1}$
is
$K_{k+1}$
is
![]() $p^k(N-k) = n-o(n)$
. Similarly, the expected number of extensions of a red
$p^k(N-k) = n-o(n)$
. Similarly, the expected number of extensions of a red
![]() $K_k$
to a red
$K_k$
to a red
![]() $K_{k+1}$
is
$K_{k+1}$
is
![]() $(1-p)^k(N-k) = ((1-p)/p)^k n - o(n)=cn-o(n)$
, by our choice of
$(1-p)^k(N-k) = ((1-p)/p)^k n - o(n)=cn-o(n)$
, by our choice of
![]() $p$
. A standard application of the Chernoff bound and the union bound then implies that w.h.p.Footnote 2 this colouring contains no blue
$p$
. A standard application of the Chernoff bound and the union bound then implies that w.h.p.Footnote 2 this colouring contains no blue
![]() $B_n ^{(k)}$
and no red
$B_n ^{(k)}$
and no red
![]() $B_{cn}^{(k)}$
, assuming the
$B_{cn}^{(k)}$
, assuming the
![]() $o(n)$
terms are chosen appropriately. This implies that for any
$o(n)$
terms are chosen appropriately. This implies that for any
![]() $k \in \mathbb{N}$
and any
$k \in \mathbb{N}$
and any
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
while the lower bound in (1) is that
![]() $r(B_{cn} ^{(k)},B_n ^{(k)}) \geq (k+o(1))n$
. If
$r(B_{cn} ^{(k)},B_n ^{(k)}) \geq (k+o(1))n$
. If
![]() $c\gt ((1+o(1))\frac{\log k}{k})^k$
, then the quantity
$c\gt ((1+o(1))\frac{\log k}{k})^k$
, then the quantity
![]() $(c^{1/k}+1)^k$
is larger than
$(c^{1/k}+1)^k$
is larger than
![]() $k+o(1)$
, where the logarithm is to base
$k+o(1)$
, where the logarithm is to base
![]() $e$
. Thus, once
$e$
. Thus, once
![]() $c$
is sufficiently far from
$c$
is sufficiently far from
![]() $0$
, the bound in (1) is smaller than the random bound.
$0$
, the bound in (1) is smaller than the random bound.
Our next main result shows that the random bound actually becomes asymptotically tight at this point.
Theorem 1.3.
For every
![]() $k \geq 2$
, there exists some
$k \geq 2$
, there exists some
![]() $c_1=c_1(k) \in (0,1]$
such that, for any fixed
$c_1=c_1(k) \in (0,1]$
such that, for any fixed
![]() $c_1 \leq c \leq 1$
,
$c_1 \leq c \leq 1$
,
Moreover, one may take
![]() $c_1(k)=((1+o(1))\frac{\log k}{k})^k$
.
$c_1(k)=((1+o(1))\frac{\log k}{k})^k$
.
Our third main result is a corresponding structural stability theorem, which says that all near-extremal Ramsey colourings (i.e., colourings on roughly
![]() $(c^{1/k}+1)^kn$
vertices) must either contain a monochromatic book substantially larger than what is guaranteed by Theorem 1.3 or be ‘random-like’. The latter possibility is captured by the notion of quasirandomness, introduced by Chung, Graham, and Wilson [Reference Chung, Graham and Wilson6]. For parameters
$(c^{1/k}+1)^kn$
vertices) must either contain a monochromatic book substantially larger than what is guaranteed by Theorem 1.3 or be ‘random-like’. The latter possibility is captured by the notion of quasirandomness, introduced by Chung, Graham, and Wilson [Reference Chung, Graham and Wilson6]. For parameters
![]() $p,\theta \in (0,1)$
, a red/blue colouring of
$p,\theta \in (0,1)$
, a red/blue colouring of
![]() $E(K_N)$
is said to be
$E(K_N)$
is said to be
![]() $(p,\theta )$
-quasirandom if, for every pair of disjoint sets
$(p,\theta )$
-quasirandom if, for every pair of disjoint sets
![]() $X,Y \subseteq V(K_N)$
, we have that
$X,Y \subseteq V(K_N)$
, we have that
where
![]() $e_B(X,Y)$
denotes the number of blue edges between
$e_B(X,Y)$
denotes the number of blue edges between
![]() $X$
and
$X$
and
![]() $Y$
. Note that since the colours are complementary, this is equivalent to the analogous condition requiring that
$Y$
. Note that since the colours are complementary, this is equivalent to the analogous condition requiring that
![]() $e_R(X,Y)$
is within
$e_R(X,Y)$
is within
![]() $\theta N^2$
of
$\theta N^2$
of
![]() $(1-p)|X||Y|$
. In their seminal paper, Chung, Graham, and Wilson, building on previous results of Thomason [Reference Thomason25], showed that this condition is essentially equivalent to a large number of other conditions, all of which encapsulate some intuitive idea of what it means for a colouring to be similar to a random colouring with blue density
$(1-p)|X||Y|$
. In their seminal paper, Chung, Graham, and Wilson, building on previous results of Thomason [Reference Thomason25], showed that this condition is essentially equivalent to a large number of other conditions, all of which encapsulate some intuitive idea of what it means for a colouring to be similar to a random colouring with blue density
![]() $p$
. With this notion in hand, we can state our structural stability result.
$p$
. With this notion in hand, we can state our structural stability result.
Theorem 1.4.
For every
![]() $p \in [\frac 12,1)$
, there exists some
$p \in [\frac 12,1)$
, there exists some
![]() $k_0 \in \mathbb{N}$
such that the following holds for every
$k_0 \in \mathbb{N}$
such that the following holds for every
![]() $k \geq k_0$
. For every
$k \geq k_0$
. For every
![]() $\theta \gt 0$
, there exists some
$\theta \gt 0$
, there exists some
![]() $\gamma \gt 0$
such that if a red/blue colouring of
$\gamma \gt 0$
such that if a red/blue colouring of
![]() $E(K_N)$
is not
$E(K_N)$
is not
![]() $(p,\theta )$
-quasirandom, then it contains one of the following:
$(p,\theta )$
-quasirandom, then it contains one of the following:
-
at least
 $\gamma N^k$
red
$\gamma N^k$
red
 $K_k$
, each with at least
$K_k$
, each with at least
 $((1-p)^k+\gamma )N$
extensions to a red
$((1-p)^k+\gamma )N$
extensions to a red
 $K_{k+1}$
, or
$K_{k+1}$
, or
-
at least
 $\gamma N^k$
blue
$\gamma N^k$
blue
 $K_k$
, each with at least
$K_k$
, each with at least
 $(p^k+\gamma )N$
extensions to a blue
$(p^k+\gamma )N$
extensions to a blue
 $K_{k+1}$
.
$K_{k+1}$
.
Remark 1.1.
As stated, this theorem does not mention the ‘off-diagonalness’ parameter
![]() $c$
from the previous theorem. But
$c$
from the previous theorem. But
![]() $c$
can easily be recovered as
$c$
can easily be recovered as
![]() $((1-p)/p)^k$
and the theorem can then be restated to be about blue books with slightly more than
$((1-p)/p)^k$
and the theorem can then be restated to be about blue books with slightly more than
![]() $n$
pages or red books with slightly more than
$n$
pages or red books with slightly more than
![]() $cn$
pages. However, since
$cn$
pages. However, since
![]() $p$
is what matters while
$p$
is what matters while
![]() $c$
plays no real role in the argument, we instead choose to use this language and avoid
$c$
plays no real role in the argument, we instead choose to use this language and avoid
![]() $c$
entirely.
$c$
entirely.
In Theorem 5.7, we also prove a converse to Theorem 1.4, which implies that for
![]() $p$
fixed and
$p$
fixed and
![]() $k$
sufficiently large in terms of
$k$
sufficiently large in terms of
![]() $p$
, a colouring of
$p$
, a colouring of
![]() $K_N$
(or, more accurately, a sequence of colourings with
$K_N$
(or, more accurately, a sequence of colourings with
![]() $N$
tending to infinity) is
$N$
tending to infinity) is
![]() $(p, o(1))$
-quasirandom if and only if all but
$(p, o(1))$
-quasirandom if and only if all but
![]() $o(N^k)$
red
$o(N^k)$
red
![]() $K_k$
have at most
$K_k$
have at most
![]() $((1-p)^k+o(1))N$
extensions to a red
$((1-p)^k+o(1))N$
extensions to a red
![]() $K_{k+1}$
and all but
$K_{k+1}$
and all but
![]() $o(N^k)$
blue
$o(N^k)$
blue
![]() $K_k$
have at most
$K_k$
have at most
![]() $(p^k+o(1))N$
extensions to a blue
$(p^k+o(1))N$
extensions to a blue
![]() $K_{k+1}$
. Thus, we derive a new equivalent formulation for
$K_{k+1}$
. Thus, we derive a new equivalent formulation for
![]() $(p, o(1))$
-quasirandomness.
$(p, o(1))$
-quasirandomness.
The rest of the paper is organized as follows. In Section 2, we quote (mostly without proof) a number of key results that we will use repeatedly. In Section 3, we establish Theorem 1.2, the stability result for small
![]() $c$
. We prove Theorem 1.3, that the random bound is asymptotically tight once
$c$
. We prove Theorem 1.3, that the random bound is asymptotically tight once
![]() $c$
is not too small, in Section 4 and Theorem 1.4, that extremal colourings are quasirandom in this range, in Section 5. We end with some concluding remarks and open problems.
$c$
is not too small, in Section 4 and Theorem 1.4, that extremal colourings are quasirandom in this range, in Section 5. We end with some concluding remarks and open problems.
1.1. Notation and terminology
If
![]() $X$
and
$X$
and
![]() $Y$
are two vertex subsets of a graph, let
$Y$
are two vertex subsets of a graph, let
![]() $e(X,Y)$
denote the number of pairs in
$e(X,Y)$
denote the number of pairs in
![]() $X \times Y$
that are edges. We will often normalize this and consider the edge density
$X \times Y$
that are edges. We will often normalize this and consider the edge density
If we consider a red/blue colouring of the edges of a graph, then
![]() $e_B(X,Y)$
and
$e_B(X,Y)$
and
![]() $e_R(X,Y)$
will denote the number of pairs in
$e_R(X,Y)$
will denote the number of pairs in
![]() $X \times Y$
that are blue and red edges, respectively. Similarly,
$X \times Y$
that are blue and red edges, respectively. Similarly,
![]() $d_B$
and
$d_B$
and
![]() $d_R$
will denote the blue and red edge densities, respectively. Finally, for a vertex
$d_R$
will denote the blue and red edge densities, respectively. Finally, for a vertex
![]() $v$
and a set
$v$
and a set
![]() $Y$
, we will sometimes abuse notation and write
$Y$
, we will sometimes abuse notation and write
![]() $d(v,Y)$
for
$d(v,Y)$
for
![]() $d(\{v\},Y)$
and similarly for
$d(\{v\},Y)$
and similarly for
![]() $d_B$
and
$d_B$
and
![]() $d_R$
.
$d_R$
.
An equitable partition of a graph
![]() $G$
is a partition of the vertex set
$G$
is a partition of the vertex set
![]() $V(G)=V_1 \sqcup \dotsb \sqcup V_m$
with
$V(G)=V_1 \sqcup \dotsb \sqcup V_m$
with
![]() $||V_i|-|V_j||\leq 1$
for all
$||V_i|-|V_j||\leq 1$
for all
![]() $1 \leq i,j \leq m$
. A pair of vertex subsets
$1 \leq i,j \leq m$
. A pair of vertex subsets
![]() $(X,Y)$
is said to be
$(X,Y)$
is said to be
![]() $\varepsilon$
-regular if, for every
$\varepsilon$
-regular if, for every
![]() $X' \subseteq X$
,
$X' \subseteq X$
,
![]() $Y' \subseteq Y$
with
$Y' \subseteq Y$
with
![]() $|X'| \geq \varepsilon |X|$
,
$|X'| \geq \varepsilon |X|$
,
![]() $|Y'| \geq \varepsilon |Y|$
, we have
$|Y'| \geq \varepsilon |Y|$
, we have
Note that we do not require
![]() $X$
and
$X$
and
![]() $Y$
to be disjoint. In particular, we say that a single vertex subset
$Y$
to be disjoint. In particular, we say that a single vertex subset
![]() $X$
is
$X$
is
![]() $\varepsilon$
-regular if the pair
$\varepsilon$
-regular if the pair
![]() $(X,X)$
is
$(X,X)$
is
![]() $\varepsilon$
-regular. We will often need a simple fact, known as the hereditary property of regularity, which asserts that for any
$\varepsilon$
-regular. We will often need a simple fact, known as the hereditary property of regularity, which asserts that for any
![]() $0\lt \alpha \leq 1$
, if
$0\lt \alpha \leq 1$
, if
![]() $(X,Y)$
is
$(X,Y)$
is
![]() $\varepsilon$
-regular and
$\varepsilon$
-regular and
![]() $X' \subseteq X$
,
$X' \subseteq X$
,
![]() $Y' \subseteq Y$
satisfy
$Y' \subseteq Y$
satisfy
![]() $|X'| \geq \alpha |X|$
,
$|X'| \geq \alpha |X|$
,
![]() $|Y'| \geq \alpha |Y|$
, then
$|Y'| \geq \alpha |Y|$
, then
![]() $(X',Y')$
is
$(X',Y')$
is
![]() $(\!\max \{\varepsilon/\alpha, 2\varepsilon \})$
-regular.
$(\!\max \{\varepsilon/\alpha, 2\varepsilon \})$
-regular.
For real numbers
![]() $a,b$
, we denote by
$a,b$
, we denote by
![]() $a \pm b$
any quantity in the interval
$a \pm b$
any quantity in the interval
![]() $[a-b, a+b]$
. All logarithms are base
$[a-b, a+b]$
. All logarithms are base
![]() $e$
unless otherwise specified. For the sake of clarity of presentation, we systematically omit floor and ceiling signs whenever they are not crucial. In this vein, whenever we have an equitable partition of a vertex set, we will always assume that all of the parts have exactly the same size, rather than being off by at most one. Because the number of vertices in our graphs will always be ‘sufficiently large’, this has no effect on our final results.
$e$
unless otherwise specified. For the sake of clarity of presentation, we systematically omit floor and ceiling signs whenever they are not crucial. In this vein, whenever we have an equitable partition of a vertex set, we will always assume that all of the parts have exactly the same size, rather than being off by at most one. Because the number of vertices in our graphs will always be ‘sufficiently large’, this has no effect on our final results.
2. Results from earlier work
In this section, we collect some useful tools for the study of book Ramsey numbers, all of which have appeared in previous works. We begin with several results from the theory around Szemerédi’s regularity lemma and then quote two simple analytic inequalities.
2.1. Tools from regularity
We begin with a strengthened form of Szemerédi’s regularity lemma taken from our first paper [Reference Conlon, Fox and Wigderson10, Lemma 2.1].
Lemma 2.1.
For every
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $M_0 \in \mathbb N$
, there is some
$M_0 \in \mathbb N$
, there is some
![]() $M=M(\varepsilon,M_0) \geq M_0$
such that, for every graph
$M=M(\varepsilon,M_0) \geq M_0$
such that, for every graph
![]() $G$
with at least
$G$
with at least
![]() $M_0$
vertices, there is an equitable partition
$M_0$
vertices, there is an equitable partition
![]() $V(G)=V_1 \sqcup \dotsb \sqcup V_m$
into
$V(G)=V_1 \sqcup \dotsb \sqcup V_m$
into
![]() $M_0 \leq m \leq M$
parts such that the following hold:
$M_0 \leq m \leq M$
parts such that the following hold:
-
1. Each part
 $V_i$
is
$V_i$
is
 $\varepsilon$
-regular and
$\varepsilon$
-regular and
-
2. For every
 $1 \leq i \leq m$
, there are at most
$1 \leq i \leq m$
, there are at most
 $\varepsilon m$
values
$\varepsilon m$
values
 $1 \leq j \leq m$
such that the pair
$1 \leq j \leq m$
such that the pair
 $(V_i,V_j)$
is not
$(V_i,V_j)$
is not
 $\varepsilon$
-regular.
$\varepsilon$
-regular.
To complement the regularity lemma, we will also need a standard counting lemma (see, e.g., [Reference Zhao26, Theorems 2.6.2 and 4.5.1]).
Lemma 2.2.
Suppose that
![]() $V_1,\ldots,V_k$
are (not necessarily distinct) subsets of a graph
$V_1,\ldots,V_k$
are (not necessarily distinct) subsets of a graph
![]() $G$
such that all pairs
$G$
such that all pairs
![]() $(V_i,V_j)$
are
$(V_i,V_j)$
are
![]() $\varepsilon$
-regular. Then the number of labelled copies of
$\varepsilon$
-regular. Then the number of labelled copies of
![]() $K_k$
whose
$K_k$
whose
![]() $i$
-th vertex is in
$i$
-th vertex is in
![]() $V_i$
for all
$V_i$
for all
![]() $i$
is
$i$
is
 \begin{equation*} \left ( \prod _{1 \leq i\lt j\leq k}d(V_i,V_j) \pm \varepsilon \!\left (\begin{matrix} k \\[-3pt] 2 \end{matrix}\right ) \right ) \prod _{i=1}^k |V_i|. \end{equation*}
\begin{equation*} \left ( \prod _{1 \leq i\lt j\leq k}d(V_i,V_j) \pm \varepsilon \!\left (\begin{matrix} k \\[-3pt] 2 \end{matrix}\right ) \right ) \prod _{i=1}^k |V_i|. \end{equation*}
We will frequently use the following consequence of the counting lemma, proved in [Reference Conlon, Fox and Wigderson10, Corollary 2.6], designed to count monochromatic extensions of cliques and thus estimate the size of monochromatic books.
Lemma 2.3.
Fix
![]() $k \geq 2$
and let
$k \geq 2$
and let
![]() $\eta,\alpha \in (0,1)$
be parameters with
$\eta,\alpha \in (0,1)$
be parameters with
![]() $\eta \leq \alpha ^3/k^2$
. Suppose
$\eta \leq \alpha ^3/k^2$
. Suppose
![]() $U_1,\ldots,U_k$
are (not necessarily distinct) vertex sets in a graph
$U_1,\ldots,U_k$
are (not necessarily distinct) vertex sets in a graph
![]() $G$
and suppose that all pairs
$G$
and suppose that all pairs
![]() $(U_i,U_j)$
are
$(U_i,U_j)$
are
![]() $\eta$
-regular with
$\eta$
-regular with
![]() $\prod _{1 \leq i\lt j\leq k}d(U_i,U_j) \geq \alpha$
. Let
$\prod _{1 \leq i\lt j\leq k}d(U_i,U_j) \geq \alpha$
. Let
![]() $Q$
be a uniformly random copy of
$Q$
be a uniformly random copy of
![]() $K_k$
with one vertex in each
$K_k$
with one vertex in each
![]() $U_i$
, for
$U_i$
, for
![]() $1 \leq i \leq k$
, and say that a vertex
$1 \leq i \leq k$
, and say that a vertex
![]() $u$
extends
$u$
extends
![]() $Q$
if
$Q$
if
![]() $u$
is adjacent to every vertex of
$u$
is adjacent to every vertex of
![]() $Q$
. Then, for any
$Q$
. Then, for any
![]() $u \in V(G)$
,
$u \in V(G)$
,
 \begin{equation*} \mathbb {P}(u \text { extends }Q) \geq \prod _{i=1}^k d(u,U_i)-4 \alpha . \end{equation*}
\begin{equation*} \mathbb {P}(u \text { extends }Q) \geq \prod _{i=1}^k d(u,U_i)-4 \alpha . \end{equation*}
The final result in this subsection is actually a simple consequence of Markov’s inequality and so does not require any regularity tools to prove. Nonetheless, we will always use it in conjunction with Lemmas 2.2 and 2.3, which is why we include it here. Both the statement and proof are very similar to [Reference Conlon, Fox and Wigderson10, Lemma 5.2].
Lemma 2.4.
Let
![]() $\kappa,\xi \in (0,1)$
, let
$\kappa,\xi \in (0,1)$
, let
![]() $0\lt \nu \lt \xi$
, and suppose that
$0\lt \nu \lt \xi$
, and suppose that
![]() $\mathcal{Q}$
is a set of at least
$\mathcal{Q}$
is a set of at least
![]() $\kappa N^k$
copies of
$\kappa N^k$
copies of
![]() $K_k$
in an
$K_k$
in an
![]() $N$
-vertex graph. Suppose that a uniformly random
$N$
-vertex graph. Suppose that a uniformly random
![]() $Q \in \mathcal{Q}$
has at least
$Q \in \mathcal{Q}$
has at least
![]() $\xi N$
extensions to a
$\xi N$
extensions to a
![]() $K_{k+1}$
in expectation. Then the graph contains at least
$K_{k+1}$
in expectation. Then the graph contains at least
![]() $(\xi -\nu )\kappa N^k$
copies of
$(\xi -\nu )\kappa N^k$
copies of
![]() $K_k$
, each with at least
$K_k$
, each with at least
![]() $\nu N$
extensions.
$\nu N$
extensions.
Proof. Let
![]() $X$
be the random variable counting the number of extensions of a random
$X$
be the random variable counting the number of extensions of a random
![]() $Q \in \mathcal{Q}$
and let
$Q \in \mathcal{Q}$
and let
![]() $Y=N-X$
. Then
$Y=N-X$
. Then
![]() $Y$
is a non-negative random variable with
$Y$
is a non-negative random variable with
![]() $\mathbb{E}[Y]=N-\mathbb{E}[X] \leq (1-\xi )N$
. By Markov’s inequality,
$\mathbb{E}[Y]=N-\mathbb{E}[X] \leq (1-\xi )N$
. By Markov’s inequality,
Thus,
which implies that the number of
![]() $Q \in \mathcal{Q}$
with at least
$Q \in \mathcal{Q}$
with at least
![]() $\nu N$
extensions is at least
$\nu N$
extensions is at least
![]() $(\xi -\nu )|\mathcal{Q}| \geq (\xi -\nu )\kappa N^k$
, as desired.
$(\xi -\nu )|\mathcal{Q}| \geq (\xi -\nu )\kappa N^k$
, as desired.
2.2. Analytic inequalities
The following lemma is a multiplicative form of Jensen’s inequality and is a simple consequence of the standard version. For a proof, see [Reference Conlon, Fox and Wigderson10, Lemma A.1].
Lemma 2.5 (multiplicative Jensen inequality). Suppose
![]() $0\lt a\lt b$
are real numbers and
$0\lt a\lt b$
are real numbers and
![]() $x_1,\ldots,x_k \in (a,b)$
. Let
$x_1,\ldots,x_k \in (a,b)$
. Let
![]() $f\;:\; (a,b) \to \mathbb{R}$
be a function such that
$f\;:\; (a,b) \to \mathbb{R}$
be a function such that
![]() $y \mapsto f(e^y)$
is strictly convex on the interval
$y \mapsto f(e^y)$
is strictly convex on the interval
![]() $(\!\log a,\log b)$
. Then, for any
$(\!\log a,\log b)$
. Then, for any
![]() $z \in (a^k,b^k)$
, subject to the constraint
$z \in (a^k,b^k)$
, subject to the constraint
![]() $\prod _{i=1}^k x_i=z$
,
$\prod _{i=1}^k x_i=z$
,
 \begin{equation*} \frac 1k \sum _{i=1}^k f(x_i) \end{equation*}
\begin{equation*} \frac 1k \sum _{i=1}^k f(x_i) \end{equation*}
is minimized when all the
![]() $x_i$
are equal (and thus equal to
$x_i$
are equal (and thus equal to
![]() $z^{1/k}$
).
$z^{1/k}$
).
The following theorem is the well-known ‘defect’ or ‘stability’ version of Jensen’s inequality. For a proof, see [Reference Steele24, Problem 6.5].
Theorem 2.6 (Hölder’s defect formula). Suppose
![]() $\varphi \;:\;[a,b] \to \mathbb{R}$
is a twice-differentiable function with
$\varphi \;:\;[a,b] \to \mathbb{R}$
is a twice-differentiable function with
![]() $\varphi ''(y) \geq m \gt 0$
for all
$\varphi ''(y) \geq m \gt 0$
for all
![]() $y \in (a,b)$
. For any
$y \in (a,b)$
. For any
![]() $y_1,\ldots,y_k \in [a,b]$
, let
$y_1,\ldots,y_k \in [a,b]$
, let
 \begin{equation*} \mu = \frac 1k \sum _{i=1}^k y_i \qquad \text { and } \qquad \sigma ^2 = \frac 1k \sum _{i=1}^k (y_i-\mu )^2 \end{equation*}
\begin{equation*} \mu = \frac 1k \sum _{i=1}^k y_i \qquad \text { and } \qquad \sigma ^2 = \frac 1k \sum _{i=1}^k (y_i-\mu )^2 \end{equation*}
be the empirical mean and variance of
![]() $\{y_1,\ldots,y_k\}$
. Then
$\{y_1,\ldots,y_k\}$
. Then
 \begin{equation*} \frac 1k \sum _{i=1}^k \varphi (y_i) - \varphi (\mu ) \geq \frac {m\sigma ^2}{2}. \end{equation*}
\begin{equation*} \frac 1k \sum _{i=1}^k \varphi (y_i) - \varphi (\mu ) \geq \frac {m\sigma ^2}{2}. \end{equation*}
3. The
 $k$
-partite regime
$k$
-partite regime
In this section, we analyze what happens when
![]() $c$
is very small. Recall, from the introduction, that a simple
$c$
is very small. Recall, from the introduction, that a simple
![]() $k$
-partite construction yields a lower bound for
$k$
-partite construction yields a lower bound for
![]() $r\big(B_{cn}^{(k)},B_n ^{(k)}\big)$
and, by a result of Nikiforov and Rousseau [Reference Nikiforov and Rousseau19], this construction is tight for
$r\big(B_{cn}^{(k)},B_n ^{(k)}\big)$
and, by a result of Nikiforov and Rousseau [Reference Nikiforov and Rousseau19], this construction is tight for
![]() $c$
sufficiently small.
$c$
sufficiently small.
Theorem 1.1 (Nikiforov–Rousseau [Reference Nikiforov and Rousseau19, Theorem 2.12]). For every
![]() $k \geq 2$
, there exists some
$k \geq 2$
, there exists some
![]() $c_0 \in (0,1)$
such that, for any
$c_0 \in (0,1)$
such that, for any
![]() $0\lt c \leq c_0$
and
$0\lt c \leq c_0$
and
![]() $n$
sufficiently large,
$n$
sufficiently large,
Our aim here is to adapt the methods of [Reference Nikiforov and Rousseau19] to prove a stability version of this theorem, our Theorem 1.2. We first make the following definition.
Definition 3.1. For
![]() $c,\gamma \gt 0$
, we say that a red/blue colouring of
$c,\gamma \gt 0$
, we say that a red/blue colouring of
![]() $E(K_N)$
contains
$E(K_N)$
contains
![]() $(c,\gamma )$
-many books if it contains
$(c,\gamma )$
-many books if it contains
-
at least
 $\gamma N^k$
red
$\gamma N^k$
red
 $K_k$
, each with at least
$K_k$
, each with at least
 $(\frac ck +\gamma )N$
extensions to a red
$(\frac ck +\gamma )N$
extensions to a red
 $K_{k+1}$
, or
$K_{k+1}$
, or -
at least
 $\gamma N^k$
blue
$\gamma N^k$
blue
 $K_k$
, each with at least
$K_k$
, each with at least
 $(\frac 1k +\gamma )N$
extensions to a blue
$(\frac 1k +\gamma )N$
extensions to a blue
 $K_{k+1}$
.
$K_{k+1}$
.
With this definition in place, we may restate Theorem 1.2 as follows.
Theorem 1.2’.
For every
![]() $k \geq 2$
and every
$k \geq 2$
and every
![]() $\theta \gt 0$
, there exist
$\theta \gt 0$
, there exist
![]() $c,\gamma \in (0,1)$
such that the following holds. If a red/blue colouring of
$c,\gamma \in (0,1)$
such that the following holds. If a red/blue colouring of
![]() $E(K_N)$
does not have
$E(K_N)$
does not have
![]() $(c,\gamma )$
-many books, then one can recolour at most
$(c,\gamma )$
-many books, then one can recolour at most
![]() $\theta N^2$
edges to turn the red graph into a balanced complete k-partite graph.
$\theta N^2$
edges to turn the red graph into a balanced complete k-partite graph.
As well as referring to Section 2, we will need the following classical result of Andrásfai, Erdős, and Sós [Reference Andrásfai, Erdős and Sós2] (see also [Reference Brandt4] for a simpler proof).
Theorem 3.2 (Andrásfai–Erdős–Sós [Reference Andrásfai, Erdős and Sós2]). For every
![]() $k \geq 2$
, there exists
$k \geq 2$
, there exists
![]() $\rho \gt 0$
such that if
$\rho \gt 0$
such that if
![]() $G$
is a
$G$
is a
![]() $K_{k+1}$
-free graph on
$K_{k+1}$
-free graph on
![]() $m$
vertices with minimum degree greater than
$m$
vertices with minimum degree greater than
![]() $(1-\frac 1k - \rho )m$
, then
$(1-\frac 1k - \rho )m$
, then
![]() $G$
is
$G$
is
![]() $k$
-partite. Moreover, one may take
$k$
-partite. Moreover, one may take
![]() $\rho = 1/(3k^2-k)$
.
$\rho = 1/(3k^2-k)$
.
This is a stability version of Turán’s theorem. Indeed, Turán’s theorem implies that if a graph on
![]() $m$
vertices has minimum degree at least
$m$
vertices has minimum degree at least
![]() $\left(1-\frac 1k\right)m$
, then it contains a copy of
$\left(1-\frac 1k\right)m$
, then it contains a copy of
![]() $K_{k+1}$
, while the Andrásfai–Erdős–Sós theorem says that as long as the minimum degree is not too far below
$K_{k+1}$
, while the Andrásfai–Erdős–Sós theorem says that as long as the minimum degree is not too far below
![]() $(1-\frac 1k)m$
, every such graph must be
$(1-\frac 1k)m$
, every such graph must be
![]() $k$
-partite.
$k$
-partite.
Before proceeding to the technical details, let us briefly sketch the proof of Theorem 1.2. We are given a red/blue colouring of
![]() $E(K_N)$
and we wish to prove that either the colouring is close to complete
$E(K_N)$
and we wish to prove that either the colouring is close to complete
![]() $k$
-partite in red or it contains
$k$
-partite in red or it contains
![]() $(c,\gamma )$
-many books for some
$(c,\gamma )$
-many books for some
![]() $c,\gamma \gt 0$
. We begin by applying Lemma 2.1 to the red graph of the colouring to obtain an equitable partition
$c,\gamma \gt 0$
. We begin by applying Lemma 2.1 to the red graph of the colouring to obtain an equitable partition
![]() $V(K_N) = V_1 \sqcup \dotsb \sqcup V_m$
, where each part
$V(K_N) = V_1 \sqcup \dotsb \sqcup V_m$
, where each part
![]() $V_i$
and most pairs
$V_i$
and most pairs
![]() $(V_i,V_j)$
are
$(V_i,V_j)$
are
![]() $\eta$
-regular for some small
$\eta$
-regular for some small
![]() $\eta \gt 0$
. We now wish to improve our understanding of the colouring with respect to this partition.
$\eta \gt 0$
. We now wish to improve our understanding of the colouring with respect to this partition.
First, we show that all the parts
![]() $V_i$
must have very low internal red density. Indeed, if some part
$V_i$
must have very low internal red density. Indeed, if some part
![]() $V_i$
has
$V_i$
has
![]() $d_R(V_i)\geq \delta$
, for some fixed
$d_R(V_i)\geq \delta$
, for some fixed
![]() $\delta \gt 0$
, then the counting lemma, Lemma 2.2, implies that
$\delta \gt 0$
, then the counting lemma, Lemma 2.2, implies that
![]() $V_i$
contains many red
$V_i$
contains many red
![]() $K_{k+1}$
. By a simple averaging argument, this implies that some
$K_{k+1}$
. By a simple averaging argument, this implies that some
![]() $k$
-tuple of vertices in
$k$
-tuple of vertices in
![]() $V_i$
lies in many red
$V_i$
lies in many red
![]() $K_{k+1}$
, yielding a red book with
$K_{k+1}$
, yielding a red book with
![]() $\frac ck N$
pages. In fact, by using Lemma 2.4 in place of the averaging argument, we find
$\frac ck N$
pages. In fact, by using Lemma 2.4 in place of the averaging argument, we find
![]() $(c,\gamma )$
-many books if
$(c,\gamma )$
-many books if
![]() $d_R(V_i) \geq \delta$
, so we may assume that
$d_R(V_i) \geq \delta$
, so we may assume that
![]() $d_R(V_i)\lt \delta$
for all
$d_R(V_i)\lt \delta$
for all
![]() $i$
.
$i$
.
We next build a reduced graph
![]() $G$
with vertex set
$G$
with vertex set
![]() $v_1,\dots,v_m$
, where we make
$v_1,\dots,v_m$
, where we make
![]() $v_i v_j$
an edge if and only if
$v_i v_j$
an edge if and only if
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\eta$
-regular and
$\eta$
-regular and
![]() $d_R(V_i,V_j)\geq \delta$
. We claim that every vertex of
$d_R(V_i,V_j)\geq \delta$
. We claim that every vertex of
![]() $G$
has degree at least
$G$
has degree at least
![]() $(1- \frac 1k - \sigma )m$
for some small
$(1- \frac 1k - \sigma )m$
for some small
![]() $\sigma \gt 0$
. Indeed, if some vertex
$\sigma \gt 0$
. Indeed, if some vertex
![]() $v_i$
of
$v_i$
of
![]() $G$
has degree smaller than this, then we find that
$G$
has degree smaller than this, then we find that
![]() $V_i$
has very high blue density to roughly
$V_i$
has very high blue density to roughly
![]() $(\frac 1k + \sigma )m$
of the remaining parts
$(\frac 1k + \sigma )m$
of the remaining parts
![]() $V_j$
. Since
$V_j$
. Since
![]() $V_i$
also has very high internal blue density, we can use this to find many blue books with spines in
$V_i$
also has very high internal blue density, we can use this to find many blue books with spines in
![]() $V_i$
and
$V_i$
and
![]() $(\frac 1k + \gamma )N$
pages for some
$(\frac 1k + \gamma )N$
pages for some
![]() $0\lt \gamma \lt \sigma$
. This again yields
$0\lt \gamma \lt \sigma$
. This again yields
![]() $(c,\gamma )$
-many books in the colouring.
$(c,\gamma )$
-many books in the colouring.
So we may assume that the graph
![]() $G$
has high minimum degree. By applying Theorem 3.2, we find that either
$G$
has high minimum degree. By applying Theorem 3.2, we find that either
![]() $G$
is
$G$
is
![]() $k$
-partite or it contains a copy of
$k$
-partite or it contains a copy of
![]() $K_{k+1}$
. In the former case, we can show that the colouring itself is close to
$K_{k+1}$
. In the former case, we can show that the colouring itself is close to
![]() $k$
-partite in red. In the latter case, this
$k$
-partite in red. In the latter case, this
![]() $K_{k+1}$
yields
$K_{k+1}$
yields
![]() $k+1$
parts, say
$k+1$
parts, say
![]() $V_1,\dots,V_{k+1}$
, such that all pairs are
$V_1,\dots,V_{k+1}$
, such that all pairs are
![]() $\eta$
-regular and have red density at least
$\eta$
-regular and have red density at least
![]() $\delta$
. By another application of the counting lemma and an averaging argument, we can then show that this structure again yields
$\delta$
. By another application of the counting lemma and an averaging argument, we can then show that this structure again yields
![]() $(c,\gamma )$
-many red books.
$(c,\gamma )$
-many red books.
We now turn to the details of the proof. We will need the following fact about bipartite graphs, which is a simple consequence of a double-counting technique first introduced by Kővári, Sós, and Turán [Reference Kővári, Sós and Turán16].
Lemma 3.3.
Let
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $d \in (0,1)$
and let
$d \in (0,1)$
and let
![]() $\zeta = (d/4)^k$
. Let
$\zeta = (d/4)^k$
. Let
![]() $H$
be a bipartite graph with parts
$H$
be a bipartite graph with parts
![]() $A,B$
, where
$A,B$
, where
![]() $\lvert B\rvert \geq 2k/d$
, and suppose that
$\lvert B\rvert \geq 2k/d$
, and suppose that
![]() $H$
has at least
$H$
has at least
![]() $d \lvert A\rvert \lvert B\rvert$
edges. Let
$d \lvert A\rvert \lvert B\rvert$
edges. Let
![]() $\mathcal{H}$
be a
$\mathcal{H}$
be a
![]() $k$
-uniform hypergraph with vertex set
$k$
-uniform hypergraph with vertex set
![]() $B$
and at least
$B$
and at least
![]() $(1-\zeta ) \left(\substack{\lvert B\rvert \\[3pt] k}\right)$
edges. Then there are at least
$(1-\zeta ) \left(\substack{\lvert B\rvert \\[3pt] k}\right)$
edges. Then there are at least
![]() $\zeta \left(\substack{\lvert B\rvert \\[3pt] k} \right)$
edges of
$\zeta \left(\substack{\lvert B\rvert \\[3pt] k} \right)$
edges of
![]() $\mathcal{H}$
such that the vertices of each such edge have at least
$\mathcal{H}$
such that the vertices of each such edge have at least
![]() $\zeta \lvert A\rvert$
common neighbours in
$\zeta \lvert A\rvert$
common neighbours in
![]() $A$
.
$A$
.
Proof. For a
![]() $k$
-tuple
$k$
-tuple
![]() $Q \in \!\left(\substack{B\\[3pt] k } \right)$
, let
$Q \in \!\left(\substack{B\\[3pt] k } \right)$
, let
![]() $\textrm{ext}(Q)$
denote the number of common neighbours of
$\textrm{ext}(Q)$
denote the number of common neighbours of
![]() $Q$
in
$Q$
in
![]() $A$
. We double-count the number of stars
$A$
. We double-count the number of stars
![]() $K_{1,k}$
in
$K_{1,k}$
in
![]() $H$
whose central vertex is in
$H$
whose central vertex is in
![]() $A$
to find that
$A$
to find that
 \begin{equation*} \sum _{Q \in \left (\substack{ B\\[3pt] k }\right )} \textrm {ext}(Q) = \sum _{a \in A} \!\left (\begin {array}{c} \deg\!(a)\\[-3pt] k \end {array}\right )\geq \lvert A\rvert \left (\begin {array}{c} {\frac 1{\lvert A\rvert }\sum _{a \in A} \deg\!(a)}\\[-3pt] k \end {array}\right ) \geq \lvert A\rvert \left (\begin {array}{c} {d \lvert B\rvert }\\[-3pt] k \end {array}\right ), \end{equation*}
\begin{equation*} \sum _{Q \in \left (\substack{ B\\[3pt] k }\right )} \textrm {ext}(Q) = \sum _{a \in A} \!\left (\begin {array}{c} \deg\!(a)\\[-3pt] k \end {array}\right )\geq \lvert A\rvert \left (\begin {array}{c} {\frac 1{\lvert A\rvert }\sum _{a \in A} \deg\!(a)}\\[-3pt] k \end {array}\right ) \geq \lvert A\rvert \left (\begin {array}{c} {d \lvert B\rvert }\\[-3pt] k \end {array}\right ), \end{equation*}
where the first inequality follows from convexity. If we split the left-hand side into a sum over tuples
![]() $Q$
which are non-edges of
$Q$
which are non-edges of
![]() $\mathcal{H}$
, a sum over tuples
$\mathcal{H}$
, a sum over tuples
![]() $Q$
that are edges of
$Q$
that are edges of
![]() $\mathcal{H}$
with fewer than
$\mathcal{H}$
with fewer than
![]() $\zeta \lvert A\rvert$
extensions, and the remainder, we find that
$\zeta \lvert A\rvert$
extensions, and the remainder, we find that
 \begin{align*} \lvert A\rvert \left (\begin{array}{c}{d \lvert B\rvert }\\[-3pt] k \end{array}\right ) &\leq \sum _{Q \notin E(\mathcal{H})} \textrm{ext}(Q) + \sum _{\substack{Q \in E(\mathcal{H})\\ \textrm{ext}(Q) \lt \zeta \lvert A\rvert }} \textrm{ext}(Q) + \sum _{\substack{Q \in E(\mathcal{H})\\ \textrm{ext}(Q) \geq \zeta \lvert A\rvert }} \textrm{ext}(Q)\\[5pt] &\leq \zeta \lvert A\rvert \left (\begin{array}{c}{\lvert B\rvert }\\[-3pt] k \end{array}\right ) + \zeta \lvert A\rvert \left (\begin{array}{c}{\lvert B\rvert }\\[-3pt] k \end{array}\right ) + \lvert A\rvert \lvert \{Q \in E(\mathcal{H})\;:\;\textrm{ext}(Q) \geq \zeta \lvert A\rvert \}\rvert . \end{align*}
\begin{align*} \lvert A\rvert \left (\begin{array}{c}{d \lvert B\rvert }\\[-3pt] k \end{array}\right ) &\leq \sum _{Q \notin E(\mathcal{H})} \textrm{ext}(Q) + \sum _{\substack{Q \in E(\mathcal{H})\\ \textrm{ext}(Q) \lt \zeta \lvert A\rvert }} \textrm{ext}(Q) + \sum _{\substack{Q \in E(\mathcal{H})\\ \textrm{ext}(Q) \geq \zeta \lvert A\rvert }} \textrm{ext}(Q)\\[5pt] &\leq \zeta \lvert A\rvert \left (\begin{array}{c}{\lvert B\rvert }\\[-3pt] k \end{array}\right ) + \zeta \lvert A\rvert \left (\begin{array}{c}{\lvert B\rvert }\\[-3pt] k \end{array}\right ) + \lvert A\rvert \lvert \{Q \in E(\mathcal{H})\;:\;\textrm{ext}(Q) \geq \zeta \lvert A\rvert \}\rvert . \end{align*}
Therefore, the number of edges of
![]() $\mathcal{H}$
with at least
$\mathcal{H}$
with at least
![]() $\zeta \lvert A\rvert$
common neighbours is at least
$\zeta \lvert A\rvert$
common neighbours is at least
![]() $ \left(\substack{d \lvert B\rvert \\[3pt] k } \right) - 2\zeta \!\left(\substack{\lvert B\rvert \\[2pt] k} \right)$
. We note that
$ \left(\substack{d \lvert B\rvert \\[3pt] k } \right) - 2\zeta \!\left(\substack{\lvert B\rvert \\[2pt] k} \right)$
. We note that
 \begin{equation*} \frac {\left (\substack{{d \lvert B\rvert }\\[3pt] k }\right )}{\left (\substack{{\lvert B\rvert }\\[3pt] k }\right )} = \frac {d \lvert B\rvert }{\lvert B\rvert } \cdot \frac {d \lvert B\rvert -1}{\lvert B\rvert -1}\dotsb \frac {d \lvert B\rvert - (k-1)}{\lvert B\rvert -(k-1)} \geq \!\left (\frac d2\right )^k =2^k \zeta, \end{equation*}
\begin{equation*} \frac {\left (\substack{{d \lvert B\rvert }\\[3pt] k }\right )}{\left (\substack{{\lvert B\rvert }\\[3pt] k }\right )} = \frac {d \lvert B\rvert }{\lvert B\rvert } \cdot \frac {d \lvert B\rvert -1}{\lvert B\rvert -1}\dotsb \frac {d \lvert B\rvert - (k-1)}{\lvert B\rvert -(k-1)} \geq \!\left (\frac d2\right )^k =2^k \zeta, \end{equation*}
where we used our assumption that
![]() $\lvert B\rvert \geq 2k/d$
. Thus, the number of edges of
$\lvert B\rvert \geq 2k/d$
. Thus, the number of edges of
![]() $\mathcal{H}$
with at least
$\mathcal{H}$
with at least
![]() $\zeta \lvert A\rvert$
common neighbours in
$\zeta \lvert A\rvert$
common neighbours in
![]() $A$
is at least
$A$
is at least
 \begin{equation*} \left (\begin {array}{c} {d \lvert B\rvert }\\[-3pt] k \end {array}\right ) - 2\zeta \!\left (\begin {array}{c} {\lvert B\rvert }\\[-3pt] k \end {array}\right ) \geq (2^k \zeta - 2\zeta ) \left (\begin {array}{c} {\lvert B\rvert }\\[-3pt] k \end {array}\right ) \geq \zeta \!\left (\begin {array}{c} {\lvert B\rvert }\\[-3pt] k \end {array}\right ). \end{equation*}
\begin{equation*} \left (\begin {array}{c} {d \lvert B\rvert }\\[-3pt] k \end {array}\right ) - 2\zeta \!\left (\begin {array}{c} {\lvert B\rvert }\\[-3pt] k \end {array}\right ) \geq (2^k \zeta - 2\zeta ) \left (\begin {array}{c} {\lvert B\rvert }\\[-3pt] k \end {array}\right ) \geq \zeta \!\left (\begin {array}{c} {\lvert B\rvert }\\[-3pt] k \end {array}\right ). \end{equation*}
With these preliminaries in place, we are now ready to prove Theorem 1.2.
Proof of Theorem
1.2. Fix some
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\theta \in (0,1)$
, and a red/blue colouring of
$\theta \in (0,1)$
, and a red/blue colouring of
![]() $E(K_N)$
. Let
$E(K_N)$
. Let
![]() $\sigma =(\theta/(12k^4))^k$
,
$\sigma =(\theta/(12k^4))^k$
,
![]() $M_0=k$
,
$M_0=k$
,
![]() $\delta =\sigma ^2$
, and
$\delta =\sigma ^2$
, and
![]() $\eta = \delta ^{k^2}$
. Let
$\eta = \delta ^{k^2}$
. Let
![]() $M=M(\eta,M_0)$
be the parameter from Lemma 2.1 and let
$M=M(\eta,M_0)$
be the parameter from Lemma 2.1 and let
![]() $c=\delta ^{k^2}/M^4$
and
$c=\delta ^{k^2}/M^4$
and
![]() $\gamma =\delta ^{2k^2}/M^{2k}$
. We apply Lemma 2.1 to the red graph in our colouring with parameters
$\gamma =\delta ^{2k^2}/M^{2k}$
. We apply Lemma 2.1 to the red graph in our colouring with parameters
![]() $M_0$
and
$M_0$
and
![]() $\eta$
. This yields an equitable partition
$\eta$
. This yields an equitable partition
![]() $V(K_N)=V_1 \sqcup \dotsb \sqcup V_m$
with
$V(K_N)=V_1 \sqcup \dotsb \sqcup V_m$
with
![]() $M_0 \leq m \leq M$
such that each part
$M_0 \leq m \leq M$
such that each part
![]() $V_i$
is
$V_i$
is
![]() $\eta$
-regular in red and, for each
$\eta$
-regular in red and, for each
![]() $i$
, there are at most
$i$
, there are at most
![]() $\eta m$
values of
$\eta m$
values of
![]() $j \neq i$
for which
$j \neq i$
for which
![]() $(V_i,V_j)$
is not
$(V_i,V_j)$
is not
![]() $\eta$
-regular in red.
$\eta$
-regular in red.
First suppose that some part, say
![]() $V_1$
, has internal red density at least
$V_1$
, has internal red density at least
![]() $\delta$
. By the counting lemma, Lemma 2.2, we see that
$\delta$
. By the counting lemma, Lemma 2.2, we see that
![]() $V_1$
contains at least
$V_1$
contains at least
![]() $\frac{1}{(k+1)!}\Big(\delta ^{\left (\substack{k+1\\[3pt] 2} \right )}- \eta \!\left (\substack{ k+1\\[3pt] 2} \right )\Big)|V_1|^{k+1}$
red
$\frac{1}{(k+1)!}\Big(\delta ^{\left (\substack{k+1\\[3pt] 2} \right )}- \eta \!\left (\substack{ k+1\\[3pt] 2} \right )\Big)|V_1|^{k+1}$
red
![]() $K_{k+1}$
. Since each red
$K_{k+1}$
. Since each red
![]() $K_{k+1}$
contains exactly
$K_{k+1}$
contains exactly
![]() $k+1$
red
$k+1$
red
![]() $K_k$
, this implies that an average
$K_k$
, this implies that an average
![]() $k$
-tuple of vertices in
$k$
-tuple of vertices in
![]() $V_1$
lies in at least
$V_1$
lies in at least
 \begin{equation*} \frac {\frac {k+1}{(k+1)!}\left(\delta ^{\left (\substack{ k+1\\[3pt] 2 }\right )}- \eta \!\left (\begin {array}{c} k+1\\[-2pt] 2 \end {array}\right )\right)|V_1|^{k+1}}{\left (\begin {array}{c} {\lvert V_1\rvert }\\[-3pt] k \end {array}\right ) }\geq \!\left (\delta ^{\left (\substack{k+1\\[3pt] 2 }\right )}-\eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right ) |V_1|\;=\!:\; \xi M |V_1| \end{equation*}
\begin{equation*} \frac {\frac {k+1}{(k+1)!}\left(\delta ^{\left (\substack{ k+1\\[3pt] 2 }\right )}- \eta \!\left (\begin {array}{c} k+1\\[-2pt] 2 \end {array}\right )\right)|V_1|^{k+1}}{\left (\begin {array}{c} {\lvert V_1\rvert }\\[-3pt] k \end {array}\right ) }\geq \!\left (\delta ^{\left (\substack{k+1\\[3pt] 2 }\right )}-\eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right ) |V_1|\;=\!:\; \xi M |V_1| \end{equation*}
red
![]() $K_{k+1}$
. That is, if we pick a uniformly random
$K_{k+1}$
. That is, if we pick a uniformly random
![]() $k$
-tuple of vertices from
$k$
-tuple of vertices from
![]() $V_1$
, then the expected number of red
$V_1$
, then the expected number of red
![]() $K_{k+1}$
containing it is at least
$K_{k+1}$
containing it is at least
![]() $\xi M \lvert V_1\rvert$
. If we also define
$\xi M \lvert V_1\rvert$
. If we also define
![]() $\kappa = \Big(\delta ^{ \left(\substack{k\\[3pt] 2}\right)}- \eta \!\left(\substack{k\\[3pt] 2 } \right)\Big)/(k! M^k)$
, then Lemma 2.2 implies that
$\kappa = \Big(\delta ^{ \left(\substack{k\\[3pt] 2}\right)}- \eta \!\left(\substack{k\\[3pt] 2 } \right)\Big)/(k! M^k)$
, then Lemma 2.2 implies that
![]() $V_1$
contains at least
$V_1$
contains at least
![]() $\kappa N^k$
red
$\kappa N^k$
red
![]() $K_k$
, with an average one having at least
$K_k$
, with an average one having at least
![]() $\xi N$
extensions to a red
$\xi N$
extensions to a red
![]() $K_{k+1}$
, where we use the fact that
$K_{k+1}$
, where we use the fact that
![]() $|V_1| \geq N/M$
since the partition is equitable and has
$|V_1| \geq N/M$
since the partition is equitable and has
![]() $m \leq M$
parts. If we now set
$m \leq M$
parts. If we now set
![]() $\nu =\xi/2$
and apply Lemma 2.4, we conclude that
$\nu =\xi/2$
and apply Lemma 2.4, we conclude that
![]() $V_1$
contains at least
$V_1$
contains at least
![]() $(\xi \kappa/2) N^k$
red
$(\xi \kappa/2) N^k$
red
![]() $K_k$
, each with at least
$K_k$
, each with at least
![]() $(\xi/2)N$
extensions to a red
$(\xi/2)N$
extensions to a red
![]() $K_{k+1}$
. By our choice of parameters,
$K_{k+1}$
. By our choice of parameters,
 \begin{equation*} \xi = \frac 1M \!\left (\delta ^{\left (\substack{ k+1\\[3pt] 2 }\right )}-\eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right ) \geq \frac {\delta ^{k^2}}{2M} \end{equation*}
\begin{equation*} \xi = \frac 1M \!\left (\delta ^{\left (\substack{ k+1\\[3pt] 2 }\right )}-\eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right ) \geq \frac {\delta ^{k^2}}{2M} \end{equation*}
and, therefore,
![]() $\xi/2 \geq c/k +\gamma$
. Similarly,
$\xi/2 \geq c/k +\gamma$
. Similarly,
![]() $\kappa \geq \delta ^{k^2}/M^k$
and, therefore,
$\kappa \geq \delta ^{k^2}/M^k$
and, therefore,
![]() $\xi \kappa/2 \geq \gamma$
. Thus, we find that in this case the colouring contains
$\xi \kappa/2 \geq \gamma$
. Thus, we find that in this case the colouring contains
![]() $(c,\gamma )$
-many books.
$(c,\gamma )$
-many books.
Therefore, we may assume that all
![]() $V_i$
have
$V_i$
have
![]() $d_R(V_i) \lt \delta$
. We build a reduced graph
$d_R(V_i) \lt \delta$
. We build a reduced graph
![]() $G$
with vertex set
$G$
with vertex set
![]() $v_1,\ldots,v_m$
and declare
$v_1,\ldots,v_m$
and declare
![]() $\{v_i, v_j\} \in E(G)$
if
$\{v_i, v_j\} \in E(G)$
if
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\eta$
-regular and
$\eta$
-regular and
![]() $d_R(V_i,V_j) \geq \delta$
. Suppose that some vertex of
$d_R(V_i,V_j) \geq \delta$
. Suppose that some vertex of
![]() $G$
, say
$G$
, say
![]() $v_1$
, has degree less than
$v_1$
, has degree less than
![]() $(1- \frac 1k - \sigma )m$
. Since at most
$(1- \frac 1k - \sigma )m$
. Since at most
![]() $\eta m$
non-neighbours of
$\eta m$
non-neighbours of
![]() $v_1$
can come from irregular pairs, we find that
$v_1$
can come from irregular pairs, we find that
![]() $d_B(V_1,V_i) \geq 1- \delta$
for at least
$d_B(V_1,V_i) \geq 1- \delta$
for at least
![]() $(\frac 1k+\sigma -\eta )m$
choices of
$(\frac 1k+\sigma -\eta )m$
choices of
![]() $i \in [m]$
. Let
$i \in [m]$
. Let
![]() $I \subseteq [m]$
be the set of such
$I \subseteq [m]$
be the set of such
![]() $i$
. Since
$i$
. Since
![]() $d_B(V_1) \geq 1-\delta$
and
$d_B(V_1) \geq 1-\delta$
and
![]() $\delta \leq 1/k^2$
, we see that, for
$\delta \leq 1/k^2$
, we see that, for
![]() $\alpha =k \delta/4$
,
$\alpha =k \delta/4$
,
 \begin{equation*} d_B(V_1)^{\left (\substack{ k\\[3pt] 2 }\right )} \geq (1- \delta )^{\left (\substack{ k\\[3pt] 2 }\right )} \geq 1 -\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \delta \geq \alpha . \end{equation*}
\begin{equation*} d_B(V_1)^{\left (\substack{ k\\[3pt] 2 }\right )} \geq (1- \delta )^{\left (\substack{ k\\[3pt] 2 }\right )} \geq 1 -\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \delta \geq \alpha . \end{equation*}
Moreover, we have that
![]() $\eta \lt \alpha ^3/k^2$
by our choice of
$\eta \lt \alpha ^3/k^2$
by our choice of
![]() $\eta$
. Therefore, we may apply Lemma 2.3, which implies that if
$\eta$
. Therefore, we may apply Lemma 2.3, which implies that if
![]() $Q$
is a randomly chosen blue
$Q$
is a randomly chosen blue
![]() $K_k$
in
$K_k$
in
![]() $V_1$
and
$V_1$
and
![]() $u$
is some vertex in
$u$
is some vertex in
![]() $K_N$
, then
$K_N$
, then
![]() $\mathbb{P}(u\text{ extends }Q) \geq d(u,V_1)^k-4 \alpha$
. In particular, if we sum this up over all
$\mathbb{P}(u\text{ extends }Q) \geq d(u,V_1)^k-4 \alpha$
. In particular, if we sum this up over all
![]() $u \in \bigcup _{i \in I} V_i$
, we find that the expected number of blue extensions of
$u \in \bigcup _{i \in I} V_i$
, we find that the expected number of blue extensions of
![]() $Q$
is at least
$Q$
is at least
where the first inequality follows from the convexity of the function
![]() $x \mapsto x^k$
. Using
$x \mapsto x^k$
. Using
![]() $\eta \lt \sigma/2$
, we have that
$\eta \lt \sigma/2$
, we have that
where the last step follows from the bound
![]() $1/k+\sigma \leq 1/k+1/k \leq 1$
. By our choice of
$1/k+\sigma \leq 1/k+1/k \leq 1$
. By our choice of
![]() $\delta =\sigma ^2 \leq \sigma/(8k)$
, we see that the expected number of blue extensions of
$\delta =\sigma ^2 \leq \sigma/(8k)$
, we see that the expected number of blue extensions of
![]() $Q$
is at least
$Q$
is at least
![]() $(\frac 1k+\frac \sigma 4)N$
. Moreover, by Lemma 2.2, the number of choices for
$(\frac 1k+\frac \sigma 4)N$
. Moreover, by Lemma 2.2, the number of choices for
![]() $Q$
is at least
$Q$
is at least
![]() $\frac{1}{k!} \Big((1-\delta )^{\left (\substack{k\\[3pt] 2 }\right )}-\eta \!\left (\substack{k\\[3pt] 2} \right )\!\Big)(N/M)^k \geq \kappa N^k$
. Therefore, if we apply Lemma 2.4 with parameters
$\frac{1}{k!} \Big((1-\delta )^{\left (\substack{k\\[3pt] 2 }\right )}-\eta \!\left (\substack{k\\[3pt] 2} \right )\!\Big)(N/M)^k \geq \kappa N^k$
. Therefore, if we apply Lemma 2.4 with parameters
![]() $\kappa$
,
$\kappa$
,
![]() $\xi =\frac 1k+\frac \sigma 4$
, and
$\xi =\frac 1k+\frac \sigma 4$
, and
![]() $\nu =\frac 1k+\gamma$
, then we find that the colouring contains
$\nu =\frac 1k+\gamma$
, then we find that the colouring contains
![]() $(c,\gamma )$
-many books.
$(c,\gamma )$
-many books.
Therefore, we may assume that every vertex in
![]() $G$
has degree greater than
$G$
has degree greater than
![]() $(1- \frac 1k -\sigma )m$
, so, by Theorem 3.2 and the fact that
$(1- \frac 1k -\sigma )m$
, so, by Theorem 3.2 and the fact that
![]() $\sigma \lt 1/(3k^2-k)$
, we see that either
$\sigma \lt 1/(3k^2-k)$
, we see that either
![]() $G$
contains a
$G$
contains a
![]() $K_{k+1}$
or
$K_{k+1}$
or
![]() $G$
is
$G$
is
![]() $k$
-partite. Assume first that there is a
$k$
-partite. Assume first that there is a
![]() $K_{k+1}$
in
$K_{k+1}$
in
![]() $G$
. By relabelling the vertices, we may assume that
$G$
. By relabelling the vertices, we may assume that
![]() $v_1,\ldots,v_{k+1}$
form a clique. By the counting lemma, Lemma 2.2, we have that
$v_1,\ldots,v_{k+1}$
form a clique. By the counting lemma, Lemma 2.2, we have that
![]() $V_1,\ldots,V_k$
span at least
$V_1,\ldots,V_k$
span at least
![]() $\Big(\delta ^{ \left(\substack{k\\[3pt] 2 } \right)}- \eta \left(\substack{k\\[3pt] 2 } \right)\Big)(N/m)^k \geq \kappa N^k$
red
$\Big(\delta ^{ \left(\substack{k\\[3pt] 2 } \right)}- \eta \left(\substack{k\\[3pt] 2 } \right)\Big)(N/m)^k \geq \kappa N^k$
red
![]() $K_k$
and
$K_k$
and
![]() $V_1,\ldots,V_{k+1}$
span at least
$V_1,\ldots,V_{k+1}$
span at least
![]() $\Big(\delta ^{ \left(\substack{k+1\\[3pt] 2 } \right)} - \eta \left(\substack{k+1\\[3pt] 2} \right)\Big)(N/m)^{k+1}$
red
$\Big(\delta ^{ \left(\substack{k+1\\[3pt] 2 } \right)} - \eta \left(\substack{k+1\\[3pt] 2} \right)\Big)(N/m)^{k+1}$
red
![]() $K_{k+1}$
. Every such red
$K_{k+1}$
. Every such red
![]() $K_{k+1}$
contains exactly one red
$K_{k+1}$
contains exactly one red
![]() $K_k$
with one vertex in each of
$K_k$
with one vertex in each of
![]() $V_1,\dots,V_k$
, so an average
$V_1,\dots,V_k$
, so an average
![]() $k$
-tuple
$k$
-tuple
![]() $(v_1,\dots,v_k) \in V_1 \times \dotsb \times V_k$
lies in at least
$(v_1,\dots,v_k) \in V_1 \times \dotsb \times V_k$
lies in at least
 \begin{equation*} \frac {\left(\delta ^{\left (\substack{k+1\\[3pt] 2 }\right )} - \eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right)(N/m)^{k+1}}{(N/m)^k} \geq \!\left (\delta ^{\left (\substack{k+1\\[3pt] 2 }\right )} - \eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right ) \frac NM = \xi N. \end{equation*}
\begin{equation*} \frac {\left(\delta ^{\left (\substack{k+1\\[3pt] 2 }\right )} - \eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right)(N/m)^{k+1}}{(N/m)^k} \geq \!\left (\delta ^{\left (\substack{k+1\\[3pt] 2 }\right )} - \eta \!\left (\begin {array}{c} k+1\\[-3pt] 2 \end {array}\right )\right ) \frac NM = \xi N. \end{equation*}
Thus, we have a set of at least
![]() $\kappa N^k$
red
$\kappa N^k$
red
![]() $K_k$
with at least
$K_k$
with at least
![]() $\xi N$
extensions on average and so, applying Lemma 2.4 as before, our colouring has
$\xi N$
extensions on average and so, applying Lemma 2.4 as before, our colouring has
![]() $(c,\gamma )$
-many books.
$(c,\gamma )$
-many books.
Thus, we may assume that
![]() $G$
is
$G$
is
![]() $k$
-partite. Let this
$k$
-partite. Let this
![]() $k$
-partition of
$k$
-partition of
![]() $V(G)$
be
$V(G)$
be
![]() $A_1\sqcup \dotsb \sqcup A_k$
. Note that
$A_1\sqcup \dotsb \sqcup A_k$
. Note that
![]() $\lvert A_\ell \rvert \leq \left(\frac 1k+\sigma \right)m$
for every
$\lvert A_\ell \rvert \leq \left(\frac 1k+\sigma \right)m$
for every
![]() $\ell$
, since the minimum degree of
$\ell$
, since the minimum degree of
![]() $G$
is at least
$G$
is at least
![]() $(1-\frac 1k - \sigma )m$
and each
$(1-\frac 1k - \sigma )m$
and each
![]() $A_\ell$
is an independent set in
$A_\ell$
is an independent set in
![]() $G$
. This in turn implies that
$G$
. This in turn implies that
![]() $\lvert A_\ell \rvert \geq \left(\frac 1k-k\sigma \right)m$
for every
$\lvert A_\ell \rvert \geq \left(\frac 1k-k\sigma \right)m$
for every
![]() $\ell$
, since
$\ell$
, since
![]() $\lvert A_\ell \rvert = m -\sum _{\ell ' \neq \ell }\lvert A_{\ell '}\rvert \geq (\frac 1k-k\sigma )m$
. We lift this partition to a partition of the vertices of
$\lvert A_\ell \rvert = m -\sum _{\ell ' \neq \ell }\lvert A_{\ell '}\rvert \geq (\frac 1k-k\sigma )m$
. We lift this partition to a partition of the vertices of
![]() $K_N$
into
$K_N$
into
![]() $k$
parts
$k$
parts
![]() $X_1,\dots,X_k$
by letting
$X_1,\dots,X_k$
by letting
![]() $X_\ell = \bigcup _{v_i \in A_\ell }V_i$
, noting that our observations above imply that
$X_\ell = \bigcup _{v_i \in A_\ell }V_i$
, noting that our observations above imply that
![]() $\lvert X_\ell \rvert = (\frac 1k \pm k\sigma )N$
for all
$\lvert X_\ell \rvert = (\frac 1k \pm k\sigma )N$
for all
![]() $\ell$
. We claim that each
$\ell$
. We claim that each
![]() $X_\ell$
contains at most
$X_\ell$
contains at most
![]() $\frac{3\delta }2 \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2} \right )$
red edges. Indeed, observe that if
$\frac{3\delta }2 \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2} \right )$
red edges. Indeed, observe that if
![]() $v_i,v_j$
are two (not necessarily distinct) vertices of
$v_i,v_j$
are two (not necessarily distinct) vertices of
![]() $G$
that are in the same part
$G$
that are in the same part
![]() $A_\ell$
, then they must be non-adjacent in
$A_\ell$
, then they must be non-adjacent in
![]() $G$
. This means that either
$G$
. This means that either
![]() $(V_i,V_j)$
is an irregular pair or
$(V_i,V_j)$
is an irregular pair or
![]() $d_R(V_i,V_j)\lt \delta$
. There are at most
$d_R(V_i,V_j)\lt \delta$
. There are at most
![]() $\eta m^2$
irregular pairs, so the irregular pairs can contribute at most
$\eta m^2$
irregular pairs, so the irregular pairs can contribute at most
![]() $\eta N^2\leq 4k^2 \eta \lvert X_\ell \rvert ^2 \leq 10 k^2 \eta \!\left(\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right)$
red edges inside
$\eta N^2\leq 4k^2 \eta \lvert X_\ell \rvert ^2 \leq 10 k^2 \eta \!\left(\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right)$
red edges inside
![]() $X_\ell$
, where we used that
$X_\ell$
, where we used that
![]() $\lvert X_\ell \rvert \geq (\frac 1k-k\sigma )N \geq N/(2k)$
. All other pairs of parts inside each
$\lvert X_\ell \rvert \geq (\frac 1k-k\sigma )N \geq N/(2k)$
. All other pairs of parts inside each
![]() $X_\ell$
have red density at most
$X_\ell$
have red density at most
![]() $\delta$
, so the total number of red edges inside
$\delta$
, so the total number of red edges inside
![]() $X_\ell$
is at most
$X_\ell$
is at most
![]() $\delta \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right ) + 10k^2 \eta \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right ) \leq \frac{3\delta }2 \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right )$
, since
$\delta \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right ) + 10k^2 \eta \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right ) \leq \frac{3\delta }2 \!\left (\substack{\lvert X_\ell\rvert \\[3pt] 2 }\right )$
, since
![]() $\eta \leq \delta/(20k^2)$
. This implies that the number of ordered pairs of (not necessarily distinct) vertices in
$\eta \leq \delta/(20k^2)$
. This implies that the number of ordered pairs of (not necessarily distinct) vertices in
![]() $X_\ell$
which do not form a blue edge is at most
$X_\ell$
which do not form a blue edge is at most
![]() $2 \delta \lvert X_\ell \rvert ^2$
.
$2 \delta \lvert X_\ell \rvert ^2$
.
This already implies that the red graph can be made
![]() $k$
-partite by recolouring at most
$k$
-partite by recolouring at most
![]() $2\delta N^2$
edges, so it only remains to show that by recolouring a small number of additional edges, we can make the red graph balanced complete
$2\delta N^2$
edges, so it only remains to show that by recolouring a small number of additional edges, we can make the red graph balanced complete
![]() $k$
-partite. For this, suppose that
$k$
-partite. For this, suppose that
![]() $d_B(X_1,X_2) \geq \theta/k^2$
. If we sample (with repetition) a random
$d_B(X_1,X_2) \geq \theta/k^2$
. If we sample (with repetition) a random
![]() $k$
-tuple
$k$
-tuple
![]() $Q$
of vertices from
$Q$
of vertices from
![]() $X_2$
, then the probability that it does not form a blue clique is at most
$X_2$
, then the probability that it does not form a blue clique is at most
![]() $\left(\substack{ k\\[3pt] 2 } \right)\cdot 2 \delta \leq k^2 \delta$
, since each random pair of vertices does not span a blue edge with probability at most
$\left(\substack{ k\\[3pt] 2 } \right)\cdot 2 \delta \leq k^2 \delta$
, since each random pair of vertices does not span a blue edge with probability at most
![]() $2\delta$
. Moreover, the expected number of common blue neighbours of
$2\delta$
. Moreover, the expected number of common blue neighbours of
![]() $Q$
inside
$Q$
inside
![]() $X_2$
is at least
$X_2$
is at least
![]() $(1-2\delta )^k \lvert X_2\rvert - k\geq (1-2k\delta )\lvert X_2\rvert$
, by convexity. By applying Markov’s inequality as in the proof of Lemma 2.4, the probability that
$(1-2\delta )^k \lvert X_2\rvert - k\geq (1-2k\delta )\lvert X_2\rvert$
, by convexity. By applying Markov’s inequality as in the proof of Lemma 2.4, the probability that
![]() $Q$
has fewer than
$Q$
has fewer than
![]() $(1-\sqrt \delta )\lvert X_2\rvert$
common blue neighbours in
$(1-\sqrt \delta )\lvert X_2\rvert$
common blue neighbours in
![]() $X_2$
is at most
$X_2$
is at most
![]() $2k\sqrt \delta$
. Therefore, the probability that
$2k\sqrt \delta$
. Therefore, the probability that
![]() $Q$
is a blue clique with at least
$Q$
is a blue clique with at least
![]() $(1-\sqrt \delta )\lvert X_2\rvert$
common blue neighbours in
$(1-\sqrt \delta )\lvert X_2\rvert$
common blue neighbours in
![]() $X_2$
is at least
$X_2$
is at least
![]() $1-k^2 \delta -2k\sqrt \delta \geq 1-3k\sqrt \delta$
, since
$1-k^2 \delta -2k\sqrt \delta \geq 1-3k\sqrt \delta$
, since
![]() $\sqrt \delta \leq 1/k$
. Let
$\sqrt \delta \leq 1/k$
. Let
![]() $\mathcal{H}$
be the
$\mathcal{H}$
be the
![]() $k$
-uniform hypergraph with vertex set
$k$
-uniform hypergraph with vertex set
![]() $X_2$
whose edges are all blue
$X_2$
whose edges are all blue
![]() $K_k$
in
$K_k$
in
![]() $X_2$
with at least
$X_2$
with at least
![]() $(1-\sqrt \delta )\lvert X_2\rvert$
common blue neighbours in
$(1-\sqrt \delta )\lvert X_2\rvert$
common blue neighbours in
![]() $X_2$
. Then
$X_2$
. Then
![]() $\mathcal{H}$
has at least
$\mathcal{H}$
has at least
![]() $(1-3k\sqrt \delta ) \left(\substack{\lvert X_2\rvert \\[3pt] k } \right)$
edges.
$(1-3k\sqrt \delta ) \left(\substack{\lvert X_2\rvert \\[3pt] k } \right)$
edges.
We now apply Lemma 3.3 to the hypergraph
![]() $\mathcal{H}$
and to the bipartite graph of blue edges between
$\mathcal{H}$
and to the bipartite graph of blue edges between
![]() $X_1$
and
$X_1$
and
![]() $X_2$
, which has edge density
$X_2$
, which has edge density
![]() $d\geq \theta/k^2$
by assumption. We have that
$d\geq \theta/k^2$
by assumption. We have that
![]() $(d/4)^k \geq (\theta/(4k^2))^k \geq 3k\sigma = 3k\sqrt \delta$
by our choice of
$(d/4)^k \geq (\theta/(4k^2))^k \geq 3k\sigma = 3k\sqrt \delta$
by our choice of
![]() $\sigma$
and
$\sigma$
and
![]() $\delta$
, so we may indeed apply Lemma 3.3 to conclude that at least
$\delta$
, so we may indeed apply Lemma 3.3 to conclude that at least
![]() $(\theta/(4k^2))^k \left(\substack{\lvert X_2\rvert \\[3pt] k } \right)$
of the edges of
$(\theta/(4k^2))^k \left(\substack{\lvert X_2\rvert \\[3pt] k } \right)$
of the edges of
![]() $\mathcal{H}$
have at least
$\mathcal{H}$
have at least
![]() $(\theta/(4k^2))^k\lvert X_1\rvert$
common blue neighbours in
$(\theta/(4k^2))^k\lvert X_1\rvert$
common blue neighbours in
![]() $X_1$
. This yields at least
$X_1$
. This yields at least
 \begin{equation*} \left (\frac \theta {4k^2}\right )^k \left (\begin {array}{c} {\lvert X_2\rvert }\\[-3pt] k \end {array}\right ) \geq \!\left (\frac {\theta \lvert X_2\rvert }{4k^3}\right )^k \geq \!\left (\frac {\theta }{8k^4}\right )^k N^k \geq \gamma N^k \end{equation*}
\begin{equation*} \left (\frac \theta {4k^2}\right )^k \left (\begin {array}{c} {\lvert X_2\rvert }\\[-3pt] k \end {array}\right ) \geq \!\left (\frac {\theta \lvert X_2\rvert }{4k^3}\right )^k \geq \!\left (\frac {\theta }{8k^4}\right )^k N^k \geq \gamma N^k \end{equation*}
blue
![]() $K_k$
, each of which has at least
$K_k$
, each of which has at least
 \begin{align*} (1-\sqrt \delta )\lvert X_2\rvert + \left (\frac \theta{4k^2}\right )^k \lvert X_1\rvert &\geq \!\left (1-\sqrt \delta + \left (\frac \theta{4k^2}\right )^k\right ) \left (\frac 1k -k\sigma \right )N\\[5pt] &\geq \!\left (\frac 1k + \left (\frac \theta{4k^3}\right )^k -\sqrt \delta - 2k\sigma \right )N\\[5pt] &\geq \!\left (\frac 1k + \left (\frac \theta{4k^3}\right )^k - 3k\sigma \right )N\\[5pt] &\geq \!\left (\frac 1k+\gamma \right )N \end{align*}
\begin{align*} (1-\sqrt \delta )\lvert X_2\rvert + \left (\frac \theta{4k^2}\right )^k \lvert X_1\rvert &\geq \!\left (1-\sqrt \delta + \left (\frac \theta{4k^2}\right )^k\right ) \left (\frac 1k -k\sigma \right )N\\[5pt] &\geq \!\left (\frac 1k + \left (\frac \theta{4k^3}\right )^k -\sqrt \delta - 2k\sigma \right )N\\[5pt] &\geq \!\left (\frac 1k + \left (\frac \theta{4k^3}\right )^k - 3k\sigma \right )N\\[5pt] &\geq \!\left (\frac 1k+\gamma \right )N \end{align*}
extensions to a blue
![]() $K_{k+1}$
, where in both computations we used the fact that
$K_{k+1}$
, where in both computations we used the fact that
![]() $\lvert X_1\rvert,\lvert X_2\rvert \geq (\frac 1k - k\sigma )N\geq N/(2k)$
, as well as our choices of
$\lvert X_1\rvert,\lvert X_2\rvert \geq (\frac 1k - k\sigma )N\geq N/(2k)$
, as well as our choices of
![]() $\sqrt \delta = \sigma = (\theta/(12k^4))^k$
. Thus, in this case, we have again found
$\sqrt \delta = \sigma = (\theta/(12k^4))^k$
. Thus, in this case, we have again found
![]() $(c,\gamma )$
-many books, a contradiction.
$(c,\gamma )$
-many books, a contradiction.
Hence, we may assume that
![]() $d_B(X_1,X_2) \lt \theta/k^2$
. By the same argument, all the blue densities between different parts
$d_B(X_1,X_2) \lt \theta/k^2$
. By the same argument, all the blue densities between different parts
![]() $X_\ell$
can be assumed to be at most
$X_\ell$
can be assumed to be at most
![]() $\theta/k^2$
. Since we have already argued that the red density inside each part is at most
$\theta/k^2$
. Since we have already argued that the red density inside each part is at most
![]() $2\delta$
, we see that, by recolouring at most
$2\delta$
, we see that, by recolouring at most
![]() $\left( \left(\substack{k\\[3pt] 2 } \right)\theta/k^2 + 2k\delta \right)N^2$
edges, we can make the red graph complete
$\left( \left(\substack{k\\[3pt] 2 } \right)\theta/k^2 + 2k\delta \right)N^2$
edges, we can make the red graph complete
![]() $k$
-partite. Finally, we recall that each part
$k$
-partite. Finally, we recall that each part
![]() $X_\ell$
has size
$X_\ell$
has size
![]() $\lvert X_\ell \rvert = (\frac 1k \pm k\sigma )N$
. Therefore, by moving at most
$\lvert X_\ell \rvert = (\frac 1k \pm k\sigma )N$
. Therefore, by moving at most
![]() $k^2\sigma N$
arbitrary vertices into another part, we see that we can make our partition equitable. We then recolour the edges incident with any moved vertex to obtain a balanced complete
$k^2\sigma N$
arbitrary vertices into another part, we see that we can make our partition equitable. We then recolour the edges incident with any moved vertex to obtain a balanced complete
![]() $k$
-partite red graph. Doing so entails recolouring at most
$k$
-partite red graph. Doing so entails recolouring at most
![]() $k^2 \sigma N^2$
additional edges. Thus, in total, we recolour at most
$k^2 \sigma N^2$
additional edges. Thus, in total, we recolour at most
 \begin{equation*} \left (\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \frac \theta {k^2} + 2k\delta + k^2 \sigma \right )N^2 \leq \left (\frac \theta 2 + 3k^2 \sigma \right ) \leq \theta N^2 \end{equation*}
\begin{equation*} \left (\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \frac \theta {k^2} + 2k\delta + k^2 \sigma \right )N^2 \leq \left (\frac \theta 2 + 3k^2 \sigma \right ) \leq \theta N^2 \end{equation*}
edges, where we used that
![]() $\delta \leq \sigma$
and
$\delta \leq \sigma$
and
![]() $\sigma \leq (\theta/(12k^4))^k \leq \theta/(6k^2)$
.
$\sigma \leq (\theta/(12k^4))^k \leq \theta/(6k^2)$
.
4. An upper bound matching the random bound
In this section, we prove Theorem 1.3, which says that when
![]() $c$
is not too small, the random lower bound for
$c$
is not too small, the random lower bound for
![]() $r(B_{cn}^{(k)}, B_n ^{(k)})$
is asymptotically tight. To prove this theorem, we will mimic our simplified proof of the diagonal result from [Reference Conlon, Fox and Wigderson10, Section 3], though it needs to be adapted to the off-diagonal setting in several ways. Before proceeding with the details, we sketch the proof at a high level, indicating which parts require new ideas beyond those already present in [Reference Conlon, Fox and Wigderson10].
$r(B_{cn}^{(k)}, B_n ^{(k)})$
is asymptotically tight. To prove this theorem, we will mimic our simplified proof of the diagonal result from [Reference Conlon, Fox and Wigderson10, Section 3], though it needs to be adapted to the off-diagonal setting in several ways. Before proceeding with the details, we sketch the proof at a high level, indicating which parts require new ideas beyond those already present in [Reference Conlon, Fox and Wigderson10].
A key notion used in the proof is that of a red-blocked configuration. Informally, a red-blocked configuration consists of
![]() $k$
disjoint vertex sets such that each set and all pairs are
$k$
disjoint vertex sets such that each set and all pairs are
![]() $\eta$
-regular for some small
$\eta$
-regular for some small
![]() $\eta$
, every set has red density at least
$\eta$
, every set has red density at least
![]() $\delta$
for some small
$\delta$
for some small
![]() $\delta$
, and every pair has blue density at least
$\delta$
, and every pair has blue density at least
![]() $\delta$
. A blue-blocked configuration is defined similarly, except with the roles of red and blue interchanged. Like the good and great configurations defined in [Reference Conlon, Fox and Wigderson10], we care about such configurations because their existence automatically implies the existence of large monochromatic books. The precise statement is given in Lemma 4.3, but, roughly, it says that if we have a red/blue colouring of the complete graph on
$\delta$
. A blue-blocked configuration is defined similarly, except with the roles of red and blue interchanged. Like the good and great configurations defined in [Reference Conlon, Fox and Wigderson10], we care about such configurations because their existence automatically implies the existence of large monochromatic books. The precise statement is given in Lemma 4.3, but, roughly, it says that if we have a red/blue colouring of the complete graph on
![]() $(c^{1/k}+1)^k n +o(n)$
vertices which contains a red-blocked or a blue-blocked configuration and
$(c^{1/k}+1)^k n +o(n)$
vertices which contains a red-blocked or a blue-blocked configuration and
![]() $k$
is sufficiently large with respect to
$k$
is sufficiently large with respect to
![]() $c$
, then the colouring contains a red
$c$
, then the colouring contains a red
![]() $B_{cn}^{(k)}$
or a blue
$B_{cn}^{(k)}$
or a blue
![]() $B_n^{(k)}$
. This is the key lemma which underlies the entire proof. Its proof is similar to that of [Reference Conlon, Fox and Wigderson10, Lemma 3.3], but requires a few modifications. First, the analytic inequality which yields the result is more complicated in the off-diagonal setting and this is where the (necessary) assumption that
$B_n^{(k)}$
. This is the key lemma which underlies the entire proof. Its proof is similar to that of [Reference Conlon, Fox and Wigderson10, Lemma 3.3], but requires a few modifications. First, the analytic inequality which yields the result is more complicated in the off-diagonal setting and this is where the (necessary) assumption that
![]() $k$
is large with respect to
$k$
is large with respect to
![]() $c$
comes from. Second, the averaging arguments used in the proof of Lemma 4.3 require a little more care than those used in the proof of [Reference Conlon, Fox and Wigderson10, Lemma 3.3], because we must take
$c$
comes from. Second, the averaging arguments used in the proof of Lemma 4.3 require a little more care than those used in the proof of [Reference Conlon, Fox and Wigderson10, Lemma 3.3], because we must take
![]() $(p,1-p)$
-weighted averages here. Finally, though in principle one needs separate arguments to deal with red-blocked configurations and blue-blocked configurations, it turns out that the same proof works for both cases, simply by interchanging the roles of red and blue and of
$(p,1-p)$
-weighted averages here. Finally, though in principle one needs separate arguments to deal with red-blocked configurations and blue-blocked configurations, it turns out that the same proof works for both cases, simply by interchanging the roles of red and blue and of
![]() $p$
and
$p$
and
![]() $1-p$
.
$1-p$
.
The remainder of the proof now comes down to finding a red-blocked or blue-blocked configuration or else finding a large monochromatic book directly. To do this, we begin by applying Lemma 2.1 to the red graph of the colouring, obtaining a regular equitable partition
![]() $V(K_N) = V_1\sqcup \dotsb \sqcup V_m$
. Call a part red if it contains more red edges than blue edges and blue otherwise. We assume for now that at least
$V(K_N) = V_1\sqcup \dotsb \sqcup V_m$
. Call a part red if it contains more red edges than blue edges and blue otherwise. We assume for now that at least
![]() $pm$
of the parts are blue; the case where at least
$pm$
of the parts are blue; the case where at least
![]() $(1-p)m$
of the parts are red runs similarly. We build a reduced graph
$(1-p)m$
of the parts are red runs similarly. We build a reduced graph
![]() $G$
whose vertices are in bijection with the blue parts and where edges represent pairs of parts that are regular and have red density at least
$G$
whose vertices are in bijection with the blue parts and where edges represent pairs of parts that are regular and have red density at least
![]() $\delta$
for some small
$\delta$
for some small
![]() $\delta \gt 0$
. By defining
$\delta \gt 0$
. By defining
![]() $G$
in this way, we see that a
$G$
in this way, we see that a
![]() $K_k$
in
$K_k$
in
![]() $G$
corresponds to a blue-blocked configuration in the original colouring, so it suffices to find a
$G$
corresponds to a blue-blocked configuration in the original colouring, so it suffices to find a
![]() $K_k$
in
$K_k$
in
![]() $G$
.
$G$
.
To do this, we first show that every vertex in
![]() $G$
must have degree at least roughly
$G$
must have degree at least roughly
![]() $(1-p^{k-1})\lvert V(G)\rvert$
. Indeed, if this is not the case, since
$(1-p^{k-1})\lvert V(G)\rvert$
. Indeed, if this is not the case, since
![]() $\lvert V(G)\rvert \geq pm$
, we find that there is some blue part
$\lvert V(G)\rvert \geq pm$
, we find that there is some blue part
![]() $V_i$
which has very high blue density to at least roughly
$V_i$
which has very high blue density to at least roughly
![]() $p^k m$
other parts. This can then be used to find a blue
$p^k m$
other parts. This can then be used to find a blue
![]() $B_n^{(k)}$
, where
$B_n^{(k)}$
, where
![]() $n \approx p^kN$
. So we may conclude that every vertex in
$n \approx p^kN$
. So we may conclude that every vertex in
![]() $G$
has high degree. But, by Turán’s theorem, plus the fact that
$G$
has high degree. But, by Turán’s theorem, plus the fact that
![]() $p^{k-1}\lt 1/(k-1)$
for sufficiently large
$p^{k-1}\lt 1/(k-1)$
for sufficiently large
![]() $k$
, this implies that
$k$
, this implies that
![]() $G$
contains a copy of
$G$
contains a copy of
![]() $K_k$
, as desired.
$K_k$
, as desired.
We now begin the detailed proof of Theorem 1.3. The following result generalizes a key analytic inequality from the diagonal case [Reference Conlon, Fox and Wigderson10, Lemma 3.4].
Lemma 4.1.
For every
![]() $p \in (0,1)$
, there exists some
$p \in (0,1)$
, there exists some
![]() $k_1 \in \mathbb{N}$
such that if
$k_1 \in \mathbb{N}$
such that if
![]() $k \geq k_1$
and
$k \geq k_1$
and
![]() $x_1,\ldots,x_k \in [0,1]$
, then
$x_1,\ldots,x_k \in [0,1]$
, then
 \begin{equation*} p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k} \sum _{i=1}^k (1-x_i)^k \geq 1. \end{equation*}
\begin{equation*} p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k} \sum _{i=1}^k (1-x_i)^k \geq 1. \end{equation*}
Moreover, one may take
 \begin{equation*} k_1(p) = \begin {cases} 6 &\text {if }p \geq 1-5/(4e)\\[5pt] 1+\frac {5 - \log \log \frac 1{1-p} + \log (-\log \log \frac 1{1-p})}{\log \frac 1{1-p}}&\text {otherwise.} \end {cases} \end{equation*}
\begin{equation*} k_1(p) = \begin {cases} 6 &\text {if }p \geq 1-5/(4e)\\[5pt] 1+\frac {5 - \log \log \frac 1{1-p} + \log (-\log \log \frac 1{1-p})}{\log \frac 1{1-p}}&\text {otherwise.} \end {cases} \end{equation*}
Proof. First suppose that
![]() $x_j \leq \frac 1k$
for some
$x_j \leq \frac 1k$
for some
![]() $j \in [k]$
. Then we have that
$j \in [k]$
. Then we have that
 \begin{equation*} \frac {(1-p)^{1-k}}{k} \sum _{i=1}^k (1-x_i)^k \geq \frac {(1-p)^{1-k}}{k}(1-x_j)^k \geq \frac {(1-p)^{1-k}}{k} \!\left ( 1- \frac 1k \right ) ^k \geq \frac {(1-p)^{1-k}}{e^2k} \;=\!:\; f(p,k), \end{equation*}
\begin{equation*} \frac {(1-p)^{1-k}}{k} \sum _{i=1}^k (1-x_i)^k \geq \frac {(1-p)^{1-k}}{k}(1-x_j)^k \geq \frac {(1-p)^{1-k}}{k} \!\left ( 1- \frac 1k \right ) ^k \geq \frac {(1-p)^{1-k}}{e^2k} \;=\!:\; f(p,k), \end{equation*}
where we used the inequality
![]() $1-x \geq e^{-2x}$
for
$1-x \geq e^{-2x}$
for
![]() $x \in [0,\frac 12]$
. If
$x \in [0,\frac 12]$
. If
![]() $p \geq 1-5/(4e)$
, then
$p \geq 1-5/(4e)$
, then
![]() $1-p \leq 5/(4e)$
, so
$1-p \leq 5/(4e)$
, so
![]() $f(p,k) \geq (4/5)^{k-1} e^{k-3}/k$
. Once
$f(p,k) \geq (4/5)^{k-1} e^{k-3}/k$
. Once
![]() $k \geq 6$
, this last expression is at least
$k \geq 6$
, this last expression is at least
![]() $1$
, so in the case where
$1$
, so in the case where
![]() $p \geq 1-5/(4e)$
, we may take
$p \geq 1-5/(4e)$
, we may take
![]() $k_1(p)=6$
.
$k_1(p)=6$
.
For
![]() $p\lt 1-5/(4e)$
, let
$p\lt 1-5/(4e)$
, let
![]() $\lambda =\lambda (p) = \log \frac 1{1-p}$
and
$\lambda =\lambda (p) = \log \frac 1{1-p}$
and
 \begin{equation*} k_1(p)=1+\frac {5 - \log \lambda + \log \log \frac 1\lambda }{\lambda }= 1+\frac {5 - \log \log \frac 1{1-p} + \log \!\left(\!-\!\log \log \frac 1{1-p}\right)}{\log \frac 1{1-p}}. \end{equation*}
\begin{equation*} k_1(p)=1+\frac {5 - \log \lambda + \log \log \frac 1\lambda }{\lambda }= 1+\frac {5 - \log \log \frac 1{1-p} + \log \!\left(\!-\!\log \log \frac 1{1-p}\right)}{\log \frac 1{1-p}}. \end{equation*}
We now claim that
By differentiating, we see that
![]() $f(p,k)$
is monotonically increasing in
$f(p,k)$
is monotonically increasing in
![]() $k$
for
$k$
for
![]() $k \geq 1/\log \frac 1{1-p} = 1/\lambda$
. Since
$k \geq 1/\log \frac 1{1-p} = 1/\lambda$
. Since
![]() $p\lt 1-5/(4e)$
, we have that
$p\lt 1-5/(4e)$
, we have that
![]() $5-\log \lambda +\log \log \frac 1\lambda \gt 1$
and so we are in the monotonicity regime. It therefore suffices to prove the statement for
$5-\log \lambda +\log \log \frac 1\lambda \gt 1$
and so we are in the monotonicity regime. It therefore suffices to prove the statement for
![]() $k=k_1(p)$
. Note now that
$k=k_1(p)$
. Note now that
and let
![]() $g(p)=1 + \lambda/\log \frac 1 \lambda + 5/\log \frac 1\lambda + \log \log \frac 1\lambda/\log \frac 1\lambda$
. Then we have
$g(p)=1 + \lambda/\log \frac 1 \lambda + 5/\log \frac 1\lambda + \log \log \frac 1\lambda/\log \frac 1\lambda$
. Then we have
Thus, to prove that
![]() $f(p,k_1(p))\geq 1$
, it suffices to prove that
$f(p,k_1(p))\geq 1$
, it suffices to prove that
![]() $g(p) \leq e^3$
for all
$g(p) \leq e^3$
for all
![]() $p \lt 1-5/(4e)$
. By differentiating, one can check that
$p \lt 1-5/(4e)$
. By differentiating, one can check that
![]() $g(p)$
is monotonically increasing in
$g(p)$
is monotonically increasing in
![]() $p \in [0,1-5/(4e)]$
. Thus, it suffices to check that
$p \in [0,1-5/(4e)]$
. Thus, it suffices to check that
![]() $g(1-5/(4e)) \leq e^3$
. But
$g(1-5/(4e)) \leq e^3$
. But
![]() $g(1-5/(4e))\approx 18.4 \lt e^3$
, so
$g(1-5/(4e))\approx 18.4 \lt e^3$
, so
![]() $f(p,k_1(p))\geq 1$
, as claimed. Hence, from now on, we may assume that all the
$f(p,k_1(p))\geq 1$
, as claimed. Hence, from now on, we may assume that all the
![]() $x_i$
are in
$x_i$
are in
![]() $\big(\frac 1k,1\big]$
.
$\big(\frac 1k,1\big]$
.
For the moment, let’s assume that all the
![]() $x_i$
are in
$x_i$
are in
![]() $(\frac 1k,1)$
. Note that the function
$(\frac 1k,1)$
. Note that the function
![]() $\varphi \;:\;y \mapsto (1-e^y)^k$
is strictly convex on the interval
$\varphi \;:\;y \mapsto (1-e^y)^k$
is strictly convex on the interval
![]() $(\!\log \frac 1k,0)$
. By the multiplicative Jensen inequality, Lemma 2.5, this implies that, subject to the constraint
$(\!\log \frac 1k,0)$
. By the multiplicative Jensen inequality, Lemma 2.5, this implies that, subject to the constraint
![]() $\prod _{i=1}^k x_i=z$
, the term
$\prod _{i=1}^k x_i=z$
, the term
![]() $\frac 1k \sum _{i=1}^k \!(1-x_i)^k$
is minimized when all the
$\frac 1k \sum _{i=1}^k \!(1-x_i)^k$
is minimized when all the
![]() $x_i$
are equal to
$x_i$
are equal to
![]() $z^{1/k}$
. Therefore,
$z^{1/k}$
. Therefore,
 \begin{equation*} p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k} \sum _{i=1}^k (1-x_i)^k \geq p^{1-k}z+(1-p)^{1-k}(1-z^{1/k})^k. \end{equation*}
\begin{equation*} p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k} \sum _{i=1}^k (1-x_i)^k \geq p^{1-k}z+(1-p)^{1-k}(1-z^{1/k})^k. \end{equation*}
So it suffices to minimize this expression as a function of
![]() $z$
. Changing variables to
$z$
. Changing variables to
![]() $w=z^{1/k}$
, it suffices to minimize
$w=z^{1/k}$
, it suffices to minimize
as a function of
![]() $w$
. By differentiating, we find that
$w$
. By differentiating, we find that
![]() $\psi$
is minimized at
$\psi$
is minimized at
![]() $w=p$
, where
$w=p$
, where
![]() $\psi (p)=1$
. This proves the desired result as long as all the
$\psi (p)=1$
. This proves the desired result as long as all the
![]() $x_i$
are in
$x_i$
are in
![]() $[0,1)$
. By continuity, the result then extends to all
$[0,1)$
. By continuity, the result then extends to all
![]() $x_i \in [0,1]$
.
$x_i \in [0,1]$
.
Definition 4.2. Fix parameters
![]() $k \in \mathbb{N}$
and
$k \in \mathbb{N}$
and
![]() $\eta,\delta \in (0,1)$
and suppose that we are given a red/blue colouring of
$\eta,\delta \in (0,1)$
and suppose that we are given a red/blue colouring of
![]() $E(K_N)$
. Then a
$E(K_N)$
. Then a
![]() $k$
-tuple of pairwise disjoint vertex sets
$k$
-tuple of pairwise disjoint vertex sets
![]() $C_1,\ldots,C_k \subseteq V(K_N)$
is called a
$C_1,\ldots,C_k \subseteq V(K_N)$
is called a
![]() $(k,\eta,\delta )$
-red-blocked configuration if the following properties are satisfied:
$(k,\eta,\delta )$
-red-blocked configuration if the following properties are satisfied:
-
1. Each
 $C_i$
is
$C_i$
is
 $\eta$
-regular with itself,
$\eta$
-regular with itself, -
2. Each
 $C_i$
has internal red density at least
$C_i$
has internal red density at least
 $\delta$
, and
$\delta$
, and -
3. For all
 $i \neq j$
, the pair
$i \neq j$
, the pair
 $(C_i,C_j)$
is
$(C_i,C_j)$
is
 $\eta$
-regular and has blue density at least
$\eta$
-regular and has blue density at least
 $\delta$
.
$\delta$
.
Similarly, we say that
![]() $C_1,\ldots,C_k$
is a
$C_1,\ldots,C_k$
is a
![]() $(k,\eta,\delta )$
-blue-blocked configuration if properties (1–3) hold, but with the roles of red and blue interchanged.
$(k,\eta,\delta )$
-blue-blocked configuration if properties (1–3) hold, but with the roles of red and blue interchanged.
The reason we care about these configurations is that, for appropriate choices of the parameters
![]() $\eta$
and
$\eta$
and
![]() $\delta$
, their existence yields the existence of the required monochromatic books. This idea (or, rather, the version of it when red and blue play symmetric roles) already appears implicitly in the work of the first author [Reference Conlon9], but was made much more explicit in the prequel to this paper [Reference Conlon, Fox and Wigderson10]. The precise statement we will need here is given by the next lemma.
$\delta$
, their existence yields the existence of the required monochromatic books. This idea (or, rather, the version of it when red and blue play symmetric roles) already appears implicitly in the work of the first author [Reference Conlon9], but was made much more explicit in the prequel to this paper [Reference Conlon, Fox and Wigderson10]. The precise statement we will need here is given by the next lemma.
Lemma 4.3.
For every
![]() $p \in [\frac 12, 1)$
, there is
$p \in [\frac 12, 1)$
, there is
![]() $k_2 \in \mathbb{N}$
such that the following holds. Let
$k_2 \in \mathbb{N}$
such that the following holds. Let
![]() $k \geq k_2$
,
$k \geq k_2$
,
![]() $c = ((1-p)/p)^k$
, and
$c = ((1-p)/p)^k$
, and
![]() $0\lt \varepsilon \lt \frac 12$
and suppose
$0\lt \varepsilon \lt \frac 12$
and suppose
![]() $0\lt \delta \leq (1-p) \varepsilon$
and
$0\lt \delta \leq (1-p) \varepsilon$
and
![]() $0\lt \eta \leq \delta ^{4k^2}$
. Suppose that the edges of
$0\lt \eta \leq \delta ^{4k^2}$
. Suppose that the edges of
![]() $K_N$
with
$K_N$
with
![]() $N=(p^{-k}+\varepsilon )n$
are red/blue coloured and this colouring contains either a
$N=(p^{-k}+\varepsilon )n$
are red/blue coloured and this colouring contains either a
![]() $(k,\eta,\delta )$
-red-blocked configuration or a
$(k,\eta,\delta )$
-red-blocked configuration or a
![]() $(k,\eta,\delta )$
-blue-blocked configuration. Then, in either case, the colouring contains either a red
$(k,\eta,\delta )$
-blue-blocked configuration. Then, in either case, the colouring contains either a red
![]() $B_{cn}^{(k)}$
or a blue
$B_{cn}^{(k)}$
or a blue
![]() $B_n ^{(k)}$
. Moreover, one may take
$B_n ^{(k)}$
. Moreover, one may take
![]() $k_2(p) = k_1(1-p)$
, where
$k_2(p) = k_1(1-p)$
, where
![]() $k_1$
is the constant from Lemma 4.1.
$k_1$
is the constant from Lemma 4.1.
Proof. We tackle the two cases separately: suppose first that the colouring has a
![]() $(k,\eta,\delta )$
-red-blocked configuration, say
$(k,\eta,\delta )$
-red-blocked configuration, say
![]() $C_1,\ldots,C_k$
. By the counting lemma, Lemma 2.2, we know that the number of blue
$C_1,\ldots,C_k$
. By the counting lemma, Lemma 2.2, we know that the number of blue
![]() $K_k$
with one vertex in each
$K_k$
with one vertex in each
![]() $C_i$
is at least
$C_i$
is at least
 \begin{align*} \left ( \prod _{1 \leq i\lt j \leq k} d_B(C_i,C_j)-\eta \!\left (\begin{array}{c} k\\[-3pt] 2 \end{array}\right ) \right ) \prod _{i=1}^k |C_i|&\geq \!\left ( \delta ^{\left (\substack{ k\\[3pt] 2 }\right )}- \eta \left (\begin{array}{c} k\\[-3pt] 2 \end{array}\right ) \right ) \prod _{i=1}^k |C_i| \gt 0, \end{align*}
\begin{align*} \left ( \prod _{1 \leq i\lt j \leq k} d_B(C_i,C_j)-\eta \!\left (\begin{array}{c} k\\[-3pt] 2 \end{array}\right ) \right ) \prod _{i=1}^k |C_i|&\geq \!\left ( \delta ^{\left (\substack{ k\\[3pt] 2 }\right )}- \eta \left (\begin{array}{c} k\\[-3pt] 2 \end{array}\right ) \right ) \prod _{i=1}^k |C_i| \gt 0, \end{align*}
so there is at least one blue
![]() $K_k$
with one vertex in each of
$K_k$
with one vertex in each of
![]() $C_1,\ldots,C_k$
. By a similar computation, we see that each
$C_1,\ldots,C_k$
. By a similar computation, we see that each
![]() $C_i$
contains at least one red
$C_i$
contains at least one red
![]() $K_k$
.
$K_k$
.
For a vertex
![]() $v$
and
$v$
and
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $x_i(v)\;:\!=\; d_B(v,C_i) \in [0,1]$
. We observe that from the definition in Lemma 4.1, we have that
$x_i(v)\;:\!=\; d_B(v,C_i) \in [0,1]$
. We observe that from the definition in Lemma 4.1, we have that
![]() $k_1(1-p) \geq k_1(p)$
for all
$k_1(1-p) \geq k_1(p)$
for all
![]() $p \geq \frac 12$
. Therefore, Lemma 4.1 implies that since
$p \geq \frac 12$
. Therefore, Lemma 4.1 implies that since
![]() $k \geq k_2 \geq k_1(p)$
, we have that
$k \geq k_2 \geq k_1(p)$
, we have that
 \begin{equation*} p \!\left ( p^{-k}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k (1-x_i(v))^k \right ) \geq 1 \end{equation*}
\begin{equation*} p \!\left ( p^{-k}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k (1-x_i(v))^k \right ) \geq 1 \end{equation*}
for all
![]() $v \in V$
. Summing this fact up over all
$v \in V$
. Summing this fact up over all
![]() $v$
, we find that
$v$
, we find that
 \begin{equation} p \!\left ( p^{-k}\sum _{v \in V}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac{(1-p)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V} (1-x_i(v))^k \right ) \geq N. \end{equation}
\begin{equation} p \!\left ( p^{-k}\sum _{v \in V}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac{(1-p)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V} (1-x_i(v))^k \right ) \geq N. \end{equation}
This says that a
![]() $(p,1-p)$
-weighted average of two numbers is at least
$(p,1-p)$
-weighted average of two numbers is at least
![]() $N$
, which means that at least one of them is at least
$N$
, which means that at least one of them is at least
![]() $N$
. Suppose first that the first term is at least
$N$
. Suppose first that the first term is at least
![]() $N$
, that is, that
$N$
, that is, that
 \begin{equation*} \sum _{v \in V} \prod _{i=1}^k x_i(v) \geq p^k N. \end{equation*}
\begin{equation*} \sum _{v \in V} \prod _{i=1}^k x_i(v) \geq p^k N. \end{equation*}
Let
![]() $Q$
be a uniformly random blue
$Q$
be a uniformly random blue
![]() $K_k$
spanning
$K_k$
spanning
![]() $C_1,\ldots,C_k$
, which must exist by our computations above. Let
$C_1,\ldots,C_k$
, which must exist by our computations above. Let
![]() $\alpha =\delta ^{k^2} \leq \prod _{i\lt j} d_B(C_i,C_j)$
and observe that
$\alpha =\delta ^{k^2} \leq \prod _{i\lt j} d_B(C_i,C_j)$
and observe that
![]() $\eta \leq \delta ^{4k^2} = \alpha ^4 \leq \alpha ^3/k^2$
. Thus, for any
$\eta \leq \delta ^{4k^2} = \alpha ^4 \leq \alpha ^3/k^2$
. Thus, for any
![]() $v$
, we can apply Lemma 2.3 to conclude that the probability
$v$
, we can apply Lemma 2.3 to conclude that the probability
![]() $v$
extends
$v$
extends
![]() $Q$
to a blue
$Q$
to a blue
![]() $K_{k+1}$
is at least
$K_{k+1}$
is at least
![]() $\prod _i x_i(v)-4 \alpha$
. Therefore, the expected number of extensions of
$\prod _i x_i(v)-4 \alpha$
. Therefore, the expected number of extensions of
![]() $Q$
to a blue
$Q$
to a blue
![]() $K_{k+1}$
is at least
$K_{k+1}$
is at least
 \begin{align} \sum _{v \in V} \!\left ( \prod _{i=1}^k x_i(v)-4 \alpha \right ) &\geq (p^k-4 \alpha )N\notag \\[5pt] &\geq (p^k-4 \alpha )(p^{-k}+\varepsilon )n\notag \\[5pt] &\geq (1+p^k \varepsilon -8 \alpha p^{-k}) n\notag \\[5pt] &\geq n, \end{align}
\begin{align} \sum _{v \in V} \!\left ( \prod _{i=1}^k x_i(v)-4 \alpha \right ) &\geq (p^k-4 \alpha )N\notag \\[5pt] &\geq (p^k-4 \alpha )(p^{-k}+\varepsilon )n\notag \\[5pt] &\geq (1+p^k \varepsilon -8 \alpha p^{-k}) n\notag \\[5pt] &\geq n, \end{align}
where (4) uses that
![]() $\alpha =\delta ^{k^2} \leq ((1-p)\varepsilon )^{k^2}\leq (p \varepsilon )^{k^2} \leq p^{2k} \varepsilon/8$
. Therefore,
$\alpha =\delta ^{k^2} \leq ((1-p)\varepsilon )^{k^2}\leq (p \varepsilon )^{k^2} \leq p^{2k} \varepsilon/8$
. Therefore,
![]() $Q$
has at least
$Q$
has at least
![]() $n$
extensions in expectation, so there must exist some blue
$n$
extensions in expectation, so there must exist some blue
![]() $K_k$
with at least
$K_k$
with at least
![]() $n$
extensions, that is, a blue
$n$
extensions, that is, a blue
![]() $B_n ^{(k)}$
.
$B_n ^{(k)}$
.
Now assume that the other term in the weighted average in (3) is at least
![]() $N$
, that is, that
$N$
, that is, that
 \begin{equation*} \frac 1k \sum _{i=1}^k \sum _{v \in V} (1-x_i(v))^k \geq (1-p)^{k}N. \end{equation*}
\begin{equation*} \frac 1k \sum _{i=1}^k \sum _{v \in V} (1-x_i(v))^k \geq (1-p)^{k}N. \end{equation*}
Then there must exist some
![]() $i$
for which
$i$
for which
Therefore, if
![]() $Q$
is a random red
$Q$
is a random red
![]() $K_k$
inside this
$K_k$
inside this
![]() $C_i$
, then, by Lemma 2.3, the expected number of extensions of
$C_i$
, then, by Lemma 2.3, the expected number of extensions of
![]() $Q$
is at leastFootnote 3
$Q$
is at leastFootnote 3
 \begin{align} \sum _{v \in V} \!\left [ (1-x_i(v))^k-4 \alpha \right ] &\geq \left [(1-p)^k-4 \alpha \right ](p^{-k}+\varepsilon )n\notag \\[5pt] &\geq \!\left (\left ( \frac{1-p}{p} \right ) ^k+(1-p)^k \varepsilon -8 \alpha p^{-k}\right )n\notag \\[5pt] &\geq cn, \end{align}
\begin{align} \sum _{v \in V} \!\left [ (1-x_i(v))^k-4 \alpha \right ] &\geq \left [(1-p)^k-4 \alpha \right ](p^{-k}+\varepsilon )n\notag \\[5pt] &\geq \!\left (\left ( \frac{1-p}{p} \right ) ^k+(1-p)^k \varepsilon -8 \alpha p^{-k}\right )n\notag \\[5pt] &\geq cn, \end{align}
where we use the fact that
![]() $c=((1-p)/p)^k$
and that
$c=((1-p)/p)^k$
and that
since
![]() $1-p \leq p$
. Thus, the expected number of red extensions of a red
$1-p \leq p$
. Thus, the expected number of red extensions of a red
![]() $K_k$
in
$K_k$
in
![]() $C_i$
is at least
$C_i$
is at least
![]() $cn$
, so there must exist a red
$cn$
, so there must exist a red
![]() $B_{cn}^{(k)}$
. This concludes the proof under the assumption that the colouring contains a
$B_{cn}^{(k)}$
. This concludes the proof under the assumption that the colouring contains a
![]() $(k,\eta,\delta )$
-red-blocked configuration.
$(k,\eta,\delta )$
-red-blocked configuration.
Now, we instead assume that the colouring contains a
![]() $(k,\eta,\delta )$
-blue-blocked configuration and aim to conclude the same result; the proof is more or less identical, but with the role of
$(k,\eta,\delta )$
-blue-blocked configuration and aim to conclude the same result; the proof is more or less identical, but with the role of
![]() $p$
now played by
$p$
now played by
![]() $q=1-p$
. As before, we find that there is at least one red
$q=1-p$
. As before, we find that there is at least one red
![]() $K_k$
spanning
$K_k$
spanning
![]() $C_1,\ldots,C_k$
and that each
$C_1,\ldots,C_k$
and that each
![]() $C_i$
contains at least one blue
$C_i$
contains at least one blue
![]() $K_k$
. For a vertex
$K_k$
. For a vertex
![]() $v$
and
$v$
and
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $y_i(v)=d_R(v,C_i) \in [0,1]$
and write
$y_i(v)=d_R(v,C_i) \in [0,1]$
and write
![]() $q=1-p$
. Since
$q=1-p$
. Since
![]() $k \geq k_2 = k_1(q)$
, we can sum the result of applying Lemma 4.1 over all
$k \geq k_2 = k_1(q)$
, we can sum the result of applying Lemma 4.1 over all
![]() $v \in V$
to find that
$v \in V$
to find that
 \begin{equation*} q \!\left ( q^{-k} \sum _{v \in V} \prod _{i=1}^k y_i(v) \right ) +(1-q) \left ( \frac {(1-q)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V} (1-y_i(v))^k \right ) \geq N. \end{equation*}
\begin{equation*} q \!\left ( q^{-k} \sum _{v \in V} \prod _{i=1}^k y_i(v) \right ) +(1-q) \left ( \frac {(1-q)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V} (1-y_i(v))^k \right ) \geq N. \end{equation*}
As before, this is a
![]() $(q,1-q)$
-weighted average of two terms, which means that one of the terms must be at least
$(q,1-q)$
-weighted average of two terms, which means that one of the terms must be at least
![]() $N$
. Suppose first that the first term is at least
$N$
. Suppose first that the first term is at least
![]() $N$
, that is, that
$N$
, that is, that
 \begin{equation*} \sum _{v \in V} \prod _{i=1}^k y_i(v) \geq q^k N. \end{equation*}
\begin{equation*} \sum _{v \in V} \prod _{i=1}^k y_i(v) \geq q^k N. \end{equation*}
If
![]() $Q$
is a uniformly random red
$Q$
is a uniformly random red
![]() $K_k$
spanning
$K_k$
spanning
![]() $C_1,\ldots,C_k$
and
$C_1,\ldots,C_k$
and
![]() $\alpha =\delta ^{k^2}$
, then, as before, we find that the expected number of extensions of
$\alpha =\delta ^{k^2}$
, then, as before, we find that the expected number of extensions of
![]() $Q$
to a red
$Q$
to a red
![]() $K_{k+1}$
is at least
$K_{k+1}$
is at least
 \begin{equation*} \sum _{v \in V} \!\left ( \prod _{i=1}^k y_i(v)-4 \alpha \right ) \geq (q^k-4 \alpha ) N \geq ((1-p)^k- 4 \alpha )(p^{-k}+\varepsilon )n \geq cn, \end{equation*}
\begin{equation*} \sum _{v \in V} \!\left ( \prod _{i=1}^k y_i(v)-4 \alpha \right ) \geq (q^k-4 \alpha ) N \geq ((1-p)^k- 4 \alpha )(p^{-k}+\varepsilon )n \geq cn, \end{equation*}
by the computation in (5). Therefore, in this case, there must exist some red
![]() $K_k$
with at least
$K_k$
with at least
![]() $cn$
red extensions, giving the desired red
$cn$
red extensions, giving the desired red
![]() $B_{cn}^{(k)}$
. So we may assume instead that
$B_{cn}^{(k)}$
. So we may assume instead that
 \begin{equation*} \frac 1k \sum _{i=1}^k \sum _{v \in V} (1-y_i(v))^k \geq (1-q)^kN, \end{equation*}
\begin{equation*} \frac 1k \sum _{i=1}^k \sum _{v \in V} (1-y_i(v))^k \geq (1-q)^kN, \end{equation*}
which implies that for some
![]() $i \in [k]$
,
$i \in [k]$
,
Thus, if
![]() $Q$
is a random blue
$Q$
is a random blue
![]() $K_k$
inside this
$K_k$
inside this
![]() $C_i$
, we find that the expected number of blue extensions of
$C_i$
, we find that the expected number of blue extensions of
![]() $Q$
is at least
$Q$
is at least
by the same computation as in (4). This gives us our blue
![]() $B_n ^{(k)}$
, completing the proof.
$B_n ^{(k)}$
, completing the proof.
With this result in hand, we can now prove Theorem 1.3.
Proof of Theorem
1.3. Given an integer
![]() $k \geq 2$
, let
$k \geq 2$
, let
![]() $c_1(k)$
be the infimum of
$c_1(k)$
be the infimum of
![]() $c \in (0,1]$
such that
$c \in (0,1]$
such that
![]() $k_2((c^{1/k}+1)^{-1}) \leq k$
, where
$k_2((c^{1/k}+1)^{-1}) \leq k$
, where
![]() $k_2$
is the constant from Lemma 4.3. Note that we declare this infimum to equal
$k_2$
is the constant from Lemma 4.3. Note that we declare this infimum to equal
![]() $1$
if no
$1$
if no
![]() $c \in (0,1]$
satisfies this condition (as happens for
$c \in (0,1]$
satisfies this condition (as happens for
![]() $k=2$
). In this case, there is nothing to prove, since Theorem 1.3 for
$k=2$
). In this case, there is nothing to prove, since Theorem 1.3 for
![]() $c=1$
is already known [Reference Conlon9]. We now fix
$c=1$
is already known [Reference Conlon9]. We now fix
![]() $c\in [c_1,1]$
and
$c\in [c_1,1]$
and
![]() $p = 1/(c^{1/k}+1) \in (\frac 12,1]$
, noting that we have
$p = 1/(c^{1/k}+1) \in (\frac 12,1]$
, noting that we have
![]() $k \geq k_2(p)$
.
$k \geq k_2(p)$
.
Fix
![]() $0\lt \varepsilon \lt \frac 12$
and suppose we are given a red/blue colouring of
$0\lt \varepsilon \lt \frac 12$
and suppose we are given a red/blue colouring of
![]() $E(K_N)$
where
$E(K_N)$
where
![]() $N=(p^{-k}+\varepsilon )n$
. Our goal is to prove that if
$N=(p^{-k}+\varepsilon )n$
. Our goal is to prove that if
![]() $n$
is sufficiently large in terms of
$n$
is sufficiently large in terms of
![]() $\varepsilon$
, then this colouring contains a red
$\varepsilon$
, then this colouring contains a red
![]() $B_{cn} ^{(k)}$
or a blue
$B_{cn} ^{(k)}$
or a blue
![]() $B_n ^{(k)}$
. To do this, we fix parameters
$B_n ^{(k)}$
. To do this, we fix parameters
![]() $\delta =(1-p)^{2k}\varepsilon/(4k)$
and
$\delta =(1-p)^{2k}\varepsilon/(4k)$
and
![]() $\eta =\min \{\delta ^{4k^2},(1-p)/(4k)\}$
depending on
$\eta =\min \{\delta ^{4k^2},(1-p)/(4k)\}$
depending on
![]() $c$
,
$c$
,
![]() $k$
, and
$k$
, and
![]() $\varepsilon$
.
$\varepsilon$
.
We apply Lemma 2.1 to the red graph from our colouring with parameters
![]() $\eta$
and
$\eta$
and
![]() $M_0=1/\eta$
to obtain an equitable partition
$M_0=1/\eta$
to obtain an equitable partition
![]() $V(K_N)=V_1 \sqcup \dotsb \sqcup V_m$
, where each
$V(K_N)=V_1 \sqcup \dotsb \sqcup V_m$
, where each
![]() $V_i$
is
$V_i$
is
![]() $\eta$
-regular and, for each
$\eta$
-regular and, for each
![]() $i$
, there are at most
$i$
, there are at most
![]() $\eta m$
values
$\eta m$
values
![]() $1 \leq j \leq m$
such that the pair
$1 \leq j \leq m$
such that the pair
![]() $(V_i,V_j)$
is not
$(V_i,V_j)$
is not
![]() $\eta$
-regular. Moreover,
$\eta$
-regular. Moreover,
![]() $M_0 \leq m \leq M=M(\eta,M_0)$
. Note that since the colours are complementary, the same properties also hold for the blue graph. Call a part
$M_0 \leq m \leq M=M(\eta,M_0)$
. Note that since the colours are complementary, the same properties also hold for the blue graph. Call a part
![]() $V_i$
blue if
$V_i$
blue if
![]() $d_B(V_i) \geq \frac 12$
and red otherwise.
$d_B(V_i) \geq \frac 12$
and red otherwise.
Suppose first that at least
![]() $m' \geq pm$
of the parts are blue and rename the parts so that
$m' \geq pm$
of the parts are blue and rename the parts so that
![]() $V_1,\ldots,V_{m'}$
are these blue parts. We build a reduced graph
$V_1,\ldots,V_{m'}$
are these blue parts. We build a reduced graph
![]() $G$
whose vertex set is
$G$
whose vertex set is
![]() $v_1,\ldots,v_{m'}$
by making
$v_1,\ldots,v_{m'}$
by making
![]() $\{v_i,v_j\}$
an edge if and only if
$\{v_i,v_j\}$
an edge if and only if
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\eta$
-regular and
$\eta$
-regular and
![]() $d_R(V_i,V_j) \geq \delta$
. Suppose that some vertex in
$d_R(V_i,V_j) \geq \delta$
. Suppose that some vertex in
![]() $G$
, say
$G$
, say
![]() $v_1$
, has degree at most
$v_1$
, has degree at most
![]() $(1-p^{k-1}-\eta/p)m'-1$
. Since
$(1-p^{k-1}-\eta/p)m'-1$
. Since
![]() $v_1$
has at most
$v_1$
has at most
![]() $\eta m \leq \eta m'/p$
non-neighbours coming from irregular pairs
$\eta m \leq \eta m'/p$
non-neighbours coming from irregular pairs
![]() $(V_1,V_j)$
, this means that there are at least
$(V_1,V_j)$
, this means that there are at least
![]() $p^{k-1} m'$
parts
$p^{k-1} m'$
parts
![]() $V_j$
such that
$V_j$
such that
![]() $(V_1,V_j)$
is
$(V_1,V_j)$
is
![]() $\eta$
-regular and
$\eta$
-regular and
![]() $d_B(V_1,V_j) \geq 1- \delta$
. Let
$d_B(V_1,V_j) \geq 1- \delta$
. Let
![]() $J$
be the set of all these indices
$J$
be the set of all these indices
![]() $j$
and
$j$
and
![]() $U=\bigcup _{j \in J}V_j$
be the union of all of these
$U=\bigcup _{j \in J}V_j$
be the union of all of these
![]() $V_j$
. We then have
$V_j$
. We then have
Let
![]() $V'_{\!\!1} \subseteq V_1$
denote the set of vertices
$V'_{\!\!1} \subseteq V_1$
denote the set of vertices
![]() $v \in V_1$
with
$v \in V_1$
with
![]() $e_B(v,U) \geq (1-2 \delta )|U|$
. Then we may write
$e_B(v,U) \geq (1-2 \delta )|U|$
. Then we may write
Combining inequalities (6) and (7), we find that
![]() $|V'_{\!\!1}| \geq \frac 12 |V_1|$
, where every vertex in
$|V'_{\!\!1}| \geq \frac 12 |V_1|$
, where every vertex in
![]() $V'_{\!\!1}$
has blue density at least
$V'_{\!\!1}$
has blue density at least
![]() $1-2 \delta$
into
$1-2 \delta$
into
![]() $U$
. Moreover, since
$U$
. Moreover, since
![]() $\eta \lt \frac 16$
, we may apply the
$\eta \lt \frac 16$
, we may apply the
![]() $\eta$
-regularity of
$\eta$
-regularity of
![]() $V_1$
to conclude that the internal blue density of
$V_1$
to conclude that the internal blue density of
![]() $V'_{\!\!1}$
is at least
$V'_{\!\!1}$
is at least
![]() $\frac 12- \eta \geq \frac 13$
, while the hereditary property of regularity implies that
$\frac 12- \eta \geq \frac 13$
, while the hereditary property of regularity implies that
![]() $V'_{\!\!1}$
is
$V'_{\!\!1}$
is
![]() $2\eta$
-regular. Then the counting lemma, Lemma 2.2, implies that
$2\eta$
-regular. Then the counting lemma, Lemma 2.2, implies that
![]() $V'_{\!\!1}$
contains at least
$V'_{\!\!1}$
contains at least
 \begin{equation*} \frac {1}{k!}\!\left ( d_B(V'_{\!\!1})^{\left(\substack{ k\\[3pt] 2 }\right )}-2\eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) |V'_{\!\!1}|^k \geq \frac {1}{k!}\left ( 3^{-\left (\substack{ k\\[3pt] 2 }\right )}-2\eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) |V'_{\!\!1}|^k \gt 0 \end{equation*}
\begin{equation*} \frac {1}{k!}\!\left ( d_B(V'_{\!\!1})^{\left(\substack{ k\\[3pt] 2 }\right )}-2\eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) |V'_{\!\!1}|^k \geq \frac {1}{k!}\left ( 3^{-\left (\substack{ k\\[3pt] 2 }\right )}-2\eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) |V'_{\!\!1}|^k \gt 0 \end{equation*}
blue
![]() $K_k$
, so that
$K_k$
, so that
![]() $V'_{\!\!1}$
contains at least one blue
$V'_{\!\!1}$
contains at least one blue
![]() $K_k$
. Every vertex of this blue
$K_k$
. Every vertex of this blue
![]() $K_k$
has at least
$K_k$
has at least
![]() $(1-2 \delta )|U|$
blue neighbours in
$(1-2 \delta )|U|$
blue neighbours in
![]() $U$
, so the blue
$U$
, so the blue
![]() $K_k$
has at least
$K_k$
has at least
![]() $(1-2 k \delta )|U|$
blue extensions into
$(1-2 k \delta )|U|$
blue extensions into
![]() $U$
. Moreover, since we assumed that
$U$
. Moreover, since we assumed that
![]() $|J| \geq p^{k-1} m' \geq p^{k} m$
and the partition is equitable, we find that
$|J| \geq p^{k-1} m' \geq p^{k} m$
and the partition is equitable, we find that
![]() $|U| \geq p^{k}N$
. Therefore,
$|U| \geq p^{k}N$
. Therefore,
 \begin{align*} (1-2 k \delta )|U| &\geq (1-2 k \delta )p^k (p^{-k}+\varepsilon )n\\[5pt] &= (1-2 k \delta )(1+p^k \varepsilon )n\\[5pt] &\geq (1+p^k \varepsilon -4 k \delta )n\\[5pt] &\geq n, \end{align*}
\begin{align*} (1-2 k \delta )|U| &\geq (1-2 k \delta )p^k (p^{-k}+\varepsilon )n\\[5pt] &= (1-2 k \delta )(1+p^k \varepsilon )n\\[5pt] &\geq (1+p^k \varepsilon -4 k \delta )n\\[5pt] &\geq n, \end{align*}
since our choice of
![]() $\delta$
yields
$\delta$
yields
![]() $4k \delta = (1-p)^{2k} \varepsilon \leq p^k \varepsilon$
. Thus, we find that any blue
$4k \delta = (1-p)^{2k} \varepsilon \leq p^k \varepsilon$
. Thus, we find that any blue
![]() $K_k$
inside
$K_k$
inside
![]() $V'_{\!\!1}$
must have at least
$V'_{\!\!1}$
must have at least
![]() $n$
blue extensions, giving us our blue
$n$
blue extensions, giving us our blue
![]() $B_n ^{(k)}$
.
$B_n ^{(k)}$
.
So we may assume that every vertex in
![]() $G$
has degree at least
$G$
has degree at least
![]() $(1-p^{k-1}-\eta/p)m'$
. Recall from (2) that
$(1-p^{k-1}-\eta/p)m'$
. Recall from (2) that
![]() $f(1-p,k) = p^{1-k}/(e^2k) \geq 1$
for
$f(1-p,k) = p^{1-k}/(e^2k) \geq 1$
for
![]() $k \geq k_1(1-p)$
. Since we assume that
$k \geq k_1(1-p)$
. Since we assume that
![]() $k \geq k_2(p) = k_1(1-p)$
, this implies that
$k \geq k_2(p) = k_1(1-p)$
, this implies that
Additionally, by our choice of
![]() $\eta \leq (1-p)/(4k) \leq p/(4k)$
, we know that
$\eta \leq (1-p)/(4k) \leq p/(4k)$
, we know that
The previous two inequalities imply that
so that
![]() $G$
contains a
$G$
contains a
![]() $K_k$
by Turán’s theorem. Let
$K_k$
by Turán’s theorem. Let
![]() $v_{i_1},\ldots,v_{i_k}$
be the vertices of this
$v_{i_1},\ldots,v_{i_k}$
be the vertices of this
![]() $K_k$
and let
$K_k$
and let
![]() $C_j=V_{i_j}$
for
$C_j=V_{i_j}$
for
![]() $1 \leq j \leq k$
. Then we claim that
$1 \leq j \leq k$
. Then we claim that
![]() $C_1,\ldots,C_k$
is a
$C_1,\ldots,C_k$
is a
![]() $(k,\eta,\delta )$
-blue-blocked configuration. The fact that each
$(k,\eta,\delta )$
-blue-blocked configuration. The fact that each
![]() $C_i$
is
$C_i$
is
![]() $\eta$
-regular follows immediately from our application of Lemma 2.1 and the fact that
$\eta$
-regular follows immediately from our application of Lemma 2.1 and the fact that
![]() $d_B(C_i) \geq \delta$
follows from the fact that we assumed
$d_B(C_i) \geq \delta$
follows from the fact that we assumed
![]() $d_B(C_i) \geq \frac 12$
. Finally, the definition of edges in
$d_B(C_i) \geq \frac 12$
. Finally, the definition of edges in
![]() $G$
implies that
$G$
implies that
![]() $(C_i,C_j)$
is
$(C_i,C_j)$
is
![]() $\eta$
-regular with
$\eta$
-regular with
![]() $d_R(C_i,C_j) \geq \delta$
for all
$d_R(C_i,C_j) \geq \delta$
for all
![]() $i \neq j$
. Thus, our colouring contains a
$i \neq j$
. Thus, our colouring contains a
![]() $(k,\eta,\delta )$
-blue-blocked configuration with
$(k,\eta,\delta )$
-blue-blocked configuration with
![]() $\delta \leq (1-p) \varepsilon$
and
$\delta \leq (1-p) \varepsilon$
and
![]() $\eta \leq \delta ^{4k^2}$
, so Lemma 4.3 implies that the colouring contains either a red
$\eta \leq \delta ^{4k^2}$
, so Lemma 4.3 implies that the colouring contains either a red
![]() $B_{cn} ^{(k)}$
or a blue
$B_{cn} ^{(k)}$
or a blue
![]() $B_n ^{(k)}$
.
$B_n ^{(k)}$
.
We have now finished the proof if at least
![]() $pm$
of the parts
$pm$
of the parts
![]() $V_i$
are blue. Therefore, we may assume instead that at least
$V_i$
are blue. Therefore, we may assume instead that at least
![]() $m'' \geq (1-p) m$
of the parts are red and again rename the parts so that these red parts are
$m'' \geq (1-p) m$
of the parts are red and again rename the parts so that these red parts are
![]() $V_1,\ldots,V_{m''}$
. We construct a reduced graph
$V_1,\ldots,V_{m''}$
. We construct a reduced graph
![]() $G$
on vertices
$G$
on vertices
![]() $v_1,\ldots,v_{m''}$
by connecting
$v_1,\ldots,v_{m''}$
by connecting
![]() $v_i$
to
$v_i$
to
![]() $v_j$
if
$v_j$
if
![]() $(V_i,V_j)$
is
$(V_i,V_j)$
is
![]() $\eta$
-regular with
$\eta$
-regular with
![]() $d_B(V_i,V_j) \geq \delta$
. Suppose that some vertex in
$d_B(V_i,V_j) \geq \delta$
. Suppose that some vertex in
![]() $G$
, say
$G$
, say
![]() $v_1$
, has degree at most
$v_1$
, has degree at most
![]() $(1-(1-p)^{k-1}-\eta/(1-p))m''-1$
. As before,
$(1-(1-p)^{k-1}-\eta/(1-p))m''-1$
. As before,
![]() $v_1$
has at most
$v_1$
has at most
![]() $\eta m \leq \eta m''/(1-p)$
non-neighbours coming from irregular pairs. Thus, if we let
$\eta m \leq \eta m''/(1-p)$
non-neighbours coming from irregular pairs. Thus, if we let
![]() $J$
denote the set of indices
$J$
denote the set of indices
![]() $j$
for which
$j$
for which
![]() $(V_1,V_j)$
is
$(V_1,V_j)$
is
![]() $\eta$
-regular with
$\eta$
-regular with
![]() $d_R(V_1,V_j) \geq 1- \delta$
, then we find that
$d_R(V_1,V_j) \geq 1- \delta$
, then we find that
![]() $|J| \geq (1-p)^{k-1}m'' \geq (1-p)^k m$
. Thus, if
$|J| \geq (1-p)^{k-1}m'' \geq (1-p)^k m$
. Thus, if
![]() $U=\bigcup _{j \in J}V_j$
, then we see that
$U=\bigcup _{j \in J}V_j$
, then we see that
![]() $|U| \geq (1-p)^k N$
, since the partition is equitable. Next, as above, we let
$|U| \geq (1-p)^k N$
, since the partition is equitable. Next, as above, we let
![]() $V'_{\!\!1} \subseteq V_1$
denote the set of vertices
$V'_{\!\!1} \subseteq V_1$
denote the set of vertices
![]() $v \in V_1$
with
$v \in V_1$
with
![]() $e_R(v,U) \geq (1-2 \delta )|U|$
and find that
$e_R(v,U) \geq (1-2 \delta )|U|$
and find that
![]() $|V'_{\!\!1}| \geq \frac 12 |V_1|$
. Therefore, as above, we know that
$|V'_{\!\!1}| \geq \frac 12 |V_1|$
. Therefore, as above, we know that
![]() $V'_{\!\!1}$
contains at least one red
$V'_{\!\!1}$
contains at least one red
![]() $K_k$
and this red
$K_k$
and this red
![]() $K_k$
has at least
$K_k$
has at least
![]() $(1-2 k \delta )|U|$
red extensions in
$(1-2 k \delta )|U|$
red extensions in
![]() $U$
. Moreover,
$U$
. Moreover,
 \begin{align} (1-2k \delta )|U|&\geq (1-2k \delta ) (1-p)^k N\notag \\[5pt] &=(1-2 k \delta )(1-p)^k (p^{-k}+\varepsilon )n \notag \\[5pt] &=(1-2 k \delta )(c+(1-p)^k \varepsilon )n \end{align}
\begin{align} (1-2k \delta )|U|&\geq (1-2k \delta ) (1-p)^k N\notag \\[5pt] &=(1-2 k \delta )(1-p)^k (p^{-k}+\varepsilon )n \notag \\[5pt] &=(1-2 k \delta )(c+(1-p)^k \varepsilon )n \end{align}
 \begin{align} &\qquad\;\;\; \geq (c+(1-p)^k \varepsilon -4 k \delta )n\notag \\[5pt] & \qquad\;\;\;\geq cn, \end{align}
\begin{align} &\qquad\;\;\; \geq (c+(1-p)^k \varepsilon -4 k \delta )n\notag \\[5pt] & \qquad\;\;\;\geq cn, \end{align}
where in (9) we used the definition of
![]() $p$
, which implies that
$p$
, which implies that
![]() $((1-p)/p)^k=c$
, and in (10) we used our choice of
$((1-p)/p)^k=c$
, and in (10) we used our choice of
![]() $\delta$
to see that
$\delta$
to see that
![]() $\delta \leq (1-p)^k \varepsilon/(4k)$
. Thus, in this case, we can find a red
$\delta \leq (1-p)^k \varepsilon/(4k)$
. Thus, in this case, we can find a red
![]() $B_{cn}^{(k)}$
.
$B_{cn}^{(k)}$
.
We may therefore assume that every vertex in
![]() $G$
has degree at least
$G$
has degree at least
![]() $(1- (1-p)^{k-1}-\eta/(1-p))m''$
. As before, we know that, since
$(1- (1-p)^{k-1}-\eta/(1-p))m''$
. As before, we know that, since
![]() $k \geq k_2(p)$
,
$k \geq k_2(p)$
,
and our choice of
![]() $\eta \leq (1-p)/(4k)$
implies that
$\eta \leq (1-p)/(4k)$
implies that
Thus, by Turán’s theorem,
![]() $G$
must contain a
$G$
must contain a
![]() $K_k$
, with vertices
$K_k$
, with vertices
![]() $v_{i_1},\ldots,v_{i_k}$
. If we let
$v_{i_1},\ldots,v_{i_k}$
. If we let
![]() $C_j=V_{i_j}$
, then
$C_j=V_{i_j}$
, then
![]() $C_1,\ldots,C_k$
will be a
$C_1,\ldots,C_k$
will be a
![]() $(k,\eta,\delta )$
-red-blocked configuration, by the definition of edges in
$(k,\eta,\delta )$
-red-blocked configuration, by the definition of edges in
![]() $G$
and the assumption that
$G$
and the assumption that
![]() $N$
is sufficiently large in terms of
$N$
is sufficiently large in terms of
![]() $\varepsilon$
. Thus, by Lemma 4.3, we can again conclude that the colouring contains either a red
$\varepsilon$
. Thus, by Lemma 4.3, we can again conclude that the colouring contains either a red
![]() $B_{cn}^{(k)}$
or a blue
$B_{cn}^{(k)}$
or a blue
![]() $B_n ^{(k)}$
.
$B_n ^{(k)}$
.
To finish, we note that, as claimed, we may take
![]() $c_1(k) \leq \!\left((1+o(1))\frac{\log k}{k}\right)^k$
. Indeed, for any
$c_1(k) \leq \!\left((1+o(1))\frac{\log k}{k}\right)^k$
. Indeed, for any
![]() $c$
and
$c$
and
![]() $k$
, let
$k$
, let
![]() $p(c,k) = (c^{1/k}+1)^{-1}$
and
$p(c,k) = (c^{1/k}+1)^{-1}$
and
![]() $y = y(c,k) = 1/\log [1/p(c,k)]$
. Then, from Lemma 4.3 and 4.1, we see that
$y = y(c,k) = 1/\log [1/p(c,k)]$
. Then, from Lemma 4.3 and 4.1, we see that
![]() $k_2(p(c,k)) = 1+y(5+\log y+\log \log y)$
. Thus, if
$k_2(p(c,k)) = 1+y(5+\log y+\log \log y)$
. Thus, if
![]() $y\leq (1+o(1))k/\log k$
, then
$y\leq (1+o(1))k/\log k$
, then
![]() $k \geq k_2(p(c,k))$
. Since
$k \geq k_2(p(c,k))$
. Since
![]() $y = 1/\log \!(1+c^{1/k})$
, this condition is equivalent to
$y = 1/\log \!(1+c^{1/k})$
, this condition is equivalent to
![]() $c^{1/k} \geq \exp\!\left((1+o(1))\frac{\log k}{k}\right)-1= (1+o(1))\frac{\log k}{k}$
, which yields the desired bound.
$c^{1/k} \geq \exp\!\left((1+o(1))\frac{\log k}{k}\right)-1= (1+o(1))\frac{\log k}{k}$
, which yields the desired bound.
5. Quasirandomness
In the previous section, we showed that for a certain range of
![]() $c$
and
$c$
and
![]() $k$
, the Ramsey number
$k$
, the Ramsey number
![]() $r\!\left(B_{cn}^{(k)},B_n^{(k)}\right)$
is, as
$r\!\left(B_{cn}^{(k)},B_n^{(k)}\right)$
is, as
![]() $n \to \infty$
, asymptotically equal to the lower bound coming from a
$n \to \infty$
, asymptotically equal to the lower bound coming from a
![]() $p$
-random construction. In this section, we strengthen this result, showing that all colourings whose number of vertices is close to the Ramsey number must either be quasirandom or else contain substantially larger books than the Ramsey property implies. We make the following definition.
$p$
-random construction. In this section, we strengthen this result, showing that all colourings whose number of vertices is close to the Ramsey number must either be quasirandom or else contain substantially larger books than the Ramsey property implies. We make the following definition.
Definition 5.1. For
![]() $p \in \!\big[\frac 12,1\big)$
and
$p \in \!\big[\frac 12,1\big)$
and
![]() $\gamma \gt 0$
, we say that a red/blue colouring of
$\gamma \gt 0$
, we say that a red/blue colouring of
![]() $E(K_N)$
contains
$E(K_N)$
contains
![]() $(p,\gamma )$
-many books if it contains
$(p,\gamma )$
-many books if it contains
-
at least
 $\gamma N^k$
red
$\gamma N^k$
red
 $K_k$
, each with at least
$K_k$
, each with at least
 $((1-p)^k +\gamma )N$
extensions to a red
$((1-p)^k +\gamma )N$
extensions to a red
 $K_{k+1}$
, or
$K_{k+1}$
, or -
at least
 $\gamma N^k$
blue
$\gamma N^k$
blue
 $K_k$
, each with at least
$K_k$
, each with at least
 $(p^k +\gamma )N$
extensions to a blue
$(p^k +\gamma )N$
extensions to a blue
 $K_{k+1}$
.
$K_{k+1}$
.
Here is the restatement of Theorem 1.4 in terms of
![]() $(p, \gamma )$
-many books that we will prove.
$(p, \gamma )$
-many books that we will prove.
Theorem 1.4. For every
![]() $p \in [\frac 12,1)$
, there exists some
$p \in [\frac 12,1)$
, there exists some
![]() $k_0 \in \mathbb{N}$
such that the following holds for every
$k_0 \in \mathbb{N}$
such that the following holds for every
![]() $k \geq k_0$
. For every
$k \geq k_0$
. For every
![]() $\theta \gt 0$
, there exists some
$\theta \gt 0$
, there exists some
![]() $\gamma \gt 0$
such that if a red/blue colouring of
$\gamma \gt 0$
such that if a red/blue colouring of
![]() $E(K_N)$
is not
$E(K_N)$
is not
![]() $(p,\theta )$
-quasirandom, then it contains
$(p,\theta )$
-quasirandom, then it contains
![]() $(p,\gamma )$
-many books.
$(p,\gamma )$
-many books.
To prove Theorem 1.4, we will need a few technical lemmas. At a high level, the proof closely follows the proof of the main quasirandomness theorem in [Reference Conlon, Fox and Wigderson10, Section 5], as follows. First, we prove a strengthening of Lemma 4.1, which can be thought of as a stability version of that result; it says that if our vector
![]() $(x_1,\ldots,x_k)$
is bounded in
$(x_1,\ldots,x_k)$
is bounded in
![]() $\ell _\infty$
away from the minimizing point
$\ell _\infty$
away from the minimizing point
![]() $(p,\ldots,p)$
, then the value of the function in Lemma 4.1 is bounded away from its minimum of
$(p,\ldots,p)$
, then the value of the function in Lemma 4.1 is bounded away from its minimum of
![]() $1$
. Using this, we can strengthen Lemma 4.3 to say that not only does a blocked configuration imply the existence of the desired monochromatic book, but in fact it implies the existence of a larger book unless every part of the blocked configuration is
$1$
. Using this, we can strengthen Lemma 4.3 to say that not only does a blocked configuration imply the existence of the desired monochromatic book, but in fact it implies the existence of a larger book unless every part of the blocked configuration is
![]() $\varepsilon$
-regular to the entire vertex set. Therefore, assuming our colouring does not contain many blue
$\varepsilon$
-regular to the entire vertex set. Therefore, assuming our colouring does not contain many blue
![]() $B^{(k)}_{(p^k+\gamma )N}$
or red
$B^{(k)}_{(p^k+\gamma )N}$
or red
![]() $B^{(k)}_{((1-p)^k+\gamma )N}$
, we will be able to repeatedly pull out vertex subsets that are
$B^{(k)}_{((1-p)^k+\gamma )N}$
, we will be able to repeatedly pull out vertex subsets that are
![]() $\varepsilon$
-regular to the entire vertex set until we have almost partitioned all the vertices into such subsets. At that point, we can use the structure coming from this partition to deduce that the colouring is
$\varepsilon$
-regular to the entire vertex set until we have almost partitioned all the vertices into such subsets. At that point, we can use the structure coming from this partition to deduce that the colouring is
![]() $(p,\theta )$
-quasirandom, as desired.
$(p,\theta )$
-quasirandom, as desired.
We begin with the strengthening of Lemma 4.1.
Lemma 5.2.
For
![]() $p \in (0,1)$
, let
$p \in (0,1)$
, let
![]() $k_1=k_1(p)$
be as in Lemma
4.1
. Then, for every integer
$k_1=k_1(p)$
be as in Lemma
4.1
. Then, for every integer
![]() $k \geq k_1$
and any
$k \geq k_1$
and any
![]() $\varepsilon _0\gt 0$
, there exists some
$\varepsilon _0\gt 0$
, there exists some
![]() $\delta _0\gt 0$
such that if
$\delta _0\gt 0$
such that if
![]() $x_1,\ldots,x_k \in [0,1]$
are numbers with
$x_1,\ldots,x_k \in [0,1]$
are numbers with
![]() $|x_j-p| \geq \varepsilon _0$
for some
$|x_j-p| \geq \varepsilon _0$
for some
![]() $j$
, then
$j$
, then
 \begin{equation*} p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k}\sum _{i=1}^k (1-x_i)^k \geq 1+\delta _0. \end{equation*}
\begin{equation*} p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k}\sum _{i=1}^k (1-x_i)^k \geq 1+\delta _0. \end{equation*}
Proof. Let
 \begin{equation*} F(x_1,\ldots,x_k)=p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k}\sum _{i=1}^k (1-x_i)^k \end{equation*}
\begin{equation*} F(x_1,\ldots,x_k)=p^{1-k} \prod _{i=1}^k x_i+\frac {(1-p)^{1-k}}{k}\sum _{i=1}^k (1-x_i)^k \end{equation*}
and
![]() $\varphi (y)=(1-e^y)^k$
. The goal is to apply Hölder’s defect formula, Theorem 2.6, using the strict convexity of the function
$\varphi (y)=(1-e^y)^k$
. The goal is to apply Hölder’s defect formula, Theorem 2.6, using the strict convexity of the function
![]() $\varphi$
. However,
$\varphi$
. However,
![]() $\varphi$
is only strictly convex on the interval
$\varphi$
is only strictly convex on the interval
![]() $(\!\log \frac 1k,0)$
and, in order to apply Theorem 2.6, we in fact need a positive lower bound on
$(\!\log \frac 1k,0)$
and, in order to apply Theorem 2.6, we in fact need a positive lower bound on
![]() $\varphi ''$
, but no such bound exists for the whole interval
$\varphi ''$
, but no such bound exists for the whole interval
![]() $(\!\log \frac 1k,0)$
. Because of this, we need to separately analyze the cases where all the variables are inside a large subinterval of
$(\!\log \frac 1k,0)$
. Because of this, we need to separately analyze the cases where all the variables are inside a large subinterval of
![]() $\big(\frac 1k,1\big)$
and when one of them is outside such a subinterval.
$\big(\frac 1k,1\big)$
and when one of them is outside such a subinterval.
First, suppose that one of the variables, say
![]() $x_1$
, is in the interval
$x_1$
, is in the interval
![]() $\big[0,\frac{1+\varepsilon _1}k\big]$
, for some small constant
$\big[0,\frac{1+\varepsilon _1}k\big]$
, for some small constant
![]() $\varepsilon _1\gt 0$
. Then we have that
$\varepsilon _1\gt 0$
. Then we have that
From the proof of Lemma 4.1, we see that this quantity is strictly larger than
![]() $1$
for all
$1$
for all
![]() $k \geq k_1(p)$
, so, by choosing
$k \geq k_1(p)$
, so, by choosing
![]() $\delta _0$
appropriately, we see that
$\delta _0$
appropriately, we see that
![]() $F(x_1,\dots,x_k) \geq 1+\delta _0$
in this case. We may therefore assume from now on that all the variables are at least
$F(x_1,\dots,x_k) \geq 1+\delta _0$
in this case. We may therefore assume from now on that all the variables are at least
![]() $\frac{1+\varepsilon _1}k$
.
$\frac{1+\varepsilon _1}k$
.
Next, suppose that there exist values
![]() $x_1,\ldots,x_{k-1} \in \big[\frac{1+\varepsilon _1}k,1\big]$
such that
$x_1,\ldots,x_{k-1} \in \big[\frac{1+\varepsilon _1}k,1\big]$
such that
![]() $F(x_1,\ldots,x_{k-1},1)=1$
. We observe that
$F(x_1,\ldots,x_{k-1},1)=1$
. We observe that
 \begin{align*} \left . \mathchoice{\frac{\partial F}{\partial x_k}}{\partial F/\partial x_k}{\partial F/\partial x_k}{\partial F/\partial x_k} \right |_{x_k=1}=\left [ p^{1-k} \prod _{i=1}^{k-1}x_i-(1-p)^{1-k}(1-x_k)^{k-1} \right ] _{x_k=1}=p^{1-k} \prod _{i=1}^{k-1} x_i \gt 0. \end{align*}
\begin{align*} \left . \mathchoice{\frac{\partial F}{\partial x_k}}{\partial F/\partial x_k}{\partial F/\partial x_k}{\partial F/\partial x_k} \right |_{x_k=1}=\left [ p^{1-k} \prod _{i=1}^{k-1}x_i-(1-p)^{1-k}(1-x_k)^{k-1} \right ] _{x_k=1}=p^{1-k} \prod _{i=1}^{k-1} x_i \gt 0. \end{align*}
This implies that if we move from
![]() $x_k=1$
to
$x_k=1$
to
![]() $x_k=1- \varepsilon _2$
for some sufficiently small
$x_k=1- \varepsilon _2$
for some sufficiently small
![]() $\varepsilon _2$
, the value of
$\varepsilon _2$
, the value of
![]() $F$
will decrease. Therefore, there will exist a vector
$F$
will decrease. Therefore, there will exist a vector
![]() $(x_1,\ldots,x_k)$
for which
$(x_1,\ldots,x_k)$
for which
![]() $F(x_1,\ldots,x_k)\lt 1$
, contradicting Lemma 4.1 as long as
$F(x_1,\ldots,x_k)\lt 1$
, contradicting Lemma 4.1 as long as
![]() $k \geq k_1(p)$
. Thus, for every choice of
$k \geq k_1(p)$
. Thus, for every choice of
![]() $x_1,\ldots,x_{k-1} \in \big[\frac{1+\varepsilon _1}k,1\big]$
, we have that
$x_1,\ldots,x_{k-1} \in \big[\frac{1+\varepsilon _1}k,1\big]$
, we have that
![]() $F(x_1,\ldots,x_{k-1},1)\gt 1$
. Since the space
$F(x_1,\ldots,x_{k-1},1)\gt 1$
. Since the space
![]() $\big[\frac{1+\varepsilon _1}k,1\big]^{k-1} \times \{1\}$
is compact, we in fact find that
$\big[\frac{1+\varepsilon _1}k,1\big]^{k-1} \times \{1\}$
is compact, we in fact find that
![]() $F(x_1,\ldots,x_{k-1},1) \geq 1+\delta' _{\!\!1}$
for all
$F(x_1,\ldots,x_{k-1},1) \geq 1+\delta' _{\!\!1}$
for all
![]() $x_1,\ldots,x_{k-1} \in \big[\frac{1+\varepsilon _1}k,1\big]$
, for some sufficiently small
$x_1,\ldots,x_{k-1} \in \big[\frac{1+\varepsilon _1}k,1\big]$
, for some sufficiently small
![]() $\delta'_{\!\!1}$
depending on
$\delta'_{\!\!1}$
depending on
![]() $p$
and
$p$
and
![]() $k$
. Finally, by continuity of
$k$
. Finally, by continuity of
![]() $F$
, we have that
$F$
, we have that
![]() $F(x_1,\ldots,x_k) \geq 1+\delta _1$
whenever
$F(x_1,\ldots,x_k) \geq 1+\delta _1$
whenever
![]() $x_k \geq 1- \varepsilon _2$
for some other
$x_k \geq 1- \varepsilon _2$
for some other
![]() $\delta _1,\varepsilon _2\gt 0$
. Since
$\delta _1,\varepsilon _2\gt 0$
. Since
![]() $F$
is a symmetric function of its variables, the same conclusion holds if
$F$
is a symmetric function of its variables, the same conclusion holds if
![]() $x_i \geq 1- \varepsilon _2$
for any
$x_i \geq 1- \varepsilon _2$
for any
![]() $i$
. Thus, as long as we take the
$i$
. Thus, as long as we take the
![]() $\delta _0$
in the lemma statement to be smaller than
$\delta _0$
in the lemma statement to be smaller than
![]() $\delta _1$
, we can assume from now on that
$\delta _1$
, we can assume from now on that
![]() $x_i \in [\frac{1+\varepsilon _1}k, 1- \varepsilon _2]$
for all
$x_i \in [\frac{1+\varepsilon _1}k, 1- \varepsilon _2]$
for all
![]() $i$
.
$i$
.
By Lemma 2.5, subject to the constraint
![]() $\prod _{i=1}^k x_i = z$
, the term
$\prod _{i=1}^k x_i = z$
, the term
![]() $\frac 1k \sum _{i=1}^k \!(1-x_i)^k$
is minimized when
$\frac 1k \sum _{i=1}^k \!(1-x_i)^k$
is minimized when
![]() $x_i= z^{1/k}$
for all
$x_i= z^{1/k}$
for all
![]() $i$
. As in the proof of Lemma 4.1, this shows that
$i$
. As in the proof of Lemma 4.1, this shows that
![]() $F(x_1,\dots,x_k) \geq \psi (z^{1/k})$
, where
$F(x_1,\dots,x_k) \geq \psi (z^{1/k})$
, where
![]() $\psi (w) = p^{1-k}w^k + (1-p)^{1-k}(1-w)^k$
. The function
$\psi (w) = p^{1-k}w^k + (1-p)^{1-k}(1-w)^k$
. The function
![]() $\psi$
has a global minimum at
$\psi$
has a global minimum at
![]() $w=p$
, where its value is
$w=p$
, where its value is
![]() $1$
. This shows that
$1$
. This shows that
![]() $F(x_1,\dots,x_k)\geq 1+\delta _0$
if
$F(x_1,\dots,x_k)\geq 1+\delta _0$
if
![]() $\lvert z^{1/k}-p\rvert \geq \varepsilon _3$
, for some
$\lvert z^{1/k}-p\rvert \geq \varepsilon _3$
, for some
![]() $\varepsilon _3\gt 0$
depending on
$\varepsilon _3\gt 0$
depending on
![]() $p,k$
, and
$p,k$
, and
![]() $\delta _0$
. Moreover, by picking
$\delta _0$
. Moreover, by picking
![]() $\delta _0$
sufficiently small, we can make
$\delta _0$
sufficiently small, we can make
![]() $\varepsilon _3$
as small as we wish. Therefore, we may now assume that
$\varepsilon _3$
as small as we wish. Therefore, we may now assume that
![]() $z^{1/k} = p \pm \varepsilon _3$
, which implies that
$z^{1/k} = p \pm \varepsilon _3$
, which implies that
![]() $\log (z^{1/k}) = (\!\log p) \pm \varepsilon _4$
for some
$\log (z^{1/k}) = (\!\log p) \pm \varepsilon _4$
for some
![]() $\varepsilon _4\gt 0$
, which can also be made arbitrarily small by picking
$\varepsilon _4\gt 0$
, which can also be made arbitrarily small by picking
![]() $\delta _0$
appropriately.
$\delta _0$
appropriately.
We are now ready to apply Hölder’s defect formula. First, we observe that for
![]() $y \in [\!\log \frac{1+\varepsilon _1}k,\log (1-\varepsilon _2)]$
, we have
$y \in [\!\log \frac{1+\varepsilon _1}k,\log (1-\varepsilon _2)]$
, we have
where
![]() $m$
is a fixed, strictly positive constant. Let
$m$
is a fixed, strictly positive constant. Let
![]() $y_i = \log x_i$
for
$y_i = \log x_i$
for
![]() $1 \leq i \leq k$
, so that
$1 \leq i \leq k$
, so that
![]() $\frac 1k \sum _{i=1}^k y_i = \log (z^{1/k})$
. We assumed that
$\frac 1k \sum _{i=1}^k y_i = \log (z^{1/k})$
. We assumed that
![]() $\lvert x_j-p\rvert \geq \varepsilon _0$
for some
$\lvert x_j-p\rvert \geq \varepsilon _0$
for some
![]() $j$
, which implies that
$j$
, which implies that
![]() $\lvert y_j-\log p\rvert \geq \varepsilon _0$
as well, since the derivative of
$\lvert y_j-\log p\rvert \geq \varepsilon _0$
as well, since the derivative of
![]() $\log x$
is bounded below by
$\log x$
is bounded below by
![]() $1$
on the interval
$1$
on the interval
![]() $(0,1)$
. Therefore, choosing
$(0,1)$
. Therefore, choosing
![]() $\delta _0$
small enough that
$\delta _0$
small enough that
![]() $\varepsilon _4\lt \varepsilon _0$
, we see that
$\varepsilon _4\lt \varepsilon _0$
, we see that
 \begin{equation*} \frac 1k \sum _{i=1}^k \big(y_i-\log \big(z^{1/k}\big)\big)^2 \geq \frac 1k \big(y_j-\log \big(z^{1/k}\big)\big)^2 \geq \frac 1k (\varepsilon _0-\varepsilon _4)^2, \end{equation*}
\begin{equation*} \frac 1k \sum _{i=1}^k \big(y_i-\log \big(z^{1/k}\big)\big)^2 \geq \frac 1k \big(y_j-\log \big(z^{1/k}\big)\big)^2 \geq \frac 1k (\varepsilon _0-\varepsilon _4)^2, \end{equation*}
since
![]() $\log (z^{1/k}) = (\!\log p)\pm \varepsilon _4$
and
$\log (z^{1/k}) = (\!\log p)\pm \varepsilon _4$
and
![]() $\lvert y_j-\log p\rvert \geq \varepsilon _0$
. Hence, by Theorem 2.6, we have that
$\lvert y_j-\log p\rvert \geq \varepsilon _0$
. Hence, by Theorem 2.6, we have that
 \begin{align*} F(x_1,\dots,x_k) &= p^{1-k} z +\frac{(1-p)^{1-k}}k \sum _{i=1}^k (1-x_i)^k\\[5pt] &= p^{1-k}z + (1-p)^{1-k}\cdot \frac 1k \sum _{i=1}^k \varphi (y_i) \\[5pt] &\geq p^{1-k}z + \varphi \big(\!\log \big(z^{1/k}\big)\big)+ \frac m{2k}(\varepsilon _0-\varepsilon _4)^2\\[5pt] &=\psi (z^{1/k}) + \frac m{2k} (\varepsilon _0-\varepsilon _4)^2\\[5pt] &\geq 1+\delta _0, \end{align*}
\begin{align*} F(x_1,\dots,x_k) &= p^{1-k} z +\frac{(1-p)^{1-k}}k \sum _{i=1}^k (1-x_i)^k\\[5pt] &= p^{1-k}z + (1-p)^{1-k}\cdot \frac 1k \sum _{i=1}^k \varphi (y_i) \\[5pt] &\geq p^{1-k}z + \varphi \big(\!\log \big(z^{1/k}\big)\big)+ \frac m{2k}(\varepsilon _0-\varepsilon _4)^2\\[5pt] &=\psi (z^{1/k}) + \frac m{2k} (\varepsilon _0-\varepsilon _4)^2\\[5pt] &\geq 1+\delta _0, \end{align*}
where we use the fact that
![]() $\psi (w)\geq 1$
for all
$\psi (w)\geq 1$
for all
![]() $w \in [0,1]$
and take
$w \in [0,1]$
and take
![]() $\delta _0$
sufficiently small.
$\delta _0$
sufficiently small.
Using Lemma 5.2, we can now prove the following strengthening of Lemma 4.3, which says that if we have a blocked configuration
![]() $C_1,\ldots,C_k$
and many vertices whose blue density into
$C_1,\ldots,C_k$
and many vertices whose blue density into
![]() $C_i$
is far from
$C_i$
is far from
![]() $p$
, then we can find a substantially larger monochromatic book than what is guaranteed by Lemma 4.3.
$p$
, then we can find a substantially larger monochromatic book than what is guaranteed by Lemma 4.3.
Lemma 5.3.
Fix
![]() $p \in \big[\frac 12,1\big)$
and let
$p \in \big[\frac 12,1\big)$
and let
![]() $k \geq k_2(p)$
, where
$k \geq k_2(p)$
, where
![]() $k_2$
is the constant from Lemma 4.3. Suppose
$k_2$
is the constant from Lemma 4.3. Suppose
![]() $0\lt \varepsilon _0\lt \frac 14$
and let
$0\lt \varepsilon _0\lt \frac 14$
and let
![]() $\delta _0=\delta _0(\varepsilon _0)$
be the parameter from Lemma 5.2. Let
$\delta _0=\delta _0(\varepsilon _0)$
be the parameter from Lemma 5.2. Let
![]() $0\lt \delta \leq (1-p)\delta _0 \varepsilon _0$
and
$0\lt \delta \leq (1-p)\delta _0 \varepsilon _0$
and
![]() $0\lt \eta \leq \delta ^{4k^2}$
and suppose that
$0\lt \eta \leq \delta ^{4k^2}$
and suppose that
![]() $C_1,\ldots,C_k$
is either a
$C_1,\ldots,C_k$
is either a
![]() $(k,\eta,\delta )$
-red-blocked configuration or a
$(k,\eta,\delta )$
-red-blocked configuration or a
![]() $(k,\eta,\delta )$
-blue-blocked configuration in a red/blue colouring of
$(k,\eta,\delta )$
-blue-blocked configuration in a red/blue colouring of
![]() $K_N$
. Define
$K_N$
. Define
Then the following hold:
-
(a) If
 $|B_i| \geq \varepsilon _0 N$
for some
$|B_i| \geq \varepsilon _0 N$
for some
 $i$
, then the colouring contains a blue
$i$
, then the colouring contains a blue
 $B_{(p^k+\beta )N}^{(k)}$
or a red
$B_{(p^k+\beta )N}^{(k)}$
or a red
 $B_{((1-p)^k+\beta )N}^{(k)}$
, where
$B_{((1-p)^k+\beta )N}^{(k)}$
, where
 $\beta =(1-p)^k\delta _0 \varepsilon _0/2$
.
$\beta =(1-p)^k\delta _0 \varepsilon _0/2$
. -
(b) If, in addition,
 $|C_i| \geq \tau N$
for all
$|C_i| \geq \tau N$
for all
 $i$
and some
$i$
and some
 $\tau \gt 0$
, then there exists some
$\tau \gt 0$
, then there exists some
 $0\lt \gamma \lt \beta$
depending on
$0\lt \gamma \lt \beta$
depending on
 $\varepsilon _0,\tau,$
and
$\varepsilon _0,\tau,$
and
 $\delta$
such that the colouring contains
$\delta$
such that the colouring contains
 $(p,\gamma )$
-many books.
$(p,\gamma )$
-many books.
Proof. We may assume without loss of generality that
![]() $|B_1| \geq \varepsilon _0 N$
. As in the proof of Lemma 4.3, we need to split into two cases, depending on whether
$|B_1| \geq \varepsilon _0 N$
. As in the proof of Lemma 4.3, we need to split into two cases, depending on whether
![]() $C_1,\ldots,C_k$
is blue-blocked or red-blocked. We begin by assuming that it is
$C_1,\ldots,C_k$
is blue-blocked or red-blocked. We begin by assuming that it is
![]() $(k,\eta,\delta )$
-red-blocked.
$(k,\eta,\delta )$
-red-blocked.
First, as in the proof of Lemma 4.3, observe that each
![]() $C_i$
contains at least one red
$C_i$
contains at least one red
![]() $K_k$
and there is at least one blue
$K_k$
and there is at least one blue
![]() $K_k$
spanning
$K_k$
spanning
![]() $C_1,\ldots,C_k$
. Moreover, if we assume that
$C_1,\ldots,C_k$
. Moreover, if we assume that
![]() $|C_i| \geq \tau N$
for all
$|C_i| \geq \tau N$
for all
![]() $i$
, then Lemma 2.2 shows that the number of blue
$i$
, then Lemma 2.2 shows that the number of blue
![]() $K_k$
spanning
$K_k$
spanning
![]() $C_1,\ldots,C_k$
is at least
$C_1,\ldots,C_k$
is at least
 \begin{equation*} \left ( \prod _{1 \leq i \lt j \leq k}d_B(C_i,C_j)- \eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) \prod _{i=1}^k |C_i| \geq \!\left ( \delta ^{\left (\substack{k \\[3pt] 2 }\right )}-\eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) (\tau N)^k \geq \!\left ( \frac {\delta ^{\left (\substack{k\\[3pt] 2 }\right )}\tau ^k}{2} \right ) N^k \end{equation*}
\begin{equation*} \left ( \prod _{1 \leq i \lt j \leq k}d_B(C_i,C_j)- \eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) \prod _{i=1}^k |C_i| \geq \!\left ( \delta ^{\left (\substack{k \\[3pt] 2 }\right )}-\eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right ) \right ) (\tau N)^k \geq \!\left ( \frac {\delta ^{\left (\substack{k\\[3pt] 2 }\right )}\tau ^k}{2} \right ) N^k \end{equation*}
and similarly, with an additional factor of
![]() $1/k!$
, for the number of red
$1/k!$
, for the number of red
![]() $K_k$
inside each
$K_k$
inside each
![]() $C_i$
.
$C_i$
.
For a vertex
![]() $v$
and
$v$
and
![]() $i \in [k]$
, let
$i \in [k]$
, let
![]() $x_i(v)=d_B(v,C_i)$
. Lemma 4.1 implies that, for any
$x_i(v)=d_B(v,C_i)$
. Lemma 4.1 implies that, for any
![]() $v \in V$
,
$v \in V$
,
 \begin{equation*} p \!\left ( p^{-k}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k (1-x_i(v))^k \right ) \geq 1. \end{equation*}
\begin{equation*} p \!\left ( p^{-k}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k (1-x_i(v))^k \right ) \geq 1. \end{equation*}
Additionally, if
![]() $v \in B_1$
, then
$v \in B_1$
, then
![]() $|x_1(v)-p|\geq \varepsilon _0$
, so Lemma 5.2 implies that, for
$|x_1(v)-p|\geq \varepsilon _0$
, so Lemma 5.2 implies that, for
![]() $v \in B_1$
,
$v \in B_1$
,
 \begin{equation*} p \!\left ( p^{-k}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k (1-x_i(v))^k \right ) \geq 1+\delta _0. \end{equation*}
\begin{equation*} p \!\left ( p^{-k}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k (1-x_i(v))^k \right ) \geq 1+\delta _0. \end{equation*}
Adding these two equations up over all
![]() $v \in V$
shows that
$v \in V$
shows that
 \begin{equation*} p \!\left ( p^{-k} \sum _{v \in V}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V}(1-x_i(v))^k \right ) \geq N+\delta _0|B_1| \geq (1+\delta _0 \varepsilon _0)N. \end{equation*}
\begin{equation*} p \!\left ( p^{-k} \sum _{v \in V}\prod _{i=1}^k x_i(v) \right ) +(1-p) \left ( \frac {(1-p)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V}(1-x_i(v))^k \right ) \geq N+\delta _0|B_1| \geq (1+\delta _0 \varepsilon _0)N. \end{equation*}
That is, a
![]() $(p,1-p)$
-weighted average of two quantities is at least
$(p,1-p)$
-weighted average of two quantities is at least
![]() $(1+\delta _0 \varepsilon _0)N$
, which implies that one of the quantities must itself be at least
$(1+\delta _0 \varepsilon _0)N$
, which implies that one of the quantities must itself be at least
![]() $(1+\delta _0 \varepsilon _0)N$
. Suppose first that
$(1+\delta _0 \varepsilon _0)N$
. Suppose first that
 \begin{equation*} p^{-k} \sum _{v \in V} \prod _{i=1}^k x_i(v) \geq (1+\delta _0 \varepsilon _0)N. \end{equation*}
\begin{equation*} p^{-k} \sum _{v \in V} \prod _{i=1}^k x_i(v) \geq (1+\delta _0 \varepsilon _0)N. \end{equation*}
Let
![]() $Q$
be a uniformly random blue
$Q$
be a uniformly random blue
![]() $K_k$
with one vertex in each of
$K_k$
with one vertex in each of
![]() $C_1,\ldots,C_k$
. Let
$C_1,\ldots,C_k$
. Let
![]() $\alpha =\delta ^{k^2} \leq \prod _{i\lt j} d_B(C_i,C_j)$
, so that
$\alpha =\delta ^{k^2} \leq \prod _{i\lt j} d_B(C_i,C_j)$
, so that
![]() $\eta \leq \delta ^{4k^2} = \alpha ^4 \leq \alpha ^3/k^2$
. Therefore, applying Lemma 2.3 to each
$\eta \leq \delta ^{4k^2} = \alpha ^4 \leq \alpha ^3/k^2$
. Therefore, applying Lemma 2.3 to each
![]() $v$
and summing up the result, we find that the expected number of blue extensions of
$v$
and summing up the result, we find that the expected number of blue extensions of
![]() $Q$
is at least
$Q$
is at least
 \begin{align*} \sum _{v \in V} \!\left ( \prod _{i=1}^k x_i(v)-4 \alpha \right ) &\geq (p^k+ p^k\delta _0 \varepsilon _0-4 \alpha )N. \end{align*}
\begin{align*} \sum _{v \in V} \!\left ( \prod _{i=1}^k x_i(v)-4 \alpha \right ) &\geq (p^k+ p^k\delta _0 \varepsilon _0-4 \alpha )N. \end{align*}
Next, observe that
which implies that the expected number of blue extensions of
![]() $Q$
is at least
$Q$
is at least
![]() $(p^k+\beta )N$
, where
$(p^k+\beta )N$
, where
![]() $\beta =(1-p)^k \delta _0 \varepsilon _0/2$
. Thus, there exists a blue
$\beta =(1-p)^k \delta _0 \varepsilon _0/2$
. Thus, there exists a blue
![]() $B_{(p^k+\beta )N}^{(k)}$
, proving (a) in this case. Moreover, if we assume that
$B_{(p^k+\beta )N}^{(k)}$
, proving (a) in this case. Moreover, if we assume that
![]() $|C_i| \geq \tau N$
for all
$|C_i| \geq \tau N$
for all
![]() $i$
, then our earlier computation shows that
$i$
, then our earlier computation shows that
![]() $Q$
is chosen uniformly at random from a set of at least
$Q$
is chosen uniformly at random from a set of at least
![]() $\kappa N^k$
monochromatic cliques, where
$\kappa N^k$
monochromatic cliques, where
![]() $\kappa =\delta ^{ \left(\substack{ k\\[3pt] 2} \right)} \tau ^k/2$
. We may therefore apply Lemma 2.4 with
$\kappa =\delta ^{ \left(\substack{ k\\[3pt] 2} \right)} \tau ^k/2$
. We may therefore apply Lemma 2.4 with
![]() $\xi =p^k+\beta$
and
$\xi =p^k+\beta$
and
![]() $\nu =p^k+\gamma$
, for some appropriately chosen
$\nu =p^k+\gamma$
, for some appropriately chosen
![]() $0\lt \gamma \lt \beta$
, to conclude that in this case our colouring contains at least
$0\lt \gamma \lt \beta$
, to conclude that in this case our colouring contains at least
![]() $\gamma N^k$
blue cliques, each with at least
$\gamma N^k$
blue cliques, each with at least
![]() $(p^k+\gamma )N$
blue extensions, proving (b).
$(p^k+\gamma )N$
blue extensions, proving (b).
Therefore, we may assume that the second term in the weighted average is the large one, that is, that
 \begin{equation*} \frac {(1-p)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V}(1-x_i(v))^k\geq (1+\delta _0 \varepsilon _0)N, \end{equation*}
\begin{equation*} \frac {(1-p)^{-k}}{k}\sum _{i=1}^k \sum _{v \in V}(1-x_i(v))^k\geq (1+\delta _0 \varepsilon _0)N, \end{equation*}
which implies that, for some
![]() $i$
,
$i$
,
Therefore, if
![]() $Q$
is now a random red
$Q$
is now a random red
![]() $K_k$
inside this
$K_k$
inside this
![]() $C_i$
, Lemma 2.3 implies that the expected number of red extensions of
$C_i$
, Lemma 2.3 implies that the expected number of red extensions of
![]() $Q$
is at least
$Q$
is at least
But, by (11),
![]() $4 \alpha \leq (1-p)^k \delta _0 \varepsilon _0/2$
, which implies that the expected number of red extensions of
$4 \alpha \leq (1-p)^k \delta _0 \varepsilon _0/2$
, which implies that the expected number of red extensions of
![]() $Q$
is at least
$Q$
is at least
![]() $((1-p)^k+\beta )N$
, proving (a). As before, if we also assume that
$((1-p)^k+\beta )N$
, proving (a). As before, if we also assume that
![]() $|C_i| \geq \tau N$
for all
$|C_i| \geq \tau N$
for all
![]() $i$
, then we may apply Lemma 2.4 with
$i$
, then we may apply Lemma 2.4 with
![]() $\kappa =\delta ^{ \left(\substack{ k \\[3pt] 2} \right)}\tau ^k/2k!$
,
$\kappa =\delta ^{ \left(\substack{ k \\[3pt] 2} \right)}\tau ^k/2k!$
,
![]() $\xi =(1-p)^k+\beta$
, and
$\xi =(1-p)^k+\beta$
, and
![]() $\nu = (1-p)^k+\gamma$
to find that our colouring contains at least
$\nu = (1-p)^k+\gamma$
to find that our colouring contains at least
![]() $\gamma N^k$
red
$\gamma N^k$
red
![]() $K_k$
, each with at least
$K_k$
, each with at least
![]() $((1-p)^k+\gamma )N$
red extensions for some appropriately chosen
$((1-p)^k+\gamma )N$
red extensions for some appropriately chosen
![]() $\gamma \in (0,\beta )$
, yielding (b). This concludes the proof of the lemma in the case where
$\gamma \in (0,\beta )$
, yielding (b). This concludes the proof of the lemma in the case where
![]() $C_1,\ldots,C_k$
is a
$C_1,\ldots,C_k$
is a
![]() $(k,\eta,\delta )$
-red-blocked configuration.
$(k,\eta,\delta )$
-red-blocked configuration.
As in the proof of Lemma 4.3, the other case, where
![]() $C_1,\ldots,C_k$
is a
$C_1,\ldots,C_k$
is a
![]() $(k,\eta,\delta )$
-blue-blocked configuration, follows in an almost identical fashion. We define
$(k,\eta,\delta )$
-blue-blocked configuration, follows in an almost identical fashion. We define
![]() $y_i(v)=d_R(v,C_i)$
for all
$y_i(v)=d_R(v,C_i)$
for all
![]() $v \in V$
and
$v \in V$
and
![]() $i \in [k]$
and let
$i \in [k]$
and let
![]() $q=1-p$
. We then apply Lemma 4.1 and 5.2 with these
$q=1-p$
. We then apply Lemma 4.1 and 5.2 with these
![]() $y$
variables and with
$y$
variables and with
![]() $q$
instead of
$q$
instead of
![]() $p$
. The remaining details are exactly the same.
$p$
. The remaining details are exactly the same.
Next, we strengthen Lemma 5.3 by showing that not only does every part of a blocked configuration have density roughly
![]() $p$
to most vertices, but it is in fact
$p$
to most vertices, but it is in fact
![]() $(p,\varepsilon )$
-regular to the entire vertex set. Here, by saying that a pair of vertex subsets
$(p,\varepsilon )$
-regular to the entire vertex set. Here, by saying that a pair of vertex subsets
![]() $(X,Y)$
is
$(X,Y)$
is
![]() $(p,\varepsilon )$
-regular, we mean that
$(p,\varepsilon )$
-regular, we mean that
![]() $|d(X',Y')-p| \leq \varepsilon$
for every
$|d(X',Y')-p| \leq \varepsilon$
for every
![]() $X' \subseteq X$
,
$X' \subseteq X$
,
![]() $Y' \subseteq Y$
with
$Y' \subseteq Y$
with
![]() $|X'| \geq \varepsilon |X|$
,
$|X'| \geq \varepsilon |X|$
,
![]() $|Y'| \geq \varepsilon |Y|$
. Note that
$|Y'| \geq \varepsilon |Y|$
. Note that
![]() $(p,\varepsilon )$
-regularity is equivalent, up to a linear change in the parameters, to
$(p,\varepsilon )$
-regularity is equivalent, up to a linear change in the parameters, to
![]() $\varepsilon$
-regularity with density
$\varepsilon$
-regularity with density
![]() $p \pm \varepsilon$
.
$p \pm \varepsilon$
.
Lemma 5.4.
Fix
![]() $p \in [\frac 12, 1)$
and let
$p \in [\frac 12, 1)$
and let
![]() $k \geq k_2(p)$
. Suppose
$k \geq k_2(p)$
. Suppose
![]() $0\lt \varepsilon _1\lt \frac 14$
,
$0\lt \varepsilon _1\lt \frac 14$
,
![]() $\varepsilon _0=\varepsilon _1^2/2$
, and let
$\varepsilon _0=\varepsilon _1^2/2$
, and let
![]() $\delta _0=\delta _0(\varepsilon _0)$
be the parameter from Lemma
5.2
. Let
$\delta _0=\delta _0(\varepsilon _0)$
be the parameter from Lemma
5.2
. Let
![]() $0\lt \delta \leq (1-p)\delta _0 \varepsilon _0$
and
$0\lt \delta \leq (1-p)\delta _0 \varepsilon _0$
and
![]() $0\lt \eta \leq \varepsilon _1 2^{-4k^2}\delta ^{4k^2}$
and suppose that
$0\lt \eta \leq \varepsilon _1 2^{-4k^2}\delta ^{4k^2}$
and suppose that
![]() $C_1,\ldots,C_k$
is either a
$C_1,\ldots,C_k$
is either a
![]() $(k,\eta,\delta )$
-red-blocked or a
$(k,\eta,\delta )$
-red-blocked or a
![]() $(k,\eta,\delta )$
-blue-blocked configuration in a red/blue colouring of
$(k,\eta,\delta )$
-blue-blocked configuration in a red/blue colouring of
![]() $K_N$
. Then the following hold:
$K_N$
. Then the following hold:
-
(a) If, for some
 $i$
, the pair
$i$
, the pair
 $(C_i,V)$
is not
$(C_i,V)$
is not
 $(p,\varepsilon _1)$
-regular in blue, then the colouring contains a blue
$(p,\varepsilon _1)$
-regular in blue, then the colouring contains a blue
 $B^{(k)}_{(p^{k}+\beta )N}$
or a red
$B^{(k)}_{(p^{k}+\beta )N}$
or a red
 $B^{(k)} _{((1-p)^k+\beta )N}$
, where
$B^{(k)} _{((1-p)^k+\beta )N}$
, where
 $\beta =(1-p)^k\delta _0 \varepsilon _0/2$
.
$\beta =(1-p)^k\delta _0 \varepsilon _0/2$
. -
(b) If, in addition,
 $|C_i| \geq \tau N$
for all
$|C_i| \geq \tau N$
for all
 $i$
and some
$i$
and some
 $\tau \gt 0$
, then the colouring contains
$\tau \gt 0$
, then the colouring contains
 $(p,\gamma )$
-many books for some
$(p,\gamma )$
-many books for some
 $0\lt \gamma \lt \beta$
depending on
$0\lt \gamma \lt \beta$
depending on
 $\varepsilon _1,\delta$
, and
$\varepsilon _1,\delta$
, and
 $\tau$
.
$\tau$
.
Proof. Without loss of generality, suppose that
![]() $(C_1,V)$
is not
$(C_1,V)$
is not
![]() $(p,\varepsilon _1)$
-regular in blue. Then there exist
$(p,\varepsilon _1)$
-regular in blue. Then there exist
![]() $C'_{\!\!1} \subseteq C_1, D \subseteq V$
with
$C'_{\!\!1} \subseteq C_1, D \subseteq V$
with
![]() $|C'_{\!\!1}| \geq \varepsilon _1 |C_1|, |D| \geq \varepsilon _1 N$
such that
$|C'_{\!\!1}| \geq \varepsilon _1 |C_1|, |D| \geq \varepsilon _1 N$
such that
![]() $|d_B(C'_{\!\!1},D)-p| \gt \varepsilon _1$
. Assume first that
$|d_B(C'_{\!\!1},D)-p| \gt \varepsilon _1$
. Assume first that
![]() $d_B(C'_{\!\!1},D) \geq p+\varepsilon _1$
. Let
$d_B(C'_{\!\!1},D) \geq p+\varepsilon _1$
. Let
![]() $D_1 \subseteq D$
denote the set of vertices
$D_1 \subseteq D$
denote the set of vertices
![]() $v \in D$
with
$v \in D$
with
![]() $d_B(v,C'_{\!\!1})\lt p +\frac{\varepsilon _1}{2}$
and let
$d_B(v,C'_{\!\!1})\lt p +\frac{\varepsilon _1}{2}$
and let
![]() $D_2=D \setminus D_1$
. Then we have that
$D_2=D \setminus D_1$
. Then we have that
which implies that
![]() $|D_2| \geq \frac{\varepsilon _1}{2}|D| \geq \frac{\varepsilon _1^2}{2}N=\varepsilon _0 N$
, where each
$|D_2| \geq \frac{\varepsilon _1}{2}|D| \geq \frac{\varepsilon _1^2}{2}N=\varepsilon _0 N$
, where each
![]() $v \in D_2$
has
$v \in D_2$
has
![]() $d_B(v,C'_{\!\!1}) \geq p+\frac{\varepsilon _1}{2}$
. Now, consider the
$d_B(v,C'_{\!\!1}) \geq p+\frac{\varepsilon _1}{2}$
. Now, consider the
![]() $k$
-tuple of sets
$k$
-tuple of sets
![]() $C'_{\!\!1},C_2,\ldots,C_k$
; by the hereditary property of regularity, we see that this is a
$C'_{\!\!1},C_2,\ldots,C_k$
; by the hereditary property of regularity, we see that this is a
![]() $(k,\eta ',\delta ')$
-blocked configuration, where
$(k,\eta ',\delta ')$
-blocked configuration, where
![]() $\eta '=\eta/\varepsilon _1$
and
$\eta '=\eta/\varepsilon _1$
and
![]() $\delta '=\delta - \eta \geq \delta/2$
. This implies that
$\delta '=\delta - \eta \geq \delta/2$
. This implies that
![]() $\delta ' \leq (1-p) \delta _0 \varepsilon _0$
and
$\delta ' \leq (1-p) \delta _0 \varepsilon _0$
and
![]() $\eta ' \leq (\delta ')^{4k^2}$
. Therefore, we may apply Lemma 5.3 to the
$\eta ' \leq (\delta ')^{4k^2}$
. Therefore, we may apply Lemma 5.3 to the
![]() $(k,\eta ',\delta ')$
-blocked configuration
$(k,\eta ',\delta ')$
-blocked configuration
![]() $C'_{\!\!1},C_2,\ldots,C_k$
to conclude that the colouring contains a blue
$C'_{\!\!1},C_2,\ldots,C_k$
to conclude that the colouring contains a blue
![]() $B_{(p^k+\beta )N}^{(k)}$
or a red
$B_{(p^k+\beta )N}^{(k)}$
or a red
![]() $B_{((1-p)^k+\beta )N}^{(k)}$
. Moreover, if we assume that
$B_{((1-p)^k+\beta )N}^{(k)}$
. Moreover, if we assume that
![]() $|C_i| \geq \tau N$
for all
$|C_i| \geq \tau N$
for all
![]() $i$
, then
$i$
, then
![]() $|C_i'| \geq \varepsilon _1 \tau N$
for all
$|C_i'| \geq \varepsilon _1 \tau N$
for all
![]() $i$
, where
$i$
, where
![]() $C_i'=C_i$
if
$C_i'=C_i$
if
![]() $i\geq 2$
. Thus, Lemma 5.3 implies that in this case the colouring contains
$i\geq 2$
. Thus, Lemma 5.3 implies that in this case the colouring contains
![]() $(p,\gamma )$
-many books for some
$(p,\gamma )$
-many books for some
![]() $0\lt \gamma \lt \beta$
depending on
$0\lt \gamma \lt \beta$
depending on
![]() $\varepsilon _1,\delta$
, and
$\varepsilon _1,\delta$
, and
![]() $\tau$
.
$\tau$
.
To complete the proof of the lemma, we also need to check the case where
![]() $d_B(C'_{\!\!1},D) \leq p- \varepsilon _1$
. However, the proof is essentially identical: we find a subset
$d_B(C'_{\!\!1},D) \leq p- \varepsilon _1$
. However, the proof is essentially identical: we find a subset
![]() $D_2 \subseteq D$
such that every vertex
$D_2 \subseteq D$
such that every vertex
![]() $v \in D_2$
has
$v \in D_2$
has
![]() $d_B(v,C'_{\!\!1}) \leq p- \frac{\varepsilon _1}{2}$
and such that
$d_B(v,C'_{\!\!1}) \leq p- \frac{\varepsilon _1}{2}$
and such that
![]() $|D_2| \geq \frac{\varepsilon _1}{2}|D|$
and then the rest of the proof is as above.
$|D_2| \geq \frac{\varepsilon _1}{2}|D|$
and then the rest of the proof is as above.
Our next technical lemma gives the inductive step for our proof of Theorem 1.4. The proof mimics that of Theorem 1.3, except that the vertex set is split into parts that were already pulled out as regular and a part that has not yet been touched. Inside the untouched part, we build a reduced graph and use it to find either many large monochromatic books or a blocked configuration, at which point Lemma 5.4 implies that the induction can continue.
Lemma 5.5.
Fix
![]() $p \in \big[\frac 12,1\big)$
and let
$p \in \big[\frac 12,1\big)$
and let
![]() $k \geq k_2(p)$
. Fix
$k \geq k_2(p)$
. Fix
![]() $0\lt \varepsilon \leq p/(20 k)$
and suppose that the edges of the complete graph
$0\lt \varepsilon \leq p/(20 k)$
and suppose that the edges of the complete graph
![]() $K_N$
with vertex set
$K_N$
with vertex set
![]() $V$
have been red/blue coloured. Suppose that
$V$
have been red/blue coloured. Suppose that
![]() $A_1,\ldots,A_\ell$
are disjoint subsets of
$A_1,\ldots,A_\ell$
are disjoint subsets of
![]() $V$
such that
$V$
such that
![]() $(A_i,V)$
is
$(A_i,V)$
is
![]() $(p, \varepsilon ^2)$
-regular for all
$(p, \varepsilon ^2)$
-regular for all
![]() $i$
. Let
$i$
. Let
![]() $W= V \setminus (A_1 \cup \dotsb \cup A_\ell )$
and suppose that
$W= V \setminus (A_1 \cup \dotsb \cup A_\ell )$
and suppose that
![]() $|W| \geq \varepsilon N$
. Then either there is some
$|W| \geq \varepsilon N$
. Then either there is some
![]() $A_{\ell +1} \subseteq W$
such that
$A_{\ell +1} \subseteq W$
such that
![]() $(A_{\ell +1},V)$
is
$(A_{\ell +1},V)$
is
![]() $(p, \varepsilon ^2)$
-regular or else the colouring contains
$(p, \varepsilon ^2)$
-regular or else the colouring contains
![]() $(p,\gamma )$
-many books for some
$(p,\gamma )$
-many books for some
![]() $\gamma \gt 0$
depending on
$\gamma \gt 0$
depending on
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $p,$
and
$p,$
and
![]() $k$
.
$k$
.
Proof. Let
![]() $\varepsilon _1=\varepsilon ^2$
,
$\varepsilon _1=\varepsilon ^2$
,
![]() $\varepsilon _0=\varepsilon _1^2/2,$
and
$\varepsilon _0=\varepsilon _1^2/2,$
and
![]() $\delta _0=\delta _0(\varepsilon _0)$
be the parameter from Lemma 5.2 and set
$\delta _0=\delta _0(\varepsilon _0)$
be the parameter from Lemma 5.2 and set
![]() $\delta =(1-p)\delta _0 \varepsilon _0$
,
$\delta =(1-p)\delta _0 \varepsilon _0$
,
![]() $\eta =\varepsilon ^2 2^{-4k^2} \delta ^{4k^2}$
,
$\eta =\varepsilon ^2 2^{-4k^2} \delta ^{4k^2}$
,
![]() $\beta =k p^{k-1}\varepsilon ^2$
, and
$\beta =k p^{k-1}\varepsilon ^2$
, and
![]() $\beta '=4 \varepsilon$
. We apply Lemma 2.1 to the subgraph induced on
$\beta '=4 \varepsilon$
. We apply Lemma 2.1 to the subgraph induced on
![]() $W$
, with parameters
$W$
, with parameters
![]() $\eta$
and
$\eta$
and
![]() $M_0=1/\eta$
, to obtain an equitable partition
$M_0=1/\eta$
, to obtain an equitable partition
![]() $W=W_1 \sqcup \dotsb \sqcup W_m$
, where
$W=W_1 \sqcup \dotsb \sqcup W_m$
, where
![]() $M_0 \leq m \leq M=M(\eta,M_0)$
. Call a part
$M_0 \leq m \leq M=M(\eta,M_0)$
. Call a part
![]() $W_i$
blue if
$W_i$
blue if
![]() $d_B(W_i) \geq \frac 12$
and red otherwise. As in the proof of Theorem 1.3, we first assume that at least
$d_B(W_i) \geq \frac 12$
and red otherwise. As in the proof of Theorem 1.3, we first assume that at least
![]() $m' \geq pm$
of the parts are blue and rename them so that
$m' \geq pm$
of the parts are blue and rename them so that
![]() $W_1,\ldots,W_{m'}$
are the blue parts.
$W_1,\ldots,W_{m'}$
are the blue parts.
We build a reduced graph
![]() $G$
on vertex set
$G$
on vertex set
![]() $w_1,\ldots,w_{m'}$
, connecting
$w_1,\ldots,w_{m'}$
, connecting
![]() $w_{i_1}$
and
$w_{i_1}$
and
![]() $w_{i_2}$
by an edge if
$w_{i_2}$
by an edge if
![]() $(W_{i_1},W_{i_2})$
is
$(W_{i_1},W_{i_2})$
is
![]() $\eta$
-regular and
$\eta$
-regular and
![]() $d_R(W_{i_1},W_{i_2}) \geq \delta$
. Suppose that
$d_R(W_{i_1},W_{i_2}) \geq \delta$
. Suppose that
![]() $w_1$
has at most
$w_1$
has at most
![]() $(1-p^{k-1}-\beta '/p-\eta/p)m'-1$
neighbours in
$(1-p^{k-1}-\beta '/p-\eta/p)m'-1$
neighbours in
![]() $G$
. Since
$G$
. Since
![]() $w_1$
has at most
$w_1$
has at most
![]() $\eta m \leq \eta m'/p$
non-neighbours coming from irregular pairs, this means that there are at least
$\eta m \leq \eta m'/p$
non-neighbours coming from irregular pairs, this means that there are at least
![]() $(p^{k-1}+\beta '/p)m'$
parts
$(p^{k-1}+\beta '/p)m'$
parts
![]() $W_j$
with
$W_j$
with
![]() $2 \leq j \leq m'$
such that
$2 \leq j \leq m'$
such that
![]() $(W_1,W_j)$
is
$(W_1,W_j)$
is
![]() $\eta$
-regular and
$\eta$
-regular and
![]() $d_B(W_1,W_j) \geq 1-\delta$
. Let
$d_B(W_1,W_j) \geq 1-\delta$
. Let
![]() $J$
be the set of these indices
$J$
be the set of these indices
![]() $j$
and set
$j$
and set
![]() $U=\bigcup _{j \in J} W_j$
. By the counting lemma, Lemma 2.2,
$U=\bigcup _{j \in J} W_j$
. By the counting lemma, Lemma 2.2,
![]() $W_1$
contains at least
$W_1$
contains at least
![]() $\frac{1}{k!}\!\left (2^{-\left (\substack{ k\\[3pt] 2 }\right )}-\eta \!\left (\substack{k\\[3pt] 2 }\right )\right )|W_1|^k$
blue copies of
$\frac{1}{k!}\!\left (2^{-\left (\substack{ k\\[3pt] 2 }\right )}-\eta \!\left (\substack{k\\[3pt] 2 }\right )\right )|W_1|^k$
blue copies of
![]() $K_k$
and
$K_k$
and
 \begin{equation*} \frac {1}{k!}\!\left (2^{-\left (\substack{ k\\[3pt] 2 }\right )}- \eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right )\right )|W_1|^k \geq \frac {2^{-k^2}}{k!} \left ( \frac {|W|}{M} \right ) ^k \geq \!\left (\frac { \varepsilon N}{k 2^k M}\right )^k, \end{equation*}
\begin{equation*} \frac {1}{k!}\!\left (2^{-\left (\substack{ k\\[3pt] 2 }\right )}- \eta \!\left (\begin {array}{c} k\\[-3pt] 2 \end {array}\right )\right )|W_1|^k \geq \frac {2^{-k^2}}{k!} \left ( \frac {|W|}{M} \right ) ^k \geq \!\left (\frac { \varepsilon N}{k 2^k M}\right )^k, \end{equation*}
where we use that
![]() $\eta \leq \delta ^{4k^2} \leq \delta ^{ \left(\substack{ k\\[3pt] 2 } \right)}/ \left(\substack{ k\\[3pt] 2} \right)$
and that
$\eta \leq \delta ^{4k^2} \leq \delta ^{ \left(\substack{ k\\[3pt] 2 } \right)}/ \left(\substack{ k\\[3pt] 2} \right)$
and that
![]() $2^{- \left(\substack{ k\\[3pt] 2 } \right)}-\delta ^{ \left(\substack{k\\[3pt] 2} \right)} \gt 2^{-k^2}$
, along with our assumption that
$2^{- \left(\substack{ k\\[3pt] 2 } \right)}-\delta ^{ \left(\substack{k\\[3pt] 2} \right)} \gt 2^{-k^2}$
, along with our assumption that
![]() $|W| \geq \varepsilon N$
. If we set
$|W| \geq \varepsilon N$
. If we set
![]() $\kappa =( \varepsilon/k 2^k M)^k$
, then this implies that
$\kappa =( \varepsilon/k 2^k M)^k$
, then this implies that
![]() $W_1$
contains at least
$W_1$
contains at least
![]() $\kappa N^k$
blue
$\kappa N^k$
blue
![]() $K_k$
. If we pick a uniformly random such blue
$K_k$
. If we pick a uniformly random such blue
![]() $K_k$
, then Lemma 2.3 with
$K_k$
, then Lemma 2.3 with
![]() $\alpha =\delta ^{k^2} \leq 2^{- \left(\substack{ k\\[3pt] 2 } \right)}\leq d_B(W_1)^{ \left(\substack{ k\\[3pt] 2 } \right)}$
implies that its expected number of blue extensions inside
$\alpha =\delta ^{k^2} \leq 2^{- \left(\substack{ k\\[3pt] 2 } \right)}\leq d_B(W_1)^{ \left(\substack{ k\\[3pt] 2 } \right)}$
implies that its expected number of blue extensions inside
![]() $U$
is at least
$U$
is at least
where we first use Jensen’s inequality applied to the convex function
![]() $x \mapsto x^k$
to lower bound
$x \mapsto x^k$
to lower bound
![]() $\sum _u d_B(u,W_1)^k$
by
$\sum _u d_B(u,W_1)^k$
by
![]() $(1- \delta )^k|U|$
and then use that
$(1- \delta )^k|U|$
and then use that
![]() $(1- \delta )^k \geq 1-k \delta$
and
$(1- \delta )^k \geq 1-k \delta$
and
![]() $4 \delta ^{k^2} \leq \delta ^k \leq k \delta$
. Since we assumed that
$4 \delta ^{k^2} \leq \delta ^k \leq k \delta$
. Since we assumed that
![]() $J$
was large and the partition is equitable, we find that
$J$
was large and the partition is equitable, we find that
Thus, a random blue
![]() $K_k$
inside
$K_k$
inside
![]() $W_1$
has at least
$W_1$
has at least
![]() $(1-2k \delta )(p^{k}+\beta ')|W|$
blue extensions in
$(1-2k \delta )(p^{k}+\beta ')|W|$
blue extensions in
![]() $W$
.
$W$
.
Now, suppose that instead of just
![]() $w_1$
having low degree in
$w_1$
having low degree in
![]() $G$
, we have a set of at least
$G$
, we have a set of at least
![]() $\varepsilon m$
vertices
$\varepsilon m$
vertices
![]() $w_j \in V(G)$
, each with at most
$w_j \in V(G)$
, each with at most
![]() $(1-p^{k-1}-\beta '/p-\eta/p)m'-1$
neighbours in
$(1-p^{k-1}-\beta '/p-\eta/p)m'-1$
neighbours in
![]() $G$
. Let
$G$
. Let
![]() $S$
be the set of these
$S$
be the set of these
![]() $j$
and
$j$
and
![]() $T=\bigcup _{j \in S} W_j$
. By the above argument, for every
$T=\bigcup _{j \in S} W_j$
. By the above argument, for every
![]() $j\in S$
, we have that
$j\in S$
, we have that
![]() $W_j$
contains at least
$W_j$
contains at least
![]() $\kappa N^k$
blue
$\kappa N^k$
blue
![]() $K_k$
such that a uniformly average one among them has at least
$K_k$
such that a uniformly average one among them has at least
![]() $(1-2k \delta )(p^{k}+\beta ')|W|$
blue extensions into
$(1-2k \delta )(p^{k}+\beta ')|W|$
blue extensions into
![]() $W$
. Moreover, we have that
$W$
. Moreover, we have that
We may therefore apply the
![]() $(p,\varepsilon ^2)$
regularity of
$(p,\varepsilon ^2)$
regularity of
![]() $(A_i, V)$
to conclude that
$(A_i, V)$
to conclude that
![]() $d_B(A_i,T)=p \pm \varepsilon ^2$
for all
$d_B(A_i,T)=p \pm \varepsilon ^2$
for all
![]() $i$
. Thus, if we pick
$i$
. Thus, if we pick
![]() $j \in S$
randomly, then
$j \in S$
randomly, then
![]() $\mathbb{E}[d_B(W_j,A_i)]=p \pm \varepsilon ^2$
. Therefore, if we first sample
$\mathbb{E}[d_B(W_j,A_i)]=p \pm \varepsilon ^2$
. Therefore, if we first sample
![]() $j \in S$
randomly and then pick a random blue
$j \in S$
randomly and then pick a random blue
![]() $K_k$
inside
$K_k$
inside
![]() $W_j$
, then Lemma 2.3 implies that this random blue
$W_j$
, then Lemma 2.3 implies that this random blue
![]() $K_k$
will have in expectation at least
$K_k$
will have in expectation at least
 \begin{align*} \sum _{a \in A_i} \!\left ( d_B(a,W_j)^k-4 \delta ^{k^2} \right ) &\geq \left [ \left ( p- \varepsilon ^2 \right ) ^k- \delta ^k \right ] |A_i| \\[5pt] &\geq \left [ p^k \!\left ( 1- \frac{k\varepsilon ^2}{p} \right ) -\delta ^k \right ] |A_i|\\[5pt] &\geq p^k \!\left ( 1- \frac{2k\varepsilon ^2}{p} \right ) |A_i| \end{align*}
\begin{align*} \sum _{a \in A_i} \!\left ( d_B(a,W_j)^k-4 \delta ^{k^2} \right ) &\geq \left [ \left ( p- \varepsilon ^2 \right ) ^k- \delta ^k \right ] |A_i| \\[5pt] &\geq \left [ p^k \!\left ( 1- \frac{k\varepsilon ^2}{p} \right ) -\delta ^k \right ] |A_i|\\[5pt] &\geq p^k \!\left ( 1- \frac{2k\varepsilon ^2}{p} \right ) |A_i| \end{align*}
blue extensions into
![]() $A_i$
, again by Jensen’s inequality. This implies that this random
$A_i$
, again by Jensen’s inequality. This implies that this random
![]() $K_k$
has in expectation at least
$K_k$
has in expectation at least
![]() $(1 -2k \varepsilon ^2/p) p^{k}|A_1 \cup \dotsb \cup A_\ell |$
extensions into
$(1 -2k \varepsilon ^2/p) p^{k}|A_1 \cup \dotsb \cup A_\ell |$
extensions into
![]() $A_1 \cup \dotsb \cup A_\ell$
. Adding up the extensions into this set and into
$A_1 \cup \dotsb \cup A_\ell$
. Adding up the extensions into this set and into
![]() $W$
, its complement, shows that this random blue
$W$
, its complement, shows that this random blue
![]() $K_k$
has in expectation at least
$K_k$
has in expectation at least
![]() $\xi N$
blue extensions, where
$\xi N$
blue extensions, where
![]() $\xi$
is a weighted average of
$\xi$
is a weighted average of
![]() $(1-2k \varepsilon ^2/p)p^{k}$
and
$(1-2k \varepsilon ^2/p)p^{k}$
and
![]() $(1-2k \delta )(p^{k}+\beta ')$
, and where the latter quantity receives weight at least
$(1-2k \delta )(p^{k}+\beta ')$
, and where the latter quantity receives weight at least
![]() $\varepsilon$
, since
$\varepsilon$
, since
![]() $|W| \geq \varepsilon N$
. Thus,
$|W| \geq \varepsilon N$
. Thus,
 \begin{align*} \xi &\geq (1- \varepsilon )\left (1-\frac{2k \varepsilon ^2}p\right ) p^{k}+\varepsilon (1-2k \delta )(p^{k}+\beta ')\\[5pt] &\geq \!\left (1-\frac{2k \varepsilon ^2}p- \varepsilon \right )p^k+\varepsilon (1-2k \delta )(1+p^{-k} \beta ')p^k\\[5pt] &\geq \!\left (1-\frac{2k \varepsilon ^2}p- \varepsilon \right )p^k+\varepsilon \!\left (1+\frac{3k \varepsilon }p\right )p^k\\[5pt] &=p^k\!\left (1+\frac{k \varepsilon ^2}p\right )\\[5pt] &=p^k+\beta, \end{align*}
\begin{align*} \xi &\geq (1- \varepsilon )\left (1-\frac{2k \varepsilon ^2}p\right ) p^{k}+\varepsilon (1-2k \delta )(p^{k}+\beta ')\\[5pt] &\geq \!\left (1-\frac{2k \varepsilon ^2}p- \varepsilon \right )p^k+\varepsilon (1-2k \delta )(1+p^{-k} \beta ')p^k\\[5pt] &\geq \!\left (1-\frac{2k \varepsilon ^2}p- \varepsilon \right )p^k+\varepsilon \!\left (1+\frac{3k \varepsilon }p\right )p^k\\[5pt] &=p^k\!\left (1+\frac{k \varepsilon ^2}p\right )\\[5pt] &=p^k+\beta, \end{align*}
where we used the definition of
![]() $\beta$
, the fact that
$\beta$
, the fact that
![]() $2k\delta \lt p^{-k}\beta '/4$
, that
$2k\delta \lt p^{-k}\beta '/4$
, that
![]() $(1-x/4)(1+x) \geq 1+x/2$
for all
$(1-x/4)(1+x) \geq 1+x/2$
for all
![]() $x \in [0,1]$
, and that
$x \in [0,1]$
, and that
![]() $p^{-k} \beta ' \geq 6k \varepsilon/p$
, which follows since
$p^{-k} \beta ' \geq 6k \varepsilon/p$
, which follows since
![]() $\beta '=4\varepsilon$
and, as in the proof of Lemma 4.1,
$\beta '=4\varepsilon$
and, as in the proof of Lemma 4.1,
![]() $p^{1-k} \geq e^2 k \geq \frac 32 k$
for
$p^{1-k} \geq e^2 k \geq \frac 32 k$
for
![]() $k \geq k_2(p)$
. Therefore, by Lemma 2.4, we can find at least
$k \geq k_2(p)$
. Therefore, by Lemma 2.4, we can find at least
![]() $\gamma N^k$
blue
$\gamma N^k$
blue
![]() $K_k$
, each with at least
$K_k$
, each with at least
![]() $(p^{k}+\gamma )N$
blue extensions, for some
$(p^{k}+\gamma )N$
blue extensions, for some
![]() $\gamma \lt \beta$
depending on
$\gamma \lt \beta$
depending on
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $\beta$
and, thus, only on
$\beta$
and, thus, only on
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $p$
, and
$p$
, and
![]() $k$
.
$k$
.
Therefore, we may assume that in
![]() $G$
, all but
$G$
, all but
![]() $\varepsilon m\leq \varepsilon m'/p$
of the vertices have degree at least
$\varepsilon m\leq \varepsilon m'/p$
of the vertices have degree at least
![]() $(1-p^{k-1}-\beta '/p- \eta/p)m'$
. Hence, the average degree in
$(1-p^{k-1}-\beta '/p- \eta/p)m'$
. Hence, the average degree in
![]() $G$
is at least
$G$
is at least
since
![]() $\beta '=4 \varepsilon$
,
$\beta '=4 \varepsilon$
,
![]() $\eta \leq \varepsilon$
, and
$\eta \leq \varepsilon$
, and
![]() $\varepsilon \leq p/(20k)$
. By (8), the fact that
$\varepsilon \leq p/(20k)$
. By (8), the fact that
![]() $k \geq k_2(p)$
implies that
$k \geq k_2(p)$
implies that
![]() $p^{k-1} \leq 1/(3k)$
. Therefore, the average degree in
$p^{k-1} \leq 1/(3k)$
. Therefore, the average degree in
![]() $G$
is greater than
$G$
is greater than
![]() $(1-1/(k-1))m'$
, so, by Turán’s theorem,
$(1-1/(k-1))m'$
, so, by Turán’s theorem,
![]() $G$
will contain a
$G$
will contain a
![]() $K_k$
. Let
$K_k$
. Let
![]() $w_{i_1},\ldots,w_{i_k}$
be the vertices of this
$w_{i_1},\ldots,w_{i_k}$
be the vertices of this
![]() $K_k$
and let
$K_k$
and let
![]() $C_j=W_{i_j}$
for
$C_j=W_{i_j}$
for
![]() $1 \leq j \leq k$
. Then, by the definition of
$1 \leq j \leq k$
. Then, by the definition of
![]() $G$
, we see that
$G$
, we see that
![]() $C_1,\ldots,C_k$
is a
$C_1,\ldots,C_k$
is a
![]() $(k,\eta,\delta )$
-blue-blocked configuration with
$(k,\eta,\delta )$
-blue-blocked configuration with
![]() $|C_i| \geq \tau N$
for all
$|C_i| \geq \tau N$
for all
![]() $i$
, where
$i$
, where
![]() $\tau =\varepsilon/M$
depends only on
$\tau =\varepsilon/M$
depends only on
![]() $\varepsilon$
,
$\varepsilon$
,
![]() $p$
, and
$p$
, and
![]() $k$
. Thus, by Lemma 5.4, we see that either the colouring contains
$k$
. Thus, by Lemma 5.4, we see that either the colouring contains
![]() $(p,\gamma )$
-many books for some
$(p,\gamma )$
-many books for some
![]() $\gamma$
depending on
$\gamma$
depending on
![]() $\varepsilon,p,$
and
$\varepsilon,p,$
and
![]() $k$
or else
$k$
or else
![]() $(C_j,V)$
is
$(C_j,V)$
is
![]() $(p,\varepsilon ^2)$
-regular for all
$(p,\varepsilon ^2)$
-regular for all
![]() $j$
. In the latter case, we can set
$j$
. In the latter case, we can set
![]() $A_{\ell +1}=C_1$
(or any other
$A_{\ell +1}=C_1$
(or any other
![]() $C_j$
) and get the desired result.
$C_j$
) and get the desired result.
Now, we need to assume instead that at least
![]() $m'' \geq (1-p)m$
of the parts
$m'' \geq (1-p)m$
of the parts
![]() $W_i$
are red. However, just as in the proof of Theorem 1.3, the argument is essentially identical: we first rule out the existence of too many low-degree vertices in the reduced graph by counting extensions to
$W_i$
are red. However, just as in the proof of Theorem 1.3, the argument is essentially identical: we first rule out the existence of too many low-degree vertices in the reduced graph by counting extensions to
![]() $W$
and to
$W$
and to
![]() $A_1\cup \dotsb \cup A_\ell$
and then apply Turán’s theorem to find a
$A_1\cup \dotsb \cup A_\ell$
and then apply Turán’s theorem to find a
![]() $K_k$
in the reduced graph, which completes the proof by Lemma 5.4.
$K_k$
in the reduced graph, which completes the proof by Lemma 5.4.
By repeatedly applying Lemma 5.5 until
![]() $W$
has fewer than
$W$
has fewer than
![]() $\varepsilon N$
vertices, we can partition
$\varepsilon N$
vertices, we can partition
![]() $K_N$
into a collection of subsets
$K_N$
into a collection of subsets
![]() $A_i$
such that
$A_i$
such that
![]() $(A_i,V)$
is
$(A_i,V)$
is
![]() $(p,\varepsilon ^2)$
-regular, plus a small remainder set
$(p,\varepsilon ^2)$
-regular, plus a small remainder set
![]() $A_{\ell +1}$
about which we have no such information. Our final technical lemma shows that such a structural decomposition suffices to conclude that the colouring is
$A_{\ell +1}$
about which we have no such information. Our final technical lemma shows that such a structural decomposition suffices to conclude that the colouring is
![]() $(p,\theta )$
-quasirandom.
$(p,\theta )$
-quasirandom.
Lemma 5.6.
Let
![]() $\varepsilon \leq \theta/3$
. Suppose we have a partition
$\varepsilon \leq \theta/3$
. Suppose we have a partition
where
![]() $(A_i,V)$
is
$(A_i,V)$
is
![]() $(p,\varepsilon )$
-regular for each
$(p,\varepsilon )$
-regular for each
![]() $1 \leq i\leq \ell$
and
$1 \leq i\leq \ell$
and
![]() $|A_{\ell +1}| \leq \varepsilon N$
. Then the colouring is
$|A_{\ell +1}| \leq \varepsilon N$
. Then the colouring is
![]() $(p,\theta )$
-quasirandom.
$(p,\theta )$
-quasirandom.
Proof. Fix disjoint
![]() $X,Y \subseteq V(K_N)$
. We need to check that
$X,Y \subseteq V(K_N)$
. We need to check that
First, observe that if
![]() $|Y| \leq \varepsilon N$
, then
$|Y| \leq \varepsilon N$
, then
Therefore, from now on, we may assume that
![]() $|Y| \geq \varepsilon N$
. For
$|Y| \geq \varepsilon N$
. For
![]() $1 \leq i \leq \ell +1$
, let
$1 \leq i \leq \ell +1$
, let
![]() $X_i=A_i \cap X$
and define
$X_i=A_i \cap X$
and define
![]() $I_X=\{1 \leq i \leq \ell \;:\; |X_i| \geq \varepsilon |A_i|\}$
. Then we have that
$I_X=\{1 \leq i \leq \ell \;:\; |X_i| \geq \varepsilon |A_i|\}$
. Then we have that
 \begin{equation*} \sum _{i \notin I_X} |X _i| \leq |A_{\ell +1}|+ \varepsilon \sum _{i=1}^\ell |A_i| \leq 2\varepsilon N. \end{equation*}
\begin{equation*} \sum _{i \notin I_X} |X _i| \leq |A_{\ell +1}|+ \varepsilon \sum _{i=1}^\ell |A_i| \leq 2\varepsilon N. \end{equation*}
We now write
 \begin{equation*} e_B(X,Y)-p |X||Y|=\sum _{i=1}^{\ell +1} \left ( e_B(X_i,Y)-p |X_i||Y| \right ) . \end{equation*}
\begin{equation*} e_B(X,Y)-p |X||Y|=\sum _{i=1}^{\ell +1} \left ( e_B(X_i,Y)-p |X_i||Y| \right ) . \end{equation*}
We will split this sum into two parts, depending on whether
![]() $i \in I_X$
or not. First, suppose that
$i \in I_X$
or not. First, suppose that
![]() $i \in I_X$
. Then
$i \in I_X$
. Then
![]() $|X_i| \geq \varepsilon |A_i|$
and
$|X_i| \geq \varepsilon |A_i|$
and
![]() $|Y| \geq \varepsilon |V|$
, so we may apply the
$|Y| \geq \varepsilon |V|$
, so we may apply the
![]() $(p, \varepsilon )$
-regularity of
$(p, \varepsilon )$
-regularity of
![]() $(A_i,V)$
to conclude that
$(A_i,V)$
to conclude that
On the other hand, since
![]() $\sum _{i \notin I_X} |X_i| \leq 2 \varepsilon N$
, we have that
$\sum _{i \notin I_X} |X_i| \leq 2 \varepsilon N$
, we have that
Adding these together, we conclude that
as desired.
With all these pieces in place, the proof of Theorem 1.4 becomes quite straightforward.
Proof of Theorem
1.4. Fix
![]() $p \in [\frac 12,1)$
and suppose
$p \in [\frac 12,1)$
and suppose
![]() $k \geq k_0 \;:\!=\; k_2(p)$
. Fix
$k \geq k_0 \;:\!=\; k_2(p)$
. Fix
![]() $\theta \gt 0$
and set
$\theta \gt 0$
and set
![]() $\varepsilon =\min \{\theta/3,p/(20k)\}$
. Let
$\varepsilon =\min \{\theta/3,p/(20k)\}$
. Let
![]() $\gamma =\gamma (\theta,p,k)$
be the parameter from Lemma 5.5. Suppose we are given a colouring of
$\gamma =\gamma (\theta,p,k)$
be the parameter from Lemma 5.5. Suppose we are given a colouring of
![]() $K_N$
without
$K_N$
without
![]() $(p,\gamma )$
-many books. We wish to prove that the colouring is
$(p,\gamma )$
-many books. We wish to prove that the colouring is
![]() $(p,\theta )$
-quasirandom. We inductively apply Lemma 5.5 to find a sequence
$(p,\theta )$
-quasirandom. We inductively apply Lemma 5.5 to find a sequence
![]() $A_1,\ldots,A_\ell$
of vertex subsets such that
$A_1,\ldots,A_\ell$
of vertex subsets such that
![]() $(A_i,V)$
is
$(A_i,V)$
is
![]() $(p,\varepsilon ^2)$
-regular for all
$(p,\varepsilon ^2)$
-regular for all
![]() $i$
and, therefore,
$i$
and, therefore,
![]() $(p,\varepsilon )$
-regular for all
$(p,\varepsilon )$
-regular for all
![]() $i$
. We continue until the remainder set
$i$
. We continue until the remainder set
![]() $W=V \setminus (A_1 \cup \dotsb \cup A_\ell )$
satisfies
$W=V \setminus (A_1 \cup \dotsb \cup A_\ell )$
satisfies
![]() $|W| \leq \varepsilon N$
, at which point the assumptions of Lemma 5.5 are no longer met, so we set
$|W| \leq \varepsilon N$
, at which point the assumptions of Lemma 5.5 are no longer met, so we set
![]() $A_{\ell +1} = W$
. However, at this point, we can apply Lemma 5.6 to conclude that our colouring is indeed
$A_{\ell +1} = W$
. However, at this point, we can apply Lemma 5.6 to conclude that our colouring is indeed
![]() $(p,\theta )$
-quasirandom.
$(p,\theta )$
-quasirandom.
5.1. The converse
In this section, we prove a converse to Theorem 1.4, which implies that not containing
![]() $(p,\gamma )$
-many books is an equivalent characterization of
$(p,\gamma )$
-many books is an equivalent characterization of
![]() $p$
-quasirandomness.
$p$
-quasirandomness.
Theorem 5.7.
Fix
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $p \in (0,1)$
. Then, for every
$p \in (0,1)$
. Then, for every
![]() $\gamma \gt 0$
, there exists some
$\gamma \gt 0$
, there exists some
![]() $\theta \gt 0$
such that the following holds for every
$\theta \gt 0$
such that the following holds for every
![]() $(p,\theta )$
-quasirandom colouring of
$(p,\theta )$
-quasirandom colouring of
![]() $E(K_N)$
with
$E(K_N)$
with
![]() $N$
sufficiently large. Apart from fewer than
$N$
sufficiently large. Apart from fewer than
![]() $\gamma N^k$
exceptions, every red
$\gamma N^k$
exceptions, every red
![]() $K_k$
has
$K_k$
has
![]() $((1-p)^k \pm \gamma )N$
extensions to a red
$((1-p)^k \pm \gamma )N$
extensions to a red
![]() $K_{k+1}$
and every blue
$K_{k+1}$
and every blue
![]() $K_k$
has
$K_k$
has
![]() $(p^k \pm \gamma )N$
extensions to a blue
$(p^k \pm \gamma )N$
extensions to a blue
![]() $K_{k+1}$
. In particular, the colouring does not contain
$K_{k+1}$
. In particular, the colouring does not contain
![]() $(p,\gamma )$
-many books.
$(p,\gamma )$
-many books.
Remark 5.2.
In this direction, there is no dependence between
![]() $p$
and the range of
$p$
and the range of
![]() $k$
for which the result holds. As we know from the fact that the
$k$
for which the result holds. As we know from the fact that the
![]() $k$
-partite structure is the extremal structure for small
$k$
-partite structure is the extremal structure for small
![]() $c$
, such a dependence is necessary in the forward direction. However, here, all we are saying is that almost all monochromatic books in a quasirandom colouring are of essentially the correct size, that is, asymptotic to what they would be in a random colouring.
$c$
, such a dependence is necessary in the forward direction. However, here, all we are saying is that almost all monochromatic books in a quasirandom colouring are of essentially the correct size, that is, asymptotic to what they would be in a random colouring.
Proof. We will use the well-known result of Chung, Graham, and Wilson [Reference Chung, Graham and Wilson6], that a quasirandom colouring contains roughly the correct count of any fixed monochromatic subgraph. Specifically, for every
![]() $\delta \gt 0$
, there is some
$\delta \gt 0$
, there is some
![]() $\theta \gt 0$
, such that, in any
$\theta \gt 0$
, such that, in any
![]() $(p,\theta )$
-quasirandom colouring of
$(p,\theta )$
-quasirandom colouring of
![]() $E(K_N)$
,
$E(K_N)$
,
 \begin{align*} B(K_k)&\;:\!=\; \#(\text{blue }K_k)=p^{\left (\substack{ k\\[3pt] 2 }\right )} \left (\begin{array}{c} N\\[-3pt] k \end{array}\right ) \pm \delta N^k,\\[5pt] B(K_{k+1})&\;:\!=\; \#(\text{blue }K_{k+1})=p^{\left (\substack{ k+1\\[3pt] 2 }\right )} \left (\begin{array}{c} N\\[-3pt] k+1 \end{array}\right ) \pm \delta N^{k+1},\\[5pt] B(K_{k+2}-e)&\;:\!=\; \#(\text{blue }K_{k+2}-e)=p^{\left (\substack{ k+2\\[3pt] 2 }\right )-1}\!\left (\begin{array}{c} N\\[-3pt] k+2 \end{array}\right ) \left (\begin{array}{c} k+2\\[-3pt] 2 \end{array}\right ) \pm \delta N^{k+2}, \end{align*}
\begin{align*} B(K_k)&\;:\!=\; \#(\text{blue }K_k)=p^{\left (\substack{ k\\[3pt] 2 }\right )} \left (\begin{array}{c} N\\[-3pt] k \end{array}\right ) \pm \delta N^k,\\[5pt] B(K_{k+1})&\;:\!=\; \#(\text{blue }K_{k+1})=p^{\left (\substack{ k+1\\[3pt] 2 }\right )} \left (\begin{array}{c} N\\[-3pt] k+1 \end{array}\right ) \pm \delta N^{k+1},\\[5pt] B(K_{k+2}-e)&\;:\!=\; \#(\text{blue }K_{k+2}-e)=p^{\left (\substack{ k+2\\[3pt] 2 }\right )-1}\!\left (\begin{array}{c} N\\[-3pt] k+2 \end{array}\right ) \left (\begin{array}{c} k+2\\[-3pt] 2 \end{array}\right ) \pm \delta N^{k+2}, \end{align*}
where
![]() $K_{k+2}-e$
is the graph formed by deleting one edge from
$K_{k+2}-e$
is the graph formed by deleting one edge from
![]() $K_{k+2}$
; note that for this count we have an extra factor of
$K_{k+2}$
; note that for this count we have an extra factor of
![]() $\left(\substack{ k+2\\[3pt] 2 } \right)$
to account for the fact that this graph is not vertex-transitive. On the other hand, we can observe that every blue copy of
$\left(\substack{ k+2\\[3pt] 2 } \right)$
to account for the fact that this graph is not vertex-transitive. On the other hand, we can observe that every blue copy of
![]() $K_{k+2}-e$
corresponds to two distinct extensions of a single blue
$K_{k+2}-e$
corresponds to two distinct extensions of a single blue
![]() $K_k$
to a blue
$K_k$
to a blue
![]() $K_{k+1}$
. Therefore,
$K_{k+1}$
. Therefore,
 \begin{equation*} B(K_{k+2}-e)=\sum _{Q} \!\left (\begin {array}{c} {\#(\text {blue extensions of }Q)}\\[-3pt] 2 \end {array}\right ), \end{equation*}
\begin{equation*} B(K_{k+2}-e)=\sum _{Q} \!\left (\begin {array}{c} {\#(\text {blue extensions of }Q)}\\[-3pt] 2 \end {array}\right ), \end{equation*}
where the sum is over all blue
![]() $K_k$
. Let
$K_k$
. Let
![]() $\textrm{ext}_B(Q)$
denote the number of blue extensions of
$\textrm{ext}_B(Q)$
denote the number of blue extensions of
![]() $Q$
. Then we can also observe that
$Q$
. Then we can also observe that
![]() $\sum _Q \textrm{ext}_B(Q)$
counts the total number of ways of extending a blue
$\sum _Q \textrm{ext}_B(Q)$
counts the total number of ways of extending a blue
![]() $K_k$
into a blue
$K_k$
into a blue
![]() $K_{k+1}$
, which is precisely
$K_{k+1}$
, which is precisely
![]() $(k+1)B(K_{k+1})$
, since each blue
$(k+1)B(K_{k+1})$
, since each blue
![]() $K_{k+1}$
contributes exactly
$K_{k+1}$
contributes exactly
![]() $k+1$
terms to this sum.
$k+1$
terms to this sum.
Now, we consider the quantity
On the one hand, we have that if
![]() $\delta \geq 1/N$
, then
$\delta \geq 1/N$
, then
 \begin{align*} E&=\sum _Q \textrm{ext}_B(Q)^2-2p^kN \sum _Q \textrm{ext}_B(Q)+\sum _Q p^{2k} N^2\\[5pt] &=\left ( 2 \sum _Q \!\left (\begin{array}{c}{\textrm{ext}_B(Q)}\\[-3pt] 2 \end{array}\right ) +\sum _Q \textrm{ext}_B(Q) \right ) -2p^k N(k+1)B(K_{k+1})+p^{2k} N^2 B(K_k)\\[5pt] &=2 B(K_{k+2}-e)+(1-2p^k N)(k+1)B(K_{k+1})+p^{2k} N^2 B(K_k)\\[5pt] &\leq 2p^{\left (\substack{ k+2\\[3pt] 2 }\right )-1} \!\left (\begin{array}{c} N\\[-3pt] k+2 \end{array}\right )\left (\begin{array}{c} k+2\\[-3pt] 2 \end{array}\right )-2p^k N(k+1)p^{\left (\substack{ k+1\\[3pt] 2 }\right )}\left (\begin{array}{c} N\\[-3pt] k+1 \end{array}\right )\!+p^{2k} N^2 p^{\left (\substack{k\\[3pt] 2 }\right )} \left (\begin{array}{c} N\\[-3pt] k \end{array}\right )\! +5k \delta N^{k+2}\\[5pt] &=p^{\frac{k^2+3k}2} \left (\begin{array}{c} N\\[-3pt] k \end{array}\right ) (\!-\!N+k^2+k) + 5k \delta N^{k+2}\\[5pt] &\lt 5k \delta N^{k+2}. \end{align*}
\begin{align*} E&=\sum _Q \textrm{ext}_B(Q)^2-2p^kN \sum _Q \textrm{ext}_B(Q)+\sum _Q p^{2k} N^2\\[5pt] &=\left ( 2 \sum _Q \!\left (\begin{array}{c}{\textrm{ext}_B(Q)}\\[-3pt] 2 \end{array}\right ) +\sum _Q \textrm{ext}_B(Q) \right ) -2p^k N(k+1)B(K_{k+1})+p^{2k} N^2 B(K_k)\\[5pt] &=2 B(K_{k+2}-e)+(1-2p^k N)(k+1)B(K_{k+1})+p^{2k} N^2 B(K_k)\\[5pt] &\leq 2p^{\left (\substack{ k+2\\[3pt] 2 }\right )-1} \!\left (\begin{array}{c} N\\[-3pt] k+2 \end{array}\right )\left (\begin{array}{c} k+2\\[-3pt] 2 \end{array}\right )-2p^k N(k+1)p^{\left (\substack{ k+1\\[3pt] 2 }\right )}\left (\begin{array}{c} N\\[-3pt] k+1 \end{array}\right )\!+p^{2k} N^2 p^{\left (\substack{k\\[3pt] 2 }\right )} \left (\begin{array}{c} N\\[-3pt] k \end{array}\right )\! +5k \delta N^{k+2}\\[5pt] &=p^{\frac{k^2+3k}2} \left (\begin{array}{c} N\\[-3pt] k \end{array}\right ) (\!-\!N+k^2+k) + 5k \delta N^{k+2}\\[5pt] &\lt 5k \delta N^{k+2}. \end{align*}
On the other hand, suppose there were at least
![]() $\gamma N^k/2$
blue
$\gamma N^k/2$
blue
![]() $K_k$
with at least
$K_k$
with at least
![]() $(p^{k}+\gamma )N$
or at most
$(p^{k}+\gamma )N$
or at most
![]() $(p^k-\gamma )N$
blue extensions. Then, by only keeping these cliques in the sum defining
$(p^k-\gamma )N$
blue extensions. Then, by only keeping these cliques in the sum defining
![]() $E$
, we would have that
$E$
, we would have that
 \begin{align*} E&=\sum _Q (\textrm{ext}_B(Q)-p^{k}N)^2 \geq \frac{\gamma N^k}2 (\gamma N)^2=\frac{\gamma ^3}2 N^{k+2}. \end{align*}
\begin{align*} E&=\sum _Q (\textrm{ext}_B(Q)-p^{k}N)^2 \geq \frac{\gamma N^k}2 (\gamma N)^2=\frac{\gamma ^3}2 N^{k+2}. \end{align*}
Therefore, if we pick
![]() $\delta \lt \gamma ^3/10k$
, we get a contradiction. The same argument with
$\delta \lt \gamma ^3/10k$
, we get a contradiction. The same argument with
![]() $p$
replaced by
$p$
replaced by
![]() $1-p$
and blue replaced by red shows that there are also fewer than
$1-p$
and blue replaced by red shows that there are also fewer than
![]() $\gamma N^k/2$
red
$\gamma N^k/2$
red
![]() $K_k$
with at least
$K_k$
with at least
![]() $((1-p)^k+\gamma )N$
or at most
$((1-p)^k+\gamma )N$
or at most
![]() $((1-p)^k-\gamma )N$
red extensions. This proves the theorem, since the total number of exceptional cliques is at most
$((1-p)^k-\gamma )N$
red extensions. This proves the theorem, since the total number of exceptional cliques is at most
![]() $\gamma N^k$
.
$\gamma N^k$
.
6. Concluding remarks
Putting together the main results of this paper, we obtain the following picture. For every
![]() $k \geq 2$
, there exist two numbers
$k \geq 2$
, there exist two numbers
![]() $c_0(k),c_1(k) \in (0,1]$
such that if
$c_0(k),c_1(k) \in (0,1]$
such that if
![]() $0 \lt c\leq c_0$
, then
$0 \lt c\leq c_0$
, then
![]() $r\big(B_{cn}^{(k)},B_n ^{(k)}\big) =k(n+k-1)+1$
, while if
$r\big(B_{cn}^{(k)},B_n ^{(k)}\big) =k(n+k-1)+1$
, while if
![]() $1\geq c\geq c_1$
, then
$1\geq c\geq c_1$
, then
![]() $r\big(B_{cn} ^{(k)}, B_n ^{(k)}\big) = (c^{1/k}+1)^k n+o_k(n)$
. Moreover, in both these regimes, there are stability results: there exist
$r\big(B_{cn} ^{(k)}, B_n ^{(k)}\big) = (c^{1/k}+1)^k n+o_k(n)$
. Moreover, in both these regimes, there are stability results: there exist
![]() $c'_{\!\!0}(k)\leq c_0(k)$
and
$c'_{\!\!0}(k)\leq c_0(k)$
and
![]() $c'_{\!\!1}(k)\geq c_1(k)$
such that for
$c'_{\!\!1}(k)\geq c_1(k)$
such that for
![]() $0 \lt c \leq c'_{\!\!0}$
, all the near-extremal colourings are close to
$0 \lt c \leq c'_{\!\!0}$
, all the near-extremal colourings are close to
![]() $k$
-partite,Footnote 4 while for all
$k$
-partite,Footnote 4 while for all
![]() $1 \geq c \geq c'_{\!\!1}$
, all near-extremal colourings are quasirandom. Of course, the most natural question remaining is to understand what happens in the interval
$1 \geq c \geq c'_{\!\!1}$
, all near-extremal colourings are quasirandom. Of course, the most natural question remaining is to understand what happens in the interval
![]() $(c'_{\!\!0},c'_{\!\!1})$
, where our results say nothing. Note that this gap is real, since below
$(c'_{\!\!0},c'_{\!\!1})$
, where our results say nothing. Note that this gap is real, since below
![]() $c'_{\!\!0}$
all extremal colourings must be
$c'_{\!\!0}$
all extremal colourings must be
![]() $k$
-partite, whereas above
$k$
-partite, whereas above
![]() $c'_{\!\!1}$
all extremal colourings must be quasirandom. On the other hand, it is possible that there is no gap between
$c'_{\!\!1}$
all extremal colourings must be quasirandom. On the other hand, it is possible that there is no gap between
![]() $c_0$
and
$c_0$
and
![]() $c_1$
, since it is conceivable that at the point where the random and
$c_1$
, since it is conceivable that at the point where the random and
![]() $k$
-partite constructions yield comparable lower bounds on
$k$
-partite constructions yield comparable lower bounds on
![]() $r(B_{cn}^{(k)}, B_n^{(k)})$
, both are tight.
$r(B_{cn}^{(k)}, B_n^{(k)})$
, both are tight.
This question about the gap really comprises at least two separate questions: what happens for fixed
![]() $k$
and what happens as
$k$
and what happens as
![]() $k \to \infty$
? To address the second question first, our results give some indication. Indeed, we have shown that both
$k \to \infty$
? To address the second question first, our results give some indication. Indeed, we have shown that both
![]() $c_0(k)$
and
$c_0(k)$
and
![]() $c_1(k)$
tend to
$c_1(k)$
tend to
![]() $0$
as
$0$
as
![]() $k \to \infty$
and thus the gap interval shrinks as
$k \to \infty$
and thus the gap interval shrinks as
![]() $k \to \infty$
. More precisely, we have that
$k \to \infty$
. More precisely, we have that
Moreover, the results of [Reference Fox, He and Wigderson14] show that
![]() $1/c_0$
is at most single-exponential in a power of
$1/c_0$
is at most single-exponential in a power of
![]() $k$
. On the other hand, because we used the regularity lemma, our upper bound for
$k$
. On the other hand, because we used the regularity lemma, our upper bound for
![]() $1/c'_{\!\!0}$
is only of tower-type. However, it seems likely that the methods of [Reference Fox, He and Wigderson14] could also be adapted to improve this.
$1/c'_{\!\!0}$
is only of tower-type. However, it seems likely that the methods of [Reference Fox, He and Wigderson14] could also be adapted to improve this.
The other question is what happens for fixed
![]() $k$
. Here, our understanding is much more limited, even for the simplest case
$k$
. Here, our understanding is much more limited, even for the simplest case
![]() $k=2$
. In this case, Nikiforov and Rousseau [Reference Nikiforov and Rousseau18] proved that
$k=2$
. In this case, Nikiforov and Rousseau [Reference Nikiforov and Rousseau18] proved that
![]() $c_0(2)=1/6$
, in the sense that, for all
$c_0(2)=1/6$
, in the sense that, for all
![]() $c\lt 1/6$
and all
$c\lt 1/6$
and all
![]() $n$
sufficiently large,
$n$
sufficiently large,
![]() $r(B_{cn}^{(2)}, B_n ^{(2)}) = 2n+3$
, whereas, for any
$r(B_{cn}^{(2)}, B_n ^{(2)}) = 2n+3$
, whereas, for any
![]() $c\gt 1/6$
and all
$c\gt 1/6$
and all
![]() $n$
sufficiently large, there is a construction showing that
$n$
sufficiently large, there is a construction showing that
![]() $r(B_{cn} ^{(2)}, B_n ^{(2)})\gt 2n+3$
. Curiously, our results do not say anything non-trivial about
$r(B_{cn} ^{(2)}, B_n ^{(2)})\gt 2n+3$
. Curiously, our results do not say anything non-trivial about
![]() $c_1(2)$
, other than the fact that the random bound is correct for
$c_1(2)$
, other than the fact that the random bound is correct for
![]() $c=1$
; in other words, we cannot prove that
$c=1$
; in other words, we cannot prove that
![]() $c_1(2) \lt 1$
and in fact believe this to not be the case.
$c_1(2) \lt 1$
and in fact believe this to not be the case.
Conjecture 6.1.
For every
![]() $c\lt 1$
, the random bound for
$c\lt 1$
, the random bound for
![]() $r\big(B_{cn}^{(2)},B_n ^{(2)}\big)$
is not tight. In other words, there exists some
$r\big(B_{cn}^{(2)},B_n ^{(2)}\big)$
is not tight. In other words, there exists some
![]() $\beta =\beta (c)\gt 0$
such that
$\beta =\beta (c)\gt 0$
such that
![]() $r(B_{cn}^{(2)},B_n ^{(2)}) \geq ((\sqrt c+1)^2 + \beta )n$
for all
$r(B_{cn}^{(2)},B_n ^{(2)}) \geq ((\sqrt c+1)^2 + \beta )n$
for all
![]() $n$
sufficiently large.
$n$
sufficiently large.
Of course, this conjecture is really only the tip of an iceberg, with the general open question being to understand
![]() $r(B_{cn}^{(2)},B_n ^{(2)})$
for
$r(B_{cn}^{(2)},B_n ^{(2)})$
for
![]() $c\in (1/6,1)$
and
$c\in (1/6,1)$
and
![]() $n\to \infty$
. There are many conjectures one could make about the behaviour of this quantity as a function of
$n\to \infty$
. There are many conjectures one could make about the behaviour of this quantity as a function of
![]() $c$
; for instance, perhaps there are a number of thresholds in the interval
$c$
; for instance, perhaps there are a number of thresholds in the interval
![]() $(1/6,1)$
at which new extremal structures emerge, each dictating the value of
$(1/6,1)$
at which new extremal structures emerge, each dictating the value of
![]() $r\big(B_{cn}^{(2)}, B_n ^{(2)}\big)$
until the next threshold. Because we know that the random bound is correct for
$r\big(B_{cn}^{(2)}, B_n ^{(2)}\big)$
until the next threshold. Because we know that the random bound is correct for
![]() $c=1$
and that quasirandom colourings are the only extremal ones, such a sequence of extremal examples would need to converge, in some appropriate sense, to the quasirandom colouring as
$c=1$
and that quasirandom colourings are the only extremal ones, such a sequence of extremal examples would need to converge, in some appropriate sense, to the quasirandom colouring as
![]() $c \to 1$
. However, at the moment we are not even able to conjecture a single such extremal structure or threshold.
$c \to 1$
. However, at the moment we are not even able to conjecture a single such extremal structure or threshold.
Acknowledgments
We are grateful to the anonymous referee for helpful comments which improved the presentation of this paper.