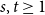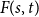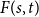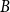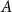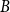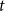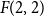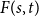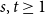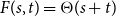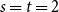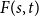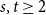1. Introduction
A well-researched area in modern graph theory is that of graph splitting. It is concerned with problems in which the vertex set of a given graph is to be split into a given number of parts while meeting specific degree conditions within or between the parts. One of the first instances of such a result is a classical theorem by Lovász [Reference Lovász13] from 1966, stating that for all numbers
![]() $s, t \in \mathbb {N}$
, every graph
$s, t \in \mathbb {N}$
, every graph
![]() $G$
of maximum degree
$G$
of maximum degree
![]() $\Delta (G)\le s+t+1$
admits a partition of its vertex set into sets
$\Delta (G)\le s+t+1$
admits a partition of its vertex set into sets
![]() $A$
and
$A$
and
![]() $B$
such that
$B$
such that
![]() $\Delta (G[A])\le s$
and
$\Delta (G[A])\le s$
and
![]() $\Delta (G[B])\le t$
. In the opposite direction, looking for splittings that preserve a given minimum degree, Thomassen [Reference Thomassen18] proved in 1983 that for all integers
$\Delta (G[B])\le t$
. In the opposite direction, looking for splittings that preserve a given minimum degree, Thomassen [Reference Thomassen18] proved in 1983 that for all integers
![]() $s,t \ge 1$
there exists some
$s,t \ge 1$
there exists some
![]() $f(s,t) \in \mathbb {N}$
such that every graph
$f(s,t) \in \mathbb {N}$
such that every graph
![]() $G$
of minimum degree
$G$
of minimum degree
![]() $\delta (G)\ge f(s,t)$
admits a partition of its vertex set into non-empty sets
$\delta (G)\ge f(s,t)$
admits a partition of its vertex set into non-empty sets
![]() $A$
and
$A$
and
![]() $B$
such that
$B$
such that
![]() $\delta (G[A])\ge s$
and
$\delta (G[A])\ge s$
and
![]() $\delta (G[B])\ge t$
. He also conjectured that the function
$\delta (G[B])\ge t$
. He also conjectured that the function
![]() $f(s,t)$
can be taken to be
$f(s,t)$
can be taken to be
![]() $s+t+1$
, which is best-possible as can be seen by considering complete graphs. In 1996, Stiebitz [Reference Stiebitz16] proved Thomassen’s conjecture.
$s+t+1$
, which is best-possible as can be seen by considering complete graphs. In 1996, Stiebitz [Reference Stiebitz16] proved Thomassen’s conjecture.
The perhaps most natural way of extending the above problems to directed graphs is to consider the out-degrees of vertices in a directed graph instead of their total degrees. Alon [Reference Alon3] has written a short survey about the arising problems in 2006. Maybe surprisingly, most of them turn out to be either false or much harder than their undirected cousins. In the following, we briefly summarise what is known.
1.1 Maximum out-degree
The natural analogue of Lovász’s theorem for directed graphs would state that for all
![]() $s,t \ge 1$
, every directed graph
$s,t \ge 1$
, every directed graph
![]() $D$
of maximum out-degree
$D$
of maximum out-degree
![]() $\Delta ^+(D)\le s+t+1$
admits a partition
$\Delta ^+(D)\le s+t+1$
admits a partition
![]() $A, B$
of its vertex set such that
$A, B$
of its vertex set such that
![]() $\Delta ^+(D[A])\le s, \Delta ^+(D[B])\le t$
. However, this turns out to be completely false – in 1983, Thomassen [Reference Thomassen20] constructed a sequence
$\Delta ^+(D[A])\le s, \Delta ^+(D[B])\le t$
. However, this turns out to be completely false – in 1983, Thomassen [Reference Thomassen20] constructed a sequence
![]() $(D_k)_{k=1}^{\infty }$
of digraphs such that
$(D_k)_{k=1}^{\infty }$
of digraphs such that
![]() $\Delta ^+(D_k)=k$
for every
$\Delta ^+(D_k)=k$
for every
![]() $k$
and in every partition
$k$
and in every partition
![]() $A, B$
of
$A, B$
of
![]() $V(D_k)$
, we either have
$V(D_k)$
, we either have
![]() $\Delta ^+(D_k[A])=k$
or
$\Delta ^+(D_k[A])=k$
or
![]() $\Delta ^+(D_k[B])=k$
. In other words, no matter how we split
$\Delta ^+(D_k[B])=k$
. In other words, no matter how we split
![]() $D_k$
into two parts, the maximum out-degree of one of the two parts will not be reduced. However, the situation changes when allowing more than
$D_k$
into two parts, the maximum out-degree of one of the two parts will not be reduced. However, the situation changes when allowing more than
![]() $2$
parts in the partition of the vertex set: Alon [Reference Alon3] was the first to prove that every directed graph of maximum out-degree at most
$2$
parts in the partition of the vertex set: Alon [Reference Alon3] was the first to prove that every directed graph of maximum out-degree at most
![]() $\Delta$
can be split into three parts
$\Delta$
can be split into three parts
![]() $A, B, C$
such that the maximum out-degree in each part is bounded by
$A, B, C$
such that the maximum out-degree in each part is bounded by
![]() $\frac {2}{3}\Delta$
. More generally, Alon’s proof yields that for every digraph
$\frac {2}{3}\Delta$
. More generally, Alon’s proof yields that for every digraph
![]() $D$
the vertex set of
$D$
the vertex set of
![]() $D$
can be partitioned into three sets
$D$
can be partitioned into three sets
![]() $A,B,C$
such that for every vertex
$A,B,C$
such that for every vertex
![]() $v$
, at most
$v$
, at most
![]() $\frac {2}{3}d^+(v)$
of its out-neighbors lie in the same part of the partition as
$\frac {2}{3}d^+(v)$
of its out-neighbors lie in the same part of the partition as
![]() $v$
. This statement has been independently reproved and strengthened several times, see [Reference Anholcer, Bosek and Grytczuk7, Reference Girão, Kittipassorn and Popielarz9, Reference Knox and Sámal10]. A popular conjecture due to Kreutzer, Oum, Seymour, van der Zypen and Wood [Reference Kreutzer, Oum, Seymour, van der Zypen and Wood11] from 2017, known as the Majority Coloring Conjecture, states that the constant
$v$
. This statement has been independently reproved and strengthened several times, see [Reference Anholcer, Bosek and Grytczuk7, Reference Girão, Kittipassorn and Popielarz9, Reference Knox and Sámal10]. A popular conjecture due to Kreutzer, Oum, Seymour, van der Zypen and Wood [Reference Kreutzer, Oum, Seymour, van der Zypen and Wood11] from 2017, known as the Majority Coloring Conjecture, states that the constant
![]() $\frac {2}{3}$
in the above result can be improved to
$\frac {2}{3}$
in the above result can be improved to
![]() $\frac {1}{2}$
, which would be best-possible. While this remains widely open, some special cases have been solved, such as tournaments and random graphs, see [Reference Anastos, Lamaison, Steiner and Szabó5, Reference Anastos, Cooley, Kang and Kwan6, Reference Girão, Kittipassorn and Popielarz9].
$\frac {1}{2}$
, which would be best-possible. While this remains widely open, some special cases have been solved, such as tournaments and random graphs, see [Reference Anastos, Lamaison, Steiner and Szabó5, Reference Anastos, Cooley, Kang and Kwan6, Reference Girão, Kittipassorn and Popielarz9].
1.2 Minimum out-degree
The natural analogue of Stiebitz’s theorem for directed graphs would state that for all
![]() $s,t \ge 1$
, every directed graph
$s,t \ge 1$
, every directed graph
![]() $D$
of minimum out-degree
$D$
of minimum out-degree
![]() $\delta ^+(D) \ge s+t+1$
admits a partition of its vertex set into non-empty sets
$\delta ^+(D) \ge s+t+1$
admits a partition of its vertex set into non-empty sets
![]() $A, B$
such that
$A, B$
such that
![]() $\delta ^+(D[A]) \ge s$
and
$\delta ^+(D[A]) \ge s$
and
![]() $\delta ^+(D[B]) \ge t$
. This statement, too, turns out to be quite false. Namely, Alon [Reference Alon1] proved in 1984 that for every integer
$\delta ^+(D[B]) \ge t$
. This statement, too, turns out to be quite false. Namely, Alon [Reference Alon1] proved in 1984 that for every integer
![]() $k \ge 1$
and every prime number
$k \ge 1$
and every prime number
![]() $p\gt k^2\cdot 2^{2k-2}$
with
$p\gt k^2\cdot 2^{2k-2}$
with
![]() $p\equiv 3 \text { }(\text {mod }4)$
, there exists a digraph
$p\equiv 3 \text { }(\text {mod }4)$
, there exists a digraph
![]() $D$
of order
$D$
of order
![]() $p$
such that
$p$
such that
![]() $\delta ^+(D)=\frac {p-1}{2}$
and such that for every non-empty
$\delta ^+(D)=\frac {p-1}{2}$
and such that for every non-empty
![]() $X\subseteq V(D)$
we have that
$X\subseteq V(D)$
we have that
![]() $\delta ^+(D[X])\lt \frac {k}{2}$
if
$\delta ^+(D[X])\lt \frac {k}{2}$
if
![]() $|X| \le k$
and
$|X| \le k$
and
![]() $\delta ^+(D[X])\lt \frac {p-1}{2}-k$
if
$\delta ^+(D[X])\lt \frac {p-1}{2}-k$
if
![]() $|X| \le p-k$
. Setting
$|X| \le p-k$
. Setting
![]() $s=\frac {k}{2}$
and
$s=\frac {k}{2}$
and
![]() $t=\frac {p-1}{2}-k$
, we can see that
$t=\frac {p-1}{2}-k$
, we can see that
![]() $\delta ^+(D)\gt s+t+1$
but in every partition of
$\delta ^+(D)\gt s+t+1$
but in every partition of
![]() $V(D)$
into non-empty sets
$V(D)$
into non-empty sets
![]() $A, B$
, we either have
$A, B$
, we either have
![]() $|A|\le k$
and thus
$|A|\le k$
and thus
![]() $\delta ^+(D[A]) \lt s$
, or
$\delta ^+(D[A]) \lt s$
, or
![]() $|B|\le p-k$
and thus
$|B|\le p-k$
and thus
![]() $\delta ^+(D[B])\lt t$
. More recently, the third author [Reference Steiner15] answered a question of Alon [Reference Alon3] by proving that for arbitrarily large values of
$\delta ^+(D[B])\lt t$
. More recently, the third author [Reference Steiner15] answered a question of Alon [Reference Alon3] by proving that for arbitrarily large values of
![]() $s=t$
, there exists a digraph
$s=t$
, there exists a digraph
![]() $D$
with
$D$
with
![]() $\delta ^+(D)\gt 2s+(1+o(1))\log _3(s)\gt s+t+1$
such that for every non-empty
$\delta ^+(D)\gt 2s+(1+o(1))\log _3(s)\gt s+t+1$
such that for every non-empty
![]() $X\subseteq V(D)$
with
$X\subseteq V(D)$
with
![]() $|X| \le \frac {|V(D)|}{2}$
, we have
$|X| \le \frac {|V(D)|}{2}$
, we have
![]() $\delta ^+(D[X])\lt s$
. Similarly as above this implies a negative answer to the direct extension of Stiebitz’s theorem when
$\delta ^+(D[X])\lt s$
. Similarly as above this implies a negative answer to the direct extension of Stiebitz’s theorem when
![]() $s=t$
.
$s=t$
.
The main open problem in this area is the intriguing question asked independently by Stiebitz [Reference Stiebitz17] in 1995 and Alon [Reference Alon2, Reference Alon3] in 1996 and again in 2006 whether the qualitative version of Stiebitz’s theorem extends to directed graphs. We also refer to the open problem garden entry [14].
Problem 1.
Does there exist, for all
![]() $s,t \ge 1$
, a number
$s,t \ge 1$
, a number
![]() $F(s,t) \in \mathbb {N}$
such that every digraph
$F(s,t) \in \mathbb {N}$
such that every digraph
![]() $D$
with
$D$
with
![]() $\delta ^+(D) \ge F(s,t)$
has a partition
$\delta ^+(D) \ge F(s,t)$
has a partition
![]() $V(D)=A\sqcup B$
such that
$V(D)=A\sqcup B$
such that
![]() $\delta ^+(D[A]) \ge s$
and
$\delta ^+(D[A]) \ge s$
and
![]() $\delta ^+(D[B])\ge t$
?
$\delta ^+(D[B])\ge t$
?
In the rest of this paper, we write
![]() $F(s,t)$
for the smallest possible integer satisfying the statement in Problem 1 if it does exist, and set
$F(s,t)$
for the smallest possible integer satisfying the statement in Problem 1 if it does exist, and set
![]() $F(s,t)=\infty$
otherwise.
$F(s,t)=\infty$
otherwise.
So far,
![]() $F(s,t)\lt \infty$
is only known in the case
$F(s,t)\lt \infty$
is only known in the case
![]() $s=t=1$
, in which it is equivalent to the statement that every digraph of large enough minimum out-degree contains two disjoint directed cycles, see [Reference Alon2, Reference Bucić8, Reference Thomassen19] for proofs and extensions of this statement. However, already whether
$s=t=1$
, in which it is equivalent to the statement that every digraph of large enough minimum out-degree contains two disjoint directed cycles, see [Reference Alon2, Reference Bucić8, Reference Thomassen19] for proofs and extensions of this statement. However, already whether
![]() $F(2,2)\lt \infty$
or even
$F(2,2)\lt \infty$
or even
![]() $F(1,2)\lt \infty$
remain open problems. The only other known results on Problem2 are for restricted classes of digraphs, for instance [Reference Alon, Bang-Jensen and Bessy4] and [Reference Yang, Bai, Wang and Wu21] gave positive answers for tournaments and digraphs with balanced out- and in-degrees.
$F(1,2)\lt \infty$
remain open problems. The only other known results on Problem2 are for restricted classes of digraphs, for instance [Reference Alon, Bang-Jensen and Bessy4] and [Reference Yang, Bai, Wang and Wu21] gave positive answers for tournaments and digraphs with balanced out- and in-degrees.
1.3 Our result
As the main contribution of this paper, we show that in order to solve Problem 1 in full generality, it suffices to decide whether
![]() $F(2,2)\lt \infty$
. Moreover, under the assumption of
$F(2,2)\lt \infty$
. Moreover, under the assumption of
![]() $F(2,2)\lt \infty$
, we settle the question of the asymptotic growth of
$F(2,2)\lt \infty$
, we settle the question of the asymptotic growth of
![]() $F(s,t)$
by showing that it is within a constant factor of the trivial lower bound
$F(s,t)$
by showing that it is within a constant factor of the trivial lower bound
![]() $s+t+1$
for all values
$s+t+1$
for all values
![]() $s,t \ge 1$
. We also obtain similar results for the values
$s,t \ge 1$
. We also obtain similar results for the values
![]() $F(s,1)$
if we assume that
$F(s,1)$
if we assume that
![]() $F(2,1)\lt \infty$
.
$F(2,1)\lt \infty$
.
Theorem 2.
-
(1) If
 $F(2,2)\lt \infty$
, then
$F(2,2)\lt \infty$
, then
 $F(s,t)=\Theta (s+t)$
for
$F(s,t)=\Theta (s+t)$
for
 $s,t \ge 1$
. More precisely, we have
$s,t \ge 1$
. More precisely, we have
 \begin{equation*}F(s,t)\lt \frac {e^2}{3}\cdot F(2,2)^6\cdot \max \{s,t\}.\end{equation*}
\begin{equation*}F(s,t)\lt \frac {e^2}{3}\cdot F(2,2)^6\cdot \max \{s,t\}.\end{equation*}
-
(2) If
 $F(2,1)\lt \infty$
, then
$F(2,1)\lt \infty$
, then
 $F(s,1)=\Theta (s)$
for
$F(s,1)=\Theta (s)$
for
 $s\ge 1$
. More precisely, we have
$s\ge 1$
. More precisely, we have
 \begin{equation*}F(s,1)\lt \frac {e^2}{3}\cdot F(2,1)^6\cdot s.\end{equation*}
\begin{equation*}F(s,1)\lt \frac {e^2}{3}\cdot F(2,1)^6\cdot s.\end{equation*}
Remark. Upon receiving the reviews for this paper, one of the referees pointed out to us that the fact that the existence of
![]() $F(2,2)$
implies the existence of
$F(2,2)$
implies the existence of
![]() $F(s,s)$
was independently shown by William Lochet in his PhD thesis [Reference Lochet12]. However, the upper bound of
$F(s,s)$
was independently shown by William Lochet in his PhD thesis [Reference Lochet12]. However, the upper bound of
![]() $F(s,s)\le F(2,2)^{s+1}$
proved by Lochet is exponential and thus much worse than the linear bound obtained in the main result of the paper at hand.
$F(s,s)\le F(2,2)^{s+1}$
proved by Lochet is exponential and thus much worse than the linear bound obtained in the main result of the paper at hand.
2. Proof of Theorem2
Towards proving Theorem2, we start with the following two lemmas.
Lemma 3.
For every integer
![]() $k \ge 3$
there exists a constant
$k \ge 3$
there exists a constant
![]() $\varepsilon = \frac {3}{e^2k^3}$
such that for every
$\varepsilon = \frac {3}{e^2k^3}$
such that for every
![]() $n \geq k$
there exists a bipartite graph
$n \geq k$
there exists a bipartite graph
![]() $G$
on
$G$
on
![]() $2n$
vertices with bipartition
$2n$
vertices with bipartition
![]() $V(G)=S \sqcup T$
, such that
$V(G)=S \sqcup T$
, such that
![]() $|S|=|T|=n$
and all of the following hold.
$|S|=|T|=n$
and all of the following hold.
-
(i) Every vertex in
 $S$
has degree exactly
$S$
has degree exactly
 $k$
.
$k$
. -
(ii) For every non-empty
 $X\subseteq S$
with
$X\subseteq S$
with
 $|X| \le \varepsilon n$
and every
$|X| \le \varepsilon n$
and every
 $Y\subseteq T$
such that
$Y\subseteq T$
such that
 $|N_G(x)\cap Y| \ge 3$
for all
$|N_G(x)\cap Y| \ge 3$
for all
 $x \in X$
, we have that
$x \in X$
, we have that
 $|Y|\gt |X|$
.
$|Y|\gt |X|$
.
Proof. Let
![]() $G$
be the random graph on vertex set
$G$
be the random graph on vertex set
![]() $S\sqcup T$
obtained by choosing independently for each vertex
$S\sqcup T$
obtained by choosing independently for each vertex
![]() $v\in S$
uniformly at random
$v\in S$
uniformly at random
![]() $k$
neighbours in
$k$
neighbours in
![]() $T$
. Then, 1 follows immediately, so let us show that 2 also holds with positive probability. Given
$T$
. Then, 1 follows immediately, so let us show that 2 also holds with positive probability. Given
![]() $Y\subseteq T$
and a set
$Y\subseteq T$
and a set
![]() $U\subseteq T$
of three distinct vertices chosen uniformly at random, we get
$U\subseteq T$
of three distinct vertices chosen uniformly at random, we get
It follows by a union bound that given a vertex
![]() $v\in S$
and a set
$v\in S$
and a set
![]() $Y\subseteq T$
,
$Y\subseteq T$
,
Thus, for any non-empty sets
![]() $X\subseteq S$
and
$X\subseteq S$
and
![]() $Y\subseteq T$
we have
$Y\subseteq T$
we have
There are at most
![]() $\binom {n}{|X|}\binom {n}{|Y|}$
choices of
$\binom {n}{|X|}\binom {n}{|Y|}$
choices of
![]() $X$
and
$X$
and
![]() $Y$
. Note that we only have to consider
$Y$
. Note that we only have to consider
![]() $X\subseteq S$
and
$X\subseteq S$
and
![]() $Y\subseteq T$
with
$Y\subseteq T$
with
![]() $|X|=|Y|$
, since if 2 is not satisfied then there exist equal sized
$|X|=|Y|$
, since if 2 is not satisfied then there exist equal sized
![]() $X$
and
$X$
and
![]() $Y$
contradicting it. By a union bound, it follows that the probability that there exist such
$Y$
contradicting it. By a union bound, it follows that the probability that there exist such
![]() $X\subseteq S$
and
$X\subseteq S$
and
![]() $Y\subseteq T$
not satisfying 2 is at most
$Y\subseteq T$
not satisfying 2 is at most
 \begin{equation*} \sum _{i = 1}^{\lfloor \varepsilon n\rfloor }\binom {n}{i}^2\left (\frac {1}{6}\right )^i\left (\frac {ki}{n}\right )^{3i}\leq \sum _{i = 1}^{\lfloor \varepsilon n\rfloor }\left (\frac {en}{i}\right )^{2i}\left (\frac {1}{6}\right )^i\left (\frac {ki}{n}\right )^{3i}\end{equation*}
\begin{equation*} \sum _{i = 1}^{\lfloor \varepsilon n\rfloor }\binom {n}{i}^2\left (\frac {1}{6}\right )^i\left (\frac {ki}{n}\right )^{3i}\leq \sum _{i = 1}^{\lfloor \varepsilon n\rfloor }\left (\frac {en}{i}\right )^{2i}\left (\frac {1}{6}\right )^i\left (\frac {ki}{n}\right )^{3i}\end{equation*}
 \begin{equation*} = \sum _{i = 1}^{\lfloor \varepsilon n\rfloor }\left (\frac {e^2k^3i}{6n}\right )^{i} \lt \sum _{i = 1}^{\infty }\left (\frac {e^2k^3\varepsilon }{6}\right )^{i}=\frac {e^2k^3\varepsilon }{6-e^2k^3\varepsilon }=1. \end{equation*}
\begin{equation*} = \sum _{i = 1}^{\lfloor \varepsilon n\rfloor }\left (\frac {e^2k^3i}{6n}\right )^{i} \lt \sum _{i = 1}^{\infty }\left (\frac {e^2k^3\varepsilon }{6}\right )^{i}=\frac {e^2k^3\varepsilon }{6-e^2k^3\varepsilon }=1. \end{equation*}
Thus, there exists a graph
![]() $G$
which satisfies both conditions.
$G$
which satisfies both conditions.
Lemma 4.
If
![]() $F(2,2)\lt \infty$
, then
$F(2,2)\lt \infty$
, then
![]() $F(4,4)\leq F(2,2)^2$
and similarly, if
$F(4,4)\leq F(2,2)^2$
and similarly, if
![]() $F(2,1)\lt \infty$
, then
$F(2,1)\lt \infty$
, then
![]() $F(4,1)\leq F(2,1)^2$
.
$F(4,1)\leq F(2,1)^2$
.
Proof. We prove both statements simultaneously, where replacing
![]() $b(k)$
with either
$b(k)$
with either
![]() $k$
or
$k$
or
![]() $1$
gives the two arguments. Using this notation, we have to show that
$1$
gives the two arguments. Using this notation, we have to show that
![]() $F(4,b(4)) \leq F(2,b(2))^2$
.
$F(4,b(4)) \leq F(2,b(2))^2$
.
Let
![]() $D$
be a digraph with
$D$
be a digraph with
![]() $\delta ^+(D) \geq F(2,b(2))^2$
and
$\delta ^+(D) \geq F(2,b(2))^2$
and
![]() $V(D) = \{v_1, \ldots, v_N\}$
. Let
$V(D) = \{v_1, \ldots, v_N\}$
. Let
![]() $D^{\prime}$
be the digraph obtained from
$D^{\prime}$
be the digraph obtained from
![]() $D$
by taking
$D$
by taking
and the following arcs. For each
![]() $v_{i,j}\in V(D^{\prime})$
, the arc
$v_{i,j}\in V(D^{\prime})$
, the arc
![]() $(v_i, v_{i,j})$
is in
$(v_i, v_{i,j})$
is in
![]() $A(D^{\prime})$
. Moreover, for each
$A(D^{\prime})$
. Moreover, for each
![]() $i \in [N]$
, if
$i \in [N]$
, if
![]() $N^+_D(v_i) = \{u_i^1, \ldots, u_i^{k_i}\}$
with
$N^+_D(v_i) = \{u_i^1, \ldots, u_i^{k_i}\}$
with
![]() $k_i \geq F(2,b(2))^2$
, then for each
$k_i \geq F(2,b(2))^2$
, then for each
![]() $j=1,\ldots, F(2,b(2))$
, we have that all the arcs
$j=1,\ldots, F(2,b(2))$
, we have that all the arcs
are in
![]() $A(D^{\prime})$
. Intuitively, to obtain
$A(D^{\prime})$
. Intuitively, to obtain
![]() $D^{\prime}$
, we have split the neighbourhood of each vertex
$D^{\prime}$
, we have split the neighbourhood of each vertex
![]() $v_i$
into
$v_i$
into
![]() $F(2,b(2))$
groups of size
$F(2,b(2))$
groups of size
![]() $F(2,b(2))$
each, and added a different intermediate vertex on the path from
$F(2,b(2))$
each, and added a different intermediate vertex on the path from
![]() $v_i$
to each group of its neighbourhood in
$v_i$
to each group of its neighbourhood in
![]() $D$
.
$D$
.
Claim 5.
Let
![]() $W^{\prime}\subseteq V(D^{\prime})$
be non-empty and
$W^{\prime}\subseteq V(D^{\prime})$
be non-empty and
![]() $W:=W^{\prime}\cap V(D)$
.
$W:=W^{\prime}\cap V(D)$
.
-
(a) If
 $\delta ^+(D^{\prime}[W^{\prime}])\ge 1$
, then
$\delta ^+(D^{\prime}[W^{\prime}])\ge 1$
, then
 $W$
is non-empty and
$W$
is non-empty and
 $\delta ^+(D[W])\ge 1$
.
$\delta ^+(D[W])\ge 1$
. -
(b) If
 $\delta ^+(D^{\prime}[W^{\prime}])\geq 2$
then
$\delta ^+(D^{\prime}[W^{\prime}])\geq 2$
then
 $W$
is non-empty and
$W$
is non-empty and
 $\delta ^+(D[W])\geq 4$
.
$\delta ^+(D[W])\geq 4$
.
Proof.
-
(a) Suppose
 $\delta ^+(D^{\prime}[W^{\prime}])\geq 1$
. This condition implies that
$\delta ^+(D^{\prime}[W^{\prime}])\geq 1$
. This condition implies that
 $D^{\prime}[W^{\prime}]$
contains a directed cycle
$D^{\prime}[W^{\prime}]$
contains a directed cycle
 $C$
. It is easy to see by definition that
$C$
. It is easy to see by definition that
 $D^{\prime}-V(D)$
is an acyclic digraph, hence
$D^{\prime}-V(D)$
is an acyclic digraph, hence
 $C$
must meet at least one vertex in
$C$
must meet at least one vertex in
 $V(D)$
. This shows that
$V(D)$
. This shows that
 $V(C)\cap V(D)$
and hence also
$V(C)\cap V(D)$
and hence also
 $W=W^{\prime}\cap V(D)$
is non-empty.
$W=W^{\prime}\cap V(D)$
is non-empty.Now, consider any vertex
 $v_i\in W$
. Then there exists a vertex
$v_i\in W$
. Then there exists a vertex
 $v$
in
$v$
in
 $W^{\prime}\cap \{v_{i,j} | 1\le j \le F(2,b(2))\}$
which in turn has an out-neighbor in
$W^{\prime}\cap \{v_{i,j} | 1\le j \le F(2,b(2))\}$
which in turn has an out-neighbor in
 $W^{\prime}\cap N^+_D(v_i)$
. This latter vertex is then an out-neighbor of
$W^{\prime}\cap N^+_D(v_i)$
. This latter vertex is then an out-neighbor of
 $v_i$
in
$v_i$
in
 $D[W]$
. Since
$D[W]$
. Since
 $v_i \in W$
was chosen arbitrarily, this shows that
$v_i \in W$
was chosen arbitrarily, this shows that
 $\delta ^+(D[W])\ge 1$
.
$\delta ^+(D[W])\ge 1$
. -
(b) Similarly, suppose that
 $\delta ^+(D^{\prime}[W^{\prime}])\geq 2$
. It follows from the previous part that
$\delta ^+(D^{\prime}[W^{\prime}])\geq 2$
. It follows from the previous part that
 $W$
is non-empty. Let
$W$
is non-empty. Let
 $v_i\in W$
be an arbitrary vertex. Since
$v_i\in W$
be an arbitrary vertex. Since
 $\text {deg}^+_{D^{\prime}[W^{\prime}]}(v_i) \geq 2$
, there exist at least two vertices in
$\text {deg}^+_{D^{\prime}[W^{\prime}]}(v_i) \geq 2$
, there exist at least two vertices in
 $W^{\prime}\cap \{v_{i,j} | 1 \le j \le F(2,b(2))\}$
. Since each of them has at least
$W^{\prime}\cap \{v_{i,j} | 1 \le j \le F(2,b(2))\}$
. Since each of them has at least
 $2$
out-neighbors in
$2$
out-neighbors in
 $D^{\prime}[W^{\prime}]$
, at least
$D^{\prime}[W^{\prime}]$
, at least
 $4$
vertices among
$4$
vertices among
 $N^+_D(v_i)$
are in
$N^+_D(v_i)$
are in
 $W^{\prime}$
and so also in
$W^{\prime}$
and so also in
 $W$
. Since
$W$
. Since
 $v_i \in W$
was chosen arbitrarily, this shows that
$v_i \in W$
was chosen arbitrarily, this shows that
 $\delta ^+(D[W])\ge 4$
.
$\delta ^+(D[W])\ge 4$
.
By construction,
![]() $\delta ^+(D^{\prime}) \geq F(2,b(2))$
, so there is a partition of
$\delta ^+(D^{\prime}) \geq F(2,b(2))$
, so there is a partition of
![]() $V(D^{\prime})$
into non-empty sets
$V(D^{\prime})$
into non-empty sets
![]() $A^{\prime}$
and
$A^{\prime}$
and
![]() $B^{\prime}$
such that
$B^{\prime}$
such that
![]() $\delta ^+(D^{\prime}[A^{\prime}])\geq 2$
and
$\delta ^+(D^{\prime}[A^{\prime}])\geq 2$
and
![]() $\delta ^+(D^{\prime}[B^{\prime}]) \geq b(2)$
. By Claim 5, we get that
$\delta ^+(D^{\prime}[B^{\prime}]) \geq b(2)$
. By Claim 5, we get that
![]() $(A:=A^{\prime}\cap V(D),B\,:\!=B^{\prime} \cap V(D))$
is a partition of
$(A:=A^{\prime}\cap V(D),B\,:\!=B^{\prime} \cap V(D))$
is a partition of
![]() $V(D)$
into non-empty sets with
$V(D)$
into non-empty sets with
![]() $\delta ^+(D[A])\geq 4$
and
$\delta ^+(D[A])\geq 4$
and
![]() $\delta ^+(D[B]) \geq b(4)$
.
$\delta ^+(D[B]) \geq b(4)$
.
Proof of Theorem 2. Similarly as in the proof of Lemma 4, we prove both 1 and 2 simultaneously. Towards this, for
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $b(k) = k$
correspond to the proof of 1 and
$b(k) = k$
correspond to the proof of 1 and
![]() $b(k)=1$
to the proof of 2. Furthermore, in the case of 1, suppose w.l.o.g. that
$b(k)=1$
to the proof of 2. Furthermore, in the case of 1, suppose w.l.o.g. that
![]() $s \geq t$
. Now, we show
$s \geq t$
. Now, we show
from which the result follows since
![]() $F$
is non-decreasing and, by Lemma 4,
$F$
is non-decreasing and, by Lemma 4,
![]() $F(3,b(3))^3\leq F(4,b(4))^3\leq F(2,b(2))^6$
.
$F(3,b(3))^3\leq F(4,b(4))^3\leq F(2,b(2))^6$
.
Let
![]() $D$
be a digraph with
$D$
be a digraph with
![]() $\delta ^+(D) \geq d$
and
$\delta ^+(D) \geq d$
and
![]() $V(D) = \{v_1, \ldots, v_N\}$
. Let us define the digraph
$V(D) = \{v_1, \ldots, v_N\}$
. Let us define the digraph
![]() $D^{\prime\prime}$
obtained from
$D^{\prime\prime}$
obtained from
![]() $D$
with vertex set
$D$
with vertex set
 \begin{equation*}V(D^{\prime\prime}) = V(D) \cup \bigcup _{\substack {1 \le i \le N,\\3\leq j \leq s-1}} U_{i,j},\end{equation*}
\begin{equation*}V(D^{\prime\prime}) = V(D) \cup \bigcup _{\substack {1 \le i \le N,\\3\leq j \leq s-1}} U_{i,j},\end{equation*}
where each
![]() $U_{i,j}$
is a disjoint set of
$U_{i,j}$
is a disjoint set of
![]() $d$
new vertices. Furthermore, for each
$d$
new vertices. Furthermore, for each
![]() $i=1,\ldots, N$
, we select an arbitrary subset of size
$i=1,\ldots, N$
, we select an arbitrary subset of size
![]() $d$
of
$d$
of
![]() $N^+_D(v_i)$
and denote it by
$N^+_D(v_i)$
and denote it by
![]() $U_{i,s}$
. For each
$U_{i,s}$
. For each
![]() $i=1,\ldots, N$
and each
$i=1,\ldots, N$
and each
![]() $u \in U_{i,3}$
, we have that the arc
$u \in U_{i,3}$
, we have that the arc
![]() $(v_i,u)$
is in
$(v_i,u)$
is in
![]() $A(D^{\prime\prime})$
. Additionally, let
$A(D^{\prime\prime})$
. Additionally, let
![]() $G$
be the graph with bipartition
$G$
be the graph with bipartition
![]() $S$
and
$S$
and
![]() $T$
given by Lemma 3 applied with
$T$
given by Lemma 3 applied with
![]() $n\,:\!=d$
and
$n\,:\!=d$
and
![]() $k\,:\!= F(3,b(3))$
. Thus,
$k\,:\!= F(3,b(3))$
. Thus,
![]() $\varepsilon =\frac {3}{e^2F(3,b(3))^3}$
. Then for all
$\varepsilon =\frac {3}{e^2F(3,b(3))^3}$
. Then for all
![]() $1 \le i \le N$
and
$1 \le i \le N$
and
![]() $3\leq j \leq s-1$
, we add a copy of
$3\leq j \leq s-1$
, we add a copy of
![]() $G$
between
$G$
between
![]() $U_{i,j}$
and
$U_{i,j}$
and
![]() $U_{i,j+1}$
to
$U_{i,j+1}$
to
![]() $D^{\prime\prime}$
, identifying
$D^{\prime\prime}$
, identifying
![]() $U_{i,j}$
with
$U_{i,j}$
with
![]() $S$
and
$S$
and
![]() $U_{i,j+1}$
with
$U_{i,j+1}$
with
![]() $T$
, and directing all the edges from
$T$
, and directing all the edges from
![]() $U_{i,j}$
to
$U_{i,j}$
to
![]() $U_{i,j+1}$
. Those are all the arcs in
$U_{i,j+1}$
. Those are all the arcs in
![]() $D^{\prime\prime}$
. Thus, by Lemma 3, for each
$D^{\prime\prime}$
. Thus, by Lemma 3, for each
![]() $3\leq j \leq s-1$
, every vertex in
$3\leq j \leq s-1$
, every vertex in
![]() $U_{i,j}$
has out-degree exactly
$U_{i,j}$
has out-degree exactly
![]() $F(3,b(3))$
in
$F(3,b(3))$
in
![]() $D^{\prime\prime}$
. Now consider any non-empty subset
$D^{\prime\prime}$
. Now consider any non-empty subset
![]() $X \subseteq U_{i,j}$
with
$X \subseteq U_{i,j}$
with
![]() $|X|\leq s-1$
. Then we have
$|X|\leq s-1$
. Then we have
Thus by the second item of Lemma 3, for every
![]() $Y \subseteq U_{i,j+1}$
with
$Y \subseteq U_{i,j+1}$
with
![]() $|N^+_{D^{\prime\prime}}(x) \cap Y| \geq 3$
for all
$|N^+_{D^{\prime\prime}}(x) \cap Y| \geq 3$
for all
![]() $x \in X$
, we have
$x \in X$
, we have
![]() $|Y| \gt |X|$
.
$|Y| \gt |X|$
.
Claim 6.
Let
![]() $W^{\prime}\subseteq V(D^{\prime\prime})$
be non-empty and
$W^{\prime}\subseteq V(D^{\prime\prime})$
be non-empty and
![]() $W:=W^{\prime}\cap V(D)$
.
$W:=W^{\prime}\cap V(D)$
.
-
(a) If
 $\delta ^+(D^{\prime\prime}[W^{\prime}])\ge 1$
, then
$\delta ^+(D^{\prime\prime}[W^{\prime}])\ge 1$
, then
 $W$
is non-empty and
$W$
is non-empty and
 $\delta ^+(D[W])\ge 1$
.
$\delta ^+(D[W])\ge 1$
. -
(b) If
 $\delta ^+(D^{\prime\prime}[W^{\prime}])\geq 3$
then
$\delta ^+(D^{\prime\prime}[W^{\prime}])\geq 3$
then
 $W$
is non-empty and
$W$
is non-empty and
 $\delta ^+(D[W])\geq s$
.
$\delta ^+(D[W])\geq s$
.
Proof.
-
(a) Suppose
 $\delta ^+(D^{\prime\prime}[W^{\prime}])\geq 1$
. Therefore,
$\delta ^+(D^{\prime\prime}[W^{\prime}])\geq 1$
. Therefore,
 $D^{\prime\prime}[W^{\prime}]$
contains a directed cycle
$D^{\prime\prime}[W^{\prime}]$
contains a directed cycle
 $C$
. But
$C$
. But
 $D^{\prime\prime}-V(D)$
is acyclic, and thus, we must have that
$D^{\prime\prime}-V(D)$
is acyclic, and thus, we must have that
 $V(C)\cap V(D) \subseteq W^{\prime}\cap V(D)=W$
is non-empty. Furthermore, from
$V(C)\cap V(D) \subseteq W^{\prime}\cap V(D)=W$
is non-empty. Furthermore, from
 $\delta ^+(D^{\prime\prime}[W^{\prime}])\ge 1$
we get that for every
$\delta ^+(D^{\prime\prime}[W^{\prime}])\ge 1$
we get that for every
 $v_i\in W$
there exists
$v_i\in W$
there exists
 $W_{i,j} \subseteq U_{i,j} \cap W^{\prime}$
with
$W_{i,j} \subseteq U_{i,j} \cap W^{\prime}$
with
 $|W_{i,j}| = 1$
for every
$|W_{i,j}| = 1$
for every
 $3\leq j\leq s$
, implying that
$3\leq j\leq s$
, implying that \begin{equation*}|N^+_{D[W]}(v_i)| \geq |W_{i,s}| \geq 1.\end{equation*}
\begin{equation*}|N^+_{D[W]}(v_i)| \geq |W_{i,s}| \geq 1.\end{equation*}
-
(b) Suppose
 $\delta ^+(D^{\prime\prime}[W^{\prime}])\geq 3$
. By the previous part, we get that
$\delta ^+(D^{\prime\prime}[W^{\prime}])\geq 3$
. By the previous part, we get that
 $W$
is non-empty. Let us consider some
$W$
is non-empty. Let us consider some
 $v_i \in W$
. We now show by induction on
$v_i \in W$
. We now show by induction on
 $j$
that for each
$j$
that for each
 $3\leq j\leq s$
, there is a set
$3\leq j\leq s$
, there is a set
 $W_{i,j} \subseteq U_{i,j} \cap W^{\prime}$
with
$W_{i,j} \subseteq U_{i,j} \cap W^{\prime}$
with
 $|W_{i,j}| = j$
. For the base case
$|W_{i,j}| = j$
. For the base case
 $j=3$
, since
$j=3$
, since
 $\text {deg}^+_{D^{\prime\prime}[W^{\prime}]}(v_i) \geq 3$
, there is some
$\text {deg}^+_{D^{\prime\prime}[W^{\prime}]}(v_i) \geq 3$
, there is some
 $W_{i,3} \subseteq U_{i,3} \cap W^{\prime}$
with
$W_{i,3} \subseteq U_{i,3} \cap W^{\prime}$
with
 $|W_{i,3}| = 3$
. Suppose we have shown that the statement holds for some
$|W_{i,3}| = 3$
. Suppose we have shown that the statement holds for some
 $3\leq j \leq s-1$
, we now show it holds for
$3\leq j \leq s-1$
, we now show it holds for
 $j+1$
. Let
$j+1$
. Let
 $X:=W_{i,j}$
and
$X:=W_{i,j}$
and
 $Y := U_{i,j+1} \cap W^{\prime}$
. Since
$Y := U_{i,j+1} \cap W^{\prime}$
. Since
 $W_{i,j} \subseteq W^{\prime}$
, it must hold that for each
$W_{i,j} \subseteq W^{\prime}$
, it must hold that for each
 $x \in X$
, we haveThus, as
$x \in X$
, we haveThus, as \begin{equation*}|N^+_{D^{\prime\prime}[W^{\prime}]}(x)| = |N^+_{D^{\prime\prime}}(x) \cap Y| \geq 3.\end{equation*}
\begin{equation*}|N^+_{D^{\prime\prime}[W^{\prime}]}(x)| = |N^+_{D^{\prime\prime}}(x) \cap Y| \geq 3.\end{equation*}
 $|X|=|W_{i,j}| = j \leq s-1$
, by the above-mentioned properties coming from Lemma 3 we have that
$|X|=|W_{i,j}| = j \leq s-1$
, by the above-mentioned properties coming from Lemma 3 we have that
 $|Y| \gt |X|=|W_{i,j}| = j$
. Taking
$|Y| \gt |X|=|W_{i,j}| = j$
. Taking
 $W_{i,j+1}$
to be an arbitrary subset of
$W_{i,j+1}$
to be an arbitrary subset of
 $Y$
of size
$Y$
of size
 $j+1$
finishes the induction step. In particular, this shows thatas desired.
$j+1$
finishes the induction step. In particular, this shows thatas desired. \begin{equation*}|N^+_{D[W]}(v_i)| \geq |U_{i,s} \cap W| = |U_{i,s} \cap W^{\prime}| \geq |W_{i,s}| \geq s,\end{equation*}
\begin{equation*}|N^+_{D[W]}(v_i)| \geq |U_{i,s} \cap W| = |U_{i,s} \cap W^{\prime}| \geq |W_{i,s}| \geq s,\end{equation*}
Since
![]() $\delta ^+(D^{\prime\prime}) \geq k=F(3,b(3))$
by construction, there is a partition of
$\delta ^+(D^{\prime\prime}) \geq k=F(3,b(3))$
by construction, there is a partition of
![]() $V(D^{\prime\prime})$
into non-empty sets
$V(D^{\prime\prime})$
into non-empty sets
![]() $A^{\prime}$
and
$A^{\prime}$
and
![]() $B^{\prime}$
such that
$B^{\prime}$
such that
![]() $\delta ^+(D^{\prime\prime}[A^{\prime}])\geq 3$
and
$\delta ^+(D^{\prime\prime}[A^{\prime}])\geq 3$
and
![]() $\delta ^+(D^{\prime\prime}[B^{\prime}]) \geq b(3)$
. It follows by Claim 6 that
$\delta ^+(D^{\prime\prime}[B^{\prime}]) \geq b(3)$
. It follows by Claim 6 that
![]() $A:=A^{\prime} \cap V(D)$
and
$A:=A^{\prime} \cap V(D)$
and
![]() $B:= B^{\prime} \cap V(D)$
are non-empty and satisfy
$B:= B^{\prime} \cap V(D)$
are non-empty and satisfy
![]() $\delta ^+(D[A]) \ge s$
and
$\delta ^+(D[A]) \ge s$
and
![]() $\delta ^+(D[B])\ge b(s)$
, as desired. This shows that
$\delta ^+(D[B])\ge b(s)$
, as desired. This shows that
![]() $F(s,b(s))\le d$
, concluding the proof.
$F(s,b(s))\le d$
, concluding the proof.
Acknowledgements
Funded by SNSF Ambizione grant No. 216071. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No, 101034413. Funded by SNSF grant CRSII5, 173721.