Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T05:20:23.281Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-increasing tree growth process for recursive trees and applications

Part of: Combinatorial probability Graph theory

Published online by Cambridge University Press:  19 October 2020

Laura Eslava
Laura Eslava*
Affiliation:
Universidad Nacional Autonoma Mexico, Instituto de investigaciones en matematicas aplicadas y en sistemas, CDMX 04510, Mexico
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a non-increasing tree growth 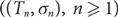process $((T_n,{\sigma}_n),\, n\ge 1)$ , where Tn is a rooted labelled tree on n vertices and σn is a permutation of the vertex labels. The construction of (Tn, σn) from (Tn−1, σn−1) involves rewiring a random (possibly empty) subset of edges in Tn−1 towards the newly added vertex; as a consequence Tn−1 ⊄ Tn with positive probability. The key feature of the process is that the shape of Tn has the same law as that of a random recursive tree, while the degree distribution of any given vertex is not monotone in the process.

We present two applications. First, while couplings between Kingman’s coalescent and random recursive trees were known for any fixed n, this new process provides a non-standard coupling of all finite Kingman’s coalescents. Second, we use the new process and the Chen–Stein method to extend the well-understood properties of degree distribution of random recursive trees to extremal-range cases. Namely, we obtain convergence rates on the number of vertices with degree at least 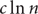$c\ln n$ , c ∈ (1, 2), in trees with n vertices. Further avenues of research are discussed.

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 05C80: Random graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 1 , January 2021 , pp. 79 - 104
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addario-Berry, L. (2015) Partition functions of discrete coalescents: from Cayley’s formula to Frieze’s ζ (3) limit theorem. In XI Symposium on Probability and Stochastic Processes, Vol. 68 of Progress in Probability, Birkhäuser.Google Scholar
Addario-Berry, L. and Eslava, L. (2018) High degree of random recursive trees. Random Struct. Algorithms 52 560–575.CrossRefGoogle Scholar
Anderson, C. W. (1970) Extreme value theory for a class of discrete distributions with applications to some stochastic processes. J. Appl. Probab. 7 99–113.CrossRefGoogle Scholar
Blum, M., François, O and Janson, S. (2006) The mean, the variance and limiting distributions of two statistics sensitive to phylogenetic tree balance. Ann. Appl. Probab. 16 2195–2114.CrossRefGoogle Scholar
Chang, H. and Fuchs, M. (2010) Limit theorems for patterns in phylogenetic trees. J. Math. Biol. 60 481–512.CrossRefGoogle ScholarPubMed
Devroye, L. (1987) Branching processes in the analysis of the heights of trees. Acta Inform. 24 277–298.Google Scholar
Devroye, L. and Lu, J. (1995) The strong convergence of maximal degrees in uniform random recursive trees and dags. Random Struct. Algorithms 7 1–14.Google Scholar
Dubhashi, D. and Ranjan, D. (1998) Balls and bins: a study in negative dependence. Random Struct. Algorithms 13 99–124.3.0.CO;2-M>CrossRefGoogle Scholar
Durrett, R. (1996) Probability: Theory and Examples, second edition, Duxbury.Google Scholar
Eslava, L. (2016) Depth of vertices with high degree in random recursive trees. arXiv:1611.07466Google Scholar
Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics, Cambridge University Press.CrossRefGoogle Scholar
Fuchs, M. (2008) Subtree sizes in recursive trees and binary search trees: Berry–Esseen bounds and Poisson approximations. Combin. Probab. Comput. 17 661–680.Google Scholar
Goh, W. and Schmutz, E. (2002) Limit distribution for the maximum degree of a random recursive tree. J. Comput. Appl. Math. 142 61–82.Google Scholar
Goldschmidt, C. (2000) The Chen–Stein method for convergence of distributions. https://www.stats.ox.ac.uk/~goldschm/chen-stein.ps.gz Google Scholar
Gumbel, E. J. (1935) Les valeurs extrêmes des distributions statistiques. Ann. Inst. H. Poincaré 5 115–158.Google Scholar
Holmgren, C. and Janson, S. (2015) Limit laws for functions of fringe trees for binary search trees and random recursive trees. Electron. J. Probab. 20 4.CrossRefGoogle Scholar
Janson, S. (2005) Asymptotic degree distribution in random recursive trees. Random Struct. Algorithms 26 69–83.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs , Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley-Interscience.Google Scholar
Lindvall, T. (1999) On Strassen’s theorem on stochastic domination. Electron. Comm. Probab. 4 51–59.CrossRefGoogle Scholar
Luczak, M. and Winkler, P. (2004) Building uniformly random subtrees. Random Struct. Algorithms 24 420–443.CrossRefGoogle Scholar
Na, H. S. and Rapoport, A. (1970) Distribution of nodes of a tree by degree. Math. Biosci. 6 313–329.Google Scholar
Pitman, J. (1999) Coalescent random forests. J. Combin. Theory Ser. A 85 165–193.CrossRefGoogle Scholar
Pittel, B. (1994) Note on the heights of random recursive trees and random m-ary search trees. Random Struct. Algorithms 5 337–347.Google Scholar
Standish, T. A. (1980) Data Structure Techniques, Addison-Wesley Longman.Google Scholar