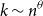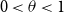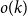1. Introduction
1.1. Background and motivation
Few mathematical disciplines offer as abundant a supply of easy-to-state but hard-to-crack problems as combinatorics does. Group testing is a prime example. The problem goes back to the 1940s [Reference Dorfman15]. Within a population of size
![]() $n$
, we are to identify a subset of
$n$
, we are to identify a subset of
![]() $k$
infected individuals. To this end, we test groups of individuals simultaneously. In an idealised scenario called ‘noiseless group testing’, each test returns a positive result if and only if at least one member of the group is infected. All tests are conducted in parallel. The problem is to devise a (possibly randomised) test design that minimises the total number of tests required.
$k$
infected individuals. To this end, we test groups of individuals simultaneously. In an idealised scenario called ‘noiseless group testing’, each test returns a positive result if and only if at least one member of the group is infected. All tests are conducted in parallel. The problem is to devise a (possibly randomised) test design that minimises the total number of tests required.
Noiseless group testing has inspired a long line of research, which has led to optimal or near-optimal results for several parameter regimes [Reference Aldridge, Johnson and Scarlett4, Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9]. But the assumption of perfectly accurate tests is unrealistic. Real tests are noisy [Reference Long, Prober and Fischer29]. More precisely, in medical terms, the sensitivity of a test is defined as the probability that a test detects an actual infection, namely, that a group that contains an infected individual displays a positive test result. Moreover, the specificity of a test refers to the probability that a healthy group returns a negative test result. If these accuracies are reasonably high (say 99%), one might be tempted to think that noiseless testing provides a good enough approximation. Yet remarkably, we will discover that this is far from correct. Even a seemingly tiny amount of noise has a discernible impact not only on the number of tests required but also on the choice of a good test design; we will revisit this point in Section 1.5. Hence, in group testing, like in several other inference problems, the presence of noise adds substantial mathematical depth. As a rough analogy, think of error-correcting linear codes. In the absence of noise, the decoding problem just boils down to solving linear equations. By contrast, the noisy version, the closest vector problem, is NP-hard [Reference Dinur, Kindler, Raz and Safra13].
In the present paper, we consider a very general noise model that allows for arbitrary sensitivities and specificities. To be precise, we assume that if a test group contains an infected individual, then the test displays a positive result with probability
![]() $p_{11}$
and a negative result with probability
$p_{11}$
and a negative result with probability
![]() $p_{10}=1-p_{11}$
. Similarly, if the group consists of healthy individuals only, then the test result will display a negative outcome with probability
$p_{10}=1-p_{11}$
. Similarly, if the group consists of healthy individuals only, then the test result will display a negative outcome with probability
![]() $p_{00}$
and a positive result with probability
$p_{00}$
and a positive result with probability
![]() $p_{01}=1-p_{00}$
. Every test is subjected to noise independently.
$p_{01}=1-p_{00}$
. Every test is subjected to noise independently.
Under the common assumption that the number
![]() $k$
of infected individuals scales as a power
$k$
of infected individuals scales as a power
![]() $k\sim n^\theta$
of the population size
$k\sim n^\theta$
of the population size
![]() $n$
with an exponent
$n$
with an exponent
![]() $0\lt \theta \lt 1$
, we contribute new approximate and exact recovery algorithms SPARC and SPEX. These new algorithms come with randomised test designs. We will identify a threshold
$0\lt \theta \lt 1$
, we contribute new approximate and exact recovery algorithms SPARC and SPEX. These new algorithms come with randomised test designs. We will identify a threshold
![]() $m_{\mathrm{\texttt{SPARC}}}=m_{\mathrm{\texttt{SPARC}}}(n,k,\boldsymbol{p})$
such that SPARC correctly identifies the set of infected individuals up to
$m_{\mathrm{\texttt{SPARC}}}=m_{\mathrm{\texttt{SPARC}}}(n,k,\boldsymbol{p})$
such that SPARC correctly identifies the set of infected individuals up to
![]() $o(k)$
errors with high probability over the choice of the test design, provided that at least
$o(k)$
errors with high probability over the choice of the test design, provided that at least
![]() $(1+\varepsilon )m_{\mathrm{\texttt{SPARC}}}$
tests are deployed. SPARC is efficient, that is, has polynomial running time in terms of
$(1+\varepsilon )m_{\mathrm{\texttt{SPARC}}}$
tests are deployed. SPARC is efficient, that is, has polynomial running time in terms of
![]() $n$
. By contrast, we will prove that with
$n$
. By contrast, we will prove that with
![]() $(1-\varepsilon )m_{\mathrm{\texttt{SPARC}}}$
tests it is impossible to identify the set of infected individuals up to
$(1-\varepsilon )m_{\mathrm{\texttt{SPARC}}}$
tests it is impossible to identify the set of infected individuals up to
![]() $o(k)$
errors, regardless of the choice of test design or the running time allotted. In other words, SPARC solves the approximate recovery problem optimally.
$o(k)$
errors, regardless of the choice of test design or the running time allotted. In other words, SPARC solves the approximate recovery problem optimally.
In addition, we develop a polynomial time algorithm SPEX that correctly identifies the status of all individuals w.h.p., provided that at least
![]() $(1+\varepsilon )m_{\mathrm{\texttt{SPEX}}}$
tests are available, for a certain
$(1+\varepsilon )m_{\mathrm{\texttt{SPEX}}}$
tests are available, for a certain
![]() $m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})$
. Exact recovery has been the focus of much of the previous literature on group testing [Reference Aldridge, Johnson and Scarlett4]. In particular, for noisy group testing, the best previous exact recovery algorithm is the DD algorithm from [Reference Gebhard, Johnson, Loick and Rolvien19]. DD comes with a simple randomised test design called the constant column design. Complementing the positive result on SPEX, we show that on the constant column design, exact recovery is information-theoretically impossible with
$m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})$
. Exact recovery has been the focus of much of the previous literature on group testing [Reference Aldridge, Johnson and Scarlett4]. In particular, for noisy group testing, the best previous exact recovery algorithm is the DD algorithm from [Reference Gebhard, Johnson, Loick and Rolvien19]. DD comes with a simple randomised test design called the constant column design. Complementing the positive result on SPEX, we show that on the constant column design, exact recovery is information-theoretically impossible with
![]() $(1-\varepsilon )m_{\mathrm{\texttt{SPEX}}}$
tests. As a consequence, the number
$(1-\varepsilon )m_{\mathrm{\texttt{SPEX}}}$
tests. As a consequence, the number
![]() $m_{\mathrm{\texttt{SPEX}}}$
of tests required by SPEX is an asymptotic lower bound on the number of tests required by any algorithm on the constant column design, including DD. Indeed, as we will see in Section 1.5, for most choices of the specificity/sensitivity and of the infection density
$m_{\mathrm{\texttt{SPEX}}}$
of tests required by SPEX is an asymptotic lower bound on the number of tests required by any algorithm on the constant column design, including DD. Indeed, as we will see in Section 1.5, for most choices of the specificity/sensitivity and of the infection density
![]() $\theta$
, SPEX outperforms DD dramatically.
$\theta$
, SPEX outperforms DD dramatically.
Throughout the paper, we write
![]() $\boldsymbol{p}=(p_{00},p_{01},p_{10},p_{11})$
for the noisy channel to which the test results are subjected. We may assume without loss of generality that
$\boldsymbol{p}=(p_{00},p_{01},p_{10},p_{11})$
for the noisy channel to which the test results are subjected. We may assume without loss of generality that
that is, that a test is more likely to display a positive result if the test group actually contains an infected individual; otherwise, we could just invert the test results. A test design can be described succinctly by a (possibly random) bipartite graph
![]() $G=(V\cup F,E)$
, where
$G=(V\cup F,E)$
, where
![]() $V$
is a set of
$V$
is a set of
![]() $n$
individuals and
$n$
individuals and
![]() $F$
is a set of
$F$
is a set of
![]() $m$
tests. Write
$m$
tests. Write
![]() $\boldsymbol{\sigma }\in \{0,1\}^V$
for the (unknown) vector of Hamming weight
$\boldsymbol{\sigma }\in \{0,1\}^V$
for the (unknown) vector of Hamming weight
![]() $k$
whose
$k$
whose
![]() $1$
-entries mark the infected individuals. Further, let
$1$
-entries mark the infected individuals. Further, let
![]() $\boldsymbol{\sigma }^{\prime}\in \{0,1\}^F$
be the vector of actual test results, that is,
$\boldsymbol{\sigma }^{\prime}\in \{0,1\}^F$
be the vector of actual test results, that is,
![]() $\boldsymbol{\sigma }^{\prime}_a=1$
if and only if
$\boldsymbol{\sigma }^{\prime}_a=1$
if and only if
![]() $\boldsymbol{\sigma }_v=1$
for at least one individual
$\boldsymbol{\sigma }_v=1$
for at least one individual
![]() $v$
in test
$v$
in test
![]() $a$
. Finally, let
$a$
. Finally, let
![]() $\boldsymbol{\sigma }^{\prime\prime}\in \{0,1\}^F$
be the vector of displayed test results, where noise has been applied to
$\boldsymbol{\sigma }^{\prime\prime}\in \{0,1\}^F$
be the vector of displayed test results, where noise has been applied to
![]() $\boldsymbol{\sigma }^{\prime}$
, that is,
$\boldsymbol{\sigma }^{\prime}$
, that is,
The objective is to infer
![]() $\boldsymbol{\sigma }$
from
$\boldsymbol{\sigma }$
from
![]() $\boldsymbol{\sigma }^{\prime\prime}$
given
$\boldsymbol{\sigma }^{\prime\prime}$
given
![]() $G$
. As per common practice in the group testing literature, we assume throughout that
$G$
. As per common practice in the group testing literature, we assume throughout that
![]() $k=\lceil n^\theta \rceil$
and that
$k=\lceil n^\theta \rceil$
and that
![]() $k$
and the channel
$k$
and the channel
![]() $\boldsymbol{p}$
are known to the algorithm [Reference Aldridge, Johnson and Scarlett4].Footnote
1
$\boldsymbol{p}$
are known to the algorithm [Reference Aldridge, Johnson and Scarlett4].Footnote
1
1.2. Approximate recovery
The first main result provides an algorithm that identifies the status of all but
![]() $o(k)$
individuals correctly with the optimal number of tests. For a number
$o(k)$
individuals correctly with the optimal number of tests. For a number
![]() $z\in [0,1]$
, let
$z\in [0,1]$
, let
![]() $h(z)=-z\ln (z)-(1-z)\ln (1-z)$
. Further, for
$h(z)=-z\ln (z)-(1-z)\ln (1-z)$
. Further, for
![]() $y,z\in [0,1]$
, let
$y,z\in [0,1]$
, let
![]() $D_{\mathrm{KL}}\left ({{{y}\|{z}}}\right )=y\ln (y/z)+(1-y)\ln ((1-y)/(1-z))$
signify the Kullback–Leibler divergence. We use the convention that
$D_{\mathrm{KL}}\left ({{{y}\|{z}}}\right )=y\ln (y/z)+(1-y)\ln ((1-y)/(1-z))$
signify the Kullback–Leibler divergence. We use the convention that
![]() $0\ln 0=0\ln \frac{0}{0}=0$
. Given the channel
$0\ln 0=0\ln \frac{0}{0}=0$
. Given the channel
![]() $\boldsymbol{p}$
define
$\boldsymbol{p}$
define
The value
![]() $1/c_{\mathrm{Sh}}=D_{\mathrm{KL}}\left ({{{p_{10}}\|{(1-\tanh (\phi /2))/2}}}\right )$
equals the capacity of the
$1/c_{\mathrm{Sh}}=D_{\mathrm{KL}}\left ({{{p_{10}}\|{(1-\tanh (\phi /2))/2}}}\right )$
equals the capacity of the
![]() $\boldsymbol{p}$
-channel [Reference Gebhard, Johnson, Loick and Rolvien19, Lemma F.1]. Let
$\boldsymbol{p}$
-channel [Reference Gebhard, Johnson, Loick and Rolvien19, Lemma F.1]. Let
Theorem 1.1.
For any
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $0\lt \theta \lt 1$
and
$0\lt \theta \lt 1$
and
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for every
$n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for every
![]() $n\gt n_0$
, there exists a randomised test design
$n\gt n_0$
, there exists a randomised test design
![]() $\mathbf{G}_{\mathrm{sc}}$
with
$\mathbf{G}_{\mathrm{sc}}$
with
![]() $m\leq (1+\varepsilon )m_{\mathrm{\texttt{SPARC}}}(n,k,\boldsymbol{p})$
tests and a deterministic polynomial time inference algorithm
$m\leq (1+\varepsilon )m_{\mathrm{\texttt{SPARC}}}(n,k,\boldsymbol{p})$
tests and a deterministic polynomial time inference algorithm
![]() $\mathrm{\texttt{SPARC}}$
such that
$\mathrm{\texttt{SPARC}}$
such that
In other words, once the number of tests exceeds
![]() $m_{\mathrm{\texttt{SPARC}}}=c_{\mathrm{Sh}} k\ln (n/k)$
, SPARC applied to the test design
$m_{\mathrm{\texttt{SPARC}}}=c_{\mathrm{Sh}} k\ln (n/k)$
, SPARC applied to the test design
![]() $\mathbf{G}_{\mathrm{sc}}$
identifies the status of all but
$\mathbf{G}_{\mathrm{sc}}$
identifies the status of all but
![]() $o(k)$
individuals correctly w.h.p. The test design
$o(k)$
individuals correctly w.h.p. The test design
![]() $\mathbf{G}_{\mathrm{sc}}$
employs an idea from coding theory called ‘spatial coupling’ [Reference Takeuchi, Tanaka and Kawabata37, Reference Wang, Li, Zhang and Zhang41]. As we will elaborate in Section 2, spatial coupling blends a randomised and a topological construction. A closely related design has been used in noiseless group testing [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9].
$\mathbf{G}_{\mathrm{sc}}$
employs an idea from coding theory called ‘spatial coupling’ [Reference Takeuchi, Tanaka and Kawabata37, Reference Wang, Li, Zhang and Zhang41]. As we will elaborate in Section 2, spatial coupling blends a randomised and a topological construction. A closely related design has been used in noiseless group testing [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9].
The following theorem shows that Theorem 1.1 is optimal in the strong sense that it is information-theoretically impossible to approximately recover the set of infected individuals with fewer than
![]() $(1-\varepsilon )m_{\mathrm{\texttt{SPARC}}}$
tests on any test design. In fact, approximate recovery w.h.p. is impossible even if we allow adaptive group testing, where tests are conducted one by one and the choice of the next group to be tested may depend on all previous results.
$(1-\varepsilon )m_{\mathrm{\texttt{SPARC}}}$
tests on any test design. In fact, approximate recovery w.h.p. is impossible even if we allow adaptive group testing, where tests are conducted one by one and the choice of the next group to be tested may depend on all previous results.
Theorem 1.2.
For any
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $0\lt \theta \lt 1$
and
$0\lt \theta \lt 1$
and
![]() $\varepsilon \gt 0$
, there exist
$\varepsilon \gt 0$
, there exist
![]() $\delta =\delta (\boldsymbol{p},\theta, \varepsilon )\gt 0$
and
$\delta =\delta (\boldsymbol{p},\theta, \varepsilon )\gt 0$
and
![]() $n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for all
$n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for all
![]() $n\gt n_0$
, all adaptive test designs with
$n\gt n_0$
, all adaptive test designs with
![]() $m\leq (1-\varepsilon )m_{\mathrm{\texttt{SPARC}}}(n,k,\boldsymbol{p})$
tests in total and any function
$m\leq (1-\varepsilon )m_{\mathrm{\texttt{SPARC}}}(n,k,\boldsymbol{p})$
tests in total and any function
![]() $\mathscr{A}\,:\,\{0,1\}^m\to \{0,1\}^n$
, we have
$\mathscr{A}\,:\,\{0,1\}^m\to \{0,1\}^n$
, we have
Theorem 1.2 and its proof are a relatively simple adaptation of [Reference Gebhard, Johnson, Loick and Rolvien19, Corollary 2.3], where
![]() $c_{\mathrm{Sh}} k\ln (n/k)$
was established as a lower bound on the number of tests required for exact recovery.
$c_{\mathrm{Sh}} k\ln (n/k)$
was established as a lower bound on the number of tests required for exact recovery.
1.3. Exact recovery
How many tests are required in order to infer the set of infected individuals precisely, not just up to
![]() $o(k)$
mistakes? Intuitively, apart from an information-theoretic condition such as (1.3), exact recovery requires a kind of local stability condition. More precisely, imagine that we managed to correctly diagnose all individuals
$o(k)$
mistakes? Intuitively, apart from an information-theoretic condition such as (1.3), exact recovery requires a kind of local stability condition. More precisely, imagine that we managed to correctly diagnose all individuals
![]() $y\neq x$
that share a test with individual
$y\neq x$
that share a test with individual
![]() $x$
. Then towards ascertaining the status of
$x$
. Then towards ascertaining the status of
![]() $x$
itself, only those tests are relevant that contain
$x$
itself, only those tests are relevant that contain
![]() $x$
but no other infected individual
$x$
but no other infected individual
![]() $y$
, for the outcome of these tests hinges on the status of
$y$
, for the outcome of these tests hinges on the status of
![]() $x$
. Hence, to achieve exact recovery, we need to make certain that it is possible to tell the status of
$x$
. Hence, to achieve exact recovery, we need to make certain that it is possible to tell the status of
![]() $x$
itself from these tests w.h.p.
$x$
itself from these tests w.h.p.
The required number of tests to guarantee local stability on the test design
![]() $\mathbf{G}_{\mathrm{sc}}$
from Theorem 1.1 can be expressed in terms of a mildly involved optimisation problem. For
$\mathbf{G}_{\mathrm{sc}}$
from Theorem 1.1 can be expressed in terms of a mildly involved optimisation problem. For
![]() $c,d\gt 0$
and
$c,d\gt 0$
and
![]() $\theta \in (0,1)$
, let
$\theta \in (0,1)$
, let
This set is a nonempty interval because
![]() $y\mapsto D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )$
is convex and
$y\mapsto D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )$
is convex and
![]() $y=\exp ({-}d)\in \mathscr{Y}(c,d,\theta )$
. Let
$y=\exp ({-}d)\in \mathscr{Y}(c,d,\theta )$
. Let
 \begin{align} c_{\mathrm{ex},0}(d,\theta )&= \begin{cases} \inf \left \{c\gt 0\,:\,\inf _{y\in \mathscr{Y}(c,d,\theta )}cd(1-\theta )\left (D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )\right.\right. & \text{if }p_{11}\lt 1,\\\left.\left. +yD_{\mathrm{KL}}\left ({{{p_{01}}\|{p_{11}}}}\right )\right )\geq \theta \right \}&\\[3pt] \inf \{c\gt 0\,:\,0\not \in \mathscr{Y}(c,d,\theta )\}&\text{otherwise}. \end{cases} \end{align}
\begin{align} c_{\mathrm{ex},0}(d,\theta )&= \begin{cases} \inf \left \{c\gt 0\,:\,\inf _{y\in \mathscr{Y}(c,d,\theta )}cd(1-\theta )\left (D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )\right.\right. & \text{if }p_{11}\lt 1,\\\left.\left. +yD_{\mathrm{KL}}\left ({{{p_{01}}\|{p_{11}}}}\right )\right )\geq \theta \right \}&\\[3pt] \inf \{c\gt 0\,:\,0\not \in \mathscr{Y}(c,d,\theta )\}&\text{otherwise}. \end{cases} \end{align}
If
![]() $p_{11}=1$
, let
$p_{11}=1$
, let
![]() $\mathfrak z(y)=1$
for all
$\mathfrak z(y)=1$
for all
![]() $y\in \mathscr{Y}(c,d,\theta )$
. Further, if
$y\in \mathscr{Y}(c,d,\theta )$
. Further, if
![]() $p_{11}\lt 1$
, then the function
$p_{11}\lt 1$
, then the function
![]() $z\mapsto D_{\mathrm{KL}}\left ({{{z}\|{p_{11}}}}\right )$
is strictly decreasing on
$z\mapsto D_{\mathrm{KL}}\left ({{{z}\|{p_{11}}}}\right )$
is strictly decreasing on
![]() $[p_{01},p_{11}]$
; therefore, for any
$[p_{01},p_{11}]$
; therefore, for any
![]() $c\gt c_{\mathrm{ex},0}(d,\theta )$
and
$c\gt c_{\mathrm{ex},0}(d,\theta )$
and
![]() $y\in \mathscr{Y}(c,d,\theta )$
, there exists a unique
$y\in \mathscr{Y}(c,d,\theta )$
, there exists a unique
![]() $\mathfrak z(y)=\mathfrak z_{c,d,\theta }(y)\in [p_{01},p_{11}]$
such that
$\mathfrak z(y)=\mathfrak z_{c,d,\theta }(y)\in [p_{01},p_{11}]$
such that
In either case set
 \begin{align} c_{\mathrm{ex},1}(d,\theta )&= \begin{cases} \inf \left \{c\gt c_{\mathrm{ex},0}(d,\theta )\,:\,\inf _{y\in \mathscr{Y}(c,d,\theta )}cd(1-\theta )\left (D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )\right.\right. &\text{if }p_{01}\gt 0,\\\left.\left.+yD_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{01}}}}\right )\right )\geq 1\right \} & \\[3pt] c_{\mathrm{ex},0}(d,\theta )&\text{otherwise}. \end{cases} \end{align}
\begin{align} c_{\mathrm{ex},1}(d,\theta )&= \begin{cases} \inf \left \{c\gt c_{\mathrm{ex},0}(d,\theta )\,:\,\inf _{y\in \mathscr{Y}(c,d,\theta )}cd(1-\theta )\left (D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )\right.\right. &\text{if }p_{01}\gt 0,\\\left.\left.+yD_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{01}}}}\right )\right )\geq 1\right \} & \\[3pt] c_{\mathrm{ex},0}(d,\theta )&\text{otherwise}. \end{cases} \end{align}
Finally, define
 \begin{align} c_{\mathrm{ex},2}(d)&=1\big /\left (h(p_{00}\exp ({-}d)+p_{10}(1-\exp ({-}d)))-\exp ({-}d) h(p_{00})\right.\nonumber\\[5pt]& \left. \quad -(1-\exp ({-}d))h(p_{10})\right ), \end{align}
\begin{align} c_{\mathrm{ex},2}(d)&=1\big /\left (h(p_{00}\exp ({-}d)+p_{10}(1-\exp ({-}d)))-\exp ({-}d) h(p_{00})\right.\nonumber\\[5pt]& \left. \quad -(1-\exp ({-}d))h(p_{10})\right ), \end{align}
 \begin{align} c_{\mathrm{ex}}(\theta )&=\inf _{d\gt 0}\max \{c_{\mathrm{ex},1}(d,\theta ),c_{\mathrm{ex},2}(d)\},\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})&=c_{\mathrm{ex}}(\theta ) k\ln (n/k).\nonumber \end{align}
\begin{align} c_{\mathrm{ex}}(\theta )&=\inf _{d\gt 0}\max \{c_{\mathrm{ex},1}(d,\theta ),c_{\mathrm{ex},2}(d)\},\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})&=c_{\mathrm{ex}}(\theta ) k\ln (n/k).\nonumber \end{align}
Theorem 1.3.
For any
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $0\lt \theta \lt 1$
and
$0\lt \theta \lt 1$
and
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for every
$n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for every
![]() $n\gt n_0$
, there exists a randomised test design
$n\gt n_0$
, there exists a randomised test design
![]() $\mathbf{G}_{\mathrm{sc}}$
with
$\mathbf{G}_{\mathrm{sc}}$
with
![]() $m\leq (1+\varepsilon )m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})$
tests and a deterministic polynomial time inference algorithm
$m\leq (1+\varepsilon )m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})$
tests and a deterministic polynomial time inference algorithm
![]() $\mathrm{\texttt{SPEX}}$
such that
$\mathrm{\texttt{SPEX}}$
such that
Like SPARC from Theorem 1.1, SPEX uses the spatially coupled test design
![]() $\mathbf{G}_{\mathrm{sc}}$
. Crucially, apart from the numbers
$\mathbf{G}_{\mathrm{sc}}$
. Crucially, apart from the numbers
![]() $n$
and
$n$
and
![]() $m$
of individuals and tests, the value of
$m$
of individuals and tests, the value of
![]() $d$
at which the infimum (1.11) is attained also enters into the construction of that test design. Specifically, the average size of a test group equals
$d$
at which the infimum (1.11) is attained also enters into the construction of that test design. Specifically, the average size of a test group equals
![]() $dn/k$
. Remarkably, while the optimal value of
$dn/k$
. Remarkably, while the optimal value of
![]() $d$
for approximate recovery turns out to depend on the channel
$d$
for approximate recovery turns out to depend on the channel
![]() $\boldsymbol{p}$
only, a different value of
$\boldsymbol{p}$
only, a different value of
![]() $d$
that also depends on
$d$
that also depends on
![]() $k$
can be the right choice to facilitate exact recovery. We will revisit this point in Section 1.5.
$k$
can be the right choice to facilitate exact recovery. We will revisit this point in Section 1.5.
1.4. Lower bound on the constant column design
Unlike in the case of approximate recovery, we do not have a proof that the positive result on exact recovery from Theorem 1.3 is optimal for any choice of test design. However, we can show that exact recovery with
![]() $(1-\varepsilon )c_{\mathrm{ex}} k\ln (n/k)$
tests is impossible on the constant column design
$(1-\varepsilon )c_{\mathrm{ex}} k\ln (n/k)$
tests is impossible on the constant column design
![]() $\mathbf{G}_{\mathrm{cc}}$
. Under
$\mathbf{G}_{\mathrm{cc}}$
. Under
![]() $\mathbf{G}_{\mathrm{cc}}$
, each of the
$\mathbf{G}_{\mathrm{cc}}$
, each of the
![]() $n$
individuals independently joins an equal number
$n$
individuals independently joins an equal number
![]() $\Delta$
of tests, drawn uniformly without replacement from the set of all
$\Delta$
of tests, drawn uniformly without replacement from the set of all
![]() $m$
available tests. Let
$m$
available tests. Let
![]() $\mathbf{G}_{\mathrm{cc}}=\mathbf{G}_{\mathrm{cc}}(n,m,\Delta )$
signify the outcome. The following theorem shows that exact recovery on
$\mathbf{G}_{\mathrm{cc}}=\mathbf{G}_{\mathrm{cc}}(n,m,\Delta )$
signify the outcome. The following theorem shows that exact recovery on
![]() $\mathbf{G}_{\mathrm{cc}}$
is information-theoretically impossible with fewer than
$\mathbf{G}_{\mathrm{cc}}$
is information-theoretically impossible with fewer than
![]() $m_{\mathrm{\texttt{SPEX}}}$
tests.
$m_{\mathrm{\texttt{SPEX}}}$
tests.
Theorem 1.4.
For any
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $0\lt \theta \lt 1$
and
$0\lt \theta \lt 1$
and
![]() $\varepsilon \gt 0$
, there exists
$\varepsilon \gt 0$
, there exists
![]() $n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for every
$n_0=n_0(\boldsymbol{p},\theta, \varepsilon )$
such that for every
![]() $n\gt n_0$
and all
$n\gt n_0$
and all
![]() $m\leq (1-\varepsilon )m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})$
,
$m\leq (1-\varepsilon )m_{\mathrm{\texttt{SPEX}}}(n,k,\boldsymbol{p})$
,
![]() $\Delta \gt 0$
and any
$\Delta \gt 0$
and any
![]() $\mathscr{A}_{\mathbf{G}_{\mathrm{cc}}}\,:\,\{0,1\}^m\to \{0,1\}^n$
, we have
$\mathscr{A}_{\mathbf{G}_{\mathrm{cc}}}\,:\,\{0,1\}^m\to \{0,1\}^n$
, we have
An immediate implication of Theorem 1.4 is that the positive result from Theorem 1.3 is at least as good as the best prior results on exact noisy recovery from [Reference Gebhard, Johnson, Loick and Rolvien19], which are based on running a simple combinatorial algorithm called DD on
![]() $\mathbf{G}_{\mathrm{cc}}$
. In fact, in Section 1.5, we will see that the new bound from Theorem 1.3 improves over the bounds from [Reference Gebhard, Johnson, Loick and Rolvien19] rather significantly for most
$\mathbf{G}_{\mathrm{cc}}$
. In fact, in Section 1.5, we will see that the new bound from Theorem 1.3 improves over the bounds from [Reference Gebhard, Johnson, Loick and Rolvien19] rather significantly for most
![]() $\theta, \boldsymbol{p}$
.
$\theta, \boldsymbol{p}$
.
The proof of Theorem 1.4 confirms the combinatorial meaning of the threshold
![]() $c_{\mathrm{ex}}(\theta )$
. Specifically, for
$c_{\mathrm{ex}}(\theta )$
. Specifically, for
![]() $c=m/(k\ln (n/k))\lt c_{\mathrm{ex},2}(d)$
from (1.10), a moment calculation reveals that w.h.p.,
$c=m/(k\ln (n/k))\lt c_{\mathrm{ex},2}(d)$
from (1.10), a moment calculation reveals that w.h.p.,
![]() $\mathbf{G}_{\mathrm{cc}}$
contains ‘solutions’
$\mathbf{G}_{\mathrm{cc}}$
contains ‘solutions’
![]() $\sigma$
of at least the same posterior likelihood as the true
$\sigma$
of at least the same posterior likelihood as the true
![]() $\boldsymbol{\sigma }$
such that
$\boldsymbol{\sigma }$
such that
![]() $\sigma$
and
$\sigma$
and
![]() $\boldsymbol{\sigma }$
differ significantly, that is,
$\boldsymbol{\sigma }$
differ significantly, that is,
![]() $\|\boldsymbol{\sigma }-\sigma \|_1=\Omega (k)$
. By contrast, the threshold
$\|\boldsymbol{\sigma }-\sigma \|_1=\Omega (k)$
. By contrast, the threshold
![]() $c_{\mathrm{ex},1}(d,\theta )$
marks the onset of local stability. This means that for
$c_{\mathrm{ex},1}(d,\theta )$
marks the onset of local stability. This means that for
![]() $c\lt c_{\mathrm{ex},1}(d,\theta )$
, there will be numerous
$c\lt c_{\mathrm{ex},1}(d,\theta )$
, there will be numerous
![]() $\sigma$
close to but not identical to
$\sigma$
close to but not identical to
![]() $\boldsymbol{\sigma }$
(i.e.
$\boldsymbol{\sigma }$
(i.e.
![]() $0\lt \|\boldsymbol{\sigma }-\sigma \|_1=o(k)$
) of the at least same posterior likelihood. In either case, any inference algorithm, efficient or not, is at a loss identifying the actual
$0\lt \|\boldsymbol{\sigma }-\sigma \|_1=o(k)$
) of the at least same posterior likelihood. In either case, any inference algorithm, efficient or not, is at a loss identifying the actual
![]() $\boldsymbol{\sigma }$
.
$\boldsymbol{\sigma }$
.
In recent independent work, Chen and Scarlett [Reference Chen and Scarlett7] obtained Theorem 1.4 in the special case of symmetric noise (i.e.
![]() $p_{00}=p_{11}$
). While syntactically their expression for the threshold
$p_{00}=p_{11}$
). While syntactically their expression for the threshold
![]() $c_{\mathrm{ex}}(\theta )$
differs from (1.6)–(1.11), it can be checked that both formulas yield identical results (see Appendix F). Apart from the information-theoretic lower bound (which is the part most relevant to the present work), Chen and Scarlett also proved that it is information-theoretically possible (by means of an exponential-time algorithm) to infer
$c_{\mathrm{ex}}(\theta )$
differs from (1.6)–(1.11), it can be checked that both formulas yield identical results (see Appendix F). Apart from the information-theoretic lower bound (which is the part most relevant to the present work), Chen and Scarlett also proved that it is information-theoretically possible (by means of an exponential-time algorithm) to infer
![]() $\boldsymbol{\sigma }$
w.h.p. on the constant column design with
$\boldsymbol{\sigma }$
w.h.p. on the constant column design with
![]() $m\geq (1+\varepsilon )c_{\mathrm{ex}}(\theta )k\ln (n/k)$
tests if
$m\geq (1+\varepsilon )c_{\mathrm{ex}}(\theta )k\ln (n/k)$
tests if
![]() $p_{00}=p_{11}$
. Hence, the bound
$p_{00}=p_{11}$
. Hence, the bound
![]() $c_{\mathrm{ex}}(\theta )$
is tight in the case of symmetric noise.
$c_{\mathrm{ex}}(\theta )$
is tight in the case of symmetric noise.
1.5. Examples
We illustrate the improvements that Theorems 1.1 and 1.3 contribute by way of concrete examples of channels
![]() $\boldsymbol{p}$
. Specifically, for the binary symmetric channel and the
$\boldsymbol{p}$
. Specifically, for the binary symmetric channel and the
![]() $Z$
-channel, it is possible to obtain partial analytic results on the optimisation behind
$Z$
-channel, it is possible to obtain partial analytic results on the optimisation behind
![]() $c_{\mathrm{ex}}(\theta )$
from (1.11) (see Appendices D–E). As we will see, even a tiny amount of noise has a dramatic impact on both the number of tests required and the parameters that make a good test design.
$c_{\mathrm{ex}}(\theta )$
from (1.11) (see Appendices D–E). As we will see, even a tiny amount of noise has a dramatic impact on both the number of tests required and the parameters that make a good test design.
1.5.1. The binary symmetric channel
Although symmetry is an unrealistic assumption from the viewpoint of applications [Reference Long, Prober and Fischer29], the expression (1.3) and the optimisations (1.9)–(1.11) get much simpler on the binary symmetric channel, that is, in the case
![]() $p_{00}=p_{11}$
. For instance, the value of
$p_{00}=p_{11}$
. For instance, the value of
![]() $d$
that minimises
$d$
that minimises
![]() $c_{\mathrm{ex},2}(d)$
from (1.10) turns out to be
$c_{\mathrm{ex},2}(d)$
from (1.10) turns out to be
![]() $d=\ln 2$
. The parameter
$d=\ln 2$
. The parameter
![]() $d$
enters into the constructions of the randomised test designs
$d$
enters into the constructions of the randomised test designs
![]() $\mathbf{G}_{\mathrm{sc}}$
and
$\mathbf{G}_{\mathrm{sc}}$
and
![]() $\mathbf{G}_{\mathrm{cc}}$
in a crucial role. Specifically, the average size of a test group equals
$\mathbf{G}_{\mathrm{cc}}$
in a crucial role. Specifically, the average size of a test group equals
![]() $dn/k$
. In effect, any test is actually negative with probability
$dn/k$
. In effect, any test is actually negative with probability
![]() $\exp ({-}d+o(1))$
(see Proposition 2.3 and Lemma 5.1 below). Hence, if
$\exp ({-}d+o(1))$
(see Proposition 2.3 and Lemma 5.1 below). Hence, if
![]() $d=\ln 2$
, then w.h.p. about half the tests contain an infected individual. In effect, since
$d=\ln 2$
, then w.h.p. about half the tests contain an infected individual. In effect, since
![]() $p_{11}=p_{00}$
, after the application of noise about half the tests display a positive result w.h.p.
$p_{11}=p_{00}$
, after the application of noise about half the tests display a positive result w.h.p.
In particular, in the noiseless case
![]() $p_{11}=p_{00}=1$
, a bit of calculus reveals that the value
$p_{11}=p_{00}=1$
, a bit of calculus reveals that the value
![]() $d=\ln 2$
also minimises the other parameter
$d=\ln 2$
also minimises the other parameter
![]() $c_{\mathrm{ex},1}(d,\theta )$
from (1.9) that enters into
$c_{\mathrm{ex},1}(d,\theta )$
from (1.9) that enters into
![]() $c_{\mathrm{ex}}(\theta )$
from (1.11). Therefore, in noiseless group testing,
$c_{\mathrm{ex}}(\theta )$
from (1.11). Therefore, in noiseless group testing,
![]() $d=\ln 2$
unequivocally is the optimal choice, the optimisation on
$d=\ln 2$
unequivocally is the optimal choice, the optimisation on
![]() $d$
(1.11) effectively disappears, and we obtain
$d$
(1.11) effectively disappears, and we obtain
thereby reproducing the optimal result on noiseless group testing from [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9].
But remarkably, as we verify analytically in Appendix D at positive noise
![]() $\frac{1}{2}\lt p_{11}=p_{00}\lt 1$
, the value of
$\frac{1}{2}\lt p_{11}=p_{00}\lt 1$
, the value of
![]() $d$
that minimises
$d$
that minimises
![]() $c_{\mathrm{ex},1}(d,\theta )$
does not generally equal
$c_{\mathrm{ex},1}(d,\theta )$
does not generally equal
![]() $\ln 2$
. Hence, if we aim for exact recovery, then at positive noise, it is no longer optimal for all
$\ln 2$
. Hence, if we aim for exact recovery, then at positive noise, it is no longer optimal for all
![]() $0\lt \theta \lt 1$
to aim for about half the tests being positive/negative. The reason is the occurrence of a phase transition in terms of
$0\lt \theta \lt 1$
to aim for about half the tests being positive/negative. The reason is the occurrence of a phase transition in terms of
![]() $\theta$
where the ‘local stability’ term
$\theta$
where the ‘local stability’ term
![]() $c_{\mathrm{ex},1}(d,\theta )$
takes over as the overall maximiser in (1.10). Consequently, the objective of minimising
$c_{\mathrm{ex},1}(d,\theta )$
takes over as the overall maximiser in (1.10). Consequently, the objective of minimising
![]() $c_{\mathrm{ex},1}(d,\theta )$
and the optimal choice
$c_{\mathrm{ex},1}(d,\theta )$
and the optimal choice
![]() $d=\ln 2$
for
$d=\ln 2$
for
![]() $c_{\mathrm{ex},2}(d)$
clash. In effect, the overall minimiser
$c_{\mathrm{ex},2}(d)$
clash. In effect, the overall minimiser
![]() $d$
for
$d$
for
![]() $c_{\mathrm{ex}}(d,\theta )$
depends on both
$c_{\mathrm{ex}}(d,\theta )$
depends on both
![]() $\boldsymbol{p}$
and the infection density parameter
$\boldsymbol{p}$
and the infection density parameter
![]() $\theta$
in a nontrivial way. Thus, the presence and level of noise have a discernible impact on the choice of a good test design.Footnote
2
$\theta$
in a nontrivial way. Thus, the presence and level of noise have a discernible impact on the choice of a good test design.Footnote
2

Figure 1. Information rates on different channels in nats. The horizontal axis displays the infection density parameter
![]() $0\lt \theta \lt 1$
. The colour indicates the optimal value of
$0\lt \theta \lt 1$
. The colour indicates the optimal value of
![]() $d$
for a given
$d$
for a given
![]() $\theta$
.
$\theta$
.
Figure 1 displays the performance of the algorithms
![]() $\mathrm{\texttt{SPARC}}$
and
$\mathrm{\texttt{SPARC}}$
and
![]() $\mathrm{\texttt{SPEX}}$
from Theorems 1.1 and 1.3 on the binary symmetric channel. For the purpose of graphical representation, the figure does not display the values of
$\mathrm{\texttt{SPEX}}$
from Theorems 1.1 and 1.3 on the binary symmetric channel. For the purpose of graphical representation, the figure does not display the values of
![]() $c_{\mathrm{ex}}(\theta )$
, which diverge as
$c_{\mathrm{ex}}(\theta )$
, which diverge as
![]() $\theta \to 1$
, but the value
$\theta \to 1$
, but the value
![]() $1/c_{\mathrm{ex}}(\theta )$
. This value has a natural information-theoretic interpretation: it is the average amount of information that a test reveals about the set of infected individuals, measured in ‘nats’. In other words, the plots display the information rate of a single test (higher is better). The optimal values of
$1/c_{\mathrm{ex}}(\theta )$
. This value has a natural information-theoretic interpretation: it is the average amount of information that a test reveals about the set of infected individuals, measured in ‘nats’. In other words, the plots display the information rate of a single test (higher is better). The optimal values of
![]() $d$
are colour-coded into the curves. While in the noiseless case,
$d$
are colour-coded into the curves. While in the noiseless case,
![]() $d=\ln 2$
remains constant, in the noisy cases,
$d=\ln 2$
remains constant, in the noisy cases,
![]() $d$
varies substantially with both
$d$
varies substantially with both
![]() $\theta$
and
$\theta$
and
![]() $p_{00}=p_{11}$
.
$p_{00}=p_{11}$
.
For comparison, the figure also displays the rate in the noiseless case (dashed line on top) and the best previous rates realised by the DD algorithm on
![]() $\mathbf{G}_{\mathrm{cc}}$
from [Reference Gebhard, Johnson, Loick and Rolvien19] (dotted lines). As is evident from Figure 1, even noise as small as
$\mathbf{G}_{\mathrm{cc}}$
from [Reference Gebhard, Johnson, Loick and Rolvien19] (dotted lines). As is evident from Figure 1, even noise as small as
![]() $1\%$
already reduces the rate markedly: the upper coloured curve remains significantly below the noiseless black line. That said, Figure 1 also illustrates how the rate achieved by SPEX improves over the best previous algorithm DD from [Reference Gebhard, Johnson, Loick and Rolvien19]. Somewhat remarkably, the
$1\%$
already reduces the rate markedly: the upper coloured curve remains significantly below the noiseless black line. That said, Figure 1 also illustrates how the rate achieved by SPEX improves over the best previous algorithm DD from [Reference Gebhard, Johnson, Loick and Rolvien19]. Somewhat remarkably, the
![]() $10\%$
-line for
$10\%$
-line for
![]() $c_{\mathrm{ex}}(\theta )$
intersects the
$c_{\mathrm{ex}}(\theta )$
intersects the
![]() $1\%$
-line for DD for an interval of
$1\%$
-line for DD for an interval of
![]() $\theta$
. Hence, for these
$\theta$
. Hence, for these
![]() $\theta$
, the algorithm from Theorem 1.3 at
$\theta$
, the algorithm from Theorem 1.3 at
![]() $10\%$
noise requires fewer tests than DD at
$10\%$
noise requires fewer tests than DD at
![]() $1\%$
.
$1\%$
.
Figure 1 also illustrates how approximate and exact recovery compare. Both coloured curves start out as black horizontal lines. These bits of the curves coincide with the rate of the SPARC algorithm from Theorem 1.1. The rate achieved by SPARC, which does not depend on
![]() $\theta$
, is therefore just the extension of this horizontal line to the entire interval
$\theta$
, is therefore just the extension of this horizontal line to the entire interval
![]() $0\lt \theta \lt 1$
at the height
$0\lt \theta \lt 1$
at the height
![]() $c_{\mathrm{Sh}}$
from (1.3). Hence, particularly for large
$c_{\mathrm{Sh}}$
from (1.3). Hence, particularly for large
![]() $\theta$
, approximate recovery achieves much better rates than exact recovery.
$\theta$
, approximate recovery achieves much better rates than exact recovery.
1.5.2. The
 $Z$
-channel
$Z$
-channel
In the case
![]() $p_{00}=1$
of perfect specificity, known as the
$p_{00}=1$
of perfect specificity, known as the
![]() $Z$
-channel, it is possible to derive simple expressions for the optimisation problems (1.6)–(1.11) (see Appendix E):
$Z$
-channel, it is possible to derive simple expressions for the optimisation problems (1.6)–(1.11) (see Appendix E):
As in the symmetric case, there is a tension between the value of
![]() $d$
that minimises (1.15) and the objective of minimising (1.16). Recall that since the size of the test groups is proportional to
$d$
that minimises (1.15) and the objective of minimising (1.16). Recall that since the size of the test groups is proportional to
![]() $d$
, the optimiser
$d$
, the optimiser
![]() $d$
has a direct impact on the construction of the test design.
$d$
has a direct impact on the construction of the test design.
Figure 1b displays the rates achieved by SPEX (solid line) and, for comparison, the DD algorithm from [Reference Gebhard, Johnson, Loick and Rolvien19] (dotted grey) on the
![]() $Z$
-channel with sensitivities
$Z$
-channel with sensitivities
![]() $p_{11}=0.9$
and
$p_{11}=0.9$
and
![]() $p_{11}=0.5$
. Additionally, the dashed red line indicates the noiseless rate. Once again, the optimal value of
$p_{11}=0.5$
. Additionally, the dashed red line indicates the noiseless rate. Once again, the optimal value of
![]() $d$
is colour-coded into the solid SPEX line. Remarkably, the SPEX rate at
$d$
is colour-coded into the solid SPEX line. Remarkably, the SPEX rate at
![]() $p_{11}=0.5$
(high noise) exceeds the DD rate at
$p_{11}=0.5$
(high noise) exceeds the DD rate at
![]() $p_{11}=0.9$
for a wide range of
$p_{11}=0.9$
for a wide range of
![]() $\theta$
. As in the symmetric case, the horizontal
$\theta$
. As in the symmetric case, the horizontal
![]() $c_{\mathrm{Sh}}$
-lines indicate the performance of the SPARC approximate recovery algorithm.
$c_{\mathrm{Sh}}$
-lines indicate the performance of the SPARC approximate recovery algorithm.
1.5.3. General (asymmetric) noise
While in the symmetric case, the term
![]() $c_{\mathrm{ex},2}(d)$
from (1.10) attains its minimum simply at
$c_{\mathrm{ex},2}(d)$
from (1.10) attains its minimum simply at
![]() $d=\ln 2$
, with
$d=\ln 2$
, with
![]() $\phi$
from (1.3), the minimum for general
$\phi$
from (1.3), the minimum for general
![]() $\boldsymbol{p}$
is attained at
$\boldsymbol{p}$
is attained at
Once again, the design of
![]() $\mathbf{G}_{\mathrm{sc}}$
(as well as
$\mathbf{G}_{\mathrm{sc}}$
(as well as
![]() $\mathbf{G}_{\mathrm{cc}}$
) ensures that w.h.p., a
$\mathbf{G}_{\mathrm{cc}}$
) ensures that w.h.p., a
![]() $\exp ({-}d)$
-fraction of tests is actually negative w.h.p. The choice (1.17) ensures that under the
$\exp ({-}d)$
-fraction of tests is actually negative w.h.p. The choice (1.17) ensures that under the
![]() $\boldsymbol{p}$
-channel, the mutual information between the channel input and the channel output is maximised (Reference Gebhard, Johnson, Loick and Rolvien19, LemmaF.1):
$\boldsymbol{p}$
-channel, the mutual information between the channel input and the channel output is maximised (Reference Gebhard, Johnson, Loick and Rolvien19, LemmaF.1):
As can be checked numerically, the second contributor
![]() $c_{\mathrm{ex},1}(d,\theta )$
to
$c_{\mathrm{ex},1}(d,\theta )$
to
![]() $c_{\mathrm{ex}}(\theta )$
may take its minimum at another
$c_{\mathrm{ex}}(\theta )$
may take its minimum at another
![]() $d$
. However, we are not aware of simple explicit expressions for
$d$
. However, we are not aware of simple explicit expressions for
![]() $c_{\mathrm{ex},2}(\theta )$
from (1.10) for general noise.
$c_{\mathrm{ex},2}(\theta )$
from (1.10) for general noise.
1.6. Related work
The monograph of Aldridge, Johnson, and Scarlett [Reference Aldridge, Johnson and Scarlett4] provides an excellent overview of the group testing literature. The group testing problem comes in various different flavours: non-adaptive (where all tests are conducted concurrently) or adaptive (where tests are conducted in subsequent stages such that the tests at later stages may depend on the outcomes of earlier stages), as well as noiseless or noisy. An important result of Aldridge shows that noiseless non-adaptive group testing does not perform better than plain individual testing if
![]() $k=\Omega (n)$
, that is, if the number of infected individuals is linear in the size of the population [Reference Aldridge3]. Therefore, research on non-adaptive group testing focuses on the case
$k=\Omega (n)$
, that is, if the number of infected individuals is linear in the size of the population [Reference Aldridge3]. Therefore, research on non-adaptive group testing focuses on the case
![]() $k\sim n^\theta$
with
$k\sim n^\theta$
with
![]() $0\lt \theta \lt 1$
. For non-adaptive noiseless group testing with this scaling of
$0\lt \theta \lt 1$
. For non-adaptive noiseless group testing with this scaling of
![]() $k$
, two different test designs (Bernoulli and constant column) and various elementary algorithms have been proposed [Reference Chan, Che, Jaggi and Saligrama6]. Among these elementary designs and algorithms, the best performance to date is achieved by the DD greedy algorithm on the constant column design [Reference Johnson, Aldridge and Scarlett24]. However, the DD algorithm does not match the information-theoretic bound on the constant column design for all
$k$
, two different test designs (Bernoulli and constant column) and various elementary algorithms have been proposed [Reference Chan, Che, Jaggi and Saligrama6]. Among these elementary designs and algorithms, the best performance to date is achieved by the DD greedy algorithm on the constant column design [Reference Johnson, Aldridge and Scarlett24]. However, the DD algorithm does not match the information-theoretic bound on the constant column design for all
![]() $\theta$
[Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick8].
$\theta$
[Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick8].
Coja-Oghlan, Gebhard, Hahn-Klimroth, and Loick proposed a more sophisticated test design for noiseless group testing based on spatial coupling [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9], along with an efficient inference algorithm called SPIV. Additionally, they improved the information-theoretic lower bound for non-adaptive noiseless group testing. The number of tests required by the SPIV algorithm matches this new lower bound. In effect, the combination of SPIV with the spatially coupled test design solves the noiseless non-adaptive group testing problem optimally both for exact and approximate recovery.
The present article deals with the noisy non-adaptive variant of group testing. A noisy version of the efficient DD algorithm was previously studied on both the Bernoulli and the constant column design [Reference Gebhard, Johnson, Loick and Rolvien19, Reference Scarlett and Johnson35]. The best previous exact recovery results for general noise were obtained by Johnson, Gebhard, Loick, and Rolvien [Reference Gebhard, Johnson, Loick and Rolvien19] by means of DD on the constant column design (see Theorem 2.1 below). Theorem 1.4 shows in combination with Theorem 1.3 that the new SPEX algorithm performs at least as well as any algorithm on the constant column design, including and particularly DD.
Apart from the articles [Reference Gebhard, Johnson, Loick and Rolvien19, Reference Scarlett and Johnson35] that dealt with the same general noise model as we consider here, several contributions focused on special noise models, particularly symmetric noise (
![]() $p_{00}=p_{11}$
). In this scenario, Chen and Scarlett [Reference Chen and Scarlett7] recently determined the information-theoretically optimal number of tests required for exact recovery on the Bernoulli and constant column designs.
$p_{00}=p_{11}$
). In this scenario, Chen and Scarlett [Reference Chen and Scarlett7] recently determined the information-theoretically optimal number of tests required for exact recovery on the Bernoulli and constant column designs.
For both designs, Chen and Scarlett considered the “low overlap” and the “high overlap” regime separately. This corresponds to decodings that align weakly/strongly with the ground truth. For the low overlap regime, they bounded the mutual information by using results of [Reference Scarlett and Cevher33]. For the high overlap regime, they worked out a local stability analysis for the symmetric case while taking the degree fluctuations for the Bernoulli design into account. The local stability analysis of Chen and Scarlett for the constant column design is equivalent to the special case of symmetric noise of the corresponding analysis that we perform towards the proof of Theorem 1.3. Indeed, the information-theoretic threshold identified by Chen and Scarlett matches the threshold
![]() $c_{\mathrm{ex}}(\theta )$
from (1.10) in the special case of symmetric noise; see Appendix F for details. In contrast to the present work, Chen and Scarlett do not investigate the issue of efficient inference algorithms. Instead, they pose the existence of an efficient inference algorithm that matches the information-theoretic threshold as an open problem. Theorem 1.3 applied to symmetric noise answers their question in the affirmative. While it might be interesting to investigate whether the present approach for exact recovery extends to (a spatially coupled variant of) the Bernoulli design, we expect that this would lead to weaker bounds than obtained in Theorem 1.3. In fact, there is no known case where the Bernoulli design outperformed the constant column design. Furthermore, for noiseless group testing, the constant column design outperforms the Bernoulli design [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9, Reference Aldridge1, Reference Truong, Aldridge and Scarlett39], although it is not proven yet that this holds in general for the noisy case [Reference Aldridge, Johnson and Scarlett4, Reference Chen and Scarlett7]. In addition, the question of a tight lower bound for exact recovery for general noise and arbitrary test designs remains open.
$c_{\mathrm{ex}}(\theta )$
from (1.10) in the special case of symmetric noise; see Appendix F for details. In contrast to the present work, Chen and Scarlett do not investigate the issue of efficient inference algorithms. Instead, they pose the existence of an efficient inference algorithm that matches the information-theoretic threshold as an open problem. Theorem 1.3 applied to symmetric noise answers their question in the affirmative. While it might be interesting to investigate whether the present approach for exact recovery extends to (a spatially coupled variant of) the Bernoulli design, we expect that this would lead to weaker bounds than obtained in Theorem 1.3. In fact, there is no known case where the Bernoulli design outperformed the constant column design. Furthermore, for noiseless group testing, the constant column design outperforms the Bernoulli design [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9, Reference Aldridge1, Reference Truong, Aldridge and Scarlett39], although it is not proven yet that this holds in general for the noisy case [Reference Aldridge, Johnson and Scarlett4, Reference Chen and Scarlett7]. In addition, the question of a tight lower bound for exact recovery for general noise and arbitrary test designs remains open.
A further contribution of Scarlett and Cevher [Reference Scarlett and Cevher33] contains a result on approximate recovery under the assumption of symmetric noise. In this case, Scarlett and Cevher obtain matching information-theoretic upper and lower bounds, albeit without addressing the question of efficient inference algorithms. Theorem 1.1 applied to the special case of symmetric noise provides a polynomial time inference algorithm that matches their lower bound.
From a practical viewpoint, non-adaptive group testing (where all tests are conducted in parallel) is preferable because results are available more rapidly than in the adaptive setting, where several rounds of testing are required. That said, adaptive schemes may require a smaller total number of tests. The case of noiseless adaptive group testing has been studied since the seminal work of Dorfman [Reference Dorfman15] from the 1940s. For the case
![]() $k\sim n^\theta$
, a technique known as generalised binary splitting gets by with the optimal number of tests [Reference Baldassini, Johnson and Aldridge5, Reference Hwang22]. Aldridge [Reference Aldridge2] extended this approach to the case
$k\sim n^\theta$
, a technique known as generalised binary splitting gets by with the optimal number of tests [Reference Baldassini, Johnson and Aldridge5, Reference Hwang22]. Aldridge [Reference Aldridge2] extended this approach to the case
![]() $k=\Theta (n)$
, obtaining near-optimal rates. Recently, there has been significant progress on upper and lower bounds for noisy and adaptive group testing, although general optimal results remain elusive [Reference Scarlett32, Reference Teo and Scarlett38].
$k=\Theta (n)$
, obtaining near-optimal rates. Recently, there has been significant progress on upper and lower bounds for noisy and adaptive group testing, although general optimal results remain elusive [Reference Scarlett32, Reference Teo and Scarlett38].
Beyond group testing, in recent years, important progress has been made on several inference problems by means of a combination of spatial coupling and message passing ideas. Perhaps the most prominent case in point is the compressed sensing problem [Reference Donoho, Javanmard and Montanari14, Reference Krzakala, Mézard, Sausset, Sun and Zdeborová25]. Further applications include the pooled data problem [Reference El Alaoui, Ramdas, Krzakala, Zdeborová and Jordan17–Reference Hahn-Klimroth and Müller20] and CDMA [Reference Takeuchi, Tanaka and Kawabata37], a signal processing problem. The basic idea of spatial coupling, which we are going to discuss in some detail in Section 2.3, goes back to work on capacity-achieving linear codes [Reference Takeuchi, Tanaka and Kawabata37, Reference Wang, Li, Zhang and Zhang41, Reference Kudekar and Pfister26–Reference Kumar, Young, Macris and Pfister28]. The SPIV algorithm from [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9] combines a test design inspired by spatial coupling with a combinatorial inference algorithm. A novelty of the present work is that we replace this elementary algorithm with a novel variant of the Belief Propagation (BP) message passing algorithm [Reference Mézard and Montanari30, Reference Pearl31] that lends itself to a rigorous analysis.
The standard variant of BP has been studied for variants of group testing [Reference El Alaoui, Ramdas, Krzakala, Zdeborová and Jordan17, Reference Sejdinovic and Johnson36, Reference Zhang, Krzakala, Mézard and Zdeborová43]. Additionally there have been empirical studies on BP for group testing [Reference Coja-Oghlan, Hahn-Klimroth, Loick and Penschuck11, Reference Wang and Huang40].
1.7. Organisation
After introducing a bit of notation and recalling some background in Section 1.8, we give an outline of the proofs of the main results in Section 2. Subsequently, Section 3 deals with the details of the proof of Theorem 1.1. Moreover, Section 4 deals with the proof of Theorem 1.3, while in Section 5, we prove Theorem 1.4. The proof of Theorem 1.2, which is quite short and uses arguments that are well established in the literature, follows in Appendix B. Appendix C contains the proof of a routine expansion property of the test design
![]() $\mathbf{G}_{\mathrm{sc}}$
. Finally, in Appendices D and E, we investigate the optimisation problems (1.9)–(1.11) on the binary symmetric channel and the
$\mathbf{G}_{\mathrm{sc}}$
. Finally, in Appendices D and E, we investigate the optimisation problems (1.9)–(1.11) on the binary symmetric channel and the
![]() $Z$
-channel, and in Appendix F, we compare our result to the recent result of Chen and Scarlett [Reference Chen and Scarlett7]. A table of used notations can be found in Appendix A.
$Z$
-channel, and in Appendix F, we compare our result to the recent result of Chen and Scarlett [Reference Chen and Scarlett7]. A table of used notations can be found in Appendix A.
1.8. Preliminaries
As explained in Section 1.1, a test design is a bipartite graph
![]() $G=(V\cup F,E)$
whose vertex set consists of a set
$G=(V\cup F,E)$
whose vertex set consists of a set
![]() $V$
individuals and a set
$V$
individuals and a set
![]() $F$
of tests. The ground truth, that is, the set of infected individuals, is encoded as a vector
$F$
of tests. The ground truth, that is, the set of infected individuals, is encoded as a vector
![]() $\boldsymbol{\sigma }\in \{0,1\}^V$
of Hamming weight
$\boldsymbol{\sigma }\in \{0,1\}^V$
of Hamming weight
![]() $k$
. Since we will deal with randomised test designs, we may assume that
$k$
. Since we will deal with randomised test designs, we may assume that
![]() $\boldsymbol{\sigma }$
is a uniformly random vector of Hamming weight
$\boldsymbol{\sigma }$
is a uniformly random vector of Hamming weight
![]() $k$
(by shuffling the set of individuals). Also recall that for a test
$k$
(by shuffling the set of individuals). Also recall that for a test
![]() $a$
, we let
$a$
, we let
![]() $\boldsymbol{\sigma }^{\prime}_a\in \{0,1\}$
denote the actual result of test
$\boldsymbol{\sigma }^{\prime}_a\in \{0,1\}$
denote the actual result of test
![]() $a$
(equal to one if and only if
$a$
(equal to one if and only if
![]() $a$
contains an infected individual), while
$a$
contains an infected individual), while
![]() $\boldsymbol{\sigma }^{\prime\prime}_a\in \{0,1\}$
signifies the displayed test result obtained via (1.2). It is convenient to introduce the shorthands
$\boldsymbol{\sigma }^{\prime\prime}_a\in \{0,1\}$
signifies the displayed test result obtained via (1.2). It is convenient to introduce the shorthands
for the set of infected/healthy individuals, the set of actually negative/positive tests, the set of negatively/positively displayed tests, and the tests that are actually negative/positive and display a positive/negative result, respectively. For each node
![]() $u$
of
$u$
of
![]() $G$
, we denote
$G$
, we denote
![]() $\partial u=\partial _Gu$
be the set of neighbours of
$\partial u=\partial _Gu$
be the set of neighbours of
![]() $u$
. For an individual
$u$
. For an individual
![]() $x\in V$
, we also let
$x\in V$
, we also let
![]() $\partial ^{\pm } x=\partial _G^{\pm } x=\partial _G x\cap F^{\pm }$
be the set of positively/negatively displayed tests that contain
$\partial ^{\pm } x=\partial _G^{\pm } x=\partial _G x\cap F^{\pm }$
be the set of positively/negatively displayed tests that contain
![]() $x$
.
$x$
.
We need Chernoff bounds for the binomial and the hypergeometric distribution. Recall that the hypergeometric distribution
![]() $\textrm{Hyp}(L,M,N)$
is defined by
$\textrm{Hyp}(L,M,N)$
is defined by
(Out of a total of
![]() $L$
items of which
$L$
items of which
![]() $M$
are special, we draw
$M$
are special, we draw
![]() $N$
items without replacement and count the number of special items in the draw.) The mean of the hypergeometric distribution equals
$N$
items without replacement and count the number of special items in the draw.) The mean of the hypergeometric distribution equals
![]() $MN/L$
.
$MN/L$
.
Lemma 1.5 ([Reference Janson, Luczak and Rucinski23, Equation 2.4] ). Let
![]() $\boldsymbol{X}$
be a binomial random variable with parameters
$\boldsymbol{X}$
be a binomial random variable with parameters
![]() $N,p$
. Then
$N,p$
. Then
Lemma 1.6 ([Reference Hoeffding, Fisher and Sen21]). For a hypergeometric variable
![]() $\boldsymbol{X}\sim \textrm{Hyp}(L,M,N)$
, the bounds
(1.20)
–
(1.21)
hold with
$\boldsymbol{X}\sim \textrm{Hyp}(L,M,N)$
, the bounds
(1.20)
–
(1.21)
hold with
![]() $p=M/L$
.
$p=M/L$
.
Throughout, we use asymptotic notation
![]() $o(\cdot),\omega (\cdot),O(\cdot),\Omega (\cdot),\Theta (\cdot)$
to refer to limit
$o(\cdot),\omega (\cdot),O(\cdot),\Omega (\cdot),\Theta (\cdot)$
to refer to limit
![]() $n\to \infty$
. It is understood that the constants hidden in, for example, a
$n\to \infty$
. It is understood that the constants hidden in, for example, a
![]() $O(\cdot)$
-term may depend on
$O(\cdot)$
-term may depend on
![]() $\theta, \boldsymbol{p}$
or other parameters and that a
$\theta, \boldsymbol{p}$
or other parameters and that a
![]() $O(\cdot)$
-term may have a positive or a negative sign. To avoid case distinctions, we sometimes take the liberty of calculating with the values
$O(\cdot)$
-term may have a positive or a negative sign. To avoid case distinctions, we sometimes take the liberty of calculating with the values
![]() $\pm \infty$
. The usual conventions
$\pm \infty$
. The usual conventions
![]() $\infty +\infty =\infty \cdot \infty =\infty$
and
$\infty +\infty =\infty \cdot \infty =\infty$
and
![]() $0\cdot \infty =0$
apply. Furthermore, we set
$0\cdot \infty =0$
apply. Furthermore, we set
![]() $\tanh (\pm \infty )=\pm 1$
. Also recall that
$\tanh (\pm \infty )=\pm 1$
. Also recall that
![]() $0\ln 0=0\ln \frac{0}{0}=0$
. Additionally,
$0\ln 0=0\ln \frac{0}{0}=0$
. Additionally,
![]() $\ln 0=-\infty$
and
$\ln 0=-\infty$
and
![]() $\frac{1}{0} = \ln \frac{1}{0}=\infty$
.
$\frac{1}{0} = \ln \frac{1}{0}=\infty$
.
Finally, for two random variables
![]() $\boldsymbol{X},\boldsymbol{Y}$
defined on the same finite probability space
$\boldsymbol{X},\boldsymbol{Y}$
defined on the same finite probability space
![]() $(\Omega, {\mathbb{P}}\left \lbrack{\cdot}\right \rbrack )$
, we write
$(\Omega, {\mathbb{P}}\left \lbrack{\cdot}\right \rbrack )$
, we write
 \begin{align*} I(\boldsymbol{X},\boldsymbol{Y})&=\sum _{\omega, \omega ^{\prime}\in \Omega }{\mathbb{P}}\left \lbrack{\boldsymbol{X}=\omega, \,\boldsymbol{Y}=\omega ^{\prime}}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{X}=\omega, \,\boldsymbol{Y}=\omega ^{\prime}}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{X}=\omega }\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{Y}=\omega ^{\prime}}\right \rbrack } \end{align*}
\begin{align*} I(\boldsymbol{X},\boldsymbol{Y})&=\sum _{\omega, \omega ^{\prime}\in \Omega }{\mathbb{P}}\left \lbrack{\boldsymbol{X}=\omega, \,\boldsymbol{Y}=\omega ^{\prime}}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{X}=\omega, \,\boldsymbol{Y}=\omega ^{\prime}}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{X}=\omega }\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{Y}=\omega ^{\prime}}\right \rbrack } \end{align*}
for the mutual information of
![]() $\boldsymbol{X},\boldsymbol{Y}$
. We recall that
$\boldsymbol{X},\boldsymbol{Y}$
. We recall that
![]() $I(\boldsymbol{X},\boldsymbol{Y})\geq 0$
.
$I(\boldsymbol{X},\boldsymbol{Y})\geq 0$
.
2. Overview
We proceed to survey the functioning of the algorithms SPARC and SPEX. To get started, we briefly discuss the best previously known algorithm for noisy group testing, the DD algorithm from [Reference Gebhard, Johnson, Loick and Rolvien19], which operates on the constant column design. We will discover that DD can be viewed as a truncated version of the BP message passing algorithm. BP is a generic heuristic for inference problems backed by physics intuition [Reference Mézard and Montanari30, Reference Zdeborová and Krzakala42]. Yet unfortunately, BP is notoriously difficult to analyse. Even worse, it seems unlikely that full BP will significantly outperform DD on the constant column design; evidence of this was provided in [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth, Wein and Zadik10] in the noiseless case. The basic issue is the lack of a good initialisation of the BP messages.
To remedy this issue, we resort to the spatially coupled test design
![]() $\mathbf{G}_{\mathrm{sc}}$
, which combines a randomised and a spatial construction. The basic idea resembles domino toppling. Starting from an easy-to-diagnose ‘seed’, the algorithm works its way forward in a well-defined direction until all individuals have been diagnosed. Spatial coupling has proved useful in related inference problems, including noiseless group testing [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9]. Therefore, a natural stab at group testing would be to run BP on
$\mathbf{G}_{\mathrm{sc}}$
, which combines a randomised and a spatial construction. The basic idea resembles domino toppling. Starting from an easy-to-diagnose ‘seed’, the algorithm works its way forward in a well-defined direction until all individuals have been diagnosed. Spatial coupling has proved useful in related inference problems, including noiseless group testing [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9]. Therefore, a natural stab at group testing would be to run BP on
![]() $\mathbf{G}_{\mathrm{sc}}$
. Indeed, the BP intuition provides a key ingredient to the SPARC algorithm, namely, the update equations (see [2.30] below), of which the correct choice of the weights (Eq. [2.29] below) is the most important ingredient. But in light of the difficulty of analysing textbook BP, SPARC relies on a modified version of BP that better lends itself to a rigorous analysis. Furthermore, the SPEX algorithm for exact recovery combines SPARC with a cleanup step.
$\mathbf{G}_{\mathrm{sc}}$
. Indeed, the BP intuition provides a key ingredient to the SPARC algorithm, namely, the update equations (see [2.30] below), of which the correct choice of the weights (Eq. [2.29] below) is the most important ingredient. But in light of the difficulty of analysing textbook BP, SPARC relies on a modified version of BP that better lends itself to a rigorous analysis. Furthermore, the SPEX algorithm for exact recovery combines SPARC with a cleanup step.
SPARC and SPEX can be viewed as generalised versions of the noiseless group testing algorithm called SPIV from [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9]. However, [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9] did not exploit the connection with BP. Instead, in the noiseless case, the correct weights were simply ‘guessed’ based on combinatorial intuition, an approach that it seems difficult to generalise. Hence, the present, systematic derivation of the weights (2.29) also casts new light on the noiseless case. In fact, we expect that the paradigm behind SPARC and SPEX, namely, to use BP heuristically to find the correct parameters for a simplified message passing algorithm, potentially generalises to other inference problems as well.
2.1. The DD algorithm
The noisy DD algorithm is the best previously known efficient algorithm for exact recovery [Reference Gebhard, Johnson, Loick and Rolvien19]. SPEX uses DD as a subroutine for diagnosing a small fraction of individuals. Later, we compare the number of tests needed by SPEX with the one needed by DD. The DD algorithm from [Reference Gebhard, Johnson, Loick and Rolvien19] utilises the constant column design
![]() $\mathbf{G}_{\mathrm{cc}}$
.Thus, each individual independently joins an equal number
$\mathbf{G}_{\mathrm{cc}}$
.Thus, each individual independently joins an equal number
![]() $\Delta$
of random tests. Given the displayed test results, DD first declares certain individuals as uninfected by thresholding the number of negatively displayed tests. More precisely, DD declares as uninfected any individual that appears in at least
$\Delta$
of random tests. Given the displayed test results, DD first declares certain individuals as uninfected by thresholding the number of negatively displayed tests. More precisely, DD declares as uninfected any individual that appears in at least
![]() $\alpha \Delta$
negatively displayed tests, with
$\alpha \Delta$
negatively displayed tests, with
![]() $\alpha$
a diligently chosen threshold. Having identified the respective individuals as uninfected, DD looks out for tests
$\alpha$
a diligently chosen threshold. Having identified the respective individuals as uninfected, DD looks out for tests
![]() $a$
that display a positive result and that only contain a single individual
$a$
that display a positive result and that only contain a single individual
![]() $x$
that has not been identified as uninfected yet. Since such tests
$x$
that has not been identified as uninfected yet. Since such tests
![]() $a$
hint at
$a$
hint at
![]() $x$
being infected, in its second step, DD declares as infected any individual
$x$
being infected, in its second step, DD declares as infected any individual
![]() $x$
that appears in at least
$x$
that appears in at least
![]() $\beta \Delta$
positively displayed tests
$\beta \Delta$
positively displayed tests
![]() $a$
where all other individuals
$a$
where all other individuals
![]() $y\in \partial a\setminus x$
were declared uninfected by the first step. Once again,
$y\in \partial a\setminus x$
were declared uninfected by the first step. Once again,
![]() $\beta$
is a carefully chosen threshold. Finally, DD declares as uninfected all remaining individuals.
$\beta$
is a carefully chosen threshold. Finally, DD declares as uninfected all remaining individuals.
The DD algorithm exactly recovers the infected set w.h.p. provided the total number
![]() $m$
of tests is sufficiently large such that the aforementioned thresholds
$m$
of tests is sufficiently large such that the aforementioned thresholds
![]() $\alpha, \beta$
exist. The required number of tests, which comes out in terms of a mildly delicate optimisation problem, was determined in [Reference Gebhard, Johnson, Loick and Rolvien19]. Let
$\alpha, \beta$
exist. The required number of tests, which comes out in terms of a mildly delicate optimisation problem, was determined in [Reference Gebhard, Johnson, Loick and Rolvien19]. Let
Theorem 2.1 ([Reference Gebhard, Johnson, Loick and Rolvien19, Theorem 2.2]). Let
![]() $\varepsilon \gt 0$
and with
$\varepsilon \gt 0$
and with
![]() $\alpha \in (p_{10},q_0^-)$
and
$\alpha \in (p_{10},q_0^-)$
and
![]() $\beta \in (0,\exp ({-}d)p_{11})$
, let
$\beta \in (0,\exp ({-}d)p_{11})$
, let
 \begin{align*} c_{\mathrm{\texttt{DD}}}&=\min _{\alpha, \beta, d} \max \left \{{c_{\mathrm{\texttt{DD}},1}(\alpha, d),c_{\mathrm{\texttt{DD}},2}(\alpha, d),c_{\mathrm{\texttt{DD}},3}(\beta, d),c_{\mathrm{\texttt{DD}},4}(\alpha, \beta, d)}\right \},\qquad \text{ where}\\ c_{\mathrm{\texttt{DD}},1}(\alpha, d)&=\frac{\theta }{(1-\theta )D_{\mathrm{KL}}\left ({{{\alpha }\|{p_{10}}}}\right )},\qquad c_{\mathrm{\texttt{DD}},2}(\alpha, d)=\frac{1}{dD_{\mathrm{KL}}\left ({{{\alpha }\|{q_0^-}}}\right )},\\ & \qquad c_{\mathrm{\texttt{DD}},3}(\beta, d)=\frac{\theta }{d(1-\theta )D_{\mathrm{KL}}\left ({{{\beta }\|{p_{11}\exp ({-}d)}}}\right )},\\ c_{\mathrm{\texttt{DD}},4}(\alpha, \beta, d) & =\max _{(1-\alpha )\vee \beta \leq z\leq 1}\left (d(1-\theta )\left (D_{\mathrm{KL}}\left ({{{z}\|{q_0^+}}}\right )\right.\right.\\ &\qquad \left.\left. +\unicode{x1D7D9}\left \{{\beta \gt \frac{z\exp ({-}d)p_{01}}{q_0^+}}\right \}zD_{\mathrm{KL}}\left ({{{\beta /z}\|{\exp ({-}d)p_{01}/q_0^+}}}\right )\right )\right )^{-1}. \end{align*}
\begin{align*} c_{\mathrm{\texttt{DD}}}&=\min _{\alpha, \beta, d} \max \left \{{c_{\mathrm{\texttt{DD}},1}(\alpha, d),c_{\mathrm{\texttt{DD}},2}(\alpha, d),c_{\mathrm{\texttt{DD}},3}(\beta, d),c_{\mathrm{\texttt{DD}},4}(\alpha, \beta, d)}\right \},\qquad \text{ where}\\ c_{\mathrm{\texttt{DD}},1}(\alpha, d)&=\frac{\theta }{(1-\theta )D_{\mathrm{KL}}\left ({{{\alpha }\|{p_{10}}}}\right )},\qquad c_{\mathrm{\texttt{DD}},2}(\alpha, d)=\frac{1}{dD_{\mathrm{KL}}\left ({{{\alpha }\|{q_0^-}}}\right )},\\ & \qquad c_{\mathrm{\texttt{DD}},3}(\beta, d)=\frac{\theta }{d(1-\theta )D_{\mathrm{KL}}\left ({{{\beta }\|{p_{11}\exp ({-}d)}}}\right )},\\ c_{\mathrm{\texttt{DD}},4}(\alpha, \beta, d) & =\max _{(1-\alpha )\vee \beta \leq z\leq 1}\left (d(1-\theta )\left (D_{\mathrm{KL}}\left ({{{z}\|{q_0^+}}}\right )\right.\right.\\ &\qquad \left.\left. +\unicode{x1D7D9}\left \{{\beta \gt \frac{z\exp ({-}d)p_{01}}{q_0^+}}\right \}zD_{\mathrm{KL}}\left ({{{\beta /z}\|{\exp ({-}d)p_{01}/q_0^+}}}\right )\right )\right )^{-1}. \end{align*}
If
![]() $m\geq (1+\varepsilon )c_{\mathrm{\texttt{DD}}}k\ln (n/k)$
, then there exists
$m\geq (1+\varepsilon )c_{\mathrm{\texttt{DD}}}k\ln (n/k)$
, then there exists
![]() $\Delta \gt 0$
and
$\Delta \gt 0$
and
![]() $0\leq \alpha, \beta \leq 1$
such that the DD algorithm outputs
$0\leq \alpha, \beta \leq 1$
such that the DD algorithm outputs
![]() $\boldsymbol{\sigma }$
w.h.p.
$\boldsymbol{\sigma }$
w.h.p.
The distinct feature of DD is its simplicity. However, the thresholding that DD applies does seem to leave something on the table. For a start, whether DD identifies a certain individual
![]() $x$
as infected depends only on the results of tests that have a distance of at most three from
$x$
as infected depends only on the results of tests that have a distance of at most three from
![]() $x$
in the graph
$x$
in the graph
![]() $\mathbf{G}_{\mathrm{cc}}$
. Moreover, it seems wasteful that DD takes only those positively displayed tests into consideration where all but one individual were already identified as uninfected.
$\mathbf{G}_{\mathrm{cc}}$
. Moreover, it seems wasteful that DD takes only those positively displayed tests into consideration where all but one individual were already identified as uninfected.
2.2. Belief propagation
BP is a message passing algorithm that is expected to overcome these deficiencies. In fact, heuristic arguments suggest that BP might be the ultimate recovery algorithm for a wide class of inference algorithms on random graphs [Reference Zdeborová and Krzakala42]. That said, rigorous analyses of BP are few and far between.
Following the general framework from [Reference Mézard and Montanari30], in order to apply BP to a group testing design
![]() $G=(V\cup F,E)$
, we equip each test
$G=(V\cup F,E)$
, we equip each test
![]() $a\in F$
with a weight function
$a\in F$
with a weight function
 \begin{align} \psi _a=\psi _{G,\boldsymbol{\sigma }^{\prime\prime},a}&\,:\,\{0,1\}^{\partial a}\to \mathbb{R}_{\geq 0},& \sigma _{\partial a_i}&\mapsto \begin{cases} \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{00}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{10}&\text{ if } a\in F^-\\ \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{01}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{11}&\text{ if } a\in F^+. \end{cases} \end{align}
\begin{align} \psi _a=\psi _{G,\boldsymbol{\sigma }^{\prime\prime},a}&\,:\,\{0,1\}^{\partial a}\to \mathbb{R}_{\geq 0},& \sigma _{\partial a_i}&\mapsto \begin{cases} \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{00}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{10}&\text{ if } a\in F^-\\ \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{01}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{11}&\text{ if } a\in F^+. \end{cases} \end{align}
Thus,
![]() $\psi _a$
takes as argument a
$\psi _a$
takes as argument a
![]() $\{0,1\}$
-vector
$\{0,1\}$
-vector
![]() $\sigma =(\sigma _x)_{x\in \partial a}$
indexed by the individuals that take part in test
$\sigma =(\sigma _x)_{x\in \partial a}$
indexed by the individuals that take part in test
![]() $a$
. The weight
$a$
. The weight
![]() $\psi _a(\sigma )$
equals the probability of observing the result that
$\psi _a(\sigma )$
equals the probability of observing the result that
![]() $a$
displays if the infection status were
$a$
displays if the infection status were
![]() $\sigma _x$
for every individual
$\sigma _x$
for every individual
![]() $x\in \partial a$
. In other words,
$x\in \partial a$
. In other words,
![]() $\psi _a$
encodes the posterior under the
$\psi _a$
encodes the posterior under the
![]() $\boldsymbol{p}$
-channel. Given
$\boldsymbol{p}$
-channel. Given
![]() $G,\boldsymbol{\sigma }^{\prime\prime}$
, the weight functions give rise to the total weight of
$G,\boldsymbol{\sigma }^{\prime\prime}$
, the weight functions give rise to the total weight of
![]() $\sigma \in \{0,1\}^V$
by letting
$\sigma \in \{0,1\}^V$
by letting
Thus, we just multiply up the contributions (2.2) of the various tests and add in the prior assumption that precisely
![]() $k$
individuals are infected. The total weight (2.3) induces a probability distribution
$k$
individuals are infected. The total weight (2.3) induces a probability distribution
A simple application of Bayes’ rule shows that
![]() $\mu _G$
matches the posterior of the ground truth
$\mu _G$
matches the posterior of the ground truth
![]() $\boldsymbol{\sigma }$
given the test results.
$\boldsymbol{\sigma }$
given the test results.
Fact 2.2.
For any test design
![]() $G$
, we have
$G$
, we have
![]() $\mu _{G,\boldsymbol{\sigma }^{\prime\prime}}(\sigma )={\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=\sigma \mid \boldsymbol{\sigma }^{\prime\prime}}\right \rbrack$
.
$\mu _{G,\boldsymbol{\sigma }^{\prime\prime}}(\sigma )={\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=\sigma \mid \boldsymbol{\sigma }^{\prime\prime}}\right \rbrack$
.
BP is a heuristic to calculate the marginals of
![]() $\mu _{G,\boldsymbol{\sigma }^{\prime\prime}}$
or, in light of Fact 2.2, the posterior probabilities
$\mu _{G,\boldsymbol{\sigma }^{\prime\prime}}$
or, in light of Fact 2.2, the posterior probabilities
![]() ${\mathbb{P}}[\boldsymbol{\sigma }_{x_i}=1\mid \boldsymbol{\sigma }^{\prime\prime}]$
. To this end, BP associates messages with the edges of
${\mathbb{P}}[\boldsymbol{\sigma }_{x_i}=1\mid \boldsymbol{\sigma }^{\prime\prime}]$
. To this end, BP associates messages with the edges of
![]() $G$
. Specifically, for any adjacent individual/test pair
$G$
. Specifically, for any adjacent individual/test pair
![]() $x,a$
, there is a message
$x,a$
, there is a message
![]() $\mu _{x\to a,t}(\cdot)$
from
$\mu _{x\to a,t}(\cdot)$
from
![]() $x$
to
$x$
to
![]() $a$
and another one
$a$
and another one
![]() $\mu _{a\to x,t}(\cdot)$
in the reverse direction. The messages are updated in rounds and therefore come with a time parameter
$\mu _{a\to x,t}(\cdot)$
in the reverse direction. The messages are updated in rounds and therefore come with a time parameter
![]() $t\in \mathbb{Z}_{\geq 0}$
. Moreover, being probability distributions on
$t\in \mathbb{Z}_{\geq 0}$
. Moreover, being probability distributions on
![]() $\{0,1\}$
, the messages always satisfy
$\{0,1\}$
, the messages always satisfy
The intended semantics is that
![]() $\mu _{x\to a,t}(1)$
estimates the probability that
$\mu _{x\to a,t}(1)$
estimates the probability that
![]() $x$
is infected given all known information except the result of test
$x$
is infected given all known information except the result of test
![]() $a$
. Analogously,
$a$
. Analogously,
![]() $\mu _{a\to x,t}(1)$
estimates the probability that
$\mu _{a\to x,t}(1)$
estimates the probability that
![]() $x$
is infected if we disregard all other tests
$x$
is infected if we disregard all other tests
![]() $b\in \partial x\setminus \{a\}$
.
$b\in \partial x\setminus \{a\}$
.
This slightly convoluted interpretation of the messages facilitates simple heuristic formulas for computing the messages iteratively. To elaborate, in the absence of a better a priori estimate, at time
![]() $t=0$
, we simply initialise in accordance with the prior, that is,
$t=0$
, we simply initialise in accordance with the prior, that is,
Subsequently, we use the weight function (2.2) to update the messages: inductively for
![]() $t\geq 1$
and
$t\geq 1$
and
![]() $r\in \{0,1\}$
, let
$r\in \{0,1\}$
, let
 \begin{align} \mu _{a\to x,t}(r)&\propto \begin{cases} p_{11}&\text{if }r=1,\,a\in F^+,\\ p_{11}+(p_{01}-p_{11})\prod _{y\in \partial a\setminus \{x\}}\mu _{y\to a,t-1}(0)&\text{if }r=0,\,a\in F^+,\\ p_{10}& \text{ if }r=1,\,a\in F^-,\\ p_{10}+(p_{00}-p_{10})\prod _{y\in \partial a\setminus \{x\}}\mu _{y\to a,t-1}(0)&\text{ if }r=0,\,a\in F^-, \end{cases} \end{align}
\begin{align} \mu _{a\to x,t}(r)&\propto \begin{cases} p_{11}&\text{if }r=1,\,a\in F^+,\\ p_{11}+(p_{01}-p_{11})\prod _{y\in \partial a\setminus \{x\}}\mu _{y\to a,t-1}(0)&\text{if }r=0,\,a\in F^+,\\ p_{10}& \text{ if }r=1,\,a\in F^-,\\ p_{10}+(p_{00}-p_{10})\prod _{y\in \partial a\setminus \{x\}}\mu _{y\to a,t-1}(0)&\text{ if }r=0,\,a\in F^-, \end{cases} \end{align}
 \begin{align} \mu _{x\to a,t}(r)&\propto \left ({\frac{k}{n}}\right )^r\left ({1-\frac{k}{n}}\right )^{1-r}\prod _{b\in \partial x\setminus \{a\}}\mu _{b\to x,t-1}(r). \end{align}
\begin{align} \mu _{x\to a,t}(r)&\propto \left ({\frac{k}{n}}\right )^r\left ({1-\frac{k}{n}}\right )^{1-r}\prod _{b\in \partial x\setminus \{a\}}\mu _{b\to x,t-1}(r). \end{align}
The
![]() $\propto$
-symbol hides the necessary normalisation to ensure that the messages satisfy (2.5). Furthermore, the
$\propto$
-symbol hides the necessary normalisation to ensure that the messages satisfy (2.5). Furthermore, the
![]() $(k/n)^r$
and
$(k/n)^r$
and
![]() $(1-k/n)^{1-r}$
-prefactors in (2.8) encode the prior that precisely
$(1-k/n)^{1-r}$
-prefactors in (2.8) encode the prior that precisely
![]() $k$
individuals are infected. The expressions (2.7)–(2.8) are motivated by the hunch that for most tests
$k$
individuals are infected. The expressions (2.7)–(2.8) are motivated by the hunch that for most tests
![]() $a$
, the values
$a$
, the values
![]() $(\boldsymbol{\sigma }_y)_{y\in \partial a}$
should be stochastically dependent primarily through their joint membership in test
$(\boldsymbol{\sigma }_y)_{y\in \partial a}$
should be stochastically dependent primarily through their joint membership in test
![]() $a$
. An excellent exposition of BP can be found in [Reference Mézard and Montanari30].
$a$
. An excellent exposition of BP can be found in [Reference Mézard and Montanari30].
How do we utilise the BP messages to infer the actual infection status of each individual? The idea is to perform the update (2.7)–(2.8) for a ‘sufficiently large’ number of rounds, say, until an approximate fixed point is reached. The (heuristic) BP estimate of the posterior marginals after
![]() $t$
rounds then reads
$t$
rounds then reads
 \begin{align} \mu _{x,t}(r)&\propto \left ({\frac{k}{n}}\right )^r\left ({1-\frac{k}{n}}\right )^{1-r}\prod _{b\in \partial x}\mu _{b\to x,t-1}(r)&&(r\in \{0,1\}). \end{align}
\begin{align} \mu _{x,t}(r)&\propto \left ({\frac{k}{n}}\right )^r\left ({1-\frac{k}{n}}\right )^{1-r}\prod _{b\in \partial x}\mu _{b\to x,t-1}(r)&&(r\in \{0,1\}). \end{align}
Thus, by comparison to (2.8), we just take the incoming messages from all tests
![]() $b\in \partial x$
into account. In summary, we ‘hope’ that after sufficiently many updates, we have
$b\in \partial x$
into account. In summary, we ‘hope’ that after sufficiently many updates, we have
![]() $\mu _{x,t}(r)\approx{\mathbb{P}}[\boldsymbol{\sigma }_x=r\mid \boldsymbol{\sigma }^{\prime\prime}]$
. We could then, for instance, declare the
$\mu _{x,t}(r)\approx{\mathbb{P}}[\boldsymbol{\sigma }_x=r\mid \boldsymbol{\sigma }^{\prime\prime}]$
. We could then, for instance, declare the
![]() $k$
individuals with the greatest
$k$
individuals with the greatest
![]() $\mu _{x,t}(1)$
infected and everybody else uninfected.
$\mu _{x,t}(1)$
infected and everybody else uninfected.
For later reference, we point out that the BP updates (2.7)–(2.8) and (2.9) can be simplified slightly by passing to log-likelihood ratios. Thus, define
with the initialisation
![]() $\eta _{G,\boldsymbol{\sigma }^{\prime\prime},x\to a,0}=\ln (k/(n-k))\sim (\theta -1)\ln n$
from (2.6). Then (2.7)–(2.9) transform into
$\eta _{G,\boldsymbol{\sigma }^{\prime\prime},x\to a,0}=\ln (k/(n-k))\sim (\theta -1)\ln n$
from (2.6). Then (2.7)–(2.9) transform into
 \begin{align} \eta _{a\to x,t}&=\begin{cases} \ln p_{11}-\ln \left \lbrack{p_{11}+(p_{01}-p_{11})\prod _{y\in \partial a\setminus \{x\}}\frac{1}{2}\left ({1-\tanh \left ({\frac{1}{2}\eta _{y\to a,t-1}}\right )}\right )}\right \rbrack &\text{ if }a\in F^+,\\ \ln p_{10}-\ln \left \lbrack{p_{10}+(p_{00}-p_{10})\prod _{y\in \partial a\setminus \{x\}}\frac{1}{2}\left ({1-\tanh \left ({\frac{1}{2}\eta _{y\to a,t-1}}\right )}\right )}\right \rbrack &\text{ if }a\in F^-,\\ \end{cases} \end{align}
\begin{align} \eta _{a\to x,t}&=\begin{cases} \ln p_{11}-\ln \left \lbrack{p_{11}+(p_{01}-p_{11})\prod _{y\in \partial a\setminus \{x\}}\frac{1}{2}\left ({1-\tanh \left ({\frac{1}{2}\eta _{y\to a,t-1}}\right )}\right )}\right \rbrack &\text{ if }a\in F^+,\\ \ln p_{10}-\ln \left \lbrack{p_{10}+(p_{00}-p_{10})\prod _{y\in \partial a\setminus \{x\}}\frac{1}{2}\left ({1-\tanh \left ({\frac{1}{2}\eta _{y\to a,t-1}}\right )}\right )}\right \rbrack &\text{ if }a\in F^-,\\ \end{cases} \end{align}
In this formulation, BP ultimately diagnoses the
![]() $k$
individuals with the largest
$k$
individuals with the largest
![]() $\eta _{x,t}$
as infected.
$\eta _{x,t}$
as infected.
Under the assumptions of Theorem 2.1, the DD algorithm can be viewed as the special case of BP with
![]() $t=2$
applied to
$t=2$
applied to
![]() $\mathbf{G}_{\mathrm{cc}}$
. Indeed, the analysis of DD evinces that on
$\mathbf{G}_{\mathrm{cc}}$
. Indeed, the analysis of DD evinces that on
![]() $\mathbf{G}_{\mathrm{cc}}$
, the largest
$\mathbf{G}_{\mathrm{cc}}$
, the largest
![]() $k$
BP estimates (2.9) with
$k$
BP estimates (2.9) with
![]() $t\geq 2$
correctly identify the infected individuals w.h.p.Footnote
3
$t\geq 2$
correctly identify the infected individuals w.h.p.Footnote
3
It is therefore an obvious question whether BP on the constant column design fits the bill of Theorem 1.1. Clearly, BP remedies the obvious deficiencies of DD by taking into account information from a larger radius around an individual (if we iterate beyond
![]() $t=2$
). Also in contrast to DD’s hard thresholding, the update rules (2.7)–(2.8) take information into account in a more subtle, soft manner. Nonetheless, we do not expect that BP applied to the constant column design meets the information-theoretically optimal bound from Theorem 1.1. In fact, there is strong evidence that BP does not suffice to meet the information-threshold for all
$t=2$
). Also in contrast to DD’s hard thresholding, the update rules (2.7)–(2.8) take information into account in a more subtle, soft manner. Nonetheless, we do not expect that BP applied to the constant column design meets the information-theoretically optimal bound from Theorem 1.1. In fact, there is strong evidence that BP does not suffice to meet the information-threshold for all
![]() $\theta$
even in the noiseless case [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth, Wein and Zadik10]. The fundamental obstacle appears to be the ‘cold’ initialisation (2.6), which (depending on the parameters) can cause the BP messages to approach a meaningless fixed point. Yet for symmetry reasons on the constant column design, no better starting point than the prior (2.6) springs to mind; after all,
$\theta$
even in the noiseless case [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth, Wein and Zadik10]. The fundamental obstacle appears to be the ‘cold’ initialisation (2.6), which (depending on the parameters) can cause the BP messages to approach a meaningless fixed point. Yet for symmetry reasons on the constant column design, no better starting point than the prior (2.6) springs to mind; after all,
![]() $\mathbf{G}_{\mathrm{cc}}$
is a nearly biregular random graph, and thus, all individuals look alike. To overcome this issue, we will employ a different type of test design that enables a warm start for BP. This technique goes by the name of spatial coupling.
$\mathbf{G}_{\mathrm{cc}}$
is a nearly biregular random graph, and thus, all individuals look alike. To overcome this issue, we will employ a different type of test design that enables a warm start for BP. This technique goes by the name of spatial coupling.
2.3. Spatial coupling
The thrust of spatial coupling is to blend a randomised construction, in our case, the constant column design, with a spatial arrangement so as to provide a propitious starting point for BP. Originally hailing from coding theory, spatial coupling has also been used in previous work on noiseless group testing [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9]. In fact, the construction that we use is essentially identical to that from [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9] (with suitably adapted parameters).
To set up the spatially coupled test design
![]() $\mathbf{G}_{\mathrm{sc}}$
, we divide the set
$\mathbf{G}_{\mathrm{sc}}$
, we divide the set
![]() $V=V_n=\{x_1,\ldots, x_n\}$
of individuals into
$V=V_n=\{x_1,\ldots, x_n\}$
of individuals into
pairwise disjoint compartments
![]() $V[1],\ldots, V[\ell ]\subseteq V$
such that
$V[1],\ldots, V[\ell ]\subseteq V$
such that
![]() $\lfloor n/\ell \rfloor \leq |V[i]|\leq \lceil n/\ell \rceil$
. We think of these compartments as being spatially arranged so that
$\lfloor n/\ell \rfloor \leq |V[i]|\leq \lceil n/\ell \rceil$
. We think of these compartments as being spatially arranged so that
![]() $V[i+1]$
comes ‘to the right’ of
$V[i+1]$
comes ‘to the right’ of
![]() $V[i]$
for
$V[i]$
for
![]() $1\leq i\lt \ell$
. More precisely, we arrange the compartments in a ring topology such that
$1\leq i\lt \ell$
. More precisely, we arrange the compartments in a ring topology such that
![]() $V[\ell ]$
is followed again by
$V[\ell ]$
is followed again by
![]() $V[1]$
. Hence, for notational convenience, let
$V[1]$
. Hence, for notational convenience, let
![]() $V[\ell +j]=V[j]$
and
$V[\ell +j]=V[j]$
and
![]() $V[1-j]=V[\ell -j+1]$
for
$V[1-j]=V[\ell -j+1]$
for
![]() $1\leq j\leq \ell$
. Additionally, we introduce
$1\leq j\leq \ell$
. Additionally, we introduce
![]() $\ell$
compartments
$\ell$
compartments
![]() $F[1],\ldots, F[\ell ]$
of tests arranged in the same way: think of
$F[1],\ldots, F[\ell ]$
of tests arranged in the same way: think of
![]() $F[i]$
as sitting ‘above’
$F[i]$
as sitting ‘above’
![]() $V[i]$
. We assume that the total number
$V[i]$
. We assume that the total number
![]() $m$
of tests in
$m$
of tests in
![]() $F[1]\cup \ldots \cup F[\ell ]$
is divisible by
$F[1]\cup \ldots \cup F[\ell ]$
is divisible by
![]() $\ell$
and satisfies
$\ell$
and satisfies
![]() $m=\Theta (k\ln (n/k))$
. Hence, let each compartment
$m=\Theta (k\ln (n/k))$
. Hence, let each compartment
![]() $F[i]$
contain precisely
$F[i]$
contain precisely
![]() $m/\ell$
tests. As in the case of the individuals, we let
$m/\ell$
tests. As in the case of the individuals, we let
![]() $F[\ell +j]=F[j]$
for
$F[\ell +j]=F[j]$
for
![]() $0\lt j\leq \ell$
. Additionally, let
$0\lt j\leq \ell$
. Additionally, let
be integers such that
![]() $\Delta$
is divisible by
$\Delta$
is divisible by
![]() $s$
. Construct
$s$
. Construct
![]() $\mathbf{G}_{\mathrm{sc}}$
by letting each
$\mathbf{G}_{\mathrm{sc}}$
by letting each
![]() $x\in V[i]$
join precisely
$x\in V[i]$
join precisely
![]() $\Delta /s$
tests from
$\Delta /s$
tests from
![]() $F[i+j-1]$
for
$F[i+j-1]$
for
![]() $j=1,\ldots, s$
. These tests are chosen uniformly without replacement and independently for different
$j=1,\ldots, s$
. These tests are chosen uniformly without replacement and independently for different
![]() $x$
and
$x$
and
![]() $j$
. Additionally,
$j$
. Additionally,
![]() $\mathbf{G}_{\mathrm{sc}}$
contains a compartment
$\mathbf{G}_{\mathrm{sc}}$
contains a compartment
![]() $F[0]$
of
$F[0]$
of
tests. Every individual
![]() $x$
from the first
$x$
from the first
![]() $s$
compartments
$s$
compartments
![]() $V[1],\ldots, V[s]$
joins an equal number
$V[1],\ldots, V[s]$
joins an equal number
![]() $\Delta _0$
of tests from
$\Delta _0$
of tests from
![]() $F[0]$
. These tests are drawn uniformly without replacement and independently. For future reference, we let
$F[0]$
. These tests are drawn uniformly without replacement and independently. For future reference, we let
the aforementioned assumptions on
![]() $m,\Delta$
ensure that
$m,\Delta$
ensure that
![]() $c,d=\Theta (1)$
and the total number of tests of
$c,d=\Theta (1)$
and the total number of tests of
![]() $\mathbf{G}_{\mathrm{sc}}$
comes to
$\mathbf{G}_{\mathrm{sc}}$
comes to
 \begin{align} \sum _{i=0}^{\ell }|F[i]|&=(c+o(1))k\ln (n/k). \end{align}
\begin{align} \sum _{i=0}^{\ell }|F[i]|&=(c+o(1))k\ln (n/k). \end{align}
In summary,
![]() $\mathbf{G}_{\mathrm{sc}}$
consists of
$\mathbf{G}_{\mathrm{sc}}$
consists of
![]() $\ell$
equally sized compartments
$\ell$
equally sized compartments
![]() $V[i]$
,
$V[i]$
,
![]() $F[i]$
of tests plus one extra serving
$F[i]$
of tests plus one extra serving
![]() $F[0]$
of tests. Each individual
$F[0]$
of tests. Each individual
![]() $V[i]$
joins random tests in the
$V[i]$
joins random tests in the
![]() $s$
consecutive compartments
$s$
consecutive compartments
![]() $F[i+j-1]$
with
$F[i+j-1]$
with
![]() $1\leq j\leq s$
. Additionally, the individuals in the first
$1\leq j\leq s$
. Additionally, the individuals in the first
![]() $s$
compartments
$s$
compartments
![]() $V[1]\cup \cdots \cup V[s]$
, which we refer to as the seed, also join the tests in
$V[1]\cup \cdots \cup V[s]$
, which we refer to as the seed, also join the tests in
![]() $F[0]$
.
$F[0]$
.
We will discover momentarily how
![]() $\mathbf{G}_{\mathrm{sc}}$
facilitates inference via BP. But first let us make a note of some basic properties of
$\mathbf{G}_{\mathrm{sc}}$
facilitates inference via BP. But first let us make a note of some basic properties of
![]() $\mathbf{G}_{\mathrm{sc}}$
. Recall that
$\mathbf{G}_{\mathrm{sc}}$
. Recall that
![]() $\boldsymbol{\sigma }\in \{0,1\}^V$
, which encodes the true infection status of each individual, is chosen uniformly and independently of
$\boldsymbol{\sigma }\in \{0,1\}^V$
, which encodes the true infection status of each individual, is chosen uniformly and independently of
![]() $\mathbf{G}_{\mathrm{sc}}$
from all vectors of Hamming weight
$\mathbf{G}_{\mathrm{sc}}$
from all vectors of Hamming weight
![]() $k$
. Let
$k$
. Let
![]() $V_1=\{x\in V\,:\,\boldsymbol{\sigma }_x=1\}$
,
$V_1=\{x\in V\,:\,\boldsymbol{\sigma }_x=1\}$
,
![]() $V_0=V\setminus V_1$
, and let
$V_0=V\setminus V_1$
, and let
![]() $V_r[i]=V_r\cap V[i]$
be the set of individuals with infection status
$V_r[i]=V_r\cap V[i]$
be the set of individuals with infection status
![]() $r\in \{0,1\}$
in compartment
$r\in \{0,1\}$
in compartment
![]() $i$
. Furthermore, recall that
$i$
. Furthermore, recall that
![]() $\boldsymbol{\sigma }^{\prime}_a\in \{0,1\}$
denotes the actual result of test
$\boldsymbol{\sigma }^{\prime}_a\in \{0,1\}$
denotes the actual result of test
![]() $a\in F=F[0]\cup \cdots \cup F[\ell ]$
and that
$a\in F=F[0]\cup \cdots \cup F[\ell ]$
and that
![]() $\boldsymbol{\sigma }^{\prime\prime}_a$
signifies the displayed result of
$\boldsymbol{\sigma }^{\prime\prime}_a$
signifies the displayed result of
![]() $a$
as per (1.2). For
$a$
as per (1.2). For
![]() $r\in \{0,1\}$
and
$r\in \{0,1\}$
and
![]() $0\leq i\leq \ell$
, let
$0\leq i\leq \ell$
, let
Thus, the subscript indicates the actual test result, while the superscript indicates the displayed result. In Section 3.1, we will prove the following.
Proposition 2.3.
The test design
![]() $\mathbf{G}_{\mathrm{sc}}$
enjoys the following properties with probability
$\mathbf{G}_{\mathrm{sc}}$
enjoys the following properties with probability
![]() $1-o(n^{-2})$
.
$1-o(n^{-2})$
.
-
G1 The number of infected individuals in the various compartments satisfies
(2.18) \begin{align} \frac{k}{\ell }-\sqrt{\frac{k}{\ell }}\ln n\leq \min _{i\in [\ell ]}|V_1[i]|\leq \max _{i\in [\ell ]}|V_1[i]|\leq \frac{k}{\ell }+\sqrt{\frac{k}{\ell }}\ln n. \end{align}
\begin{align} \frac{k}{\ell }-\sqrt{\frac{k}{\ell }}\ln n\leq \min _{i\in [\ell ]}|V_1[i]|\leq \max _{i\in [\ell ]}|V_1[i]|\leq \frac{k}{\ell }+\sqrt{\frac{k}{\ell }}\ln n. \end{align}
-
G2 For all
 $i\in [\ell ]$
, the numbers of tests that are actually/displayed positive/negative satisfy (2.19)
$i\in [\ell ]$
, the numbers of tests that are actually/displayed positive/negative satisfy (2.19) \begin{align} \frac{m}{\ell }\exp ({-}d)p_{00}-\sqrt m\ln ^3 n&\leq \left |{F_0^-[i]}\right |\leq \frac{m}{\ell }\exp ({-}d)p_{00}+\sqrt m\ln ^3 n, \end{align}
(2.20)
\begin{align} \frac{m}{\ell }\exp ({-}d)p_{00}-\sqrt m\ln ^3 n&\leq \left |{F_0^-[i]}\right |\leq \frac{m}{\ell }\exp ({-}d)p_{00}+\sqrt m\ln ^3 n, \end{align}
(2.20) \begin{align} \frac{m}{\ell }\exp ({-}d)p_{01}-\sqrt m\ln ^3 n&\leq \left |{F_0^+[i]}\right |\leq \frac{m}{\ell }\exp ({-}d)p_{01}+\sqrt m\ln ^3 n, &\!\!\!\!\!\! \text{comment} \end{align}
(2.21)
\begin{align} \frac{m}{\ell }\exp ({-}d)p_{01}-\sqrt m\ln ^3 n&\leq \left |{F_0^+[i]}\right |\leq \frac{m}{\ell }\exp ({-}d)p_{01}+\sqrt m\ln ^3 n, &\!\!\!\!\!\! \text{comment} \end{align}
(2.21) \begin{align} \frac{m}{\ell }(1-\exp ({-}d))p_{10}-\sqrt m\ln ^3 n&\leq \left |{F_1^-[i]}\right |\leq \frac{m}{\ell }(1-\exp ({-}d))p_{10}+\sqrt m\ln ^3 n, \end{align}
(2.22)
\begin{align} \frac{m}{\ell }(1-\exp ({-}d))p_{10}-\sqrt m\ln ^3 n&\leq \left |{F_1^-[i]}\right |\leq \frac{m}{\ell }(1-\exp ({-}d))p_{10}+\sqrt m\ln ^3 n, \end{align}
(2.22) \begin{align} \frac{m}{\ell }(1-\exp ({-}d))p_{11}-\sqrt m\ln ^3 n&\leq \left |{F_1^+[i]}\right |\leq \frac{m}{\ell }(1-\exp ({-}d))p_{11}+\sqrt m\ln ^3 n. \end{align}
\begin{align} \frac{m}{\ell }(1-\exp ({-}d))p_{11}-\sqrt m\ln ^3 n&\leq \left |{F_1^+[i]}\right |\leq \frac{m}{\ell }(1-\exp ({-}d))p_{11}+\sqrt m\ln ^3 n. \end{align}
2.4. Approximate recovery
We are going to exploit the spatial structure of
![]() $\mathbf{G}_{\mathrm{sc}}$
in a manner reminiscent of domino toppling. To get started, we will run DD on the seed
$\mathbf{G}_{\mathrm{sc}}$
in a manner reminiscent of domino toppling. To get started, we will run DD on the seed
![]() $V[1]\cup \cdots \cup V[s]$
and the tests
$V[1]\cup \cdots \cup V[s]$
and the tests
![]() $F[0]$
only; this is our first domino. The choice (2.15) of
$F[0]$
only; this is our first domino. The choice (2.15) of
![]() $m_0$
ensures that DD diagnoses all individuals in
$m_0$
ensures that DD diagnoses all individuals in
![]() $V[1]\cup \cdots \cup V[s]$
correctly w.h.p. The seed could then be used as an informed starting point from which we could iterate BP to infer the status of the individuals in
$V[1]\cup \cdots \cup V[s]$
correctly w.h.p. The seed could then be used as an informed starting point from which we could iterate BP to infer the status of the individuals in
![]() $V[s+1]\cup \ldots \cup V[\ell ]$
. However, this algorithm appears to be difficult to analyse. Instead, we will show under that the assumptions of Theorem 1.1 a modified, ‘paced’ version of BP that diagnoses one compartment (or ‘domino’) at a time and then re-initialises the messages ultimately classifies all but
$V[s+1]\cup \ldots \cup V[\ell ]$
. However, this algorithm appears to be difficult to analyse. Instead, we will show under that the assumptions of Theorem 1.1 a modified, ‘paced’ version of BP that diagnoses one compartment (or ‘domino’) at a time and then re-initialises the messages ultimately classifies all but
![]() $o(k)$
individuals correctly. Let us flesh this strategy out in detail.
$o(k)$
individuals correctly. Let us flesh this strategy out in detail.
2.4.1. The seed
Recall that each individual
![]() $x\in V[1]\cup \cdots \cup V[s]$
independently joins
$x\in V[1]\cup \cdots \cup V[s]$
independently joins
![]() $\Delta _0$
random tests from
$\Delta _0$
random tests from
![]() $F[0]$
. In the initial step,
$F[0]$
. In the initial step,
![]() $\mathrm{\texttt{SPARC}}$
runs DD on the test design
$\mathrm{\texttt{SPARC}}$
runs DD on the test design
![]() ${\boldsymbol{G}}_0$
comprising
${\boldsymbol{G}}_0$
comprising
![]() $V[1]\cup \cdots \cup V[s]$
and the tests
$V[1]\cup \cdots \cup V[s]$
and the tests
![]() $F[0]$
only. Throughout,
$F[0]$
only. Throughout,
![]() $\mathrm{\texttt{SPARC}}$
maintains a vector
$\mathrm{\texttt{SPARC}}$
maintains a vector
![]() $\tau \in \{0,1,*\}^{V}$
that represents the algorithm’s current estimate of the ground truth
$\tau \in \{0,1,*\}^{V}$
that represents the algorithm’s current estimate of the ground truth
![]() $\boldsymbol{\sigma }$
, with
$\boldsymbol{\sigma }$
, with
![]() $*$
indicating ‘undetermined as yet’.
$*$
indicating ‘undetermined as yet’.
Since Proposition 2.3 shows that the seed contains
![]() $(1+o(1))ks/\ell$
infected individuals w.h.p., the choice (2.15) of
$(1+o(1))ks/\ell$
infected individuals w.h.p., the choice (2.15) of
![]() $m_0$
and Theorem 2.1 imply that DD will succeed to diagnose the seed correctly for a suitable
$m_0$
and Theorem 2.1 imply that DD will succeed to diagnose the seed correctly for a suitable
![]() $\Delta _0$
.
$\Delta _0$
.
Proposition 2.4 ([Reference Gebhard, Johnson, Loick and Rolvien19, Theorem 2.2]). There exists
![]() $\Delta _0=\Theta (\ln n)$
such that the output of DD satisfies
$\Delta _0=\Theta (\ln n)$
such that the output of DD satisfies
![]() $\tau _x=\boldsymbol{\sigma }_x$
for all
$\tau _x=\boldsymbol{\sigma }_x$
for all
![]() $x\in V[1]\cup \cdots \cup V[s]$
w.h.p.
$x\in V[1]\cup \cdots \cup V[s]$
w.h.p.
2.4.2. A combinatorial condition
To simplify the analysis of the message passing step in Section 2.4.3, we observe that certain individuals can be identified as likely uninfected purely on combinatorial grounds. More precisely, consider
![]() $x\in V[i]$
for
$x\in V[i]$
for
![]() $s\lt i\leq \ell$
. If
$s\lt i\leq \ell$
. If
![]() $x$
is infected, then any test
$x$
is infected, then any test
![]() $a\in \partial x$
is actually positive. Hence, we expect that
$a\in \partial x$
is actually positive. Hence, we expect that
![]() $x$
appears in about
$x$
appears in about
![]() $p_{11}\Delta$
tests that display a positive result. In fact, the choice (2.14) of
$p_{11}\Delta$
tests that display a positive result. In fact, the choice (2.14) of
![]() $s$
ensures that w.h.p. even within each separate compartment
$s$
ensures that w.h.p. even within each separate compartment
![]() $F[i+j-1]$
,
$F[i+j-1]$
,
![]() $1\leq j\leq s$
the individual
$1\leq j\leq s$
the individual
![]() $x$
appears in about
$x$
appears in about
![]() $p_{11}\Delta /s$
positively displayed tests. Thus, let
$p_{11}\Delta /s$
positively displayed tests. Thus, let
 \begin{align} V^+[i]&=\left \{{x\in V[i]\,:\,\sum _{j=1}^s\left |{|\partial x\cap F^+[i+j-1]|-\Delta p_{11}/s}\right |\leq \ln ^{4/7}n}\right \}. \end{align}
\begin{align} V^+[i]&=\left \{{x\in V[i]\,:\,\sum _{j=1}^s\left |{|\partial x\cap F^+[i+j-1]|-\Delta p_{11}/s}\right |\leq \ln ^{4/7}n}\right \}. \end{align}
The following proposition confirms that all but
![]() $o(k/s)$
infected individuals
$o(k/s)$
infected individuals
![]() $x\in V[i]$
belong to
$x\in V[i]$
belong to
![]() $V^+[i]$
. Additionally, the proposition determines the approximate size of
$V^+[i]$
. Additionally, the proposition determines the approximate size of
![]() $V^+[i]$
. For notational convenience, we define
$V^+[i]$
. For notational convenience, we define
Recall
![]() $q_0^+$
from (2.1). The proof of the following proposition can be found in Section 3.2.
$q_0^+$
from (2.1). The proof of the following proposition can be found in Section 3.2.
Algorithm 1 SPARC, steps 1–2

Proposition 2.5. W.h.p., we have
 \begin{align} \sum _{i=s+1}^\ell |V_1[i]\setminus V^+[i]|&\leq k\exp ({-}\Omega (\ln ^{1/7}n))&&\text{ and} \end{align}
\begin{align} \sum _{i=s+1}^\ell |V_1[i]\setminus V^+[i]|&\leq k\exp ({-}\Omega (\ln ^{1/7}n))&&\text{ and} \end{align}
2.4.3. Belief propagation redux
The main phase of the SPARC algorithm employs a simplified version of the BP update rules (2.7)–(2.8) to diagnose one compartment
![]() $V[i]$
,
$V[i]$
,
![]() $s\lt i\leq \ell$
, after the other. The textbook way to employ BP would be to diagnose the seed, initialise the BP messages emanating from the seed accordingly, and then run BP updates until the messages converge. However, towards the proof of Theorem 1.1, this way of applying BP seems too complicated to analyse. Instead, SPARC relies on a ‘paced’ version of BP. Rather than updating the messages to convergence from the seed, we perform one round of message updates, then diagnose the next compartment, re-initialise the messages to coincide with the newly diagnosed compartment, and proceed to the next undiagnosed compartment.
$s\lt i\leq \ell$
, after the other. The textbook way to employ BP would be to diagnose the seed, initialise the BP messages emanating from the seed accordingly, and then run BP updates until the messages converge. However, towards the proof of Theorem 1.1, this way of applying BP seems too complicated to analyse. Instead, SPARC relies on a ‘paced’ version of BP. Rather than updating the messages to convergence from the seed, we perform one round of message updates, then diagnose the next compartment, re-initialise the messages to coincide with the newly diagnosed compartment, and proceed to the next undiagnosed compartment.
We work with the log-likelihood versions of the BP messages from (2.10) to (2.12). Suppose we aim to process compartment
![]() $V[i]$
,
$V[i]$
,
![]() $s\lt i\leq \ell$
, having completed
$s\lt i\leq \ell$
, having completed
![]() $V[1],\ldots, V[i-1]$
already. Then for a test
$V[1],\ldots, V[i-1]$
already. Then for a test
![]() $a\in F[i+j-1]$
,
$a\in F[i+j-1]$
,
![]() $j\in [s]$
, and an adjacent variable
$j\in [s]$
, and an adjacent variable
![]() $x\in V[i+j-s]\cup V[i+j-1]$
, we initialise
$x\in V[i+j-s]\cup V[i+j-1]$
, we initialise
 \begin{align} \eta _{x\to a,0}&=\begin{cases} -\infty &\text{ if }\tau _x=0,\\ +\infty &\text{ if }\tau _x=1,\\ \ln (k/(n-k))&\text{ if }\tau _x=*. \end{cases} \end{align}
\begin{align} \eta _{x\to a,0}&=\begin{cases} -\infty &\text{ if }\tau _x=0,\\ +\infty &\text{ if }\tau _x=1,\\ \ln (k/(n-k))&\text{ if }\tau _x=*. \end{cases} \end{align}
The third case above occurs if and only if
![]() $x\in V[i]\cup \cdots \cup V[i+j-1]$
, that is, if
$x\in V[i]\cup \cdots \cup V[i+j-1]$
, that is, if
![]() $x$
belongs to an as yet undiagnosed compartment. For the compartments that have been diagnosed already, we set
$x$
belongs to an as yet undiagnosed compartment. For the compartments that have been diagnosed already, we set
![]() $\eta _{x\to a,0}$
to
$\eta _{x\to a,0}$
to
![]() $\pm \infty$
, depending on whether
$\pm \infty$
, depending on whether
![]() $x$
has been classified as infected or uninfected.
$x$
has been classified as infected or uninfected.
Let us now investigate the ensuing messages
![]() $\eta _{a\to x,1}$
for
$\eta _{a\to x,1}$
for
![]() $x\in V[i]$
and tests
$x\in V[i]$
and tests
![]() $a\in \partial x\cap F[i+j-1]$
. A glimpse at (2.11) reveals that for any test
$a\in \partial x\cap F[i+j-1]$
. A glimpse at (2.11) reveals that for any test
![]() $a$
that contains an individual
$a$
that contains an individual
![]() $y\in V[i+j-s]\cup \cdots \cup V[i-1]$
with
$y\in V[i+j-s]\cup \cdots \cup V[i-1]$
with
![]() $\tau _y=1$
, we have
$\tau _y=1$
, we have
![]() $\eta _{a\to x,1}=0$
. This is because (2.26) ensures that
$\eta _{a\to x,1}=0$
. This is because (2.26) ensures that
![]() $\eta _{y\to a,0}=\infty$
and
$\eta _{y\to a,0}=\infty$
and
![]() $\tanh (\infty )=1$
. Hence, the test
$\tanh (\infty )=1$
. Hence, the test
![]() $a$
contains no further information as to the status of
$a$
contains no further information as to the status of
![]() $x$
. Therefore, we call a test
$x$
. Therefore, we call a test
![]() $a\in F[i+j-1]$
informative towards
$a\in F[i+j-1]$
informative towards
![]() $V[i]$
if
$V[i]$
if
![]() $\tau _y=0$
for all
$\tau _y=0$
for all
![]() $y\in \partial a\cap (V[i+j-s]\cup \cdots \cup V[i-1])$
.
$y\in \partial a\cap (V[i+j-s]\cup \cdots \cup V[i-1])$
.
Let
![]() $\boldsymbol{W}_{i,j}(\tau )$
be the set of all informative
$\boldsymbol{W}_{i,j}(\tau )$
be the set of all informative
![]() $a\in F[i+j-1]$
. Then any
$a\in F[i+j-1]$
. Then any
![]() $a\in \boldsymbol{W}_{i,j}(\tau )$
receives
$a\in \boldsymbol{W}_{i,j}(\tau )$
receives
![]() $\eta _{y\to a,0}=-\infty$
from all individuals
$\eta _{y\to a,0}=-\infty$
from all individuals
![]() $y$
that have been diagnosed already, that is, all
$y$
that have been diagnosed already, that is, all
![]() $y\in V[h]$
with
$y\in V[h]$
with
![]() $i+j-s\leq h\lt i$
. Another glance at the update rule shows that the corresponding terms simply disappear from the product on the r.h.s. of (2.11) because
$i+j-s\leq h\lt i$
. Another glance at the update rule shows that the corresponding terms simply disappear from the product on the r.h.s. of (2.11) because
![]() $\tanh ({-}\infty )=-1$
. Consequently, only the factors corresponding to undiagnosed individuals
$\tanh ({-}\infty )=-1$
. Consequently, only the factors corresponding to undiagnosed individuals
![]() $y\in V[i]\cup \cdots \cup V[i+j-1]$
remain. Hence, with
$y\in V[i]\cup \cdots \cup V[i+j-1]$
remain. Hence, with
![]() $r=\unicode{x1D7D9}\{a\in F^+\}$
, the update rule (2.11) simplifies to
$r=\unicode{x1D7D9}\{a\in F^+\}$
, the update rule (2.11) simplifies to
The only random element in the expression (2.27) is the number
![]() $\left |{\partial a\cap (V[i]\cup \cdots \cup V[i+j-1])}\right |$
of members of test
$\left |{\partial a\cap (V[i]\cup \cdots \cup V[i+j-1])}\right |$
of members of test
![]() $a$
from compartments
$a$
from compartments
![]() $V[i]\cup \cdots \cup V[i+j-1]$
. But by the construction of
$V[i]\cup \cdots \cup V[i+j-1]$
. But by the construction of
![]() $\mathbf{G}_{\mathrm{sc}}$
, this number has a binomial distribution with mean
$\mathbf{G}_{\mathrm{sc}}$
, this number has a binomial distribution with mean
Since the fluctuations of
![]() $\left |{\partial a\cap (V[i]\cup \cdots \cup V[i+j-1])}\right |$
are of smaller order than the mean, we conclude that w.h.p., (2.27) can be well approximated by a deterministic quantity:
$\left |{\partial a\cap (V[i]\cup \cdots \cup V[i+j-1])}\right |$
are of smaller order than the mean, we conclude that w.h.p., (2.27) can be well approximated by a deterministic quantity:
 \begin{align} \eta _{a\to x,1}&=\begin{cases} w_j^++o(1),&\text{ if }a\in F^+,\\ -w_j^-+o(1),&\text{ if }a\in F^- \end{cases},\qquad \text{ where } \end{align}
\begin{align} \eta _{a\to x,1}&=\begin{cases} w_j^++o(1),&\text{ if }a\in F^+,\\ -w_j^-+o(1),&\text{ if }a\in F^- \end{cases},\qquad \text{ where } \end{align}
Note that in the case
![]() $p_{10} = 0$
, the negative test weight
$p_{10} = 0$
, the negative test weight
![]() $W_j^-$
evaluates to
$W_j^-$
evaluates to
![]() $w_j^- = \infty$
, indicating that individual contained in negative test definitely are uninfected. Finally, the messages (2.28) lead to the BP estimate of the posterior marginal of
$w_j^- = \infty$
, indicating that individual contained in negative test definitely are uninfected. Finally, the messages (2.28) lead to the BP estimate of the posterior marginal of
![]() $x$
via (2.12), that is, by summing on all informative tests
$x$
via (2.12), that is, by summing on all informative tests
![]() $a\in \partial x$
. To be precise, letting
$a\in \partial x$
. To be precise, letting
be the positively/negatively displayed informative tests adjacent to
![]() $x$
and setting
$x$
and setting
 \begin{align} \boldsymbol{W}_x^+(\tau )& = \sum _{j=1}^{s} w_j^+\left |{\boldsymbol{W}_{x,j}^+(\tau )}\right |,& \boldsymbol{W}_x^-(\tau )&=\sum _{j=1}^{s}w_j^- \left |{\boldsymbol{W}_{x,j}^-(\tau )}\right |, \end{align}
\begin{align} \boldsymbol{W}_x^+(\tau )& = \sum _{j=1}^{s} w_j^+\left |{\boldsymbol{W}_{x,j}^+(\tau )}\right |,& \boldsymbol{W}_x^-(\tau )&=\sum _{j=1}^{s}w_j^- \left |{\boldsymbol{W}_{x,j}^-(\tau )}\right |, \end{align}
we obtain
One issue with the formula (2.28) is the analysis of the ‘lower order fluctuations’, which come from the random variables
![]() $|\partial a\cap (V^+[i]\cup \cdots \cup V^+[i+s-1])|$
. Of course, one could try to analyse these deviations carefully by resorting to some kind of a normal approximation. But for our purposes, this is unnecessary. It turns out that we may simply use the sum on the r.h.s. of (2.31) to identify which individuals are infected. Specifically, instead of computing the actual BP approximation
$|\partial a\cap (V^+[i]\cup \cdots \cup V^+[i+s-1])|$
. Of course, one could try to analyse these deviations carefully by resorting to some kind of a normal approximation. But for our purposes, this is unnecessary. It turns out that we may simply use the sum on the r.h.s. of (2.31) to identify which individuals are infected. Specifically, instead of computing the actual BP approximation
![]() $\eta _{x,1}$
after one round of updating, we just compare
$\eta _{x,1}$
after one round of updating, we just compare
![]() $\boldsymbol{W}_x^+(\tau )$
and
$\boldsymbol{W}_x^+(\tau )$
and
![]() $\boldsymbol{W}_x^-(\tau )$
with the values that we would expect these random variables to take if
$\boldsymbol{W}_x^-(\tau )$
with the values that we would expect these random variables to take if
![]() $x$
were infected. These conditional expectations work out to be
$x$
were infected. These conditional expectations work out to be
 \begin{align} W^+&=p_{11}\Delta \sum _{j=1}^{s}\exp (d(j-s)/s)w_j^+,& W^-&= \begin{cases} p_{10}\Delta \sum _{j=1}^{s}\exp (d(j-s)/s)w_j^- &\text{ if } p_{10}\gt 0\\ 0 &\text{ otherwise. } \end{cases} \end{align}
\begin{align} W^+&=p_{11}\Delta \sum _{j=1}^{s}\exp (d(j-s)/s)w_j^+,& W^-&= \begin{cases} p_{10}\Delta \sum _{j=1}^{s}\exp (d(j-s)/s)w_j^- &\text{ if } p_{10}\gt 0\\ 0 &\text{ otherwise. } \end{cases} \end{align}
Thus, SPARC will diagnose
![]() $V[i]$
by comparing
$V[i]$
by comparing
![]() $\boldsymbol{W}_x^{\pm }(\tau )$
with
$\boldsymbol{W}_x^{\pm }(\tau )$
with
![]() $W^{\pm }$
. Additionally, SPARC takes into account that infected individuals likely belong to
$W^{\pm }$
. Additionally, SPARC takes into account that infected individuals likely belong to
![]() $V^+[i]$
, as we learned from Proposition 2.5.
$V^+[i]$
, as we learned from Proposition 2.5.
Algorithm 2 SPARC, steps 3–9.

Let
be a term that tends to zero slowly enough to absorb error terms. The following proposition, which we prove in Section 3.3, summarises the analysis of phase 3. Recall from (2.16) that
![]() $c=m/(k\ln (n/k))$
.
$c=m/(k\ln (n/k))$
.
Proposition 2.6.
Assume that for a fixed
![]() $\varepsilon \gt 0$
, we have
$\varepsilon \gt 0$
, we have
Then w.h.p., the output
![]() $\tau$
of SPARC satisfies
$\tau$
of SPARC satisfies
The proof of Proposition 2.6, which can be found in Section 3.3, is the centrepiece of the analysis of SPARC. The proof is based on a large deviations analysis that bounds the number of individuals
![]() $x\in V^+[i]$
whose corresponding sums
$x\in V^+[i]$
whose corresponding sums
![]() $\boldsymbol{W}_x^{\pm }(\tau )$
deviate from their conditional expectations given
$\boldsymbol{W}_x^{\pm }(\tau )$
deviate from their conditional expectations given
![]() $\boldsymbol{\sigma }_x$
. We have all the pieces in place to complete the proof of the first theorem.
$\boldsymbol{\sigma }_x$
. We have all the pieces in place to complete the proof of the first theorem.
2.5. Exact recovery
As we saw in Section 1.3, the threshold
![]() $c_{\mathrm{ex},1}(d,\theta )$
encodes a local stability condition. This condition is intended to ensure that w.h.p., no other ‘solution’
$c_{\mathrm{ex},1}(d,\theta )$
encodes a local stability condition. This condition is intended to ensure that w.h.p., no other ‘solution’
![]() $\sigma \neq \boldsymbol{\sigma }$
with
$\sigma \neq \boldsymbol{\sigma }$
with
![]() $\|\sigma -\boldsymbol{\sigma }\|_1=o(k)$
of a similarly large posterior likelihood exists. In fact, because
$\|\sigma -\boldsymbol{\sigma }\|_1=o(k)$
of a similarly large posterior likelihood exists. In fact, because
![]() $\mathbf{G}_{\mathrm{sc}}$
enjoys fairly good expansion properties, the test results provide sufficient clues for us to home in on
$\mathbf{G}_{\mathrm{sc}}$
enjoys fairly good expansion properties, the test results provide sufficient clues for us to home in on
![]() $\boldsymbol{\sigma }$
once we get close, provided the number of tests is as large as prescribed by Theorem 1.3. Thus, the idea behind exact recovery is to run SPARC first and then apply local corrections to fully recover
$\boldsymbol{\sigma }$
once we get close, provided the number of tests is as large as prescribed by Theorem 1.3. Thus, the idea behind exact recovery is to run SPARC first and then apply local corrections to fully recover
![]() $\boldsymbol{\sigma }$
; a similar strategy was employed in the noiseless case in [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9].
$\boldsymbol{\sigma }$
; a similar strategy was employed in the noiseless case in [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9].
Though this may sound easy and a simple greedy strategy does indeed do the trick in the noiseless case [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9], in the presence of noise, it takes a good bit of care to get the local search step right. Hence, as per (1.11), suppose that
![]() $c,d$
from (2.16) satisfy
$c,d$
from (2.16) satisfy
![]() $c\gt \max \{c_{\mathrm{ex},2}(d),c_{\mathrm{ex},1}(d,\theta )\}+\varepsilon$
. Also suppose that we already ran SPARC to obtain
$c\gt \max \{c_{\mathrm{ex},2}(d),c_{\mathrm{ex},1}(d,\theta )\}+\varepsilon$
. Also suppose that we already ran SPARC to obtain
![]() $\tau \in \{0,1\}^V$
with
$\tau \in \{0,1\}^V$
with
![]() $\|\tau -\boldsymbol{\sigma }\|_1=o(k)$
(as provided by Proposition 2.6). How can we set about learning the status of an individual
$\|\tau -\boldsymbol{\sigma }\|_1=o(k)$
(as provided by Proposition 2.6). How can we set about learning the status of an individual
![]() $x$
with perfect confidence?
$x$
with perfect confidence?
Assume for the sake of argument that
![]() $\tau _y=\boldsymbol{\sigma }_y$
for all
$\tau _y=\boldsymbol{\sigma }_y$
for all
![]() $y$
that share a test
$y$
that share a test
![]() $a\in \partial x$
with
$a\in \partial x$
with
![]() $x$
. If
$x$
. If
![]() $a$
contains another infected individual
$a$
contains another infected individual
![]() $y\neq x$
, then unfortunately, nothing can be learned from
$y\neq x$
, then unfortunately, nothing can be learned from
![]() $a$
about the status of
$a$
about the status of
![]() $x$
. In this case, we call the test
$x$
. In this case, we call the test
![]() $a$
tainted. By contrast, if
$a$
tainted. By contrast, if
![]() $\tau _y=0$
for all
$\tau _y=0$
for all
![]() $y\in \partial a\setminus \{x\}$
, that is, if
$y\in \partial a\setminus \{x\}$
, that is, if
![]() $a$
is untainted, then the displayed result
$a$
is untainted, then the displayed result
![]() $\boldsymbol{\sigma }^{\prime\prime}_a$
hinges on the infection status of
$\boldsymbol{\sigma }^{\prime\prime}_a$
hinges on the infection status of
![]() $x$
itself. Hence, the larger the number of untainted positively displayed
$x$
itself. Hence, the larger the number of untainted positively displayed
![]() $a\in \partial x$
, the likelier
$a\in \partial x$
, the likelier
![]() $x$
is infected. Consequently, to accomplish exact recovery, we are going to threshold the number of untainted positively displayed
$x$
is infected. Consequently, to accomplish exact recovery, we are going to threshold the number of untainted positively displayed
![]() $a\in \partial x$
. But crucially, to obtain an optimal algorithm, we cannot just use a scalar, one-size-fits-all threshold. Instead, we need to carefully choose a threshold function that takes into account the total number of untainted tests
$a\in \partial x$
. But crucially, to obtain an optimal algorithm, we cannot just use a scalar, one-size-fits-all threshold. Instead, we need to carefully choose a threshold function that takes into account the total number of untainted tests
![]() $a\in \partial x$
.
$a\in \partial x$
.
To elaborate, let
be the total number of untainted tests
![]() $a\in \partial x$
; to avoid case distinctions, we omit seed tests
$a\in \partial x$
; to avoid case distinctions, we omit seed tests
![]() $a\in F[0]$
. Routine calculations reveal that
$a\in F[0]$
. Routine calculations reveal that
![]() $\boldsymbol{Y}_x$
is well approximated by a binomial variable with mean
$\boldsymbol{Y}_x$
is well approximated by a binomial variable with mean
![]() $\exp ({-}d)\Delta$
. Therefore, the fluctuations of
$\exp ({-}d)\Delta$
. Therefore, the fluctuations of
![]() $\boldsymbol{Y}_x$
can be estimated via the Chernoff bound. Specifically, the numbers of infected/uninfected individuals with
$\boldsymbol{Y}_x$
can be estimated via the Chernoff bound. Specifically, the numbers of infected/uninfected individuals with
![]() $\boldsymbol{Y}_x=\alpha \Delta$
can be approximated as
$\boldsymbol{Y}_x=\alpha \Delta$
can be approximated as
Consequently, since
![]() $k=\lceil n^\theta \rceil =o(n)$
‘atypical’ values of
$k=\lceil n^\theta \rceil =o(n)$
‘atypical’ values of
![]() $\boldsymbol{Y}_x$
occur more frequently in healthy than in infected individuals. In fact, recalling (1.6), we learn from a brief calculation that for
$\boldsymbol{Y}_x$
occur more frequently in healthy than in infected individuals. In fact, recalling (1.6), we learn from a brief calculation that for
![]() $\alpha \not \in \mathscr{Y}(c,d,\theta )$
not a single
$\alpha \not \in \mathscr{Y}(c,d,\theta )$
not a single
![]() $x\in V_1$
with
$x\in V_1$
with
![]() $\boldsymbol{Y}_x=\alpha \Delta$
exists w.h.p. Hence, if
$\boldsymbol{Y}_x=\alpha \Delta$
exists w.h.p. Hence, if
![]() $\boldsymbol{Y}_x/\Delta \not \in \mathscr{Y}(c,d,\theta )$
, we deduce that
$\boldsymbol{Y}_x/\Delta \not \in \mathscr{Y}(c,d,\theta )$
, we deduce that
![]() $x$
is uninfected.
$x$
is uninfected.
For
![]() $x$
such that
$x$
such that
![]() $\boldsymbol{Y}_x/\Delta \in \mathscr{Y}(c,d,\theta )$
, more care is required. In this case, we need to compare the number
$\boldsymbol{Y}_x/\Delta \in \mathscr{Y}(c,d,\theta )$
, more care is required. In this case, we need to compare the number
of positively displayed untainted tests to the total number
![]() $\boldsymbol{Y}_x$
of untainted tests. Since the test results are put through the
$\boldsymbol{Y}_x$
of untainted tests. Since the test results are put through the
![]() $\boldsymbol{p}$
-channel independently,
$\boldsymbol{p}$
-channel independently,
![]() $\boldsymbol{Z}_x$
is a binomial variable given
$\boldsymbol{Z}_x$
is a binomial variable given
![]() $\boldsymbol{Y}_x$
. The conditional mean of
$\boldsymbol{Y}_x$
. The conditional mean of
![]() $\boldsymbol{Z}_x$
equals
$\boldsymbol{Z}_x$
equals
![]() $p_{11}\boldsymbol{Y}_x$
if
$p_{11}\boldsymbol{Y}_x$
if
![]() $x$
is infected and
$x$
is infected and
![]() $p_{01}\boldsymbol{Y}_x$
otherwise. Therefore, the Chernoff bound shows that
$p_{01}\boldsymbol{Y}_x$
otherwise. Therefore, the Chernoff bound shows that
In light of (2.39), we set up the definition (1.9) of
![]() $c_{\mathrm{ex},1}(d,\theta )$
so that
$c_{\mathrm{ex},1}(d,\theta )$
so that
![]() $\mathfrak z(\cdot)$
can be used as a threshold function to tell infected from uninfected individuals. Indeed, given
$\mathfrak z(\cdot)$
can be used as a threshold function to tell infected from uninfected individuals. Indeed, given
![]() $\boldsymbol{Y}_x,\boldsymbol{Z}_x$
, we should declare
$\boldsymbol{Y}_x,\boldsymbol{Z}_x$
, we should declare
![]() $x$
uninfected if either
$x$
uninfected if either
![]() $\boldsymbol{Y}_x/\Delta \not \in \mathscr{Y}(c,d,\theta )$
or
$\boldsymbol{Y}_x/\Delta \not \in \mathscr{Y}(c,d,\theta )$
or
![]() $\boldsymbol{Z}_x/\boldsymbol{Y}_x\lt \mathfrak z(\boldsymbol{Z}_x/\Delta )$
and infected otherwise; then the choice of
$\boldsymbol{Z}_x/\boldsymbol{Y}_x\lt \mathfrak z(\boldsymbol{Z}_x/\Delta )$
and infected otherwise; then the choice of
![]() $\mathfrak z(\cdot)$
and
$\mathfrak z(\cdot)$
and
![]() $c_{\mathrm{ex}}(\theta )$
would ensure that all individuals get diagnosed correctly w.h.p. Figure 2 displays a characteristic specimen of the function
$c_{\mathrm{ex}}(\theta )$
would ensure that all individuals get diagnosed correctly w.h.p. Figure 2 displays a characteristic specimen of the function
![]() $\mathfrak z(\cdot)$
and the corresponding rate function from (1.9).
$\mathfrak z(\cdot)$
and the corresponding rate function from (1.9).

Figure 2. The threshold function
![]() $\mathfrak z(\cdot)$
(red) on the interval
$\mathfrak z(\cdot)$
(red) on the interval
![]() $\mathscr{Y}(c_{\mathrm{ex},1}(d,\theta ),d,\theta )$
and the resulting large deviations rate
$\mathscr{Y}(c_{\mathrm{ex},1}(d,\theta ),d,\theta )$
and the resulting large deviations rate
![]() $c_{\mathrm{ex},1}(d,\theta )d(1-\theta )({D_{\mathrm{KL}}({{{\alpha }\|{\exp ({-}d)}}})+\alpha D_{\mathrm{KL}}({{{\mathfrak z(\alpha )}\|{p_{01}}}})})$
(black) with
$c_{\mathrm{ex},1}(d,\theta )d(1-\theta )({D_{\mathrm{KL}}({{{\alpha }\|{\exp ({-}d)}}})+\alpha D_{\mathrm{KL}}({{{\mathfrak z(\alpha )}\|{p_{01}}}})})$
(black) with
![]() $\theta =1/2$
,
$\theta =1/2$
,
![]() $p_{00}=0.972$
,
$p_{00}=0.972$
,
![]() $p_{11}=0.9$
at the optimal choice of
$p_{11}=0.9$
at the optimal choice of
![]() $d$
.
$d$
.
Yet trying to distil an algorithm from these considerations, we run into two obvious obstacles. First, the threshold
![]() $\mathfrak z(\cdot)$
may be hard to compute precisely. Similarly, the limits of the interval
$\mathfrak z(\cdot)$
may be hard to compute precisely. Similarly, the limits of the interval
![]() $\mathscr{Y}(c,d,\theta )$
may be irrational (or worse). The following proposition, which we prove in Section 4.1, remedies these issues.
$\mathscr{Y}(c,d,\theta )$
may be irrational (or worse). The following proposition, which we prove in Section 4.1, remedies these issues.
Proposition 2.7.
Let
![]() $\varepsilon \gt 0$
and assume that
$\varepsilon \gt 0$
and assume that
![]() $c\gt c_{\mathrm{ex}}(d,\theta )+\varepsilon$
. Then there exist
$c\gt c_{\mathrm{ex}}(d,\theta )+\varepsilon$
. Then there exist
![]() $\delta \gt 0$
and an open interval
$\delta \gt 0$
and an open interval
![]() $\emptyset \neq \mathscr{I}=(l,r)\subseteq [\delta, 1-\delta ]$
with endpoints
$\emptyset \neq \mathscr{I}=(l,r)\subseteq [\delta, 1-\delta ]$
with endpoints
![]() $l,r\in \mathbb{Q}$
such that for any
$l,r\in \mathbb{Q}$
such that for any
![]() $\varepsilon ^{\prime}\gt 0$
, there exist
$\varepsilon ^{\prime}\gt 0$
, there exist
![]() $\delta ^{\prime}\gt 0$
and a step function
$\delta ^{\prime}\gt 0$
and a step function
![]() $\mathscr{Z}\,:\,\mathscr{I}\to (p_{01},p_{11})\cap \mathbb{Q}$
such that the following conditions are satisfied.
$\mathscr{Z}\,:\,\mathscr{I}\to (p_{01},p_{11})\cap \mathbb{Q}$
such that the following conditions are satisfied.
-
Z1:
 $cd(1-\theta )D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )\gt \theta +\delta$
for all
$cd(1-\theta )D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )\gt \theta +\delta$
for all
 $y\in (0,1)\setminus (l+\delta, r-\delta )$
.
$y\in (0,1)\setminus (l+\delta, r-\delta )$
. -
Z2:
 $cd(1-\theta )\left ({D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{11}}}}\right )}\right )\gt \theta +\delta$
for all
$cd(1-\theta )\left ({D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{11}}}}\right )}\right )\gt \theta +\delta$
for all
 $y\in \mathscr{I}$
.
$y\in \mathscr{I}$
. -
Z3:
 $cd(1-\theta )\left ({D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{01}}}}\right )}\right )\gt 1+\delta$
for all
$cd(1-\theta )\left ({D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{01}}}}\right )}\right )\gt 1+\delta$
for all
 $y\in \mathscr{I}$
.
$y\in \mathscr{I}$
. -
Z4: If
 $y,y^{\prime}\in \mathscr{I}$
satisfy
$y,y^{\prime}\in \mathscr{I}$
satisfy
 $|y-y^{\prime}|\lt \delta ^{\prime}$
, then
$|y-y^{\prime}|\lt \delta ^{\prime}$
, then
 $|\mathscr{Z}(y)-\mathscr{Z}(y^{\prime})|\lt \varepsilon ^{\prime}$
.
$|\mathscr{Z}(y)-\mathscr{Z}(y^{\prime})|\lt \varepsilon ^{\prime}$
.
The second obstacle is that in the above discussion, we assumed that
![]() $\tau _y=\boldsymbol{\sigma }_y$
for all
$\tau _y=\boldsymbol{\sigma }_y$
for all
![]() $y\in \partial a\setminus \{x\}$
. But all that the analysis of SPARC provides is that w.h.p.
$y\in \partial a\setminus \{x\}$
. But all that the analysis of SPARC provides is that w.h.p.
![]() $\tau _y\neq \boldsymbol{\sigma }_y$
for at most
$\tau _y\neq \boldsymbol{\sigma }_y$
for at most
![]() $o(k)$
individuals
$o(k)$
individuals
![]() $y$
. To cope with this issue, we resort to the expansion properties of
$y$
. To cope with this issue, we resort to the expansion properties of
![]() $\mathbf{G}_{\mathrm{sc}}$
. Roughly speaking, we show that w.h.p. for any small set
$\mathbf{G}_{\mathrm{sc}}$
. Roughly speaking, we show that w.h.p. for any small set
![]() $S$
of individuals (such as
$S$
of individuals (such as
![]() $\{y\,:\,\tau _y\neq \boldsymbol{\sigma }_y\}$
), the set of individuals
$\{y\,:\,\tau _y\neq \boldsymbol{\sigma }_y\}$
), the set of individuals
![]() $x$
that occur in ‘many’ tests that also contain a second individual from
$x$
that occur in ‘many’ tests that also contain a second individual from
![]() $S$
is significantly smaller than
$S$
is significantly smaller than
![]() $S$
. As a consequence, as we apply the thresholding procedure repeatedly, the number of misclassified individuals decays geometrically. We thus arrive at the following algorithm.
$S$
. As a consequence, as we apply the thresholding procedure repeatedly, the number of misclassified individuals decays geometrically. We thus arrive at the following algorithm.
Algorithm 3 The SPEX algorithm.

Proposition 2.8.
Suppose that
![]() $c\gt c_{\mathrm{ex}}(d,\theta )+\varepsilon$
for a fixed
$c\gt c_{\mathrm{ex}}(d,\theta )+\varepsilon$
for a fixed
![]() $\varepsilon \gt 0$
. There exists
$\varepsilon \gt 0$
. There exists
![]() $\varepsilon ^{\prime}\gt 0$
, a rational interval
$\varepsilon ^{\prime}\gt 0$
, a rational interval
![]() $\mathscr{I}$
and a rational step function
$\mathscr{I}$
and a rational step function
![]() $\mathscr{Z}$
such that w.h.p. for all
$\mathscr{Z}$
such that w.h.p. for all
![]() $1\leq i\lt \ln n$
, we have
$1\leq i\lt \ln n$
, we have
We prove Proposition 2.8 in Section 4.2.
Proof of Theorem
1.3
(upper bound on exact recovery by SPEX). Since Proposition 2.8 shows that the number of misclassified individuals decreases geometrically as we iterate Steps 3–5 of SPEX, we have
![]() $\tau ^{(\lceil \ln n\rceil )}=\boldsymbol{\sigma }$
w.h.p. Furthermore, thanks to Theorem 1.1 and Proposition 2.7, SPEX is indeed a polynomial time algorithm.
$\tau ^{(\lceil \ln n\rceil )}=\boldsymbol{\sigma }$
w.h.p. Furthermore, thanks to Theorem 1.1 and Proposition 2.7, SPEX is indeed a polynomial time algorithm.
Remark 2.9. In the noiseless case
![]() $p_{00}=p_{11}=1$
, Theorem 1.3 reproduces the analysis of the SPIV algorithm from [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9]. One key difference between SPARC and SPEX on the one hand and SPIV on the other is that the former are based on BP, while the latter relies on combinatorial intuition. More precisely, the SPIV algorithm infers from positive tests by means of a weighted sum identical to
$p_{00}=p_{11}=1$
, Theorem 1.3 reproduces the analysis of the SPIV algorithm from [Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9]. One key difference between SPARC and SPEX on the one hand and SPIV on the other is that the former are based on BP, while the latter relies on combinatorial intuition. More precisely, the SPIV algorithm infers from positive tests by means of a weighted sum identical to
![]() $\boldsymbol{W}_x^+(\tau )$
from (2.30) with the special values
$\boldsymbol{W}_x^+(\tau )$
from (2.30) with the special values
![]() $p_{00}=p_{11}=1$
and
$p_{00}=p_{11}=1$
and
![]() $d=\ln 2$
. In the noiseless case, the weights
$d=\ln 2$
. In the noiseless case, the weights
![]() $w_j^+$
were ‘guessed’ based on combinatorial intuition. Furthermore, in noiseless case, we can be certain that any individual contained in a negative test is healthy, and therefore, the SPIV algorithm only takes negative tests into account in this simple, deterministic manner. By contrast, in the noisy case, the negative tests give rise to a second weighted sum
$w_j^+$
were ‘guessed’ based on combinatorial intuition. Furthermore, in noiseless case, we can be certain that any individual contained in a negative test is healthy, and therefore, the SPIV algorithm only takes negative tests into account in this simple, deterministic manner. By contrast, in the noisy case, the negative tests give rise to a second weighted sum
![]() $\boldsymbol{W}^-_x(\tau )$
. An important novelty is that rather than ‘guessing’ the weights
$\boldsymbol{W}^-_x(\tau )$
. An important novelty is that rather than ‘guessing’ the weights
![]() $w_j^{\pm }$
, here we discovered how they can be derived systematically from the BP formalism. Apart from shedding new light on the noiseless case as well, we expect that this type of approach can be generalised to other inference problems as well. A second novelty in the design of SPEX is the use of the threshold function
$w_j^{\pm }$
, here we discovered how they can be derived systematically from the BP formalism. Apart from shedding new light on the noiseless case as well, we expect that this type of approach can be generalised to other inference problems as well. A second novelty in the design of SPEX is the use of the threshold function
![]() $\mathscr{Z}(\cdot)$
that depends on the number untainted tests. The need for such a threshold function is encoded in the optimisation problem (1.9) that gives rise to a nontrivial choice of the coefficient
$\mathscr{Z}(\cdot)$
that depends on the number untainted tests. The need for such a threshold function is encoded in the optimisation problem (1.9) that gives rise to a nontrivial choice of the coefficient
![]() $d$
that governs the size of the tests. This type of optimisation is unnecessary in the noiseless case, where simply
$d$
that governs the size of the tests. This type of optimisation is unnecessary in the noiseless case, where simply
![]() $d=\ln 2$
is the optimal choice for all
$d=\ln 2$
is the optimal choice for all
![]() $\theta \in (0,1)$
.
$\theta \in (0,1)$
.
2.6. The constant column lower bound
Having completed the discussion of the algorithms SPARC and SPEX for Theorems 1.1 and 1.3, we turn to the proof of Theorem 1.4 on the information-theoretic lower bound for the constant column design. The goal is to show that for
![]() $m\lt (c_{\mathrm{ex}}(\theta )-\varepsilon )k\ln (n/k)$
, no algorithm, efficient or otherwise, can exactly recover
$m\lt (c_{\mathrm{ex}}(\theta )-\varepsilon )k\ln (n/k)$
, no algorithm, efficient or otherwise, can exactly recover
![]() $\boldsymbol{\sigma }$
on
$\boldsymbol{\sigma }$
on
![]() $\mathbf{G}_{\mathrm{cc}}$
.
$\mathbf{G}_{\mathrm{cc}}$
.
To this end, we are going to estimate the probability of the actual ground truth
![]() $\boldsymbol{\sigma }$
under the posterior given the test results. We recall from Fact 2.2 that the posterior coincides with the Boltzmann distribution from (2.4). The following proposition, whose proof can be found in Section 5.1, estimates the Boltzmann weight
$\boldsymbol{\sigma }$
under the posterior given the test results. We recall from Fact 2.2 that the posterior coincides with the Boltzmann distribution from (2.4). The following proposition, whose proof can be found in Section 5.1, estimates the Boltzmann weight
![]() $\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}(\boldsymbol{\sigma })$
of the ground truth. Recall from (2.16) that
$\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}(\boldsymbol{\sigma })$
of the ground truth. Recall from (2.16) that
![]() $d=k\Delta /m$
. Also recall the weight function from (2.3).
$d=k\Delta /m$
. Also recall the weight function from (2.3).
Proposition 2.10.
W.h.p., the weight of
![]() $\boldsymbol{\sigma }$
satisfies
$\boldsymbol{\sigma }$
satisfies
We are now going to argue that for
![]() $c\lt c_{\mathrm{ex}}(\theta )$
the partition function
$c\lt c_{\mathrm{ex}}(\theta )$
the partition function
![]() $Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
dwarfs the Boltzmann weight (2.40) w.h.p. The definition (1.11) of
$Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
dwarfs the Boltzmann weight (2.40) w.h.p. The definition (1.11) of
![]() $c_{\mathrm{ex}}(\theta )$
suggests that there are two possible ways how this may come about. The first occurs when
$c_{\mathrm{ex}}(\theta )$
suggests that there are two possible ways how this may come about. The first occurs when
![]() $c=m/(k\ln (n/k))$
is smaller than the local stability bound
$c=m/(k\ln (n/k))$
is smaller than the local stability bound
![]() $c_{\mathrm{ex},1}(d,\theta )$
from (1.9). In this case, we will essentially put the analysis of SPEX into reverse gear. That is, we will show that there are plenty of individuals
$c_{\mathrm{ex},1}(d,\theta )$
from (1.9). In this case, we will essentially put the analysis of SPEX into reverse gear. That is, we will show that there are plenty of individuals
![]() $x$
whose status could be flipped from infected to healthy or vice versa without reducing the posterior likelihood. In effect, the partition function will be far greater than the Boltzmann weight of
$x$
whose status could be flipped from infected to healthy or vice versa without reducing the posterior likelihood. In effect, the partition function will be far greater than the Boltzmann weight of
![]() $\boldsymbol{\sigma }$
.
$\boldsymbol{\sigma }$
.
Proposition 2.11.
Assume that there exists
![]() $y\in \mathscr{Y}(c,d,\theta )$
such that there exists
$y\in \mathscr{Y}(c,d,\theta )$
such that there exists
![]() $z\in (p_{01},p_{11})$
such that
$z\in (p_{01},p_{11})$
such that
Then w.h.p., there exist
![]() $n^{\Omega (1)}$
pairs
$n^{\Omega (1)}$
pairs
![]() $(v,w)\in V_1\times V_0$
such that for the configuration
$(v,w)\in V_1\times V_0$
such that for the configuration
![]() $\boldsymbol{\sigma }^{[v,w]}$
obtained from
$\boldsymbol{\sigma }^{[v,w]}$
obtained from
![]() $\boldsymbol{\sigma }$
by inverting the
$\boldsymbol{\sigma }$
by inverting the
![]() $v,w$
-entries, we have
$v,w$
-entries, we have
We prove Proposition 2.11 in Section 5.2.
The second case is that
![]() $c$
is smaller than the entropy bound
$c$
is smaller than the entropy bound
![]() $c_{\mathrm{ex},2}(d)$
from (1.10). In this case, we will show by way of a moment computation that
$c_{\mathrm{ex},2}(d)$
from (1.10). In this case, we will show by way of a moment computation that
![]() $Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
exceeds the Boltzmann weight of
$Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
exceeds the Boltzmann weight of
![]() $\boldsymbol{\sigma }$
w.h.p. More precisely, in Section 5.3, we prove the following.
$\boldsymbol{\sigma }$
w.h.p. More precisely, in Section 5.3, we prove the following.
Proposition 2.12.
Let
![]() $\varepsilon \gt 0$
. If
$\varepsilon \gt 0$
. If
![]() $c\lt c_{\mathrm{ex},2}(d)-\varepsilon$
, then
$c\lt c_{\mathrm{ex},2}(d)-\varepsilon$
, then
Proof of Theorem
1.4
(lower bound on exact recovery on Gcc). Proposition 2.11 readily implies that
![]() $\mu _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}(\boldsymbol{\sigma })=o(1)$
w.h.p. if
$\mu _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}(\boldsymbol{\sigma })=o(1)$
w.h.p. if
![]() $c\lt c_{\mathrm{ex},1}(d,\theta )$
. Furthermore, in the case
$c\lt c_{\mathrm{ex},1}(d,\theta )$
. Furthermore, in the case
![]() $c\lt c_{\mathrm{ex},2}(d)$
, the assertion follows from Propositions 2.10 and 2.12.
$c\lt c_{\mathrm{ex},2}(d)$
, the assertion follows from Propositions 2.10 and 2.12.
3. Analysis of the approximate recovery algorithm
In this section, we carry out the proofs of the various propositions leading up to the proof of Theorem 1.1 (Propositions 2.3, 2.5, and 2.6).
Proposition 2.3 contains some basic properties about
![]() $\mathbf{G}_{\mathrm{sc}}$
that we need further on. Further Proposition 2.5 justifies to only consider
$\mathbf{G}_{\mathrm{sc}}$
that we need further on. Further Proposition 2.5 justifies to only consider
![]() $V^+$
in the main step of SPARC. The most important part of the analysis is contained in the proof of Proposition 2.6 that shows the correctness for the main step of SPARC. Here we consider three different sets of possibly misclassified individuals (Lemmas 3.1, 3.2, and 3.3) that we analyse separately to show that the in total the number of misclassified individuals is small.
$V^+$
in the main step of SPARC. The most important part of the analysis is contained in the proof of Proposition 2.6 that shows the correctness for the main step of SPARC. Here we consider three different sets of possibly misclassified individuals (Lemmas 3.1, 3.2, and 3.3) that we analyse separately to show that the in total the number of misclassified individuals is small.
Throughout, we work with the spatially coupled test design
![]() $\mathbf{G}_{\mathrm{sc}}$
from Section 2.3. Hence, we keep the notation and assumptions from (2.13) to (2.17). We also make a note of the fact that for any
$\mathbf{G}_{\mathrm{sc}}$
from Section 2.3. Hence, we keep the notation and assumptions from (2.13) to (2.17). We also make a note of the fact that for any
![]() $x\in V[i]$
and any
$x\in V[i]$
and any
![]() $a\in F[i+j-1]$
,
$a\in F[i+j-1]$
,
![]() $j=1,\ldots, s$
,
$j=1,\ldots, s$
,
 \begin{align} {\mathbb{P}}\left \lbrack{x\in \partial a}\right \rbrack &=1-{\mathbb{P}}\left \lbrack{x\not \in \partial a}\right \rbrack =1-\binom{|F[i+j-1]|-1}{\Delta /s}\binom{|F[i+j-1]|}{\Delta /s}^{-1}=\frac{\Delta \ell }{ms}+O\left ({\left ({\frac{\Delta \ell }{ms}}\right )^2}\right ); \end{align}
\begin{align} {\mathbb{P}}\left \lbrack{x\in \partial a}\right \rbrack &=1-{\mathbb{P}}\left \lbrack{x\not \in \partial a}\right \rbrack =1-\binom{|F[i+j-1]|-1}{\Delta /s}\binom{|F[i+j-1]|}{\Delta /s}^{-1}=\frac{\Delta \ell }{ms}+O\left ({\left ({\frac{\Delta \ell }{ms}}\right )^2}\right ); \end{align}
this is because the construction of
![]() $\mathbf{G}_{\mathrm{sc}}$
ensures that
$\mathbf{G}_{\mathrm{sc}}$
ensures that
![]() $x$
joins
$x$
joins
![]() $\Delta /s$
random tests in each of
$\Delta /s$
random tests in each of
![]() $F[i+j-1]$
, drawn uniformly without replacement.
$F[i+j-1]$
, drawn uniformly without replacement.
3.1. Proof of Proposition 2.3 (properties of
 $\mathbf{G}_{\mathrm{sc}}$
)
$\mathbf{G}_{\mathrm{sc}}$
)
Property G1 is a routine consequence of the Chernoff bound and was previously established as part of (Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9, Proposition 4.1). With respect to G2, we may condition on the event
![]() $\mathfrak{E}$
that the bound (2.18) from G1 is satisfied. Consider a test
$\mathfrak{E}$
that the bound (2.18) from G1 is satisfied. Consider a test
![]() $a\in F[i]$
. Recall that
$a\in F[i]$
. Recall that
![]() $a$
comprises individuals from the compartments
$a$
comprises individuals from the compartments
![]() $V[i-s+1],\ldots, V[i]$
. Since the probability that a specific individual joins a specific test is given by (3.1) and since individuals choose the tests that they join independently, on
$V[i-s+1],\ldots, V[i]$
. Since the probability that a specific individual joins a specific test is given by (3.1) and since individuals choose the tests that they join independently, on
![]() $\mathfrak{E}$
for each
$\mathfrak{E}$
for each
![]() $i-s+1\leq h\leq i$
, we have
$i-s+1\leq h\leq i$
, we have
 \begin{align} |V_1[h]\cap \partial a|\sim \textrm{Bin}\left ({\frac{k}{\ell }+O\left ({\sqrt{\frac{k}{\ell }}\ln n}\right ),\frac{\Delta \ell }{ms}+O\left ({\left ({\frac{\Delta \ell }{m s}}\right )^2}\right )}\right ). \end{align}
\begin{align} |V_1[h]\cap \partial a|\sim \textrm{Bin}\left ({\frac{k}{\ell }+O\left ({\sqrt{\frac{k}{\ell }}\ln n}\right ),\frac{\Delta \ell }{ms}+O\left ({\left ({\frac{\Delta \ell }{m s}}\right )^2}\right )}\right ). \end{align}
Combining (2.16) and (3.2), we obtain
 \begin{align} \mathbb{E}[|V_1[h]\cap \partial a|\mid \mathfrak{E}]&=\frac{\Delta k}{ms}+O\left ({\sqrt{\frac{\ell }{k}}\ln n}\right )=\frac{d}{s}+O\left ({k^{-1/2}\ln ^{3/2}n}\right ). \end{align}
\begin{align} \mathbb{E}[|V_1[h]\cap \partial a|\mid \mathfrak{E}]&=\frac{\Delta k}{ms}+O\left ({\sqrt{\frac{\ell }{k}}\ln n}\right )=\frac{d}{s}+O\left ({k^{-1/2}\ln ^{3/2}n}\right ). \end{align}
Further, combining (3.2) and (3.3), we get
 \begin{align*}{\mathbb{P}}\left \lbrack{V_1[h]\cap \partial a =\emptyset \mid \mathfrak{E}}\right \rbrack &=\exp \left \lbrack{\left ({\frac{k}{\ell }+O\left ({\sqrt{\frac{k}{\ell }}\ln n}\right )}\right )\ln \left ({1-\frac{\Delta \ell }{ms}+O\left ({\left ({\frac{\Delta \ell }{m s}}\right )^2}\right )}\right )}\right \rbrack\\& =\exp \left ({-\frac{d}{s}+O\left ({k^{-1/2}\ln ^{3/2}n}\right )}\right ). \end{align*}
\begin{align*}{\mathbb{P}}\left \lbrack{V_1[h]\cap \partial a =\emptyset \mid \mathfrak{E}}\right \rbrack &=\exp \left \lbrack{\left ({\frac{k}{\ell }+O\left ({\sqrt{\frac{k}{\ell }}\ln n}\right )}\right )\ln \left ({1-\frac{\Delta \ell }{ms}+O\left ({\left ({\frac{\Delta \ell }{m s}}\right )^2}\right )}\right )}\right \rbrack\\& =\exp \left ({-\frac{d}{s}+O\left ({k^{-1/2}\ln ^{3/2}n}\right )}\right ). \end{align*}
Multiplying these probabilities up on
![]() $i-s+1\leq h\leq i$
, we arrive at the estimate
$i-s+1\leq h\leq i$
, we arrive at the estimate
Hence,
To establish concentration, observe that the set
![]() $\partial x$
of tests that a specific infected individual
$\partial x$
of tests that a specific infected individual
![]() $x\in V_1[h]$
joins can change
$x\in V_1[h]$
joins can change
![]() $|F_0[i]|$
by
$|F_0[i]|$
by
![]() $\Delta$
at the most. Moreover, changing the neighbourhood
$\Delta$
at the most. Moreover, changing the neighbourhood
![]() $\partial x$
of a healthy individual cannot change the actual test results at all. Therefore, by Azuma–Hoeffding,
$\partial x$
of a healthy individual cannot change the actual test results at all. Therefore, by Azuma–Hoeffding,
 \begin{align} {\mathbb{P}}\left \lbrack{\left |{|F_0[i]|-\mathbb{E}\left \lbrack{|F_0[i]| \mid{\mathscr{E}}}\right \rbrack }\right |\geq \sqrt m\ln ^2n \mid{\mathscr{E}}}\right \rbrack &\leq 2\exp \left ({-\frac{m\ln ^4n}{2k\Delta ^2}}\right )=o(n^{-3}). \end{align}
\begin{align} {\mathbb{P}}\left \lbrack{\left |{|F_0[i]|-\mathbb{E}\left \lbrack{|F_0[i]| \mid{\mathscr{E}}}\right \rbrack }\right |\geq \sqrt m\ln ^2n \mid{\mathscr{E}}}\right \rbrack &\leq 2\exp \left ({-\frac{m\ln ^4n}{2k\Delta ^2}}\right )=o(n^{-3}). \end{align}
Thus, (3.4), (3.5), and G1 show that with probability
![]() $1-o(n^{-2})$
for all
$1-o(n^{-2})$
for all
![]() $1\leq i\leq \ell$
, we have
$1\leq i\leq \ell$
, we have
Since the actual test results are subjected to the
![]() $\boldsymbol{p}$
-channel independently to obtain the displayed test results, the distributions of
$\boldsymbol{p}$
-channel independently to obtain the displayed test results, the distributions of
![]() $|F_{0/1}^{\pm }[i]$
given
$|F_{0/1}^{\pm }[i]$
given
![]() $F_{0/1}[i]$
read
$F_{0/1}[i]$
read
Thus, G2 follows from (3.6), (3.7), and Lemma 1.5 (the Chernoff bound).
3.2. Proof of Proposition 2.5 (plausible number of positive tests)
Any
![]() $x\in V_1[i]$
has a total of
$x\in V_1[i]$
has a total of
![]() $\Delta /s$
neighbours in each of
$\Delta /s$
neighbours in each of
![]() $F[i],\ldots, F[i+s-1]$
. Moreover, all tests
$F[i],\ldots, F[i+s-1]$
. Moreover, all tests
![]() $a\in \partial x$
are actually positive. Since the displayed result is obtained via the
$a\in \partial x$
are actually positive. Since the displayed result is obtained via the
![]() $\boldsymbol{p}$
-channel independently for every
$\boldsymbol{p}$
-channel independently for every
![]() $a$
, the number of displayed positive neighbours
$a$
, the number of displayed positive neighbours
![]() $|\partial x\cap F^+[i+j-1]|$
is a binomial variable with distribution
$|\partial x\cap F^+[i+j-1]|$
is a binomial variable with distribution
![]() $\textrm{Bin}(\Delta /s,p_{11})$
. Since
$\textrm{Bin}(\Delta /s,p_{11})$
. Since
![]() $\Delta =\Theta (\ln n)$
and
$\Delta =\Theta (\ln n)$
and
![]() $s=\Theta (\ln \ln n)$
, the first assertion (2.24) is immediate from Lemma 1.5.
$s=\Theta (\ln \ln n)$
, the first assertion (2.24) is immediate from Lemma 1.5.
Moving on to the second assertion, we condition on the event
![]() $\mathfrak{E}$
that the bounds (2.19)–(2.22) hold for all
$\mathfrak{E}$
that the bounds (2.19)–(2.22) hold for all
![]() $i\in [\ell ]$
. Then Proposition 2.3 shows that
$i\in [\ell ]$
. Then Proposition 2.3 shows that
![]() ${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o(n^{-2})$
. Given
${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o(n^{-2})$
. Given
![]() $\mathfrak{E}$
, we know that
$\mathfrak{E}$
, we know that
Now consider an individual
![]() $x\in V_0[i]$
. Also consider any test
$x\in V_0[i]$
. Also consider any test
![]() $a\in F[i+j-1]$
for
$a\in F[i+j-1]$
for
![]() $j\in [s]$
. Then the actual result
$j\in [s]$
. Then the actual result
![]() $\boldsymbol{\sigma }^{\prime}_a$
of
$\boldsymbol{\sigma }^{\prime}_a$
of
![]() $a$
is independent of the event
$a$
is independent of the event
![]() $\{x\in a\}$
because
$\{x\in a\}$
because
![]() $x$
is uninfected. Since the displayed result
$x$
is uninfected. Since the displayed result
![]() $\boldsymbol{\sigma }^{\prime\prime}_a$
depends solely on
$\boldsymbol{\sigma }^{\prime\prime}_a$
depends solely on
![]() $\boldsymbol{\sigma }^{\prime}_a$
, we conclude that
$\boldsymbol{\sigma }^{\prime}_a$
, we conclude that
![]() $\boldsymbol{\sigma }^{\prime\prime}_a$
is independent of
$\boldsymbol{\sigma }^{\prime\prime}_a$
is independent of
![]() $\{x\in a\}$
as well. Therefore, (3.9) shows that on the event
$\{x\in a\}$
as well. Therefore, (3.9) shows that on the event
![]() $\mathfrak{E}$
, the number of displayed positive tests that
$\mathfrak{E}$
, the number of displayed positive tests that
![]() $x$
is a member has conditional distribution
$x$
is a member has conditional distribution
 \begin{align} |\partial x\cap F^+[i+j-1]|\sim \textrm{Hyp}\left ({\frac{m}{\ell },\frac{q_0^+m}\ell +O\left(\sqrt m\ln ^3n\right),\frac{\Delta }{s}}\right ). \end{align}
\begin{align} |\partial x\cap F^+[i+j-1]|\sim \textrm{Hyp}\left ({\frac{m}{\ell },\frac{q_0^+m}\ell +O\left(\sqrt m\ln ^3n\right),\frac{\Delta }{s}}\right ). \end{align}
Since the random variables
![]() $(|\partial x\cap F^+[i+j-1]|)_{1\leq j\leq s}$
are mutually independent, (2.25) follows from Lemma 1.6.
$(|\partial x\cap F^+[i+j-1]|)_{1\leq j\leq s}$
are mutually independent, (2.25) follows from Lemma 1.6.
3.3. Proof of Proposition 2.6 (correctness of SPARC for
 $V^+$
)
$V^+$
)
We reduce the proof of Proposition 2.6 to three lemmas. The first two estimate the sums from (2.30) when evaluated at the actual ground truth
![]() $\boldsymbol{\sigma }$
.
$\boldsymbol{\sigma }$
.
Lemma 3.1. Assume that (2.34) is satisfied. w.h.p., we have
 \begin{align} \sum _{s\lt i\leq \ell }\sum _{x\in V_1^+[i]}\unicode{x1D7D9}\left \{{\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \lt (1-\zeta /2) W^+\text{ or }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) \gt (1+\zeta /2) W^-}\right \}\leq k\exp \left ({-\Omega \left ({\frac{\ln n}{(\ln \ln n)^4}}\right )}\right ). \end{align}
\begin{align} \sum _{s\lt i\leq \ell }\sum _{x\in V_1^+[i]}\unicode{x1D7D9}\left \{{\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \lt (1-\zeta /2) W^+\text{ or }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) \gt (1+\zeta /2) W^-}\right \}\leq k\exp \left ({-\Omega \left ({\frac{\ln n}{(\ln \ln n)^4}}\right )}\right ). \end{align}
Lemma 3.2. Assume that (2.34) is satisfied. w.h.p., we have
We defer the proofs of Lemmas 3.1 and 3.2 to Sections 3.4 and 3.5. While the proof of Lemma 3.1 is fairly routine, the proof of Lemma 3.2 is the linchpin of the entire analysis of SPARC, as it effectively vindicates the BP heuristics that we have been invoking so liberally in designing the algorithm.
Additionally, to compare
![]() $\boldsymbol{W}_x^{\pm }(\boldsymbol{\sigma })$
with the algorithm’s estimate
$\boldsymbol{W}_x^{\pm }(\boldsymbol{\sigma })$
with the algorithm’s estimate
![]() $\boldsymbol{W}_x^{\pm }(\tau )$
, we resort to the following expansion property of
$\boldsymbol{W}_x^{\pm }(\tau )$
, we resort to the following expansion property of
![]() $\mathbf{G}_{\mathrm{sc}}$
.
$\mathbf{G}_{\mathrm{sc}}$
.
Lemma 3.3.
Let
![]() $0\lt \alpha, \beta \lt 1$
be such that
$0\lt \alpha, \beta \lt 1$
be such that
![]() $\alpha +\beta \gt 1$
. Then w.h.p. for any
$\alpha +\beta \gt 1$
. Then w.h.p. for any
![]() $T \subseteq V$
of size
$T \subseteq V$
of size
![]() $|T|\leq \exp ({-}\ln ^\alpha n)k$
,
$|T|\leq \exp ({-}\ln ^\alpha n)k$
,
 \begin{align*} \left |{\left \{{x\in V\,:\,\sum _{a\in \partial x\setminus F[0]}\unicode{x1D7D9}\left \{{T\cap \partial a\setminus \left \{{x}\right \}\neq \emptyset }\right \}\geq \ln ^{\beta }n}\right \}}\right |\leq \frac{|T|}{8\ln \ln n}. \end{align*}
\begin{align*} \left |{\left \{{x\in V\,:\,\sum _{a\in \partial x\setminus F[0]}\unicode{x1D7D9}\left \{{T\cap \partial a\setminus \left \{{x}\right \}\neq \emptyset }\right \}\geq \ln ^{\beta }n}\right \}}\right |\leq \frac{|T|}{8\ln \ln n}. \end{align*}
In a nutshell, Lemma 3.3 posits that for any ‘small’ set
![]() $T$
of individuals, there are even fewer individuals that share many tests with individuals from
$T$
of individuals, there are even fewer individuals that share many tests with individuals from
![]() $T$
. Lemma 3.3 is an generalisation of (Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9, Lemma 4.16). The proof, based on a routine union bound argument, is included in Appendix C for completeness.
$T$
. Lemma 3.3 is an generalisation of (Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9, Lemma 4.16). The proof, based on a routine union bound argument, is included in Appendix C for completeness.
Proof of Proposition
2.6
(correctness of SPARC for V+). Proposition 2.4 shows that for all individuals
![]() $x$
in the seed
$x$
in the seed
![]() $V[1],\ldots, V[s]$
, we have
$V[1],\ldots, V[s]$
, we have
![]() $\tau _x=\boldsymbol{\sigma }_x$
w.h.p. Let
$\tau _x=\boldsymbol{\sigma }_x$
w.h.p. Let
![]() $\mathscr{M}[i] = \left \{{x \in V^+[i]\,:\, \tau _x \neq \boldsymbol{\sigma }_x}\right \}$
be the set of misclassified individuals in
$\mathscr{M}[i] = \left \{{x \in V^+[i]\,:\, \tau _x \neq \boldsymbol{\sigma }_x}\right \}$
be the set of misclassified individuals in
![]() $V^+[i]$
. We are going to show that w.h.p. for all
$V^+[i]$
. We are going to show that w.h.p. for all
![]() $1\leq i\leq \ell$
and for large enough
$1\leq i\leq \ell$
and for large enough
![]() $n$
,
$n$
,
We proceed by induction on
![]() $i$
. As mentioned above, Proposition 2.4 ensures that
$i$
. As mentioned above, Proposition 2.4 ensures that
![]() $\mathscr{M}[1]\cup \cdots \cup \mathscr{M}[s]=\emptyset$
w.h.p. Now assume that (3.13) is correct for all
$\mathscr{M}[1]\cup \cdots \cup \mathscr{M}[s]=\emptyset$
w.h.p. Now assume that (3.13) is correct for all
![]() $i\lt h\leq \ell$
; we are going to show that (3.13) holds for
$i\lt h\leq \ell$
; we are going to show that (3.13) holds for
![]() $i=h$
as well. To this end, recalling
$i=h$
as well. To this end, recalling
![]() $\zeta$
from (2.33) and
$\zeta$
from (2.33) and
![]() $W^{\pm }$
from (2.32), we define for
$W^{\pm }$
from (2.32), we define for
![]() $p_{10} \gt 0$
$p_{10} \gt 0$
 \begin{align*} \mathscr{M}_1[h]&=\left \{{x\in V_1^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \lt (1- \zeta /2) W^+\text{ or }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) \gt (1+\zeta /2) W^-}\right \},\\ \mathscr{M}_2[h]&=\left \{{x\in V_0^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \gt (1- 2\zeta ) W^+\text{ and }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) \lt (1+2\zeta ) W^-}\right \},\\ \mathscr{M}_3[h]&=\left \{{x\in V^+[h]\,:\,|\boldsymbol{W}_x^+(\boldsymbol{\sigma })-\boldsymbol{W}_x^+(\tau )|+|\boldsymbol{W}_x^-(\boldsymbol{\sigma })-\boldsymbol{W}_x^-(\tau )|\gt \zeta (W^+\wedge W^-)/8}\right \} \end{align*}
\begin{align*} \mathscr{M}_1[h]&=\left \{{x\in V_1^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \lt (1- \zeta /2) W^+\text{ or }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) \gt (1+\zeta /2) W^-}\right \},\\ \mathscr{M}_2[h]&=\left \{{x\in V_0^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \gt (1- 2\zeta ) W^+\text{ and }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) \lt (1+2\zeta ) W^-}\right \},\\ \mathscr{M}_3[h]&=\left \{{x\in V^+[h]\,:\,|\boldsymbol{W}_x^+(\boldsymbol{\sigma })-\boldsymbol{W}_x^+(\tau )|+|\boldsymbol{W}_x^-(\boldsymbol{\sigma })-\boldsymbol{W}_x^-(\tau )|\gt \zeta (W^+\wedge W^-)/8}\right \} \end{align*}
and further for
![]() $p_{10} = 0$
$p_{10} = 0$
 \begin{align*} \mathscr{M}_1[h]&=\left \{{x\in V_1^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \lt (1- \zeta /2) W^+}\right \},\\ \mathscr{M}_2[h]&=\left \{{x\in V_0^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \gt (1- 2\zeta ) W^+\text{ and }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) = 0 }\right \},\\ \mathscr{M}_3[h]&=\left \{{x\in V^+[h]\,:\,|\boldsymbol{W}_x^+(\boldsymbol{\sigma })-\boldsymbol{W}_x^+(\tau )|\gt \zeta (W^+)/8}\right \}. \end{align*}
\begin{align*} \mathscr{M}_1[h]&=\left \{{x\in V_1^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \lt (1- \zeta /2) W^+}\right \},\\ \mathscr{M}_2[h]&=\left \{{x\in V_0^+[h]\,:\,\boldsymbol{W}_x^+(\boldsymbol{\sigma }) \gt (1- 2\zeta ) W^+\text{ and }\boldsymbol{W}_x^-(\boldsymbol{\sigma }) = 0 }\right \},\\ \mathscr{M}_3[h]&=\left \{{x\in V^+[h]\,:\,|\boldsymbol{W}_x^+(\boldsymbol{\sigma })-\boldsymbol{W}_x^+(\tau )|\gt \zeta (W^+)/8}\right \}. \end{align*}
We claim that
![]() $\mathscr{M}[h]\subseteq \mathscr{M}_1[h]\cup \mathscr{M}_2[h]\cup \mathscr{M}_3[h]$
. To see this, assume that
$\mathscr{M}[h]\subseteq \mathscr{M}_1[h]\cup \mathscr{M}_2[h]\cup \mathscr{M}_3[h]$
. To see this, assume that
![]() $x\in \mathscr{M}[h]\setminus (\mathscr{M}_1[h]\cup \mathscr{M}_2[h])$
. Then for SPARC to misclassify
$x\in \mathscr{M}[h]\setminus (\mathscr{M}_1[h]\cup \mathscr{M}_2[h])$
. Then for SPARC to misclassify
![]() $x$
, it must be the case that
$x$
, it must be the case that
and thus
![]() $x\in \mathscr{M}_3[h]$
.
$x\in \mathscr{M}_3[h]$
.
Thus, to complete the proof, we need to estimate
![]() $|\mathscr{M}_1[h]|,|\mathscr{M}_2[h]|,|\mathscr{M}_3[h]|$
. Lemmas 3.1 and 3.2 readily show that
$|\mathscr{M}_1[h]|,|\mathscr{M}_2[h]|,|\mathscr{M}_3[h]|$
. Lemmas 3.1 and 3.2 readily show that
Furthermore, in order to bound
![]() $|\mathscr{M}_3[h]|$
, we will employ Lemma 3.3. Specifically, consider
$|\mathscr{M}_3[h]|$
, we will employ Lemma 3.3. Specifically, consider
![]() $x\in \mathscr{M}_3[h]$
. Since
$x\in \mathscr{M}_3[h]$
. Since
![]() $W^+\wedge W^-=\Omega (\Delta )=\Omega (\ln n)$
for
$W^+\wedge W^-=\Omega (\Delta )=\Omega (\ln n)$
for
![]() $p_{10}\gt 0$
by (2.29) and (2.32), there exists
$p_{10}\gt 0$
by (2.29) and (2.32), there exists
![]() $j\in [s]$
such that
$j\in [s]$
such that
Since
![]() $W^+=\Omega (\ln n)$
for
$W^+=\Omega (\ln n)$
for
![]() $p_{10}=0$
, there exists
$p_{10}=0$
, there exists
![]() $j\in [s]$
such that
$j\in [s]$
such that
Assume without loss of generality that the left inequality holds. Then there are at least
![]() $\ln ^{1/2}n$
tests
$\ln ^{1/2}n$
tests
![]() $a\in \partial x\cap F^+[h+j-1]$
such that
$a\in \partial x\cap F^+[h+j-1]$
such that
![]() $\partial a\cap (\mathscr{M}[1]\cup \cdots \cup \mathscr{M}[h-1])\neq \emptyset$
. Therefore, Lemma 3.3 shows that
$\partial a\cap (\mathscr{M}[1]\cup \cdots \cup \mathscr{M}[h-1])\neq \emptyset$
. Therefore, Lemma 3.3 shows that
Hence, using induction to bound
![]() $|\mathscr{M}[h-s]|,\ldots, |\mathscr{M}[h-1]|$
and recalling from (2.14) that
$|\mathscr{M}[h-s]|,\ldots, |\mathscr{M}[h-1]|$
and recalling from (2.14) that
![]() $s\leq 1+\ln \ln n$
, we obtain (3.13) for
$s\leq 1+\ln \ln n$
, we obtain (3.13) for
![]() $i=h$
.
$i=h$
.
3.4. Proof of Lemma 3.1 (large deviations for infected individuals)
The thrust of Lemma 3.1 is to verify that the definition (2.23) of the set
![]() $V^+[i]$
faithfully reflects the typical statistics of positively/negatively displayed tests in the neighbourhood of an infected individual
$V^+[i]$
faithfully reflects the typical statistics of positively/negatively displayed tests in the neighbourhood of an infected individual
![]() $x\in V_1[i]$
with
$x\in V_1[i]$
with
![]() $s\lt i\leq \ell$
. Recall from the definition of
$s\lt i\leq \ell$
. Recall from the definition of
![]() $\mathbf{G}_{\mathrm{sc}}$
that such an individual
$\mathbf{G}_{\mathrm{sc}}$
that such an individual
![]() $x$
joins tests in
$x$
joins tests in
![]() $F[i+j-1]$
for
$F[i+j-1]$
for
![]() $j\in [s]$
. Moreover, apart from
$j\in [s]$
. Moreover, apart from
![]() $x$
itself, a test
$x$
itself, a test
![]() $a\in F[i+j-1]\cap \partial x$
recruits from
$a\in F[i+j-1]\cap \partial x$
recruits from
![]() $V[i+j-s],\ldots, V[i+j-1]$
. In particular,
$V[i+j-s],\ldots, V[i+j-1]$
. In particular,
![]() $a$
recruits participants from the
$a$
recruits participants from the
![]() $s-j$
compartments
$s-j$
compartments
![]() $V[i+j-s],\ldots, V[i-1]$
preceding
$V[i+j-s],\ldots, V[i-1]$
preceding
![]() $V[i]$
. Let
$V[i]$
. Let
 \begin{align} \mathscr{U}_{i,j} & ={\left \{{a\in F[i+j-1]\,:\,(V_1[1]\cup \cdots \cup V_1[i-1])\cap \partial a=\emptyset }\right \}}\nonumber\\[3pt]& ={\left \{{a\in F[i+j-1]\,:\,\bigcup _{h=i+j-s}^{i-1}V_1[h]\cap \partial a=\emptyset }\right \}} \end{align}
\begin{align} \mathscr{U}_{i,j} & ={\left \{{a\in F[i+j-1]\,:\,(V_1[1]\cup \cdots \cup V_1[i-1])\cap \partial a=\emptyset }\right \}}\nonumber\\[3pt]& ={\left \{{a\in F[i+j-1]\,:\,\bigcup _{h=i+j-s}^{i-1}V_1[h]\cap \partial a=\emptyset }\right \}} \end{align}
be the set of tests in
![]() $F[i+j-1]$
that do not contain an infected individual from
$F[i+j-1]$
that do not contain an infected individual from
![]() $V[i+j-s],\ldots, V[i-1]$
.
$V[i+j-s],\ldots, V[i-1]$
.
Claim 3.4.
With probability
![]() $1-o(n^{-2})$
for all
$1-o(n^{-2})$
for all
![]() $s\leq i\lt \ell$
,
$s\leq i\lt \ell$
,
![]() $j\in [s]$
, we have
$j\in [s]$
, we have
Proof. We condition on the event
![]() $\mathfrak{E}$
that G1 from Proposition 2.3 holds. Then for any
$\mathfrak{E}$
that G1 from Proposition 2.3 holds. Then for any
![]() $a\in F[i+j-1]$
and any
$a\in F[i+j-1]$
and any
![]() $i+j-s\leq h\lt i$
, the number
$i+j-s\leq h\lt i$
, the number
![]() $V_1[h]\cap \partial a$
of infected individuals in
$V_1[h]\cap \partial a$
of infected individuals in
![]() $a$
from
$a$
from
![]() $V[h]$
is a binomial variable as in (3.2). Since the random variables
$V[h]$
is a binomial variable as in (3.2). Since the random variables
![]() $(V_1[h]\cap \partial a)_h$
are mutually independent, we therefore obtain
$(V_1[h]\cap \partial a)_h$
are mutually independent, we therefore obtain
Hence,
Further, changing the set
![]() $\partial x$
of tests that a single
$\partial x$
of tests that a single
![]() $x\in V_1$
joins can alter
$x\in V_1$
joins can alter
![]() $|\mathscr{U}_{i,j}|$
by
$|\mathscr{U}_{i,j}|$
by
![]() $\Delta$
at the most, while changing the set of neighbours of any
$\Delta$
at the most, while changing the set of neighbours of any
![]() $x\in V_0$
does not change
$x\in V_0$
does not change
![]() $|\mathscr{U}_{i,j}|$
at all. Therefore, Azuma–Hoeffding shows that
$|\mathscr{U}_{i,j}|$
at all. Therefore, Azuma–Hoeffding shows that
 \begin{align} {\mathbb{P}}\left \lbrack{\left |{|\mathscr{U}_{i,j}|-\mathbb{E}[|\mathscr{U}_{i,j}|\mid \mathfrak{E}]}\right |\gt \sqrt m\ln ^2n\mid \mathfrak{E}}\right \rbrack &\leq 2\exp \left ({-\frac{m\ln ^4n}{2k\Delta ^2}}\right )=o(n^{-2}). \end{align}
\begin{align} {\mathbb{P}}\left \lbrack{\left |{|\mathscr{U}_{i,j}|-\mathbb{E}[|\mathscr{U}_{i,j}|\mid \mathfrak{E}]}\right |\gt \sqrt m\ln ^2n\mid \mathfrak{E}}\right \rbrack &\leq 2\exp \left ({-\frac{m\ln ^4n}{2k\Delta ^2}}\right )=o(n^{-2}). \end{align}
Let
Claim 3.5.
For all
![]() $s\lt i\leq \ell$
,
$s\lt i\leq \ell$
,
![]() $x \in V_1[i]$
, and
$x \in V_1[i]$
, and
![]() $j \in [s]$
, we have
$j \in [s]$
, we have
Proof. Fix
![]() $s\leq i\lt \ell, 1\leq j\leq s$
and
$s\leq i\lt \ell, 1\leq j\leq s$
and
![]() $x\in V_1[i]$
. In light of Proposition 2.3 and Claim 3.4, the event
$x\in V_1[i]$
. In light of Proposition 2.3 and Claim 3.4, the event
![]() $\mathfrak{E}$
that G1 from Proposition 2.3 holds and that
$\mathfrak{E}$
that G1 from Proposition 2.3 holds and that
![]() $|\mathscr{U}_{i,j}|=\exp (d(j-s)/s)\frac{m}{\ell }(1+O(n^{-\Omega (1)}))$
has probability
$|\mathscr{U}_{i,j}|=\exp (d(j-s)/s)\frac{m}{\ell }(1+O(n^{-\Omega (1)}))$
has probability
Let
![]() $\boldsymbol{U}_{i,j}=|\partial x\cap \mathscr{U}_{i,j}|$
. Given
$\boldsymbol{U}_{i,j}=|\partial x\cap \mathscr{U}_{i,j}|$
. Given
![]() $\mathscr{U}_{i,j}$
, we have
$\mathscr{U}_{i,j}$
, we have
Therefore, Lemma 1.6 shows that the event
has conditional probability
Finally, given
![]() $\boldsymbol{U}_{i,j}$
the number
$\boldsymbol{U}_{i,j}$
the number
![]() $|\boldsymbol{W}_{x,j}^+|$
of positively displayed
$|\boldsymbol{W}_{x,j}^+|$
of positively displayed
![]() $a\in \partial x\cap \mathscr{U}_{i,j}$
has distribution
$a\in \partial x\cap \mathscr{U}_{i,j}$
has distribution
![]() $\textrm{Bin}(\boldsymbol{U}_{i,j},p_{11})$
; similarly,
$\textrm{Bin}(\boldsymbol{U}_{i,j},p_{11})$
; similarly,
![]() $|\boldsymbol{W}_{x,j}^-|$
has distribution
$|\boldsymbol{W}_{x,j}^-|$
has distribution
![]() $\textrm{Bin}(\boldsymbol{U}_{i,j},p_{01})$
. Thus, since
$\textrm{Bin}(\boldsymbol{U}_{i,j},p_{01})$
. Thus, since
![]() $\Delta =\Theta (\ln n)$
while
$\Delta =\Theta (\ln n)$
while
![]() $s=O(\ln \ln n)$
by (2.14), the assertion follows from (3.20), (3.21), and Lemma 1.5.
$s=O(\ln \ln n)$
by (2.14), the assertion follows from (3.20), (3.21), and Lemma 1.5.
3.5. Proof of Lemma 3.2 (large deviations for healthy individuals)
To prove Lemma 3.2, we need to estimate the probability that an uninfected individual
![]() $x\in V[i]$
,
$x\in V[i]$
,
![]() $s\lt i\leq \ell$
, ‘disguises’ itself to look like an infected individual. In addition to the sets
$s\lt i\leq \ell$
, ‘disguises’ itself to look like an infected individual. In addition to the sets
![]() $\mathscr{U}_{i,j}$
from (3.15) towards the proof of Lemma 3.2, we also need to consider the sets
$\mathscr{U}_{i,j}$
from (3.15) towards the proof of Lemma 3.2, we also need to consider the sets
In words,
![]() $\mathscr{P}_{i,j}$
and
$\mathscr{P}_{i,j}$
and
![]() $\mathscr{N}_{i,j}$
are the sets of actually positive/negative tests in
$\mathscr{N}_{i,j}$
are the sets of actually positive/negative tests in
![]() $\mathscr{U}_{i,j}$
, that is, actually positive/negative tests
$\mathscr{U}_{i,j}$
, that is, actually positive/negative tests
![]() $a\in F[i+j-1]$
that do not contain an infected individual from
$a\in F[i+j-1]$
that do not contain an infected individual from
![]() $V[i+j-s]\cup \cdots \cup V[i-1]$
. Additionally,
$V[i+j-s]\cup \cdots \cup V[i-1]$
. Additionally,
![]() $\mathscr{P}^{\pm }_{i,j},\mathscr{N}^{\pm }_{i,j}$
discriminate based on the displayed test results. We begin by estimating the likely sizes of these sets.
$\mathscr{P}^{\pm }_{i,j},\mathscr{N}^{\pm }_{i,j}$
discriminate based on the displayed test results. We begin by estimating the likely sizes of these sets.
Claim 3.6.
Let
![]() $s\lt i\leq \ell$
and
$s\lt i\leq \ell$
and
![]() $j\in [s]$
. Then with probability
$j\in [s]$
. Then with probability
![]() $1-o(n^{-2})$
, we have
$1-o(n^{-2})$
, we have
Proof. Since
![]() $\mathscr{N}_{i,j}=F_0[i+j-1]$
, the second equation in (3.22) just follows from Proposition 2.3, G2. Furthermore, since
$\mathscr{N}_{i,j}=F_0[i+j-1]$
, the second equation in (3.22) just follows from Proposition 2.3, G2. Furthermore, since
![]() $\mathscr{P}_{i,j}=\mathscr{U}_{i,j}\setminus \mathscr{N}_{i,j}$
, the first equation (3.22) is an immediate consequence of Claim 3.4. Finally, to obtain (3.23)–(3.24), we simply notice that given
$\mathscr{P}_{i,j}=\mathscr{U}_{i,j}\setminus \mathscr{N}_{i,j}$
, the first equation (3.22) is an immediate consequence of Claim 3.4. Finally, to obtain (3.23)–(3.24), we simply notice that given
![]() $|\mathscr{P}_{i,j}|,|\mathscr{N}_{i,j}|$
, we have
$|\mathscr{P}_{i,j}|,|\mathscr{N}_{i,j}|$
, we have
Let
![]() $\mathfrak U$
be the event that G1–G2 from Proposition 2.3 hold and that the estimates (3.22)–(3.24) hold. Then by Proposition 2.3 and Claim 3.6, we have
$\mathfrak U$
be the event that G1–G2 from Proposition 2.3 hold and that the estimates (3.22)–(3.24) hold. Then by Proposition 2.3 and Claim 3.6, we have
To facilitate the following computations, we let
Additionally, we introduce the shorthand
![]() $\lambda =(\ln \ln n)/\ln ^{3/7}n$
for the error term from the definition (2.23) of
$\lambda =(\ln \ln n)/\ln ^{3/7}n$
for the error term from the definition (2.23) of
![]() $V^+[i]$
. Our next step is to determine the distribution of the random variables
$V^+[i]$
. Our next step is to determine the distribution of the random variables
![]() $|\boldsymbol{W}_{{x},{j}}^{\pm }|$
that contribute to
$|\boldsymbol{W}_{{x},{j}}^{\pm }|$
that contribute to
![]() $\boldsymbol{W}_x^{\pm }(\boldsymbol{\sigma })$
from (2.30).
$\boldsymbol{W}_x^{\pm }(\boldsymbol{\sigma })$
from (2.30).
Claim 3.7.
Let
![]() $s\lt i\leq \ell$
and
$s\lt i\leq \ell$
and
![]() $j\in [s]$
. Given
$j\in [s]$
. Given
![]() $\mathfrak U$
for every
$\mathfrak U$
for every
![]() $x \in V_{0}^+[i]$
, we have
$x \in V_{0}^+[i]$
, we have
 \begin{align} |\boldsymbol{W}_{{x},{j}}^-| \sim \textrm{Hyp} \left ({\left ({1 + O(n^{-\Omega (1)})}\right )\frac{mq_0^-}{\ell },\left ({1 + O(n^{-\Omega (1)})}\right ) \frac{mq_{0,j}^-}{2\ell },(1+O(\lambda ))\frac{\Delta }{s} p_{10}}\right ), \end{align}
\begin{align} |\boldsymbol{W}_{{x},{j}}^-| \sim \textrm{Hyp} \left ({\left ({1 + O(n^{-\Omega (1)})}\right )\frac{mq_0^-}{\ell },\left ({1 + O(n^{-\Omega (1)})}\right ) \frac{mq_{0,j}^-}{2\ell },(1+O(\lambda ))\frac{\Delta }{s} p_{10}}\right ), \end{align}
 \begin{align} |\boldsymbol{W}_{{x},{j}}^+| \sim \textrm{Hyp} \left (\left ({1 + O(n^{-\Omega (1)})}\right )\frac{mq_0^+}{\ell },\left ({1 + O(n^{-\Omega (1)})}\right ) \frac{mq_{0,j}^+}{2\ell },\left ({1+O(\lambda )}\right )\frac{\Delta s}{p_{11}}\right ). \end{align}
\begin{align} |\boldsymbol{W}_{{x},{j}}^+| \sim \textrm{Hyp} \left (\left ({1 + O(n^{-\Omega (1)})}\right )\frac{mq_0^+}{\ell },\left ({1 + O(n^{-\Omega (1)})}\right ) \frac{mq_{0,j}^+}{2\ell },\left ({1+O(\lambda )}\right )\frac{\Delta s}{p_{11}}\right ). \end{align}
Proof. The definition (2.23) of
![]() $V^+[i]$
prescribes that for any
$V^+[i]$
prescribes that for any
![]() $x\in V_0^+[i]$
, we have
$x\in V_0^+[i]$
, we have
![]() $\partial x\cap F^+[i+j-1]=(p_{11}+O(\lambda ))\Delta /s$
. The absence or presence of
$\partial x\cap F^+[i+j-1]=(p_{11}+O(\lambda ))\Delta /s$
. The absence or presence of
![]() $x\in V_0[i]$
in any test
$x\in V_0[i]$
in any test
![]() $a$
does not affect the displayed results of
$a$
does not affect the displayed results of
![]() $a$
because
$a$
because
![]() $x$
is uninfected. Therefore, the conditional distributions of
$x$
is uninfected. Therefore, the conditional distributions of
![]() $|\boldsymbol{W}^{\pm }_{x,j}|$
read
$|\boldsymbol{W}^{\pm }_{x,j}|$
read
Since on
![]() $\mathfrak U$
the bounds (2.19)–(2.22) and (3.22)–(3.24) hold, the assertion follows.
$\mathfrak U$
the bounds (2.19)–(2.22) and (3.22)–(3.24) hold, the assertion follows.
We are now ready to derive an exact expression for the probability that for
![]() $x\in V_0[i]$
, the value
$x\in V_0[i]$
, the value
![]() $\boldsymbol{W}_x^{+}$
gets (almost) as large as the value
$\boldsymbol{W}_x^{+}$
gets (almost) as large as the value
![]() $W^+$
that we would expected to see for an infected individual. Recall the values
$W^+$
that we would expected to see for an infected individual. Recall the values
![]() $q_{1,j}^{\pm }$
from (3.19).
$q_{1,j}^{\pm }$
from (3.19).
Claim 3.8. Let
 \begin{align} \mathscr{M}^+=&\min \frac{1}{s}\sum _{j=1}^{s} D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^+}{q_0^+}}}}\right )\qquad \text{ s.t.}\quad \sum _{j=1}^{s}\left ({z_j-\frac{q_{1,j}^+}{p_{11}}}\right ) w_j^+ = 0,\qquad z_1,\ldots, z_{s}\in (0,1). \end{align}
\begin{align} \mathscr{M}^+=&\min \frac{1}{s}\sum _{j=1}^{s} D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^+}{q_0^+}}}}\right )\qquad \text{ s.t.}\quad \sum _{j=1}^{s}\left ({z_j-\frac{q_{1,j}^+}{p_{11}}}\right ) w_j^+ = 0,\qquad z_1,\ldots, z_{s}\in (0,1). \end{align}
Then for all
![]() $s \lt i \leq \ell$
and all
$s \lt i \leq \ell$
and all
![]() $x\in V[i]$
, we have
$x\in V[i]$
, we have
Proof. Since
![]() $\Delta =O(\ln n)$
and
$\Delta =O(\ln n)$
and
![]() $s=O(\ln \ln n)$
by (2.14), we can write
$s=O(\ln \ln n)$
by (2.14), we can write
 \begin{align}&{\mathbb{P}}\left \lbrack{\boldsymbol{W}_{{x}}^+(\boldsymbol{\sigma })\geq (1-2\zeta )W^+ \mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack \nonumber \\ &\leq \sum _{0\leq v_1, \ldots, v_s\leq \Delta /s}\unicode{x1D7D9}\left \{{\sum _{j=1}^nv_jw_j^+\geq (1-2\zeta )W^+}\right \}{\mathbb{P}}\left \lbrack{\forall j\in [s]\,:\,\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack \nonumber \\ & \leq \exp (o(\Delta ))\max _{0\leq v_1, \ldots, v_s\leq \Delta /s}\unicode{x1D7D9}\!\!\left \{{\sum _{j=1}^nv_jw_j^+\geq (1-2\zeta )W^+}\right \}{\mathbb{P}}\left \lbrack{\forall j\in [s]\,:\,\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack . \end{align}
\begin{align}&{\mathbb{P}}\left \lbrack{\boldsymbol{W}_{{x}}^+(\boldsymbol{\sigma })\geq (1-2\zeta )W^+ \mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack \nonumber \\ &\leq \sum _{0\leq v_1, \ldots, v_s\leq \Delta /s}\unicode{x1D7D9}\left \{{\sum _{j=1}^nv_jw_j^+\geq (1-2\zeta )W^+}\right \}{\mathbb{P}}\left \lbrack{\forall j\in [s]\,:\,\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack \nonumber \\ & \leq \exp (o(\Delta ))\max _{0\leq v_1, \ldots, v_s\leq \Delta /s}\unicode{x1D7D9}\!\!\left \{{\sum _{j=1}^nv_jw_j^+\geq (1-2\zeta )W^+}\right \}{\mathbb{P}}\left \lbrack{\forall j\in [s]\,:\,\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack . \end{align}
Further, given
![]() $\mathfrak U$
and
$\mathfrak U$
and
![]() $x\in V_0^+[i]$
, the random variables
$x\in V_0^+[i]$
, the random variables
![]() $(\boldsymbol{W}^+_{x,j})_{j\in [s]}$
are mutually independent because
$(\boldsymbol{W}^+_{x,j})_{j\in [s]}$
are mutually independent because
![]() $x$
joins tests in the compartments
$x$
joins tests in the compartments
![]() $F[i+j-1]$
,
$F[i+j-1]$
,
![]() $j\in [s]$
, independently. Hence, Claim 3.7 shows that for any
$j\in [s]$
, independently. Hence, Claim 3.7 shows that for any
![]() $v_1,\ldots, v_s$
,
$v_1,\ldots, v_s$
,
 \begin{align}{\mathbb{P}}\left \lbrack{\forall j\in [s]\,:\,\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack =\prod _{j=1}^s{\mathbb{P}}\left \lbrack{\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack . \end{align}
\begin{align}{\mathbb{P}}\left \lbrack{\forall j\in [s]\,:\,\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack =\prod _{j=1}^s{\mathbb{P}}\left \lbrack{\boldsymbol{W}^+_{x,j}(\boldsymbol{\sigma })=v_j\mid \mathfrak U,\,x\in V_{0}^+[{i}]}\right \rbrack . \end{align}
Thus, consider the optimisation problem
 \begin{align} \mathscr{M}^+_t=&\min \frac{1}{s}\sum _{j=1}^{s} D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^+}{q_0^+}}}}\right )\qquad \text{ s.t.}\quad \sum _{j=1}^{s}z_j w_j^+ \geq (1-t)W^+,\quad z_1,\ldots, z_{s}\in [q_{0,j}^+/q_0^+,1]. \end{align}
\begin{align} \mathscr{M}^+_t=&\min \frac{1}{s}\sum _{j=1}^{s} D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^+}{q_0^+}}}}\right )\qquad \text{ s.t.}\quad \sum _{j=1}^{s}z_j w_j^+ \geq (1-t)W^+,\quad z_1,\ldots, z_{s}\in [q_{0,j}^+/q_0^+,1]. \end{align}
Then combining (3.30) and (3.31) with Claim 3.7 and Lemma 1.6 and using the substitution
![]() $z_j=v_j/(p_{11}\Delta )$
, we obtain
$z_j=v_j/(p_{11}\Delta )$
, we obtain
We claim that (3.33) can be sharpened to
Indeed, consider any feasible solution
![]() $z_1,\ldots, z_s$
to
$z_1,\ldots, z_s$
to
![]() $\mathscr{M}_\zeta ^+$
such that
$\mathscr{M}_\zeta ^+$
such that
![]() $\sum _{j\geq s}z_jw_j^+\lt W^+$
. Obtain
$\sum _{j\geq s}z_jw_j^+\lt W^+$
. Obtain
![]() $z^{\prime}_1,\ldots, z^{\prime}_s$
by increasing some of the values
$z^{\prime}_1,\ldots, z^{\prime}_s$
by increasing some of the values
![]() $z_1,\ldots, z_s$
such that
$z_1,\ldots, z_s$
such that
![]() $\sum _{j\leq s}z^{\prime}_jw_j^+=W^+$
. Then because the functions
$\sum _{j\leq s}z^{\prime}_jw_j^+=W^+$
. Then because the functions
![]() $z\mapsto D_{\mathrm{KL}}({z}\|{q_{0,j}^+/q_0^+})$
with
$z\mapsto D_{\mathrm{KL}}({z}\|{q_{0,j}^+/q_0^+})$
with
![]() $j\in [s]$
are equicontinuous on the compact interval
$j\in [s]$
are equicontinuous on the compact interval
![]() $[0,1]$
, we see that
$[0,1]$
, we see that
 \begin{align*} \frac{1}{s}\sum _{j=1}^sD_{\mathrm{KL}}\left ({{{z_j}\|{q_{0,j}^+/q_0^+}}}\right )\geq \frac{1}{s}\sum _{j=1}^sD_{\mathrm{KL}}\left ({{{z^{\prime}_j}\|{q_{0,j}^+/q_0^+}}}\right )+o(1) \end{align*}
\begin{align*} \frac{1}{s}\sum _{j=1}^sD_{\mathrm{KL}}\left ({{{z_j}\|{q_{0,j}^+/q_0^+}}}\right )\geq \frac{1}{s}\sum _{j=1}^sD_{\mathrm{KL}}\left ({{{z^{\prime}_j}\|{q_{0,j}^+/q_0^+}}}\right )+o(1) \end{align*}
uniformly for all
![]() $z_1,\ldots, z_s$
and
$z_1,\ldots, z_s$
and
![]() $z^{\prime}_1,\ldots, z^{\prime}_s$
. Thus, (3.34) follows from (3.33).
$z^{\prime}_1,\ldots, z^{\prime}_s$
. Thus, (3.34) follows from (3.33).
Finally, we notice that the condition
![]() $z_j\geq q_{0,j}^+/q_0^+$
in (3.32) is superfluous. Indeed, since
$z_j\geq q_{0,j}^+/q_0^+$
in (3.32) is superfluous. Indeed, since
![]() $D_{\mathrm{KL}}({q_{0,j}^+/q_0^+}\|{q_{0,j}^+/q_0^+})=0$
, there is nothing to be gained from choosing
$D_{\mathrm{KL}}({q_{0,j}^+/q_0^+}\|{q_{0,j}^+/q_0^+})=0$
, there is nothing to be gained from choosing
![]() $z_j\lt q_{0,j}^+/q_0^+$
. Furthermore, since the Kullback–Leibler divergence is strictly convex and (1.1) ensures that
$z_j\lt q_{0,j}^+/q_0^+$
. Furthermore, since the Kullback–Leibler divergence is strictly convex and (1.1) ensures that
![]() $q_{0,j}^+/q_0^+\lt q_{1,j}^+/p_{11}$
for all
$q_{0,j}^+/q_0^+\lt q_{1,j}^+/p_{11}$
for all
![]() $j$
, the optimisation problem
$j$
, the optimisation problem
![]() $\mathscr{M}^+_0$
attains a unique minimum, which is not situated at the boundary of the intervals
$\mathscr{M}^+_0$
attains a unique minimum, which is not situated at the boundary of the intervals
![]() $[q_{0,j}^+/q_0^+,1]$
. That said, the unique minimiser satisfies the weight constraint
$[q_{0,j}^+/q_0^+,1]$
. That said, the unique minimiser satisfies the weight constraint
![]() $\sum _{j\geq s}z_jw_j^+$
with equality; otherwise, we could reduce some
$\sum _{j\geq s}z_jw_j^+$
with equality; otherwise, we could reduce some
![]() $z_j$
, thereby decreasing the objective function value. In summary, we conclude that
$z_j$
, thereby decreasing the objective function value. In summary, we conclude that
![]() $\mathscr{M}_0^+=\mathscr{M}^+$
. Thus, the assertion follows from (3.34).
$\mathscr{M}_0^+=\mathscr{M}^+$
. Thus, the assertion follows from (3.34).
Claim 3.9. Let
 \begin{align} \mathscr{M}^-=& \min \frac{1}{s}\sum _{j=1}^{s} D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^-}{q_0^-}}}}\right )\qquad \text{ s.t.}\quad \sum _{j=1}^{s}\left ({z_j-\frac{q_{1,j}^-}{p_{01}}}\right ) w_j^- = 0,\qquad z_1,\ldots, z_{s}\in (0,1). \end{align}
\begin{align} \mathscr{M}^-=& \min \frac{1}{s}\sum _{j=1}^{s} D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^-}{q_0^-}}}}\right )\qquad \text{ s.t.}\quad \sum _{j=1}^{s}\left ({z_j-\frac{q_{1,j}^-}{p_{01}}}\right ) w_j^- = 0,\qquad z_1,\ldots, z_{s}\in (0,1). \end{align}
Then for all
![]() $s \lt i \leq \ell$
and all
$s \lt i \leq \ell$
and all
![]() $x\in V[i]$
, we have
$x\in V[i]$
, we have
Recall that by convention
![]() $0 \cdot \infty = 0$
. Thus for
$0 \cdot \infty = 0$
. Thus for
![]() $p_{10}=0$
, the condition of (3.35) boils down to
$p_{10}=0$
, the condition of (3.35) boils down to
![]() $z_j ={q_{1,j}^-}/{p_{01}}$
, and the optimisation becomes trivial.
$z_j ={q_{1,j}^-}/{p_{01}}$
, and the optimisation becomes trivial.
Proof. Analogous to the proof of Claim 3.8.
Clearly, as a next step, we need to solve the optimisation problems (3.29) and (3.35). We defer this task to Section 3.6, where we prove the following.
Lemma 3.10.
Let
![]() $\boldsymbol{X}$
have distribution
$\boldsymbol{X}$
have distribution
![]() ${\textrm{Be}}({\exp} ({-}d))$
, and let
${\textrm{Be}}({\exp} ({-}d))$
, and let
![]() $\boldsymbol{Y}$
be the (random) channel output given input
$\boldsymbol{Y}$
be the (random) channel output given input
![]() $\boldsymbol{X}$
. Then
$\boldsymbol{X}$
. Then
Proof of Lemma
3.2
(large deviations for healthy individuals). In light of Claims 3.8 and 3.9 and Lemma 3.10 to work out that all but
![]() $o(k)$
positive individuals are identified correctly, using Markov’s inequality, we need to verify that
$o(k)$
positive individuals are identified correctly, using Markov’s inequality, we need to verify that
Taking the logarithm of (3.36) and simplifying, we arrive at
Thus, we need to show that
This boils down to
![]() $cI(\boldsymbol{X},\boldsymbol{Y})\gt 1$
, which in turn is identical to (2.34).
$cI(\boldsymbol{X},\boldsymbol{Y})\gt 1$
, which in turn is identical to (2.34).
3.6. Proof of Lemma 3.10
We tackle the optimisation problems
![]() $\mathscr{M}^{\pm }$
via the method of Lagrange multipliers. Since the objective functions are strictly convex, these optimisation problems possess unique stationary points. As the parameters from (3.19) satisfy
$\mathscr{M}^{\pm }$
via the method of Lagrange multipliers. Since the objective functions are strictly convex, these optimisation problems possess unique stationary points. As the parameters from (3.19) satisfy
![]() $q_{1,j}^+/p_{11}=\exp (d(j-s)/s)$
, the optimisation problem (3.29) gives rise to the following Lagrangian.
$q_{1,j}^+/p_{11}=\exp (d(j-s)/s)$
, the optimisation problem (3.29) gives rise to the following Lagrangian.
Claim 3.11. The Lagrangian
 \begin{align*} \mathscr{L}^+ =& \sum _{j=1}^s D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^+}{q_0^+}}}}\right ) + \lambda w_j^+\left ({z_j - \exp ({-}d(s-j)/s)}\right ) \end{align*}
\begin{align*} \mathscr{L}^+ =& \sum _{j=1}^s D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^+}{q_0^+}}}}\right ) + \lambda w_j^+\left ({z_j - \exp ({-}d(s-j)/s)}\right ) \end{align*}
has the unique stationary point
![]() $z_j=\exp ({-}d(s-j)/s)$
,
$z_j=\exp ({-}d(s-j)/s)$
,
![]() $\lambda =-1$
.
$\lambda =-1$
.
Proof. Since the objective function
![]() $\sum _{j=1}^s D_{\mathrm{KL}}\left ({{{z_j}\|{q_{1,j}^+/p_{11}}}}\right )$
is strictly convex, we just need to verify that
$\sum _{j=1}^s D_{\mathrm{KL}}\left ({{{z_j}\|{q_{1,j}^+/p_{11}}}}\right )$
is strictly convex, we just need to verify that
![]() $\lambda =-1$
and
$\lambda =-1$
and
![]() $z_j=\exp ({-}d(s-j)/s)$
is a stationary point. To this end, we calculate
$z_j=\exp ({-}d(s-j)/s)$
is a stationary point. To this end, we calculate
 \begin{align} \frac{\partial \mathscr{L}^+}{\partial z_j} = & \ln \frac{z_j^+}{1-z_j^+}- \ln \frac{q_{1,j}^+}{p_{11}-q_{1,j}^+} + \lambda w_j^+,& \frac{\partial \mathscr{L}^+}{\partial \lambda } =& \sum _{j=1}^s \left ({z_j - \exp \left ({-d(s-j)/s}\right )}\right ) w_j^+. \end{align}
\begin{align} \frac{\partial \mathscr{L}^+}{\partial z_j} = & \ln \frac{z_j^+}{1-z_j^+}- \ln \frac{q_{1,j}^+}{p_{11}-q_{1,j}^+} + \lambda w_j^+,& \frac{\partial \mathscr{L}^+}{\partial \lambda } =& \sum _{j=1}^s \left ({z_j - \exp \left ({-d(s-j)/s}\right )}\right ) w_j^+. \end{align}
Substituting in the definition (2.29) of the weights
![]() $w_j^+$
and the definition (3.19) of
$w_j^+$
and the definition (3.19) of
![]() $p_{11},q_{1,j}^+$
and simplifying, we obtain
$p_{11},q_{1,j}^+$
and simplifying, we obtain
 \begin{align*} \frac{\partial L^+}{\partial z_j}\bigg |_{\substack{z_j=\exp ({-}d(s-j)/s)\\\lambda =-1}} & =\ln \frac{\exp ({-}d(s-j)/s)}{1-\exp ({-}d(s-j)/s)} - \ln \frac{p_{11}({\exp} \left ({dj/s}\right ) -1) + p_{01}}{p_{11}({\exp} (d)-1)+p_{01}}\\& +\ln \left (\!{1-\frac{p_{11}({\exp} (d j/s) -1) + p_{01}}{p_{11}({\exp} (d)-1)+p_{01}} }\right ) {-}\ln \frac{p_{11}}{p_{11} + (p_{01}-p_{11}) \exp ({-}d j/s )}=0. \end{align*}
\begin{align*} \frac{\partial L^+}{\partial z_j}\bigg |_{\substack{z_j=\exp ({-}d(s-j)/s)\\\lambda =-1}} & =\ln \frac{\exp ({-}d(s-j)/s)}{1-\exp ({-}d(s-j)/s)} - \ln \frac{p_{11}({\exp} \left ({dj/s}\right ) -1) + p_{01}}{p_{11}({\exp} (d)-1)+p_{01}}\\& +\ln \left (\!{1-\frac{p_{11}({\exp} (d j/s) -1) + p_{01}}{p_{11}({\exp} (d)-1)+p_{01}} }\right ) {-}\ln \frac{p_{11}}{p_{11} + (p_{01}-p_{11}) \exp ({-}d j/s )}=0. \end{align*}
Finally, (3.39) shows that setting
![]() $z_j=\exp ({-}d(s-j)/s)$
ensures that
$z_j=\exp ({-}d(s-j)/s)$
ensures that
![]() $\partial \mathscr{L}^+/\partial \lambda =0$
as well.
$\partial \mathscr{L}^+/\partial \lambda =0$
as well.
Analogous steps prove the corresponding statement for
![]() $\mathscr{M}^-$
.
$\mathscr{M}^-$
.
Claim 3.12.
Assume
![]() $p_{10} \gt 0$
. The Lagrangian
$p_{10} \gt 0$
. The Lagrangian
 \begin{align*} \mathscr{L}^- =& \sum _{j=1}^s D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^-}{p_{01}}}}}\right ) + \lambda w_j^-\left ({z_j - \exp ({-}d(s-j)/s)}\right ) \end{align*}
\begin{align*} \mathscr{L}^- =& \sum _{j=1}^s D_{\mathrm{KL}}\left ({{{z_j}\|{\frac{q_{0,j}^-}{p_{01}}}}}\right ) + \lambda w_j^-\left ({z_j - \exp ({-}d(s-j)/s)}\right ) \end{align*}
has the unique stationary point
![]() $z_j=\exp ({-}d(s-j)/s)$
,
$z_j=\exp ({-}d(s-j)/s)$
,
![]() $\lambda =-1$
.
$\lambda =-1$
.
Having identified the minimisers of
![]() $\mathscr{M}^{\pm }$
, we proceed to calculate the optimal objective function values. Note that for
$\mathscr{M}^{\pm }$
, we proceed to calculate the optimal objective function values. Note that for
![]() $\mathscr{M}^-$
, the minimisers
$\mathscr{M}^-$
, the minimisers
![]() $z_j$
for the cases
$z_j$
for the cases
![]() $p_{10}\gt 0$
and
$p_{10}\gt 0$
and
![]() $p_{10} = 0$
coincide.
$p_{10} = 0$
coincide.
Claim 3.13. Let
Then
 \begin{align*} p_{11}d\exp (d)\mathscr{M}^+=&(\lambda ^++d)\left ({p_{11}\left ({(d-1)\exp (d)+1}\right )-p_{01}}\right )+p_{01}\ln (p_{01})\\& -p_{11}\left ({(d-1)\exp (d)+1}\right )\ln (p_{11})-d(d-1)\exp (d)p_{11}+O(1/s),\\ p_{10}d\exp (d)\mathscr{M}^-=&(\lambda ^-+d)\left ({p_{10}\left ({(d-1)\exp (d)+1}\right )-p_{00}}\right )+p_{00}\ln (p_{00})\\ & -p_{10}\left ({(d-1)\exp (d)+1}\right )\ln (p_{10})-d(d-1)\exp (d)p_{10}+O(1/s)\quad \text{if } p_{10}\gt 0. \end{align*}
\begin{align*} p_{11}d\exp (d)\mathscr{M}^+=&(\lambda ^++d)\left ({p_{11}\left ({(d-1)\exp (d)+1}\right )-p_{01}}\right )+p_{01}\ln (p_{01})\\& -p_{11}\left ({(d-1)\exp (d)+1}\right )\ln (p_{11})-d(d-1)\exp (d)p_{11}+O(1/s),\\ p_{10}d\exp (d)\mathscr{M}^-=&(\lambda ^-+d)\left ({p_{10}\left ({(d-1)\exp (d)+1}\right )-p_{00}}\right )+p_{00}\ln (p_{00})\\ & -p_{10}\left ({(d-1)\exp (d)+1}\right )\ln (p_{10})-d(d-1)\exp (d)p_{10}+O(1/s)\quad \text{if } p_{10}\gt 0. \end{align*}
Proof. We perform the calculation for
![]() $\mathscr{M}^+$
in detail. Syntactically identical steps yield the expression for
$\mathscr{M}^+$
in detail. Syntactically identical steps yield the expression for
![]() $\mathscr{M}^-$
, the only required change being the obvious modification of the indices of the channel probabilities. Substituting the optimal solution
$\mathscr{M}^-$
, the only required change being the obvious modification of the indices of the channel probabilities. Substituting the optimal solution
![]() $z_j=\exp ({-}d(s-j)/s)$
and the definitions (3.19) and (2.1), (3.19), and (3.26) of
$z_j=\exp ({-}d(s-j)/s)$
and the definitions (3.19) and (2.1), (3.19), and (3.26) of
![]() $q^+_{1,j},q_0^+,q_{0,j}^+$
into (3.29), we obtain
$q^+_{1,j},q_0^+,q_{0,j}^+$
into (3.29), we obtain
 \begin{align} \mathscr{M}^+=&\frac{1}{s}\sum _{j=1}^{s}D_{\mathrm{KL}}\left ({{{\exp ({-}d(s-j)/s)}\|{\frac{p_{01}+({\exp} (dj/s)-1)p_{11}}{p_{01}+({\exp} (d)-1)p_{11}}}}}\right )=\mathscr{I}^++O(1/s),\qquad \text{ where}\\ \mathscr{I}^+=&\int _0^1D_{\mathrm{KL}}\left ({{{\exp (d(x-1))}\|{\frac{p_{11}({\exp} (dx)-1)+p_{01}}{p_{11}({\exp} (d)-1)+p_{01}}}}}\right ){\mathrm d} x;\nonumber \end{align}
\begin{align} \mathscr{M}^+=&\frac{1}{s}\sum _{j=1}^{s}D_{\mathrm{KL}}\left ({{{\exp ({-}d(s-j)/s)}\|{\frac{p_{01}+({\exp} (dj/s)-1)p_{11}}{p_{01}+({\exp} (d)-1)p_{11}}}}}\right )=\mathscr{I}^++O(1/s),\qquad \text{ where}\\ \mathscr{I}^+=&\int _0^1D_{\mathrm{KL}}\left ({{{\exp (d(x-1))}\|{\frac{p_{11}({\exp} (dx)-1)+p_{01}}{p_{11}({\exp} (d)-1)+p_{01}}}}}\right ){\mathrm d} x;\nonumber \end{align}
the
![]() $O(1/s)$
-bound in (3.40) holds because the derivative of the integrand
$O(1/s)$
-bound in (3.40) holds because the derivative of the integrand
![]() $x\mapsto D_{\mathrm{KL}}\left ({{{\exp (d(x-1))}\|{\frac{p_{11}({\exp} (dx)-1)+p_{01}}{p_{11}({\exp} (d)-1)+p_{01}}}}}\right )$
is bounded on
$x\mapsto D_{\mathrm{KL}}\left ({{{\exp (d(x-1))}\|{\frac{p_{11}({\exp} (dx)-1)+p_{01}}{p_{11}({\exp} (d)-1)+p_{01}}}}}\right )$
is bounded on
![]() $[0,1]$
. Replacing the Kullback–Leibler divergence by its definition, we obtain
$[0,1]$
. Replacing the Kullback–Leibler divergence by its definition, we obtain
![]() $\mathscr{I}^+=\mathscr{I}^+_1+\mathscr{I}^+_2$
, where
$\mathscr{I}^+=\mathscr{I}^+_1+\mathscr{I}^+_2$
, where
 \begin{align*} \mathscr{I}^+_1&=\int _{0}^{1} \exp \left ({d(x-1)}\right ) \ln \frac{\exp \left ({d(x-1)}\right ) ( p_{11}({\exp} \left ({d}\right )-1)+p_{01} ) }{p_{11}({\exp} \left ({dx}\right )-1)+p_{01} }{\mathrm d} x,\\ \mathscr{I}^+_2&=\int _{0}^{1} (1-\exp \left ({d(x-1)}\right )) \ln \left \lbrack{ \frac{ 1- \exp \left ({d(x-1)}\right ) }{ 1 - \frac{p_{11}({\exp} \left ({dx}\right )-1)+p_{01}}{p_{11}({\exp} \left ({d}\right )-1)+p_{01}} } }\right \rbrack{\mathrm d} x. \end{align*}
\begin{align*} \mathscr{I}^+_1&=\int _{0}^{1} \exp \left ({d(x-1)}\right ) \ln \frac{\exp \left ({d(x-1)}\right ) ( p_{11}({\exp} \left ({d}\right )-1)+p_{01} ) }{p_{11}({\exp} \left ({dx}\right )-1)+p_{01} }{\mathrm d} x,\\ \mathscr{I}^+_2&=\int _{0}^{1} (1-\exp \left ({d(x-1)}\right )) \ln \left \lbrack{ \frac{ 1- \exp \left ({d(x-1)}\right ) }{ 1 - \frac{p_{11}({\exp} \left ({dx}\right )-1)+p_{01}}{p_{11}({\exp} \left ({d}\right )-1)+p_{01}} } }\right \rbrack{\mathrm d} x. \end{align*}
Splitting the logarithm in the first integrand, we further obtain
![]() $\mathscr{I}^+_1=\mathscr{I}_{11}^++\mathscr{I}_{12}^+$
, where
$\mathscr{I}^+_1=\mathscr{I}_{11}^++\mathscr{I}_{12}^+$
, where
 \begin{align*} \mathscr{I}^+_{11}&=\int _{0}^{1} \exp \left ({d(x-1)}\right ) \ln \left \lbrack{ \exp \left ({d(x-1)}\right ) ( p_{11}({\exp} \left ({d}\right )-1)+p_{01} )}\right \rbrack{\mathrm d} x,\\ \mathscr{I}^+_{12}&=-\int _{0}^{1} \exp \left ({d(x-1)}\right ) \ln \left \lbrack{ p_{11}({\exp} \left ({dx}\right )-1)+p_{01} }\right \rbrack{\mathrm d} x. \end{align*}
\begin{align*} \mathscr{I}^+_{11}&=\int _{0}^{1} \exp \left ({d(x-1)}\right ) \ln \left \lbrack{ \exp \left ({d(x-1)}\right ) ( p_{11}({\exp} \left ({d}\right )-1)+p_{01} )}\right \rbrack{\mathrm d} x,\\ \mathscr{I}^+_{12}&=-\int _{0}^{1} \exp \left ({d(x-1)}\right ) \ln \left \lbrack{ p_{11}({\exp} \left ({dx}\right )-1)+p_{01} }\right \rbrack{\mathrm d} x. \end{align*}
Setting
![]() $\Lambda ^+=\ln ( p_{11}({\exp} \left ({d}\right )-1)+p_{01})=\lambda ^++d$
and introducing
$\Lambda ^+=\ln ( p_{11}({\exp} \left ({d}\right )-1)+p_{01})=\lambda ^++d$
and introducing
![]() $ u = \exp \left ({d(x-1)}\right )$
, we calculate
$ u = \exp \left ({d(x-1)}\right )$
, we calculate
 \begin{align} \mathscr{I}_{11}^+&=\frac{1}{d} \left \lbrack{\int _{\exp \left ({-d}\right )}^{1} \ln ( u){\mathrm d} u + \int _{\exp \left ({-d}\right )}^{1} \Lambda ^+{\mathrm d} u }\right \rbrack =\frac{1}{d} \left \lbrack{(d+1)\exp ({-}d) -1 + (1 - \exp \left ({-d}\right ) ) \Lambda ^+}\right \rbrack . \end{align}
\begin{align} \mathscr{I}_{11}^+&=\frac{1}{d} \left \lbrack{\int _{\exp \left ({-d}\right )}^{1} \ln ( u){\mathrm d} u + \int _{\exp \left ({-d}\right )}^{1} \Lambda ^+{\mathrm d} u }\right \rbrack =\frac{1}{d} \left \lbrack{(d+1)\exp ({-}d) -1 + (1 - \exp \left ({-d}\right ) ) \Lambda ^+}\right \rbrack . \end{align}
Concerning
![]() $\mathscr{I}_{12}^+$
, we once again substitute
$\mathscr{I}_{12}^+$
, we once again substitute
![]() $ u = \exp \left ({d(x-1)}\right )$
to obtain
$ u = \exp \left ({d(x-1)}\right )$
to obtain
 \begin{align} \nonumber \mathscr{I}_{12}^+&=-\frac{1}{d}\int _{\exp ({-}d)}^1\ln \left ({p_{11}\exp (d)u+p_{01}-p_{11}}\right ){\mathrm d} u\\[4pt] &= - \frac{1}{d} \left \lbrack{ \left ({\frac{ p_{01}}{p_{11}}\exp \left ({-d}\right )-\exp \left ({-d}\right )+1}\right )\Lambda ^+ - \exp \left ({-d}\right )\frac{p_{01}}{p_{11}} \ln (p_{01}) + \exp \left ({-d}\right )-1 }\right \rbrack \end{align}
\begin{align} \nonumber \mathscr{I}_{12}^+&=-\frac{1}{d}\int _{\exp ({-}d)}^1\ln \left ({p_{11}\exp (d)u+p_{01}-p_{11}}\right ){\mathrm d} u\\[4pt] &= - \frac{1}{d} \left \lbrack{ \left ({\frac{ p_{01}}{p_{11}}\exp \left ({-d}\right )-\exp \left ({-d}\right )+1}\right )\Lambda ^+ - \exp \left ({-d}\right )\frac{p_{01}}{p_{11}} \ln (p_{01}) + \exp \left ({-d}\right )-1 }\right \rbrack \end{align}
Proceeding to
![]() $\mathscr{I}_2$
, we obtain
$\mathscr{I}_2$
, we obtain
 \begin{align} \nonumber \mathscr{I}_2^+ &= \int _{0}^{1} (1- \exp \left ({d(x-1)}\right )) \ln \frac{ p_{11} ({\exp} \left ({d}\right ) - 1) + p_{01} }{ p_{11}\exp (d) }{\mathrm d} x\nonumber\\ & = \int _{0}^{1} (1- \exp \left ({d(x-1)}\right )) \ln \left ({ p_{11} ({\exp} (d) - 1) + p_{01} }\right ){\mathrm d} x\nonumber\\ & \quad - \int _{0}^{1} (1- \exp \left ({d(x-1)}\right )) \ln ( p_{11}\exp (d) ){\mathrm d} x\nonumber \\ &=\frac{ (\Lambda ^+ - \ln ( p_{11}) - d ) ( d-1 + \exp \left ({-d}\right ) )}{d}. \end{align}
\begin{align} \nonumber \mathscr{I}_2^+ &= \int _{0}^{1} (1- \exp \left ({d(x-1)}\right )) \ln \frac{ p_{11} ({\exp} \left ({d}\right ) - 1) + p_{01} }{ p_{11}\exp (d) }{\mathrm d} x\nonumber\\ & = \int _{0}^{1} (1- \exp \left ({d(x-1)}\right )) \ln \left ({ p_{11} ({\exp} (d) - 1) + p_{01} }\right ){\mathrm d} x\nonumber\\ & \quad - \int _{0}^{1} (1- \exp \left ({d(x-1)}\right )) \ln ( p_{11}\exp (d) ){\mathrm d} x\nonumber \\ &=\frac{ (\Lambda ^+ - \ln ( p_{11}) - d ) ( d-1 + \exp \left ({-d}\right ) )}{d}. \end{align}
Finally, recalling that
![]() $\mathscr{I}^+=\mathscr{I}_1+\mathscr{I}_2=\mathscr{I}^+_{11}+\mathscr{I}^+_{12}+\mathscr{I}_2^+$
and combining (3.40)–(3.43) and simplifying, we arrive at the desired expression for
$\mathscr{I}^+=\mathscr{I}_1+\mathscr{I}_2=\mathscr{I}^+_{11}+\mathscr{I}^+_{12}+\mathscr{I}_2^+$
and combining (3.40)–(3.43) and simplifying, we arrive at the desired expression for
![]() $\mathscr{M}^+$
.
$\mathscr{M}^+$
.
Proof of Lemma 3.10 . We have
Hence, Claim 3.13 yields
 \begin{align*} p_{11}\mathscr{M}^++p_{10}\mathscr{M}^-=&-\frac{h(p_{00})}{d\exp (d)}-\frac{(1-\exp ({-}d))h(p_{11})}{d}+h(p_{11})\\[3pt] &+\frac{(p_{11}-p_{01})\lambda ^++(p_{10}-p_{00})\lambda ^-}{d\exp (d)}+\frac{d-1}d\left \lbrack{p_{11}\lambda ^++p_{10}\lambda ^-}\right \rbrack \\[3pt] &=-\frac{h(p_{00})}{d\exp (d)}-\frac{(1-\exp ({-}d))h(p_{11})}{d}-D_{\mathrm{KL}}\left ({{{p_{11}}\|{q_0^+}}}\right )-\frac{\lambda ^+}d\exp (\lambda ^+)\\ & \quad -\frac{\lambda ^-}d\exp (\lambda ^-)\\[3pt] &=\frac{I(\boldsymbol{X},\boldsymbol{Y})}d-D_{\mathrm{KL}}\left ({{{p_{11}}\|{q_0^+}}}\right ), \end{align*}
\begin{align*} p_{11}\mathscr{M}^++p_{10}\mathscr{M}^-=&-\frac{h(p_{00})}{d\exp (d)}-\frac{(1-\exp ({-}d))h(p_{11})}{d}+h(p_{11})\\[3pt] &+\frac{(p_{11}-p_{01})\lambda ^++(p_{10}-p_{00})\lambda ^-}{d\exp (d)}+\frac{d-1}d\left \lbrack{p_{11}\lambda ^++p_{10}\lambda ^-}\right \rbrack \\[3pt] &=-\frac{h(p_{00})}{d\exp (d)}-\frac{(1-\exp ({-}d))h(p_{11})}{d}-D_{\mathrm{KL}}\left ({{{p_{11}}\|{q_0^+}}}\right )-\frac{\lambda ^+}d\exp (\lambda ^+)\\ & \quad -\frac{\lambda ^-}d\exp (\lambda ^-)\\[3pt] &=\frac{I(\boldsymbol{X},\boldsymbol{Y})}d-D_{\mathrm{KL}}\left ({{{p_{11}}\|{q_0^+}}}\right ), \end{align*}
as desired.
4. Analysis of the exact recovery algorithm
In this section, we establish Propositions 2.7 and 2.8, which are the building blocks of the proof of Theorem 1.3. Remember that SPEX uses the result of SPARC and performs
![]() $O(\ln (n))$
cleanup steps to fix possible mistakes. Each of these cleanup steps updates the estimate via thresholding for every individual. Proposition 2.7 ensures that this thresholding is algorithmically possible as intended. Proposition 2.8 then guarantees that every single cleanup step decreases the number of mistakes enough. We continue to work with the spatially coupled design
$O(\ln (n))$
cleanup steps to fix possible mistakes. Each of these cleanup steps updates the estimate via thresholding for every individual. Proposition 2.7 ensures that this thresholding is algorithmically possible as intended. Proposition 2.8 then guarantees that every single cleanup step decreases the number of mistakes enough. We continue to work with the spatially coupled design
![]() $\mathbf{G}_{\mathrm{sc}}$
from Section 2.3 and keep the notation and assumptions from (2.13)–(2.17).
$\mathbf{G}_{\mathrm{sc}}$
from Section 2.3 and keep the notation and assumptions from (2.13)–(2.17).
4.1. Proof of Proposition 2.7
Assume that
![]() $c\gt c_{\mathrm{ex},1}(d,\theta )+\varepsilon$
, and let
$c\gt c_{\mathrm{ex},1}(d,\theta )+\varepsilon$
, and let
![]() $c^{\prime}=c_{\mathrm{ex},1}(d,\theta )+\varepsilon /2$
. Since
$c^{\prime}=c_{\mathrm{ex},1}(d,\theta )+\varepsilon /2$
. Since
![]() $c\gt c^{\prime}+\varepsilon /2$
, the definitions (1.11) of
$c\gt c^{\prime}+\varepsilon /2$
, the definitions (1.11) of
![]() $c_{\mathrm{ex},1}(d,\theta )$
and (1.6) of
$c_{\mathrm{ex},1}(d,\theta )$
and (1.6) of
![]() $\mathscr{Y}(c^{\prime},d,\theta )$
ensure that for small enough
$\mathscr{Y}(c^{\prime},d,\theta )$
ensure that for small enough
![]() $\delta \gt 0$
, we can find an open interval
$\delta \gt 0$
, we can find an open interval
![]() $\mathscr{I}\subseteq \mathscr{Y}(c^{\prime},d,\theta )$
with rational boundary points such that Z1 is satisfied.
$\mathscr{I}\subseteq \mathscr{Y}(c^{\prime},d,\theta )$
with rational boundary points such that Z1 is satisfied.
Let
![]() $\,\,\,\bar{\!\!\!\mathscr{I}}\,$
be the closure of
$\,\,\,\bar{\!\!\!\mathscr{I}}\,$
be the closure of
![]() $\mathscr{I}$
. Then by the definition of
$\mathscr{I}$
. Then by the definition of
![]() $c_{\mathrm{ex},1}(d,\theta )$
, there exists a function
$c_{\mathrm{ex},1}(d,\theta )$
, there exists a function
![]() $z\,:\, \,\,\,\bar{\!\!\!\mathscr{I}}\,\to [p_{01},p_{11}]$
such that for all
$z\,:\, \,\,\,\bar{\!\!\!\mathscr{I}}\,\to [p_{01},p_{11}]$
such that for all
![]() $y\in \,\,\,\bar{\!\!\!\mathscr{I}}\,$
we have
$y\in \,\,\,\bar{\!\!\!\mathscr{I}}\,$
we have
In fact, because the Kullback–Leibler divergence is strictly convex, the equation (4.1) defines
![]() $z(y)$
uniquely. The inverse function theorem implies that the function
$z(y)$
uniquely. The inverse function theorem implies that the function
![]() $z(y)$
is continuous and therefore uniformly continuous on
$z(y)$
is continuous and therefore uniformly continuous on
![]() $\,\,\,\bar{\!\!\!\mathscr{I}}\,$
. Additionally, once again, because the Kullback–Leibler divergence is convex and
$\,\,\,\bar{\!\!\!\mathscr{I}}\,$
. Additionally, once again, because the Kullback–Leibler divergence is convex and
![]() $c\gt c_{\mathrm{ex},1}(d,\theta )$
, for all
$c\gt c_{\mathrm{ex},1}(d,\theta )$
, for all
![]() $y\in \,\,\,\bar{\!\!\!\mathscr{I}}\,$
, we have
$y\in \,\,\,\bar{\!\!\!\mathscr{I}}\,$
, we have
Therefore, there exists
![]() $\hat \delta =\hat \delta (c,d,\theta )\gt 0$
such that for all
$\hat \delta =\hat \delta (c,d,\theta )\gt 0$
such that for all
![]() $y\in \,\,\,\bar{\!\!\!\mathscr{I}}\,$
, we have
$y\in \,\,\,\bar{\!\!\!\mathscr{I}}\,$
, we have
Combining (4.1) and (4.2), we find a continuous
![]() $\hat z \,:\, \,\,\,\bar{\!\!\!\mathscr{I}}\,\to [p_{01},p_{11}]$
such that for small enough
$\hat z \,:\, \,\,\,\bar{\!\!\!\mathscr{I}}\,\to [p_{01},p_{11}]$
such that for small enough
![]() $\delta \gt 0$
for all
$\delta \gt 0$
for all
![]() $y\in [0,1]$
, we have
$y\in [0,1]$
, we have
Additionally, by uniform continuity for any given
![]() $0\lt \varepsilon ^{\prime}\lt \delta /2$
(which may depend arbitrarily on
$0\lt \varepsilon ^{\prime}\lt \delta /2$
(which may depend arbitrarily on
![]() $\delta$
and
$\delta$
and
![]() $\mathscr{I}$
), we can choose
$\mathscr{I}$
), we can choose
![]() $\delta ^{\prime}\gt 0$
small enough so that
$\delta ^{\prime}\gt 0$
small enough so that
Finally, let
![]() $y_0,\ldots, y_\nu$
with
$y_0,\ldots, y_\nu$
with
![]() $\nu =\nu (\delta ^{\prime},\varepsilon ^{\prime})\gt 0$
be a large enough number of equally spaced points in
$\nu =\nu (\delta ^{\prime},\varepsilon ^{\prime})\gt 0$
be a large enough number of equally spaced points in
![]() $\,\,\,\bar{\!\!\!\mathscr{I}}\,=[y_0,y_\nu ]$
. Then for each
$\,\,\,\bar{\!\!\!\mathscr{I}}\,=[y_0,y_\nu ]$
. Then for each
![]() $i$
, we pick
$i$
, we pick
![]() $\mathscr{Z}(y_i)\in [p_{01},p_{11}]\cap \mathbb{Q}$
such that
$\mathscr{Z}(y_i)\in [p_{01},p_{11}]\cap \mathbb{Q}$
such that
![]() $|\hat z(y_i)-\mathscr{Z}(y_i)|$
is small enough. Extend
$|\hat z(y_i)-\mathscr{Z}(y_i)|$
is small enough. Extend
![]() $\mathscr{Z}$
to a step function
$\mathscr{Z}$
to a step function
![]() $\,\,\,\bar{\!\!\!\mathscr{I}}\,\to \mathbb{Q}\cap [0,1]$
by letting
$\,\,\,\bar{\!\!\!\mathscr{I}}\,\to \mathbb{Q}\cap [0,1]$
by letting
![]() $\mathscr{Z}(y)=\mathscr{Z}(y_{i-1})$
for all
$\mathscr{Z}(y)=\mathscr{Z}(y_{i-1})$
for all
![]() $y\in (y_{i-1},y_i)$
for
$y\in (y_{i-1},y_i)$
for
![]() $1\leq i\leq \nu$
. Since
$1\leq i\leq \nu$
. Since
![]() $y\mapsto \hat z(y)$
is uniformly continuous, we can choose
$y\mapsto \hat z(y)$
is uniformly continuous, we can choose
![]() $\nu$
large enough so that (4.3)–(4.5) imply
$\nu$
large enough so that (4.3)–(4.5) imply
 \begin{align*} cd(1-\theta )\left \lbrack{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{11}}}}\right )}\right \rbrack &\gt \theta +\delta &&\text{for all }y\in \,\,\bar{\!\!\!\mathscr{I}},\\ cd(1-\theta )\left \lbrack{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{01}}}}\right )}\right \rbrack &\gt 1+\delta &&\text{ for all }y\in \,\,\bar{\!\!\!\mathscr{I}},\\ |\mathscr{Z}(y)-\mathscr{Z}(y^{\prime})|&\lt \varepsilon ^{\prime}&&\text{ for all } y,y^{\prime}\in \,\,\bar{\!\!\!\mathscr{I}}\, \text{ such that } |y-y^{\prime}|\lt \delta ^{\prime}, \end{align*}
\begin{align*} cd(1-\theta )\left \lbrack{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{11}}}}\right )}\right \rbrack &\gt \theta +\delta &&\text{for all }y\in \,\,\bar{\!\!\!\mathscr{I}},\\ cd(1-\theta )\left \lbrack{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right )+yD_{\mathrm{KL}}\left ({{{\mathscr{Z}(y)}\|{p_{01}}}}\right )}\right \rbrack &\gt 1+\delta &&\text{ for all }y\in \,\,\bar{\!\!\!\mathscr{I}},\\ |\mathscr{Z}(y)-\mathscr{Z}(y^{\prime})|&\lt \varepsilon ^{\prime}&&\text{ for all } y,y^{\prime}\in \,\,\bar{\!\!\!\mathscr{I}}\, \text{ such that } |y-y^{\prime}|\lt \delta ^{\prime}, \end{align*}
as claimed.
4.2. Proof of Proposition 2.8
As in the proof of Proposition 2.6 in Section 3.3, we will first investigate an idealised scenario where we assume that the ground truth
![]() $\boldsymbol{\sigma }$
is known. Then we will use the expansion property provided by Lemma 3.3 to connect this idealised scenario with the actual steps of the algorithm.
$\boldsymbol{\sigma }$
is known. Then we will use the expansion property provided by Lemma 3.3 to connect this idealised scenario with the actual steps of the algorithm.
In order to study the idealised scenario, for
![]() $x\in V[i]$
and
$x\in V[i]$
and
![]() $j\in [s]$
, we introduce
$j\in [s]$
, we introduce
 \begin{align*} \boldsymbol{Y}_{x,j}&= \left |{ \left \{{ a \in F[i+j-1]\cap \partial x\,:\, V_1\cap \partial a\subseteq \left \{{x}\right \}}\right \}}\right |,& \boldsymbol{Z}_{x,j}&= \left |{ \left \{{ a \in F^+[i+j-1]\cap \partial x\,:\, V_1\cap \partial a\subseteq \left \{{x}\right \}}\right \}}\right |,\\ \boldsymbol{Y}_x&= \sum _{j=1}^s\boldsymbol{Y}_{x,j},&\boldsymbol{Z}_x&= \sum _{j=1}^s\boldsymbol{Z}_{x,j}. \end{align*}
\begin{align*} \boldsymbol{Y}_{x,j}&= \left |{ \left \{{ a \in F[i+j-1]\cap \partial x\,:\, V_1\cap \partial a\subseteq \left \{{x}\right \}}\right \}}\right |,& \boldsymbol{Z}_{x,j}&= \left |{ \left \{{ a \in F^+[i+j-1]\cap \partial x\,:\, V_1\cap \partial a\subseteq \left \{{x}\right \}}\right \}}\right |,\\ \boldsymbol{Y}_x&= \sum _{j=1}^s\boldsymbol{Y}_{x,j},&\boldsymbol{Z}_x&= \sum _{j=1}^s\boldsymbol{Z}_{x,j}. \end{align*}
Thus,
![]() $\boldsymbol{Y}_{x,j}$
is the number of untainted tests in compartment
$\boldsymbol{Y}_{x,j}$
is the number of untainted tests in compartment
![]() $F[i+j-1]$
that contain
$F[i+j-1]$
that contain
![]() $x$
, that is, test that does not contain another infected individual. Moreover,
$x$
, that is, test that does not contain another infected individual. Moreover,
![]() $\boldsymbol{Z}_{x,j}$
is the number of positively displayed untainted tests. Finally,
$\boldsymbol{Z}_{x,j}$
is the number of positively displayed untainted tests. Finally,
![]() $\boldsymbol{Y}_x,\boldsymbol{Z}_x$
are the sums of these quantities on
$\boldsymbol{Y}_x,\boldsymbol{Z}_x$
are the sums of these quantities on
![]() $j\in [s]$
. The following lemma provides an estimate of the number of individuals
$j\in [s]$
. The following lemma provides an estimate of the number of individuals
![]() $x$
with a certain value of
$x$
with a certain value of
![]() $\boldsymbol{Y}_x$
.
$\boldsymbol{Y}_x$
.
Lemma 4.1.
w.h.p., for all
![]() $0\leq Y\leq \Delta$
and all
$0\leq Y\leq \Delta$
and all
![]() $i\in [\ell ]$
, we have
$i\in [\ell ]$
, we have
Proof. Let
![]() $1\leq i\leq \ell$
and consider any
$1\leq i\leq \ell$
and consider any
![]() $x\in V[i]$
. Further, obtain
$x\in V[i]$
. Further, obtain
![]() $\mathbf{G}_{\mathrm{sc}}-x$
from
$\mathbf{G}_{\mathrm{sc}}-x$
from
![]() $\mathbf{G}_{\mathrm{sc}}$
by deleting individual
$\mathbf{G}_{\mathrm{sc}}$
by deleting individual
![]() $x$
(and, of course, removing
$x$
(and, of course, removing
![]() $x$
from all tests). Additionally, obtain
$x$
from all tests). Additionally, obtain
![]() $\mathbf{G}_{\mathrm{sc}}^{\prime}$
from
$\mathbf{G}_{\mathrm{sc}}^{\prime}$
from
![]() $\mathbf{G}_{\mathrm{sc}}-x$
by re-inserting
$\mathbf{G}_{\mathrm{sc}}-x$
by re-inserting
![]() $x$
and assigning
$x$
and assigning
![]() $x$
to
$x$
to
![]() $\Delta /s$
random tests in the compartments
$\Delta /s$
random tests in the compartments
![]() $F[i+j-1]$
for
$F[i+j-1]$
for
![]() $j\in [s]$
as per the construction of the spatially coupled test design. Then the random test designs
$j\in [s]$
as per the construction of the spatially coupled test design. Then the random test designs
![]() $\mathbf{G}_{\mathrm{sc}}$
and
$\mathbf{G}_{\mathrm{sc}}$
and
![]() $\mathbf{G}_{\mathrm{sc}}^{\prime}$
are identically distributed.
$\mathbf{G}_{\mathrm{sc}}^{\prime}$
are identically distributed.
Let
![]() $\mathfrak{E}$
be the event that
$\mathfrak{E}$
be the event that
![]() $\mathbf{G}_{\mathrm{sc}}$
enjoys properties G1 and G2 from Proposition 2.3. Then Proposition 2.3 shows that
$\mathbf{G}_{\mathrm{sc}}$
enjoys properties G1 and G2 from Proposition 2.3. Then Proposition 2.3 shows that
Moreover, given
![]() $\mathfrak{E}$
for every
$\mathfrak{E}$
for every
![]() $j\in [s]$
, the number of tests in
$j\in [s]$
, the number of tests in
![]() $F[i+j-1]$
that contain no infected individual aside from
$F[i+j-1]$
that contain no infected individual aside from
![]() $x$
satisfies
$x$
satisfies
this follows from the bounds on
![]() $F_0[i+j-1]$
provided by G2 and the fact that discarding
$F_0[i+j-1]$
provided by G2 and the fact that discarding
![]() $x$
can change the numbers of actually positive/negative tests by no more than
$x$
can change the numbers of actually positive/negative tests by no more than
![]() $\Delta$
.
$\Delta$
.
Now consider the process of re-inserting
![]() $x$
to obtain
$x$
to obtain
![]() $\mathbf{G}_{\mathrm{sc}}^{\prime}$
. Then (4.9) shows that given
$\mathbf{G}_{\mathrm{sc}}^{\prime}$
. Then (4.9) shows that given
![]() $\mathfrak{E}$
, we have
$\mathfrak{E}$
, we have
These hypergeometric variables are mutually independent given
![]() $\mathbf{G}_{\mathrm{sc}}-x$
. Therefore, Lemma 1.6 implies that on
$\mathbf{G}_{\mathrm{sc}}-x$
. Therefore, Lemma 1.6 implies that on
![]() $\mathfrak{E}$
,
$\mathfrak{E}$
,
This estimate holds independently of the infection status
![]() $\boldsymbol{\sigma }_x$
. Thus, the assertion follows from (4.8), (4.10), and Markov’s inequality.
$\boldsymbol{\sigma }_x$
. Thus, the assertion follows from (4.8), (4.10), and Markov’s inequality.
As a next step, we argue that for
![]() $c$
beyond the threshold
$c$
beyond the threshold
![]() $c_{\mathrm{ex},1}(d,\theta )$
, the function
$c_{\mathrm{ex},1}(d,\theta )$
, the function
![]() $\mathscr{Z}$
from Proposition 2.7 separates the infected from the uninfected individuals w.h.p.
$\mathscr{Z}$
from Proposition 2.7 separates the infected from the uninfected individuals w.h.p.
Lemma 4.2.
Assume that
![]() $c\gt c^*(d,\theta )+\varepsilon$
. Let
$c\gt c^*(d,\theta )+\varepsilon$
. Let
![]() $\mathscr{I}=(l,r),\delta \gt 0$
be the interval and the number from Proposition 2.7
, choose
$\mathscr{I}=(l,r),\delta \gt 0$
be the interval and the number from Proposition 2.7
, choose
![]() $\varepsilon ^{\prime}\gt 0$
sufficiently small, and let
$\varepsilon ^{\prime}\gt 0$
sufficiently small, and let
![]() $\delta ^{\prime},\mathscr{Z}$
be such that
Z1
–
Z4
are satisfied.
$\delta ^{\prime},\mathscr{Z}$
be such that
Z1
–
Z4
are satisfied.
-
(i) For all
 $x\in V_1$
, we have
$x\in V_1$
, we have
 $\boldsymbol{Y}_x/\Delta \in (l+\varepsilon ^{\prime},r-\varepsilon ^{\prime})$
and
$\boldsymbol{Y}_x/\Delta \in (l+\varepsilon ^{\prime},r-\varepsilon ^{\prime})$
and
 $\boldsymbol{Z}_x/\Delta \gt \mathscr{Z}(\boldsymbol{Y}_x/\Delta )+3\varepsilon ^{\prime}$
.
$\boldsymbol{Z}_x/\Delta \gt \mathscr{Z}(\boldsymbol{Y}_x/\Delta )+3\varepsilon ^{\prime}$
. -
(ii) For all
 $x\in V_0$
with
$x\in V_0$
with
 $\boldsymbol{Y}_x/\Delta \in \mathscr{I}$
, we have
$\boldsymbol{Y}_x/\Delta \in \mathscr{I}$
, we have
 $\boldsymbol{Z}_x/\Delta \lt \mathscr{Z}(\boldsymbol{Y}_x/\Delta )-3\varepsilon ^{\prime}$
.
$\boldsymbol{Z}_x/\Delta \lt \mathscr{Z}(\boldsymbol{Y}_x/\Delta )-3\varepsilon ^{\prime}$
.
Proof. Let
![]() $\mathfrak{E}$
be the event that the bounds (4.6)–(4.7) hold for all
$\mathfrak{E}$
be the event that the bounds (4.6)–(4.7) hold for all
![]() $0\leq Y\leq \Delta$
. Then (4.7) and Proposition 2.7, Z1 show that w.h.p.
$0\leq Y\leq \Delta$
. Then (4.7) and Proposition 2.7, Z1 show that w.h.p.
![]() $\boldsymbol{Y}_x/\Delta \in (l+\varepsilon ^{\prime},r-\varepsilon ^{\prime})$
for all
$\boldsymbol{Y}_x/\Delta \in (l+\varepsilon ^{\prime},r-\varepsilon ^{\prime})$
for all
![]() $x\in V_1$
, provided
$x\in V_1$
, provided
![]() $\varepsilon ^{\prime}\gt 0$
is small enough. Moreover, for a fixed
$\varepsilon ^{\prime}\gt 0$
is small enough. Moreover, for a fixed
![]() $0\leq Y\leq \Delta$
such that
$0\leq Y\leq \Delta$
such that
![]() $Y/\Delta \in \mathscr{I}$
and
$Y/\Delta \in \mathscr{I}$
and
![]() $i\in [\ell ]$
, let
$i\in [\ell ]$
, let
![]() $\boldsymbol{X}_1(Y)$
be the number of variables
$\boldsymbol{X}_1(Y)$
be the number of variables
![]() $x\in V_1[i]$
such that
$x\in V_1[i]$
such that
![]() $\boldsymbol{Y}_x=Y$
and
$\boldsymbol{Y}_x=Y$
and
![]() $\boldsymbol{Z}_x\leq \Delta \mathscr{Z}(Y/\Delta )+3\varepsilon ^{\prime}\Delta$
. Since
$\boldsymbol{Z}_x\leq \Delta \mathscr{Z}(Y/\Delta )+3\varepsilon ^{\prime}\Delta$
. Since
![]() $x$
itself is infected, all tests
$x$
itself is infected, all tests
![]() $a\in \partial x$
are actually positive. Therefore,
$a\in \partial x$
are actually positive. Therefore,
![]() $a$
is displayed positively with probability
$a$
is displayed positively with probability
![]() $p_{11}$
. As a consequence, Lemma 1.5 shows that
$p_{11}$
. As a consequence, Lemma 1.5 shows that
Combining (4.7) and (4.11), recalling that
![]() $k=\lceil n^\theta \rceil$
and choosing
$k=\lceil n^\theta \rceil$
and choosing
![]() $\varepsilon ^{\prime}\gt 0$
sufficiently small, we obtain
$\varepsilon ^{\prime}\gt 0$
sufficiently small, we obtain
 \begin{align} \mathbb{E}&\left \lbrack{\sum _{x\in V_1[i]}\unicode{x1D7D9}\left \{{\boldsymbol{Y}_x=Y,\,\boldsymbol{Z}_x\leq \Delta \mathscr{Z}(\boldsymbol{Y}_x/\Delta )+3\varepsilon ^{\prime}\Delta }\right \}\mid \mathfrak{E}}\right \rbrack\nonumber\\&\leq k\exp \left ({-\Delta D_{\mathrm{KL}}\left ({{{Y/\Delta }\|{\exp ({-}d)}}}\right )-YD_{\mathrm{KL}}\left ({{{\mathscr{Z}(Y/\Delta )+3\varepsilon ^{\prime}\Delta /Y}\|{p_{11}}}}\right )+o(\Delta )}\right ) \end{align}
\begin{align} \mathbb{E}&\left \lbrack{\sum _{x\in V_1[i]}\unicode{x1D7D9}\left \{{\boldsymbol{Y}_x=Y,\,\boldsymbol{Z}_x\leq \Delta \mathscr{Z}(\boldsymbol{Y}_x/\Delta )+3\varepsilon ^{\prime}\Delta }\right \}\mid \mathfrak{E}}\right \rbrack\nonumber\\&\leq k\exp \left ({-\Delta D_{\mathrm{KL}}\left ({{{Y/\Delta }\|{\exp ({-}d)}}}\right )-YD_{\mathrm{KL}}\left ({{{\mathscr{Z}(Y/\Delta )+3\varepsilon ^{\prime}\Delta /Y}\|{p_{11}}}}\right )+o(\Delta )}\right ) \end{align}
Taking a union bound on the
![]() $O(\ln ^2n)$
possible combinations
$O(\ln ^2n)$
possible combinations
![]() $(i,Y)$
, we see that (i) follows from (4.13). A similar argument based on Proposition 2.7, Z3 yields (ii).
$(i,Y)$
, we see that (i) follows from (4.13). A similar argument based on Proposition 2.7, Z3 yields (ii).
Proof of Proposition
2.8
. For
![]() $t = 1 \dots \left \lceil \ln n\right \rceil$
, consider the set of misclassified individuals after
$t = 1 \dots \left \lceil \ln n\right \rceil$
, consider the set of misclassified individuals after
![]() $t-1$
iterations:
$t-1$
iterations:
Propositions 2.5 and 2.6 show that w.h.p., the size of the initial set satisfies
We are going to argue by induction that
![]() $|\mathscr{M}_t|$
decays geometrically. Apart from the bound (4.14), this argument depends on only two conditions. First, that the random graph
$|\mathscr{M}_t|$
decays geometrically. Apart from the bound (4.14), this argument depends on only two conditions. First, that the random graph
![]() $\mathbf{G}_{\mathrm{sc}}$
indeed enjoys the expansion property from Lemma 3.3. Second, that (i)–(ii) from Lemma 4.2 hold. Let
$\mathbf{G}_{\mathrm{sc}}$
indeed enjoys the expansion property from Lemma 3.3. Second, that (i)–(ii) from Lemma 4.2 hold. Let
![]() $\mathfrak{E}$
be the event that these two conditions are satisfied and that (4.14) holds. Propositions 2.5 and 2.6 and Lemmas 3.3 and 4.2 show that
$\mathfrak{E}$
be the event that these two conditions are satisfied and that (4.14) holds. Propositions 2.5 and 2.6 and Lemmas 3.3 and 4.2 show that
![]() ${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o(1)$
.
${\mathbb{P}}\left \lbrack{\mathfrak{E}}\right \rbrack =1-o(1)$
.
To complete the proof, we are going to show by induction on
![]() $t\geq 2$
that on
$t\geq 2$
that on
![]() $\mathfrak{E}$
,
$\mathfrak{E}$
,
Indeed, consider the set
 \begin{align*} \mathscr{M}_{t}^*=\left \{{x\in V[s+1]\cup \cdots V[\ell ]\,:\, \sum _{a\in \partial x\setminus F[0]}\left |{\partial a \cap \mathscr{M}_{t-1}\setminus \left \{{x}\right \}}\right | \geq \Delta /\ln \ln n}\right \}. \end{align*}
\begin{align*} \mathscr{M}_{t}^*=\left \{{x\in V[s+1]\cup \cdots V[\ell ]\,:\, \sum _{a\in \partial x\setminus F[0]}\left |{\partial a \cap \mathscr{M}_{t-1}\setminus \left \{{x}\right \}}\right | \geq \Delta /\ln \ln n}\right \}. \end{align*}
Since by (4.14) and induction we know that
![]() $\left |{\mathscr{M}_{t-1}}\right | \leq k\exp \left ({-\Omega (\ln ^{1/8} n)}\right )$
, the expansion property from Lemma 3.3 implies that
$\left |{\mathscr{M}_{t-1}}\right | \leq k\exp \left ({-\Omega (\ln ^{1/8} n)}\right )$
, the expansion property from Lemma 3.3 implies that
![]() $\mathscr{M}_t^*\leq \mathscr{M}_{t-1}/3$
. Therefore, to complete the proof of (4.15), it suffices to show that
$\mathscr{M}_t^*\leq \mathscr{M}_{t-1}/3$
. Therefore, to complete the proof of (4.15), it suffices to show that
![]() $\mathscr{M}_{t}\subseteq \mathscr{M}_{t}^*$
.
$\mathscr{M}_{t}\subseteq \mathscr{M}_{t}^*$
.
To see this, suppose that
![]() $x\in \mathscr{M}_{t}$
.
$x\in \mathscr{M}_{t}$
.
-
Case 1:
 $x\in V_1$
but
$x\in V_1$
but
 $Y_x(\tau ^{(t-1)})/\Delta \not \in \mathscr{I}$
Lemma 4.2 (i) ensures that
$Y_x(\tau ^{(t-1)})/\Delta \not \in \mathscr{I}$
Lemma 4.2 (i) ensures that
 $\boldsymbol{Y}_x/\Delta \in (l+\varepsilon ^{\prime},r-\varepsilon ^{\prime})$
. Therefore, the case
$\boldsymbol{Y}_x/\Delta \in (l+\varepsilon ^{\prime},r-\varepsilon ^{\prime})$
. Therefore, the case
 $Y_x(\tau ^{(t-1)})/\Delta \not \in \mathscr{I}$
can occur only if at least
$Y_x(\tau ^{(t-1)})/\Delta \not \in \mathscr{I}$
can occur only if at least
 $\varepsilon ^{\prime}\Delta$
tests
$\varepsilon ^{\prime}\Delta$
tests
 $a\in \partial x$
contain a misclassified individual
$a\in \partial x$
contain a misclassified individual
 $x^{\prime}\in \mathscr{M}_{t-1}$
. Hence,
$x^{\prime}\in \mathscr{M}_{t-1}$
. Hence,
 $x\in \mathscr{M}_t^*$
.
$x\in \mathscr{M}_t^*$
. -
Case 2:
 $x\in V_1$
and
$x\in V_1$
and
 $Y_x(\tau ^{(t-1)})/\Delta \not \in \mathscr{I}$
but
$Y_x(\tau ^{(t-1)})/\Delta \not \in \mathscr{I}$
but
 $Z_x(\tau ^{(i)})/\Delta \leq \mathscr{Z}(Y_x(\tau ^{(i)})/\Delta )$
by Lemma 4.2, (i) we have
$Z_x(\tau ^{(i)})/\Delta \leq \mathscr{Z}(Y_x(\tau ^{(i)})/\Delta )$
by Lemma 4.2, (i) we have
 $\boldsymbol{Z}_x/\Delta \gt \mathscr{Z}(\boldsymbol{Y}_x/\Delta )+2\varepsilon ^{\prime}$
. Thus, if
$\boldsymbol{Z}_x/\Delta \gt \mathscr{Z}(\boldsymbol{Y}_x/\Delta )+2\varepsilon ^{\prime}$
. Thus, if
 $Z_x(\tau ^{(t-1)})/\Delta \leq \mathscr{Z}(Y_x(\tau ^{(t-1)})/\Delta )$
, then by the continuity property Z4, we have
$Z_x(\tau ^{(t-1)})/\Delta \leq \mathscr{Z}(Y_x(\tau ^{(t-1)})/\Delta )$
, then by the continuity property Z4, we have
 $|Y_x(\tau ^{(t-1)})-\boldsymbol{Y}_x|\gt \varepsilon ^{\prime}\Delta$
. Consequently, as in Case 1 we have
$|Y_x(\tau ^{(t-1)})-\boldsymbol{Y}_x|\gt \varepsilon ^{\prime}\Delta$
. Consequently, as in Case 1 we have
 $x\in \mathscr{M}_t^*$
.
$x\in \mathscr{M}_t^*$
. -
Case 3:
 $x\in V_0$
as in the previous cases, due to Z4 and Lemma 4.2, (ii) the event
$x\in V_0$
as in the previous cases, due to Z4 and Lemma 4.2, (ii) the event
 $x\in \mathscr{M}_t$
can occur only if
$x\in \mathscr{M}_t$
can occur only if
 $|\boldsymbol{Y}_x-Y_v(\tau ^{(t-1)})|\gt \varepsilon ^{\prime}\Delta$
. Thus,
$|\boldsymbol{Y}_x-Y_v(\tau ^{(t-1)})|\gt \varepsilon ^{\prime}\Delta$
. Thus,
 $x\in \mathscr{M}_t^*$
.
$x\in \mathscr{M}_t^*$
.
Hence,
![]() $\mathscr{M}_{t}\subseteq \mathscr{M}_{t}^*$
, which completes the proof.
$\mathscr{M}_{t}\subseteq \mathscr{M}_{t}^*$
, which completes the proof.
5. Lower bound on the constant column design
5.1. Proof of Proposition 2.10
The following lemma is an adaptation of Proposition 2.3 (G2) to
![]() $\mathbf{G}_{\mathrm{cc}}$
.
$\mathbf{G}_{\mathrm{cc}}$
.
Lemma 5.1.
The random graph
![]() $\mathbf{G}_{\mathrm{cc}}$
enjoys the following properties with probability
$\mathbf{G}_{\mathrm{cc}}$
enjoys the following properties with probability
![]() $1-o(n^{-2})$
:
$1-o(n^{-2})$
:
The proof of Lemma 5.1 is similar to that of Proposition 2.3 (see Section 3.1); the details are thus omitted.
Proof of Proposition 2.10 . The definition (2.2) of the weight functions ensures that
Substituting in the estimates from (5.1) to (5.4) completes the proof.
5.2. Proof of Proposition 2.11 (indistinguishable configurations with high overlap)
Let
![]() $\mathscr{X}_r(Y)$
be the set of individuals
$\mathscr{X}_r(Y)$
be the set of individuals
![]() $x\in V_r$
such that
$x\in V_r$
such that
Hence,
![]() $x$
participates in precisely
$x$
participates in precisely
![]() $Y$
tests that do not contain another infected individual.
$Y$
tests that do not contain another infected individual.
Lemma 5.2.
Let
![]() $y\in \mathscr{Y}(c,d,\theta )$
be such that
$y\in \mathscr{Y}(c,d,\theta )$
be such that
![]() $y\Delta$
is an integer. Then w.h.p., we have
$y\Delta$
is an integer. Then w.h.p., we have
Proof. Let
![]() $Y=y\Delta$
, and let
$Y=y\Delta$
, and let
![]() $\mathscr{E}$
be the event that the bounds (5.1)–(5.4) hold. We begin by computing
$\mathscr{E}$
be the event that the bounds (5.1)–(5.4) hold. We begin by computing
![]() $\mathbb{E}|\mathscr{X}_1(Y)|$
. By exchangeability, we may condition on the event
$\mathbb{E}|\mathscr{X}_1(Y)|$
. By exchangeability, we may condition on the event
![]() $\mathscr{S}=\{\boldsymbol{\sigma }_{x_1}=\cdots =\boldsymbol{\sigma }_{x_k}=1\}$
, that is, precisely the first
$\mathscr{S}=\{\boldsymbol{\sigma }_{x_1}=\cdots =\boldsymbol{\sigma }_{x_k}=1\}$
, that is, precisely the first
![]() $k$
individuals are infected. Hence, by the linearity of expectation, it suffices to prove that
$k$
individuals are infected. Hence, by the linearity of expectation, it suffices to prove that
Let
![]() ${\boldsymbol{G}}^{\prime}=\mathbf{G}_{\mathrm{cc}}-x_1$
be the random design without
${\boldsymbol{G}}^{\prime}=\mathbf{G}_{\mathrm{cc}}-x_1$
be the random design without
![]() $x_1$
, and let
$x_1$
, and let
![]() $F^{\prime}_0$
be the set of actually negative tests of
$F^{\prime}_0$
be the set of actually negative tests of
![]() ${\boldsymbol{G}}^{\prime}$
. Given
${\boldsymbol{G}}^{\prime}$
. Given
![]() $\boldsymbol{m}^{\prime}_0=|F^{\prime}_0|$
, the number of tests
$\boldsymbol{m}^{\prime}_0=|F^{\prime}_0|$
, the number of tests
![]() $a\in \partial x_1$
such that
$a\in \partial x_1$
such that
![]() $\partial a\setminus \{x_1\}\subseteq V_0$
has distribution
$\partial a\setminus \{x_1\}\subseteq V_0$
has distribution
![]() $\textrm{Hyp}(m,\boldsymbol{m}^{\prime}_0,\Delta )$
because
$\textrm{Hyp}(m,\boldsymbol{m}^{\prime}_0,\Delta )$
because
![]() $x_1$
joins precisely
$x_1$
joins precisely
![]() $\Delta$
tests independently of all other individuals. Hence, (1.19) yields
$\Delta$
tests independently of all other individuals. Hence, (1.19) yields
Expanding (5.8) via Stirling’s formula and using the bounds (5.1)–(5.2), we obtain (5.7), which implies that
Since the above argument does not depend on the infection status of
![]() $x_1$
, analogously we obtain
$x_1$
, analogously we obtain
To turn (5.9)–(5.10) into “with high probability” bounds, we resort to the second moment method. Specifically, we are going to show that
Then the assertion is an immediate consequence of (5.9)–(5.12) and Lemma 5.1.
For similar reasons as above, it suffices to prove (5.11). More precisely, we merely need to show that
To compute the probability on the l.h.s., obtain
![]() ${\boldsymbol{G}}^{\prime\prime}=\mathbf{G}_{\mathrm{cc}}-x_1-x_2$
by removing
${\boldsymbol{G}}^{\prime\prime}=\mathbf{G}_{\mathrm{cc}}-x_1-x_2$
by removing
![]() $x_1,x_2$
. Let
$x_1,x_2$
. Let
![]() $\boldsymbol{m}^{\prime\prime}_0$
be the number of actually negative tests of
$\boldsymbol{m}^{\prime\prime}_0$
be the number of actually negative tests of
![]() ${\boldsymbol{G}}^{\prime\prime}$
. We claim that on
${\boldsymbol{G}}^{\prime\prime}$
. We claim that on
![]() $\mathscr{E}$
,
$\mathscr{E}$
,
 \begin{align} {\mathbb{P}}\left \lbrack{x_1,x_2\in \mathscr{X}_1(Y)\mid \mathscr{S},\boldsymbol{m}^{\prime\prime}_0}\right \rbrack =\sum _{I=0}^{\Delta -Y}\binom{\boldsymbol{m}^{\prime\prime}_0}{I}\binom{\boldsymbol{m}^{\prime\prime}_0}{Y}\binom{\boldsymbol{m}^{\prime\prime}_0-Y}{Y}\binom{m-\boldsymbol{m}^{\prime\prime}_0}{\Delta -Y-I}\binom{m-\boldsymbol{m}^{\prime\prime}_0}{\Delta -Y-I} \binom{m}{\Delta }^{-2}. \end{align}
\begin{align} {\mathbb{P}}\left \lbrack{x_1,x_2\in \mathscr{X}_1(Y)\mid \mathscr{S},\boldsymbol{m}^{\prime\prime}_0}\right \rbrack =\sum _{I=0}^{\Delta -Y}\binom{\boldsymbol{m}^{\prime\prime}_0}{I}\binom{\boldsymbol{m}^{\prime\prime}_0}{Y}\binom{\boldsymbol{m}^{\prime\prime}_0-Y}{Y}\binom{m-\boldsymbol{m}^{\prime\prime}_0}{\Delta -Y-I}\binom{m-\boldsymbol{m}^{\prime\prime}_0}{\Delta -Y-I} \binom{m}{\Delta }^{-2}. \end{align}
Indeed, we first choose
![]() $0\leq I\leq \Delta -Y$
tests that are actually negative in
$0\leq I\leq \Delta -Y$
tests that are actually negative in
![]() ${\boldsymbol{G}}^{\prime\prime}$
that both
${\boldsymbol{G}}^{\prime\prime}$
that both
![]() $x_1,x_2$
will join. Observe that these tests
$x_1,x_2$
will join. Observe that these tests
![]() $a$
do not satisfy
$a$
do not satisfy
![]() $\partial a\setminus \{x_{1/2}\}\subseteq V_0$
. Then we choose
$\partial a\setminus \{x_{1/2}\}\subseteq V_0$
. Then we choose
![]() $Y$
distinct actually negative tests for
$Y$
distinct actually negative tests for
![]() $x_1$
and
$x_1$
and
![]() $x_2$
to join. Finally, we choose the remaining
$x_2$
to join. Finally, we choose the remaining
![]() $\Delta -Y-I$
tests for
$\Delta -Y-I$
tests for
![]() $x_1,x_2$
among the actually positive tests of
$x_1,x_2$
among the actually positive tests of
![]() ${\boldsymbol{G}}^{\prime\prime}$
.
${\boldsymbol{G}}^{\prime\prime}$
.
Since on
![]() $\mathscr{E}$
, the total number
$\mathscr{E}$
, the total number
![]() $\boldsymbol{m}^{\prime\prime}_0$
is much bigger than
$\boldsymbol{m}^{\prime\prime}_0$
is much bigger than
![]() $\Delta$
, it is easily verified that the sum (5.14) is dominated by the term
$\Delta$
, it is easily verified that the sum (5.14) is dominated by the term
![]() $I=0$
; thus, on
$I=0$
; thus, on
![]() $\mathscr{E}$
, we have
$\mathscr{E}$
, we have
the error term
![]() $O(\Delta ^2/m)$
hides the terms for
$O(\Delta ^2/m)$
hides the terms for
![]() $I\gt 0$
. Furthermore, a careful expansion of the binomial coefficients from (5.15) shows that uniformly for all
$I\gt 0$
. Furthermore, a careful expansion of the binomial coefficients from (5.15) shows that uniformly for all
![]() $m^{\prime}_0,m^{\prime\prime}_0=m\exp ({-}d)+O\left(\sqrt m\ln ^3n\right)$
, we have
$m^{\prime}_0,m^{\prime\prime}_0=m\exp ({-}d)+O\left(\sqrt m\ln ^3n\right)$
, we have
 \begin{align*} \frac{{\mathbb{P}}\left \lbrack{x_1,x_2\in \mathscr{X}_1(Y)\mid \mathscr{S},\boldsymbol{m}^{\prime\prime}_0=m^{\prime\prime}_0}\right \rbrack }{{\mathbb{P}}\left \lbrack{x_1\in \mathscr{X}_1(Y)\mid \mathscr{S},\boldsymbol{m}^{\prime}_0=m^{\prime}_0}\right \rbrack ^2}\sim 1, \end{align*}
\begin{align*} \frac{{\mathbb{P}}\left \lbrack{x_1,x_2\in \mathscr{X}_1(Y)\mid \mathscr{S},\boldsymbol{m}^{\prime\prime}_0=m^{\prime\prime}_0}\right \rbrack }{{\mathbb{P}}\left \lbrack{x_1\in \mathscr{X}_1(Y)\mid \mathscr{S},\boldsymbol{m}^{\prime}_0=m^{\prime}_0}\right \rbrack ^2}\sim 1, \end{align*}
whence we obtain (5.13). A similar argument applies to
![]() $|\mathscr{X}_0(Y)|$
.
$|\mathscr{X}_0(Y)|$
.
As a next step, consider the set
![]() $\mathscr{X}_r(Y,Z)$
of all
$\mathscr{X}_r(Y,Z)$
of all
![]() $x\in \mathscr{X}_r(Y)$
such that
$x\in \mathscr{X}_r(Y)$
such that
Corollary 5.3.
Let
![]() $y\in \mathscr{Y}(c,d,\theta )$
be such that
$y\in \mathscr{Y}(c,d,\theta )$
be such that
![]() $y\Delta$
is an integer, and let
$y\Delta$
is an integer, and let
![]() $z\in (p_{01},p_{11})$
be such that
$z\in (p_{01},p_{11})$
be such that
![]() $z\Delta$
is an integer and such that
(2.41)
–
(2.42)
are satisfied. Then w.h.p., we have
$z\Delta$
is an integer and such that
(2.41)
–
(2.42)
are satisfied. Then w.h.p., we have
Proof. Let
![]() $Y=y\Delta$
and
$Y=y\Delta$
and
![]() $Z=z\Delta$
. We deal with
$Z=z\Delta$
. We deal with
![]() $|\mathscr{X}_0(y\Delta, z\Delta )|$
and
$|\mathscr{X}_0(y\Delta, z\Delta )|$
and
![]() $|\mathscr{X}_1(y\Delta, z\Delta )|$
by two related but slightly different arguments. The computation of
$|\mathscr{X}_1(y\Delta, z\Delta )|$
by two related but slightly different arguments. The computation of
![]() $|\mathscr{X}_1(y\Delta, z\Delta )|$
is pretty straightforward. Indeed, Lemma 5.2 shows that w.h.p., the set
$|\mathscr{X}_1(y\Delta, z\Delta )|$
is pretty straightforward. Indeed, Lemma 5.2 shows that w.h.p., the set
![]() $\mathscr{X}_1(Y)$
has the size displayed in (5.6). Furthermore, since (1.2) provides that tests are subjected to noise independently, Lemma 1.5 shows that
$\mathscr{X}_1(Y)$
has the size displayed in (5.6). Furthermore, since (1.2) provides that tests are subjected to noise independently, Lemma 1.5 shows that
Moreover, as we saw in the proof of Lemma 5.2, any
![]() $x_1,x_2\in \mathscr{X}_1(Y)$
have disjoint sets of untainted tests. Hence, in perfect analogy to (5.18), we obtain
$x_1,x_2\in \mathscr{X}_1(Y)$
have disjoint sets of untainted tests. Hence, in perfect analogy to (5.18), we obtain
Thus, (5.17) follows from (5.18) to (5.19) and Chebyshev’s inequality.
Let us proceed to prove (5.16). As in the case of
![]() $|\mathscr{X}_1(y\Delta, z\Delta )|$
, we obtain
$|\mathscr{X}_1(y\Delta, z\Delta )|$
, we obtain
Hence, as in (5.10) from the proof of Lemma 5.10,
With respect to the second moment calculation, it is not necessarily true that
![]() $x_i,x_j\in \mathscr{X}_0(Y,Z)$
with
$x_i,x_j\in \mathscr{X}_0(Y,Z)$
with
![]() $k\lt i\lt j\leq n$
have disjoint sets of untainted tests. Thus, as in the expression (5.14), let
$k\lt i\lt j\leq n$
have disjoint sets of untainted tests. Thus, as in the expression (5.14), let
![]() $\boldsymbol{m}^{\prime\prime}_0$
be the number of actually negative tests of
$\boldsymbol{m}^{\prime\prime}_0$
be the number of actually negative tests of
![]() ${\boldsymbol{G}}^{\prime\prime}=\mathbf{G}_{\mathrm{cc}}-x_i-x_j$
and introduce
${\boldsymbol{G}}^{\prime\prime}=\mathbf{G}_{\mathrm{cc}}-x_i-x_j$
and introduce
![]() $0\leq I\leq \Delta$
to count the untainted tests that
$0\leq I\leq \Delta$
to count the untainted tests that
![]() $x_i,x_j$
have in common. Additionally, write
$x_i,x_j$
have in common. Additionally, write
![]() $0\leq I_1\leq \min \{I,Z\}$
for the number of common untainted tests that display a negative result. Then
$0\leq I_1\leq \min \{I,Z\}$
for the number of common untainted tests that display a negative result. Then
 \begin{align} {\mathbb{P}}\left \lbrack{x_i,x_j\in \mathscr{X}_0(Y,Z)\mid \mathscr{S},\boldsymbol{m}^{\prime\prime}_0}\right \rbrack & =\sum _{I,I_1}\binom{\boldsymbol{m}^{\prime\prime}_0}{I}\binom{\boldsymbol{m}^{\prime\prime}_0-I}{Y-I}\binom{\boldsymbol{m}^{\prime\prime}_0-Y}{Y-I}\binom{m-\boldsymbol{m}^{\prime\prime}_0}{\Delta -Y}^2\binom{m}{\Delta }^{-2}\nonumber\\ & \qquad \cdot\binom{I}{I_1} p_{00}^{I-I_1}p_{01}^{I_1}\left \lbrack{\binom{Y-I}{Z-I_1}p_{00}^{Y-Z-I+I_1}p_{01}^{Z-I_1}}\right \rbrack ^2. \end{align}
\begin{align} {\mathbb{P}}\left \lbrack{x_i,x_j\in \mathscr{X}_0(Y,Z)\mid \mathscr{S},\boldsymbol{m}^{\prime\prime}_0}\right \rbrack & =\sum _{I,I_1}\binom{\boldsymbol{m}^{\prime\prime}_0}{I}\binom{\boldsymbol{m}^{\prime\prime}_0-I}{Y-I}\binom{\boldsymbol{m}^{\prime\prime}_0-Y}{Y-I}\binom{m-\boldsymbol{m}^{\prime\prime}_0}{\Delta -Y}^2\binom{m}{\Delta }^{-2}\nonumber\\ & \qquad \cdot\binom{I}{I_1} p_{00}^{I-I_1}p_{01}^{I_1}\left \lbrack{\binom{Y-I}{Z-I_1}p_{00}^{Y-Z-I+I_1}p_{01}^{Z-I_1}}\right \rbrack ^2. \end{align}
As in the proof of Lemma 5.2, it is easily checked that the summand
![]() $I=I_1=0$
dominates (5.22) and that therefore
$I=I_1=0$
dominates (5.22) and that therefore
Thus, (5.16) follows from (5.21), (5.23), and Chebyshev’s inequality.
Proof of Proposition
2.11
. By continuity, we can find
![]() $y,z$
that satisfy (2.41)–(2.42) such that
$y,z$
that satisfy (2.41)–(2.42) such that
![]() $y\Delta$
,
$y\Delta$
,
![]() $z\Delta$
are integers, provided that
$z\Delta$
are integers, provided that
![]() $n$
is large enough. Now, if (2.41)–(2.42) are satisfied, then Corollary 5.3 shows that
$n$
is large enough. Now, if (2.41)–(2.42) are satisfied, then Corollary 5.3 shows that
Hence, take any pair
![]() $(v,w)\in \mathscr{X}_1(y\Delta, z\Delta )\times \mathscr{X}_0(y\Delta, z\Delta )$
. Then
$(v,w)\in \mathscr{X}_1(y\Delta, z\Delta )\times \mathscr{X}_0(y\Delta, z\Delta )$
. Then
![]() $\{a\in \partial v\,:\,\partial a\setminus \{v\}\subseteq V_0\}$
and
$\{a\in \partial v\,:\,\partial a\setminus \{v\}\subseteq V_0\}$
and
![]() $\{a\in \partial w\,:\,a\in F_0\}$
are disjoint because
$\{a\in \partial w\,:\,a\in F_0\}$
are disjoint because
![]() $v\in V_1$
. Therefore, any such pair
$v\in V_1$
. Therefore, any such pair
![]() $(v,w)$
satisfies (2.43).
$(v,w)$
satisfies (2.43).
5.3. Proof of Proposition 2.12
We are going to lower bound the partition function
![]() $Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
by way of a moment computation. To this end, we are going to couple the constant column design
$Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
by way of a moment computation. To this end, we are going to couple the constant column design
![]() $(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime})$
with the displayed test results
$(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime})$
with the displayed test results
![]() $\boldsymbol{\sigma }^{\prime\prime}$
with another random pair
$\boldsymbol{\sigma }^{\prime\prime}$
with another random pair
![]() $(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
where the test results indicated by the vector
$(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
where the test results indicated by the vector
![]() $\boldsymbol{\sigma }^{\prime\prime\prime}$
are purely random, that is, do not derive from an actual vector
$\boldsymbol{\sigma }^{\prime\prime\prime}$
are purely random, that is, do not derive from an actual vector
![]() $\boldsymbol{\sigma }$
of infected individuals. One can think of
$\boldsymbol{\sigma }$
of infected individuals. One can think of
![]() $(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
as a ‘null model’. Conversely, in the language of random constraint satisfaction problems [Reference Coja-Oghlan, Krzakala, Perkins and Zdeborová12], ultimately
$(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
as a ‘null model’. Conversely, in the language of random constraint satisfaction problems [Reference Coja-Oghlan, Krzakala, Perkins and Zdeborová12], ultimately
![]() $(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime})$
will turn out to be the ‘planted model’ associated with
$(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime})$
will turn out to be the ‘planted model’ associated with
![]() $(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
.
$(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
.
Hence, let
![]() $\boldsymbol{m}^+$
be the number
$\boldsymbol{m}^+$
be the number
![]() $\|\boldsymbol{\sigma }^{\prime\prime}\|_1$
of positively displayed tests of
$\|\boldsymbol{\sigma }^{\prime\prime}\|_1$
of positively displayed tests of
![]() $(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime})$
. Moreover, for a given integer
$(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime})$
. Moreover, for a given integer
![]() $0\leq m^+\leq m$
, let
$0\leq m^+\leq m$
, let
![]() $\boldsymbol{\sigma }^{\prime\prime\prime}\in \{0,1\}^F$
be a uniformly random vector of Hamming weight
$\boldsymbol{\sigma }^{\prime\prime\prime}\in \{0,1\}^F$
be a uniformly random vector of Hamming weight
![]() $m^+$
, drawn independently of
$m^+$
, drawn independently of
![]() $\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime}$
. In other words, in the null model
$\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime}$
. In other words, in the null model
![]() $(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
, we simply choose a set of uniformly random tests to display positively.
$(\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime})$
, we simply choose a set of uniformly random tests to display positively.
Let
![]() $\hat F^+=\{a\in F\,:\,\boldsymbol{\sigma }^{\prime\prime\prime}_a=1\}$
and
$\hat F^+=\{a\in F\,:\,\boldsymbol{\sigma }^{\prime\prime\prime}_a=1\}$
and
![]() $\hat F^-=F\setminus F^+$
. Moreover, just as in (2.2) define weight functions
$\hat F^-=F\setminus F^+$
. Moreover, just as in (2.2) define weight functions
 \begin{align} \psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime},a}&\,:\,\{0,1\}^{\partial a}\to \mathbb{R}_{\geq 0},& \sigma _{\partial a_i}&\mapsto \begin{cases} \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{00}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{10}&\text{ if } \boldsymbol{\sigma }^{\prime\prime\prime}_a=0,\\ \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{01}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{11}&\text{ if } \boldsymbol{\sigma }^{\prime\prime\prime}_a=1. \end{cases} \end{align}
\begin{align} \psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime},a}&\,:\,\{0,1\}^{\partial a}\to \mathbb{R}_{\geq 0},& \sigma _{\partial a_i}&\mapsto \begin{cases} \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{00}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{10}&\text{ if } \boldsymbol{\sigma }^{\prime\prime\prime}_a=0,\\ \unicode{x1D7D9}\{\|\sigma \|_{1}=0\}p_{01}+\unicode{x1D7D9}\{\|\sigma \|_{1}\gt 0\}p_{11}&\text{ if } \boldsymbol{\sigma }^{\prime\prime\prime}_a=1. \end{cases} \end{align}
In addition, exactly as in (2.3)–(2.4), let
 \begin{align} \psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma ) & =\unicode{x1D7D9}\left \{{\|\sigma \|_1=k}\right \}\prod _{a\in F}\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime},a}(\sigma _{\partial a}), Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}=\sum _{\sigma \in \{0,1\}^V}\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma ), \mu _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma )\nonumber\\& =\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma )/Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}. \end{align}
\begin{align} \psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma ) & =\unicode{x1D7D9}\left \{{\|\sigma \|_1=k}\right \}\prod _{a\in F}\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime},a}(\sigma _{\partial a}), Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}=\sum _{\sigma \in \{0,1\}^V}\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma ), \mu _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma )\nonumber\\& =\psi _{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}(\sigma )/Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}. \end{align}
We begin by computing the mean of the partition function (aka the ‘annealed average’).
Lemma 5.4.
For any
![]() $0\leq m^+\leq m$
, we have
$0\leq m^+\leq m$
, we have
![]() $\mathbb{E}\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}}\right \rbrack =\binom nk\binom{m}{m^+}^{-1}{{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }.$
$\mathbb{E}\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}}\right \rbrack =\binom nk\binom{m}{m^+}^{-1}{{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }.$
Proof. Writing out the definitions of
![]() $\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}$
, we obtain
$\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}$
, we obtain
 \begin{align*} \mathbb{E}\left \lbrack{\boldsymbol{Z}_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}}\right \rbrack & = \binom{m}{m^+}^{-1}\sum _G\sum _{\substack{\sigma ^{\prime\prime}\in \{0,1\}^F\,:\,\|\sigma ^{\prime\prime}\|_1=\boldsymbol{m}^+\\\sigma \in \{0,1\}\,:\,\|\sigma \|_1=k}}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack \psi _{\mathbf{G}_{\mathrm{cc}},\sigma ^{\prime\prime}}(\sigma )\\& =\binom{m}{m^+}^{-1}\sum _{G,\sigma ^{\prime\prime},\sigma \,:\,\|\sigma ^{\prime\prime}\|_1=m^+,\|\sigma \|_1=k}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\\[5pt]& \qquad\qquad\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \mathbf{G}_{\mathrm{cc}}=G,\,\boldsymbol{\sigma }=\sigma }\right \rbrack \qquad\qquad\quad\qquad\qquad\qquad\text{[by (5.24)-(5.25)]}\\& \binom{n}{k}\binom{m}{m^+}^{-1}\!\!\!\!\sum _{G,\sigma ^{\prime\prime},\sigma \,:\,\|\sigma ^{\prime\prime}\|_1=m^+,\|\sigma \|_1=k}\!\!{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=\sigma }\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \mathbf{G}_{\mathrm{cc}}=G,\,\boldsymbol{\sigma }=\sigma }\right \rbrack \\& \binom{n}{k}\binom{m}{m^+}^{-1}\sum _{\sigma ^{\prime\prime}\,:\,\|\sigma ^{\prime\prime}\|_1=m^+}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}}\right \rbrack =\binom nk\binom{m}{m^+}^{-1}{{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }, \end{align*}
\begin{align*} \mathbb{E}\left \lbrack{\boldsymbol{Z}_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}}\right \rbrack & = \binom{m}{m^+}^{-1}\sum _G\sum _{\substack{\sigma ^{\prime\prime}\in \{0,1\}^F\,:\,\|\sigma ^{\prime\prime}\|_1=\boldsymbol{m}^+\\\sigma \in \{0,1\}\,:\,\|\sigma \|_1=k}}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack \psi _{\mathbf{G}_{\mathrm{cc}},\sigma ^{\prime\prime}}(\sigma )\\& =\binom{m}{m^+}^{-1}\sum _{G,\sigma ^{\prime\prime},\sigma \,:\,\|\sigma ^{\prime\prime}\|_1=m^+,\|\sigma \|_1=k}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\\[5pt]& \qquad\qquad\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \mathbf{G}_{\mathrm{cc}}=G,\,\boldsymbol{\sigma }=\sigma }\right \rbrack \qquad\qquad\quad\qquad\qquad\qquad\text{[by (5.24)-(5.25)]}\\& \binom{n}{k}\binom{m}{m^+}^{-1}\!\!\!\!\sum _{G,\sigma ^{\prime\prime},\sigma \,:\,\|\sigma ^{\prime\prime}\|_1=m^+,\|\sigma \|_1=k}\!\!{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=\sigma }\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \mathbf{G}_{\mathrm{cc}}=G,\,\boldsymbol{\sigma }=\sigma }\right \rbrack \\& \binom{n}{k}\binom{m}{m^+}^{-1}\sum _{\sigma ^{\prime\prime}\,:\,\|\sigma ^{\prime\prime}\|_1=m^+}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}}\right \rbrack =\binom nk\binom{m}{m^+}^{-1}{{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }, \end{align*}
as claimed.
As a next step, we sort out the relationship of the null model and of the ‘real’ group testing instance.
Lemma 5.5.
Let
![]() $0\leq m^+\leq m$
be an integer. Then for any
$0\leq m^+\leq m$
be an integer. Then for any
![]() $G$
and any
$G$
and any
![]() $\sigma ^{\prime\prime}\in \{0,1\}^F$
with
$\sigma ^{\prime\prime}\in \{0,1\}^F$
with
![]() $\|\sigma ^{\prime\prime}\|_1=m^+$
, we have
$\|\sigma ^{\prime\prime}\|_1=m^+$
, we have
Proof. We have
 \begin{align*}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \boldsymbol{m}^+=m^+}\right \rbrack &=\sum _{\sigma \,:\,\|\sigma \|_1=k}\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }=\sigma }\right \rbrack }{\binom nk{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\\[6pt] &=\sum _{\sigma \,:\,\|\sigma \|_1=k}\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack \psi _{G,\sigma ^{\prime\prime}}(\sigma )}{\binom nk{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\qquad\qquad\qquad\qquad\!\!\text{[by (2.2)-(2.3)]}\\[6pt] &=\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack Z_{G,\sigma ^{\prime\prime}}}{\binom nk{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\qquad\qquad\qquad\qquad\qquad\qquad\text{[by (2.4)]}\\[6pt] &=\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}}\right \rbrack Z_{G,\sigma ^{\prime\prime}}}{\binom nk\binom m{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\qquad\qquad\qquad\quad[\text{as} \boldsymbol{\sigma }^{\prime\prime\prime} \text{ is uniformly random]}\\[6pt] &=\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}}\right \rbrack Z_{G,\sigma ^{\prime\prime}}}{\mathbb{E}\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}}\right \rbrack }\qquad\qquad\qquad\qquad\,\,[\text{by Lemma,5.4}], \end{align*}
\begin{align*}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \boldsymbol{m}^+=m^+}\right \rbrack &=\sum _{\sigma \,:\,\|\sigma \|_1=k}\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=\sigma ^{\prime\prime}\mid \mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }=\sigma }\right \rbrack }{\binom nk{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\\[6pt] &=\sum _{\sigma \,:\,\|\sigma \|_1=k}\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack \psi _{G,\sigma ^{\prime\prime}}(\sigma )}{\binom nk{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\qquad\qquad\qquad\qquad\!\!\text{[by (2.2)-(2.3)]}\\[6pt] &=\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack Z_{G,\sigma ^{\prime\prime}}}{\binom nk{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\qquad\qquad\qquad\qquad\qquad\qquad\text{[by (2.4)]}\\[6pt] &=\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}}\right \rbrack Z_{G,\sigma ^{\prime\prime}}}{\binom nk\binom m{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\qquad\qquad\qquad\quad[\text{as} \boldsymbol{\sigma }^{\prime\prime\prime} \text{ is uniformly random]}\\[6pt] &=\frac{{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}}\right \rbrack Z_{G,\sigma ^{\prime\prime}}}{\mathbb{E}\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime\prime}}}\right \rbrack }\qquad\qquad\qquad\qquad\,\,[\text{by Lemma,5.4}], \end{align*}
as claimed.
Combining Lemmas 5.4–5.5, we obtain the following lower bound on
![]() $Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
.
$Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}$
.
Corollary 5.6.
Let
![]() $0\leq m^+\leq m$
be an integer. For any
$0\leq m^+\leq m$
be an integer. For any
![]() $\delta \gt 0$
, we have
$\delta \gt 0$
, we have
 \begin{align*}{\mathbb{P}}\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}\lt \delta \binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack \mid \boldsymbol{m}^+=m^+}\right \rbrack \lt \delta . \end{align*}
\begin{align*}{\mathbb{P}}\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}\lt \delta \binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack \mid \boldsymbol{m}^+=m^+}\right \rbrack \lt \delta . \end{align*}
Proof. Lemmas 5.4 and 5.5 yield
 \begin{align*}{\mathbb{P}}&\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}\lt \delta \binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack \mid \boldsymbol{m}^+=m^+}\right \rbrack \\ &=\sum _{G,\sigma ^{\prime\prime}\,:\,\|\sigma ^{\prime\prime}\|_1=m^+}\frac{\unicode{x1D7D9}\{Z_{G,\sigma ^{\prime\prime}}\lt \delta \binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack \}Z_{G,\sigma ^{\prime\prime}}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}\mid \boldsymbol{m}^+=m^+}\right \rbrack }{\binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\\ &\lt \sum _{G,\sigma ^{\prime\prime}\,:\,\|\sigma ^{\prime\prime}\|_1=m^+}\delta \cdot{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}\mid \boldsymbol{m}^+=m^+}\right \rbrack \leq \delta, \end{align*}
\begin{align*}{\mathbb{P}}&\left \lbrack{Z_{\mathbf{G}_{\mathrm{cc}},\boldsymbol{\sigma }^{\prime\prime}}\lt \delta \binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack \mid \boldsymbol{m}^+=m^+}\right \rbrack \\ &=\sum _{G,\sigma ^{\prime\prime}\,:\,\|\sigma ^{\prime\prime}\|_1=m^+}\frac{\unicode{x1D7D9}\{Z_{G,\sigma ^{\prime\prime}}\lt \delta \binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack \}Z_{G,\sigma ^{\prime\prime}}{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}\mid \boldsymbol{m}^+=m^+}\right \rbrack }{\binom nk\binom{m}{m^+}^{-1}{\mathbb{P}}\left \lbrack{\boldsymbol{m}^+=m^+}\right \rbrack }\\ &\lt \sum _{G,\sigma ^{\prime\prime}\,:\,\|\sigma ^{\prime\prime}\|_1=m^+}\delta \cdot{\mathbb{P}}\left \lbrack{\mathbf{G}_{\mathrm{cc}}=G,\boldsymbol{\sigma }^{\prime\prime\prime}=\sigma ^{\prime\prime}\mid \boldsymbol{m}^+=m^+}\right \rbrack \leq \delta, \end{align*}
as desired.
Acknowledgement
We thank Petra Berenbrink and Jonathan Scarlett for helpful comments and discussions.
Appendix A. Table of notation
Table 1. Overview of notation

Appendix B. Proof of Theorem 1.2 (lower bound for approximate recovery)
The basic idea is to compute the mutual information of
![]() $\boldsymbol{\sigma }$
and
$\boldsymbol{\sigma }$
and
![]() $\boldsymbol{\sigma }^{\prime\prime}$
. What makes matters tricky is that we are dealing with the adaptive scenario where tests may be conducted one by one. To deal with this issue, we closely follow the arguments from [Reference Gebhard, Johnson, Loick and Rolvien19]. Furthermore, the displayed test results are obtained by putting the actual test results through the noisy channel.
$\boldsymbol{\sigma }^{\prime\prime}$
. What makes matters tricky is that we are dealing with the adaptive scenario where tests may be conducted one by one. To deal with this issue, we closely follow the arguments from [Reference Gebhard, Johnson, Loick and Rolvien19]. Furthermore, the displayed test results are obtained by putting the actual test results through the noisy channel.
As a first step, we bound the mutual information between
![]() $\boldsymbol{\sigma }$
and
$\boldsymbol{\sigma }$
and
![]() $\boldsymbol{\sigma }^{\prime\prime}$
from above under the assumption that the statistician applies an adaptive scheme where the next test to be conducted depends deterministically on the previously displayed test results. Let
$\boldsymbol{\sigma }^{\prime\prime}$
from above under the assumption that the statistician applies an adaptive scheme where the next test to be conducted depends deterministically on the previously displayed test results. Let
![]() $m$
be the fixed total number of tests that are conducted.
$m$
be the fixed total number of tests that are conducted.
Lemma B.1.
For a deterministic adaptive algorithm, we have
![]() $I(\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime})\leq m/c_{\mathrm{Sh}}$
.
$I(\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime})\leq m/c_{\mathrm{Sh}}$
.
Proof. Let
![]() $\boldsymbol{\sigma }^{\prime}$
be the vector of actual test results. Then
$\boldsymbol{\sigma }^{\prime}$
be the vector of actual test results. Then
 \begin{align*} I(\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime})&=\sum _{s,s^{\prime\prime}}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=s}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}}\right \rbrack }\\ &=\sum _{s,s^{\prime},s^{\prime\prime}}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime}=s^{\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=s}\right \rbrack\\ &\qquad \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime}=s^{\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}}\right \rbrack }\\ &=I(\boldsymbol{\sigma }^{\prime\prime},\boldsymbol{\sigma }^{\prime})-H(\boldsymbol{\sigma }^{\prime}\mid \boldsymbol{\sigma })\leq I(\boldsymbol{\sigma }^{\prime\prime},\boldsymbol{\sigma }^{\prime}). \end{align*}
\begin{align*} I(\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime})&=\sum _{s,s^{\prime\prime}}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=s}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}}\right \rbrack }\\ &=\sum _{s,s^{\prime},s^{\prime\prime}}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime}=s^{\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }=s}\right \rbrack\\ &\qquad \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}\mid \boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime}=s^{\prime}\mid \boldsymbol{\sigma }=s}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}}\right \rbrack }\\ &=I(\boldsymbol{\sigma }^{\prime\prime},\boldsymbol{\sigma }^{\prime})-H(\boldsymbol{\sigma }^{\prime}\mid \boldsymbol{\sigma })\leq I(\boldsymbol{\sigma }^{\prime\prime},\boldsymbol{\sigma }^{\prime}). \end{align*}
Furthermore,
 \begin{align*} I(\boldsymbol{\sigma }^{\prime},\boldsymbol{\sigma }^{\prime\prime})&=\sum _{s^{\prime\prime},s^{\prime}}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime},\boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime},\boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack }. \end{align*}
\begin{align*} I(\boldsymbol{\sigma }^{\prime},\boldsymbol{\sigma }^{\prime\prime})&=\sum _{s^{\prime\prime},s^{\prime}}{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime},\boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime},\boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}=s^{\prime\prime}}\right \rbrack{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime}=s^{\prime}}\right \rbrack }. \end{align*}
Since the tests are conducted adaptively, we obtain
Hence,
 \begin{align*} & I(\boldsymbol{\sigma }^{\prime},\boldsymbol{\sigma }^{\prime\prime})=\sum _{i=1}^m\sum _{s^{\prime\prime}_1,\ldots, s^{\prime\prime}_i,s^{\prime}_i}{\mathbb{P}}\left \lbrack{\forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j,\boldsymbol{\sigma }^{\prime}_i=s^{\prime}_i}\right \rbrack \\& \cdot{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}_i=s^{\prime\prime}_i\mid \forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j,\boldsymbol{\sigma }^{\prime}_i=s^{\prime}_i}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}_i=s^{\prime\prime}_i\mid \forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j,\boldsymbol{\sigma }^{\prime}_i=s^{\prime}_i}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}_i=s^{\prime\prime}_i\mid \forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j}\right \rbrack }. \end{align*}
\begin{align*} & I(\boldsymbol{\sigma }^{\prime},\boldsymbol{\sigma }^{\prime\prime})=\sum _{i=1}^m\sum _{s^{\prime\prime}_1,\ldots, s^{\prime\prime}_i,s^{\prime}_i}{\mathbb{P}}\left \lbrack{\forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j,\boldsymbol{\sigma }^{\prime}_i=s^{\prime}_i}\right \rbrack \\& \cdot{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}_i=s^{\prime\prime}_i\mid \forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j,\boldsymbol{\sigma }^{\prime}_i=s^{\prime}_i}\right \rbrack \ln \frac{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}_i=s^{\prime\prime}_i\mid \forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j,\boldsymbol{\sigma }^{\prime}_i=s^{\prime}_i}\right \rbrack }{{\mathbb{P}}\left \lbrack{\boldsymbol{\sigma }^{\prime\prime}_i=s^{\prime\prime}_i\mid \forall j\lt i\,:\,\boldsymbol{\sigma }^{\prime\prime}_j=s^{\prime\prime}_j}\right \rbrack }. \end{align*}
In the last term,
![]() $\boldsymbol{\sigma }^{\prime}_i$
is a Bernoulli random variable (whose distribution is determined by
$\boldsymbol{\sigma }^{\prime}_i$
is a Bernoulli random variable (whose distribution is determined by
![]() $\boldsymbol{\sigma }^{\prime\prime}_j$
for
$\boldsymbol{\sigma }^{\prime\prime}_j$
for
![]() $j\lt i$
), and
$j\lt i$
), and
![]() $\boldsymbol{\sigma }^{\prime\prime}_i$
is the output of that variable upon transmission through our channel. Furthermore, the expression in the second line above is the mutual information of these quantities. Hence, the definition of the channel capacity implies that
$\boldsymbol{\sigma }^{\prime\prime}_i$
is the output of that variable upon transmission through our channel. Furthermore, the expression in the second line above is the mutual information of these quantities. Hence, the definition of the channel capacity implies that
![]() $I(\boldsymbol{\sigma }^{\prime},\boldsymbol{\sigma }^{\prime\prime})\leq m/c_{\mathrm{Sh}}$
.
$I(\boldsymbol{\sigma }^{\prime},\boldsymbol{\sigma }^{\prime\prime})\leq m/c_{\mathrm{Sh}}$
.
Proof of Theorem
1.2
(lower bound for approximate recovery). As a first step, we argue that it suffices to investigate deterministic adaptive group testing algorithms (under the assumption that the ground truth
![]() $\boldsymbol{\sigma }$
is random). Indeed, a randomised adaptive algorithm
$\boldsymbol{\sigma }$
is random). Indeed, a randomised adaptive algorithm
![]() $\mathscr{A}(\cdot)$
can be modelled as having access to a (single) sample
$\mathscr{A}(\cdot)$
can be modelled as having access to a (single) sample
![]() $\boldsymbol{\omega }$
from a random source that is independent of
$\boldsymbol{\omega }$
from a random source that is independent of
![]() $\boldsymbol{\sigma }$
. Now, if we assume that for an arbitrarily small
$\boldsymbol{\sigma }$
. Now, if we assume that for an arbitrarily small
![]() $\delta \gt 0$
, we have
$\delta \gt 0$
, we have
where the expectation is on both
![]() $\boldsymbol{\omega }$
and
$\boldsymbol{\omega }$
and
![]() $\boldsymbol{\sigma }$
, then there exists some outcome
$\boldsymbol{\sigma }$
, then there exists some outcome
![]() $\omega$
such that
$\omega$
such that
where the expectation is on
![]() $\boldsymbol{\sigma }$
only.
$\boldsymbol{\sigma }$
only.
Thus, assume that
![]() $\mathscr{A}(\cdot)$
is deterministic. We have
$\mathscr{A}(\cdot)$
is deterministic. We have
![]() $I(\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime})=H(\boldsymbol{\sigma })-H(\boldsymbol{\sigma }\mid \boldsymbol{\sigma }^{\prime\prime})$
. Furthermore,
$I(\boldsymbol{\sigma },\boldsymbol{\sigma }^{\prime\prime})=H(\boldsymbol{\sigma })-H(\boldsymbol{\sigma }\mid \boldsymbol{\sigma }^{\prime\prime})$
. Furthermore,
![]() $H(\boldsymbol{\sigma })\sim k\ln (n/k)$
. Hence, Lemma B.1 yields
$H(\boldsymbol{\sigma })\sim k\ln (n/k)$
. Hence, Lemma B.1 yields
which implies the assertion.
Remark B.2. Alternatively, as pointed out to us by Jonathan Scarlett, Theorem 1.2 could be derived from Fano’s inequality via a straightforward adaptation of the proof of (33, Theorem 5).
Appendix C. Proof of Lemma 3.3
This proof is a straightforward adaption of (Reference Coja-Oghlan, Gebhard, Hahn-Klimroth and Loick9, proof of Lemma 4.16). Fix
![]() $T\subseteq V$
of size
$T\subseteq V$
of size
![]() $t=|T|\leq \exp ({-}\ln ^{\alpha } n)k$
as well as a set
$t=|T|\leq \exp ({-}\ln ^{\alpha } n)k$
as well as a set
![]() $R\subseteq V$
of size
$R\subseteq V$
of size
![]() $r=\lceil t/\lambda \rceil$
with
$r=\lceil t/\lambda \rceil$
with
![]() $\lambda =8\ln \ln n$
. Let
$\lambda =8\ln \ln n$
. Let
![]() $\gamma =\lceil \ln ^{\beta }n\rceil$
. Further, let
$\gamma =\lceil \ln ^{\beta }n\rceil$
. Further, let
![]() $U\subseteq F[1]\cup \cdots \cup F[\ell ]$
be a set of size
$U\subseteq F[1]\cup \cdots \cup F[\ell ]$
be a set of size
![]() $\gamma r\leq u\leq \Delta t$
. Additionally, let
$\gamma r\leq u\leq \Delta t$
. Additionally, let
![]() ${\mathscr{E}}(R,T,U)$
be the event that every test
${\mathscr{E}}(R,T,U)$
be the event that every test
![]() $a\in U$
contains two individuals from
$a\in U$
contains two individuals from
![]() $R\cup T$
. Then
$R\cup T$
. Then
 \begin{align} {\mathbb{P}}\left \lbrack{R\subseteq \left \{{x\in V\,:\,\sum _{a\in \partial x\setminus F[0]}\unicode{x1D7D9}\left \{{T\cap \partial a\setminus \left \{{x}\right \}\neq \emptyset }\right \}\geq \gamma }\right \}}\right \rbrack \leq{\mathbb{P}}\left \lbrack{{\mathscr{E}}(R,T,U)}\right \rbrack . \end{align}
\begin{align} {\mathbb{P}}\left \lbrack{R\subseteq \left \{{x\in V\,:\,\sum _{a\in \partial x\setminus F[0]}\unicode{x1D7D9}\left \{{T\cap \partial a\setminus \left \{{x}\right \}\neq \emptyset }\right \}\geq \gamma }\right \}}\right \rbrack \leq{\mathbb{P}}\left \lbrack{{\mathscr{E}}(R,T,U)}\right \rbrack . \end{align}
Hence, it suffices to bound
![]() ${\mathbb{P}}\left \lbrack{{\mathscr{E}}(R,T,U)}\right \rbrack$
.
${\mathbb{P}}\left \lbrack{{\mathscr{E}}(R,T,U)}\right \rbrack$
.
For a test
![]() $a\in U$
, there are no more than
$a\in U$
, there are no more than
![]() $\binom{r+t}2$
ways to choose distinct individuals
$\binom{r+t}2$
ways to choose distinct individuals
![]() $x_a,x^{\prime}_a\in R\cup T$
. Moreover, (3.1) shows that the probability of the event
$x_a,x^{\prime}_a\in R\cup T$
. Moreover, (3.1) shows that the probability of the event
![]() $\{x_a,x^{\prime}_a \in \partial a\}$
is bounded by
$\{x_a,x^{\prime}_a \in \partial a\}$
is bounded by
![]() $(1+o(1))(\Delta \ell /(ms))^2$
; in fact, this probability might be zero if we choose an individual that cannot join
$(1+o(1))(\Delta \ell /(ms))^2$
; in fact, this probability might be zero if we choose an individual that cannot join
![]() $a$
due to the spatially coupled construction of
$a$
due to the spatially coupled construction of
![]() $\mathbf{G}_{\mathrm{sc}}$
. Hence, due to negative association [Reference Dubhashi and Ranjan16, Lemma 2]
$\mathbf{G}_{\mathrm{sc}}$
. Hence, due to negative association [Reference Dubhashi and Ranjan16, Lemma 2]
 \begin{align*}{\mathbb{P}}\left \lbrack{{\mathscr{E}}(R,T,U)}\right \rbrack &\leq \left \lbrack{\binom{r+t}2\left ({\frac{(1+o(1))\Delta \ell }{ms}}\right )^2}\right \rbrack ^u. \end{align*}
\begin{align*}{\mathbb{P}}\left \lbrack{{\mathscr{E}}(R,T,U)}\right \rbrack &\leq \left \lbrack{\binom{r+t}2\left ({\frac{(1+o(1))\Delta \ell }{ms}}\right )^2}\right \rbrack ^u. \end{align*}
Consequently, by the union bound the event
![]() $\mathfrak{E}(r,t,u)$
that there exist sets
$\mathfrak{E}(r,t,u)$
that there exist sets
![]() $R,T,U$
of sizes
$R,T,U$
of sizes
![]() $|R|=r,|T|=t,|U|=u$
such that
$|R|=r,|T|=t,|U|=u$
such that
![]() ${\mathscr{E}}(R,T,U)$
occurs has probability
${\mathscr{E}}(R,T,U)$
occurs has probability
 \begin{align*}{\mathbb{P}}\left \lbrack{\mathfrak{E}(r,t,u)}\right \rbrack &\leq \binom nr\binom nt\binom mu\left \lbrack{\binom{r+t}2\left ({\frac{(1+o(1))\Delta \ell }{ms}}\right )^2}\right \rbrack ^u. \end{align*}
\begin{align*}{\mathbb{P}}\left \lbrack{\mathfrak{E}(r,t,u)}\right \rbrack &\leq \binom nr\binom nt\binom mu\left \lbrack{\binom{r+t}2\left ({\frac{(1+o(1))\Delta \ell }{ms}}\right )^2}\right \rbrack ^u. \end{align*}
Hence, the bounds
![]() $\gamma t/\lambda \leq \gamma r\leq u\leq \Delta t$
yield
$\gamma t/\lambda \leq \gamma r\leq u\leq \Delta t$
yield
 \begin{align*}{\mathbb{P}}\left \lbrack{\mathfrak{E}(r,t,u)}\right \rbrack &\leq \binom nt^2\binom m{u}\left \lbrack{\binom{2t}2\left ({\frac{(1+o(1))\Delta \ell }{ms}}\right )^2}\right \rbrack ^{u} \leq \left ({\frac{\mathrm{e} n}{t}}\right )^{2t}\left ({\frac{2\mathrm{e} \Delta ^2\ell ^2t^2}{ms^2u}}\right )^u\\ &\leq \left \lbrack{\left ({\frac{\mathrm{e} n}{t}}\right )^{\lambda /\gamma }\frac{2\mathrm{e}\lambda \Delta ^2\ell ^2t}{\gamma ms^2}}\right \rbrack ^u \leq \left \lbrack{\left ({\frac{\mathrm{e} n}{t}}\right )^{\lambda /\gamma }\cdot \frac{t\ln ^4n}m}\right \rbrack ^u \qquad\qquad\text{[due to (2.13), (2.14)]}. \end{align*}
\begin{align*}{\mathbb{P}}\left \lbrack{\mathfrak{E}(r,t,u)}\right \rbrack &\leq \binom nt^2\binom m{u}\left \lbrack{\binom{2t}2\left ({\frac{(1+o(1))\Delta \ell }{ms}}\right )^2}\right \rbrack ^{u} \leq \left ({\frac{\mathrm{e} n}{t}}\right )^{2t}\left ({\frac{2\mathrm{e} \Delta ^2\ell ^2t^2}{ms^2u}}\right )^u\\ &\leq \left \lbrack{\left ({\frac{\mathrm{e} n}{t}}\right )^{\lambda /\gamma }\frac{2\mathrm{e}\lambda \Delta ^2\ell ^2t}{\gamma ms^2}}\right \rbrack ^u \leq \left \lbrack{\left ({\frac{\mathrm{e} n}{t}}\right )^{\lambda /\gamma }\cdot \frac{t\ln ^4n}m}\right \rbrack ^u \qquad\qquad\text{[due to (2.13), (2.14)]}. \end{align*}
Further, since
![]() $\gamma =\Omega (\ln ^{\beta }n)$
and
$\gamma =\Omega (\ln ^{\beta }n)$
and
![]() $m=\Omega (k\ln n)$
while
$m=\Omega (k\ln n)$
while
![]() $t\leq \exp ({-}\ln ^{\alpha } n)k$
and
$t\leq \exp ({-}\ln ^{\alpha } n)k$
and
![]() $\alpha +\beta \gt 1$
, we obtain
$\alpha +\beta \gt 1$
, we obtain
Thus, summing on
![]() $1\leq t\leq \exp ({-}\ln ^\alpha n)k$
,
$1\leq t\leq \exp ({-}\ln ^\alpha n)k$
,
![]() $\gamma r\leq u\leq \Delta t$
and recalling
$\gamma r\leq u\leq \Delta t$
and recalling
![]() $r=\lceil t/\lambda \rceil$
, we obtain
$r=\lceil t/\lambda \rceil$
, we obtain
Appendix D. Parameter optimisation for the binary symmetric channel
Let
![]() $\mathscr{D}(\theta, \boldsymbol{p}) = \{d \gt 0 \,:\, \max \{c_{\mathrm{ex},1}(d,\theta ), c_{\mathrm{ex},2}(d)\} = c_{\mathrm{ex}}(\theta )\}$
be the set of those
$\mathscr{D}(\theta, \boldsymbol{p}) = \{d \gt 0 \,:\, \max \{c_{\mathrm{ex},1}(d,\theta ), c_{\mathrm{ex},2}(d)\} = c_{\mathrm{ex}}(\theta )\}$
be the set of those
![]() $d$
where the minimum in the optimisation problem (1.10) is attained. The goal in this section is to show that for the binary symmetric channel, this minimum is not always attained at the information-theoretic value
$d$
where the minimum in the optimisation problem (1.10) is attained. The goal in this section is to show that for the binary symmetric channel, this minimum is not always attained at the information-theoretic value
![]() $d_{\mathrm{Sh}}=\ln 2$
that minimises the term
$d_{\mathrm{Sh}}=\ln 2$
that minimises the term
![]() $c_{\mathrm{ex},2}(d)$
from (1.10).
$c_{\mathrm{ex},2}(d)$
from (1.10).
Proposition D.1.
For any binary symmetric channel
![]() $\boldsymbol{p}$
given by
$\boldsymbol{p}$
given by
![]() $0 \lt p_{01} = p_{10} \lt 1/2$
, there is
$0 \lt p_{01} = p_{10} \lt 1/2$
, there is
![]() $\hat{\theta }(p_{01})$
such that for all
$\hat{\theta }(p_{01})$
such that for all
![]() $\theta \gt \hat{\theta }(p_{01})$
, we have
$\theta \gt \hat{\theta }(p_{01})$
, we have
![]() $d_{\mathrm{Sh}} = \ln (2) \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
$d_{\mathrm{Sh}} = \ln (2) \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
In order to show that
![]() $d_{\mathrm{Sh}}$
is suboptimal, we will use the following analytic bound on
$d_{\mathrm{Sh}}$
is suboptimal, we will use the following analytic bound on
![]() $c_{\mathrm{ex},1}(d, \theta )$
for binary symmetric channels.
$c_{\mathrm{ex},1}(d, \theta )$
for binary symmetric channels.
Lemma D.2.
For a binary symmetric channel
![]() $\boldsymbol{p}$
given by
$\boldsymbol{p}$
given by
![]() $p_{01} \lt 1/2$
, we have
$p_{01} \lt 1/2$
, we have
The proof of Lemma D.2 uses the following fact, which can be verified by elementary calculus.
Fact D.3.
For all
![]() $d \gt 0$
,
$d \gt 0$
,
![]() $0 \lt p \lt 1$
, and
$0 \lt p \lt 1$
, and
![]() $0 \leq z \leq 1$
, we have
$0 \leq z \leq 1$
, we have
 \begin{align*} \textrm{argmin}_{0 \leq y \leq 1} \left \{{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right ) + y D_{\mathrm{KL}}\left ({{{z}\|{p}}}\right )}\right \} &= \frac{a\exp ({-}d)}{1 - (1-a)\exp ({-}d)},\\& \qquad \qquad \text{where }a = \exp \left ({-D_{\mathrm{KL}}\left ({{{z}\|{p}}}\right )}\right ),\quad \text{ and}\\ \min _{0 \leq y \leq 1} \left \{{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right ) + y D_{\mathrm{KL}}\left ({{{z}\|{p}}}\right )}\right \} &= -\ln (1-(1-a)\exp ({-}d)). \end{align*}
\begin{align*} \textrm{argmin}_{0 \leq y \leq 1} \left \{{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right ) + y D_{\mathrm{KL}}\left ({{{z}\|{p}}}\right )}\right \} &= \frac{a\exp ({-}d)}{1 - (1-a)\exp ({-}d)},\\& \qquad \qquad \text{where }a = \exp \left ({-D_{\mathrm{KL}}\left ({{{z}\|{p}}}\right )}\right ),\quad \text{ and}\\ \min _{0 \leq y \leq 1} \left \{{D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right ) + y D_{\mathrm{KL}}\left ({{{z}\|{p}}}\right )}\right \} &= -\ln (1-(1-a)\exp ({-}d)). \end{align*}
Proof of Lemma D.2 (bounding c ex,1(d,θ)). Fact D.3 shows that
with
![]() $a$
as in (D.2). Hence, it is sufficient to show that
$a$
as in (D.2). Hence, it is sufficient to show that
Let us first prove the upper bound. Choose
![]() $\hat{c}(d, \theta )$
such that
$\hat{c}(d, \theta )$
such that
we need to show that
![]() $c_{\mathrm{ex},1}(d, \theta ) \leq \hat{c}(d, \theta )$
. By the channel symmetry and because
$c_{\mathrm{ex},1}(d, \theta ) \leq \hat{c}(d, \theta )$
. By the channel symmetry and because
![]() $p_{01} \lt 1/2 \lt p_{11}$
, we have
$p_{01} \lt 1/2 \lt p_{11}$
, we have
Therefore, the definition of
![]() $\hat{c}(d, \theta )$
ensures that for all
$\hat{c}(d, \theta )$
ensures that for all
![]() $y \in [0, 1]$
, we have
$y \in [0, 1]$
, we have
and thus
![]() $\hat{c}(d, \theta ) \geq c_{\mathrm{ex},0}(d, \theta )$
. Once again by channel symmetry and the definitions of
$\hat{c}(d, \theta ) \geq c_{\mathrm{ex},0}(d, \theta )$
. Once again by channel symmetry and the definitions of
![]() $\hat{c}(d, \theta )$
and
$\hat{c}(d, \theta )$
and
![]() $\mathfrak z(y)$
(see [1.8]), we see that
$\mathfrak z(y)$
(see [1.8]), we see that
![]() $D_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{11}}}}\right ) \leq D_{\mathrm{KL}}\left ({{{1/2}\|{p_{11}}}}\right ) = D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right )$
and hence
$D_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{11}}}}\right ) \leq D_{\mathrm{KL}}\left ({{{1/2}\|{p_{11}}}}\right ) = D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right )$
and hence
![]() $D_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{01}}}}\right ) \geq D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right )$
for all
$D_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{01}}}}\right ) \geq D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right )$
for all
![]() $y$
. Consequently, the definition of
$y$
. Consequently, the definition of
![]() $\hat{c}(d, \theta )$
ensures we see that for all
$\hat{c}(d, \theta )$
ensures we see that for all
![]() $y \in [0, 1]$
,
$y \in [0, 1]$
,
Hence,
![]() $\hat{c}(d, \theta ) \geq c_{\mathrm{ex},1}(d, \theta )$
, which is the right inequality in (D.3).
$\hat{c}(d, \theta ) \geq c_{\mathrm{ex},1}(d, \theta )$
, which is the right inequality in (D.3).
Moving on to the lower bound, choose
![]() $\check{c}(d, \theta )$
such that
$\check{c}(d, \theta )$
such that
we need to show that
![]() $c_{\mathrm{ex},1}(d, \theta ) \gt \check{c}(d, \theta )$
. The
$c_{\mathrm{ex},1}(d, \theta ) \gt \check{c}(d, \theta )$
. The
![]() $y = \hat{y}$
where the minimum (D.4) is attained satisfies
$y = \hat{y}$
where the minimum (D.4) is attained satisfies
![]() $\hat{y} \in \mathscr{Y}(c,d,\theta )$
because
$\hat{y} \in \mathscr{Y}(c,d,\theta )$
because
![]() $D_{\mathrm{KL}}\left ({{{1/2}\|{p_{11}}}}\right ) \gt 0$
(due to
$D_{\mathrm{KL}}\left ({{{1/2}\|{p_{11}}}}\right ) \gt 0$
(due to
![]() $p_{11} \gt 1/2$
). Moreover,
$p_{11} \gt 1/2$
). Moreover,
![]() $\mathfrak z(\hat{y}) = 1/2$
by the definition of
$\mathfrak z(\hat{y}) = 1/2$
by the definition of
![]() $\mathfrak z(\cdot)$
. But since
$\mathfrak z(\cdot)$
. But since
![]() $D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right ) = D_{\mathrm{KL}}\left ({{{1/2}\|{p_{11}}}}\right )$
by symmetry of the channel, we have
$D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right ) = D_{\mathrm{KL}}\left ({{{1/2}\|{p_{11}}}}\right )$
by symmetry of the channel, we have
Hence, we obtain
![]() $\check{c}(d, \theta ) \lt c_{\mathrm{ex},1}(d, \theta )$
, which is the left inequality in (D.3).
$\check{c}(d, \theta ) \lt c_{\mathrm{ex},1}(d, \theta )$
, which is the left inequality in (D.3).
To complete the proof of Proposition D.1, we need a second elementary fact.
Fact D.4.
The function
![]() $f(x, p) = \ln (x) \ln (1-p x)$
is concave in its first argument for
$f(x, p) = \ln (x) \ln (1-p x)$
is concave in its first argument for
![]() $x, p \in (0, 1)$
, and for any given
$x, p \in (0, 1)$
, and for any given
![]() $p \in (0, 1)$
, any
$p \in (0, 1)$
, any
![]() $x$
maximising
$x$
maximising
![]() $f(x, p)$
is strictly less than
$f(x, p)$
is strictly less than
![]() $\frac{1}{2}$
.
$\frac{1}{2}$
.
Proof of Proposition
D.1
(d = ln [2] can be suboptimal). We reparameterise the bounds on
![]() $c_{\mathrm{ex},1}(d, \theta )$
from Lemma D.2 in terms of
$c_{\mathrm{ex},1}(d, \theta )$
from Lemma D.2 in terms of
![]() $\exp ({-}d)$
, obtaining
$\exp ({-}d)$
, obtaining
 \begin{align*} \frac{\theta }{-(1-\theta )f({\exp} ({-}d), 1-a)}&\lt c_{\mathrm{ex},1}(d, \theta ) \leq \frac{1}{-(1-\theta )f({\exp} ({-}d), 1-a)},\quad \text{where}\\ f(x, p) &= \ln (x)\ln (1 - px),\quad a = \exp \left ({-D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right )}\right ). \end{align*}
\begin{align*} \frac{\theta }{-(1-\theta )f({\exp} ({-}d), 1-a)}&\lt c_{\mathrm{ex},1}(d, \theta ) \leq \frac{1}{-(1-\theta )f({\exp} ({-}d), 1-a)},\quad \text{where}\\ f(x, p) &= \ln (x)\ln (1 - px),\quad a = \exp \left ({-D_{\mathrm{KL}}\left ({{{1/2}\|{p_{01}}}}\right )}\right ). \end{align*}
As
![]() $0 \lt a \lt 1$
Fact D.4 shows that any
$0 \lt a \lt 1$
Fact D.4 shows that any
![]() $x$
maximising
$x$
maximising
![]() $f(x, 1-a)$
is strictly less than
$f(x, 1-a)$
is strictly less than
![]() $1/2$
. Hence, for
$1/2$
. Hence, for
![]() $\hat{d} \gt \ln (2)$
minimising
$\hat{d} \gt \ln (2)$
minimising
![]() $f({\exp} ({-}d), 1-a)$
, we have
$f({\exp} ({-}d), 1-a)$
, we have
![]() $f({\exp} ({-}d), 1-a) \lt f(1/2, 1-a) = f({\exp} ({-}d_{\mathrm{Sh}}), 1-a)$
. In particular, the value
$f({\exp} ({-}d), 1-a) \lt f(1/2, 1-a) = f({\exp} ({-}d_{\mathrm{Sh}}), 1-a)$
. In particular, the value
 \begin{align*}\hat {\theta }(p_{01}) & = \inf \left \{0 \lt \theta \lt 1 \,:\, \frac {c_{\mathrm {ex},2}(\hat {d})}{\theta } \lt \frac {1}{-\hat {d}(1-\theta )\ln (1-(1-a)\exp ({-}\hat {d}))}\right.\\& \left.\lt \frac {\theta }{-d_{\mathrm {Sh}}(1-\theta )\ln (1-(1-a)\exp ({-}d_{\mathrm {Sh}}))}\right \}\end{align*}
\begin{align*}\hat {\theta }(p_{01}) & = \inf \left \{0 \lt \theta \lt 1 \,:\, \frac {c_{\mathrm {ex},2}(\hat {d})}{\theta } \lt \frac {1}{-\hat {d}(1-\theta )\ln (1-(1-a)\exp ({-}\hat {d}))}\right.\\& \left.\lt \frac {\theta }{-d_{\mathrm {Sh}}(1-\theta )\ln (1-(1-a)\exp ({-}d_{\mathrm {Sh}}))}\right \}\end{align*}
is well defined. Hence, for all
![]() $\theta \gt \hat{\theta }(p_{01})$
, we have
$\theta \gt \hat{\theta }(p_{01})$
, we have
and thus
![]() $d_{\mathrm{Sh}} \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
$d_{\mathrm{Sh}} \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
Appendix E. Parameter optimisation for the
 $Z$
-channel
$Z$
-channel
Much as in Appendix D, the goal here is to show that also for the
![]() $Z$
-channel, the value
$Z$
-channel, the value
![]() $d_{\mathrm{Sh}}$
from (1.17) at which
$d_{\mathrm{Sh}}$
from (1.17) at which
![]() $c_{\mathrm{ex},2}(d)$
from (1.10) attains its minimum is not generally the optimal choice to minimise
$c_{\mathrm{ex},2}(d)$
from (1.10) attains its minimum is not generally the optimal choice to minimise
![]() $\max \{c_{\mathrm{ex},1}(d,\theta ),c_{\mathrm{ex},2}(d)\}$
and thus obtain the optimal bound
$\max \{c_{\mathrm{ex},1}(d,\theta ),c_{\mathrm{ex},2}(d)\}$
and thus obtain the optimal bound
![]() $c_{\mathrm{ex}}(\theta )$
. To this end, we derive the explicit formula (1.15) for
$c_{\mathrm{ex}}(\theta )$
. To this end, we derive the explicit formula (1.15) for
![]() $c_{\mathrm{ex},1}(d,\theta )$
; the derivation of the second formula (1.16) is elementary.
$c_{\mathrm{ex},1}(d,\theta )$
; the derivation of the second formula (1.16) is elementary.
Proposition E.1.
For a
![]() $Z$
-channel
$Z$
-channel
![]() $\boldsymbol{p}$
given by
$\boldsymbol{p}$
given by
![]() $p_{01} = 0$
and
$p_{01} = 0$
and
![]() $0 \lt p_{11} \lt 1$
, we have
$0 \lt p_{11} \lt 1$
, we have
![]() $c_{\mathrm{ex},1}(d, \theta ) = \frac{\theta }{-(1-\theta ) d \ln (1 - \exp ({-}d) p_{11})}$
.
$c_{\mathrm{ex},1}(d, \theta ) = \frac{\theta }{-(1-\theta ) d \ln (1 - \exp ({-}d) p_{11})}$
.
Proof. We observe that for a
![]() $Z$
-channel, we have
$Z$
-channel, we have
![]() $c_{\mathrm{ex},1}(d, \theta ) = c_{\mathrm{ex},0}(d, \theta )$
. Indeed, fix any
$c_{\mathrm{ex},1}(d, \theta ) = c_{\mathrm{ex},0}(d, \theta )$
. Indeed, fix any
![]() $c \gt c_{\mathrm{ex},0}(d, \theta )$
. Then by the definitions (1.7) of
$c \gt c_{\mathrm{ex},0}(d, \theta )$
. Then by the definitions (1.7) of
![]() $c_{\mathrm{ex},0}(d, \theta )$
and of
$c_{\mathrm{ex},0}(d, \theta )$
and of
![]() $\mathfrak z(y)$
, we have
$\mathfrak z(y)$
, we have
![]() $\mathfrak z(y) \gt p_{01}$
. Since the
$\mathfrak z(y) \gt p_{01}$
. Since the
![]() $Z$
-channel satisfies
$Z$
-channel satisfies
![]() $p_{01} = 0$
, the value
$p_{01} = 0$
, the value
![]() $D_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{01}}}}\right )$
diverges for all
$D_{\mathrm{KL}}\left ({{{\mathfrak z(y)}\|{p_{01}}}}\right )$
diverges for all
![]() $c \gt c_{\mathrm{ex},0}(d, \theta )$
, rendering the condition in the definition of
$c \gt c_{\mathrm{ex},0}(d, \theta )$
, rendering the condition in the definition of
![]() $c_{\mathrm{ex},1}(d, \theta )$
void for all
$c_{\mathrm{ex},1}(d, \theta )$
void for all
![]() $y \gt 0$
. Moreover, since
$y \gt 0$
. Moreover, since
![]() $c \gt c_{\mathrm{ex},0}(d,\theta )$
, we also have
$c \gt c_{\mathrm{ex},0}(d,\theta )$
, we also have
![]() $0 \not \in \mathscr{Y}(c,d,\theta )$
and thus
$0 \not \in \mathscr{Y}(c,d,\theta )$
and thus
![]() $c \geq c_{\mathrm{ex},1}(d, \theta )$
. Since
$c \geq c_{\mathrm{ex},1}(d, \theta )$
. Since
![]() $c_{\mathrm{ex},1}(d, \theta ) \geq c_{\mathrm{ex},0}(d, \theta )$
by definition, this implies that
$c_{\mathrm{ex},1}(d, \theta ) \geq c_{\mathrm{ex},0}(d, \theta )$
by definition, this implies that
![]() $c_{\mathrm{ex},1}(d, \theta ) = c_{\mathrm{ex},0}(d, \theta )$
on the
$c_{\mathrm{ex},1}(d, \theta ) = c_{\mathrm{ex},0}(d, \theta )$
on the
![]() $Z$
-channel.
$Z$
-channel.
Hence, it remains to verify that
![]() $c_{\mathrm{ex},1}(d,\theta ) = c_{\mathrm{ex},0}(d,\theta )$
has the claimed value. This is a direct consequence of Fact D.3 (with
$c_{\mathrm{ex},1}(d,\theta ) = c_{\mathrm{ex},0}(d,\theta )$
has the claimed value. This is a direct consequence of Fact D.3 (with
![]() $z=p_{01}$
and
$z=p_{01}$
and
![]() $p=p_{11}$
) in combination with the fact that
$p=p_{11}$
) in combination with the fact that
![]() $D_{\mathrm{KL}}\left ({{{p_{01}}\|{p_{11}}}}\right ) = D_{\mathrm{KL}}\left ({{{0}\|{p_{11}}}}\right ) = -\ln (p_{10})$
and thus
$D_{\mathrm{KL}}\left ({{{p_{01}}\|{p_{11}}}}\right ) = D_{\mathrm{KL}}\left ({{{0}\|{p_{11}}}}\right ) = -\ln (p_{10})$
and thus
![]() $1 - \exp ({-}D_{\mathrm{KL}}\left ({{{p_{01}}\|{p_{11}}}}\right )) = 1 - p_{10} = p_{11}$
.
$1 - \exp ({-}D_{\mathrm{KL}}\left ({{{p_{01}}\|{p_{11}}}}\right )) = 1 - p_{10} = p_{11}$
.
The following proposition shows that indeed
![]() $d=d_{\mathrm{Sh}}$
is not generally the optimal choice. Recall that
$d=d_{\mathrm{Sh}}$
is not generally the optimal choice. Recall that
![]() $\mathscr{D}(\theta, \boldsymbol{p})$
is the set of
$\mathscr{D}(\theta, \boldsymbol{p})$
is the set of
![]() $d$
where the minimum in the optimisation problem defining
$d$
where the minimum in the optimisation problem defining
![]() $c_{\mathrm{ex}}(\theta )$
is attained for a given channel
$c_{\mathrm{ex}}(\theta )$
is attained for a given channel
![]() $\boldsymbol{p}$
.
$\boldsymbol{p}$
.
Proposition E.2.
For a
![]() $Z$
-channel
$Z$
-channel
![]() $\boldsymbol{p}$
given by
$\boldsymbol{p}$
given by
![]() $p_{01} = 0$
and any
$p_{01} = 0$
and any
![]() $0 \lt p_{11} \lt 1$
, there is a
$0 \lt p_{11} \lt 1$
, there is a
![]() $\hat{\theta }(p_{11}) \lt 1$
such that for all
$\hat{\theta }(p_{11}) \lt 1$
such that for all
![]() $\theta \gt \hat{\theta }(p_{11})$
, we have
$\theta \gt \hat{\theta }(p_{11})$
, we have
![]() $d_{\mathrm{Sh}} \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
$d_{\mathrm{Sh}} \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
Towards the proof of Proposition E.2, we state the following fact whose proof comes down to basic calculus.
Fact E.3.
For a
![]() $Z$
-channel
$Z$
-channel
![]() $\boldsymbol{p}$
where
$\boldsymbol{p}$
where
![]() $p_{01} = 0$
and
$p_{01} = 0$
and
![]() $0 \lt p_{10} \lt 1$
, we have
$0 \lt p_{10} \lt 1$
, we have
![]() $\exp ({-}d_{\mathrm{Sh}}(\boldsymbol{p})) \gt \frac{1}{2}$
.
$\exp ({-}d_{\mathrm{Sh}}(\boldsymbol{p})) \gt \frac{1}{2}$
.
Proof of Proposition
E.2
(dSh is suboptimal for the z-channel). First we show that
![]() $d = d_{\mathrm{Sh}}$
does not minimise
$d = d_{\mathrm{Sh}}$
does not minimise
![]() $c_{\mathrm{ex},1}(d, \theta )$
for all
$c_{\mathrm{ex},1}(d, \theta )$
for all
![]() $0 \lt p_{11} \lt 1$
. We reparameterise the expression for
$0 \lt p_{11} \lt 1$
. We reparameterise the expression for
![]() $c_{\mathrm{ex},1}(d, \theta )$
from Proposition E.1 in terms of
$c_{\mathrm{ex},1}(d, \theta )$
from Proposition E.1 in terms of
![]() $\exp ({-}d)$
, obtaining
$\exp ({-}d)$
, obtaining
Hence, for any given
![]() $p_{11}$
, the value of
$p_{11}$
, the value of
![]() $c_{\mathrm{ex},1}$
(
$c_{\mathrm{ex},1}$
(
![]() $d, \theta$
) is minimised when
$d, \theta$
) is minimised when
![]() $f({\exp} ({-}d), p_{11})$
is minimised. Using elementary calculus, we check that
$f({\exp} ({-}d), p_{11})$
is minimised. Using elementary calculus, we check that
![]() $f$
is concave in its first argument on the interval
$f$
is concave in its first argument on the interval
![]() $(0, 1)$
and that for all
$(0, 1)$
and that for all
![]() $0 \lt p_{11} \lt 1$
, the value of
$0 \lt p_{11} \lt 1$
, the value of
![]() $x$
maximising
$x$
maximising
![]() $f(x, p_{11})$
is strictly smaller than
$f(x, p_{11})$
is strictly smaller than
![]() $\frac{1}{2}$
(see Fact D.4). Now for any
$\frac{1}{2}$
(see Fact D.4). Now for any
![]() $Z$
-channel with
$Z$
-channel with
![]() $0 \lt p_{10} \lt 1$
, we have
$0 \lt p_{10} \lt 1$
, we have
![]() $\exp ({-}d_{\mathrm{Sh}}) \gt \frac{1}{2}$
(using Fact E.3). Hence, for the
$\exp ({-}d_{\mathrm{Sh}}) \gt \frac{1}{2}$
(using Fact E.3). Hence, for the
![]() $Z$
-channel,
$Z$
-channel,
![]() $d_{\mathrm{Sh}}$
does not minimise
$d_{\mathrm{Sh}}$
does not minimise
![]() $c_{\mathrm{ex},1}(d, \theta )$
.
$c_{\mathrm{ex},1}(d, \theta )$
.
Now let
![]() $d_1$
be a
$d_1$
be a
![]() $d$
minimising
$d$
minimising
![]() $c_{\mathrm{ex},1}(d, \theta )$
; in particular,
$c_{\mathrm{ex},1}(d, \theta )$
; in particular,
![]() $d_1 \neq d_{\mathrm{Sh}}$
. Since
$d_1 \neq d_{\mathrm{Sh}}$
. Since
![]() $\frac{\theta }{1-\theta }$
is increasing in
$\frac{\theta }{1-\theta }$
is increasing in
![]() $\theta$
and unbounded as
$\theta$
and unbounded as
![]() $\theta \to 1$
, the same holds for
$\theta \to 1$
, the same holds for
![]() $c_{\mathrm{ex},1}(d_1, \theta )$
and
$c_{\mathrm{ex},1}(d_1, \theta )$
and
![]() $c_{\mathrm{ex},1}(d_{\mathrm{Sh}}, \theta )$
. Hence, we may consider
$c_{\mathrm{ex},1}(d_{\mathrm{Sh}}, \theta )$
. Hence, we may consider
check that it is strictly less than
![]() $1$
, and that by definition of
$1$
, and that by definition of
![]() $\hat{\theta }(p_{11})$
, it holds for all
$\hat{\theta }(p_{11})$
, it holds for all
![]() $\theta \gt \hat{\theta }(p_{11})$
that
$\theta \gt \hat{\theta }(p_{11})$
that
Consequently,
![]() $d_{\mathrm{Sh}} \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
$d_{\mathrm{Sh}} \not \in \mathscr{D}(\theta, \boldsymbol{p})$
.
Appendix F. Comparison with the results of Chen and Scarlett on the symmetric channel
Chen and Scarlett [Reference Chen and Scarlett7] recently derive the preci,se information-theoretic threshold of the constant column design
![]() $\mathbf{G}_{\mathrm{cc}}$
for the symmetric channel (i.e.
$\mathbf{G}_{\mathrm{cc}}$
for the symmetric channel (i.e.
![]() $p_{11}=p_{00}$
). The aim of this section is to verify that their threshold coincides with
$p_{11}=p_{00}$
). The aim of this section is to verify that their threshold coincides with
![]() $m\sim c_{\mathrm{ex}}(\theta )k\ln (n/k)$
, with
$m\sim c_{\mathrm{ex}}(\theta )k\ln (n/k)$
, with
![]() $c_{\mathrm{ex}}(\theta )$
from (1.11) on the symmetric channel. The threshold quoted in (Reference Chen and Scarlett7, Theorems 3 and 4) reads
$c_{\mathrm{ex}}(\theta )$
from (1.11) on the symmetric channel. The threshold quoted in (Reference Chen and Scarlett7, Theorems 3 and 4) reads
![]() $m\sim \min _{d\gt 0}c_{\mathrm{CS}}(d,\theta )k\ln (n/k)$
, where
$m\sim \min _{d\gt 0}c_{\mathrm{CS}}(d,\theta )k\ln (n/k)$
, where
![]() $c_{\mathrm{CS}}(d,\theta )$
is the solution to the following optimisation problem:
$c_{\mathrm{CS}}(d,\theta )$
is the solution to the following optimisation problem:
 \begin{align} & c_{\mathrm{ls}}(d, \theta ) = \bigg [(1-\theta ) d \min _{y \in (0,1), z \in (0,1)} \max \bigg \{\frac{1}{\theta } \big( D_{\mathrm{KL}}\big({{{y}\|{\mathrm{e}^{-d} + y D_{\mathrm{KL}}\big({{{z}\|{\mathrm{e}^{-d}}}}\big)}}}\big)\big),\nonumber \\ &\qquad\qquad\qquad\qquad\qquad \min _{y^{\prime}\in [\left |{y(2z-1)}\right |, 1]}\big( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\big({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\big)\big) \bigg \} \bigg ]^{-1}\\[5pt]& z^{\prime}(z,y,y^{\prime}) = \frac{1}{2} + \frac{y(2z-1)}{2y^{\prime}}. \nonumber \end{align}
\begin{align} & c_{\mathrm{ls}}(d, \theta ) = \bigg [(1-\theta ) d \min _{y \in (0,1), z \in (0,1)} \max \bigg \{\frac{1}{\theta } \big( D_{\mathrm{KL}}\big({{{y}\|{\mathrm{e}^{-d} + y D_{\mathrm{KL}}\big({{{z}\|{\mathrm{e}^{-d}}}}\big)}}}\big)\big),\nonumber \\ &\qquad\qquad\qquad\qquad\qquad \min _{y^{\prime}\in [\left |{y(2z-1)}\right |, 1]}\big( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\big({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\big)\big) \bigg \} \bigg ]^{-1}\\[5pt]& z^{\prime}(z,y,y^{\prime}) = \frac{1}{2} + \frac{y(2z-1)}{2y^{\prime}}. \nonumber \end{align}
Lemma F.1.
For symmetric noise (
![]() $p_{00} = p_{11}$
) and any
$p_{00} = p_{11}$
) and any
![]() $d\gt 0$
, we have
$d\gt 0$
, we have
![]() $c_{\mathrm{CS}}(d,\theta )= \max \{c_{\mathrm{ex},1}(d,\theta ),c_{\mathrm{ex},2}(d)\}$
.
$c_{\mathrm{CS}}(d,\theta )= \max \{c_{\mathrm{ex},1}(d,\theta ),c_{\mathrm{ex},2}(d)\}$
.
Proof. The definition (F.2) of
![]() $c_{\mathrm{ls}}(d)$
can be equivalently rephrased as follows:
$c_{\mathrm{ls}}(d)$
can be equivalently rephrased as follows:
 \begin{align*} c_{\mathrm{ls}}(d,\theta ) =& \inf \big \{c\gt 0\,:\, \forall y,z\in \left [0,1\right ] \forall y^{\prime}\in \left \lbrack{\left |{y(2z-1)}\right |, 1}\right \rbrack \,:\, \\& \left ( f_1(c,d,\theta, y, z) \geq \theta \lor f_2(c,d,\theta, y, z, y^{\prime}, z^{\prime}(z,y,y^{\prime})) \geq 1 \right ) \big \}, \qquad \text{ where}\\ f_1(c,d,\theta, y, z) = & c d (1-\theta ) \left ( D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right ) + y D_{\mathrm{KL}}\left ({{{z}\|{p_{11}}}}\right ) \right ),\\ f_2(c,d,\theta, y, z, y^{\prime}, z^{\prime}) = & c d (1-\theta ) \left ( D_{\mathrm{KL}}\left ({{{y^{\prime}}\|{\exp ({-}d)}}}\right ) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right ) \right ). \end{align*}
\begin{align*} c_{\mathrm{ls}}(d,\theta ) =& \inf \big \{c\gt 0\,:\, \forall y,z\in \left [0,1\right ] \forall y^{\prime}\in \left \lbrack{\left |{y(2z-1)}\right |, 1}\right \rbrack \,:\, \\& \left ( f_1(c,d,\theta, y, z) \geq \theta \lor f_2(c,d,\theta, y, z, y^{\prime}, z^{\prime}(z,y,y^{\prime})) \geq 1 \right ) \big \}, \qquad \text{ where}\\ f_1(c,d,\theta, y, z) = & c d (1-\theta ) \left ( D_{\mathrm{KL}}\left ({{{y}\|{\exp ({-}d)}}}\right ) + y D_{\mathrm{KL}}\left ({{{z}\|{p_{11}}}}\right ) \right ),\\ f_2(c,d,\theta, y, z, y^{\prime}, z^{\prime}) = & c d (1-\theta ) \left ( D_{\mathrm{KL}}\left ({{{y^{\prime}}\|{\exp ({-}d)}}}\right ) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right ) \right ). \end{align*}
Consequently,
![]() $c\lt c_{\mathrm{ls}}(d,\theta )$
iff
$c\lt c_{\mathrm{ls}}(d,\theta )$
iff
Recall that
![]() $c\lt c_{\mathrm{ex},1}(d,\theta )$
iff
$c\lt c_{\mathrm{ex},1}(d,\theta )$
iff
Since
![]() $z^{\prime}(z,y,y) = z$
, we conclude that if
$z^{\prime}(z,y,y) = z$
, we conclude that if
![]() $c\lt c_{\mathrm{ex},1}(d,\theta )$
, then
$c\lt c_{\mathrm{ex},1}(d,\theta )$
, then
![]() $c\lt c_{\mathrm{ls}}(d,\theta )$
. Hence,
$c\lt c_{\mathrm{ls}}(d,\theta )$
. Hence,
![]() $c_{\mathrm{ex},1}(d,\theta )\leq c_{\mathrm{ls}}(d,\theta )$
.
$c_{\mathrm{ex},1}(d,\theta )\leq c_{\mathrm{ls}}(d,\theta )$
.
To prove the converse inequality, we are going to show that any
![]() $c\lt c_{\mathrm{ls}}(d,\theta )$
also satisfies
$c\lt c_{\mathrm{ls}}(d,\theta )$
also satisfies
![]() $c\lt c_{\mathrm{ex},1}(d,\theta )$
. Hence, assume for contradiction that
$c\lt c_{\mathrm{ex},1}(d,\theta )$
. Hence, assume for contradiction that
![]() $c \lt c_{\mathrm{ls}}(d,\theta )$
and
$c \lt c_{\mathrm{ls}}(d,\theta )$
and
![]() $c \geq c_{\mathrm{ex},1}(d,\theta )$
. Then the following four inequalities hold:
$c \geq c_{\mathrm{ex},1}(d,\theta )$
. Then the following four inequalities hold:
 \begin{align} & c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right )\right )\lt 1,\nonumber\\& \qquad c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}}\|{p_{11}}}}\right ) \right ) \geq \theta . \end{align}
\begin{align} & c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right )\right )\lt 1,\nonumber\\& \qquad c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}}\|{p_{11}}}}\right ) \right ) \geq \theta . \end{align}
The two inequalities on the left are a direct consequence of
![]() $c \lt c_{\mathrm{ls}}(d,\theta )$
. Note that if one of the right two inequalities is violated, then
$c \lt c_{\mathrm{ls}}(d,\theta )$
. Note that if one of the right two inequalities is violated, then
![]() $c \lt c_{\mathrm{ex},1}(d,\theta )$
. Combining the inequalities of (F.3) leads us to
$c \lt c_{\mathrm{ex},1}(d,\theta )$
. Combining the inequalities of (F.3) leads us to
 \begin{align} \nonumber c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y}\|{\mathrm{e}^{-d}}}}\big) + y D_{\mathrm{KL}}\left ({{{z}\|{p_{01}}}}\right ) \right ) - & c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y}\|{\mathrm{e}^{-d}}}}\big) + y D_{\mathrm{KL}}\left ({{{z}\|{p_{11}}}}\right ) \right ) \\ = c d (1- \theta ) y \left ( D_{\mathrm{KL}}\left ({{{z}\|{p_{01}}}}\right ) - D_{\mathrm{KL}}\left ({{{z}\|{1- p_{01}}}}\right )\right ) = & c d (1-\theta ) y (1-2z) \ln \left (\frac{p_{01}}{1-p_{01}}\right ) \gt 1-\theta . \end{align}
\begin{align} \nonumber c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y}\|{\mathrm{e}^{-d}}}}\big) + y D_{\mathrm{KL}}\left ({{{z}\|{p_{01}}}}\right ) \right ) - & c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y}\|{\mathrm{e}^{-d}}}}\big) + y D_{\mathrm{KL}}\left ({{{z}\|{p_{11}}}}\right ) \right ) \\ = c d (1- \theta ) y \left ( D_{\mathrm{KL}}\left ({{{z}\|{p_{01}}}}\right ) - D_{\mathrm{KL}}\left ({{{z}\|{1- p_{01}}}}\right )\right ) = & c d (1-\theta ) y (1-2z) \ln \left (\frac{p_{01}}{1-p_{01}}\right ) \gt 1-\theta . \end{align}
The remaining inequalities given by (F.4) imply
 \begin{align*} & c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right )\right ) - c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}}\|{p_{11}}}}\right ) \right )\\&\qquad\qquad = c d (1-\theta ) y^{\prime} \left ( D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right ) - D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{1-p_{01}}}}\right ) \right )\\&\qquad\qquad = c d (1-\theta ) y^{\prime} \frac{y}{y^{\prime}} (1-2z) \ln \left (\frac{p_{01}}{1-p_{01}}\right ) \lt 1-\theta, \end{align*}
\begin{align*} & c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right )\right ) - c d (1-\theta ) \left ( D_{\mathrm{KL}}\big({{{y^{\prime}}\|{\mathrm{e}^{-d}}}}\big) + y^{\prime} D_{\mathrm{KL}}\left ({{{z^{\prime}}\|{p_{11}}}}\right ) \right )\\&\qquad\qquad = c d (1-\theta ) y^{\prime} \left ( D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{p_{01}}}}\right ) - D_{\mathrm{KL}}\left ({{{z^{\prime}(z,y,y^{\prime})}\|{1-p_{01}}}}\right ) \right )\\&\qquad\qquad = c d (1-\theta ) y^{\prime} \frac{y}{y^{\prime}} (1-2z) \ln \left (\frac{p_{01}}{1-p_{01}}\right ) \lt 1-\theta, \end{align*}
which contradicts (F.5).