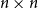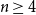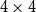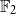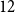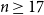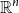1. Introduction
The determinant and permanent of an
![]() $n \times n$
matrix
$n \times n$
matrix
![]() $A$
are defined by
$A$
are defined by
 \begin{align} {\mathrm{det}}(A) = \sum _{\sigma \in S_n} \left ({\mathrm{sgn}}(\sigma )\prod _{i=1}^n a_{i,\sigma (i)}\right ) \quad \text{and} \quad \mathrm{per}(A) = \sum _{\sigma \in S_n} \left (\prod _{i=1}^n a_{i,\sigma (i)}\right ), \end{align}
\begin{align} {\mathrm{det}}(A) = \sum _{\sigma \in S_n} \left ({\mathrm{sgn}}(\sigma )\prod _{i=1}^n a_{i,\sigma (i)}\right ) \quad \text{and} \quad \mathrm{per}(A) = \sum _{\sigma \in S_n} \left (\prod _{i=1}^n a_{i,\sigma (i)}\right ), \end{align}
respectively, where
![]() $S_n$
is the symmetric group over the set
$S_n$
is the symmetric group over the set
![]() $[n] = \{1,2,\ldots,n\}$
. There are numerous other explicit formulas for the permanent of a matrix, such as Ryser’s formula [Reference Brualdi and Ryser1]
$[n] = \{1,2,\ldots,n\}$
. There are numerous other explicit formulas for the permanent of a matrix, such as Ryser’s formula [Reference Brualdi and Ryser1]
 \begin{align} \mathrm{per}(A) & = \sum _{S \subseteq [n]}\left ({\,\mathrm{sgn}}(S)\prod _{i=1}^n \sum _{j \in S} a_{i,j}\right ), \end{align}
\begin{align} \mathrm{per}(A) & = \sum _{S \subseteq [n]}\left ({\,\mathrm{sgn}}(S)\prod _{i=1}^n \sum _{j \in S} a_{i,j}\right ), \end{align}
where
![]() ${\,\mathrm{sgn}}(S) = (-1)^{|S|+n}$
, as well as Glynn’s formula [Reference Glynn6]
${\,\mathrm{sgn}}(S) = (-1)^{|S|+n}$
, as well as Glynn’s formula [Reference Glynn6]
 \begin{align} \mathrm{per}(A) & = \frac{1}{2^{n-1}}\sum _\delta \left ({\,\mathrm{sgn}}(\delta )\prod _{i=1}^n\sum _{j=1}^n\delta _ia_{i,j} \right ), \end{align}
\begin{align} \mathrm{per}(A) & = \frac{1}{2^{n-1}}\sum _\delta \left ({\,\mathrm{sgn}}(\delta )\prod _{i=1}^n\sum _{j=1}^n\delta _ia_{i,j} \right ), \end{align}
where
![]() ${\,\mathrm{sgn}}(\delta ) = \prod _{k=1}^n \delta _k$
and the outer sum ranges over all vectors
${\,\mathrm{sgn}}(\delta ) = \prod _{k=1}^n \delta _k$
and the outer sum ranges over all vectors
![]() $\delta \in \{-1,1\}^n$
with
$\delta \in \{-1,1\}^n$
with
![]() $\delta _1 = 1$
.
$\delta _1 = 1$
.
These alternative formulas for the permanent, despite looking more complicated than the defining formula of equation (1), have a very similar form: they each consist of a sum of products of
![]() $n$
factors, with each factor in the product being a linear combination of entries from a single row of
$n$
factors, with each factor in the product being a linear combination of entries from a single row of
![]() $A$
. One of the advantages of the formulas in equations (2) and (3) is that there are fewer terms in the outer sum (
$A$
. One of the advantages of the formulas in equations (2) and (3) is that there are fewer terms in the outer sum (
![]() $2^n - 1$
and
$2^n - 1$
and
![]() $2^{n-1}$
, respectively, instead of the
$2^{n-1}$
, respectively, instead of the
![]() $n!$
terms of the defining equation (1)), so they can be implemented via fewer multiplications.
$n!$
terms of the defining equation (1)), so they can be implemented via fewer multiplications.
On the other hand, while there are numerous known methods of computing the determinant of a matrix, most of them do not provide an explicit formula with fewer terms being summed than the defining formula of equation (1). For example, cofactor expansions are just factored forms of equation (1) that still consist of a sum of
![]() $n!$
terms, and most numerical methods (e.g., those based on Gaussian elimination or matrix decompositions) are iterative (see [Reference Rote13], for example) and/or require division by entries of the matrix. The only progress in the direction of finding more efficient explicit formulas for the determinant that we are aware of comes from the fact that, when
$n!$
terms, and most numerical methods (e.g., those based on Gaussian elimination or matrix decompositions) are iterative (see [Reference Rote13], for example) and/or require division by entries of the matrix. The only progress in the direction of finding more efficient explicit formulas for the determinant that we are aware of comes from the fact that, when
![]() $n = 3$
, there are several ways that are known to write the determinant as a sum of just
$n = 3$
, there are several ways that are known to write the determinant as a sum of just
![]() $5$
terms instead of
$5$
terms instead of
![]() $3! = 6$
(see [Reference Derksen4, Reference Ilten and Teitler7, Reference Krishna and Makam10], and the references therein, for example), such as
$3! = 6$
(see [Reference Derksen4, Reference Ilten and Teitler7, Reference Krishna and Makam10], and the references therein, for example), such as
 \begin{align} \begin{split}{\mathrm{det}}(A) & = (a_{1,2} + a_{1,3})(a_{2,1} + a_{2,3})(a_{3,1} + a_{3,2}) \\ & \quad - a_{1,2}a_{2,1}(a_{3,1} + a_{3,2} + a_{3,3}) \\ & \quad - a_{1,3}(a_{2,1} + a_{2,2} + a_{2,3})a_{3,1} \\ & \quad - (a_{1,1} + a_{1,2} + a_{1,3})a_{2,3}a_{3,2} \\ & \quad + a_{1,1}a_{2,2}a_{3,3}. \end{split} \end{align}
\begin{align} \begin{split}{\mathrm{det}}(A) & = (a_{1,2} + a_{1,3})(a_{2,1} + a_{2,3})(a_{3,1} + a_{3,2}) \\ & \quad - a_{1,2}a_{2,1}(a_{3,1} + a_{3,2} + a_{3,3}) \\ & \quad - a_{1,3}(a_{2,1} + a_{2,2} + a_{2,3})a_{3,1} \\ & \quad - (a_{1,1} + a_{1,2} + a_{1,3})a_{2,3}a_{3,2} \\ & \quad + a_{1,1}a_{2,2}a_{3,3}. \end{split} \end{align}
Derksen noticed that, when combined with cofactor expansions, formulas like equation (4) generalise to give explicit formulas for the
![]() $n \times n$
determinant that consist of a sum of
$n \times n$
determinant that consist of a sum of
![]() $(5/6)^{\lfloor n/3\rfloor }n!$
terms [Reference Derksen4]. This formula has the fewest terms in the sum known until now, except over fields of characteristic
$(5/6)^{\lfloor n/3\rfloor }n!$
terms [Reference Derksen4]. This formula has the fewest terms in the sum known until now, except over fields of characteristic
![]() $2$
, where
$2$
, where
![]() ${\mathrm{det}}(A) = \mathrm{per}(A)$
(since
${\mathrm{det}}(A) = \mathrm{per}(A)$
(since
![]() $-1 = 1$
) and Ryser’s formula of equation (2) is a sum of just
$-1 = 1$
) and Ryser’s formula of equation (2) is a sum of just
![]() $2^n - 1$
terms.Footnote 1
$2^n - 1$
terms.Footnote 1
Our main contribution is to present a new explicit formula for the determinant (Theorem 2) that improves upon both of these bounds. Our formula reduces to exactly the
![]() $5$
-term formula of equation (4) when
$5$
-term formula of equation (4) when
![]() $n = 3$
, and in general it consists of a sum of exactly
$n = 3$
, and in general it consists of a sum of exactly
![]() $B_n$
terms, where
$B_n$
terms, where
![]() $B_n$
denotes the
$B_n$
denotes the
![]() $n$
-th Bell number (i.e., the number of partitions of
$n$
-th Bell number (i.e., the number of partitions of
![]() $[n]$
). Since
$[n]$
). Since
for all
![]() $n \geq 1$
(the first inequality above uses the bound
$n \geq 1$
(the first inequality above uses the bound
![]() $B_n \leq (4n/5)^n/(\ln (n+1))^n$
from [Reference Berend and Tassa2]), our formula has superexponentially fewer terms than the previously best-known formula. When working over fields of non-zero characteristic, our formula simplifies even further (Corollary 11), to the point of giving a
$B_n \leq (4n/5)^n/(\ln (n+1))^n$
from [Reference Berend and Tassa2]), our formula has superexponentially fewer terms than the previously best-known formula. When working over fields of non-zero characteristic, our formula simplifies even further (Corollary 11), to the point of giving a
![]() $(2^n - n)$
-term formula when the characteristic is
$(2^n - n)$
-term formula when the characteristic is
![]() $2$
(Corollary 13), narrowly surpassing Ryser’s
$2$
(Corollary 13), narrowly surpassing Ryser’s
![]() $(2^n - 1$
)-term formula.
$(2^n - 1$
)-term formula.
1.1 Tensor rank
We can regard the
![]() $n \times n$
determinant over a field
$n \times n$
determinant over a field
![]() $\mathbb{F}$
as a tensor living in
$\mathbb{F}$
as a tensor living in
![]() $({\mathbb{F}}^n)^{\otimes n}$
, and we can then ask questions of it like we ask of any tensor. In particular, we can ask what its tensor rank is [Reference Landsberg11]. That is, if we use
$({\mathbb{F}}^n)^{\otimes n}$
, and we can then ask questions of it like we ask of any tensor. In particular, we can ask what its tensor rank is [Reference Landsberg11]. That is, if we use
![]() ${{\mathrm{det}}^n_{{\mathbb{F}}}} \in ({\mathbb{F}}^n)^{\otimes n}$
to denote the
${{\mathrm{det}}^n_{{\mathbb{F}}}} \in ({\mathbb{F}}^n)^{\otimes n}$
to denote the
![]() $n \times n$
determinant tensor over the field
$n \times n$
determinant tensor over the field
![]() $\mathbb{F}$
, what is the least integer
$\mathbb{F}$
, what is the least integer
![]() $r$
for which there exist
$r$
for which there exist
![]() $\{\mathbf{v_{j,k}}\} \subset{\mathbb{F}}^n$
with
$\{\mathbf{v_{j,k}}\} \subset{\mathbb{F}}^n$
with
We denote tensor rank (i.e., minimal
![]() $r$
) by
$r$
) by
![]() $\mathrm{Trank}$
, so the tensor rank of the determinant is denoted by
$\mathrm{Trank}$
, so the tensor rank of the determinant is denoted by
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
.
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
.
Our interest in the tensor rank comes from the fact that every determinant formula present in this paper corresponds to a tensor decomposition of the form of equation (5) by replacing each occurrence of
![]() $a_{i,j}$
in the formula by
$a_{i,j}$
in the formula by
![]() $\mathbf{e_j}$
(the
$\mathbf{e_j}$
(the
![]() $j$
-th standard basis vector of
$j$
-th standard basis vector of
![]() ${\mathbb{F}}^n$
) in the
${\mathbb{F}}^n$
) in the
![]() $i$
-th tensor factor of the tensor decomposition. For example, the defining formula (1) corresponds to the tensor decomposition
$i$
-th tensor factor of the tensor decomposition. For example, the defining formula (1) corresponds to the tensor decomposition
which shows that
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq |S_n| = n!$
. Similarly, the formula for the
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq |S_n| = n!$
. Similarly, the formula for the
![]() $3 \times 3$
determinant from equation (4) immediately gives us the following tensor decomposition of
$3 \times 3$
determinant from equation (4) immediately gives us the following tensor decomposition of
![]() ${\mathrm{det}}^3_{{\mathbb{F}}}$
, which demonstrates that
${\mathrm{det}}^3_{{\mathbb{F}}}$
, which demonstrates that
![]() ${\mathrm{Trank}}({\mathrm{det}}^3_{{\mathbb{F}}}) \leq 5$
:
${\mathrm{Trank}}({\mathrm{det}}^3_{{\mathbb{F}}}) \leq 5$
:
 \begin{align*}{\mathrm{det}}^3_{{\mathbb{F}}} & = (\mathbf{e_2} + \mathbf{e_3}) \otimes (\mathbf{e_1} + \mathbf{e_3}) \otimes (\mathbf{e_1} + \mathbf{e_2}) \\ & \quad - \mathbf{e_2} \otimes \mathbf{e_1} \otimes (\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3}) \\ & \quad - \mathbf{e_3} \otimes (\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3}) \otimes \mathbf{e_1} \\ & \quad - (\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3}) \otimes \mathbf{e_3} \otimes \mathbf{e_2} \\ & \quad + \mathbf{e_1} \otimes \mathbf{e_2} \otimes \mathbf{e_3}. \end{align*}
\begin{align*}{\mathrm{det}}^3_{{\mathbb{F}}} & = (\mathbf{e_2} + \mathbf{e_3}) \otimes (\mathbf{e_1} + \mathbf{e_3}) \otimes (\mathbf{e_1} + \mathbf{e_2}) \\ & \quad - \mathbf{e_2} \otimes \mathbf{e_1} \otimes (\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3}) \\ & \quad - \mathbf{e_3} \otimes (\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3}) \otimes \mathbf{e_1} \\ & \quad - (\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3}) \otimes \mathbf{e_3} \otimes \mathbf{e_2} \\ & \quad + \mathbf{e_1} \otimes \mathbf{e_2} \otimes \mathbf{e_3}. \end{align*}
In fact, it is known that
![]() ${\mathrm{Trank}}({\mathrm{det}}^3_{{\mathbb{F}}}) = 5$
over every field [Reference Krishna and Makam10], so this decomposition is optimal. When
${\mathrm{Trank}}({\mathrm{det}}^3_{{\mathbb{F}}}) = 5$
over every field [Reference Krishna and Makam10], so this decomposition is optimal. When
![]() $n \geq 4$
, the exact value of
$n \geq 4$
, the exact value of
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
is not known, and until now the best-known upper bounds on it were exactly the bounds that we discussed earlier:Footnote 2
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
is not known, and until now the best-known upper bounds on it were exactly the bounds that we discussed earlier:Footnote 2
Our formula improves upon these bounds by showing that
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq B_n$
regardless of the field
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq B_n$
regardless of the field
![]() $\mathbb{F}$
(Corollary 3), and
$\mathbb{F}$
(Corollary 3), and
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^n - n$
if
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^n - n$
if
![]() $\mathbb{F}$
has characteristic
$\mathbb{F}$
has characteristic
![]() $2$
(Corollary 13). These upper bounds are already known to be tight when
$2$
(Corollary 13). These upper bounds are already known to be tight when
![]() $n = 3$
, and we show that they are also tight when
$n = 3$
, and we show that they are also tight when
![]() $n = 4$
and the ground field has two elements (i.e., the tensor rank is exactly
$n = 4$
and the ground field has two elements (i.e., the tensor rank is exactly
![]() $2^n - n = 12$
in this case; see Theorem 17). We also obtain some other (tighter than
$2^n - n = 12$
in this case; see Theorem 17). We also obtain some other (tighter than
![]() $B_n$
) upper bounds when
$B_n$
) upper bounds when
![]() $\mathbb{F}$
has any non-zero characteristic (Corollaries 11 and 12).
$\mathbb{F}$
has any non-zero characteristic (Corollaries 11 and 12).
1.2 Waring rank
Another notion of the rank of the determinant comes from thinking of it as a homogeneous polynomial in the
![]() $n^2$
entries of the matrix on which it acts. That is, we can think of the determinant as the following degree-
$n^2$
entries of the matrix on which it acts. That is, we can think of the determinant as the following degree-
![]() $n$
polynomial in the
$n$
polynomial in the
![]() $n^2$
variables
$n^2$
variables
![]() $\{x_{i,j}\}$
(we abuse notation slightly and use
$\{x_{i,j}\}$
(we abuse notation slightly and use
![]() ${{\mathrm{det}}^n_{{\mathbb{F}}}}$
to refer to both this polynomial, as well as the tensor from equation (5), but which one we mean will always be clear from context):
${{\mathrm{det}}^n_{{\mathbb{F}}}}$
to refer to both this polynomial, as well as the tensor from equation (5), but which one we mean will always be clear from context):
 \begin{align} {{\mathrm{det}}^n_{{\mathbb{F}}}}(x_{1,1},x_{1,2},\ldots,x_{n,n}) = \sum _{\sigma \in S_n} \left ({\mathrm{sgn}}(\sigma )\prod _{i=1}^n x_{i,\sigma (i)}\right ). \end{align}
\begin{align} {{\mathrm{det}}^n_{{\mathbb{F}}}}(x_{1,1},x_{1,2},\ldots,x_{n,n}) = \sum _{\sigma \in S_n} \left ({\mathrm{sgn}}(\sigma )\prod _{i=1}^n x_{i,\sigma (i)}\right ). \end{align}
We are interested in the Waring rank of this polynomial. That is, what is the least integer
![]() $r$
for which there exist linear forms
$r$
for which there exist linear forms
![]() $\{\ell _k\} \subset \mathrm{Hom}(\mathbb{F}^{n\times n},\mathbb{F})$
and scalars
$\{\ell _k\} \subset \mathrm{Hom}(\mathbb{F}^{n\times n},\mathbb{F})$
and scalars
![]() $\{c_k\}\subset \mathbb{F}$
with
$\{c_k\}\subset \mathbb{F}$
with
We denote the Waring rank of this determinant polynomial by
![]() $\mathrm{Wrank}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
.
$\mathrm{Wrank}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
.
For example, if
![]() $\mathbb{F}$
has characteristic not equal to
$\mathbb{F}$
has characteristic not equal to
![]() $2$
then the Waring rank of the degree-
$2$
then the Waring rank of the degree-
![]() $2$
polynomial
$2$
polynomial
![]() $xy$
is
$xy$
is
![]() $2$
, since
$2$
, since
is a linear combination of
![]() $2$
squares of linear forms, and it is not possible to write
$2$
squares of linear forms, and it is not possible to write
![]() $xy$
as a linear combination (i.e., scalar multiple) of the square of just a single linear form. Similarly, it is well-known that if the characteristic of
$xy$
as a linear combination (i.e., scalar multiple) of the square of just a single linear form. Similarly, it is well-known that if the characteristic of
![]() $\mathbb{F}$
is
$\mathbb{F}$
is
![]() $0$
or strictly larger than
$0$
or strictly larger than
![]() $n$
then the Waring rank of the
$n$
then the Waring rank of the
![]() $n$
-variable polynomial
$n$
-variable polynomial
![]() $x_1x_2\cdots x_n$
is exactly
$x_1x_2\cdots x_n$
is exactly
![]() $2^{n-1}$
as shown in ref. [Reference Ranestad and Schreyer14].Footnote 3 By replacing each term in a formula for the determinant with a linear combination of
$2^{n-1}$
as shown in ref. [Reference Ranestad and Schreyer14].Footnote 3 By replacing each term in a formula for the determinant with a linear combination of
![]() $2^{n-1}$
different
$2^{n-1}$
different
![]() $n$
-th powers of linear forms, we immediately get the following (also well-known) simple relationship between the tensor and Waring ranks of the determinant:
$n$
-th powers of linear forms, we immediately get the following (also well-known) simple relationship between the tensor and Waring ranks of the determinant:
Lemma 1.
Let
![]() $\mathbb{F}$
be a field with characteristic
$\mathbb{F}$
be a field with characteristic
![]() $p$
. If
$p$
. If
![]() $p = 0$
or
$p = 0$
or
![]() $p \gt n$
then
$p \gt n$
then
When combined with the bounds on
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
from Section 1.1, this lemma tells us that if
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
from Section 1.1, this lemma tells us that if
![]() $\mathbb{F}$
is a field with characteristic
$\mathbb{F}$
is a field with characteristic
![]() $0$
or strictly larger than
$0$
or strictly larger than
![]() $n$
, then
$n$
, then
This upper bound was improved in ref. [Reference Johns and Teitler9], in the case when
![]() $\mathbb{F}$
also contains a primitive root of unity (e.g., if
$\mathbb{F}$
also contains a primitive root of unity (e.g., if
![]() $\mathbb{F} = \mathbb{C}$
), to
$\mathbb{F} = \mathbb{C}$
), to
Our formula improves upon these bounds by showing that
![]() $\mathrm{Wrank}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^{n-1} \cdot B_n$
, even without the primitive root of unity assumption (Corollary 3). Our bound is strictly better (i.e., smaller) than the one provided by Inequality (8) for all
$\mathrm{Wrank}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^{n-1} \cdot B_n$
, even without the primitive root of unity assumption (Corollary 3). Our bound is strictly better (i.e., smaller) than the one provided by Inequality (8) for all
![]() $n \geq 4$
, and is better than the one provided by Inequality (9) for all
$n \geq 4$
, and is better than the one provided by Inequality (9) for all
![]() $n \geq 17$
.
$n \geq 17$
.
1.3 Arrangement of the paper
In Section 2, we present our main contribution, which is a new formula for the determinant of a matrix (Theorem 2). As an immediate corollary, we obtain our new field-independent upper bounds on the tensor and Waring ranks of the determinant (Corollary 3).
We present two independent proofs of our formula. First, we present a combinatorial proof in Section 3. This proof has the advantage of being rather mechanical (and thus easy to verify), but the disadvantage of not providing much insight into the formula. Second, we present a geometric proof in Section 4 (this section can be read or skipped quite independently of the rest of the paper). This proof has the advantage of providing some insight into why the formula works and how it was actually found, but is less direct: it is established for all matrices
![]() $A$
in a small open ball in the space of
$A$
in a small open ball in the space of
![]() $n \times n$
real matrices, which is sufficient to prove equality of the determinant polynomial and the polynomial in Theorem 2, thereby proving the result in full generality over arbitrary commutative rings. This proof also demonstrates some new axis-aligned polytope tilings of
$n \times n$
real matrices, which is sufficient to prove equality of the determinant polynomial and the polynomial in Theorem 2, thereby proving the result in full generality over arbitrary commutative rings. This proof also demonstrates some new axis-aligned polytope tilings of
![]() $\mathbb{R}^n$
, where the 1-skeleta of the polytopes can be naturally identified with flip graphs for ordered partial partitions.
$\mathbb{R}^n$
, where the 1-skeleta of the polytopes can be naturally identified with flip graphs for ordered partial partitions.
In Section 5, we investigate what our formula says about the tensor rank of the determinant over fields with non-zero characteristic, and we obtain tighter upper bounds than the field-independent one (Corollaries 11, 12, and 13). Finally, in Section 6, we (very slightly) improve upon the best-known lower bound for the tensor rank of the determinant over arbitrary fields (Theorem 14), we provide a further improvement for the determinant over finite fields (Theorem 15), and we show that the
![]() $4 \times 4$
determinant over the field with two elements has tensor rank equal to exactly
$4 \times 4$
determinant over the field with two elements has tensor rank equal to exactly
![]() $12$
(Theorem 17), demonstrating optimality of our formula in this case.
$12$
(Theorem 17), demonstrating optimality of our formula in this case.
2. The formula
Before presenting our formula for the determinant, we first need the concept of a partial partition of
![]() $[n]$
, which is a set of disjoint subsets (called parts) of
$[n]$
, which is a set of disjoint subsets (called parts) of
![]() $[n]$
. If the union of a partial partition is
$[n]$
. If the union of a partial partition is
![]() $[n]$
then it is a (non-partial) partition. There is a natural bijective correspondence between partial partitions of
$[n]$
then it is a (non-partial) partition. There is a natural bijective correspondence between partial partitions of
![]() $[n]$
with no singleton parts and (non-partial) partitions of
$[n]$
with no singleton parts and (non-partial) partitions of
![]() $[n]$
, which works by erasing all singleton sets from a partition or adding singletons of all members that are missing from a partial partition. For example, when
$[n]$
, which works by erasing all singleton sets from a partition or adding singletons of all members that are missing from a partial partition. For example, when
![]() $n = 3$
, there are
$n = 3$
, there are
![]() $5$
partial partitions of
$5$
partial partitions of
![]() $[n]$
with no singletons and also
$[n]$
with no singletons and also
![]() $5$
partitions of
$5$
partitions of
![]() $[n]$
as follows:
$[n]$
as follows:
 \begin{align} \begin{array}{ccc} \underline{\text{Partitions}} && \underline{\text{Partial partitions with no singletons}}\\ \{\{1,2,3\}\} && \{\{1,2,3\}\} \\ \{\{1,2\},\{3\}\} && \{\{1,2\}\} \\ \{\{1,3\},\{2\}\} && \{\{1,3\}\} \\ \{\{2,3\},\{1\}\} && \{\{2,3\}\} \\ \{\{1\},\{2\},\{3\}\} && \{\} \end{array} \end{align}
\begin{align} \begin{array}{ccc} \underline{\text{Partitions}} && \underline{\text{Partial partitions with no singletons}}\\ \{\{1,2,3\}\} && \{\{1,2,3\}\} \\ \{\{1,2\},\{3\}\} && \{\{1,2\}\} \\ \{\{1,3\},\{2\}\} && \{\{1,3\}\} \\ \{\{2,3\},\{1\}\} && \{\{2,3\}\} \\ \{\{1\},\{2\},\{3\}\} && \{\} \end{array} \end{align}
We denote the set of partial partitions of
![]() $[n]$
by
$[n]$
by
![]() ${\mathrm{PP}}(n)$
. Just like (non-partial) partitions of
${\mathrm{PP}}(n)$
. Just like (non-partial) partitions of
![]() $[n]$
give rise to equivalence relations on
$[n]$
give rise to equivalence relations on
![]() $[n]$
, partial partitions give rise to partial equivalence relations on
$[n]$
, partial partitions give rise to partial equivalence relations on
![]() $[n]$
: relations that are symmetric and transitive, but need not be reflexive. We denote the partial equivalence relation induced by the partial partition
$[n]$
: relations that are symmetric and transitive, but need not be reflexive. We denote the partial equivalence relation induced by the partial partition
![]() $P$
by
$P$
by
![]() $\underset{P}{\sim }$
. In other words, for
$\underset{P}{\sim }$
. In other words, for
![]() $i, j \in [n]$
,
$i, j \in [n]$
,
![]() $i \underset{P}{\sim } j$
means that there is a part in
$i \underset{P}{\sim } j$
means that there is a part in
![]() $P$
containing both
$P$
containing both
![]() $i$
and
$i$
and
![]() $j$
. Moreover, for
$j$
. Moreover, for
![]() $k \in [n]$
,
$k \in [n]$
,
![]() $k \underset{P}{\sim } k$
is not guaranteed, since
$k \underset{P}{\sim } k$
is not guaranteed, since
![]() $k$
might not be in any part of
$k$
might not be in any part of
![]() $P$
.
$P$
.
With the above preliminaries out of the way, we now present our formula for the determinant, which works over any field:
Theorem 2.
Let
![]() $A$
be an
$A$
be an
![]() $n \times n$
matrix. Then
$n \times n$
matrix. Then
 \begin{align} {\mathrm{det}}(A) & = \, \sum _{P \in{\mathrm{PP}}(n)} \,{\mathrm{sgn}}(P) |P|! \prod _{i=1}^n \begin{cases}\displaystyle \, \, \sum _{j \underset{P}{\sim } i, j \neq i} a_{i,j} & \text{ if } i \underset{P}{\sim } i; \\ \displaystyle a_{i,i} + \sum _{j \underset{P}{\sim } j}a_{i,j} & \text{ if } i \underset{P}{\not \sim } i,\end{cases} \end{align}
\begin{align} {\mathrm{det}}(A) & = \, \sum _{P \in{\mathrm{PP}}(n)} \,{\mathrm{sgn}}(P) |P|! \prod _{i=1}^n \begin{cases}\displaystyle \, \, \sum _{j \underset{P}{\sim } i, j \neq i} a_{i,j} & \text{ if } i \underset{P}{\sim } i; \\ \displaystyle a_{i,i} + \sum _{j \underset{P}{\sim } j}a_{i,j} & \text{ if } i \underset{P}{\not \sim } i,\end{cases} \end{align}
where
![]() $\displaystyle{\mathrm{sgn}}(P) = \prod _{S \in P}(-1)^{|S|+1}$
.
$\displaystyle{\mathrm{sgn}}(P) = \prod _{S \in P}(-1)^{|S|+1}$
.
We note that the quantity
![]() ${\mathrm{sgn}}(P)$
is equal to the sign of a permutation with cycle type
${\mathrm{sgn}}(P)$
is equal to the sign of a permutation with cycle type
![]() $\{|S|\,{:}\, S \in P\}$
, which seems like a quite natural notion for the “sign” of a partial partition (e.g., the partial partition
$\{|S|\,{:}\, S \in P\}$
, which seems like a quite natural notion for the “sign” of a partial partition (e.g., the partial partition
![]() $\{\{1,2,3\},\{4,5\}\}$
has the same sign as the permutation
$\{\{1,2,3\},\{4,5\}\}$
has the same sign as the permutation
![]() $(1,2,3)(4,5)$
). While the sum described by Theorem 2 is over all of
$(1,2,3)(4,5)$
). While the sum described by Theorem 2 is over all of
![]() $P \in{\mathrm{PP}}(n)$
, if
$P \in{\mathrm{PP}}(n)$
, if
![]() $P$
contains a singleton part
$P$
contains a singleton part
![]() $\{i\}$
then that term in the sum equals
$\{i\}$
then that term in the sum equals
![]() $0$
since
$0$
since
is an empty sum. The formula (11) can thus be rewritten as a sum over the
![]() $P \in{\mathrm{PP}}(n)$
with no singleton parts. For example, if
$P \in{\mathrm{PP}}(n)$
with no singleton parts. For example, if
![]() $n = 2$
then there are two partial partitions of
$n = 2$
then there are two partial partitions of
![]() $[n]$
with no singletons:
$[n]$
with no singletons:
![]() $P_1 = \{\{1,2\}\}$
and
$P_1 = \{\{1,2\}\}$
and
![]() $P_2 = \{\}$
. We can compute
$P_2 = \{\}$
. We can compute
![]() ${\mathrm{sgn}}(P_1) = -1$
,
${\mathrm{sgn}}(P_1) = -1$
,
![]() ${\mathrm{sgn}}(P_2) = 1$
,
${\mathrm{sgn}}(P_2) = 1$
,
![]() $|P_1|! = 1! = 1$
and
$|P_1|! = 1! = 1$
and
![]() $|P_2|! = 0! = 1$
, so Theorem 2 says that
$|P_2|! = 0! = 1$
, so Theorem 2 says that
which is of course the same as the usual formula for the determinant from equation (1). When
![]() $n = 3$
, the
$n = 3$
, the
![]() $5$
partial partitions with no singletons from equation (10) result in exactly the
$5$
partial partitions with no singletons from equation (10) result in exactly the
![]() $5$
-term formula for the determinant that we saw in equation (4). When
$5$
-term formula for the determinant that we saw in equation (4). When
![]() $n = 4$
, Theorem 2 gives the following
$n = 4$
, Theorem 2 gives the following
![]() $15$
-term formula for the determinant (surpassing the prior state of the art formula, which has
$15$
-term formula for the determinant (surpassing the prior state of the art formula, which has
![]() $20$
terms):
$20$
terms):
 \begin{align} \begin{split}{\mathrm{det}}(A) & = a_{1,1}a_{2,2}a_{3,3}a_{4,4} \\ & \quad - (a_{1,2}+a_{1,3}+a_{1,4})(a_{2,1}+a_{2,3}+a_{2,4})(a_{3,1}+a_{3,2}+a_{3,4})(a_{4,1}+a_{4,2}+a_{4,3}) \\ & \quad + (a_{1,1}+a_{1,2}+a_{1,3}+a_{1,4})(a_{2,3}+a_{2,4})(a_{3,2}+a_{3,4})(a_{4,2}+a_{4,3}) \\ & \quad + (a_{1,3}+a_{1,4})(a_{2,1}+a_{2,2}+a_{2,3}+a_{2,4})(a_{3,1}+a_{3,4})(a_{4,1}+a_{4,3}) \\ & \quad + (a_{1,2}+a_{1,4})(a_{2,1}+a_{2,4})(a_{3,1}+a_{3,2}+a_{3,3}+a_{3,4})(a_{4,1}+a_{4,2}) \\ & \quad + (a_{1,2}+a_{1,3})(a_{2,1}+a_{2,3})(a_{3,1}+a_{3,2})(a_{4,1}+a_{4,2}+a_{4,3}+a_{4,4}) \\ & \quad - a_{1,2}a_{2,1}(a_{3,1}+a_{3,2}+a_{3,3})(a_{4,1}+a_{4,2}+a_{4,4}) \\ & \quad - a_{1,3}(a_{2,1}+a_{2,2}+a_{2,3})a_{3,1}(a_{4,1}+a_{4,3}+a_{4,4}) \\ & \quad - a_{1,4}(a_{2,1}+a_{2,2}+a_{2,4})(a_{3,1}+a_{3,3}+a_{3,4})a_{4,1} \\ & \quad - (a_{1,1}+a_{1,2}+a_{1,3})a_{2,3}a_{3,2}(a_{4,2}+a_{4,3}+a_{4,4}) \\ & \quad - (a_{1,1}+a_{1,2}+a_{1,4})a_{2,4}(a_{3,2}+a_{3,3}+a_{3,4})a_{4,2} \\ & \quad - (a_{1,1}+a_{1,3}+a_{1,4})(a_{2,2}+a_{2,3}+a_{2,4})a_{3,4}a_{4,3} \\ & \quad + 2a_{1,2}a_{2,1}a_{3,4}a_{4,3} \\ & \quad + 2a_{1,3}a_{2,4}a_{3,1}a_{4,2} \\ & \quad + 2a_{1,4}a_{2,3}a_{3,2}a_{4,1}. \end{split} \end{align}
\begin{align} \begin{split}{\mathrm{det}}(A) & = a_{1,1}a_{2,2}a_{3,3}a_{4,4} \\ & \quad - (a_{1,2}+a_{1,3}+a_{1,4})(a_{2,1}+a_{2,3}+a_{2,4})(a_{3,1}+a_{3,2}+a_{3,4})(a_{4,1}+a_{4,2}+a_{4,3}) \\ & \quad + (a_{1,1}+a_{1,2}+a_{1,3}+a_{1,4})(a_{2,3}+a_{2,4})(a_{3,2}+a_{3,4})(a_{4,2}+a_{4,3}) \\ & \quad + (a_{1,3}+a_{1,4})(a_{2,1}+a_{2,2}+a_{2,3}+a_{2,4})(a_{3,1}+a_{3,4})(a_{4,1}+a_{4,3}) \\ & \quad + (a_{1,2}+a_{1,4})(a_{2,1}+a_{2,4})(a_{3,1}+a_{3,2}+a_{3,3}+a_{3,4})(a_{4,1}+a_{4,2}) \\ & \quad + (a_{1,2}+a_{1,3})(a_{2,1}+a_{2,3})(a_{3,1}+a_{3,2})(a_{4,1}+a_{4,2}+a_{4,3}+a_{4,4}) \\ & \quad - a_{1,2}a_{2,1}(a_{3,1}+a_{3,2}+a_{3,3})(a_{4,1}+a_{4,2}+a_{4,4}) \\ & \quad - a_{1,3}(a_{2,1}+a_{2,2}+a_{2,3})a_{3,1}(a_{4,1}+a_{4,3}+a_{4,4}) \\ & \quad - a_{1,4}(a_{2,1}+a_{2,2}+a_{2,4})(a_{3,1}+a_{3,3}+a_{3,4})a_{4,1} \\ & \quad - (a_{1,1}+a_{1,2}+a_{1,3})a_{2,3}a_{3,2}(a_{4,2}+a_{4,3}+a_{4,4}) \\ & \quad - (a_{1,1}+a_{1,2}+a_{1,4})a_{2,4}(a_{3,2}+a_{3,3}+a_{3,4})a_{4,2} \\ & \quad - (a_{1,1}+a_{1,3}+a_{1,4})(a_{2,2}+a_{2,3}+a_{2,4})a_{3,4}a_{4,3} \\ & \quad + 2a_{1,2}a_{2,1}a_{3,4}a_{4,3} \\ & \quad + 2a_{1,3}a_{2,4}a_{3,1}a_{4,2} \\ & \quad + 2a_{1,4}a_{2,3}a_{3,2}a_{4,1}. \end{split} \end{align}
In general, since there are
![]() $B_n$
partitions of
$B_n$
partitions of
![]() $[n]$
, there are also
$[n]$
, there are also
![]() $B_n$
partial partitions of
$B_n$
partial partitions of
![]() $[n]$
with no singleton parts, and thus
$[n]$
with no singleton parts, and thus
![]() $B_n$
(potentially) non-zero terms in the formula (11). This demonstrates part (a) of the following corollary (part (b) then follows from Lemma 1):
$B_n$
(potentially) non-zero terms in the formula (11). This demonstrates part (a) of the following corollary (part (b) then follows from Lemma 1):
Corollary 3.
Let
![]() $\mathbb{F}$
be a field. Then
$\mathbb{F}$
be a field. Then
-
(a)
 ${\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}}^n) \leq B_n$
, and
${\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}}^n) \leq B_n$
, and
-
(b) if
 $\mathbb{F}$
has characteristic
$\mathbb{F}$
has characteristic
 $0$
or strictly larger than
$0$
or strictly larger than
 $n$
then
$n$
then
 $\mathrm{Wrank}({\mathrm{det}}_{{\mathbb{F}}}^n) \leq 2^{n-1} \cdot B_n$
.
$\mathrm{Wrank}({\mathrm{det}}_{{\mathbb{F}}}^n) \leq 2^{n-1} \cdot B_n$
.
3. Combinatorial proof
We now present a combinatorial proof of Theorem 2. This proof works by just brute-force showing that the formula (11), when expanded as a linear combination of monomials, gives the exact same quantity as the defining formula (1). More precisely, let
![]() $f\,{:}\, [n] \rightarrow [n]$
be a function (not necessarily a permutation). Our goal is to show that the coefficient of
$f\,{:}\, [n] \rightarrow [n]$
be a function (not necessarily a permutation). Our goal is to show that the coefficient of
![]() $a_{1,f(1)}a_{2,f(2)}\cdots a_{n,f(n)}$
is the same in equation (11) as it is in the defining formula for the determinant (1).
$a_{1,f(1)}a_{2,f(2)}\cdots a_{n,f(n)}$
is the same in equation (11) as it is in the defining formula for the determinant (1).
To this end we say that a partial partition
![]() $P \in{\mathrm{PP}}(n)$
is algebraically compatible with
$P \in{\mathrm{PP}}(n)$
is algebraically compatible with
![]() $f$
if, for all
$f$
if, for all
![]() $i \in [n]$
, we have the following two properties:
$i \in [n]$
, we have the following two properties:
-
(
 $\alpha$
) If
$\alpha$
) If
 $i \underset{P}{\sim } i$
then
$i \underset{P}{\sim } i$
then
 $f(i) \neq i$
and
$f(i) \neq i$
and
 $f(i) \underset{P}{\sim } i$
, and
$f(i) \underset{P}{\sim } i$
, and -
(
 $\beta$
) If
$\beta$
) If
 $i \underset{P}{\not \sim } i$
then
$i \underset{P}{\not \sim } i$
then
 $f(i) = i$
or
$f(i) = i$
or
 $f(i) \underset{P}{\sim } f(i)$
.
$f(i) \underset{P}{\sim } f(i)$
.
If we let
![]() $\mathrm{ACPP}(f)$
denote the set of partial partitions that are algebraically compatible with
$\mathrm{ACPP}(f)$
denote the set of partial partitions that are algebraically compatible with
![]() $f$
, then equation (11) says exactly that the coefficient
$f$
, then equation (11) says exactly that the coefficient
![]() $c_{f}$
of the coefficient of
$c_{f}$
of the coefficient of
![]() $a_{1,f(1)}a_{2,f(2)}\cdots a_{n,f(n)}$
in an expansion of the determinant is equal to
$a_{1,f(1)}a_{2,f(2)}\cdots a_{n,f(n)}$
in an expansion of the determinant is equal to
Lemma 4.
Let
![]() $c_{f}$
be the coefficient of
$c_{f}$
be the coefficient of
![]() $a_{1,f(1)}a_{2,f(2)}\cdots a_{n,f(n)}$
after expanding the polynomial in the right-hand side of equation (11). Then
$a_{1,f(1)}a_{2,f(2)}\cdots a_{n,f(n)}$
after expanding the polynomial in the right-hand side of equation (11). Then
![]() $c_f ={\mathrm{sgn}}(f)$
if
$c_f ={\mathrm{sgn}}(f)$
if
![]() $f$
is a permutation and
$f$
is a permutation and
![]() $c_f = 0$
otherwise.
$c_f = 0$
otherwise.
Proof. To prove Lemma 4 (and thus Theorem 2), we now split into two cases.
Case 1:
![]() $f$
is not a permutation.
$f$
is not a permutation.
As
![]() $f$
is not surjective, there exists
$f$
is not surjective, there exists
![]() $i \notin \mathop{\mathrm{range}}\nolimits (f)$
. Let
$i \notin \mathop{\mathrm{range}}\nolimits (f)$
. Let
![]() $j = f(i)$
and observe that
$j = f(i)$
and observe that
![]() $j \neq i$
. Take an arbitrary
$j \neq i$
. Take an arbitrary
![]() $P \in \mathrm{ACPP}(f)$
. Note that
$P \in \mathrm{ACPP}(f)$
. Note that
![]() $j \sim j$
and, if
$j \sim j$
and, if
![]() $i \sim i$
, we have
$i \sim i$
, we have
![]() $i \sim j$
. If
$i \sim j$
. If
![]() $P'$
is obtained by removing
$P'$
is obtained by removing
![]() $i$
from the part of
$i$
from the part of
![]() $j$
(if
$j$
(if
![]() $i \sim i$
) or introducing
$i \sim i$
) or introducing
![]() $i$
into the part of
$i$
into the part of
![]() $j$
(otherwise), then
$j$
(otherwise), then
![]() $P' \in \mathrm{ACPP}(f)$
and has the opposite sign to
$P' \in \mathrm{ACPP}(f)$
and has the opposite sign to
![]() $P$
. This defines an involution on
$P$
. This defines an involution on
![]() $\mathrm{ACPP}(f)$
mapping each algebraically compatible partial partition to one of opposite sign, so
$\mathrm{ACPP}(f)$
mapping each algebraically compatible partial partition to one of opposite sign, so
![]() $c_f = 0$
.
$c_f = 0$
.
Case 2:
![]() $f$
is a permutation.
$f$
is a permutation.
We can write
![]() $f$
as a product of disjoint cycles of length at least
$f$
as a product of disjoint cycles of length at least
![]() $2$
:
$2$
:
![]() $f = \sigma _1 \sigma _2 \cdots \sigma _k$
. Each cycle
$f = \sigma _1 \sigma _2 \cdots \sigma _k$
. Each cycle
![]() $\sigma = (i_1 \ i_2 \, \ldots \ i_\ell )$
corresponds naturally to a subset
$\sigma = (i_1 \ i_2 \, \ldots \ i_\ell )$
corresponds naturally to a subset
![]() $S_{\sigma } \,{:\!=}\, \{i_1,i_2,\ldots,i_\ell \} \subseteq [n]$
(though this correspondence is many-to-one since the order of the entries
$S_{\sigma } \,{:\!=}\, \{i_1,i_2,\ldots,i_\ell \} \subseteq [n]$
(though this correspondence is many-to-one since the order of the entries
![]() $\sigma$
matters, whereas it does not matter in
$\sigma$
matters, whereas it does not matter in
![]() $S_{\sigma }$
). Similarly, from
$S_{\sigma }$
). Similarly, from
![]() $f$
we can build the partial partition
$f$
we can build the partial partition
![]() $P_f \,{:\!=}\, \{S_{\sigma _1}, S_{\sigma _2},\ldots,S_{\sigma _k}\}$
.
$P_f \,{:\!=}\, \{S_{\sigma _1}, S_{\sigma _2},\ldots,S_{\sigma _k}\}$
.
If
![]() $i_1$
and
$i_1$
and
![]() $i_2$
are in the same cycle of
$i_2$
are in the same cycle of
![]() $f$
then, for any
$f$
then, for any
![]() $P \in \mathrm{ACPP}(f)$
we have
$P \in \mathrm{ACPP}(f)$
we have
![]() $i_1 \underset{P}{\sim } i_2$
. It follows that
$i_1 \underset{P}{\sim } i_2$
. It follows that
![]() $P \in \mathrm{ACPP}(f)$
if and only if
$P \in \mathrm{ACPP}(f)$
if and only if
![]() $P = P_f$
or
$P = P_f$
or
![]() $P$
can be obtained from
$P$
can be obtained from
![]() $P_f$
by unioning together some of its parts. In other words, there exists a (non-partial) partition
$P_f$
by unioning together some of its parts. In other words, there exists a (non-partial) partition
![]() $K = \{K_1,\ldots,K_m\}$
of
$K = \{K_1,\ldots,K_m\}$
of
![]() $[k]$
such that
$[k]$
such that
 \begin{align} P = \left \{ \bigcup _{i \in K_j} S_{\sigma _i}\,{:}\, j \in [m] \right \}. \end{align}
\begin{align} P = \left \{ \bigcup _{i \in K_j} S_{\sigma _i}\,{:}\, j \in [m] \right \}. \end{align}
If
![]() $\left\{ \begin{smallmatrix}k\\m\end{smallmatrix} \right\}$
denotes the
$\left\{ \begin{smallmatrix}k\\m\end{smallmatrix} \right\}$
denotes the
![]() $(k,m)$
-th Stirling number of the 2nd kind, then there are
$(k,m)$
-th Stirling number of the 2nd kind, then there are
![]() $\left\{ \begin{smallmatrix}k\\m\end{smallmatrix} \right\}$
partitions of
$\left\{ \begin{smallmatrix}k\\m\end{smallmatrix} \right\}$
partitions of
![]() $[k]$
with exactly
$[k]$
with exactly
![]() $m$
parts, so there are
$m$
parts, so there are
![]() $\left\{ \begin{smallmatrix}k\\m\end{smallmatrix} \right\}$
partial partitions
$\left\{ \begin{smallmatrix}k\\m\end{smallmatrix} \right\}$
partial partitions
![]() $P$
of the form (14) with exactly
$P$
of the form (14) with exactly
![]() $m$
parts. Each one has
$m$
parts. Each one has
![]() $|P| = m$
and
$|P| = m$
and
![]() ${\mathrm{sgn}}(P) = (-1)^{k+m}{\,\mathrm{sgn}}(f)$
, so equation (13) can be written more explicitly as
${\mathrm{sgn}}(P) = (-1)^{k+m}{\,\mathrm{sgn}}(f)$
, so equation (13) can be written more explicitly as
 \begin{align} \begin{split} c_f & = \, \, \sum _{P \in \mathrm{ACPP}(f)} \,{\mathrm{sgn}}(P)|P|! \\ & = \sum _{m = 1}^k (-1)^{k+m}{\,\mathrm{sgn}}(f)\left \{\!\begin{array}{c}k\\ m\end{array}\!\right \} m! \\ & = (-1)^k{\,\mathrm{sgn}}(f)\left (\sum _{m = 1}^k \left \{\!\begin{array}{c}k\\ m\end{array}\!\right \}(-1)^{m}m!\right ). \end{split} \end{align}
\begin{align} \begin{split} c_f & = \, \, \sum _{P \in \mathrm{ACPP}(f)} \,{\mathrm{sgn}}(P)|P|! \\ & = \sum _{m = 1}^k (-1)^{k+m}{\,\mathrm{sgn}}(f)\left \{\!\begin{array}{c}k\\ m\end{array}\!\right \} m! \\ & = (-1)^k{\,\mathrm{sgn}}(f)\left (\sum _{m = 1}^k \left \{\!\begin{array}{c}k\\ m\end{array}\!\right \}(-1)^{m}m!\right ). \end{split} \end{align}
We now plug
![]() $x = -1$
into the well-known formula
$x = -1$
into the well-known formula
 \begin{equation*} \sum _{m = 1}^k \left \{\!\begin {array}{c}k\\ m\end {array}\!\right \} x(x-1)(x-2)\cdots (x-m+1) = x^k \end{equation*}
\begin{equation*} \sum _{m = 1}^k \left \{\!\begin {array}{c}k\\ m\end {array}\!\right \} x(x-1)(x-2)\cdots (x-m+1) = x^k \end{equation*}
to see that
 \begin{align} \sum _{m = 1}^k \left \{\!\begin{array}{c}k\\ m\end{array}\!\right \}(-1)^{m}m! = (-1)^k. \end{align}
\begin{align} \sum _{m = 1}^k \left \{\!\begin{array}{c}k\\ m\end{array}\!\right \}(-1)^{m}m! = (-1)^k. \end{align}
Substituting equation (16) into the bottom line of equation (15) shows that
![]() $c_f = (-1)^{2k}{\,\mathrm{sgn}}(f) ={\mathrm{sgn}}(f)$
, which completes the proof.
$c_f = (-1)^{2k}{\,\mathrm{sgn}}(f) ={\mathrm{sgn}}(f)$
, which completes the proof.
4. Geometric interpretation and proof
We now present an alternate proof of Theorem 2 that perhaps provides a bit more insight into why the formula (11) works. We take the base field to be
![]() $\mathbb{R}$
throughout this section, but remark that this does not lose any generality: proving Theorem 2 over
$\mathbb{R}$
throughout this section, but remark that this does not lose any generality: proving Theorem 2 over
![]() $\mathbb{R}$
establishes equality between two polynomials in the ring
$\mathbb{R}$
establishes equality between two polynomials in the ring
![]() $\mathbb{Z}[a_{1,1}, a_{1,2}, \dots, a_{n,n}]$
, which must therefore also hold over any commutative ring.
$\mathbb{Z}[a_{1,1}, a_{1,2}, \dots, a_{n,n}]$
, which must therefore also hold over any commutative ring.
Throughout the rest of this section, we use 3D terminology (e.g., “volume” and “parallelepiped”) if the dimension
![]() $n$
is unknown or greater than
$n$
is unknown or greater than
![]() $2$
. The
$2$
. The
![]() $n$
standard basis vectors are denoted
$n$
standard basis vectors are denoted
![]() $\mathbf{e_1}, \ldots, \mathbf{e_n}$
. It is notationally convenient to also define
$\mathbf{e_1}, \ldots, \mathbf{e_n}$
. It is notationally convenient to also define
![]() $\mathbf{e_0}$
to be the negated sum of the standard basis vectors, so that
$\mathbf{e_0}$
to be the negated sum of the standard basis vectors, so that
![]() $\mathbf{e_0} + \mathbf{e_1} + \cdots + \mathbf{e_n} = 0$
.
$\mathbf{e_0} + \mathbf{e_1} + \cdots + \mathbf{e_n} = 0$
.
4.1 Tilings in general
We consider the matrix
![]() $A$
as defining a lattice in
$A$
as defining a lattice in
![]() $\mathbb{R}^n$
, where the lattice points consist of integer linear combinations of the columns of the matrix. More specifically, this lattice is
$\mathbb{R}^n$
, where the lattice points consist of integer linear combinations of the columns of the matrix. More specifically, this lattice is
The usual connection between the determinant and this lattice is the fact that a parallelepiped with side vectors equal to the columns of
![]() $A$
tiles
$A$
tiles
![]() $\mathbb{R}^n$
by translates in the lattice
$\mathbb{R}^n$
by translates in the lattice
![]() $\Lambda _A$
and has signed volume equal to
$\Lambda _A$
and has signed volume equal to
![]() ${\mathrm{det}}(A)$
(see Fig. 1a). We will prove Theorem 2 by constructing a polytope whose volume is given by the formula in equation (11), but that also tiles
${\mathrm{det}}(A)$
(see Fig. 1a). We will prove Theorem 2 by constructing a polytope whose volume is given by the formula in equation (11), but that also tiles
![]() $\mathbb{R}^n$
by translates in the lattice
$\mathbb{R}^n$
by translates in the lattice
![]() $\Lambda _A$
and thus must also have signed volume equal to
$\Lambda _A$
and thus must also have signed volume equal to
![]() ${\mathrm{det}}(A)$
(see Fig. 1b).Footnote 4
${\mathrm{det}}(A)$
(see Fig. 1b).Footnote 4

Figure 1. Two tilings of
![]() $\mathbb{R}^2$
on the same lattice in which the tiles have area equal to
$\mathbb{R}^2$
on the same lattice in which the tiles have area equal to
![]() $\mathrm{det}\,\left(\left[\begin{smallmatrix}5 & -2 \\ -1 & 3\end{smallmatrix}\right]\right) = 13$
.
$\mathrm{det}\,\left(\left[\begin{smallmatrix}5 & -2 \\ -1 & 3\end{smallmatrix}\right]\right) = 13$
.
For now, instead of placing the usual parallelepiped at each lattice point, we place a cuboid with dimensions
![]() $a_{1,1} \times a_{2,2} \times \cdots \times a_{n,n}$
, extending in the positive direction. That is, we define the cuboid
$a_{1,1} \times a_{2,2} \times \cdots \times a_{n,n}$
, extending in the positive direction. That is, we define the cuboid
![]() $C_A$
to be the Cartesian product of closed intervals of lengths given by the diagonal entries of
$C_A$
to be the Cartesian product of closed intervals of lengths given by the diagonal entries of
![]() $A$
:
$A$
:
and we consider the set of cuboids
![]() $\{C_A + \mathbf{z}\,{:}\, \mathbf{z} \in \Lambda _A\}$
. Depending on the values of the off-diagonal entries of
$\{C_A + \mathbf{z}\,{:}\, \mathbf{z} \in \Lambda _A\}$
. Depending on the values of the off-diagonal entries of
![]() $A$
, these cuboids may overlap and/or there may be gaps between them (see Fig. 2).
$A$
, these cuboids may overlap and/or there may be gaps between them (see Fig. 2).

Figure 2. Two
![]() $5 \times 3$
rectangular not-quite-tilings of
$5 \times 3$
rectangular not-quite-tilings of
![]() $\mathbb{R}^2$
coming from matrices with diagonal entries
$\mathbb{R}^2$
coming from matrices with diagonal entries
![]() $5$
and
$5$
and
![]() $3$
. The shaded rectangle is
$3$
. The shaded rectangle is
![]() $C_A$
, while the other rectangles are its translates on the lattice
$C_A$
, while the other rectangles are its translates on the lattice
![]() $\Lambda _A$
.
$\Lambda _A$
.
Since these cuboids may overlap and/or have gaps between them, they do not typically form a valid tiling of
![]() $\mathbb{R}^n$
. In order to “fix” the fact that these cuboids can overlap, we define
$\mathbb{R}^n$
. In order to “fix” the fact that these cuboids can overlap, we define
![]() $F_A$
to be the axis-aligned polytope obtained from
$F_A$
to be the axis-aligned polytope obtained from
![]() $C_A$
by removing copies of
$C_A$
by removing copies of
![]() $C_A$
translated by sums of non-empty subsets of the columns of
$C_A$
translated by sums of non-empty subsets of the columns of
![]() $A$
.Footnote 5 We take the closure so that
$A$
.Footnote 5 We take the closure so that
![]() $F_A$
contains its boundary:
$F_A$
contains its boundary:

In order to similarly “fix” the fact that there may be gaps between the cuboids, for the remainder of the proof we only consider matrices
![]() $A$
with the following properties:
$A$
with the following properties:
-
(a) Each diagonal entry
 $a_{i,i}$
is strictly positive;
$a_{i,i}$
is strictly positive; -
(b) Each off-diagonal entry,
 $a_{i,j}$
with
$a_{i,j}$
with
 $i\neq j$
, is strictly negative; and
$i\neq j$
, is strictly negative; and -
(c) Each row has strictly positive sum, i.e.,
 $A$
is strictly diagonally dominant.
$A$
is strictly diagonally dominant.
Doing so simplifies the rest of the proof considerably (since the determinant for these matrices is strictly positive, so it equals a volume instead of a signed volume, for example), and it does not result in any loss of generality. Indeed, if two polynomials agree on some open set then they must agree everywhere; the definitional formula of the determinant from equation (1) and the formula described by Theorem 2 are both polynomials in the
![]() $n^2$
entries of the matrix
$n^2$
entries of the matrix
![]() $A$
, so if they agree on some open set (like the set of matrices described by conditions (a)–(c), or even just the smaller set described by the upcoming Lemma 5) then they must agree everywhere.
$A$
, so if they agree on some open set (like the set of matrices described by conditions (a)–(c), or even just the smaller set described by the upcoming Lemma 5) then they must agree everywhere.
In the next section we establish that, subject to these conditions (a)–(c), the translates of
![]() $F_A$
by vectors in
$F_A$
by vectors in
![]() $\Lambda _A$
tile the ambient space
$\Lambda _A$
tile the ambient space
![]() $\mathbb{R}^n$
: their union covers all of space, and any two distinct translates intersect on a set of measure zero (i.e., on their boundary or not at all). We also show that two tiles
$\mathbb{R}^n$
: their union covers all of space, and any two distinct translates intersect on a set of measure zero (i.e., on their boundary or not at all). We also show that two tiles
![]() $F_A + A\mathbf{u}$
and
$F_A + A\mathbf{u}$
and
![]() $F_A + A\mathbf{v}$
share a common boundary if and only if the difference
$F_A + A\mathbf{v}$
share a common boundary if and only if the difference
![]() $\mathbf{u} - \mathbf{v}$
is the sum of some non-empty proper subset of the vectors
$\mathbf{u} - \mathbf{v}$
is the sum of some non-empty proper subset of the vectors
![]() $\{ \mathbf{e_0}, \mathbf{e_1}, \ldots, \mathbf{e_n} \}$
, in which case we describe these two translates as “neighbours”. This is equivalent to
$\{ \mathbf{e_0}, \mathbf{e_1}, \ldots, \mathbf{e_n} \}$
, in which case we describe these two translates as “neighbours”. This is equivalent to
![]() $\mathbf{u} - \mathbf{v}$
being a non-zero vector with all entries in
$\mathbf{u} - \mathbf{v}$
being a non-zero vector with all entries in
![]() $\{0, 1\}$
or all entries in
$\{0, 1\}$
or all entries in
![]() $\{0, -1\}$
. Each tile has exactly
$\{0, -1\}$
. Each tile has exactly
![]() $2(2^n - 1)$
neighbours.
$2(2^n - 1)$
neighbours.
This tiling admits a proper
![]() $(n+1)$
-colouring, where
$(n+1)$
-colouring, where
![]() $F_A + A\mathbf{v}$
is coloured according to the sum of the coordinates of
$F_A + A\mathbf{v}$
is coloured according to the sum of the coordinates of
![]() $\mathbf{v}$
modulo
$\mathbf{v}$
modulo
![]() $n+1$
. Observe that if two tiles
$n+1$
. Observe that if two tiles
![]() $F_A + A\mathbf{u}$
and
$F_A + A\mathbf{u}$
and
![]() $F_A + A\mathbf{v}$
are neighbours, then the coordinate sum of
$F_A + A\mathbf{v}$
are neighbours, then the coordinate sum of
![]() $\mathbf{u} - \mathbf{v}$
is in
$\mathbf{u} - \mathbf{v}$
is in
![]() $[-n, -1] \cup [1, n]$
and is therefore non-zero modulo
$[-n, -1] \cup [1, n]$
and is therefore non-zero modulo
![]() $n + 1$
, so the tiles are assigned distinct colours. Figure 1b shows
$n + 1$
, so the tiles are assigned distinct colours. Figure 1b shows
![]() $F_A$
and its neighbours coloured in this manner.
$F_A$
and its neighbours coloured in this manner.
Moreover, the tiling is homeomorphic to the standard permutohedral tiling of
![]() $\mathbb{R}^n$
obtained by taking the Voronoi tessellation of the lattice
$\mathbb{R}^n$
obtained by taking the Voronoi tessellation of the lattice
![]() $A_n^{\star }$
defined in [Reference Conway and Sloane3]. For
$A_n^{\star }$
defined in [Reference Conway and Sloane3]. For
![]() $n = 2$
, this is the familiar hexagonal tessellation; for
$n = 2$
, this is the familiar hexagonal tessellation; for
![]() $n = 3$
, this is the tessellation by truncated octahedra whose centres form the body-centred cubic lattice.
$n = 3$
, this is the tessellation by truncated octahedra whose centres form the body-centred cubic lattice.
4.2 The proof itself
For an arbitrary
![]() $n \times n$
matrix
$n \times n$
matrix
![]() $A$
, we shall consider five different propositions (each of which may be true or false, depending on
$A$
, we shall consider five different propositions (each of which may be true or false, depending on
![]() $A$
):
$A$
):
-
 $P_1(A)$
:
$P_1(A)$
:
 ${\mathrm{det}}(A)$
is equal to the formula described by equation (11).
${\mathrm{det}}(A)$
is equal to the formula described by equation (11). -
 $P_2(A)$
: the translates
$P_2(A)$
: the translates
 $\{F_A + \mathbf{z}\,{:}\, \mathbf{z} \in \Lambda _A\}$
have pairwise measure-zero intersections.
$\{F_A + \mathbf{z}\,{:}\, \mathbf{z} \in \Lambda _A\}$
have pairwise measure-zero intersections. -
 $P_3(A)$
: the translates
$P_3(A)$
: the translates
 $\{F_A + \mathbf{z}\,{:}\, \mathbf{z} \in \Lambda _A\}$
cover all of
$\{F_A + \mathbf{z}\,{:}\, \mathbf{z} \in \Lambda _A\}$
cover all of
 $\mathbb{R}^n$
.
$\mathbb{R}^n$
. -
 $P_4(A)$
: the volume of
$P_4(A)$
: the volume of
 $F_A$
is equal to the formula described by equation (11).
$F_A$
is equal to the formula described by equation (11). -
 $P_5(A)$
: the volume of
$P_5(A)$
: the volume of
 $F_A$
is equal to
$F_A$
is equal to
 ${\mathrm{det}}(A)$
.
${\mathrm{det}}(A)$
.
Any two of
![]() $P_2(A), P_3(A), P_5(A)$
together imply the third (being equivalent to the claim that the translates of
$P_2(A), P_3(A), P_5(A)$
together imply the third (being equivalent to the claim that the translates of
![]() $F_A$
by the vectors in the lattice
$F_A$
by the vectors in the lattice
![]() $\Lambda _A$
tile space). Also, any two of
$\Lambda _A$
tile space). Also, any two of
![]() $P_1(A), P_4(A), P_5(A)$
together imply the third (by transitivity of equality). We summarise these relationships in Fig. 3.
$P_1(A), P_4(A), P_5(A)$
together imply the third (by transitivity of equality). We summarise these relationships in Fig. 3.

Figure 3. A summary of the relationship between the properties
![]() $P_1(A)$
–
$P_1(A)$
–
![]() $P_5(A)$
. Any two of the properties in the left Y-shape imply the third, and any two of the properties in the right Y-shape imply the third.
$P_5(A)$
. Any two of the properties in the left Y-shape imply the third, and any two of the properties in the right Y-shape imply the third.
Theorem 2 is equivalent to
![]() $P_1(A)$
being true for all matrices
$P_1(A)$
being true for all matrices
![]() $A$
. The proof proceeds by showing that
$A$
. The proof proceeds by showing that
![]() $P_3(A)$
and
$P_3(A)$
and
![]() $P_4(A)$
are true for all matrices
$P_4(A)$
are true for all matrices
![]() $A$
satisfying the three conditions (a)–(c), and that
$A$
satisfying the three conditions (a)–(c), and that
![]() $P_2(A)$
is true for all matrices
$P_2(A)$
is true for all matrices
![]() $A$
in a small open neighbourhood of a canonical matrix
$A$
in a small open neighbourhood of a canonical matrix
![]() $B$
. We deduce that
$B$
. We deduce that
![]() $P_1(A)$
holds on a non-empty open set, and therefore (being an equality between two polynomials) holds in general, completing the proof of Theorem 2. Note that, by traversing the implications in the other direction, it follows that
$P_1(A)$
holds on a non-empty open set, and therefore (being an equality between two polynomials) holds in general, completing the proof of Theorem 2. Note that, by traversing the implications in the other direction, it follows that
![]() $P_5(A)$
and
$P_5(A)$
and
![]() $P_2(A)$
are true for all matrices
$P_2(A)$
are true for all matrices
![]() $A$
satisfying conditions (a)–(c), and not just those in the small neighbourhood for which we prove
$A$
satisfying conditions (a)–(c), and not just those in the small neighbourhood for which we prove
![]() $P_2(A)$
directly.
$P_2(A)$
directly.
Lemma 5.
Consider the
![]() $n \times n$
matrix
$n \times n$
matrix
where
![]() $J$
is the matrix with all entries equal to
$J$
is the matrix with all entries equal to
![]() $1$
. There is some
$1$
. There is some
![]() $\varepsilon$
-neighbourhood
$\varepsilon$
-neighbourhood
![]() $N_\varepsilon$
of
$N_\varepsilon$
of
![]() $B$
with the property that, for all
$B$
with the property that, for all
![]() $A \in N_\varepsilon$
and all
$A \in N_\varepsilon$
and all
![]() $\mathbf{y} \neq \mathbf{z} \in \Lambda _A$
, it is the case that
$\mathbf{y} \neq \mathbf{z} \in \Lambda _A$
, it is the case that
![]() $(F_A + \mathbf{y}) \cap (F_A + \mathbf{z})$
has measure zero (i.e., any two tiles in the tiling overlap only on their boundary or not at all).
$(F_A + \mathbf{y}) \cap (F_A + \mathbf{z})$
has measure zero (i.e., any two tiles in the tiling overlap only on their boundary or not at all).
Before proving the above lemma, we note that we will choose the
![]() $\varepsilon$
-neighbourhood
$\varepsilon$
-neighbourhood
![]() $N_\varepsilon$
to be small enough that every
$N_\varepsilon$
to be small enough that every
![]() $A \in N_\varepsilon$
satisfies the three conditions (a)–(c) that we described earlier (which is possible since
$A \in N_\varepsilon$
satisfies the three conditions (a)–(c) that we described earlier (which is possible since
![]() $B$
satisfies those three conditions and they define an open set).
$B$
satisfies those three conditions and they define an open set).
![]() $B$
is a positive-definite symmetric matrix with eigenvalues
$B$
is a positive-definite symmetric matrix with eigenvalues
![]() $1$
(with multiplicity
$1$
(with multiplicity
![]() $1$
) and
$1$
) and
![]() $n+1$
(with multiplicity
$n+1$
(with multiplicity
![]() $n-1$
). The singular values of
$n-1$
). The singular values of
![]() $B$
are equal to its eigenvalues, so the minimum singular value of
$B$
are equal to its eigenvalues, so the minimum singular value of
![]() $B$
is also equal to
$B$
is also equal to
![]() $1$
. By choosing
$1$
. By choosing
![]() $\varepsilon$
small enough, we can ensure that every
$\varepsilon$
small enough, we can ensure that every
![]() $A \in N_\varepsilon$
has minimum singular value greater than
$A \in N_\varepsilon$
has minimum singular value greater than
![]() $\frac{1}{2}$
.
$\frac{1}{2}$
.
For concreteness, let
![]() $\varepsilon _0 \gt 0$
be a constant (depending only on
$\varepsilon _0 \gt 0$
be a constant (depending only on
![]() $n$
) that ensures that every
$n$
) that ensures that every
![]() $A \in N_\varepsilon$
satisfies conditions (a)–(c) and has minimum singular value greater than
$A \in N_\varepsilon$
satisfies conditions (a)–(c) and has minimum singular value greater than
![]() $\frac{1}{2}$
.
$\frac{1}{2}$
.
Proof of Lemma
5. It suffices to prove that
![]() $F_A \cap (F_A + \mathbf{z})$
has measure zero whenever
$F_A \cap (F_A + \mathbf{z})$
has measure zero whenever
![]() $\mathbf{z} \in \Lambda _A$
is non-zero. Since
$\mathbf{z} \in \Lambda _A$
is non-zero. Since
![]() $A$
is strictly diagonally dominant and thus invertible,
$A$
is strictly diagonally dominant and thus invertible,
![]() $\mathbf{z} \in \Lambda _A$
being non-zero is equivalent to
$\mathbf{z} \in \Lambda _A$
being non-zero is equivalent to
![]() $\mathbf{z} = A\mathbf{v}$
for some non-zero
$\mathbf{z} = A\mathbf{v}$
for some non-zero
![]() $\mathbf{v} \in \mathbb{Z}^n$
.
$\mathbf{v} \in \mathbb{Z}^n$
.
If
![]() $\mathbf{v}$
is non-zero and has all entries in
$\mathbf{v}$
is non-zero and has all entries in
![]() $\{0,1\}$
or all entries in
$\{0,1\}$
or all entries in
![]() $\{0,-1\}$
then, by the construction of
$\{0,-1\}$
then, by the construction of
![]() $F_A$
given in equation (17), we know that
$F_A$
given in equation (17), we know that
![]() $F_A \cap (F_A + A\mathbf{v})$
has measure zero (we call these
$F_A \cap (F_A + A\mathbf{v})$
has measure zero (we call these
![]() $2(2^n\,{-}\,1)$
tiles
$2(2^n\,{-}\,1)$
tiles
![]() $F_A + A\mathbf{v}$
the “neighbours” of
$F_A + A\mathbf{v}$
the “neighbours” of
![]() $F_A$
; when
$F_A$
; when
![]() $n = 2$
they are exactly the
$n = 2$
they are exactly the
![]() $6$
tiles that touch the central shaded tile in Fig. 1b). Our goal now is to show that every non-neighbour of
$6$
tiles that touch the central shaded tile in Fig. 1b). Our goal now is to show that every non-neighbour of
![]() $F_A$
has empty intersection with
$F_A$
has empty intersection with
![]() $F_A$
.
$F_A$
.
To this end, first consider the matrix
![]() $B$
from equation (18). For this matrix, the polytope under consideration is
$B$
from equation (18). For this matrix, the polytope under consideration is
where
![]() $x_i^\uparrow$
is the
$x_i^\uparrow$
is the
![]() $i$
-th smallest entry of
$i$
-th smallest entry of
![]() $(x_1,x_2,\ldots,x_n)$
(see Fig. 4). Equivalently,
$(x_1,x_2,\ldots,x_n)$
(see Fig. 4). Equivalently,
![]() $F_B$
is the union of the
$F_B$
is the union of the
![]() $n!$
images of the cuboid
$n!$
images of the cuboid
![]() $[0, 1] \times [0, 2] \times \cdots \times [0, n]$
under arbitrary permutations of the coordinates. We claim that
$[0, 1] \times [0, 2] \times \cdots \times [0, n]$
under arbitrary permutations of the coordinates. We claim that
![]() $F_B$
does not intersect
$F_B$
does not intersect
![]() $F_B + B\mathbf{v}$
if
$F_B + B\mathbf{v}$
if
![]() $F_B + B\mathbf{v}$
is not a neighbour of
$F_B + B\mathbf{v}$
is not a neighbour of
![]() $F_B$
.
$F_B$
.

Figure 4. The polytope
![]() $F_B$
for the matrix
$F_B$
for the matrix
![]() $B = (n+1)I - J$
, with
$B = (n+1)I - J$
, with
![]() $n = 3$
. Its volume is equal to the sum and difference of the volumes of
$n = 3$
. Its volume is equal to the sum and difference of the volumes of
![]() $5$
different cubes, corresponding to the
$5$
different cubes, corresponding to the
![]() $5$
-term formula for the determinant (4).
$5$
-term formula for the determinant (4).
To prove this claim, suppose that
![]() $F_B + B\mathbf{v}$
is not a neighbour of
$F_B + B\mathbf{v}$
is not a neighbour of
![]() $F_B$
.
$F_B$
.
Firstly, consider the case where there exist indices
![]() $i$
and
$i$
and
![]() $j$
such that
$j$
such that
![]() $\mathbf{v_i} - \mathbf{v_j} \geq 2$
. Then
$\mathbf{v_i} - \mathbf{v_j} \geq 2$
. Then
![]() $(B\mathbf{v})_i - (B\mathbf{v})_j = (n + 1)(\mathbf{v_i} - \mathbf{v_j}) \geq 2(n+1)$
. Consequently, one of
$(B\mathbf{v})_i - (B\mathbf{v})_j = (n + 1)(\mathbf{v_i} - \mathbf{v_j}) \geq 2(n+1)$
. Consequently, one of
![]() $(B\mathbf{v})_i$
and
$(B\mathbf{v})_i$
and
![]() $(B\mathbf{v})_j$
has absolute value
$(B\mathbf{v})_j$
has absolute value
![]() $\geq n\,{+}\,1$
, which means that the bounding cubes of
$\geq n\,{+}\,1$
, which means that the bounding cubes of
![]() $F_B + B\mathbf{v}$
and
$F_B + B\mathbf{v}$
and
![]() $F_B$
(which each have sidelength
$F_B$
(which each have sidelength
![]() $n$
) are disjoint.
$n$
) are disjoint.
This leaves the case where all entries of
![]() $\mathbf{v}$
differ by at most 1. In other words, there exists
$\mathbf{v}$
differ by at most 1. In other words, there exists
![]() $c \in \mathbb{Z}$
such that for all
$c \in \mathbb{Z}$
such that for all
![]() $i$
, we have
$i$
, we have
![]() $\mathbf{v_i} \in \{c-1, c\}$
, and moreover there exists at least one such
$\mathbf{v_i} \in \{c-1, c\}$
, and moreover there exists at least one such
![]() $j$
such that
$j$
such that
![]() $\mathbf{v_j} = c$
.
$\mathbf{v_j} = c$
.
We can assume without loss of generality that
![]() $c$
is positive (because
$c$
is positive (because
![]() $F_B + B\mathbf{v}$
is disjoint from
$F_B + B\mathbf{v}$
is disjoint from
![]() $F_B$
if and only if
$F_B$
if and only if
![]() $F_B - B\mathbf{v}$
is disjoint from
$F_B - B\mathbf{v}$
is disjoint from
![]() $F_B$
). Moreover, if
$F_B$
). Moreover, if
![]() $c \in \{0, 1\}$
then the polytopes are neighbours, so we have
$c \in \{0, 1\}$
then the polytopes are neighbours, so we have
![]() $c \geq 2$
.
$c \geq 2$
.
By permuting the coordinates, we can assume that
![]() $\mathbf{v_1}, \dots, \mathbf{v_k} = c$
and
$\mathbf{v_1}, \dots, \mathbf{v_k} = c$
and
![]() $\mathbf{v_{k+1}}, \dots, \mathbf{v_n} = c - 1$
. Then we can compute that:
$\mathbf{v_{k+1}}, \dots, \mathbf{v_n} = c - 1$
. Then we can compute that:
and, because
![]() $c \geq 2$
, this means that at least
$c \geq 2$
, this means that at least
![]() $k$
of the entries
$k$
of the entries
![]() $(B\mathbf{v})_i \geq n - k + 2$
. As such,
$(B\mathbf{v})_i \geq n - k + 2$
. As such,
![]() $B\mathbf{v} \notin F_B$
, because every point
$B\mathbf{v} \notin F_B$
, because every point
![]() $x \in F_B$
has at least
$x \in F_B$
has at least
![]() $n - k + 1$
entries
$n - k + 1$
entries
![]() $x_i \leq n - k + 1$
. Moreover, because
$x_i \leq n - k + 1$
. Moreover, because
![]() $F_B$
is contained in the positive orthant, we also have
$F_B$
is contained in the positive orthant, we also have
![]() $x + B\mathbf{v} \notin F_B$
for all
$x + B\mathbf{v} \notin F_B$
for all
![]() $x \in F_B$
, establishing that the two polytopes are disjoint.
$x \in F_B$
, establishing that the two polytopes are disjoint.
Since
![]() $F_B$
has empty intersection with
$F_B$
has empty intersection with
![]() $F_B + B\mathbf{v}$
whenever they are non-neighbours, and
$F_B + B\mathbf{v}$
whenever they are non-neighbours, and
![]() $B$
has integer entries, the distance between non-neighbours
$B$
has integer entries, the distance between non-neighbours
![]() $F_B$
and
$F_B$
and
![]() $F_B + B\mathbf{v}$
must be at least
$F_B + B\mathbf{v}$
must be at least
![]() $1$
. Since the coordinates of
$1$
. Since the coordinates of
![]() $F_A$
and
$F_A$
and
![]() $F_A + A\mathbf{v}$
are continuous in the entries of
$F_A + A\mathbf{v}$
are continuous in the entries of
![]() $A$
, we conclude that there is some
$A$
, we conclude that there is some
![]() $\varepsilon$
-neighbourhood
$\varepsilon$
-neighbourhood
![]() $N_\varepsilon$
of
$N_\varepsilon$
of
![]() $B$
with the property that
$B$
with the property that
![]() $F_A \cap (F_A + A\mathbf{v}) = \oslash\,$
whenever
$F_A \cap (F_A + A\mathbf{v}) = \oslash\,$
whenever
![]() $A \in N_\varepsilon$
and
$A \in N_\varepsilon$
and
![]() $F_A + A\mathbf{v}$
is not a neighbour of
$F_A + A\mathbf{v}$
is not a neighbour of
![]() $F_A$
.
$F_A$
.
However, the particular choice of
![]() $\varepsilon$
can depend on the vector
$\varepsilon$
can depend on the vector
![]() $\mathbf{v}$
, so we denote it by
$\mathbf{v}$
, so we denote it by
![]() $\varepsilon _{\mathbf{v}}$
. To fix this problem, note that if
$\varepsilon _{\mathbf{v}}$
. To fix this problem, note that if
![]() $\|\mathbf{v}\| \geq 2K$
then
$\|\mathbf{v}\| \geq 2K$
then
![]() $\|A\mathbf{v}\| \gt K$
(since the minimum singular value of
$\|A\mathbf{v}\| \gt K$
(since the minimum singular value of
![]() $A$
is at least
$A$
is at least
![]() $\frac{1}{2}$
), so there are only finitely many
$\frac{1}{2}$
), so there are only finitely many
![]() $\mathbf{v} \in \mathbb{Z}^n$
for which
$\mathbf{v} \in \mathbb{Z}^n$
for which
![]() $F_A \cap (F_A + A\mathbf{v})$
is potentially non-empty: choose
$F_A \cap (F_A + A\mathbf{v})$
is potentially non-empty: choose
![]() $K$
to be an upper bound on the diameter of
$K$
to be an upper bound on the diameter of
![]() $F_A$
; the only
$F_A$
; the only
![]() $\mathbf{v} \in \mathbb{Z}^n$
that need to be considered are those in the ball of radius
$\mathbf{v} \in \mathbb{Z}^n$
that need to be considered are those in the ball of radius
![]() $2K$
. Defining
$2K$
. Defining
![]() $\varepsilon$
to be the minimum of
$\varepsilon$
to be the minimum of
![]() $\varepsilon _0$
(defined at the beginning of this proof) and these finitely many
$\varepsilon _0$
(defined at the beginning of this proof) and these finitely many
![]() $\varepsilon _{\mathbf{v}}$
’s completes the proof.
$\varepsilon _{\mathbf{v}}$
’s completes the proof.
Lemma 6.
If
![]() $A$
satisfies conditions (a)–(c) above then
$A$
satisfies conditions (a)–(c) above then
![]() $F_A + \Lambda _A ={\mathbb{R}}^n$
(i.e., there are no gaps in the tiling).
$F_A + \Lambda _A ={\mathbb{R}}^n$
(i.e., there are no gaps in the tiling).
Proof. We first note that it suffices to show that, for each
![]() $\mathbf{x} \in{\mathbb{R}}^n$
, there exists
$\mathbf{x} \in{\mathbb{R}}^n$
, there exists
![]() $\mathbf{z} \in \Lambda _A$
such that
$\mathbf{z} \in \Lambda _A$
such that
![]() $\mathbf{x} + \mathbf{z} \in C_A$
. To see this, recall from equation (17) that
$\mathbf{x} + \mathbf{z} \in C_A$
. To see this, recall from equation (17) that
![]() $F_A$
is constructed from
$F_A$
is constructed from
![]() $C_A$
by removing its immediate neighbours in the positive direction, so if
$C_A$
by removing its immediate neighbours in the positive direction, so if
![]() $\mathbf{x} + \mathbf{z} \in C_A$
then
$\mathbf{x} + \mathbf{z} \in C_A$
then
![]() $\mathbf{x} \in (F_A + A\mathbf{b}) - \mathbf{z}$
for some binary vector
$\mathbf{x} \in (F_A + A\mathbf{b}) - \mathbf{z}$
for some binary vector
![]() $\mathbf{b} \in \{0,1\}^n$
. Since
$\mathbf{b} \in \{0,1\}^n$
. Since
![]() $A\mathbf{b} - \mathbf{z} \in \Lambda _A$
, this implies
$A\mathbf{b} - \mathbf{z} \in \Lambda _A$
, this implies
![]() $\mathbf{x} \in F_A + \Lambda _A$
.
$\mathbf{x} \in F_A + \Lambda _A$
.
To find
![]() $\mathbf{z}$
, first pick some
$\mathbf{z}$
, first pick some
![]() $\mathbf{z^{(0)}} \in \Lambda _A$
such that each entry of
$\mathbf{z^{(0)}} \in \Lambda _A$
such that each entry of
![]() $\mathbf{y^{(0)}} \,{:\!=}\, \mathbf{x} + \mathbf{z^{(0)}}$
is non-negative (such a
$\mathbf{y^{(0)}} \,{:\!=}\, \mathbf{x} + \mathbf{z^{(0)}}$
is non-negative (such a
![]() $\mathbf{z^{(0)}}$
exists since
$\mathbf{z^{(0)}}$
exists since
![]() $A$
is strictly diagonally dominant and thus invertible). Set
$A$
is strictly diagonally dominant and thus invertible). Set
![]() $k = 0$
and proceed inductively as follows:
$k = 0$
and proceed inductively as follows:
-
(i) If
 $\mathbf{y}^{\mathbf{(k)}}_i \leq a_{i,i}$
for all
$\mathbf{y}^{\mathbf{(k)}}_i \leq a_{i,i}$
for all
 $1 \leq i \leq n$
then
$1 \leq i \leq n$
then
 $\mathbf{y^{(k)}} \in C_A$
, so we can choose
$\mathbf{y^{(k)}} \in C_A$
, so we can choose
 $\mathbf{z} = \mathbf{z^{(k)}}$
and be done.
$\mathbf{z} = \mathbf{z^{(k)}}$
and be done. -
(ii) Otherwise, pick an index
 $1 \leq i \leq n$
for which
$1 \leq i \leq n$
for which
 $\mathbf{y}^{\mathbf{(k)}}_i \gt a_{i,i}$
and set
$\mathbf{y}^{\mathbf{(k)}}_i \gt a_{i,i}$
and set
 $\mathbf{y}^{\mathbf{(k+1)}}_i = \mathbf{y}^{\mathbf{(k)}}_i - A\mathbf{e_i}$
and
$\mathbf{y}^{\mathbf{(k+1)}}_i = \mathbf{y}^{\mathbf{(k)}}_i - A\mathbf{e_i}$
and
 $\mathbf{z}^{\mathbf{(k+1)}}_i = \mathbf{z}^{\mathbf{(k)}}_i - A\mathbf{e_i}$
. Increase
$\mathbf{z}^{\mathbf{(k+1)}}_i = \mathbf{z}^{\mathbf{(k)}}_i - A\mathbf{e_i}$
. Increase
 $k$
by
$k$
by
 $1$
and then repeat these bullet points.
$1$
and then repeat these bullet points.
Since the diagonal entries of
![]() $A$
are strictly positive, it is clear that
$A$
are strictly positive, it is clear that
![]() $0 \leq \mathbf{y}^{\mathbf{(k+1)}}_i \lt \mathbf{y}^{\mathbf{(k)}}_i$
. However, decreasing the
$0 \leq \mathbf{y}^{\mathbf{(k+1)}}_i \lt \mathbf{y}^{\mathbf{(k)}}_i$
. However, decreasing the
![]() $i$
-th entry like this comes at the expense of increasing the other entries (since the off-diagonal entries of
$i$
-th entry like this comes at the expense of increasing the other entries (since the off-diagonal entries of
![]() $A$
are negative). It is thus not obvious that the inductive procedure described above terminates. To see that it does, we demonstrate the existence of a vector
$A$
are negative). It is thus not obvious that the inductive procedure described above terminates. To see that it does, we demonstrate the existence of a vector
![]() $\mathbf{v} \in{\mathbb{R}}^n$
and a scalar
$\mathbf{v} \in{\mathbb{R}}^n$
and a scalar
![]() $0 \lt d \in{\mathbb{R}}$
with the properties that
$0 \lt d \in{\mathbb{R}}$
with the properties that
![]() $\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}} \geq 0$
for all
$\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}} \geq 0$
for all
![]() $k$
and
$k$
and
![]() $(\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}}) - (\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k+1)}}) \geq d$
for all
$(\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}}) - (\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k+1)}}) \geq d$
for all
![]() $k$
, implying that the procedure terminates for some
$k$
, implying that the procedure terminates for some
![]() $k \leq (\mathbf{v} \cdot \mathbf{y}^{\mathbf{(0)}})/ d$
.
$k \leq (\mathbf{v} \cdot \mathbf{y}^{\mathbf{(0)}})/ d$
.
To construct such a
![]() $\mathbf{v}$
and
$\mathbf{v}$
and
![]() $d$
, let
$d$
, let
![]() $c \in{\mathbb{R}}$
be large enough that
$c \in{\mathbb{R}}$
be large enough that
![]() $cI - A^T$
has all entries strictly positive. The Perron–Frobenius theorem tells us that there is a strictly positive real eigenvalue
$cI - A^T$
has all entries strictly positive. The Perron–Frobenius theorem tells us that there is a strictly positive real eigenvalue
![]() $\lambda$
with a corresponding entrywise strictly positive eigenvector
$\lambda$
with a corresponding entrywise strictly positive eigenvector
![]() $\mathbf{v}$
such that
$\mathbf{v}$
such that
![]() $(cI - A^T)\mathbf{v} = \lambda \mathbf{v}$
. Since
$(cI - A^T)\mathbf{v} = \lambda \mathbf{v}$
. Since
![]() $\mathbf{v}$
and
$\mathbf{v}$
and
![]() $\mathbf{y}^{\mathbf{(k)}}$
are both entrywise non-negative, we have
$\mathbf{y}^{\mathbf{(k)}}$
are both entrywise non-negative, we have
![]() $\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}} \geq 0$
for all
$\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}} \geq 0$
for all
![]() $k$
. Furthermore, since
$k$
. Furthermore, since
![]() $(c-\lambda,\mathbf{v})$
is also an eigenvalue-eigenvector pair of
$(c-\lambda,\mathbf{v})$
is also an eigenvalue-eigenvector pair of
![]() $A^T$
, and
$A^T$
, and
![]() $A$
is strictly diagonally dominant (and
$A$
is strictly diagonally dominant (and
![]() $c$
and
$c$
and
![]() $\lambda$
are both real), we know that
$\lambda$
are both real), we know that
![]() $c - \lambda \gt 0$
. It follows that
$c - \lambda \gt 0$
. It follows that
If we choose
![]() $d \,{:\!=}\, (c-\lambda )\min _i\{v_i\} \gt 0$
then it follows that
$d \,{:\!=}\, (c-\lambda )\min _i\{v_i\} \gt 0$
then it follows that
![]() $(\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}}) - (\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k+1)}}) = \mathbf{v} \cdot (A\mathbf{e_i}) \geq d$
, which completes the proof.
$(\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k)}}) - (\mathbf{v} \cdot \mathbf{y}^{\mathbf{(k+1)}}) = \mathbf{v} \cdot (A\mathbf{e_i}) \geq d$
, which completes the proof.
Lemma 7.
If
![]() $A$
satisfies conditions (a)–(c) above then the volume of
$A$
satisfies conditions (a)–(c) above then the volume of
![]() $F_A$
is given by the expression in Equation (11).
$F_A$
is given by the expression in Equation (11).
Proof. The volume of the cuboid
![]() $C_A$
is clearly equal to
$C_A$
is clearly equal to
![]() $a_{1,1}a_{2,2}\cdots a_{n,n}$
, which is one of the terms in the sum (11) (it is the term corresponding to the empty partial partition). We now use inclusion-exclusion to show that the rest of the terms in that sum correspond to volumes that were removed by translations of
$a_{1,1}a_{2,2}\cdots a_{n,n}$
, which is one of the terms in the sum (11) (it is the term corresponding to the empty partial partition). We now use inclusion-exclusion to show that the rest of the terms in that sum correspond to volumes that were removed by translations of
![]() $C_A$
when creating
$C_A$
when creating
![]() $F_A$
as in equation (17).
$F_A$
as in equation (17).
For a non-empty
![]() $S \subseteq [n]$
, the set
$S \subseteq [n]$
, the set
 \begin{align} C_A \cap \left (C_A + \sum _{i \in S}A\mathbf{e_i}\right ) \end{align}
\begin{align} C_A \cap \left (C_A + \sum _{i \in S}A\mathbf{e_i}\right ) \end{align}
is a cuboid with its
![]() $i$
-th side length
$i$
-th side length
![]() $\ell _i$
equal to
$\ell _i$
equal to
 \begin{equation*} \ell _i = \begin {cases} \displaystyle a_{i,i}-\sum _{j \in S}a_{i,j}, & \text {if } i \in S \\ \displaystyle a_{i,i} + \sum _{j \in S}a_{i,j}, & \text {if } i \notin S \end {cases} = \begin {cases} \displaystyle -\sum _{j \in S,j \neq i}a_{i,j}, & \text {if } i \in S \\ \displaystyle a_{i,i} + \sum _{j \in S}a_{i,j}, & \text {if } i \notin S. \end {cases}. \end{equation*}
\begin{equation*} \ell _i = \begin {cases} \displaystyle a_{i,i}-\sum _{j \in S}a_{i,j}, & \text {if } i \in S \\ \displaystyle a_{i,i} + \sum _{j \in S}a_{i,j}, & \text {if } i \notin S \end {cases} = \begin {cases} \displaystyle -\sum _{j \in S,j \neq i}a_{i,j}, & \text {if } i \in S \\ \displaystyle a_{i,i} + \sum _{j \in S}a_{i,j}, & \text {if } i \notin S. \end {cases}. \end{equation*}
Multiplying these side lengths together gives us the volume of the cuboid (19). Subtracting this quantity for all non-empty
![]() $S \subseteq [n]$
(i.e., subtracting the volume of all of these cuboids that are removed from
$S \subseteq [n]$
(i.e., subtracting the volume of all of these cuboids that are removed from
![]() $C_A$
to create
$C_A$
to create
![]() $F_A$
) results in the following (not yet correct) formula for the volume of
$F_A$
) results in the following (not yet correct) formula for the volume of
![]() $F_A$
:
$F_A$
:
 \begin{align} a_{1,1}a_{2,2}\cdots a_{n,n} - \sum _{\oslash\\, \neq S \subseteq [n]}\prod _{i=1}^n \ell _i = a_{1,1}a_{2,2}\cdots a_{n,n} - \sum _{\oslash\, \neq S \subseteq [n]}\prod _{i=1}^n\begin{cases} \displaystyle -\sum _{j \in S,j \neq i}a_{i,j}, & \text{if } i \in S \\ \displaystyle a_{i,i} + \sum _{j \in S}a_{i,j}, & \text{if } i \notin S. \end{cases} \end{align}
\begin{align} a_{1,1}a_{2,2}\cdots a_{n,n} - \sum _{\oslash\\, \neq S \subseteq [n]}\prod _{i=1}^n \ell _i = a_{1,1}a_{2,2}\cdots a_{n,n} - \sum _{\oslash\, \neq S \subseteq [n]}\prod _{i=1}^n\begin{cases} \displaystyle -\sum _{j \in S,j \neq i}a_{i,j}, & \text{if } i \in S \\ \displaystyle a_{i,i} + \sum _{j \in S}a_{i,j}, & \text{if } i \notin S. \end{cases} \end{align}
When
![]() $n \leq 3$
the formula (20) is the same as the formula (11) and indeed equals the volume of
$n \leq 3$
the formula (20) is the same as the formula (11) and indeed equals the volume of
![]() $F_A$
. In particular, if
$F_A$
. In particular, if
![]() $n = 2$
then it expresses the area of the shaded tile
$n = 2$
then it expresses the area of the shaded tile
![]() $F_A$
in Fig. 1b as the area
$F_A$
in Fig. 1b as the area
![]() $a_{1,1}a_{2,2}$
of the rectangle
$a_{1,1}a_{2,2}$
of the rectangle
![]() $C_A$
from Fig. 2b minus the area of the rectangular overlapping region at its top-right vertex, and if
$C_A$
from Fig. 2b minus the area of the rectangular overlapping region at its top-right vertex, and if
![]() $n = 3$
then it expresses the volume of
$n = 3$
then it expresses the volume of
![]() $F_A$
as the volume
$F_A$
as the volume
![]() $a_{1,1}a_{2,2}a_{3,3}$
of the cuboid
$a_{1,1}a_{2,2}a_{3,3}$
of the cuboid
![]() $C_A$
minus the volumes of
$C_A$
minus the volumes of
![]() $4$
other cuboids (these cuboids are depicted in the case of the matrix
$4$
other cuboids (these cuboids are depicted in the case of the matrix
![]() $(n+1)I - J$
in Fig. 4, and the picture for other matrices satisfying (a)–(c) is similar).
$(n+1)I - J$
in Fig. 4, and the picture for other matrices satisfying (a)–(c) is similar).
When
![]() $n \geq 4$
, however, the formula (20) is not quite correct, since there are overlaps-of-overlaps of the translates of
$n \geq 4$
, however, the formula (20) is not quite correct, since there are overlaps-of-overlaps of the translates of
![]() $C_A$
, so some volume that is removed from
$C_A$
, so some volume that is removed from
![]() $C_A$
in equation (20) is removed multiple times. To correct this mistake, we proceed via inclusion-exclusion: we add back the volumes that were subtracted too many times, then we subtract volumes that were added back too many times, and so on.
$C_A$
in equation (20) is removed multiple times. To correct this mistake, we proceed via inclusion-exclusion: we add back the volumes that were subtracted too many times, then we subtract volumes that were added back too many times, and so on.
For example, when
![]() $n = 4$
, the cuboids corresponding to the subsets
$n = 4$
, the cuboids corresponding to the subsets
![]() $S_1 = \{1,2\}$
, and
$S_1 = \{1,2\}$
, and
![]() $S_2 = \{1,2,3,4\}$
(i.e., the cuboids
$S_2 = \{1,2,3,4\}$
(i.e., the cuboids
![]() $C_A + A(\mathbf{e_1} + \mathbf{e_2})$
and
$C_A + A(\mathbf{e_1} + \mathbf{e_2})$
and
![]() $C_A + A(\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3} + \mathbf{e_4})$
) overlap with each other, so formula (20) is too small: it subtracts off the volume of the cuboid
$C_A + A(\mathbf{e_1} + \mathbf{e_2} + \mathbf{e_3} + \mathbf{e_4})$
) overlap with each other, so formula (20) is too small: it subtracts off the volume of the cuboid
twice (this volume equals
![]() $a_{1,2}a_{2,1}a_{3,4}a_{4,3}$
). In fact, there are exactly six cuboids whose volumes were subtracted off twice by formula (20), given by
$a_{1,2}a_{2,1}a_{3,4}a_{4,3}$
). In fact, there are exactly six cuboids whose volumes were subtracted off twice by formula (20), given by
![]() $S_2 = \{1,2,3,4\}$
and
$S_2 = \{1,2,3,4\}$
and
![]() $S_1$
being any
$S_1$
being any
![]() $2$
-element subset of
$2$
-element subset of
![]() $S_2$
. To correct this mistake, we simply add the volumes of these cuboids back in. The cuboids corresponding to
$S_2$
. To correct this mistake, we simply add the volumes of these cuboids back in. The cuboids corresponding to
![]() $S_1 = \{1,2\}$
and
$S_1 = \{1,2\}$
and
![]() $S_1 = \{3,4\}$
have the same volume as each other, as do the cuboids corresponding to
$S_1 = \{3,4\}$
have the same volume as each other, as do the cuboids corresponding to
![]() $S_1 = \{1,3\}$
and
$S_1 = \{1,3\}$
and
![]() $S_1 = \{2,4\}$
, as do the cuboids corresponding to
$S_1 = \{2,4\}$
, as do the cuboids corresponding to
![]() $S_1 = \{1,4\}$
and
$S_1 = \{1,4\}$
and
![]() $S_1 = \{2,3\}$
, thus giving the final three terms (each with a coefficient of
$S_1 = \{2,3\}$
, thus giving the final three terms (each with a coefficient of
![]() $2$
) in equation (12).
$2$
) in equation (12).
In general,
![]() $k$
pairwise distinct (but not necessarily disjoint) subsets
$k$
pairwise distinct (but not necessarily disjoint) subsets
![]() $S_1,S_2,\ldots,S_k \subseteq [n]$
are such that
$S_1,S_2,\ldots,S_k \subseteq [n]$
are such that
 \begin{align} \bigcap _{j=1}^k \left (C_A + \sum _{i \in S_j}A\mathbf{e_i}\right ) \end{align}
\begin{align} \bigcap _{j=1}^k \left (C_A + \sum _{i \in S_j}A\mathbf{e_i}\right ) \end{align}
has non-zero volume if and only if there is a chain of inclusions among them, which we will assume is
![]() $S_1 \subset S_2 \subset \cdots \subset S_k \subseteq [n]$
without loss of generality, and
$S_1 \subset S_2 \subset \cdots \subset S_k \subseteq [n]$
without loss of generality, and
![]() $|S_\ell \setminus S_{\ell -1}| \geq 2$
for all
$|S_\ell \setminus S_{\ell -1}| \geq 2$
for all
![]() $1 \leq \ell \leq k$
(we define
$1 \leq \ell \leq k$
(we define
![]() $S_0 = \oslash\,$
for convenience). Indeed, if
$S_0 = \oslash\,$
for convenience). Indeed, if
![]() $|S_\ell \setminus S_{\ell -1}| = 0$
then
$|S_\ell \setminus S_{\ell -1}| = 0$
then
![]() $S_\ell = S_{\ell -1}$
, and if
$S_\ell = S_{\ell -1}$
, and if
![]() $|S_\ell \setminus S_{\ell -1}| = 1$
then the two cuboids corresponding to
$|S_\ell \setminus S_{\ell -1}| = 1$
then the two cuboids corresponding to
![]() $j = \ell -1$
and
$j = \ell -1$
and
![]() $j = \ell$
in equation (21) intersect only on their boundary (
$j = \ell$
in equation (21) intersect only on their boundary (
![]() $S_\ell \setminus S_{\ell -1} = \{i\}$
for some
$S_\ell \setminus S_{\ell -1} = \{i\}$
for some
![]() $i \in [n]$
, so the cuboids are offset from each other by
$i \in [n]$
, so the cuboids are offset from each other by
![]() $a_{i,i}$
in the direction of the
$a_{i,i}$
in the direction of the
![]() $i$
-th coordinate axis, which is also their width in that direction).
$i$
-th coordinate axis, which is also their width in that direction).
The volume of the cuboid described by the intersection in equation (21) is the product of its side lengths, which equals
 \begin{align} \prod _{i=1}^n\begin{cases} \displaystyle {-}\!\!\!\!\! \sum _{j \in S_\ell \setminus S_{\ell -1},j \neq i}\!\!\!\!\!\!\! a_{i,j}, & \text{if } i \in S_\ell \setminus S_{\ell -1} (1 \leq \ell \leq k) \\ \displaystyle a_{i,i} + \sum _{j \in S_k}a_{i,j}, & \text{ if } i \notin S_k. \end{cases} \end{align}
\begin{align} \prod _{i=1}^n\begin{cases} \displaystyle {-}\!\!\!\!\! \sum _{j \in S_\ell \setminus S_{\ell -1},j \neq i}\!\!\!\!\!\!\! a_{i,j}, & \text{if } i \in S_\ell \setminus S_{\ell -1} (1 \leq \ell \leq k) \\ \displaystyle a_{i,i} + \sum _{j \in S_k}a_{i,j}, & \text{ if } i \notin S_k. \end{cases} \end{align}
The result now follows from using inclusion-exclusion, associating the chain
![]() $S_1 \subset S_2 \subset \cdots \subset S_k \subseteq [n]$
with the partial partition
$S_1 \subset S_2 \subset \cdots \subset S_k \subseteq [n]$
with the partial partition
and noting that there are exactly
![]() $k!$
different chains
$k!$
different chains
![]() $S_1 \subset S_2 \subset \cdots \subset S_k \subseteq [n]$
that give rise to this particular partial partition (since the order of the parts in
$S_1 \subset S_2 \subset \cdots \subset S_k \subseteq [n]$
that give rise to this particular partial partition (since the order of the parts in
![]() $P$
does not matter).Footnote 6 This completes the proof of Theorem 2.
$P$
does not matter).Footnote 6 This completes the proof of Theorem 2.
4.3
The Polytope
 $\mathbf{F_A}$
$\mathbf{F_A}$
For an
![]() $n \times n$
matrix
$n \times n$
matrix
![]() $A$
satisfying the conditions (a)–(c), we defined
$A$
satisfying the conditions (a)–(c), we defined
![]() $F_A$
in equation (17) by subtracting translated copies of the cuboid
$F_A$
in equation (17) by subtracting translated copies of the cuboid
![]() $C_A$
from the original cuboid
$C_A$
from the original cuboid
![]() $C_A$
. In this subsection, we study the polytope
$C_A$
. In this subsection, we study the polytope
![]() $F_A$
and its 1-skeleton (i.e., its vertices and
$F_A$
and its 1-skeleton (i.e., its vertices and
![]() $1$
-dimensional edges between them; see Fig. 5), obtaining a description of it as a flip graph associated with a family of combinatorial objects.
$1$
-dimensional edges between them; see Fig. 5), obtaining a description of it as a flip graph associated with a family of combinatorial objects.
To start, we describe the combinatorial objects that will be the vertices of the graph. An ordered partial partition (OPP) on
![]() $[n]$
is defined to be a relation
$[n]$
is defined to be a relation
![]() $\preccurlyeq$
with the following properties:
$\preccurlyeq$
with the following properties:
-
(i) Transitive: if
 $x \preccurlyeq y$
and
$x \preccurlyeq y$
and
 $y \preccurlyeq z$
, then
$y \preccurlyeq z$
, then
 $x \preccurlyeq z$
.
$x \preccurlyeq z$
. -
(ii) Weakly reflexive: if
 $x \preccurlyeq y$
, then
$x \preccurlyeq y$
, then
 $x \preccurlyeq x$
and
$x \preccurlyeq x$
and
 $y \preccurlyeq y$
.
$y \preccurlyeq y$
. -
(iii) Weakly connected: if
 $x \preccurlyeq x$
and
$x \preccurlyeq x$
and
 $y \preccurlyeq y$
, then either
$y \preccurlyeq y$
, then either
 $x \preccurlyeq y$
or
$x \preccurlyeq y$
or
 $y \preccurlyeq x$
or both.
$y \preccurlyeq x$
or both.
The set of all ordered partial partitions on
![]() $[n]$
is denoted by
$[n]$
is denoted by
![]() $\mathrm{OPP}(n)$
and the number of them is enumerated in ref. [Reference Sloane, Knuth and Singer15].
$\mathrm{OPP}(n)$
and the number of them is enumerated in ref. [Reference Sloane, Knuth and Singer15].
The name “ordered partial partition” refers to the fact that these relations on
![]() $[n]$
correspond bijectively with (ordered, possibly empty) tuples of pairwise disjoint non-empty subsets of
$[n]$
correspond bijectively with (ordered, possibly empty) tuples of pairwise disjoint non-empty subsets of
![]() $[n]$
(i.e., partial partitions of
$[n]$
(i.e., partial partitions of
![]() $[n]$
in which we care about the order of the parts):
$[n]$
in which we care about the order of the parts):
where
![]() $X_i \cap X_j = \oslash\,$
whenever
$X_i \cap X_j = \oslash\,$
whenever
![]() $i \neq j$
. This tuple of sets corresponds to the original relation in the following way:
$i \neq j$
. This tuple of sets corresponds to the original relation in the following way:
![]() $x \preccurlyeq y$
if and only if there exist integers
$x \preccurlyeq y$
if and only if there exist integers
![]() $1 \leq i \leq j$
such that
$1 \leq i \leq j$
such that
![]() $x \in X_i$
and
$x \in X_i$
and
![]() $y \in X_j$
.
$y \in X_j$
.
For each
![]() $z \in [n]$
, we define a function
$z \in [n]$
, we define a function
![]() $f_z\,{:}\, \mathrm{OPP}(n) \rightarrow \mathrm{OPP}(n)$
as follows:
$f_z\,{:}\, \mathrm{OPP}(n) \rightarrow \mathrm{OPP}(n)$
as follows:
-
(1) If
 $X_1 = \{z\}$
then discard
$X_1 = \{z\}$
then discard
 $X_1$
, obtaining the tuple
$X_1$
, obtaining the tuple
 $(X_2, \ldots, X_k)$
.
$(X_2, \ldots, X_k)$
. -
(2) If
 $X_j = \{z\}$
for some
$X_j = \{z\}$
for some
 $j \geq 2$
, then merge it into the immediately preceding part, obtaining the tuple
$j \geq 2$
, then merge it into the immediately preceding part, obtaining the tuple \begin{equation*} (X_1, \ldots, X_{j-1} \cup \{z\}, X_{j+1}, \ldots, X_k). \end{equation*}
\begin{equation*} (X_1, \ldots, X_{j-1} \cup \{z\}, X_{j+1}, \ldots, X_k). \end{equation*}
-
(3) If
 $z \in X_j \neq \{z\}$
for some
$z \in X_j \neq \{z\}$
for some
 $j \geq 1$
, then split it off into its own immediately next part, obtaining the tuple
$j \geq 1$
, then split it off into its own immediately next part, obtaining the tuple \begin{equation*} (X_1, \ldots, X_j \setminus \{z\}, \{z\}, X_{j+1}, \ldots, X_k). \end{equation*}
\begin{equation*} (X_1, \ldots, X_j \setminus \{z\}, \{z\}, X_{j+1}, \ldots, X_k). \end{equation*}
-
(4) Otherwise, if
 $z \notin \bigcup _{j=1}^k X_j$
, then make it into its own first part, obtaining the tuple
$z \notin \bigcup _{j=1}^k X_j$
, then make it into its own first part, obtaining the tuple \begin{equation*} (\{z\}, X_{1}, \ldots, X_k). \end{equation*}
\begin{equation*} (\{z\}, X_{1}, \ldots, X_k). \end{equation*}
For each
![]() $z \in [n]$
, this function
$z \in [n]$
, this function
![]() $f_z$
is an involution on
$f_z$
is an involution on
![]() $\mathrm{OPP}(n)$
with no fixed points: if
$\mathrm{OPP}(n)$
with no fixed points: if
![]() $f_z(\preccurlyeq ) = \preccurlyeq ^\prime$
, then
$f_z(\preccurlyeq ) = \preccurlyeq ^\prime$
, then
![]() $f_z(\preccurlyeq ^\prime ) = \preccurlyeq$
. Moreover, if
$f_z(\preccurlyeq ^\prime ) = \preccurlyeq$
. Moreover, if
![]() $x,y \in [n]$
with
$x,y \in [n]$
with
![]() $x \neq z$
, then
$x \neq z$
, then
![]() $x \preccurlyeq y$
if and only if
$x \preccurlyeq y$
if and only if
![]() $x \preccurlyeq ' y$
.
$x \preccurlyeq ' y$
.
We form a graph (called a flip graph) by letting its vertices be the elements of
![]() $\mathrm{OPP}(n)$
and its edges be between ordered partial partitions that are exchanged by an involution
$\mathrm{OPP}(n)$
and its edges be between ordered partial partitions that are exchanged by an involution
![]() $f_z$
for some
$f_z$
for some
![]() $z \in [n]$
. The resulting flip graph is
$z \in [n]$
. The resulting flip graph is
![]() $n$
-regular, since each vertex gets one edge for each
$n$
-regular, since each vertex gets one edge for each
![]() $z \in [n]$
; we claim that this graph is isomorphic to the 1-skeleton of the polytope
$z \in [n]$
; we claim that this graph is isomorphic to the 1-skeleton of the polytope
![]() $F_A$
(see Fig. 5).
$F_A$
(see Fig. 5).

Figure 5. The
![]() $1$
-skeleton of a polytope is the set of its vertices and
$1$
-skeleton of a polytope is the set of its vertices and
![]() $1$
-dimensional edges between them. Propositions 8 and 9 show that the
$1$
-dimensional edges between them. Propositions 8 and 9 show that the
![]() $1$
-skeleton of the polytope
$1$
-skeleton of the polytope
![]() $F_A$
is isomorphic to a graph whose vertices are the ordered partial partitions on
$F_A$
is isomorphic to a graph whose vertices are the ordered partial partitions on
![]() $[n]$
and whose edges are described by the involutions
$[n]$
and whose edges are described by the involutions
![]() $f_z$
.
$f_z$
.
Proposition 8.
Suppose that
![]() $A$
is an
$A$
is an
![]() $n \times n$
matrix satisfying conditions (a)–(c). Then the vertices of
$n \times n$
matrix satisfying conditions (a)–(c). Then the vertices of
![]() $F_A$
are in bijective correspondence with the elements of
$F_A$
are in bijective correspondence with the elements of
![]() $\mathrm{OPP}(n)$
. In particular, the coordinates of the vertex
$\mathrm{OPP}(n)$
. In particular, the coordinates of the vertex
![]() $\mathbf{v}$
corresponding to the ordered partial partition
$\mathbf{v}$
corresponding to the ordered partial partition
![]() $\preccurlyeq$
are given by
$\preccurlyeq$
are given by
Proof. Recall that we originally defined
![]() $F_A$
by subtracting translated copies of the cuboid
$F_A$
by subtracting translated copies of the cuboid
![]() $C_A$
:
$C_A$
:
 \begin{align} F_A \,{:\!=}\, \overline{C_A \setminus \bigcup _{\oslash\, \neq S \subseteq [n]}\left \{ x + \sum _{i \in S} A \mathbf{e_i}\,{:}\, x \in C_A \right \} }. \end{align}
\begin{align} F_A \,{:\!=}\, \overline{C_A \setminus \bigcup _{\oslash\, \neq S \subseteq [n]}\left \{ x + \sum _{i \in S} A \mathbf{e_i}\,{:}\, x \in C_A \right \} }. \end{align}
However,
![]() $C_A$
can itself be written as
$C_A$
can itself be written as
where
![]() $P$
is the positive orthant, consisting of all vectors where every coordinate is non-negative. As such, the definition (23) of
$P$
is the positive orthant, consisting of all vectors where every coordinate is non-negative. As such, the definition (23) of
![]() $F_A$
still works even if we replace each instance of
$F_A$
still works even if we replace each instance of
![]() $C_A$
with
$C_A$
with
![]() $P$
.
$P$
.
Given a vertex
![]() $\mathbf{v}$
of
$\mathbf{v}$
of
![]() $F_A$
, observe that it is the intersection of
$F_A$
, observe that it is the intersection of
![]() $n$
facets (codimension-1 faces)
$n$
facets (codimension-1 faces)
![]() $f_1, f_2, \dots, f_n$
of
$f_1, f_2, \dots, f_n$
of
![]() $F_A$
, where the standard basis vector
$F_A$
, where the standard basis vector
![]() $\mathbf{e_i}$
is perpendicular to the facet
$\mathbf{e_i}$
is perpendicular to the facet
![]() $f_i$
. The facet
$f_i$
. The facet
![]() $f_i$
must be contained in a facet of one of the translates of
$f_i$
must be contained in a facet of one of the translates of
![]() $P$
used to construct
$P$
used to construct
![]() $F_A$
; the vertex
$F_A$
; the vertex
![]() $\mathbf{v}$
is then the vertex of the intersection of these
$\mathbf{v}$
is then the vertex of the intersection of these
![]() $n$
(not necessarily distinct) translates of the positive orthant
$n$
(not necessarily distinct) translates of the positive orthant
![]() $P$
.
$P$
.
Each vertex of
![]() $F_A$
that arises therefore corresponds to the vertex of an intersection of translated positive orthants, which is the lowest (in terms of each coordinate) vertex of the corresponding intersection of translated copies of
$F_A$
that arises therefore corresponds to the vertex of an intersection of translated positive orthants, which is the lowest (in terms of each coordinate) vertex of the corresponding intersection of translated copies of
![]() $C_A$
. We already characterised these intersections in the proof of Lemma 7 when we performed the inclusion-exclusion calculation of the volume of
$C_A$
. We already characterised these intersections in the proof of Lemma 7 when we performed the inclusion-exclusion calculation of the volume of
![]() $F_A$
, identifying them with chains of subsets of
$F_A$
, identifying them with chains of subsets of
![]() $[n]$
, which are in turn naturally identified with ordered partial partitions.Footnote 7
$[n]$
, which are in turn naturally identified with ordered partial partitions.Footnote 7
Proposition 9.
Let
![]() $A$
be an
$A$
be an
![]() $n \times n$
matrix satisfying conditions (a)–(c) and let
$n \times n$
matrix satisfying conditions (a)–(c) and let
![]() $1 \leq i \leq n$
. Then two vertices
$1 \leq i \leq n$
. Then two vertices
![]() $\mathbf{v}$
and
$\mathbf{v}$
and
![]() $\mathbf{w}$
of
$\mathbf{w}$
of
![]() $F_A$
are connected by an edge parallel to the standard basis vector
$F_A$
are connected by an edge parallel to the standard basis vector
![]() $\mathbf{e_i}$
if and only if the corresponding (in the sense of Proposition 8) elements of
$\mathbf{e_i}$
if and only if the corresponding (in the sense of Proposition 8) elements of
![]() $\mathrm{OPP}(n)$
are swapped by the involution
$\mathrm{OPP}(n)$
are swapped by the involution
![]() $f_i$
.
$f_i$
.
Proof. Combinatorially, the polytope
![]() $F_A$
does not depend on the choice of matrix
$F_A$
does not depend on the choice of matrix
![]() $A$
(besides the fact that
$A$
(besides the fact that
![]() $A$
satisfies conditions (a)–(c)), so suppose without loss of generality that the entries are linearly independent over
$A$
satisfies conditions (a)–(c)), so suppose without loss of generality that the entries are linearly independent over
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Then we have that
![]() $v_k = w_k$
if and only if
$v_k = w_k$
if and only if
![]() $\sum _{j\,{:}\, k \preccurlyeq j} a_{k,j} = \sum _{j\,{:}\, k \preccurlyeq ' j} a_{k,j}$
if and only if
$\sum _{j\,{:}\, k \preccurlyeq j} a_{k,j} = \sum _{j\,{:}\, k \preccurlyeq ' j} a_{k,j}$
if and only if
Consequently, two vertices lie on a line parallel to the basis vector
![]() $\mathbf{e_i}$
if and only if equation (24) is true for all
$\mathbf{e_i}$
if and only if equation (24) is true for all
![]() $k \neq i$
.
$k \neq i$
.
This implies that the ordered partial partitions induced on
![]() $[n] \setminus \{i\}$
are equal, so the original ordered partial partitions can only differ in terms of where
$[n] \setminus \{i\}$
are equal, so the original ordered partial partitions can only differ in terms of where
![]() $i$
is located. It also constrains the position of
$i$
is located. It also constrains the position of
![]() $i$
relative to the other parts, namely
$i$
relative to the other parts, namely
If we remove and reinsert
![]() $i$
, there are two possibilities: it is either introduced as its own singleton part, or it is not (either by being introduced into an existing part, or being deleted completely). In each of these two cases, the position of
$i$
, there are two possibilities: it is either introduced as its own singleton part, or it is not (either by being introduced into an existing part, or being deleted completely). In each of these two cases, the position of
![]() $i$
is determined by equation (25). One of these cases corresponds to
$i$
is determined by equation (25). One of these cases corresponds to
![]() $\preccurlyeq ^\prime = \preccurlyeq$
, while the other corresponds to
$\preccurlyeq ^\prime = \preccurlyeq$
, while the other corresponds to
![]() $\preccurlyeq ^\prime = f_i(\preccurlyeq )$
.
$\preccurlyeq ^\prime = f_i(\preccurlyeq )$
.
Given that
![]() $F_A$
is an orthogonal polytope, it follows that there are at most
$F_A$
is an orthogonal polytope, it follows that there are at most
![]() $n$
other vertices that can possibly be connected to a given vertex
$n$
other vertices that can possibly be connected to a given vertex
![]() $\mathbf{v}$
by an edge, namely the vertices obtained by applying
$\mathbf{v}$
by an edge, namely the vertices obtained by applying
![]() $f_i$
to the corresponding element of
$f_i$
to the corresponding element of
![]() $\mathrm{OPP}(n)$
. Moreover, every vertex in an orthogonal polytope must have degree
$\mathrm{OPP}(n)$
. Moreover, every vertex in an orthogonal polytope must have degree
![]() $n$
, so all of these edges exist. The result follows.
$n$
, so all of these edges exist. The result follows.
We can label the edges
![]() $\{\preccurlyeq, \preccurlyeq ^\prime \}$
of the flip graph, as in Fig. 5a, with the value of
$\{\preccurlyeq, \preccurlyeq ^\prime \}$
of the flip graph, as in Fig. 5a, with the value of
![]() $i \in [n]$
for which
$i \in [n]$
for which
![]() $\preccurlyeq ^\prime = f_i(\preccurlyeq )$
. The higher-dimensional faces of
$\preccurlyeq ^\prime = f_i(\preccurlyeq )$
. The higher-dimensional faces of
![]() $F_A$
then have concise descriptions in terms of this graph: the
$F_A$
then have concise descriptions in terms of this graph: the
![]() $r$
-dimensional faces parallel to the linear subspace generated by the basis vectors
$r$
-dimensional faces parallel to the linear subspace generated by the basis vectors
![]() $\{ \mathbf{e_i}\,{:}\, i \in S \}$
(where
$\{ \mathbf{e_i}\,{:}\, i \in S \}$
(where
![]() $S \subseteq [n]$
has
$S \subseteq [n]$
has
![]() $|S| = r$
) are precisely the connected components of the subgraph obtained by taking only the edges whose labels are in
$|S| = r$
) are precisely the connected components of the subgraph obtained by taking only the edges whose labels are in
![]() $S$
.
$S$
.
This description of
![]() $F_A$
by specifying its vertex coordinates is more general than the original definition in terms of subtracting translated copies of
$F_A$
by specifying its vertex coordinates is more general than the original definition in terms of subtracting translated copies of
![]() $C_A$
: it generalises to arbitrary square matrices
$C_A$
: it generalises to arbitrary square matrices
![]() $A$
, instead of requiring that
$A$
, instead of requiring that
![]() $A$
satisfy the conditions (a)–(c). Note, however, that the resulting polytope may self-intersect and thus care is required to define “volume” in such a way that it is equal to
$A$
satisfy the conditions (a)–(c). Note, however, that the resulting polytope may self-intersect and thus care is required to define “volume” in such a way that it is equal to
![]() ${\mathrm{det}}(A)$
.
${\mathrm{det}}(A)$
.
5. Fields of non-zero characteristic
For fields
![]() $\mathbb{F}$
of characteristic
$\mathbb{F}$
of characteristic
![]() $p \gt 0$
, many of the terms in the formula (11) are multiples of
$p \gt 0$
, many of the terms in the formula (11) are multiples of
![]() $p$
and thus equal to zero. As a result, the formula simplifies and we get an even tighter upper bound on the tensor rank of
$p$
and thus equal to zero. As a result, the formula simplifies and we get an even tighter upper bound on the tensor rank of
![]() ${\mathrm{det}}_{{\mathbb{F}}}^n$
. In particular, we have the following variant of Theorem 2:
${\mathrm{det}}_{{\mathbb{F}}}^n$
. In particular, we have the following variant of Theorem 2:
Theorem 10.
Let
![]() $A$
be an
$A$
be an
![]() $n \times n$
matrix over a field
$n \times n$
matrix over a field
![]() $\mathbb{F}$
with characteristic
$\mathbb{F}$
with characteristic
![]() $p \gt 0$
. Then
$p \gt 0$
. Then
 \begin{align} {\mathrm{det}}(A) & = \, \sum _{\substack{P \in{\mathrm{PP}}(n) \\ |P| \leq p-1}} \,{\mathrm{sgn}}(P) |P|! \prod _{i=1}^n \begin{cases} \, \, \mathop{\sum}\limits _{j \underset{P}{\sim } i, j \neq i} a_{i,j} & \text{ if } i \underset{P}{\sim } i; \\ a_{i,i} + \mathop{\sum}\limits _{j \underset{P}{\sim } j}a_{i,j} & \text{ if } i \underset{P}{\not \sim } i,\end{cases} \end{align}
\begin{align} {\mathrm{det}}(A) & = \, \sum _{\substack{P \in{\mathrm{PP}}(n) \\ |P| \leq p-1}} \,{\mathrm{sgn}}(P) |P|! \prod _{i=1}^n \begin{cases} \, \, \mathop{\sum}\limits _{j \underset{P}{\sim } i, j \neq i} a_{i,j} & \text{ if } i \underset{P}{\sim } i; \\ a_{i,i} + \mathop{\sum}\limits _{j \underset{P}{\sim } j}a_{i,j} & \text{ if } i \underset{P}{\not \sim } i,\end{cases} \end{align}
where
![]() $\displaystyle{\mathrm{sgn}}(P) = \prod _{S \in P}(-1)^{|S|+1}$
.
$\displaystyle{\mathrm{sgn}}(P) = \prod _{S \in P}(-1)^{|S|+1}$
.
Proof. This formula is identical to the one provided by Theorem 2, except the partial partitions
![]() $P$
that we sum over here are restricted to have
$P$
that we sum over here are restricted to have
![]() $|P| \leq p-1$
. Since any term with
$|P| \leq p-1$
. Since any term with
![]() $|P| \geq p$
has a coefficient of
$|P| \geq p$
has a coefficient of
![]() $|P|!$
, which is a multiple of
$|P|!$
, which is a multiple of
![]() $p$
, which equals
$p$
, which equals
![]() $0$
in
$0$
in
![]() $\mathbb{F}$
, this restriction on
$\mathbb{F}$
, this restriction on
![]() $|P|$
does not change the value of the sum.
$|P|$
does not change the value of the sum.
In order to count the number of non-zero terms in the sum (26), and thus obtain a tighter an upper bound on
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
when
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
when
![]() $\mathbb{F}$
has characteristic
$\mathbb{F}$
has characteristic
![]() $p \gt 0$
, we need to introduce another combinatorial quantity. Let
$p \gt 0$
, we need to introduce another combinatorial quantity. Let
![]() $B_{n,k}$
be the number of partial partitions of
$B_{n,k}$
be the number of partial partitions of
![]() $[n]$
that contain exactly
$[n]$
that contain exactly
![]() $k$
parts and no singletons, or equivalently the number of partitions of
$k$
parts and no singletons, or equivalently the number of partitions of
![]() $[n]$
that contain exactly
$[n]$
that contain exactly
![]() $k$
parts all of which have size strictly greater than
$k$
parts all of which have size strictly greater than
![]() $1$
. The sum in equation (26) contains exactly
$1$
. The sum in equation (26) contains exactly
![]() $\sum _{k=0}^{p-1}B_{n,k}$
(potentially) non-zero terms, so we immediately get the following corollary:
$\sum _{k=0}^{p-1}B_{n,k}$
(potentially) non-zero terms, so we immediately get the following corollary:
Corollary 11.
Let
![]() $\mathbb{F}$
be a field with characteristic
$\mathbb{F}$
be a field with characteristic
![]() $p \gt 0$
. Then
$p \gt 0$
. Then
 $\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \sum _{k=0}^{p-1}B_{n,k}$
.
$\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \sum _{k=0}^{p-1}B_{n,k}$
.
By making use of Lemma 1, we could also say that if
![]() $\mathbb{F}$
has characteristic
$\mathbb{F}$
has characteristic
![]() $p \gt n$
then
$p \gt n$
then
![]() $\mathrm{Wrank}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^{n-1}\sum _{k=0}^{p-1}B_{n,k}$
. However, this provides no improvement over Corollary 3, since
$\mathrm{Wrank}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^{n-1}\sum _{k=0}^{p-1}B_{n,k}$
. However, this provides no improvement over Corollary 3, since
![]() $\sum _{k=0}^{p-1}B_{n,k} = B_n$
whenever
$\sum _{k=0}^{p-1}B_{n,k} = B_n$
whenever
![]() $p \gt n$
(in fact, whenever
$p \gt n$
(in fact, whenever
![]() $p \gt \lfloor n/2 \rfloor + 1$
, since no partial partition can contain more than
$p \gt \lfloor n/2 \rfloor + 1$
, since no partial partition can contain more than
![]() $\lfloor n/2 \rfloor$
parts unless it has some singletons).
$\lfloor n/2 \rfloor$
parts unless it has some singletons).
Numerous properties and formulas for
![]() $B_{n,k}$
are known (see [Reference Deutsch5, Reference Nabawanda, Rakotondrajao and Bamunoba12] and the references therein). We summarise those that are most relevant for us here:
$B_{n,k}$
are known (see [Reference Deutsch5, Reference Nabawanda, Rakotondrajao and Bamunoba12] and the references therein). We summarise those that are most relevant for us here:
-
(i)
 $B_{n,0} = 1$
.
$B_{n,0} = 1$
. -
(ii)
 $B_{n,1} = \binom{n}{2} + \binom{n}{3} + \cdots + \binom{n}{n} = 2^n - n - 1$
, since
$B_{n,1} = \binom{n}{2} + \binom{n}{3} + \cdots + \binom{n}{n} = 2^n - n - 1$
, since
 $\binom{n}{k}$
counts the number of partial partitions of
$\binom{n}{k}$
counts the number of partial partitions of
 $[n]$
with one part of size
$[n]$
with one part of size
 $k$
. It follows that if
$k$
. It follows that if
 $\mathbb{F}$
has characteristic
$\mathbb{F}$
has characteristic
 $2$
then
$2$
then
 ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq B_{n,0} + B_{n,1} = 2^n - n$
(we return to this special case in more detail in Section 5.1).
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq B_{n,0} + B_{n,1} = 2^n - n$
(we return to this special case in more detail in Section 5.1). -
(iii) The recurrence relation
 $B_{n,k} = (k+1)B_{n-1,k} + (n-1)B_{n-2,k-1}$
holds whenever
$B_{n,k} = (k+1)B_{n-1,k} + (n-1)B_{n-2,k-1}$
holds whenever
 $n \geq 2k \geq 2$
. When combined with the facts that
$n \geq 2k \geq 2$
. When combined with the facts that
 $B_{n,0} = 1$
for all
$B_{n,0} = 1$
for all
 $n \geq 0$
and
$n \geq 0$
and
 $B_{n,k} = 0$
whenever
$B_{n,k} = 0$
whenever
 $n \lt 2k$
, this recurrence relation can be used to compute
$n \lt 2k$
, this recurrence relation can be used to compute
 $B_{n,k}$
for all
$B_{n,k}$
for all
 $n$
and
$n$
and
 $k$
.
$k$
. -
(iv) In particular, for small values of
 $k$
we have the following additional explicit formulas:
$k$
we have the following additional explicit formulas: \begin{align*} B_{n,2} & = \frac{1}{2}\big (3^n - (n+2)2^n + (n^2 + n + 1)\big ), \\ B_{n,3} & = \frac{1}{6}\big (4^n - (n+3)3^{n} + 3(n^2 + 3n + 4)2^{n-2} - (n^3 + 2n + 1)\big ), \quad \text{and} \\ B_{n,4} & = \frac{1}{24}\big (5^n - (n + 4)4^n + 2(n^2 + 5n + 9)3^{n-1} \\ & \qquad \quad - (n^3 + 3n^2 + 8n + 8)2^{n-1} + (n^4 - 2n^3 + 5n^2 + 1)\big ). \end{align*}
\begin{align*} B_{n,2} & = \frac{1}{2}\big (3^n - (n+2)2^n + (n^2 + n + 1)\big ), \\ B_{n,3} & = \frac{1}{6}\big (4^n - (n+3)3^{n} + 3(n^2 + 3n + 4)2^{n-2} - (n^3 + 2n + 1)\big ), \quad \text{and} \\ B_{n,4} & = \frac{1}{24}\big (5^n - (n + 4)4^n + 2(n^2 + 5n + 9)3^{n-1} \\ & \qquad \quad - (n^3 + 3n^2 + 8n + 8)2^{n-1} + (n^4 - 2n^3 + 5n^2 + 1)\big ). \end{align*}
-
(v)
 $B_{n,k} \leq (k+1)^n/k!$
(furthermore, for fixed
$B_{n,k} \leq (k+1)^n/k!$
(furthermore, for fixed
 $k$
we have
$k$
we have
 $B_{n,k} \sim (k+1)^n/k!$
, so this inequality is not too lossy). To verify this inequality, consider the following function
$B_{n,k} \sim (k+1)^n/k!$
, so this inequality is not too lossy). To verify this inequality, consider the following function
 $f$
from the set of
$f$
from the set of
 $P \in \mathrm{OPP}(n)$
Footnote 8 in which there are exactly
$P \in \mathrm{OPP}(n)$
Footnote 8 in which there are exactly
 $k$
parts and no singletons to the set
$k$
parts and no singletons to the set
 $\{0,1,2,\ldots,k\}^n$
:Since
$\{0,1,2,\ldots,k\}^n$
:Since \begin{align*} f(P) \,{:\!=}\, \; & (f_1(P), f_2(P), \ldots, f_n(P)), \quad \text{where} \\ f_i(P) \; = \; & \begin{cases} 0 & \text{if } i \underset{P}{\not \sim } i, \\ j & \text{if } i \text{ is in the } j-\text{th part of } P. \end{cases} \end{align*}
\begin{align*} f(P) \,{:\!=}\, \; & (f_1(P), f_2(P), \ldots, f_n(P)), \quad \text{where} \\ f_i(P) \; = \; & \begin{cases} 0 & \text{if } i \underset{P}{\not \sim } i, \\ j & \text{if } i \text{ is in the } j-\text{th part of } P. \end{cases} \end{align*}
 $f(P)$
completely specifies the ordered partial partition
$f(P)$
completely specifies the ordered partial partition
 $P$
,
$P$
,
 $f$
is injective, so there are no more than
$f$
is injective, so there are no more than
 $|\{0,1,2,\ldots,k\}^n| = (k+1)^n$
different
$|\{0,1,2,\ldots,k\}^n| = (k+1)^n$
different
 $P \in \mathrm{OPP}(n)$
with exactly
$P \in \mathrm{OPP}(n)$
with exactly
 $k$
parts and no singletons. If we then forget about the ordering of those
$k$
parts and no singletons. If we then forget about the ordering of those
 $k$
parts, we see that there are no more than
$k$
parts, we see that there are no more than
 $(k+1)^n/k!$
members of
$(k+1)^n/k!$
members of
 ${\mathrm{PP}}(n)$
with exactly
${\mathrm{PP}}(n)$
with exactly
 $k$
parts and no singletons, so
$k$
parts and no singletons, so
 $B_{n,k} \leq (k+1)^n/k!$
.
$B_{n,k} \leq (k+1)^n/k!$
.
In summary, all of the above observations and formulas, when combined with Corollary 11, lead to the following (slightly weaker when
![]() $p \geq 7$
, but much easier to evaluate and work with) corollary:
$p \geq 7$
, but much easier to evaluate and work with) corollary:
Corollary 12.
Let
![]() $\mathbb{F}$
be a field with characteristic
$\mathbb{F}$
be a field with characteristic
![]() $p \gt 0$
.
$p \gt 0$
.
-
(a) If
 $p = 2$
then
$p = 2$
then
 $\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^n - n$
.
$\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^n - n$
. -
(b) If
 $p = 3$
then
$p = 3$
then
 $\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \frac{1}{2}\big (3^n - n2^n + (n^2 - n + 1)\big )$
.
$\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \frac{1}{2}\big (3^n - n2^n + (n^2 - n + 1)\big )$
. -
(c) If
 $p = 5$
then
$p = 5$
then
 $\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \frac{1}{24}\big (5^n - n4^n + 2(n^2 - n + 9)3^{n-1} - (n^3 - 3n^2 + 14n$
$\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \frac{1}{24}\big (5^n - n4^n + 2(n^2 - n + 9)3^{n-1} - (n^3 - 3n^2 + 14n$
 $- 16)2^{n-1}$
$- 16)2^{n-1}$
 $\displaystyle + (n^4 - 6n^3 + 17n^2 - 20n + 9)\big )$
.
$\displaystyle + (n^4 - 6n^3 + 17n^2 - 20n + 9)\big )$
. -
(d) In general,
 $\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \sum _{k=1}^p\frac{k^n}{(k-1)!}$
. In particular,
$\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq \sum _{k=1}^p\frac{k^n}{(k-1)!}$
. In particular,
 $\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \in O(p^n)$
.
$\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \in O(p^n)$
.
5.1 Rank of the permanent tensor
Glynn’s formula (3) shows that the tensor rank of the permanent tensor is at most
![]() $2^{n-1}$
, as long as the field does not have characteristic
$2^{n-1}$
, as long as the field does not have characteristic
![]() $2$
. When the characteristic is
$2$
. When the characteristic is
![]() $2$
, the permanent and determinant tensors are the same, and the best-known upper bound on their rank is now
$2$
, the permanent and determinant tensors are the same, and the best-known upper bound on their rank is now
![]() $2^n - n$
, as described by Corollary 12 (surpassing the
$2^n - n$
, as described by Corollary 12 (surpassing the
![]() $2^n - 1$
that comes from Ryser’s formula (2)). The following corollary clarifies slightly what this
$2^n - 1$
that comes from Ryser’s formula (2)). The following corollary clarifies slightly what this
![]() $2^n - n$
term formula for the determinant and permanent looks like in characteristic
$2^n - n$
term formula for the determinant and permanent looks like in characteristic
![]() $2$
. We note that the “
$2$
. We note that the “
![]() $\ominus$
” in the following corollary is the symmetric difference operation on sets, and
$\ominus$
” in the following corollary is the symmetric difference operation on sets, and
![]() $\mathrm{per}^n_{{\mathbb{F}}}$
refers to the determinant tensor
$\mathrm{per}^n_{{\mathbb{F}}}$
refers to the determinant tensor
![]() $\mathrm{per}^n_{{\mathbb{F}}} = \sum _{\sigma \in S_n} \mathbf{e}_{\sigma (1)} \otimes \mathbf{e}_{\sigma (2)} \otimes \cdots \otimes \mathbf{e}_{\sigma (n)}$
:
$\mathrm{per}^n_{{\mathbb{F}}} = \sum _{\sigma \in S_n} \mathbf{e}_{\sigma (1)} \otimes \mathbf{e}_{\sigma (2)} \otimes \cdots \otimes \mathbf{e}_{\sigma (n)}$
:
Corollary 13.
Let
![]() $A$
be an
$A$
be an
![]() $n \times n$
matrix over a field
$n \times n$
matrix over a field
![]() $\mathbb{F}$
with characteristic
$\mathbb{F}$
with characteristic
![]() $2$
. Then
$2$
. Then
 \begin{align} \mathrm{per}(A) ={\mathrm{det}}(A) & = \sum _{S \subseteq [n]} \left ( \prod _{i=1}^n \sum _{j \in S\ominus \{i\}} a_{i,j} \right ). \end{align}
\begin{align} \mathrm{per}(A) ={\mathrm{det}}(A) & = \sum _{S \subseteq [n]} \left ( \prod _{i=1}^n \sum _{j \in S\ominus \{i\}} a_{i,j} \right ). \end{align}
In particular, whenever
![]() $S$
is a singleton the inner sum is empty, so
$S$
is a singleton the inner sum is empty, so
![]() ${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}}) ={\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^n - n$
.
${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}}) ={\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \leq 2^n - n$
.
The above corollary comes directly from plugging
![]() $p = 2$
into Theorem 10 and discarding all terms coming from partial partitions that have two or more parts. The partial partitions with just zero or one part are in bijection with the subsets
$p = 2$
into Theorem 10 and discarding all terms coming from partial partitions that have two or more parts. The partial partitions with just zero or one part are in bijection with the subsets
![]() $S$
of
$S$
of
![]() $[n]$
, giving the result.
$[n]$
, giving the result.
For
![]() $n \leq 3$
, the formula provided by Corollary 12 is the same as the field-independent formula that we have seen already (except with signs ignored since
$n \leq 3$
, the formula provided by Corollary 12 is the same as the field-independent formula that we have seen already (except with signs ignored since
![]() $-1 = 1$
in characteristic
$-1 = 1$
in characteristic
![]() $2$
). The first non-trivial case comes when
$2$
). The first non-trivial case comes when
![]() $n = 4$
. In this case, the resulting formula has
$n = 4$
. In this case, the resulting formula has
![]() $12$
terms; it is the same as the formula displayed in equation (12), but without the final
$12$
terms; it is the same as the formula displayed in equation (12), but without the final
![]() $3$
terms (i.e., the terms with a coefficient of
$3$
terms (i.e., the terms with a coefficient of
![]() $2$
).
$2$
).
6. Tensor rank lower bounds
All of the results that we have presented so far bound
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
and
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
and
![]() ${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}})$
from above. In the other direction, the best-known lower bounds on
${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}})$
from above. In the other direction, the best-known lower bounds on
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
and
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
and
![]() ${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}})$
when
${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}})$
when
![]() $n \geq 4$
are due to Derksen [Reference Derksen4], who showed that
$n \geq 4$
are due to Derksen [Reference Derksen4], who showed that
(he only stated these bounds for
![]() ${\mathbb{F}} ={\mathbb{C}}$
, but his proof works over any field).Footnote 9
${\mathbb{F}} ={\mathbb{C}}$
, but his proof works over any field).Footnote 9
The known upper bounds show that this lower bound on the permanent cannot be improved by more than a factor of
![]() $\Theta (\sqrt{n})$
over any field. In particular, if
$\Theta (\sqrt{n})$
over any field. In particular, if
![]() $\mathbb{F}$
has characteristic not equal to
$\mathbb{F}$
has characteristic not equal to
![]() $2$
then Glynn’s formula (3) implies
$2$
then Glynn’s formula (3) implies
Similarly, Corollary 13 tells us that if
![]() $\mathbb{F}$
has characteristic
$\mathbb{F}$
has characteristic
![]() $2$
then we have
$2$
then we have
We can, however, make some small improvements. In particular, we refine Derksen’s analysis slightly to improve these lower bounds by
![]() $1$
:
$1$
:
Theorem 14.
Let
![]() $\mathbb{F}$
be any field. Then
$\mathbb{F}$
be any field. Then
![]() $\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \geq \binom{n}{\lfloor n/2\rfloor } + 1$
and
$\displaystyle{\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \geq \binom{n}{\lfloor n/2\rfloor } + 1$
and
![]() $\displaystyle{\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}}) \geq \binom{n}{\lfloor n/2\rfloor }\,{+}\,1$
.
$\displaystyle{\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}}) \geq \binom{n}{\lfloor n/2\rfloor }\,{+}\,1$
.
Proof. We begin by recalling the definition of the antisymmetric subspace
![]() $\mathcal{A}$
of
$\mathcal{A}$
of
![]() $(\mathbb{F}^n)^{\otimes s}$
:Footnote 10
$(\mathbb{F}^n)^{\otimes s}$
:Footnote 10
 \begin{align} \mathcal{A} \,{:\!=}\, \mathrm{span}\left \{ \sum _{\sigma \in S_s}{\,\mathrm{sgn}}(\sigma ) \mathbf{e}_{i_{\sigma (1)}} \otimes \mathbf{e}_{i_{\sigma (2)}} \otimes \cdots \otimes \mathbf{e}_{i_{\sigma (s)}}\,{:}\, 1 \leq i_1 \lt i_2 \lt \cdots \lt i_s \leq n \right \}. \end{align}
\begin{align} \mathcal{A} \,{:\!=}\, \mathrm{span}\left \{ \sum _{\sigma \in S_s}{\,\mathrm{sgn}}(\sigma ) \mathbf{e}_{i_{\sigma (1)}} \otimes \mathbf{e}_{i_{\sigma (2)}} \otimes \cdots \otimes \mathbf{e}_{i_{\sigma (s)}}\,{:}\, 1 \leq i_1 \lt i_2 \lt \cdots \lt i_s \leq n \right \}. \end{align}
We just prove the inequality in the statement of the theorem that involves
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
; the bound on
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}})$
; the bound on
![]() ${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}})$
follows similarly by just ignoring signs throughout the proof and omitting
${\mathrm{Trank}}(\mathrm{per}^n_{{\mathbb{F}}})$
follows similarly by just ignoring signs throughout the proof and omitting
![]() ${\mathrm{sgn}}(\sigma )$
from the definition (29) of the ‘antisymmetric subspace’
${\mathrm{sgn}}(\sigma )$
from the definition (29) of the ‘antisymmetric subspace’
![]() $\mathcal{A}$
.Footnote 11
$\mathcal{A}$
.Footnote 11
It is well-known that if
![]() $T$
is any matrix flattening of
$T$
is any matrix flattening of
![]() ${{\mathrm{det}}^n_{{\mathbb{F}}}}$
then
${{\mathrm{det}}^n_{{\mathbb{F}}}}$
then
![]() ${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \geq \mathrm{rank}(T)$
. We choose
${\mathrm{Trank}}({{\mathrm{det}}^n_{{\mathbb{F}}}}) \geq \mathrm{rank}(T)$
. We choose
![]() $T$
to be the flattening obtained by partitioning
$T$
to be the flattening obtained by partitioning
![]() $(\mathbb{F}^n)^{\otimes n}$
as
$(\mathbb{F}^n)^{\otimes n}$
as
![]() $(\mathbb{F}^n)^{\otimes \lfloor n/2\rfloor } \otimes (\mathbb{F}^n)^{\otimes \lceil n/2\rceil }$
, which we think of as an
$(\mathbb{F}^n)^{\otimes \lfloor n/2\rfloor } \otimes (\mathbb{F}^n)^{\otimes \lceil n/2\rceil }$
, which we think of as an
![]() $n^{\lfloor n/2\rfloor } \times n^{\lceil n/2\rceil }$
matrix. The columns of this matrix
$n^{\lfloor n/2\rfloor } \times n^{\lceil n/2\rceil }$
matrix. The columns of this matrix
![]() $T$
span the antisymmetric subspace
$T$
span the antisymmetric subspace
![]() $\mathcal{A}$
of
$\mathcal{A}$
of
![]() $(\mathbb{F}^n)^{\otimes \lfloor n/2\rfloor }$
, which has dimension
$(\mathbb{F}^n)^{\otimes \lfloor n/2\rfloor }$
, which has dimension
![]() $\binom{n}{\lfloor n/2 \rfloor }$
, so
$\binom{n}{\lfloor n/2 \rfloor }$
, so
recovering Derksen’s lower bound.
To show that Inequality (30) is actually strict (and thus complete the proof), note that for any tensor decomposition of the form
we have
In particular, this implies that the range of
![]() $T$
(i.e., the antisymmetric subspace of
$T$
(i.e., the antisymmetric subspace of
![]() $(\mathbb{F}^n)^{\otimes \lfloor n/2\rfloor }$
) is contained in the span of the
$(\mathbb{F}^n)^{\otimes \lfloor n/2\rfloor }$
) is contained in the span of the
![]() $r$
elementary tensors
$r$
elementary tensors
![]() $\mathbf{v_{1,k}} \otimes \cdots \otimes \mathbf{v_{\lfloor n/2\rfloor,k}}$
(
$\mathbf{v_{1,k}} \otimes \cdots \otimes \mathbf{v_{\lfloor n/2\rfloor,k}}$
(
![]() $1 \leq k \leq r$
). If
$1 \leq k \leq r$
). If
![]() $r \leq \binom{n}{\lfloor n/2 \rfloor }$
(the dimension of the antisymmetric subspace) then this implies that each of these elementary tensors are in the antisymmetric subspace, contradicting the fact that no non-zero elementary tensors are in the antisymmetric subspace.Footnote 12 We thus conclude that
$r \leq \binom{n}{\lfloor n/2 \rfloor }$
(the dimension of the antisymmetric subspace) then this implies that each of these elementary tensors are in the antisymmetric subspace, contradicting the fact that no non-zero elementary tensors are in the antisymmetric subspace.Footnote 12 We thus conclude that
![]() $r \gt \binom{n}{\lfloor n/2 \rfloor }$
, which completes the proof.
$r \gt \binom{n}{\lfloor n/2 \rfloor }$
, which completes the proof.
6.1 Better lower bounds over finite fields
In the case when
![]() ${\mathbb{F}} ={\mathbb{F}}_q$
is the field with
${\mathbb{F}} ={\mathbb{F}}_q$
is the field with
![]() $q$
elements, we can refine the argument of Theorem 14 even further to get even better lower bounds on
$q$
elements, we can refine the argument of Theorem 14 even further to get even better lower bounds on
![]() ${\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}_q}^n)$
. In particular, we have the following:
${\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}_q}^n)$
. In particular, we have the following:
Theorem 15.
Let
![]() $q \geq 2$
be a prime power, let
$q \geq 2$
be a prime power, let
![]() $n \geq 5$
, and let
$n \geq 5$
, and let
![]() $x$
be the (unique) positive real solution to the equation
$x$
be the (unique) positive real solution to the equation
![]() $\log _q(x + 1) = x - \binom{n}{\lfloor n/2 \rfloor }$
. Then
$\log _q(x + 1) = x - \binom{n}{\lfloor n/2 \rfloor }$
. Then
In particular,
![]() ${\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}_q}^n) \geq \binom{n}{\lfloor n/2 \rfloor } + \log _q\big (\binom{n}{\lfloor n/2 \rfloor }\big )$
.
${\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}_q}^n) \geq \binom{n}{\lfloor n/2 \rfloor } + \log _q\big (\binom{n}{\lfloor n/2 \rfloor }\big )$
.
Before we can prove this, we begin by establishing a useful lemma about the tensor rank of members of the antisymmetric subspace:Footnote 13
Lemma 16.
Suppose that
![]() $\mathbb{F}$
is a field,
$\mathbb{F}$
is a field,
![]() $n, s$
are positive integers, and
$n, s$
are positive integers, and
![]() $T$
is a non-zero element of the antisymmetric subspace of
$T$
is a non-zero element of the antisymmetric subspace of
![]() $(\mathbb{F}^n)^{\otimes s}$
. Then
$(\mathbb{F}^n)^{\otimes s}$
. Then
![]() ${\mathrm{Trank}}(T) \geq s$
.
${\mathrm{Trank}}(T) \geq s$
.
Proof. If
![]() $s = 1$
, the result is immediate, because every non-zero tensor has positive tensor rank. We shall henceforth assume that
$s = 1$
, the result is immediate, because every non-zero tensor has positive tensor rank. We shall henceforth assume that
![]() $s \geq 2$
.
$s \geq 2$
.
We view the tensor
![]() $T$
as a multilinear form from
$T$
as a multilinear form from
![]() $(\mathbb{F}^n)^{s}$
to
$(\mathbb{F}^n)^{s}$
to
![]() $\mathbb{F}$
. By assumption that it is non-zero, there must exist vectors
$\mathbb{F}$
. By assumption that it is non-zero, there must exist vectors
![]() $\mathbf{x_1}, \ldots, \mathbf{x_s} \in \mathbb{F}^n$
such that
$\mathbf{x_1}, \ldots, \mathbf{x_s} \in \mathbb{F}^n$
such that
![]() $T(\mathbf{x_1}, \ldots, \mathbf{x_s})$
is non-zero. By multiplying one of these vectors by an appropriate scalar, we can assume without loss of generality that
$T(\mathbf{x_1}, \ldots, \mathbf{x_s})$
is non-zero. By multiplying one of these vectors by an appropriate scalar, we can assume without loss of generality that
![]() $T(\mathbf{x_1}, \dots, \mathbf{x_s}) = 1$
.
$T(\mathbf{x_1}, \dots, \mathbf{x_s}) = 1$
.
Note that
![]() $\{\mathbf{x_1}, \dots, \mathbf{x_s}\}$
must be linearly independent. Otherwise, we could write one of the vectors as a linear combination of the others, which we will assume without loss of generality is
$\{\mathbf{x_1}, \dots, \mathbf{x_s}\}$
must be linearly independent. Otherwise, we could write one of the vectors as a linear combination of the others, which we will assume without loss of generality is
![]() $\mathbf{x_1}$
. That is,
$\mathbf{x_1}$
. That is,
![]() $\mathbf{x_1} = \alpha _2 \mathbf{x_2} + \cdots + \alpha _s \mathbf{x_s}$
, and then we would have the following by linearity in the first argument:
$\mathbf{x_1} = \alpha _2 \mathbf{x_2} + \cdots + \alpha _s \mathbf{x_s}$
, and then we would have the following by linearity in the first argument:
By antisymmetry, each term on the right-hand side vanishes, and the left-hand side equals 1, so we obtain a contradiction. As such, it follows that
![]() $\{\mathbf{x_1}, \dots, \mathbf{x_s}\}$
is indeed linearly independent.
$\{\mathbf{x_1}, \dots, \mathbf{x_s}\}$
is indeed linearly independent.
For a fixed
![]() $1 \leq i \leq s$
, we define a covector
$1 \leq i \leq s$
, we define a covector
![]() $\mathbf{y_i}\,{:}\, \mathbb{F}^n \rightarrow \mathbb{F}$
by contracting
$\mathbf{y_i}\,{:}\, \mathbb{F}^n \rightarrow \mathbb{F}$
by contracting
![]() $T$
on its first
$T$
on its first
![]() $s - 1$
arguments with the elements of
$s - 1$
arguments with the elements of
![]() $\{\mathbf{x_1}, \dots, \mathbf{x_s}\} \setminus \{ \mathbf{x_i} \}$
and applying an appropriate sign change:
$\{\mathbf{x_1}, \dots, \mathbf{x_s}\} \setminus \{ \mathbf{x_i} \}$
and applying an appropriate sign change:
Observe that the antisymmetry properties of
![]() $T$
imply the following:
$T$
imply the following:
 \begin{equation*} \mathbf {y_i}(\mathbf {x_j}) = \begin {cases} 1 & \text { if } i = j; \\ 0 & \text { if } i \neq j. \end {cases} \end{equation*}
\begin{equation*} \mathbf {y_i}(\mathbf {x_j}) = \begin {cases} 1 & \text { if } i = j; \\ 0 & \text { if } i \neq j. \end {cases} \end{equation*}
Equivalently, if we consider the space
![]() $V$
spanned by
$V$
spanned by
![]() $\mathbf{x_1}, \ldots, \mathbf{x_s}$
, then the covectors
$\mathbf{x_1}, \ldots, \mathbf{x_s}$
, then the covectors
![]() $\mathbf{y_1}, \ldots, \mathbf{y_s}$
form a basis for
$\mathbf{y_1}, \ldots, \mathbf{y_s}$
form a basis for
![]() $V^{\star }$
, specifically the dual basis of
$V^{\star }$
, specifically the dual basis of
![]() $\mathbf{x_1}, \ldots, \mathbf{x_s}$
.
$\mathbf{x_1}, \ldots, \mathbf{x_s}$
.
Consequently, the matrix obtained from
![]() $T$
by the flattening
$T$
by the flattening
![]() $(\mathbb{F}^n)^{\otimes s} = (\mathbb{F}^n)^{\otimes (s-1)} \otimes (\mathbb{F}^n)$
has tensor rank at least
$(\mathbb{F}^n)^{\otimes s} = (\mathbb{F}^n)^{\otimes (s-1)} \otimes (\mathbb{F}^n)$
has tensor rank at least
![]() $s$
, and thus
$s$
, and thus
![]() ${\mathrm{Trank}}(T) \geq s$
.
${\mathrm{Trank}}(T) \geq s$
.
Proof of Theorem
15. We showed in the proof of Theorem 14 that if
![]() $1 \leq s \leq n$
and
$1 \leq s \leq n$
and
then the antisymmetric subspace of
![]() $(\mathbb{F}_q^n)^{\otimes s}$
must be contained in the span of the
$(\mathbb{F}_q^n)^{\otimes s}$
must be contained in the span of the
![]() $r$
elementary tensors
$r$
elementary tensors
![]() $\mathbf{v_{1,k}} \otimes \cdots \otimes \mathbf{v_{s,k}}$
(
$\mathbf{v_{1,k}} \otimes \cdots \otimes \mathbf{v_{s,k}}$
(
![]() $1 \leq k \leq r$
). We will use this fact with
$1 \leq k \leq r$
). We will use this fact with
![]() $s = \lceil n/2 \rceil$
(in the proof of Theorem 14 we instead used
$s = \lceil n/2 \rceil$
(in the proof of Theorem 14 we instead used
![]() $s = \lfloor n/2\rfloor$
).
$s = \lfloor n/2\rfloor$
).
Let
![]() $P\,{:}\, ({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil } \rightarrow ({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil }/ \mathcal{A}$
be a projection onto the quotient of the antisymmetric subspace
$P\,{:}\, ({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil } \rightarrow ({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil }/ \mathcal{A}$
be a projection onto the quotient of the antisymmetric subspace
![]() $\mathcal{A}$
inside of
$\mathcal{A}$
inside of
![]() $({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil }$
. If the antisymmetric subspace of
$({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil }$
. If the antisymmetric subspace of
![]() $(\mathbb{F}_q^n)^{\otimes \lceil n/2\rceil }$
is contained in the span of
$(\mathbb{F}_q^n)^{\otimes \lceil n/2\rceil }$
is contained in the span of
![]() $r$
elementary tensors
$r$
elementary tensors
![]() $\mathbf{v_{1,j}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,j}}$
(
$\mathbf{v_{1,j}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,j}}$
(
![]() $1 \leq j \leq r$
), then the span of the set
$1 \leq j \leq r$
), then the span of the set
must have dimension at most
![]() $r - \binom{n}{\lfloor n/2 \rfloor }$
. Since we are working over
$r - \binom{n}{\lfloor n/2 \rfloor }$
. Since we are working over
![]() ${\mathbb{F}}_q$
, there are thus at most
${\mathbb{F}}_q$
, there are thus at most
non-zero vectors in
![]() $B$
.
$B$
.
Next, we note that there are exactly
![]() $r$
members in
$r$
members in
![]() $B$
(i.e., the vectors
$B$
(i.e., the vectors
![]() $P(\mathbf{v_{1,i}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,i}})$
and
$P(\mathbf{v_{1,i}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,i}})$
and
![]() $P(\mathbf{v_{1,j}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,j}})$
are distinct whenever
$P(\mathbf{v_{1,j}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,j}})$
are distinct whenever
![]() $i \neq j$
). To see why this is the case, we apply Lemma 16: given any tensor
$i \neq j$
). To see why this is the case, we apply Lemma 16: given any tensor
![]() $T$
in the antisymmetric subspace of
$T$
in the antisymmetric subspace of
![]() $(\mathbb{F}_q^n)^{\otimes \lceil n/2\rceil }$
, we have
$(\mathbb{F}_q^n)^{\otimes \lceil n/2\rceil }$
, we have
![]() ${\mathrm{Trank}}(T) \geq \lceil n/2 \rceil \geq 3$
, which implies that
${\mathrm{Trank}}(T) \geq \lceil n/2 \rceil \geq 3$
, which implies that
![]() $P(\mathbf{v_{1,i}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,i}} - \mathbf{v_{1,j}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,j}}) = \mathbf{0}$
never occurs.
$P(\mathbf{v_{1,i}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,i}} - \mathbf{v_{1,j}} \otimes \cdots \otimes \mathbf{v_{\lceil n/2\rceil,j}}) = \mathbf{0}$
never occurs.
It follows that the set
![]() $B$
consists of exactly
$B$
consists of exactly
![]() $r$
non-zero vectors, but also no more than
$r$
non-zero vectors, but also no more than
![]() $q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
non-zero vectors, so we must have
$q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
non-zero vectors, so we must have
![]() $r \leq q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
. Rearranging shows that
$r \leq q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
. Rearranging shows that
![]() $\log _q(r + 1) \leq r - \binom{n}{\lfloor n/2 \rfloor }$
. Since the function
$\log _q(r + 1) \leq r - \binom{n}{\lfloor n/2 \rfloor }$
. Since the function
is monotonically decreasing on
![]() $(0,\infty )$
, has
$(0,\infty )$
, has
![]() $f(1) \gt 0$
, and
$f(1) \gt 0$
, and
![]() $\lim _{x\rightarrow \infty }f(x) = -\infty$
, we conclude that there is exactly one positive
$\lim _{x\rightarrow \infty }f(x) = -\infty$
, we conclude that there is exactly one positive
![]() $\widetilde{x} \in{\mathbb{R}}$
for which
$\widetilde{x} \in{\mathbb{R}}$
for which
![]() $f(\widetilde{x}) = 0$
. The least integer
$f(\widetilde{x}) = 0$
. The least integer
![]() $r \geq 1$
for which
$r \geq 1$
for which
![]() $\log _q(r + 1) \leq r - \binom{n}{\lfloor n/2 \rfloor }$
is
$\log _q(r + 1) \leq r - \binom{n}{\lfloor n/2 \rfloor }$
is
![]() $r = \lceil \widetilde{x} \rceil$
. The “in particular” statement of the theorem comes from the fact that
$r = \lceil \widetilde{x} \rceil$
. The “in particular” statement of the theorem comes from the fact that
![]() $f(x) \gt 0$
when
$f(x) \gt 0$
when
![]() $x = \binom{n}{\lfloor n/2 \rfloor } + \log _q\big (\binom{n}{\lfloor n/2 \rfloor }\big )$
too.
$x = \binom{n}{\lfloor n/2 \rfloor } + \log _q\big (\binom{n}{\lfloor n/2 \rfloor }\big )$
too.
When
![]() $n = 4$
, if we apply the same reasoning as in the proof of Theorem 15 then we have to be slightly careful, since in this case
$n = 4$
, if we apply the same reasoning as in the proof of Theorem 15 then we have to be slightly careful, since in this case
![]() $\lceil n/2\rceil = 2$
so there are antisymmetric tensors in
$\lceil n/2\rceil = 2$
so there are antisymmetric tensors in
![]() $({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil }$
with rank
$({\mathbb{F}}_q^n)^{\otimes \lceil n/2\rceil }$
with rank
![]() $2$
, leading to fewer than
$2$
, leading to fewer than
![]() $r$
members of the set
$r$
members of the set
![]() $B$
from equation (32). Instead of the inequality
$B$
from equation (32). Instead of the inequality
![]() $r \leq q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
, we obtain the weaker inequality
$r \leq q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
, we obtain the weaker inequality
![]() $r/2 \leq q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
, which leads to the bound
$r/2 \leq q^{r - \binom{n}{\lfloor n/2 \rfloor }} - 1$
, which leads to the bound
 \begin{align} {\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}_q}^4) \geq \begin{cases}9 & \text{ if } q = 2; \\ 8 & \text{ if } q \in \{3, 4\}; \\ 7 & \text{ if } q \geq 5 \text{is any other prime power.}\end{cases} \end{align}
\begin{align} {\mathrm{Trank}}({\mathrm{det}}_{{\mathbb{F}}_q}^4) \geq \begin{cases}9 & \text{ if } q = 2; \\ 8 & \text{ if } q \in \{3, 4\}; \\ 7 & \text{ if } q \geq 5 \text{is any other prime power.}\end{cases} \end{align}
We can actually prove a much stronger lower bound in the
![]() $n = 4$
,
$n = 4$
,
![]() $q = 2$
case, which matches our upper bound from Theorem 10. In particular, we have the following theorem, whose proof is computer-assisted and described in the next subsection:
$q = 2$
case, which matches our upper bound from Theorem 10. In particular, we have the following theorem, whose proof is computer-assisted and described in the next subsection:
Theorem 17.
Over the field of two elements, the tensor rank of the determinant and permanent of a
![]() $4 \times 4$
matrix is exactly 12:
$4 \times 4$
matrix is exactly 12:
6.2
Proof that the tensor rank of
 ${\mathrm{det}}_4^{{\mathbb{F}}_2}$
is 12
${\mathrm{det}}_4^{{\mathbb{F}}_2}$
is 12
The formula in Theorem 10 shows that the tensor rank is at most 12, and we have already shown a lower bound of 9. It suffices, therefore, to show that it is impossible to express the determinant tensor as the sum of
![]() $r \in \{ 9, 10, 11 \}$
rank-1 tensors.
$r \in \{ 9, 10, 11 \}$
rank-1 tensors.
Suppose otherwise. By considering the flattening
![]() $(\mathbb{F}_2^4)^{\otimes 4} = (\mathbb{F}_2^4)^{\otimes 2} \otimes (\mathbb{F}_2^4)^{\otimes 2}$
, we can write
$(\mathbb{F}_2^4)^{\otimes 4} = (\mathbb{F}_2^4)^{\otimes 2} \otimes (\mathbb{F}_2^4)^{\otimes 2}$
, we can write
where each
![]() $A_i$
and
$A_i$
and
![]() $B_i$
is a
$B_i$
is a
![]() $4 \times 4$
rank-1 matrix. Recall that the span of
$4 \times 4$
rank-1 matrix. Recall that the span of
![]() $\{ A_i\,{:}\, 1 \leq i \leq r \}$
must contain the (6-dimensional) antisymmetric subspace of
$\{ A_i\,{:}\, 1 \leq i \leq r \}$
must contain the (6-dimensional) antisymmetric subspace of
![]() $(\mathbb{F}_2^4)^{\otimes 2}$
.
$(\mathbb{F}_2^4)^{\otimes 2}$
.
Without loss of generality, we can assume that
![]() $A_1 \leq A_2 \leq \cdots \leq A_r$
, where
$A_1 \leq A_2 \leq \cdots \leq A_r$
, where
![]() $\leq$
denotes the lexicographical order on the space of
$\leq$
denotes the lexicographical order on the space of
![]() $4 \times 4$
matrices over
$4 \times 4$
matrices over
![]() ${\mathbb{F}}_2$
. Moreover, given any such tensor decomposition of
${\mathbb{F}}_2$
. Moreover, given any such tensor decomposition of
![]() ${\mathrm{det}}_4^{{\mathbb{F}}_2}$
and an invertible matrix
${\mathrm{det}}_4^{{\mathbb{F}}_2}$
and an invertible matrix
![]() $L$
, observe that the determinant is unaffected by the change of basis specified by
$L$
, observe that the determinant is unaffected by the change of basis specified by
![]() $L$
, so we also have
$L$
, so we also have
By applying a suitable change of basis
![]() $L$
, we can without loss of generality assume that at least one of the matrices – necessarily the lexicographically first matrix, and therefore
$L$
, we can without loss of generality assume that at least one of the matrices – necessarily the lexicographically first matrix, and therefore
![]() $A_1$
by definition – has a single
$A_1$
by definition – has a single
![]() $1$
in either the last or penultimate entry of the matrix, and zeroes in all other entries:
$1$
in either the last or penultimate entry of the matrix, and zeroes in all other entries:
 \begin{equation*} A_1 = \begin {bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end {bmatrix} \mathrm{ or } \begin {bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end {bmatrix} \end{equation*}
\begin{equation*} A_1 = \begin {bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end {bmatrix} \mathrm{ or } \begin {bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end {bmatrix} \end{equation*}
We performed a backtracking searchFootnote 14 for candidate
![]() $r$
-tuples
$r$
-tuples
![]() $(A_1, \dots, A_r)$
of rank-1 matrices subject to these constraints. If the intersection of the 6-dimensional antisymmetric subspace and the span of the initial segment
$(A_1, \dots, A_r)$
of rank-1 matrices subject to these constraints. If the intersection of the 6-dimensional antisymmetric subspace and the span of the initial segment
![]() $(A_1, \dots, A_s)$
has rank less than
$(A_1, \dots, A_s)$
has rank less than
![]() $6 - r + s$
, then it is impossible for the span of
$6 - r + s$
, then it is impossible for the span of
![]() $(A_1, \dots, A_r)$
to contain the antisymmetric subspace, and therefore we can eliminate that entire branch of the search tree.
$(A_1, \dots, A_r)$
to contain the antisymmetric subspace, and therefore we can eliminate that entire branch of the search tree.
The largest search (
![]() $r = 11$
) consumed 357 core-hours of CPU time, or 4 hours of wall-clock time when parallelised on an AWS r5a.24xlarge instance. The total CPU time grows rapidly as a function of
$r = 11$
) consumed 357 core-hours of CPU time, or 4 hours of wall-clock time when parallelised on an AWS r5a.24xlarge instance. The total CPU time grows rapidly as a function of
![]() $r$
:
$r$
:
 \begin{align*} \begin{array}{c | c} r & \text{CPU time} \\\hline 9 & \text{7 seconds} \\ 10 & \text{22 minutes} \\ 11 & \text{357 hours}\\ \end{array} \end{align*}
\begin{align*} \begin{array}{c | c} r & \text{CPU time} \\\hline 9 & \text{7 seconds} \\ 10 & \text{22 minutes} \\ 11 & \text{357 hours}\\ \end{array} \end{align*}
It transpires that, when
![]() $r \geq 9$
, there do exist
$r \geq 9$
, there do exist
![]() $r$
-tuples of rank-1 matrices
$r$
-tuples of rank-1 matrices
![]() $A_1, \dots, A_r$
which contain the antisymmetric subspace in their linear span, so additional ideas are necessary to eliminate these candidates.
$A_1, \dots, A_r$
which contain the antisymmetric subspace in their linear span, so additional ideas are necessary to eliminate these candidates.
Lemma 18.
Suppose that
![]() ${\mathrm{det}}_4^{{\mathbb{F}}_2} = \sum _{i=1}^r A_i \otimes B_i$
and
${\mathrm{det}}_4^{{\mathbb{F}}_2} = \sum _{i=1}^r A_i \otimes B_i$
and
![]() $r$
is minimal. Let
$r$
is minimal. Let
![]() $\mathbf{u}, \mathbf{v} \in{\mathbb{F}}_2^4$
be a pair of (not necessarily distinct) non-zero vectors. Then the size of the set of indices
$\mathbf{u}, \mathbf{v} \in{\mathbb{F}}_2^4$
be a pair of (not necessarily distinct) non-zero vectors. Then the size of the set of indices
![]() $\{ i\,{:}\, \mathbf{u}^T A_i \mathbf{v} = 1 \}$
is not equal to 1.
$\{ i\,{:}\, \mathbf{u}^T A_i \mathbf{v} = 1 \}$
is not equal to 1.
Proof. Suppose otherwise, namely that there is a unique index
![]() $i$
for which
$i$
for which
![]() $\mathbf{u}^T A_i \mathbf{v} = 1$
.
$\mathbf{u}^T A_i \mathbf{v} = 1$
.
If we contract both sides of the equation
![]() ${\mathrm{det}}_4^{{\mathbb{F}}_2} = \sum _{i=1}^r A_i \otimes B_i$
with
${\mathrm{det}}_4^{{\mathbb{F}}_2} = \sum _{i=1}^r A_i \otimes B_i$
with
![]() $\mathbf{u}$
and
$\mathbf{u}$
and
![]() $\mathbf{v}$
on the first tensor factor, all but the
$\mathbf{v}$
on the first tensor factor, all but the
![]() $i$
-th term of the sum will vanish and we obtain (in index notation)
$i$
-th term of the sum will vanish and we obtain (in index notation)
If
![]() $\mathbf{u} = \mathbf{v}$
, then the left-hand-side is the all-zeroes matrix, and therefore so is
$\mathbf{u} = \mathbf{v}$
, then the left-hand-side is the all-zeroes matrix, and therefore so is
![]() $B_i$
. But that means that we have a tensor decomposition of rank
$B_i$
. But that means that we have a tensor decomposition of rank
![]() $r - 1$
, contradicting minimality. Otherwise,
$r - 1$
, contradicting minimality. Otherwise,
![]() $\mathbf{u} \neq \mathbf{v}$
and we can apply a suitable change of basis so that, without loss of generality,
$\mathbf{u} \neq \mathbf{v}$
and we can apply a suitable change of basis so that, without loss of generality,
![]() $\mathbf{u} = \mathbf{e_1}$
and
$\mathbf{u} = \mathbf{e_1}$
and
![]() $\mathbf{v} = \mathbf{e_2}$
. Then the left-hand-side of the equation is the rank-2 matrix
$\mathbf{v} = \mathbf{e_2}$
. Then the left-hand-side of the equation is the rank-2 matrix
![]() $\mathbf{e_3} \otimes \mathbf{e_4} + \mathbf{e_4} \otimes \mathbf{e_3}$
, but the right-hand-side has rank 1, again obtaining a contradiction.
$\mathbf{e_3} \otimes \mathbf{e_4} + \mathbf{e_4} \otimes \mathbf{e_3}$
, but the right-hand-side has rank 1, again obtaining a contradiction.
This lemma eliminates all candidate 9-tuples and 10-tuples, establishing a tensor rank lower bound of 11, and leaves a single candidate 11-tuple up to change of basis and up to transposing the matrices
![]() $A_i$
:
$A_i$
:
 \begin{equation} \begin{gathered} A_1 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}, A_2 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, A_3 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix}, A_4 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \\{A_5 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & \textbf{1} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \end{bmatrix}}, A_6 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix}, A_7 = \begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix},{A_8 = \begin{bmatrix} 1 & 0 & \textbf{1} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \end{bmatrix}}, \\ A_9 = \begin{bmatrix} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \end{bmatrix}, A_{10} = \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \text{and} \quad{A_{11} = \begin{bmatrix} 1 & 1 & \textbf{1} & 0 \\ 1 & 1 & \textbf{1} & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 \end{bmatrix}}. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} A_1 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}, A_2 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, A_3 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix}, A_4 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \\{A_5 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & \textbf{1} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \end{bmatrix}}, A_6 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix}, A_7 = \begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix},{A_8 = \begin{bmatrix} 1 & 0 & \textbf{1} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \end{bmatrix}}, \\ A_9 = \begin{bmatrix} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \end{bmatrix}, A_{10} = \begin{bmatrix} 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \text{and} \quad{A_{11} = \begin{bmatrix} 1 & 1 & \textbf{1} & 0 \\ 1 & 1 & \textbf{1} & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 \end{bmatrix}}. \end{gathered} \end{equation}
The only matrices in this set to have a non-zero
![]() $(1,3)$
entry are
$(1,3)$
entry are
![]() $A_8$
and
$A_8$
and
![]() $A_{11}$
; the only matrices to have a non-zero
$A_{11}$
; the only matrices to have a non-zero
![]() $(2,3)$
entry are
$(2,3)$
entry are
![]() $A_5$
and
$A_5$
and
![]() $A_{11}$
. By contracting both sides of the equation
$A_{11}$
. By contracting both sides of the equation
![]() ${\mathrm{det}}_4^{{\mathbb{F}}_2} = \sum _{i=1}^r A_i \otimes B_i$
with
${\mathrm{det}}_4^{{\mathbb{F}}_2} = \sum _{i=1}^r A_i \otimes B_i$
with
![]() $\mathbf{e_1} \otimes \mathbf{e_3}$
, we get
$\mathbf{e_1} \otimes \mathbf{e_3}$
, we get
![]() $B_8 + B_{11} = \mathbf{e_2} \otimes \mathbf{e_4} + \mathbf{e_4} \otimes \mathbf{e_2}$
. Similarly, by contracting both sides of that equation by
$B_8 + B_{11} = \mathbf{e_2} \otimes \mathbf{e_4} + \mathbf{e_4} \otimes \mathbf{e_2}$
. Similarly, by contracting both sides of that equation by
![]() $\mathbf{e_2} \otimes \mathbf{e_3}$
, we get
$\mathbf{e_2} \otimes \mathbf{e_3}$
, we get
![]() $B_5 + B_{11} = \mathbf{e_1} \otimes \mathbf{e_4} + \mathbf{e_4} \otimes \mathbf{e_1}$
.
$B_5 + B_{11} = \mathbf{e_1} \otimes \mathbf{e_4} + \mathbf{e_4} \otimes \mathbf{e_1}$
.
There are only six different ways to write each of these rank-2 matrices as the sum of two rank-1 matrices. In particular, we must have
and
Observe that these two sets are disjoint, so
![]() $B_{11}$
cannot be in both of them. This is a contradiction that eliminates this single candidate solution for
$B_{11}$
cannot be in both of them. This is a contradiction that eliminates this single candidate solution for
![]() $r = 11$
, completing the proof of Theorem 17.
$r = 11$
, completing the proof of Theorem 17.
Acknowledgements
Thanks to Dan Piker for many Twitter conversations and excellent graphics, one of which set the first author on the road that led to this paper. Thanks to Zach Teitler for clarifying some facts about Waring rank that appeared in Section 1.2 [Reference Teitler17]. N.J. was supported by NSERC Discovery Grant RGPIN-2022-04098. Thanks also to an anonymous reviewer for numerous helpful corrections and suggestions.