Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T05:37:33.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Monochromatic cycle partitions in random graphs

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  14 August 2020

Richard Lang  and
Allan Lo
Richard Lang*
Affiliation:
Institute for Computer Science, Heidelberg University, 69120Heidelberg, Germany
Allan Lo
Affiliation:
School of Mathematics, University of Birmingham, BirminghamB15 2TT, UK
*
*Corresponding author. Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Erdős, Gyárfás and Pyber showed that every r-edge-coloured complete graph Kn can be covered by 25 r2 log r vertex-disjoint monochromatic cycles (independent of n). Here we extend their result to the setting of binomial random graphs. That is, we show that if 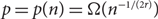$p = p(n) = \Omega(n^{-1/(2r)})$ , then with high probability any r-edge-coloured G(n, p) can be covered by at most 1000r4 log r vertex-disjoint monochromatic cycles. This answers a question of Korándi, Mousset, Nenadov, Škorić and Sudakov.

MSC classification

Primary: 05D10: Ramsey theory
Secondary: 05C38: Paths and cycles
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 1 , January 2021 , pp. 136 - 152
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Footnotes

†

The research leading to these results was supported by EPSRC, grant EP/P002420/1.

References

Allen, P., Böttcher, J., Hàn, H., Kohayakawa, Y. and Person, Y. (2016) Blow-up lemmas for sparse graphs. arXiv:1612.00622Google Scholar
Bal, D. and DeBiasio, L. Personal communication.Google Scholar
Bal, D. and DeBiasio, L. (2017) Partitioning random graphs into monochromatic components. Electron. J. Combin. 24 P1.18.Google Scholar
Balogh, J., Barát, J., Gerbner, D., Gyárfás, A. and Sárközy, G. (2014) Partitioning 2-edge-colored graphs by monochromatic paths and cycles. Combinatorica 34 507–526.CrossRefGoogle Scholar
Bessy, S. and Thomassé, S. (2010) Partitioning a graph into a cycle and an anticycle: a proof of Lehel’s conjecture. J. Combin. Theory Ser. B 100 176–180.CrossRefGoogle Scholar
Bucić, M., Korándi, D. and Sudakov, B. (2019) Covering random graphs by monochromatic trees and Helly-type results for hypergraphs. arXiv:1902.05055Google Scholar
Conlon, D. (2014) Combinatorial theorems relative to a random set. arXiv:1404.3324Google Scholar
DeBiasio, L. and Nelsen, L. (2017) Monochromatic cycle partitions of graphs with large minimum degree. J. Combin. Theory Ser. B 122 634–667.CrossRefGoogle Scholar
Erdős, P., Gyárfás, A. and Pyber, L. (1991) Vertex coverings by monochromatic cycles and trees. J. Combin. Theory Ser. B 51 90–95.CrossRefGoogle Scholar
Gyárfás, A. (2016) Vertex covers by monochromatic pieces: a survey of results and problems. Discrete Math. 339 1970–1977.CrossRefGoogle Scholar
Gyárfás, A., Jagota, A. and Schelp, R. (1997) Monochromatic path covers in nearly complete graphs. J. Combin. Math. Combin. Comput. 25 129–144.Google Scholar
Gyárfás, A., Ruszinkó, M., Sárközy, G. N. and Szemerédi, E. (2006) An improved bound for the monochromatic cycle partition number. J. Combin. Theory Ser. B 96 855–873.Google Scholar
Gyárfás, A., Ruszinkó, M., Sárközy, G. N. and Szemerédi, E. (2011) Partitioning 3-colored complete graphs into three monochromatic cycles. Electron. J. Combin. 18 P53.Google Scholar
Haxell, P. E. (1997) Partitioning complete bipartite graphs by monochromatic cycles. J. Combin. Theory Ser. B 69 210–218.Google Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs. Wiley.Google Scholar
Kohayakawa, Y., Mota, G. O. and Schacht, M. (2019) Monochromatic trees in random graphs. Math. Proc. Camb. Philos. Soc. 166, 191–208.CrossRefGoogle Scholar
Korándi, D., Lang, R., Letzter, S. and Pokrovskiy, A. (2020) Minimum degree conditions for monochromatic cycle partitioning, to appear in J. Combin. Theory Ser. B. Google Scholar
Korándi, D., Mousset, F., Nenadov, R., Škorić, N. and Sudakov, B. (2018) Monochromatic cycle covers in random graphs. Random Struct. Algorithms 53 667–691.Google Scholar
Lang, R. and Stein, M. (2017) Local colourings and monochromatic partitions in complete bipartite graphs. European J. Combin. 60 42–54.CrossRefGoogle Scholar
Letzter, S. (2015) Monochromatic cycle partitions of 2-coloured graphs with minimum degree 3n/4. arXiv:1502.07736Google Scholar
Łuczak, T. (1999) ${R}({C}_n ,{C}_n ,{C}_n ) \le (4 + o(1))n$ . J. Combin. Theory Ser. B 75 174–187.CrossRefGoogle Scholar
Łuczak, T., Rödl, V. and Szemerédi, E. (1998) Partitioning two-colored complete graphs into two monochromatic cycles. Combin. Probab. Comput. 7 423–436.Google Scholar
Pokrovskiy, A. (2014) Partitioning edge-coloured complete graphs into monochromatic cycles and paths. J. Combin. Theory Ser. B 106 70–97.CrossRefGoogle Scholar
Rödl, V. and Ruciński, A. (1995) Threshold functions for Ramsey properties. J. Amer. Math. Soc. 8 917–942.CrossRefGoogle Scholar
Sárközy, G. N. (2011) Monochromatic cycle partitions of edge-colored graphs. J. Graph Theory 66 57–64.Google Scholar