Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-16T22:25:06.148Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing properties of colourings of the ℤd lattice

Part of: Graph theory Topological dynamics

Published online by Cambridge University Press:  19 October 2020

Noga Alon ,
Raimundo Briceño ,
Nishant Chandgotia ,
Alexander Magazinov  and
Yinon Spinka
Noga Alon
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ08544, USA, and Schools of Mathematics and Computer Science, Tel Aviv University, Tel Aviv6997801, Israel
Raimundo Briceño
Affiliation:
Pontificia Universidad Católica de Chile, Santiago, Chile
Nishant Chandgotia*
Affiliation:
School of Mathematical Sciences, Hebrew University of Jerusalem, Israel
Alexander Magazinov
Affiliation:
Higher School of Economics, National Research University, 6 Usacheva Street, Moscow119048, Russia
Yinon Spinka
Affiliation:
University of British Columbia, Department of Mathematics, Vancouver, BCV6T 1Z2, Canada
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study and classify proper q-colourings of the ℤd lattice, identifying three regimes where different combinatorial behaviour holds. (1) When 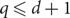$q\le d+1$ , there exist frozen colourings, that is, proper q-colourings of ℤd which cannot be modified on any finite subset. (2) We prove a strong list-colouring property which implies that, when 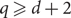$q\ge d+2$ , any proper q-colouring of the boundary of a box of side length 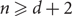$n \ge d+2$ can be extended to a proper q-colouring of the entire box. (3) When 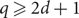$q\geq 2d+1$ , the latter holds for any 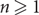$n \ge 1$ . Consequently, we classify the space of proper q-colourings of the ℤd lattice by their mixing properties.

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 37B10: Symbolic dynamics
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 3 , May 2021 , pp. 360 - 373
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, N., Krivelevich, M. and Sudakov, B. (1999) Coloring graphs with sparse neighborhoods. J. Combin. Theory Ser. B 77 73–82.Google Scholar
Alon, N. and Tarsi, M. (1992) Colorings and orientations of graphs. Combinatorica 12 125–134.Google Scholar
Boyle, M., Pavlov, R. and Schraudner, M. (2010) Multidimensional sofic shifts without separation and their factors. Trans. Amer. Math. Soc. 362 4617–4653.Google Scholar
Briceño, R. (2018) The topological strong spatial mixing property and new conditions for pressure approximation. Ergodic Theory Dynam. Systems 38 1658–1696.Google Scholar
Briceño, R. and Bulatov, A.A. and Dalmau, V. and Larose, B. (2019) Dismantlability, Connectedness, and Mixing in Relational Structures, 46th International Colloquium on Automata, Languages, and Programming (ICALP 2019), Leibniz International Proceedings in Informatics (LIPIcs) 132 1868–8969.Google Scholar
Briceño, R., McGoff, K. and Pavlov, R. (2018) Factoring onto ℤd subshifts with the finite extension property. Proc. Amer. Math. Soc. 146 5129–5140.Google Scholar
Briceño, R. and Pavlov, R. (2017) Strong spatial mixing in homomorphism spaces. SIAM J. Discrete Math. 31 2110–2137.CrossRefGoogle Scholar
Brightwell, G. R. and Winkler, P. (2000) Gibbs measures and dismantlable graphs. J. Combin. Theory Ser. B 78 141–166.CrossRefGoogle Scholar
Brightwell, G. R. and Winkler, P. (2002) Random colorings of a Cayley tree. Contemporary Combinatorics 10 247–276.Google Scholar
Burton, R. and Steif, J. E. (1994) Non-uniqueness of measures of maximal entropy for subshifts of finite type. Ergodic Theory Dynam. Systems 14 213–235.CrossRefGoogle Scholar
Chandgotia, N. (2018) A short note on the pivot property. http://math.huji.ac.il/~nishant/Research_files/Notes_files/Pivot.pdf Google Scholar
Chandgotia, N. and Marcus, B. (2018) Mixing properties for hom-shifts and the distance between walks on associated graphs. Pacific J. Math. 294 41–69.Google Scholar
Chandgotia, N. and Meyerovitch, T. (2016) Markov random fields, Markov cocycles and the 3-colored chessboard. Israel J. Math. 215 909–964.Google Scholar
Gamarnik, D., Katz, D. and Misra, S. (2015) Strong spatial mixing of list coloring of graphs. Random Struct. Algorithms 46 599–613.CrossRefGoogle Scholar
Johansson, A. (1996) Asymptotic choice number for triangle free graphs. DIMACS technical report.Google Scholar
Jonasson, J. (2002) Uniqueness of uniform random colorings of regular trees. Statist. Probab. Lett. 57 243–248.CrossRefGoogle Scholar
Marcus, B. and Pavlov, R. (2015) An integral representation for topological pressure in terms of conditional probabilities. Israel J. Math. 207 395–433.CrossRefGoogle Scholar
Pak, I., Sheffer, A. and Tassy, M. (2016) Fast domino tileability. Discrete Comput. Geom. 56 377–394.CrossRefGoogle Scholar
Peled, R. and Spinka, Y. (2018) Rigidity of proper colorings of ℤd. arXiv:1808.03597Google Scholar
Schmidt, K. (1995) The cohomology of higher-dimensional shifts of finite type. Pacific J. Math. 170 237–269.CrossRefGoogle Scholar
Sheffield, S. (2005) Random Surfaces (Astérisque 304). Société mathématique de France.Google Scholar