Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T21:37:31.094Z Has data issue: false hasContentIssue false
  • English
  • Français

Median Eigenvalues of Bipartite Subcubic Graphs

Part of: Graph theory

Published online by Cambridge University Press:  21 June 2016

BOJAN MOHAR
BOJAN MOHAR*
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC V5A 1S6, Canada (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

It is proved that the median eigenvalues of every connected bipartite graph G of maximum degree at most three belong to the interval [−1, 1] with a single exception of the Heawood graph, whose median eigenvalues are 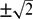$\pm\sqrt{2}$. Moreover, if G is not isomorphic to the Heawood graph, then a positive fraction of its median eigenvalues lie in the interval [−1, 1]. This surprising result has been motivated by the problem about HOMO-LUMO separation that arises in mathematical chemistry.

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 5 , September 2016 , pp. 768 - 790
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Gutman, I. and Polanski, O. E. (1986) Mathematical Concepts in Organic Chemistry, Springer.Google Scholar
[2] Fowler, P. W. and Pisanski, T. (2010) HOMO-LUMO maps for fullerenes. Acta Chim. Slov. 57 513–517.Google Scholar
[3] Fowler, P. W. and Pisanski, T. (2010) HOMO-LUMO maps for chemical graphs. MATCH Commun. Math. Comput. Chem. 64 373–390.Google Scholar
[4] Godsil, C. and Royle, G. (2001) Algebraic Graph Theory, Springer.CrossRefGoogle Scholar
[5] Jaklič, G., Fowler, P. W. and Pisanski, T. (2012) HL-index of a graph. Ars Math. Contemp. 5 99–105.Google Scholar
[6] Mohar, B. (2013) Median eigenvalues of bipartite planar graphs. MATCH Commun. Math. Comput. Chem. 70 79–84.Google Scholar
[7] Mohar, B. (2015) Median eigenvalues and the HOMO-LUMO index of graphs. J. Combin. Theory Ser. B 112 78–92.Google Scholar