Published online by Cambridge University Press: 14 May 2013
We show that the expected number of maximal empty axis-parallel boxes amidst n random points in the unit hypercube [0,1]d in 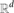 $\mathbb{R}^d$ is (1 ± o(1))
$\mathbb{R}^d$ is (1 ± o(1)) 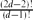 $\frac{(2d-2)!}{(d-1)!}$n lnd−1n, if d is fixed. This estimate is relevant to analysis of the performance of exact algorithms for computing the largest empty axis-parallel box amidst n given points in an axis-parallel box R, especially the algorithms that proceed by examining all maximal empty boxes. Our method for bounding the expected number of maximal empty boxes also shows that the expected number of maximal empty orthants determined by n random points in
$\frac{(2d-2)!}{(d-1)!}$n lnd−1n, if d is fixed. This estimate is relevant to analysis of the performance of exact algorithms for computing the largest empty axis-parallel box amidst n given points in an axis-parallel box R, especially the algorithms that proceed by examining all maximal empty boxes. Our method for bounding the expected number of maximal empty boxes also shows that the expected number of maximal empty orthants determined by n random points in 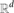 $\mathbb{R}^d$ is (1 ± o(1)) lnd−1n, if d is fixed. This estimate is related to the expected number of maximal (or minimal) points amidst random points, and has application to algorithms for coloured orthogonal range counting.
$\mathbb{R}^d$ is (1 ± o(1)) lnd−1n, if d is fixed. This estimate is related to the expected number of maximal (or minimal) points amidst random points, and has application to algorithms for coloured orthogonal range counting.