Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sambale, Holger
and
Sinulis, Arthur
2020.
Logarithmic Sobolev inequalities for finite spin systems and applications.
Bernoulli,
Vol. 26,
Issue. 3,
Erbar, Matthias
Fathi, Max
and
Schlichting, André
2020.
Entropic curvature and convergence to equilibrium for mean-field dynamics on discrete spaces
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 17,
Issue. 1,
p.
445.
Knöpfel, Holger
Löwe, Matthias
and
Sambale, Holger
2021.
Large deviations, a phase transition, and logarithmic Sobolev inequalities in the block spin Potts model.
Electronic Communications in Probability,
Vol. 26,
Issue. none,
Chen, Zongchen
Liu, Kuikui
and
Vigoda, Eric
2021.
Optimal mixing of Glauber dynamics: entropy factorization via high-dimensional expansion.
p.
1537.
Sambale, Holger
and
Sinulis, Arthur
2021.
Modified log-Sobolev inequalities and two-level concentration
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 18,
Issue. 1,
p.
855.
Eldan, Ronen
Koehler, Frederic
and
Zeitouni, Ofer
2022.
A spectral condition for spectral gap: fast mixing in high-temperature Ising models.
Probability Theory and Related Fields,
Vol. 182,
Issue. 3-4,
p.
1035.
Adamczak, Radosław
Polaczyk, Bartłomiej
and
Strzelecki, Michał
2022.
Modified log-Sobolev inequalities, Beckner inequalities and moment estimates.
Journal of Functional Analysis,
Vol. 282,
Issue. 7,
p.
109349.
De Palma, Giacomo
and
Rouzé, Cambyse
2022.
Quantum Concentration Inequalities.
Annales Henri Poincaré,
Vol. 23,
Issue. 9,
p.
3391.
Chen, Xiaoyu
Feng, Weiming
Yin, Yitong
and
Zhang, Xinyuan
2022.
Optimal mixing for two-state anti-ferromagnetic spin systems.
p.
588.
Blanca, Antonio
Caputo, Pietro
Parisi, Daniel
Sinclair, Alistair
and
Vigoda, Eric
2022.
Entropy decay in the Swendsen–Wang dynamics on Zd.
The Annals of Applied Probability,
Vol. 32,
Issue. 2,
Liu, Hongyang
and
Yin, Yitong
2022.
Simple parallel algorithms for single-site dynamics.
p.
1431.
Anari, Nima
Jain, Vishesh
Koehler, Frederic
Pham, Huy Tuan
and
Vuong, Thuy-Duong
2022.
Entropic independence: optimal mixing of down-up random walks.
p.
1418.
Blanca, Antonio
Caputo, Pietro
Chen, Zongchen
Parisi, Daniel
Štefankovič, Daniel
and
Vigoda, Eric
2022.
On mixing of Markov chains: coupling, spectral independence, and entropy factorization.
Electronic Journal of Probability,
Vol. 27,
Issue. none,
Chen, Zongchen
Liu, Kuikui
and
Vigoda, Eric
2023.
Optimal Mixing of Glauber Dynamics: Entropy Factorization via High-Dimensional Expansion.
SIAM Journal on Computing,
p.
STOC21-104.
Ganguly, Shirshendu
and
Nam, Kyeongsik
2024.
Sub-critical exponential random graphs: concentration of measure and some applications.
Transactions of the American Mathematical Society,
Koehler, Frederic
Lifshitz, Noam
Minzer, Dor
and
Mossel, Elchanan
2024.
Influences in Mixing Measures.
p.
527.
Blanca, Antonio
Chen, Zongchen
ŠTefankovič, Daniel
and
Vigoda, Eric
2025.
Complexity of High-Dimensional Identity Testing with Coordinate Conditional Sampling.
ACM Transactions on Algorithms,
Vol. 21,
Issue. 1,
p.
1.
Caputo, Pietro
Münch, Florentin
and
Salez, Justin
2025.
Entropy and curvature: Beyond the Peres-Tetali conjecture.
Transactions of the American Mathematical Society,
Liu, Hongyang
and
Yin, Yitong
2025.
Parallelize Single-Site Dynamics up to Dobrushin Criterion.
Journal of the ACM,
Vol. 72,
Issue. 1,
p.
1.
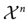 , (
, (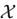 is a finite set), and any probability measure
is a finite set), and any probability measure 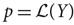 on
on 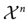 ,
(*)
,
(*)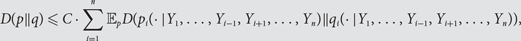 $$D(p||q){\rm{\le}}C \cdot \sum\limits_{i = 1}^n {{\rm{\mathbb{E}}}_p D(p_i ( \cdot |Y_1 ,{\rm{ }}...,{\rm{ }}Y_{i - 1} ,{\rm{ }}Y_{i + 1} ,...,{\rm{ }}Y_n )||q_i ( \cdot |Y_1 ,{\rm{ }}...,{\rm{ }}Y_{i - 1} ,{\rm{ }}Y_{i + 1} ,{\rm{ }}...,{\rm{ }}Y_n )),} $$
$$D(p||q){\rm{\le}}C \cdot \sum\limits_{i = 1}^n {{\rm{\mathbb{E}}}_p D(p_i ( \cdot |Y_1 ,{\rm{ }}...,{\rm{ }}Y_{i - 1} ,{\rm{ }}Y_{i + 1} ,...,{\rm{ }}Y_n )||q_i ( \cdot |Y_1 ,{\rm{ }}...,{\rm{ }}Y_{i - 1} ,{\rm{ }}Y_{i + 1} ,{\rm{ }}...,{\rm{ }}Y_n )),} $$

