Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
BEHRISCH, MICHAEL
COJA-OGHLAN, AMIN
and
KANG, MIHYUN
2014.
The Asymptotic Number of Connectedd-Uniform Hypergraphs.
Combinatorics, Probability and Computing,
Vol. 23,
Issue. 3,
p.
367.
Kang, Mihyun
2016.
Recent Trends in Combinatorics.
Vol. 159,
Issue. ,
p.
235.
BOLLOBÁS, BÉLA
and
RIORDAN, OLIVER
2016.
Counting Connected Hypergraphs via the Probabilistic Method.
Combinatorics, Probability and Computing,
Vol. 25,
Issue. 1,
p.
21.
Pittel, Boris
and
Poole, Daniel
2016.
Asymptotic distribution of the numbers of vertices and arcs of the giant strong component in sparse random digraphs.
Random Structures & Algorithms,
Vol. 49,
Issue. 1,
p.
3.
Bollobás, Béla
and
Riordan, Oliver
2017.
Exploring hypergraphs with martingales.
Random Structures & Algorithms,
Vol. 50,
Issue. 3,
p.
325.
COOLEY, OLIVER
KANG, MIHYUN
and
PERSON, YURY
2018.
Largest Components in Random Hypergraphs.
Combinatorics, Probability and Computing,
Vol. 27,
Issue. 5,
p.
741.
Cooley, Oliver
Kang, Mihyun
and
Koch, Christoph
2018.
The size of the giant high‐order component in random hypergraphs.
Random Structures & Algorithms,
Vol. 53,
Issue. 2,
p.
238.
Bollobás, Béla
and
Riordan, Oliver
2018.
Counting dense connected hypergraphs via the probabilistic method.
Random Structures & Algorithms,
Vol. 53,
Issue. 2,
p.
185.
Cooley, Oliver
Giudice, Nicola Del
Kang, Mihyun
and
Sprüssel, Philipp
2020.
Vanishing of cohomology groups of random simplicial complexes.
Random Structures & Algorithms,
Vol. 56,
Issue. 2,
p.
461.
Cooley, Oliver
Fang, Wenjie
Giudice, Nicola Del
and
Kang, Mihyun
2020.
Subcritical Random Hypergraphs, High-Order Components, and Hypertrees.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 4,
p.
2033.
Kang, Mihyun
Moßhammer, Michael
and
Sprüssel, Philipp
2020.
Phase transitions in graphs on orientable surfaces.
Random Structures & Algorithms,
Vol. 56,
Issue. 4,
p.
1117.
Fusy, Éric
and
Kucherov, Gregory
2023.
Algorithms and Complexity.
Vol. 13898,
Issue. ,
p.
232.
Zhou, Guangyan
and
Wang, Bin
2025.
Exploring the sharp propagation connectivity threshold in hypergraphs.
Journal of Mathematical Analysis and Applications,
Vol. 550,
Issue. 1,
p.
129509.
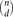 $\binom{n}{d}$ possible edges is present with probability p=p(n) independently, and let Hd(n,m) denote a uniformly distributed d-uniform hypergraph with n vertices and m edges. We derive local limit theorems for the joint distribution of the number of vertices and the number of edges in the largest component of Hd(n,p) and Hd(n,m) in the regime
$\binom{n}{d}$ possible edges is present with probability p=p(n) independently, and let Hd(n,m) denote a uniformly distributed d-uniform hypergraph with n vertices and m edges. We derive local limit theorems for the joint distribution of the number of vertices and the number of edges in the largest component of Hd(n,p) and Hd(n,m) in the regime 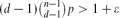 $(d-1)\binom{n-1}{d-1}p>1+\varepsilon$, resp. d(d−1)m/n>1+ϵ, where ϵ>0 is arbitrarily small but fixed as n → ∞. The proofs are based on a purely probabilistic approach.
$(d-1)\binom{n-1}{d-1}p>1+\varepsilon$, resp. d(d−1)m/n>1+ϵ, where ϵ>0 is arbitrarily small but fixed as n → ∞. The proofs are based on a purely probabilistic approach.