Hostname: page-component-5f56664f6-c65qm Total loading time: 0 Render date: 2025-05-07T19:05:45.546Z Has data issue: false hasContentIssue false
  • English
  • Français

List packing number of bounded degree graphs

Part of: Graph theory

Published online by Cambridge University Press:  18 September 2024

Stijn Cambie Open the ORCID record for Stijn Cambie [Opens in a new window] ,
Wouter Cames van Batenburg ,
Ewan Davies  and
Ross J. Kang
Stijn Cambie*
Affiliation:
Extremal Combinatorics and Probability Group (ECOPRO), Institute for Basic Science (IBS), Daejeon, South Korea Department of Computer Science, KU Leuven Campus Kulak-Kortrijk, 8500 Kortrijk, Belgium
Wouter Cames van Batenburg
Affiliation:
Delft Institute of Applied Mathematics, Delft University of Technology, Netherlands
Ewan Davies
Affiliation:
Department of Computer Science, Colorado State University, Fort Collins, USA
Ross J. Kang
Affiliation:
Korteweg–de Vries Institute for Mathematics, University of Amsterdam, Netherlands
*
Corresponding author: Stijn Cambie; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the list packing number of a graph, the least 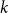$k$ such that there are always 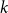$k$ disjoint proper list-colourings whenever we have lists all of size 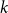$k$ associated to the vertices. We are curious how the behaviour of the list packing number contrasts with that of the list chromatic number, particularly in the context of bounded degree graphs. The main question we pursue is whether every graph with maximum degree 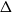$\Delta$ has list packing number at most 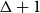$\Delta +1$. Our results highlight the subtleties of list packing and the barriers to, for example, pursuing a Brooks’-type theorem for the list packing number.

Keywords

Packing of list colouringslist packing numberlist colouringcorrespondence colouringmaximum degreetransversals

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C07: Vertex degrees 05C35: Extremal problems 05C69: Dominating sets, independent sets, cliques 05C70: Factorization, matching, partitioning, covering and packing
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 6 , November 2024 , pp. 807 - 828
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aharoni, R., Berger, E. and Ziv, R. (2007) Independent systems of representatives in weighted graphs. Combinatorica 27(3) 253–267. DOI: 10.1007/s00493-007-2086-y.CrossRefGoogle Scholar
Alon, N., Fellows, M. R. and Hare, D. R. (1996) Vertex transversals that dominate. J Graph Theory 21(1) 21–31.3.0.CO;2-O>CrossRefGoogle Scholar
Borodin, O. V. (1977) Criterion of chromaticity of a degree prescription. In:IV All-Union Conf. on Theoretical Cybernetics (Novosibirsk), pp. 27–128.Google Scholar
Cambie, S. (2022) Extremal aspects of distances and colourings in graphs, PhD thesis. Radboud University Google Scholar
Cambie, S., van Batenburg, W. Cames, Davies, E. and Kang, R. J. (2024) Packing list-colourings. Rand Struc Algorith 64(1) 62–93. to appear. arXiv: 2110.05230.CrossRefGoogle Scholar
Cambie, S. Cames van Batenburg, W. and Zhu., X. (2023) Disjoint list-colorings for planar graphs. arXiv: 2312.17233.Google Scholar
Cambie, S. and Hämäläinen, R. (2023) Packing colourings in complete bipartite graphs and the inverse problem for correspondence packing. to appear.Google Scholar
Catlin, P. A. (1980) On the Hajnal-Szemerédi theorem on disjoint cliques. Utilitas Math 17 163–177.Google Scholar
Dvořák, Z. and Postle, L. (2018) Correspondence coloring and its application to list-coloring planar graphs without cycles of lengths 4 to 8. J Combin Theory Ser B 129 38–54. DOI: 10.1016/j.jctb.2017.09.001.CrossRefGoogle Scholar
Erdős, P., Rubin, A. L. and Taylor, H. (1979) Choosability in graphs, Congress. Utilitas Math, Humboldt State Univ Arcata, California, pp. 125–157. In: Proceedings of the West Coast Conference on Combinatorics, Graph Theory and Computing.Google Scholar
Galvin, F. (1995) The List Chromatic Index of a Bipartite Multigraph. J Combin Theory Ser B 63(1) 153–158. DOI: 10.1006/jctb.1995.1011.CrossRefGoogle Scholar
Graf, A., Harris, D. G. and Haxell, P. (2021) Algorithms for weighted independent transversals and strong colouring. ACM Trans Algo 18(1) 1–16. DOI: 10.1145/3474057.Google Scholar
Graf, A. and Haxell, P. (2020) Finding independent transversals efficiently. Combin Prob Comput 29(5) 780–806. DOI: 10.1017/S0963548320000127.CrossRefGoogle Scholar
Gutner, S. and Tarsi, M. (2009) Some results on (a: b)-choosability. Discrete Math 309(8) 2260–2270. DOI: 10.1016/j.disc.2008.04.061.CrossRefGoogle Scholar
Hall, M. (1948) Distinct representatives of subsets. Bull American Math Soc 54(10) 922–926. DOI: 10.1090/S0002-9904-1948-09098-X.CrossRefGoogle Scholar
Hall, P. (1935) On representatives of subsets. J London Math Soc s1-10(1) 26–30. DOI: 10.1112/jlms/s1-10.1.128.CrossRefGoogle Scholar
Harris, D. G. (2016) Lopsidependency in the Moser-Tardos Framework: Beyond the Lopsided Lovász Local Lemma. ACM Trans Algo 13(1) 1–26. DOI: 10.1145/3015762.Google Scholar
Kelly, T. and Postle, L. (2018) Fractional coloring with local demands, DOI: 10.48550/arXiv.1811.11806.Google Scholar
Kühn, D. and Osthus, D. (2009) The minimum degree threshold for perfect graph packings. Combinatorica 29(1) 65–107. DOI: 10.48550/arXiv.1811.11806.CrossRefGoogle Scholar
Levit, M. (2018) Extensions of Galvin’s theorem, Master’s thesis. University of Waterloo Google Scholar
MacKeigan, K. (2021) Independent coverings and orthogonal colourings. Discrete Math 344(8) 112431. DOI: 10.1016/j.disc.2021.112431.CrossRefGoogle Scholar
Matula, D. W. and Beck, L. L. (1983) Smallest-last ordering and clustering and graph coloring algorithms. J Assoc Comput Mach 30(3) 417–427. DOI: 10.1145/2402.322385.CrossRefGoogle Scholar
Molloy, M. and Reed, B. (2002) Graph colouring and the probabilistic method. In: Algorithms and Combinatorics, vol. 23 Berlin, Springer-Verlag.Google Scholar
Mudrock, J. A. (2022) A short proof that the list packing number of any graph is well defined. arXiv e-prints, page arXiv: 2207.11868.Google Scholar
Schaefer, M. and Umans, C. (2002) Completeness in the polynomial-time hierarchy: A compendium. SIGACT news 33(3) 32–49.Google Scholar
van Lint, J. H. and Wilson, R. M. (1992) A course in combinatorics. Cambridge University Press, Cambridge.Google Scholar
Yuster, R. (2021) On factors of independent transversals in $k$ -partite graphs. Electron J Combin 28(4) 18. DOI: 10.37236/10529.CrossRefGoogle Scholar