Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T15:30:35.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Line-of-Sight Percolation

Published online by Cambridge University Press:  01 March 2009

BÉLA BOLLOBÁS ,
SVANTE JANSON  and
OLIVER RIORDAN
BÉLA BOLLOBÁS
Affiliation:
Department of Mathematical Sciences, University of Memphis, Memphis TN 38152, USA and Trinity College, Cambridge CB2 1TQ, UK (e-mail: [email protected])
SVANTE JANSON
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, SE-751 06 Uppsala, Sweden (e-mail: [email protected])
OLIVER RIORDAN
Affiliation:
Royal Society Research Fellow, Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK; Mathematical Institute, University of Oxford, 24–29 St Giles, Oxford OX1 3LB, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

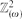Given ω ≥ 1, let be the graph with vertex set 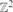in which two vertices are joined if they agree in one coordinate and differ by at most ω in the other. (Thus 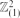is precisely 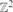.) Let pc(ω) be the critical probability for site percolation on 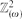. Extending recent results of Frieze, Kleinberg, Ravi and Debany, we show that limω→∞ωpc(ω)=log(3/2). We also prove analogues of this result for the n-by-n grid and in higher dimensions, the latter involving interesting connections to Gilbert's continuum percolation model. To prove our results, we explore the component of the origin in a certain non-standard way, and show that this exploration is well approximated by a certain branching random walk.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 1-2: Papers from The 2006 Oberwolfach Meeting on Combinatorics, Probability and Computing , March 2009 , pp. 83 - 106
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aizenman, M., Kesten, H. and Newman, C. M. (1987) Uniqueness of the infinite cluster and related results in percolation. In Percolation Theory and Ergodic Theory of Infinite Particle Systems, Springer, pp. 13–20.Google Scholar
[2]Athreya, K. B. and Ney, P. E. (1972) Branching Processes, Springer, Berlin.CrossRefGoogle Scholar
[3]Balister, P., Bollobás, B. and Walters, M. (2004) Continuum percolation with steps in an annulus. Ann. Appl. Probab. 14 1869–1879.CrossRefGoogle Scholar
[4]Balister, P., Bollobás, B. and Walters, M. (2005) Continuum percolation with steps in the square or the disc. Random Struct. Alg. 26 392–403.CrossRefGoogle Scholar
[5]Bollobás, B., Janson, S. and Riordan, O. (2007) The phase transition in inhomogeneous random graphs. Random Struct. Alg. 31 3–122.Google Scholar
[6]Bollobás, B., Janson, S. and Riordan, O. (2007) Spread-out percolation in . Random Struct. Alg. 31 239–246.CrossRefGoogle Scholar
[7]Bollobás, B. and Riordan, O. (2006) Percolation, Cambridge University Press.CrossRefGoogle Scholar
[8]Franceschetti, M., Booth, L., Cook, M., Meester, R. and Bruck, J. (2005) Continuum percolation with unreliable and spread-out connections. J. Statist. Phys. 118 721–734.CrossRefGoogle Scholar
[9]Frieze, A., Kleinberg, J., Ravi, R. and Debany, W. (2007) Line-of-sight networks. In Proc. 18th ACM–SIAM Symposium on Discrete Algorithms, pp. 968–977.Google Scholar
[10]Frieze, A., Kleinberg, J., Ravi, R. and Debany, W. Line-of-sight networks. Combin. Probab. Comput., to appear.Google Scholar
[11]Gilbert, E. N. (1961) Random plane networks. J. Soc. Indust. Appl. Math. 9 533–543.Google Scholar
[12]Glaz, J., Naus, J. and Wallenstein, S. (2001) Scan Statistics, Springer.Google Scholar
[13]Hall, P. (1985) On continuum percolation. Ann. Probab. 13 1250–1266.CrossRefGoogle Scholar
[14]Penrose, M. D. (1993) On the spread-out limit for bond and continuum percolation. Ann. Appl. Probab. 3 253–276.Google Scholar
[15]Stevens, W. L. (1939) Solution to a geometrical problem in probability. Ann. Eugenics 9 315–320.CrossRefGoogle Scholar