Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T23:01:25.842Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice Points of Cut Cones

Published online by Cambridge University Press:  12 September 2008

Michel Deza  and
Viatcheslav Grishukhin
Michel Deza
Affiliation:
CNRS-LIENS, Ecole Normale Supérieure, Paris
Viatcheslav Grishukhin
Affiliation:
Central Economic and Mathematical Institute of Russian Academy of Sciences (CEMI RAN), Moscow
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ℝ+(ℋn),ℤ(ℋn),ℤ+(ℋn) be, respectively, the cone over ℝ, the lattice and the cone over ℤ, generated by all cuts of the complete graph on n nodes. For i ≥ 0, let 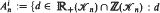has exactly i realizations in ℤ+(ℋn)}. We show that 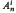is infinite, except for the undecided case 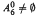and empty 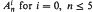and for i = 0, n ≤ 5 and for i ≥ 2, n ≤ 3. The set 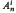contains 0,1,∞ nonsimplicial points for n ≤ 4, n = 5, n ≥ 6, respectively. On the other hand, there exists a finite number t(n) such that t(n)d ∈ ℤ+(ℋn) for any 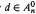; we also estimate such scales for classes of points. We construct families of points of 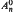and ℤ+(ℋn), especially on a 0-lifting of a simplicial facet, and points d ∈ ℝ+(ℋn) with di, n = t for 1 ≤ i ≤ n − 1.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 3 , Issue 2 , June 1994 , pp. 191 - 214
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Assouad, P. and Deza, M. (1980) Espaces métriques plongebles dans un hypercube: aspects combinatoires Annals of Discrete Math. 8 197–210.Google Scholar
[2]Avis, D. (1990) On the complexity of isometric embedding in the hypercube: In Algorithms. Springer-Verlag Lecture Notes in Computer science, 450 348–357.CrossRefGoogle Scholar
[3]Deza, M. (1960) On the Hamming geometry of unitary cubes. Doklady Academii Nauk SSSR 134, 1037–1040(in Russian)Soviet Physics Doklady (English translation) 5 940–943.Google Scholar
[4]Deza, M. (1973) Matrices de formes quadratiques non negatives pour des arguments binaires. C. R. Acad. Sci. Paris 111 873–875.Google Scholar
[5]Deza, M. (1973) Une proprieté éxtremal des plans projectifs finis dans une classe de codes equidistants. Discrete Mathematics 6 343–352.CrossRefGoogle Scholar
[6]Deza, M. and Laurent, M. (1992) Facets for the cut cone I, II. Mathematical Programming 52 121–161, 162–188.CrossRefGoogle Scholar
[7]Deza, M. and Laurent, M. (1991) Isometric hypercube embedding of generalized bipartite metrics, Research report 91706–OR, Institut für Discrete Mathematik, Universität Bonn.Google Scholar
[8]Deza, M. and Laurent, M. (1992) Extension operations for cuts. Discrete Mathematics 106–107 163–179.Google Scholar
[9]Deza, M. and Laurent, M (1992) sVariety of hypercube embeddings of the equidistant metric and designs. Journal of Combinatorics, Information and System sciences (to appear).Google Scholar
[10]Deza, M. and Laurent, M. (1993) The cut cone: simplicial faces and linear dependencies. Bulletin of the Institute of Math. Academia Sinica 21 143–182.Google Scholar
[11]Deza, M., Laurent, M. and Poljak, S. (1992) The cut cone III: on the role of triangle facets. Graphs and Combinatorics 8 125–142.CrossRefGoogle Scholar
[12]Deza, M. and Laurent, M. (1992) Applications of cut polyhedra, Research report LIENS 92–18, ENS. J. of Computational and Applied Math (to appear).Google Scholar
[13]Deza, M. and Singhi, N. M. (1988) Rigid pentagons in hypercubes. Graphs and Combinatorics 4 31–42.CrossRefGoogle Scholar
[14]Djokovic, D.Z. (1973) Distance preserving subgraphs of hypercubes. Journal of Combinatorial Theory B14 263–267.CrossRefGoogle Scholar
[15]Koolen, J. (1990) On metric properties of regular graphs, Master's thesis, Eindhoven University of Technology.Google Scholar
[16]Harary, F. (1969) Graph Theory, Addison-Wesley.CrossRefGoogle Scholar
[17]Roth, R. L. and Winkler, P. M. (1986) Collapse of the metric hierarchy for bipartite graphs. European Journal of Combinatorics 7 371–375.CrossRefGoogle Scholar
[18]Schrijver, A. (1986) Theory of linear and integer programming, Wiley.Google Scholar
[19]Shpectorov, S. V. (1993) On scale embeddings of graphs into hypercubes. European Journal of Combinatorics 14.CrossRefGoogle Scholar