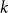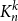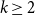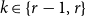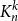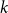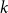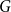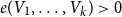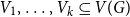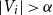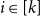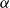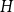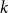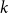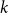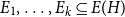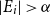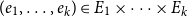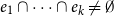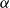1. Introduction
We say that a hypergraph
![]() $G$
is connected if the 2-shadow of
$G$
is connected if the 2-shadow of
![]() $G$
is connected (the 2-shadow of
$G$
is connected (the 2-shadow of
![]() $G$
is the graph on vertex set
$G$
is the graph on vertex set
![]() $V(G)$
and edge set
$V(G)$
and edge set
![]() $\{e\in \binom{V(G)}{2}\;:\; \exists f\in E(G), e\subseteq f\}$
). A component in a hypergraph is a maximal connected subgraph. Given a hypergraph
$\{e\in \binom{V(G)}{2}\;:\; \exists f\in E(G), e\subseteq f\}$
). A component in a hypergraph is a maximal connected subgraph. Given a hypergraph
![]() $G$
and a positive integer
$G$
and a positive integer
![]() $r$
, let
$r$
, let
![]() ${\mathrm{mc}}_r(G)$
be the largest integer
${\mathrm{mc}}_r(G)$
be the largest integer
![]() $t$
such that every
$t$
such that every
![]() $r$
-colouring of the edges of
$r$
-colouring of the edges of
![]() $G$
contains a monochromatic component of order at least
$G$
contains a monochromatic component of order at least
![]() $t$
. Let
$t$
. Let
![]() $K_n^k$
denote the complete
$K_n^k$
denote the complete
![]() $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
![]() $n$
vertices (and
$n$
vertices (and
![]() $K_n = K_n^2$
as usual). A well-studied problem has been determining the value of
$K_n = K_n^2$
as usual). A well-studied problem has been determining the value of
![]() ${\mathrm{mc}}_r(K_n^k)$
; however, this problem is still open for most values of
${\mathrm{mc}}_r(K_n^k)$
; however, this problem is still open for most values of
![]() $r$
and
$r$
and
![]() $k$
. On the other hand, Gyárfás proved the following well-known results.
$k$
. On the other hand, Gyárfás proved the following well-known results.
Theorem 1.1 (Gyárfás [Reference Gyárfás12]).
-
(i) For all
 $n\geq r\geq 2$
,
$n\geq r\geq 2$
,
 ${\mathrm{mc}}_r(K_n)\geq \frac{n}{r-1}$
. This is best possible when
${\mathrm{mc}}_r(K_n)\geq \frac{n}{r-1}$
. This is best possible when
 $(r-1)^2$
divides
$(r-1)^2$
divides
 $n$
and there exists an affine plane of order
$n$
and there exists an affine plane of order
 $r-1$
.
$r-1$
. -
(ii) For all
 $n\geq r\geq 2$
,
$n\geq r\geq 2$
,
 ${\mathrm{mc}}_r(K_n^r)=n$
.
${\mathrm{mc}}_r(K_n^r)=n$
. -
(iii) For all
 $n\geq r\geq 4$
,
$n\geq r\geq 4$
,
 ${\mathrm{mc}}_{r}(K_n^{r-1})\geq \frac{(r-1)n}{r}$
. This is best possible for all such
${\mathrm{mc}}_{r}(K_n^{r-1})\geq \frac{(r-1)n}{r}$
. This is best possible for all such
 $r$
and
$r$
and
 $n$
.
$n$
.
A natural question which has received attention lately has been to determine conditions under which a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G$
on
$G$
on
![]() $n$
vertices satisfies
$n$
vertices satisfies
![]() ${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_n^k)$
or
${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_n^k)$
or
![]() ${\mathrm{mc}}_r(G)\geq (1-o(1)){\mathrm{mc}}_r(K_n^k)$
; or, if this is too restrictive, determining the value of
${\mathrm{mc}}_r(G)\geq (1-o(1)){\mathrm{mc}}_r(K_n^k)$
; or, if this is too restrictive, determining the value of
![]() ${\mathrm{mc}}_r(G)$
in terms of some natural parameters of
${\mathrm{mc}}_r(G)$
in terms of some natural parameters of
![]() $G$
.
$G$
.
Perhaps the first such result is due to Füredi [Reference Füredi9] who proved that for all graphs
![]() $G$
on
$G$
on
![]() $n$
vertices,
$n$
vertices,
![]() ${\mathrm{mc}}_r(G)\geq \frac{n}{(r-1)\alpha (G)}$
, which is best possible when an affine plane of order
${\mathrm{mc}}_r(G)\geq \frac{n}{(r-1)\alpha (G)}$
, which is best possible when an affine plane of order
![]() $r-1$
exists (see Section 2.1.2 for more details). But note that the value of
$r-1$
exists (see Section 2.1.2 for more details). But note that the value of
![]() ${\mathrm{mc}}_r(G)$
is far from
${\mathrm{mc}}_r(G)$
is far from
![]() ${\mathrm{mc}}_r(K_n)$
in this case. In a sense that will be made precise in the coming pages, our paper is essentially a variant of Füredi’s result using a different (but related) parameter in place of independence number for which we can guarantee that
${\mathrm{mc}}_r(K_n)$
in this case. In a sense that will be made precise in the coming pages, our paper is essentially a variant of Füredi’s result using a different (but related) parameter in place of independence number for which we can guarantee that
![]() ${\mathrm{mc}}_r(G)$
is close to
${\mathrm{mc}}_r(G)$
is close to
![]() ${\mathrm{mc}}_r(K_n)$
.
${\mathrm{mc}}_r(K_n)$
.
Note that for
![]() $1\leq r\leq k$
,
$1\leq r\leq k$
,
![]() ${\mathrm{mc}}_r(G)=n={\mathrm{mc}}_r(K_n^k)$
if and only if the
${\mathrm{mc}}_r(G)=n={\mathrm{mc}}_r(K_n^k)$
if and only if the
![]() $r$
-shadow of
$r$
-shadow of
![]() $G$
is complete.Footnote
1
On the other hand, as first noted by Gyárfás and Sárközy [Reference Guggiari and Scott11], when
$G$
is complete.Footnote
1
On the other hand, as first noted by Gyárfás and Sárközy [Reference Guggiari and Scott11], when
![]() $r\gt k=2$
it is surprisingly possible for
$r\gt k=2$
it is surprisingly possible for
![]() ${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_n)$
provided
${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_n)$
provided
![]() $G$
has large enough minimum degree. See [Reference Guggiari and Scott11], [Reference Rahimi17], and [Reference Füredi and Luo10] for the best known results on this minimum degree threshold in the case
$G$
has large enough minimum degree. See [Reference Guggiari and Scott11], [Reference Rahimi17], and [Reference Füredi and Luo10] for the best known results on this minimum degree threshold in the case
![]() $k=2$
, and [Reference Bal and DeBiasio3] for a precise result on the minimum codegree threshold in the case
$k=2$
, and [Reference Bal and DeBiasio3] for a precise result on the minimum codegree threshold in the case
![]() $r=k+1\geq 4$
.
$r=k+1\geq 4$
.
For hypergraphs, Bennett, DeBiasio, Dudek, and English [Reference Bennett, DeBiasio, Dudek and English5] proved that if
![]() $G$
is an
$G$
is an
![]() $(r-1)$
-uniform hypergraph on
$(r-1)$
-uniform hypergraph on
![]() $n$
vertices with
$n$
vertices with
![]() $e(G)\geq (1-o(1))\binom{n}{r-1}$
, then
$e(G)\geq (1-o(1))\binom{n}{r-1}$
, then
![]() ${\mathrm{mc}}_{r-1}(G)\geq (1-o(1))n$
and
${\mathrm{mc}}_{r-1}(G)\geq (1-o(1))n$
and
![]() ${\mathrm{mc}}_{r}(G)\geq (\frac{r-1}{r}-o(1))n$
.
${\mathrm{mc}}_{r}(G)\geq (\frac{r-1}{r}-o(1))n$
.
As for random graphs, it was independently determined in [Reference Bal and DeBiasio2], [Reference Dudek and Prałat8] that with high probability,Footnote
2
![]() ${\mathrm{mc}}_r(G(n,p))\geq (1-o(1))\frac{n}{r-1}$
provided
${\mathrm{mc}}_r(G(n,p))\geq (1-o(1))\frac{n}{r-1}$
provided
![]() $p=\frac{\omega (1)}{n}$
, and it was determined (using the result mentioned in the previous paragraph) in [Reference Bennett, DeBiasio, Dudek and English5] that
$p=\frac{\omega (1)}{n}$
, and it was determined (using the result mentioned in the previous paragraph) in [Reference Bennett, DeBiasio, Dudek and English5] that
![]() ${\mathrm{mc}}_r(H^r(n,p))\geq (1-o(1))n$
provided
${\mathrm{mc}}_r(H^r(n,p))\geq (1-o(1))n$
provided
![]() $p=\frac{\omega (1)}{n^{r-1}}$
, and
$p=\frac{\omega (1)}{n^{r-1}}$
, and
![]() ${\mathrm{mc}}_{r}(H^{r-1}(n,p))\geq (1-o(1))\frac{(r-1)n}{r}$
provided
${\mathrm{mc}}_{r}(H^{r-1}(n,p))\geq (1-o(1))\frac{(r-1)n}{r}$
provided
![]() $p=\frac{\omega (1)}{n^{r-2}}$
. All of these results for random graphs use the sparse regularity lemma and thus only provide weak bounds on the error terms. Additionally, it was determined in [Reference DeBiasio and Tait6] that for almost all Steiner triple systems
$p=\frac{\omega (1)}{n^{r-2}}$
. All of these results for random graphs use the sparse regularity lemma and thus only provide weak bounds on the error terms. Additionally, it was determined in [Reference DeBiasio and Tait6] that for almost all Steiner triple systems
![]() $S$
on
$S$
on
![]() $n$
vertices,
$n$
vertices,
![]() ${\mathrm{mc}}_3(S)=(1-o(1))n$
. In this case, there is an explicit bound on the error term, but their result is specific to 3 colours and 3-uniform hypergraphs in which every pair of vertices is contained in at least one edge.
${\mathrm{mc}}_3(S)=(1-o(1))n$
. In this case, there is an explicit bound on the error term, but their result is specific to 3 colours and 3-uniform hypergraphs in which every pair of vertices is contained in at least one edge.
In this paper, we study a common generalisation which implies all of the results from the previous two paragraphs with more precise error terms.
1.1. Relationship between monochromatic components and partite holes
Given a hypergraph
![]() $G$
, a
$G$
, a
![]() $k$
-partite hole of size
$k$
-partite hole of size
![]() $\alpha$
is a collection of pairwise disjoint sets
$\alpha$
is a collection of pairwise disjoint sets
![]() $X_1,\ldots, X_k \subseteq V(G)$
such that
$X_1,\ldots, X_k \subseteq V(G)$
such that
![]() $|X_1|=\cdots =|X_k|=\alpha$
and no edge
$|X_1|=\cdots =|X_k|=\alpha$
and no edge
![]() $e\in E(G)$
satisfies
$e\in E(G)$
satisfies
![]() $e\cap X_i\neq \emptyset$
for all
$e\cap X_i\neq \emptyset$
for all
![]() $i\in [k].$
Define the
$i\in [k].$
Define the
![]() $k$
-partite hole number
$k$
-partite hole number
![]() $\alpha _k(G)$
to be the largest integer
$\alpha _k(G)$
to be the largest integer
![]() $\alpha$
such that
$\alpha$
such that
![]() $G$
contains an
$G$
contains an
![]() $k$
-partite hole of size
$k$
-partite hole of size
![]() $\alpha$
. Note that if
$\alpha$
. Note that if
![]() $G$
is a
$G$
is a
![]() $k$
-uniform hypergraph with
$k$
-uniform hypergraph with
![]() $\alpha _k(G)\leq \alpha$
, then for all disjoint sets
$\alpha _k(G)\leq \alpha$
, then for all disjoint sets
![]() $V_1, \ldots, V_k\subseteq V(G)$
with
$V_1, \ldots, V_k\subseteq V(G)$
with
![]() $|V_i|\gt \alpha$
for all
$|V_i|\gt \alpha$
for all
![]() $i\in [k]$
there exists
$i\in [k]$
there exists
![]() $e\in E(G)$
such that
$e\in E(G)$
such that
![]() $e\cap V_i\neq \emptyset$
for all
$e\cap V_i\neq \emptyset$
for all
![]() $i\in [k]$
. Note that this implies that
$i\in [k]$
. Note that this implies that
![]() $G$
is ‘expansive’ in a certain sense which will be made explicit in Section 2.2. As a point of comparison, note that small (ordinary) independence number does not imply expansiveness; that is, if
$G$
is ‘expansive’ in a certain sense which will be made explicit in Section 2.2. As a point of comparison, note that small (ordinary) independence number does not imply expansiveness; that is, if
![]() $G$
is a
$G$
is a
![]() $k$
-uniform hypergraph, then
$k$
-uniform hypergraph, then
![]() $\alpha (G)\leq \alpha$
does not even imply that
$\alpha (G)\leq \alpha$
does not even imply that
![]() $G$
has a connected component of order larger than
$G$
has a connected component of order larger than
![]() $\frac{n}{\alpha }$
(again, see Section 2.2 for a discussion about the relationship between
$\frac{n}{\alpha }$
(again, see Section 2.2 for a discussion about the relationship between
![]() $\alpha (G)$
and
$\alpha (G)$
and
![]() $\alpha _k(G)$
).
$\alpha _k(G)$
).
All of the results mentioned above regarding random hypergraphs and random Steiner triple systems either implicitly or explicitly make use of the fact that the
![]() $k$
-partite hole number is bounded (for further discussion, see Section 5). In this paper we consider the following general problem which attempts to pin down a more precise relationship between a
$k$
-partite hole number is bounded (for further discussion, see Section 5). In this paper we consider the following general problem which attempts to pin down a more precise relationship between a
![]() $k$
-uniform hypergraph having bounding
$k$
-uniform hypergraph having bounding
![]() $k$
-partite hole number (i.e. being ‘expansive’) and having large monochromatic components in arbitrary
$k$
-partite hole number (i.e. being ‘expansive’) and having large monochromatic components in arbitrary
![]() $r$
-colourings.
$r$
-colourings.
Problem 1.2.
Prove that for all integers
![]() $r,k\geq 2$
, there exists
$r,k\geq 2$
, there exists
![]() $c_{r,k}, d_{r,k}\gt 0$
such that for all
$c_{r,k}, d_{r,k}\gt 0$
such that for all
![]() $k$
-uniform hypergraphs
$k$
-uniform hypergraphs
![]() $G$
on
$G$
on
![]() $n$
vertices, if
$n$
vertices, if
![]() $\alpha _k(G)\lt c_{r,k} n$
, then
$\alpha _k(G)\lt c_{r,k} n$
, then
Furthermore, determine the optimal values of
![]() $c_{r,k}, d_{r,k}$
.
$c_{r,k}, d_{r,k}$
.
We solve Problem 1.2 for all
![]() $1\leq r\leq k+1$
, give the optimal values of
$1\leq r\leq k+1$
, give the optimal values of
![]() $c_{r,k}, d_{r,k}$
in the case of
$c_{r,k}, d_{r,k}$
in the case of
![]() $k=2=r$
, give the optimal value of
$k=2=r$
, give the optimal value of
![]() $c_{r,k}$
in the case
$c_{r,k}$
in the case
![]() $k=3=r$
, and give reasonable estimates on
$k=3=r$
, and give reasonable estimates on
![]() $c_{r,k}, d_{r,k}$
in the other cases. The formal statements will be given below.
$c_{r,k}, d_{r,k}$
in the other cases. The formal statements will be given below.
Our first result covers the case
![]() $k=r=2$
and thus generalises Theorem 1.1(i) in the case
$k=r=2$
and thus generalises Theorem 1.1(i) in the case
![]() $r=2$
(i.e. a graph or its complement is connected). This is the result for which we have the tightest bounds.
$r=2$
(i.e. a graph or its complement is connected). This is the result for which we have the tightest bounds.
Theorem 1.3.
-
(i) (a) For all graphs
 $G$
on
$G$
on
 $n$
vertices, if
$n$
vertices, if
 $\alpha _2(G)\lt n/6$
, then
$\alpha _2(G)\lt n/6$
, then
 ${\mathrm{mc}}_2(G)\geq n-2\alpha _2(G)$
.
${\mathrm{mc}}_2(G)\geq n-2\alpha _2(G)$
.(b)Furthermore, the bound on
 $\alpha _2(G)$
is best possible in the sense that there exists a graph on
$\alpha _2(G)$
is best possible in the sense that there exists a graph on
 $n$
vertices with
$n$
vertices with
 $\alpha _2(G)= n/6$
such that
$\alpha _2(G)= n/6$
such that
 ${\mathrm{mc}}_2(G)\leq n/3$
.
${\mathrm{mc}}_2(G)\leq n/3$
. -
(ii) For all graphs
 $G$
on
$G$
on
 $n$
vertices,
$n$
vertices,
 ${\mathrm{mc}}_2(G)\leq n-\alpha _2(G)$
.
${\mathrm{mc}}_2(G)\leq n-\alpha _2(G)$
. -
(iii) For all integers
 $n$
and
$n$
and
 $a$
with
$a$
with
 $0\leq a\leq n/4$
, there exists a graph on
$0\leq a\leq n/4$
, there exists a graph on
 $n$
vertices with
$n$
vertices with
 $\alpha _2(G)=a$
such that
$\alpha _2(G)=a$
such that
 ${\mathrm{mc}}_2(G)\leq n-2a$
.
${\mathrm{mc}}_2(G)\leq n-2a$
.
Our second result covers the case when
![]() $k=2$
and
$k=2$
and
![]() $r=3$
and thus generalises Theorem 1.1(i) in the case
$r=3$
and thus generalises Theorem 1.1(i) in the case
![]() $r=3$
. (Extending this result to the case
$r=3$
. (Extending this result to the case
![]() $r\geq 4$
is the main open problem raised by this paper. See Conjecture 4.12 and the discussion which precedes it for more details about this open case.)
$r\geq 4$
is the main open problem raised by this paper. See Conjecture 4.12 and the discussion which precedes it for more details about this open case.)
Theorem 1.4.
-
(i) For all graphs
 $G$
on
$G$
on
 $n$
vertices, if
$n$
vertices, if
 $\alpha _2(G)\leq \frac{n}{3^9}$
, then
$\alpha _2(G)\leq \frac{n}{3^9}$
, then
 ${\mathrm{mc}}_3(G)\geq \frac{n}{2}-2\alpha _2(G)$
.
${\mathrm{mc}}_3(G)\geq \frac{n}{2}-2\alpha _2(G)$
. -
(ii) For all
 $0\leq a\leq n/2$
, there exists a graph on
$0\leq a\leq n/2$
, there exists a graph on
 $n$
vertices with
$n$
vertices with
 $\alpha _2(G)=a$
such that
$\alpha _2(G)=a$
such that
 ${\mathrm{mc}}_3(G)\leq \frac{n-a}{2}$
.
${\mathrm{mc}}_3(G)\leq \frac{n-a}{2}$
.
Our third result covers the case when
![]() $k=r\geq 3$
and thus generalises Theorem 1.1(ii).
$k=r\geq 3$
and thus generalises Theorem 1.1(ii).
Theorem 1.5.
Let
![]() $r$
be an integer with
$r$
be an integer with
![]() $r\geq 3$
.
$r\geq 3$
.
-
(i) There exists
 $c_r\gt 0$
such that for all
$c_r\gt 0$
such that for all
 $r$
-uniform hypergraphs
$r$
-uniform hypergraphs
 $G$
on
$G$
on
 $n$
vertices, if
$n$
vertices, if
 $\alpha _r(G)\lt c_r n$
, then
$\alpha _r(G)\lt c_r n$
, then
 $n- \alpha _r(G)\geq{\mathrm{mc}}_r(G)\geq n-(r-1)\alpha _r(G)$
.
$n- \alpha _r(G)\geq{\mathrm{mc}}_r(G)\geq n-(r-1)\alpha _r(G)$
. -
(ii) For all
 $0 \le a \le n/(r+2)$
, there exists a
$0 \le a \le n/(r+2)$
, there exists a
 $r$
-uniform hypergraph
$r$
-uniform hypergraph
 $G$
on
$G$
on
 $n$
vertices with
$n$
vertices with
 $\alpha _r(G) = a$
such that
$\alpha _r(G) = a$
such that
 ${\mathrm{mc}}_r(G) \le n - 2\alpha _r(G)$
.
${\mathrm{mc}}_r(G) \le n - 2\alpha _r(G)$
.
Our fourth result covers the case when
![]() $r=k+1\geq 4$
and thus generalises Theorem 1.1(iii).
$r=k+1\geq 4$
and thus generalises Theorem 1.1(iii).
Theorem 1.6.
Let
![]() $r$
be an integer with
$r$
be an integer with
![]() $r\geq 4$
.
$r\geq 4$
.
-
(i) There exists
 $c_r\gt 0$
such that for all
$c_r\gt 0$
such that for all
 $(r-1)$
-uniform hypergraphs
$(r-1)$
-uniform hypergraphs
 $G$
on
$G$
on
 $n$
vertices, if
$n$
vertices, if
 $\alpha _{r-1}(G)\lt c_r n$
, then
$\alpha _{r-1}(G)\lt c_r n$
, then
 ${\mathrm{mc}}_{r}(G)\geq \frac{r-1}{r}n-\binom{r}{2} \alpha _{r-1}(G)$
.
${\mathrm{mc}}_{r}(G)\geq \frac{r-1}{r}n-\binom{r}{2} \alpha _{r-1}(G)$
. -
(ii) For all
 $0\leq a\leq n/(r-1)$
, there exists an
$0\leq a\leq n/(r-1)$
, there exists an
 $(r-1)$
-uniform hypergraph on
$(r-1)$
-uniform hypergraph on
 $n$
vertices with
$n$
vertices with
 $\alpha _{r-1}(G)=a$
such that
$\alpha _{r-1}(G)=a$
such that
 ${\mathrm{mc}}_{r}(G)\leq \frac{r-1}{r}(n-a)$
.
${\mathrm{mc}}_{r}(G)\leq \frac{r-1}{r}(n-a)$
.
While this is not the main focus of the current paper, it would also be interesting to improve the error terms in the above theorems. In particular, for Theorem 1.5 we currently have (in the context of Problem 1.2) that
![]() $2\le d_{r,r}\le (r-1)$
.
$2\le d_{r,r}\le (r-1)$
.
Regarding upper bounds on
![]() ${\mathrm{mc}}_r(G)$
, note that because of the results mentioned above regarding (hyper)graphs with large minimum (co)degree, when
${\mathrm{mc}}_r(G)$
, note that because of the results mentioned above regarding (hyper)graphs with large minimum (co)degree, when
![]() $r=k+1\geq 3$
we can’t necessarily get a
$r=k+1\geq 3$
we can’t necessarily get a
![]() $d^{\prime}_{r,k}\gt 0$
such that
$d^{\prime}_{r,k}\gt 0$
such that
![]() ${\mathrm{mc}}_r(G)\leq{\mathrm{mc}}_r(K_n)-d^{\prime}_{r,k}\alpha _k(G)$
(because it is possible to have large minimum (co)degree and large
${\mathrm{mc}}_r(G)\leq{\mathrm{mc}}_r(K_n)-d^{\prime}_{r,k}\alpha _k(G)$
(because it is possible to have large minimum (co)degree and large
![]() $\alpha _k(G)$
). However, when
$\alpha _k(G)$
). However, when
![]() $r=k$
, it is the case that
$r=k$
, it is the case that
![]() ${\mathrm{mc}}_r(G)\leq{\mathrm{mc}}_r(K_n^r)-\alpha _r(G)$
(see Observation 3.1).
${\mathrm{mc}}_r(G)\leq{\mathrm{mc}}_r(K_n^r)-\alpha _r(G)$
(see Observation 3.1).
1.2. Corollaries
As mentioned earlier, there have been a number of results showing that
![]() ${\mathrm{mc}}_r(H^k(n,p))=$
${\mathrm{mc}}_r(H^k(n,p))=$
![]() $(1-o(1)){\mathrm{mc}}_r(K_n^k)$
where
$(1-o(1)){\mathrm{mc}}_r(K_n^k)$
where
![]() $H^k(n,p)$
is the binomial random
$H^k(n,p)$
is the binomial random
![]() $k$
-uniform hypergraph. However, those results have all used the sparse regularity lemma and thus there are no reasonable estimates on the error terms. Since the value of
$k$
-uniform hypergraph. However, those results have all used the sparse regularity lemma and thus there are no reasonable estimates on the error terms. Since the value of
![]() $\alpha _k(H^k(n,p))$
is easy to estimate, we automatically recover
$\alpha _k(H^k(n,p))$
is easy to estimate, we automatically recover
![]() ${\mathrm{mc}}_r(H^k(n,p))=(1-o(1)){\mathrm{mc}}_r(K_n^k)$
(for all values of
${\mathrm{mc}}_r(H^k(n,p))=(1-o(1)){\mathrm{mc}}_r(K_n^k)$
(for all values of
![]() $k$
and
$k$
and
![]() $r$
for which Theorems 1.3
–1.6 hold) with very good estimates on the error terms.
$r$
for which Theorems 1.3
–1.6 hold) with very good estimates on the error terms.
Corollary 1.7.
For all
![]() $r\ge 2$
and
$r\ge 2$
and
![]() $p = \frac{d}{n^{r-1}}$
with
$p = \frac{d}{n^{r-1}}$
with
![]() $d\to \infty$
, we have that with high probability,
$d\to \infty$
, we have that with high probability,
 \begin{equation*}{\mathrm {mc}}_r(H^r(n,p)) = n-\Theta _r\left ( \left ( \frac {\log d}{d} \right )^{\frac {1}{r-1}}n \right ).\end{equation*}
\begin{equation*}{\mathrm {mc}}_r(H^r(n,p)) = n-\Theta _r\left ( \left ( \frac {\log d}{d} \right )^{\frac {1}{r-1}}n \right ).\end{equation*}
Additionally,
and for all
![]() $r\ge 3$
,
$r\ge 3$
,
 \begin{equation*}{\mathrm {mc}}_{r+1}(H^{r}(n,p)) \ge \frac {r}{r+1}n - O_r\left ( \left ( \frac {\log d}{d} \right )^{\frac {1}{r-1}}n \right )\end{equation*}
\begin{equation*}{\mathrm {mc}}_{r+1}(H^{r}(n,p)) \ge \frac {r}{r+1}n - O_r\left ( \left ( \frac {\log d}{d} \right )^{\frac {1}{r-1}}n \right )\end{equation*}
Proof. The statements above follow from Theorems 1.3
–1.6 and the fact that for
![]() $p$
as in the statement, w.h.p.,
$p$
as in the statement, w.h.p.,
![]() $\alpha _r(H^r(n,p)) = \Theta _r\left ( \left ( \frac{\log d}{d} \right )^{\frac{1}{r-1}}n \right )$
. The upper bound can be shown using a standard first moment calculation. The lower bound follows by taking an independent set of size
$\alpha _r(H^r(n,p)) = \Theta _r\left ( \left ( \frac{\log d}{d} \right )^{\frac{1}{r-1}}n \right )$
. The upper bound can be shown using a standard first moment calculation. The lower bound follows by taking an independent set of size
![]() $\Theta _r\left ( \left ( \frac{\log d}{d} \right )^{\frac{1}{r-1}}n \right )$
and partitioning it into
$\Theta _r\left ( \left ( \frac{\log d}{d} \right )^{\frac{1}{r-1}}n \right )$
and partitioning it into
![]() $r$
equal sized sets (see Observation 2.2). Independent sets of this size are known to exist (see e.g. [Reference Krivelevich and Sudakov15]).
$r$
equal sized sets (see Observation 2.2). Independent sets of this size are known to exist (see e.g. [Reference Krivelevich and Sudakov15]).
See Observation 3.6 and Problem 3.7 for a discussion about upper bounds on the terms in the second and third statements.
Let
![]() $\mathcal{S}_n$
be the family of all Steiner triple systems on
$\mathcal{S}_n$
be the family of all Steiner triple systems on
![]() $n$
vertices. DeBiasio and Tait [Reference DeBiasio and Tait6] proved that for all 3-uniform hypergraphs
$n$
vertices. DeBiasio and Tait [Reference DeBiasio and Tait6] proved that for all 3-uniform hypergraphs
![]() $G$
on
$G$
on
![]() $n$
vertices in which every pair of vertices is contained in at least one edge,
$n$
vertices in which every pair of vertices is contained in at least one edge,
![]() ${\mathrm{mc}}_3(G)\geq n-2\alpha _3(G)$
(note that Theorem 1.5(i) is stronger in the sense that there is no requirement that every pair of vertices is contained in at least one edge). They used this to prove that for all
${\mathrm{mc}}_3(G)\geq n-2\alpha _3(G)$
(note that Theorem 1.5(i) is stronger in the sense that there is no requirement that every pair of vertices is contained in at least one edge). They used this to prove that for all
![]() $S\in \mathcal{S}_n$
,
$S\in \mathcal{S}_n$
,
![]() ${\mathrm{mc}}_3(S)\geq 2n/3+1$
, and furthermore there exists
${\mathrm{mc}}_3(S)\geq 2n/3+1$
, and furthermore there exists
![]() $\delta \gt 0$
such that for almost all
$\delta \gt 0$
such that for almost all
![]() $S\in \mathcal{S}_n$
,
$S\in \mathcal{S}_n$
,
![]() ${\mathrm{mc}}_3(S)\geq n-n^{1-\delta }$
. This latter result was proved by showing that for almost all
${\mathrm{mc}}_3(S)\geq n-n^{1-\delta }$
. This latter result was proved by showing that for almost all
![]() $S\in \mathcal{S}_n$
,
$S\in \mathcal{S}_n$
,
![]() $\alpha _3(S)\leq n^{1-\delta }$
. Gyárfás [Reference Gyárfás13] proved in particular that for all
$\alpha _3(S)\leq n^{1-\delta }$
. Gyárfás [Reference Gyárfás13] proved in particular that for all
![]() $S\in \mathcal{S}_n$
,
$S\in \mathcal{S}_n$
,
![]() ${\mathrm{mc}}_4(S)\geq \frac{n}{3}$
(and this is best possible for infinitely many
${\mathrm{mc}}_4(S)\geq \frac{n}{3}$
(and this is best possible for infinitely many
![]() $n$
). On the other hand, we show that for almost all
$n$
). On the other hand, we show that for almost all
![]() $S\in \mathcal{S}_n$
, the value of
$S\in \mathcal{S}_n$
, the value of
![]() ${\mathrm{mc}}_4(S)$
is much larger. More precisely, using the fact (from [Reference DeBiasio and Tait6]) that for almost all
${\mathrm{mc}}_4(S)$
is much larger. More precisely, using the fact (from [Reference DeBiasio and Tait6]) that for almost all
![]() $S\in \mathcal{S}_n$
,
$S\in \mathcal{S}_n$
,
![]() $\alpha _3(S)\leq n^{1-\delta }$
, we obtain the following corollary of Theorem 1.6(i) (with
$\alpha _3(S)\leq n^{1-\delta }$
, we obtain the following corollary of Theorem 1.6(i) (with
![]() $r=4$
).
$r=4$
).
Corollary 1.8.
There exists
![]() $\delta \gt 0$
such that for almost all
$\delta \gt 0$
such that for almost all
![]() $S\in \mathcal{S}_n$
,
$S\in \mathcal{S}_n$
,
![]() ${\mathrm{mc}}_4(S)\geq \frac{3n}{4}-O(n^{1-\delta })$
.
${\mathrm{mc}}_4(S)\geq \frac{3n}{4}-O(n^{1-\delta })$
.
1.3. Outline of paper
In Section 2.1, we discuss a reformulation of our problem in the dual language of
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform hypergraphs which we will work with for the remainder of the paper. In Section 2.2, we discuss a reformulation of the notion of having bounded
$r$
-uniform hypergraphs which we will work with for the remainder of the paper. In Section 2.2, we discuss a reformulation of the notion of having bounded
![]() $k$
-partite holes in terms of expansion in hypergraphs. In Section 3, we provide examples which show the tightness of our results. In particular, this section contains proofs of Theorem 1.3(i)(b), (ii), (iii), Theorem 1.4 (ii), Theorem 1.5 (ii) and Theorem 1.6 (ii). In Section 4, we prove Theorem 1.3(i)(a), Theorem 1.4(i), Theorem 1.5(i), and Theorem 1.6(i).
$k$
-partite holes in terms of expansion in hypergraphs. In Section 3, we provide examples which show the tightness of our results. In particular, this section contains proofs of Theorem 1.3(i)(b), (ii), (iii), Theorem 1.4 (ii), Theorem 1.5 (ii) and Theorem 1.6 (ii). In Section 4, we prove Theorem 1.3(i)(a), Theorem 1.4(i), Theorem 1.5(i), and Theorem 1.6(i).
2. Duality and expansion
2.1. Duality
Throughout the rest of the paper we will be talking about multi-hypergraphs and we will always assume that all of the edges are distinguishable (and more generally, we assume that all of the elements in a multi-set are distinguishable). This means, for example, that if an edge has multiplicity
![]() $5$
, we can partition those five edges into two disjoint sets of say
$5$
, we can partition those five edges into two disjoint sets of say
![]() $3$
and
$3$
and
![]() $2$
edges respectively.
$2$
edges respectively.
Let
![]() $r,k\geq 2$
be integers. Given an
$r,k\geq 2$
be integers. Given an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph
$r$
-uniform multi-hypergraph
![]() $H$
and multisets of edges
$H$
and multisets of edges
![]() $E_1, \ldots, E_k$
, we say that
$E_1, \ldots, E_k$
, we say that
![]() $E_1, \ldots, E_k$
is cross-intersecting if there exists
$E_1, \ldots, E_k$
is cross-intersecting if there exists
![]() $(e_1, e_2, \ldots, e_k)\in E_1\times E_2\times \cdots \times E_k$
such that
$(e_1, e_2, \ldots, e_k)\in E_1\times E_2\times \cdots \times E_k$
such that
![]() $e_1\cap \cdots \cap e_k\neq \emptyset$
. Furthermore, if
$e_1\cap \cdots \cap e_k\neq \emptyset$
. Furthermore, if
![]() $S\subseteq V(H)$
, we say that
$S\subseteq V(H)$
, we say that
![]() $E_1, \ldots, E_k$
is cross-intersecting in
$E_1, \ldots, E_k$
is cross-intersecting in
![]() $S$
if there exists
$S$
if there exists
![]() $(e_1, e_2, \ldots, e_k)\in E_1\times E_2\times \cdots \times E_k$
such that
$(e_1, e_2, \ldots, e_k)\in E_1\times E_2\times \cdots \times E_k$
such that
![]() $S\cap e_1\cap \cdots \cap e_k\neq \emptyset$
.
$S\cap e_1\cap \cdots \cap e_k\neq \emptyset$
.
Let
![]() $\nu _k(H)$
be the largest integer
$\nu _k(H)$
be the largest integer
![]() $m$
such that there exists multisets of edges
$m$
such that there exists multisets of edges
![]() $E_1, \ldots, E_k$
with
$E_1, \ldots, E_k$
with
![]() $|E_i|=m$
for all
$|E_i|=m$
for all
![]() $i\in [k]$
and
$i\in [k]$
and
![]() $E_i\cap E_j=\emptyset$
for all distinct
$E_i\cap E_j=\emptyset$
for all distinct
![]() $i,j\in [k]$
such that
$i,j\in [k]$
such that
![]() $E_1, \ldots, E_k$
is not cross-intersecting; that is,
$E_1, \ldots, E_k$
is not cross-intersecting; that is,
![]() $e_1\cap e_2\cap \cdots \cap e_k=\emptyset$
for all
$e_1\cap e_2\cap \cdots \cap e_k=\emptyset$
for all
![]() $e_1\in E_1$
,
$e_1\in E_1$
,
![]() $e_2\in E_2$
,
$e_2\in E_2$
,
![]() $\ldots$
,
$\ldots$
,
![]() $e_k\in E_k$
.
$e_k\in E_k$
.
2.1.1. Monochromatic components and
 $k$
-partite holes
$k$
-partite holes
The following observation precisely describes what we mean by ‘duality’.
Observation 2.1 (Duality). Let
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $r,k\geq 2$
, and
$r,k\geq 2$
, and
![]() $s,t\geq 0$
. The following are equivalent:
$s,t\geq 0$
. The following are equivalent:
-
(i) Let
 $H$
be an
$H$
be an
 $r$
-partite
$r$
-partite
 $r$
-uniform multi-hypergraph with
$r$
-uniform multi-hypergraph with
 $n$
edges. If
$n$
edges. If
 $\nu _k(H)\leq s$
, then
$\nu _k(H)\leq s$
, then
 $\Delta (H)\geq t$
.
$\Delta (H)\geq t$
. -
(ii) Let
 $G$
be a
$G$
be a
 $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
 $n$
vertices. If
$n$
vertices. If
 $\alpha _k(G)\leq s$
, then
$\alpha _k(G)\leq s$
, then
 ${\mathrm{mc}}_r(G)\geq t$
${\mathrm{mc}}_r(G)\geq t$
Proof. ((i)
![]() $\Rightarrow$
(ii)) Suppose that (i) holds and let
$\Rightarrow$
(ii)) Suppose that (i) holds and let
![]() $G$
be a
$G$
be a
![]() $k$
-uniform hypergraph with
$k$
-uniform hypergraph with
![]() $\alpha _k(G)\leq s$
. Suppose we are given an
$\alpha _k(G)\leq s$
. Suppose we are given an
![]() $r$
-colouring of
$r$
-colouring of
![]() $G$
. We will use the
$G$
. We will use the
![]() $r$
-coloured hypergraph
$r$
-coloured hypergraph
![]() $G$
to define an
$G$
to define an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph having the property that
$r$
-uniform multi-hypergraph having the property that
![]() $\nu _k(H)\leq \alpha _k(G)\leq s$
and every vertex in
$\nu _k(H)\leq \alpha _k(G)\leq s$
and every vertex in
![]() $H$
with degree
$H$
with degree
![]() $d$
corresponds to a monochromatic component in
$d$
corresponds to a monochromatic component in
![]() $G$
with order
$G$
with order
![]() $d$
.
$d$
.
For all
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $C^i_1, \ldots, C^i_{k_i}$
be the components of
$C^i_1, \ldots, C^i_{k_i}$
be the components of
![]() $G$
of colour
$G$
of colour
![]() $i$
(note that a vertex which is incident with no edges of colour
$i$
(note that a vertex which is incident with no edges of colour
![]() $i$
is itself a component of colour
$i$
is itself a component of colour
![]() $i$
). Let
$i$
). Let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with parts
$r$
-uniform multi-hypergraph with parts
![]() $C^i=\{C^i_1, \ldots, C^i_{k_i}\}$
for all
$C^i=\{C^i_1, \ldots, C^i_{k_i}\}$
for all
![]() $i\in [r]$
where
$i\in [r]$
where
![]() $\{C^1_{j_1},\ldots, C^r_{j_r}\} \in E(H)$
is an edge of multiplicity
$\{C^1_{j_1},\ldots, C^r_{j_r}\} \in E(H)$
is an edge of multiplicity
![]() $m$
if and only if
$m$
if and only if
![]() $|\bigcap _{i\in [r]} V(C^i_{j_i})|=m$
(in
$|\bigcap _{i\in [r]} V(C^i_{j_i})|=m$
(in
![]() $G$
); note that an edge of multiplicity 0 just means a non-edge. Note that
$G$
); note that an edge of multiplicity 0 just means a non-edge. Note that
![]() $V(G)=E(H)$
since every vertex in
$V(G)=E(H)$
since every vertex in
![]() $G$
is in exactly one component of each colour. If there exists
$G$
is in exactly one component of each colour. If there exists
![]() $E_1, E_2, \ldots, E_k\subseteq E(H)$
such that
$E_1, E_2, \ldots, E_k\subseteq E(H)$
such that
![]() $E_i\cap E_j=\emptyset$
for all distinct
$E_i\cap E_j=\emptyset$
for all distinct
![]() $i,j\in [k]$
and
$i,j\in [k]$
and
![]() $e_1\cap e_2\cap \cdots \cap e_k=\emptyset$
for all
$e_1\cap e_2\cap \cdots \cap e_k=\emptyset$
for all
![]() $(e_1, \ldots, e_k)\in E_1\times \cdots \times E_k$
, then
$(e_1, \ldots, e_k)\in E_1\times \cdots \times E_k$
, then
![]() $e_G(E_1, E_2, \ldots, E_k)=0$
because any such edge intersecting all of
$e_G(E_1, E_2, \ldots, E_k)=0$
because any such edge intersecting all of
![]() $E_1, \ldots, E_k$
(in
$E_1, \ldots, E_k$
(in
![]() $G$
) would violate
$G$
) would violate
![]() $e_1\cap e_2\cap \cdots \cap e_k=\emptyset$
(in
$e_1\cap e_2\cap \cdots \cap e_k=\emptyset$
(in
![]() $H$
). So we have
$H$
). So we have
![]() $\nu _k(H)\leq \alpha _k(G)\leq s$
which by the assumption implies
$\nu _k(H)\leq \alpha _k(G)\leq s$
which by the assumption implies
![]() $\Delta (H)\geq t$
. Without loss of generality, suppose
$\Delta (H)\geq t$
. Without loss of generality, suppose
![]() $d_H(C^1_1)=\Delta (H)\geq t$
which means
$d_H(C^1_1)=\Delta (H)\geq t$
which means
![]() $C^1_1$
is a component of colour
$C^1_1$
is a component of colour
![]() $1$
in
$1$
in
![]() $G$
with at least
$G$
with at least
![]() $t$
vertices.
$t$
vertices.
((ii)
![]() $\Rightarrow$
(i)) Suppose that (ii) holds and let
$\Rightarrow$
(i)) Suppose that (ii) holds and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with
$r$
-uniform multi-hypergraph with
![]() $\nu _k(H)\leq s$
and let the parts of
$\nu _k(H)\leq s$
and let the parts of
![]() $H$
be labelled as
$H$
be labelled as
![]() $C^i=\{C^i_1, \ldots, C^i_{k_i}\}$
for all
$C^i=\{C^i_1, \ldots, C^i_{k_i}\}$
for all
![]() $i\in [r]$
(so we have
$i\in [r]$
(so we have
![]() $V(H)=\cup _{i\in [r]}C^i$
). We will use the
$V(H)=\cup _{i\in [r]}C^i$
). We will use the
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph
$r$
-uniform multi-hypergraph
![]() $H$
to define an
$H$
to define an
![]() $r$
-coloured
$r$
-coloured
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G$
having the property that
$G$
having the property that
![]() $\alpha _k(G)\leq \nu _k(H)\leq s$
and where the components of colour
$\alpha _k(G)\leq \nu _k(H)\leq s$
and where the components of colour
![]() $i$
in
$i$
in
![]() $G$
correspond to the vertices
$G$
correspond to the vertices
![]() $C^i=\{C^i_1, \ldots, C^i_{k_i}\}$
in such a way that the order of the component in
$C^i=\{C^i_1, \ldots, C^i_{k_i}\}$
in such a way that the order of the component in
![]() $G$
corresponding to
$G$
corresponding to
![]() $C^i_{i_j}$
is equal to the degree (in
$C^i_{i_j}$
is equal to the degree (in
![]() $H$
) of
$H$
) of
![]() $C^i_{i_j}$
.
$C^i_{i_j}$
.
Let
![]() $G$
be an
$G$
be an
![]() $r$
-edge coloured
$r$
-edge coloured
![]() $k$
-uniform hypergraph with
$k$
-uniform hypergraph with
![]() $V(G)=E(H)$
where
$V(G)=E(H)$
where
![]() $\{e_1,\ldots, e_k\}\in E(G)$
and of colour
$\{e_1,\ldots, e_k\}\in E(G)$
and of colour
![]() $i$
if and only if
$i$
if and only if
![]() $(e_1\cap \cdots \cap e_k)\cap C^i\neq \emptyset$
(in
$(e_1\cap \cdots \cap e_k)\cap C^i\neq \emptyset$
(in
![]() $H$
); note that an edge of
$H$
); note that an edge of
![]() $G$
may receive multiple colours. Consider a component of colour
$G$
may receive multiple colours. Consider a component of colour
![]() $i$
in
$i$
in
![]() $G$
(the vertex set of which corresponds to a collection of edges in
$G$
(the vertex set of which corresponds to a collection of edges in
![]() $H$
). By the definition of connectivity in hypergraphs, these edges of
$H$
). By the definition of connectivity in hypergraphs, these edges of
![]() $H$
must all pairwise intersect in
$H$
must all pairwise intersect in
![]() $C^i$
and since
$C^i$
and since
![]() $H$
is
$H$
is
![]() $r$
-partite, they must pairwise intersect in a single vertex
$r$
-partite, they must pairwise intersect in a single vertex
![]() $C^i_{i_j}$
of
$C^i_{i_j}$
of
![]() $C^i$
(and in this way, we can say that there is a bijection between the monochromatic components of
$C^i$
(and in this way, we can say that there is a bijection between the monochromatic components of
![]() $G$
and the vertices of
$G$
and the vertices of
![]() $H$
). Now, if
$H$
). Now, if
![]() $E_1,E_2, \ldots, E_k\subseteq V(G)$
such that
$E_1,E_2, \ldots, E_k\subseteq V(G)$
such that
![]() $e_G(E_1, E_2, \ldots, E_k)=0$
, then
$e_G(E_1, E_2, \ldots, E_k)=0$
, then
![]() $\bigcap _{i\in [k]}(\bigcup _{e\in E_i} e)=\emptyset$
(in
$\bigcap _{i\in [k]}(\bigcup _{e\in E_i} e)=\emptyset$
(in
![]() $H$
). So we have
$H$
). So we have
![]() $\alpha _k(G)\leq \nu _k(H)\leq s$
, which by the assumption implies that
$\alpha _k(G)\leq \nu _k(H)\leq s$
, which by the assumption implies that
![]() $G$
has a monochromatic component of order at least
$G$
has a monochromatic component of order at least
![]() $t$
. Without loss of generality suppose this monochromatic component corresponds to
$t$
. Without loss of generality suppose this monochromatic component corresponds to
![]() $C^1_1$
and thus by the comments above, we have that
$C^1_1$
and thus by the comments above, we have that
![]() $C_1^1$
has degree at least
$C_1^1$
has degree at least
![]() $t$
.
$t$
.
2.1.2. Monochromatic components and independence number
For expository reasons and as a comparison to the result in the last subsection, we describe Füredi’s classic example of the use of duality.
For a hypergraph
![]() $H$
, let
$H$
, let
![]() $\tau (H)$
denote the vertex cover number, let
$\tau (H)$
denote the vertex cover number, let
![]() $\nu (H)$
denote the matching number and let
$\nu (H)$
denote the matching number and let
![]() $\tau ^*(H)$
and
$\tau ^*(H)$
and
![]() $\nu ^*(H)$
denote the respective fractional versions. Ryser conjectured that for every
$\nu ^*(H)$
denote the respective fractional versions. Ryser conjectured that for every
![]() $r$
-partite (multi)hypergraph
$r$
-partite (multi)hypergraph
![]() $H$
,
$H$
,
![]() $\tau (H)\leq (r-1)\nu (H)$
. Füredi [Reference Füredi9] proved a fractional version; that is, for every
$\tau (H)\leq (r-1)\nu (H)$
. Füredi [Reference Füredi9] proved a fractional version; that is, for every
![]() $r$
-partite (multi)hypergraph
$r$
-partite (multi)hypergraph
![]() $H$
,
$H$
,
![]() $\tau ^*(H)\leq (r-1)\nu (H)$
. Now since
$\tau ^*(H)\leq (r-1)\nu (H)$
. Now since
it follows that for every
![]() $r$
-partite (multi)hypergraph
$r$
-partite (multi)hypergraph
![]() $H$
with
$H$
with
![]() $n$
edges,
$n$
edges,
![]() $\Delta (H)\geq \frac{n}{(r-1)\nu (H)}$
. In the dual language, this says for every graph
$\Delta (H)\geq \frac{n}{(r-1)\nu (H)}$
. In the dual language, this says for every graph
![]() $G$
on
$G$
on
![]() $n$
vertices,
$n$
vertices,
![]() ${\mathrm{mc}}_r(G)\geq \frac{n}{(r-1)\alpha (G)}$
.
${\mathrm{mc}}_r(G)\geq \frac{n}{(r-1)\alpha (G)}$
.
2.2. Expansion
The purpose of this section is formalise what we mean when we say that
![]() $k$
-uniform hypergraphs with small
$k$
-uniform hypergraphs with small
![]() $k$
-partite hole number are ‘expansive’.
$k$
-partite hole number are ‘expansive’.
Let
![]() $G$
be a
$G$
be a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G$
on
$G$
on
![]() $n$
vertices and let
$n$
vertices and let
![]() $S_1, \ldots, S_{k-1}\subseteq V(G)$
. Define
$S_1, \ldots, S_{k-1}\subseteq V(G)$
. Define
![]() $N(S_1,\ldots, S_{k-1})=\{v\;:\; \{v_1, \ldots, v_{k-1}, v\}\in E(G), v_i\in S_i \text{ for all } i\in [k-1]\}$
and
$N(S_1,\ldots, S_{k-1})=\{v\;:\; \{v_1, \ldots, v_{k-1}, v\}\in E(G), v_i\in S_i \text{ for all } i\in [k-1]\}$
and
![]() $N^+(S_1,\ldots, S_{k-1})=\{v\in V(G)\setminus (S_1\cup \cdots \cup S_{k-1})\;:\; \{v_1, \ldots, v_{k-1}, v\}\in E(G), v_i\in S_i \text{ for all } i\in [k-1]\}$
.
$N^+(S_1,\ldots, S_{k-1})=\{v\in V(G)\setminus (S_1\cup \cdots \cup S_{k-1})\;:\; \{v_1, \ldots, v_{k-1}, v\}\in E(G), v_i\in S_i \text{ for all } i\in [k-1]\}$
.
We say that a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G$
on
$G$
on
![]() $n$
vertices is a
$n$
vertices is a
![]() $(p,q)$
-expander if for all sets
$(p,q)$
-expander if for all sets
![]() $S_1, \ldots, S_{k-1}\subseteq V(G)$
with
$S_1, \ldots, S_{k-1}\subseteq V(G)$
with
![]() $|S_i|\gt p$
for all
$|S_i|\gt p$
for all
![]() $i\in [k-1]$
, we have
$i\in [k-1]$
, we have
![]() $|N(S_1, \ldots, S_{k-1})|\geq q$
.
$|N(S_1, \ldots, S_{k-1})|\geq q$
.
We say that a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G$
on
$G$
on
![]() $n$
vertices is a
$n$
vertices is a
![]() $(p,q)$
-outer-expander if for all disjoint sets
$(p,q)$
-outer-expander if for all disjoint sets
![]() $S_1, \ldots, S_{k-1}\subseteq V(G)$
with
$S_1, \ldots, S_{k-1}\subseteq V(G)$
with
![]() $|S_i|\gt p$
for all
$|S_i|\gt p$
for all
![]() $i\in [k-1]$
, we have
$i\in [k-1]$
, we have
![]() $|N^+(S_1, \ldots, S_{k-1})|+|S_1\cup \cdots \cup S_{k-1}|\geq q$
.
$|N^+(S_1, \ldots, S_{k-1})|+|S_1\cup \cdots \cup S_{k-1}|\geq q$
.
Given a hypergraph
![]() $G$
and an integer
$G$
and an integer
![]() $r\geq 2$
, let
$r\geq 2$
, let
![]() $\hat{\alpha }_r(G)$
be the largest integer
$\hat{\alpha }_r(G)$
be the largest integer
![]() $a$
such that there exists (not-necessarily disjoint) sets
$a$
such that there exists (not-necessarily disjoint) sets
![]() $V_1, \ldots, V_r$
with
$V_1, \ldots, V_r$
with
![]() $|V_i|=a$
for all
$|V_i|=a$
for all
![]() $i\in [r]$
such that there are no edges
$i\in [r]$
such that there are no edges
![]() $e$
such that
$e$
such that
![]() $e\cap V_i\neq \emptyset$
for all
$e\cap V_i\neq \emptyset$
for all
![]() $i\in [r]$
.
$i\in [r]$
.
We first make an observation regarding the relationship between
![]() $\alpha _k(G)$
,
$\alpha _k(G)$
,
![]() $\hat{\alpha }_k(G)$
,
$\hat{\alpha }_k(G)$
,
![]() $\alpha (G)$
. One takeaway from this observation is that it would make very little difference in our results if we considered bounding
$\alpha (G)$
. One takeaway from this observation is that it would make very little difference in our results if we considered bounding
![]() $\hat{\alpha }_k(G)$
instead of
$\hat{\alpha }_k(G)$
instead of
![]() $\alpha _k(G)$
. However, it is possible for
$\alpha _k(G)$
. However, it is possible for
![]() $\alpha (G)$
to be small and
$\alpha (G)$
to be small and
![]() $\alpha _k(G)$
to be large (the disjoint union of cliques of order
$\alpha _k(G)$
to be large (the disjoint union of cliques of order
![]() $n/k$
for instance), so it makes a big difference if we were to consider bounding
$n/k$
for instance), so it makes a big difference if we were to consider bounding
![]() $\alpha (G)$
instead of
$\alpha (G)$
instead of
![]() $\alpha _k(G)$
.
$\alpha _k(G)$
.
Observation 2.2.
For all
![]() $k$
-uniform hypergraphs
$k$
-uniform hypergraphs
![]() $G$
,
$G$
,
Proof. First note that if
![]() $S$
is an independent set, then by letting
$S$
is an independent set, then by letting
![]() $V_1=\cdots =V_k=S$
, we have
$V_1=\cdots =V_k=S$
, we have
![]() $\hat{\alpha }_k(G)\geq |S|$
. So
$\hat{\alpha }_k(G)\geq |S|$
. So
![]() $\alpha (G)\leq \hat{\alpha }_k(G)$
. Also we clearly have
$\alpha (G)\leq \hat{\alpha }_k(G)$
. Also we clearly have
![]() $\alpha _k(G)\leq \hat{\alpha }_k(G)$
since
$\alpha _k(G)\leq \hat{\alpha }_k(G)$
since
![]() $\hat{\alpha }_k$
is computed over a strictly larger domain than
$\hat{\alpha }_k$
is computed over a strictly larger domain than
![]() $\alpha _k$
(all collections of sets vs. all collections of disjoint sets).
$\alpha _k$
(all collections of sets vs. all collections of disjoint sets).
Now let
![]() $V_1, \ldots, V_k\subseteq V(G)$
(not-necessarily-disjoint) be sets such that
$V_1, \ldots, V_k\subseteq V(G)$
(not-necessarily-disjoint) be sets such that
![]() $|V_1|=\cdots =|V_k|$
, and there are no edges
$|V_1|=\cdots =|V_k|$
, and there are no edges
![]() $e$
such that
$e$
such that
![]() $e\cap X_i\neq \emptyset$
. For all
$e\cap X_i\neq \emptyset$
. For all
![]() $i\in [k]$
, there exists
$i\in [k]$
, there exists
![]() $V^{\prime}_i\subseteq V_i$
with
$V^{\prime}_i\subseteq V_i$
with
![]() $|V^{\prime}_i|\geq \lfloor \frac{|V_i|}{k}\rfloor$
such that
$|V^{\prime}_i|\geq \lfloor \frac{|V_i|}{k}\rfloor$
such that
![]() $V^{\prime}_i\cap V^{\prime}_j=\emptyset$
for all distinct
$V^{\prime}_i\cap V^{\prime}_j=\emptyset$
for all distinct
![]() $i,j\in [k]$
. Since there are no edges which intersect all of
$i,j\in [k]$
. Since there are no edges which intersect all of
![]() $V_1, \ldots, V_k$
, there are no edges which intersect all of
$V_1, \ldots, V_k$
, there are no edges which intersect all of
![]() $V^{\prime}_1, \ldots, V^{\prime}_k$
and thus we have
$V^{\prime}_1, \ldots, V^{\prime}_k$
and thus we have
![]() $\alpha _k(G)\geq \lfloor \frac{\hat{\alpha }_k(G)}{k}\rfloor$
.
$\alpha _k(G)\geq \lfloor \frac{\hat{\alpha }_k(G)}{k}\rfloor$
.
We now make an observation which provides the relationship between small
![]() $k$
-partite holes and expansion.
$k$
-partite holes and expansion.
Observation 2.3.
Let
![]() $G=(V,E)$
be a
$G=(V,E)$
be a
![]() $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
![]() $n$
vertices.
$n$
vertices.
-
(i)
 $G$
is a
$G$
is a
 $(p,n-p)$
-expander if and only if
$(p,n-p)$
-expander if and only if
 $\hat{\alpha }_k(G)\leq p$
.
$\hat{\alpha }_k(G)\leq p$
. -
(ii)
 $G$
is a
$G$
is a
 $(p,n-p)$
-outer-expander if and only if
$(p,n-p)$
-outer-expander if and only if
 $\alpha _k(G)\leq p$
.
$\alpha _k(G)\leq p$
.
Proof. (i) Let
![]() $S_1, \ldots, S_{k-1}\subseteq V$
with
$S_1, \ldots, S_{k-1}\subseteq V$
with
![]() $|S_i|\gt p$
for all
$|S_i|\gt p$
for all
![]() $i\in [k-1]$
. If
$i\in [k-1]$
. If
![]() $|N(S_1, \ldots, S_{k-1})|\lt n-p$
, then
$|N(S_1, \ldots, S_{k-1})|\lt n-p$
, then
![]() $|V\setminus N(S_1, \ldots, S_{k-1})|\gt p$
and there are no edges touching all of
$|V\setminus N(S_1, \ldots, S_{k-1})|\gt p$
and there are no edges touching all of
![]() $S_1, \ldots, S_{k-1}, V\setminus N(S_1, \ldots, S_{k-1})$
which implies
$S_1, \ldots, S_{k-1}, V\setminus N(S_1, \ldots, S_{k-1})$
which implies
![]() $\hat{\alpha }_k(G)\gt p$
.
$\hat{\alpha }_k(G)\gt p$
.
Now suppose
![]() $G$
is a
$G$
is a
![]() $(p,n-p)$
-expander and let
$(p,n-p)$
-expander and let
![]() $S_1, \ldots, S_{k}\subseteq V$
with
$S_1, \ldots, S_{k}\subseteq V$
with
![]() $|S_i|\gt p$
for all
$|S_i|\gt p$
for all
![]() $i\in [k]$
. Since
$i\in [k]$
. Since
![]() $|N(S_1, \ldots, S_{k-1})|\geq n-p$
, we have
$|N(S_1, \ldots, S_{k-1})|\geq n-p$
, we have
![]() $S_k\cap N(S_1, \ldots, S_{k-1})\neq \emptyset$
; that is, there is an edge which touches all of
$S_k\cap N(S_1, \ldots, S_{k-1})\neq \emptyset$
; that is, there is an edge which touches all of
![]() $S_1, \ldots, S_k$
and thus
$S_1, \ldots, S_k$
and thus
![]() $\hat{\alpha }_k(G)\leq p$
.
$\hat{\alpha }_k(G)\leq p$
.
(ii) Let
![]() $S_1, \ldots, S_{k-1}\subseteq V$
be disjoint sets with
$S_1, \ldots, S_{k-1}\subseteq V$
be disjoint sets with
![]() $|S_i|\gt p$
for all
$|S_i|\gt p$
for all
![]() $i\in [k-1]$
. If
$i\in [k-1]$
. If
![]() $|N^+(S_1, \ldots, S_{k-1})|+|S_1\cup \cdots \cup S_{k-1}|\lt n-p$
, then
$|N^+(S_1, \ldots, S_{k-1})|+|S_1\cup \cdots \cup S_{k-1}|\lt n-p$
, then
![]() $|V\setminus (N^+(S_1, \ldots, S_{k-1})\cup (S_1\cup \cdots \cup S_{k-1}))|\gt p$
and there are no edges touching all of
$|V\setminus (N^+(S_1, \ldots, S_{k-1})\cup (S_1\cup \cdots \cup S_{k-1}))|\gt p$
and there are no edges touching all of
![]() $S_1, \ldots, S_{k-1}, V\setminus (N^+(S_1, \ldots, S_{k-1})\cup (S_1\cup \cdots \cup S_{k-1}))$
which implies
$S_1, \ldots, S_{k-1}, V\setminus (N^+(S_1, \ldots, S_{k-1})\cup (S_1\cup \cdots \cup S_{k-1}))$
which implies
![]() $\alpha _k(G)\gt p$
.
$\alpha _k(G)\gt p$
.
Now suppose
![]() $G$
is a
$G$
is a
![]() $(p,n-p)$
-outer-expander and let
$(p,n-p)$
-outer-expander and let
![]() $S_1, \ldots, S_{k}\subseteq V$
be disjoint sets with
$S_1, \ldots, S_{k}\subseteq V$
be disjoint sets with
![]() $|S_i|\gt p$
for all
$|S_i|\gt p$
for all
![]() $i\in [k]$
. Since
$i\in [k]$
. Since
![]() $|N^+(S_1, \ldots, S_{k-1})|+|S_1\cup \cdots \cup S_{k-1}|\geq n-p$
, we have
$|N^+(S_1, \ldots, S_{k-1})|+|S_1\cup \cdots \cup S_{k-1}|\geq n-p$
, we have
![]() $S_k\cap N^+(S_1, \ldots, S_{k-1})\neq \emptyset$
; that is, there is an edge which touches all of
$S_k\cap N^+(S_1, \ldots, S_{k-1})\neq \emptyset$
; that is, there is an edge which touches all of
![]() $S_1, \ldots, S_k$
and thus
$S_1, \ldots, S_k$
and thus
![]() $\alpha _k(G)\leq p$
.
$\alpha _k(G)\leq p$
.
3. Examples
The first example provides the upper bound in Theorem 1.3.(ii).
Observation 3.1.
Let
![]() $2\leq r\leq k$
. For all
$2\leq r\leq k$
. For all
![]() $k$
-uniform hypergraphs
$k$
-uniform hypergraphs
![]() $G$
on
$G$
on
![]() $n$
vertices,
$n$
vertices,
![]() ${\mathrm{mc}}_r(G)\leq n-\alpha _r(G)$
.
${\mathrm{mc}}_r(G)\leq n-\alpha _r(G)$
.
Proof. Let
![]() $X_1, \ldots, X_r$
be disjoint sets which witness the value of
$X_1, \ldots, X_r$
be disjoint sets which witness the value of
![]() $\alpha _r(G)$
; that is, disjoint sets with
$\alpha _r(G)$
; that is, disjoint sets with
![]() $|X_i|=\alpha _r(G)$
for all
$|X_i|=\alpha _r(G)$
for all
![]() $i\in [r]$
such that
$i\in [r]$
such that
![]() $e(X_1, \ldots, X_r)=\emptyset$
. For all
$e(X_1, \ldots, X_r)=\emptyset$
. For all
![]() $i\in [r]$
, colour all edges not incident with
$i\in [r]$
, colour all edges not incident with
![]() $X_i$
with colour
$X_i$
with colour
![]() $i$
(so edges may receive many colours). Since every edge misses some
$i$
(so edges may receive many colours). Since every edge misses some
![]() $X_i$
, every edge receives at least one colour. So every component of colour
$X_i$
, every edge receives at least one colour. So every component of colour
![]() $i$
avoids
$i$
avoids
![]() $X_i$
and thus has order at most
$X_i$
and thus has order at most
![]() $n-\alpha _r(G)$
.
$n-\alpha _r(G)$
.
The next example provides the proof of Theorem 1.3.(iii) and Theorem 1.5.(ii).
Example 3.2.
For all integers
![]() $n\geq r\geq 2$
and
$n\geq r\geq 2$
and
![]() $0\leq a\leq n/(r+2)$
, there exists a
$0\leq a\leq n/(r+2)$
, there exists a
![]() $r$
-uniform hypergraph
$r$
-uniform hypergraph
![]() $G$
on
$G$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\alpha _r(G)=a$
such that
$\alpha _r(G)=a$
such that
![]() ${\mathrm{mc}}_r(G)\le n-2\alpha _r(G)$
.
${\mathrm{mc}}_r(G)\le n-2\alpha _r(G)$
.
Proof. Let
![]() $V$
be a set of order
$V$
be a set of order
![]() $n$
and let
$n$
and let
![]() $\{V_0,V_1, \ldots, V_r,V_{r+1}\}$
be a partition of
$\{V_0,V_1, \ldots, V_r,V_{r+1}\}$
be a partition of
![]() $V$
with
$V$
with
![]() $|V_0|=n-(r+1)a$
,
$|V_0|=n-(r+1)a$
,
![]() $|V_1|=\cdots =|V_{r}|=|V_{r+1}|=a$
. For
$|V_1|=\cdots =|V_{r}|=|V_{r+1}|=a$
. For
![]() $j\in [r]$
, define
$j\in [r]$
, define
![]() $\mathcal{X}_j =V_j\cup V_{r+1}$
and
$\mathcal{X}_j =V_j\cup V_{r+1}$
and
![]() $\mathcal{Y}_j = V\setminus \mathcal{X}_j = V_0\cup \bigcup _{i\in [r]\setminus \{j\}}V_i$
. Let
$\mathcal{Y}_j = V\setminus \mathcal{X}_j = V_0\cup \bigcup _{i\in [r]\setminus \{j\}}V_i$
. Let
![]() $G$
be an
$G$
be an
![]() $r$
-uniform hypergraph on
$r$
-uniform hypergraph on
![]() $V$
with edge set
$V$
with edge set
![]() $\bigcup _{j\in [r]}\binom{\mathcal{X}_j}{r}\cup \binom{\mathcal{Y}_j}{r}$
. If
$\bigcup _{j\in [r]}\binom{\mathcal{X}_j}{r}\cup \binom{\mathcal{Y}_j}{r}$
. If
![]() $e\in \binom{\mathcal{X}_j}{r}\cup \binom{\mathcal{Y}_j}{r}$
colour
$e\in \binom{\mathcal{X}_j}{r}\cup \binom{\mathcal{Y}_j}{r}$
colour
![]() $e$
with
$e$
with
![]() $j$
(so edges can receive more than one colour). Note that for all
$j$
(so edges can receive more than one colour). Note that for all
![]() $j\in [r]$
,
$j\in [r]$
,
![]() $\mathcal{X}_j$
, and
$\mathcal{X}_j$
, and
![]() $\mathcal{Y}_j$
form disjoint monochromatic components of colour
$\mathcal{Y}_j$
form disjoint monochromatic components of colour
![]() $j$
and thus the largest monochromatic component has order
$j$
and thus the largest monochromatic component has order
![]() $\max \{n-2a,2a\}=n-2a$
as desired.
$\max \{n-2a,2a\}=n-2a$
as desired.
We now check that
![]() $\alpha _r(G)=a$
. Note that
$\alpha _r(G)=a$
. Note that
![]() $V_1,\ldots, V_r$
is an
$V_1,\ldots, V_r$
is an
![]() $r$
-partite hole of size
$r$
-partite hole of size
![]() $a$
. Suppose
$a$
. Suppose
![]() $U_1, \ldots, U_r$
is an
$U_1, \ldots, U_r$
is an
![]() $r$
-partite hole of size
$r$
-partite hole of size
![]() $a+1$
. First note that for all
$a+1$
. First note that for all
![]() $j\in [r]$
, there exists
$j\in [r]$
, there exists
![]() $j\in [r]$
such that
$j\in [r]$
such that
![]() $U_{i}\subseteq \mathcal{X}_j$
. If not, then there exists
$U_{i}\subseteq \mathcal{X}_j$
. If not, then there exists
![]() $j\in [r]$
such that every
$j\in [r]$
such that every
![]() $U_i$
intersects
$U_i$
intersects
![]() $\mathcal{Y}_j$
, but since every
$\mathcal{Y}_j$
, but since every
![]() $r$
-set in
$r$
-set in
![]() $\mathcal{Y}_j$
is an edge, this is a contradiction. Also note that we cannot have
$\mathcal{Y}_j$
is an edge, this is a contradiction. Also note that we cannot have
![]() $U_i,U_j\subseteq \mathcal{X}_k$
for
$U_i,U_j\subseteq \mathcal{X}_k$
for
![]() $i\neq j$
since
$i\neq j$
since
![]() $|\mathcal{X}_k|=2a \lt |U_i\cup U_j|$
. So without loss of generality, we may assume that for all
$|\mathcal{X}_k|=2a \lt |U_i\cup U_j|$
. So without loss of generality, we may assume that for all
![]() $j\in [r]$
,
$j\in [r]$
,
![]() $U_j\subseteq \mathcal{X}_j$
. So for all
$U_j\subseteq \mathcal{X}_j$
. So for all
![]() $j\in [r]$
,
$j\in [r]$
,
![]() $U_j$
intersects
$U_j$
intersects
![]() $V_{r+1}$
since
$V_{r+1}$
since
![]() $|U_j| \gt |V_j|$
. But since every
$|U_j| \gt |V_j|$
. But since every
![]() $r$
-set in
$r$
-set in
![]() $V_{r+1}$
is an edge, this is a contradiction.
$V_{r+1}$
is an edge, this is a contradiction.
For expository reasons, we give the same example as above in the dual language.
Example 3.3.
For all integers
![]() $n\geq r\geq 2$
and
$n\geq r\geq 2$
and
![]() $a\geq 0$
with
$a\geq 0$
with
![]() $a\leq n/(r+2)$
, there exists an
$a\leq n/(r+2)$
, there exists an
![]() $r$
-uniform hypergraph
$r$
-uniform hypergraph
![]() $H$
on
$H$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\nu _r(H)=a$
such that
$\nu _r(H)=a$
such that
![]() $\Delta (H)= n-2\nu _r(H)$
.
$\Delta (H)= n-2\nu _r(H)$
.
Proof. Let
![]() $H$
be an
$H$
be an
![]() $r$
-partite hypergraph with two vertices
$r$
-partite hypergraph with two vertices
![]() $u_i, v_i$
in each part. Let
$u_i, v_i$
in each part. Let
![]() $\{v_1, \ldots, v_r\}$
be an edge of multiplicity
$\{v_1, \ldots, v_r\}$
be an edge of multiplicity
![]() $a$
. For all
$a$
. For all
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $\{u_1, \ldots, u_{i-1}, v_i, u_{i+1}, \ldots, u_r\}$
be an edge of multiplicity
$\{u_1, \ldots, u_{i-1}, v_i, u_{i+1}, \ldots, u_r\}$
be an edge of multiplicity
![]() $a$
. Finally, let
$a$
. Finally, let
![]() $\{u_1, \ldots, u_r\}$
be an edge of multiplicity
$\{u_1, \ldots, u_r\}$
be an edge of multiplicity
![]() $n-(r+1)a$
. Note that every vertex in
$n-(r+1)a$
. Note that every vertex in
![]() $\{u_1, \ldots, u_r\}$
has degree
$\{u_1, \ldots, u_r\}$
has degree
![]() $n-2a$
and every vertex in
$n-2a$
and every vertex in
![]() $\{v_1, \ldots, v_n\}$
has degree
$\{v_1, \ldots, v_n\}$
has degree
![]() $2a$
, so
$2a$
, so
![]() $\Delta (H)= \max \{n-2a,2a\}=n-2a$
as desired.
$\Delta (H)= \max \{n-2a,2a\}=n-2a$
as desired.
For
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $F_i$
be the multiset of
$F_i$
be the multiset of
![]() $a$
edges
$a$
edges
![]() $\{u_1, \ldots, u_{i-1}, v_i, u_{i+1}, \ldots, u_r\}$
. Then the collection
$\{u_1, \ldots, u_{i-1}, v_i, u_{i+1}, \ldots, u_r\}$
. Then the collection
![]() $F_1,\ldots, F_r$
shows that
$F_1,\ldots, F_r$
shows that
![]() $\nu _r(H)\ge a$
. Now suppose there is a non-cross intersecting collection
$\nu _r(H)\ge a$
. Now suppose there is a non-cross intersecting collection
![]() $E_1\ldots, E_r$
with
$E_1\ldots, E_r$
with
![]() $|E_i| = a+1$
for all
$|E_i| = a+1$
for all
![]() $i\in [r]$
. For all
$i\in [r]$
. For all
![]() $j\in [r]$
there is some
$j\in [r]$
there is some
![]() $i\in [r]$
such that no element of
$i\in [r]$
such that no element of
![]() $E_i$
contains
$E_i$
contains
![]() $u_j$
. So without loss of generality, we may assume that for all
$u_j$
. So without loss of generality, we may assume that for all
![]() $j\in [r]$
, no element of
$j\in [r]$
, no element of
![]() $E_j$
contains
$E_j$
contains
![]() $u_j$
. But now each
$u_j$
. But now each
![]() $E_j$
must contain an edge of the form
$E_j$
must contain an edge of the form
![]() $\{v_1,\ldots, v_r\}$
since there are only
$\{v_1,\ldots, v_r\}$
since there are only
![]() $a$
edges of the form
$a$
edges of the form
![]() $\{u_1, \ldots, u_{j-1}, v_j, u_{j+1}, \ldots, u_r\}$
. Thus the sets
$\{u_1, \ldots, u_{j-1}, v_j, u_{j+1}, \ldots, u_r\}$
. Thus the sets
![]() $E_1,\ldots, E_r$
are in fact cross-intersecting (in all of
$E_1,\ldots, E_r$
are in fact cross-intersecting (in all of
![]() $v_1,\ldots, v_r$
), a contradiction.
$v_1,\ldots, v_r$
), a contradiction.
The next example provides the proof of Theorem 1.6(ii).
Example 3.4.
For all
![]() $r\geq 2$
and
$r\geq 2$
and
![]() $1\leq a\leq n/k$
, there exists a
$1\leq a\leq n/k$
, there exists a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $G$
on
$G$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\alpha _k(G)=a$
such that
$\alpha _k(G)=a$
such that
![]() ${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_{n-a}^k)\lt{\mathrm{mc}}_r(K_n^k)$
.
${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_{n-a}^k)\lt{\mathrm{mc}}_r(K_n^k)$
.
Proof. Let
![]() $G$
be a complete
$G$
be a complete
![]() $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
![]() $n-a$
vertices together with
$n-a$
vertices together with
![]() $a$
isolated vertices. We have
$a$
isolated vertices. We have
![]() ${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_{n-a}^k)\lt{\mathrm{mc}}_r(K_{n}^k)$
.
${\mathrm{mc}}_r(G)={\mathrm{mc}}_r(K_{n-a}^k)\lt{\mathrm{mc}}_r(K_{n}^k)$
.
The next example provides the proof of Theorem 1.3.(i)(b). For instance when
![]() $s=3$
,
$s=3$
,
![]() $t=4$
, this gives an example of a graph
$t=4$
, this gives an example of a graph
![]() $G$
with
$G$
with
![]() $\alpha _2(G)=\frac{n}{6}$
and a 2-colouring in which the largest monochromatic component has order
$\alpha _2(G)=\frac{n}{6}$
and a 2-colouring in which the largest monochromatic component has order
![]() $\frac{n}{3}$
and thus
$\frac{n}{3}$
and thus
![]() ${\mathrm{mc}}_2(G)\leq \frac{n}{3}$
.
${\mathrm{mc}}_2(G)\leq \frac{n}{3}$
.
Example 3.5.
Let
![]() $n\geq t\geq s$
be positive integers such that
$n\geq t\geq s$
be positive integers such that
![]() $st$
divides
$st$
divides
![]() $n$
. The
$n$
. The
![]() $(s,t)$
-grid on
$(s,t)$
-grid on
![]() $n$
vertices, denoted
$n$
vertices, denoted
![]() $G_n(s,t)$
, is the graph obtained by partitioning
$G_n(s,t)$
, is the graph obtained by partitioning
![]() $[n]$
into
$[n]$
into
![]() $st$
sets
$st$
sets
![]() $A_{11}, \ldots, A_{1t}$
,
$A_{11}, \ldots, A_{1t}$
,
![]() $A_{21}, \ldots, A_{2t}$
,
$A_{21}, \ldots, A_{2t}$
,
![]() $\ldots$
,
$\ldots$
,
![]() $A_{s1}, \ldots, A_{st}$
, each of order
$A_{s1}, \ldots, A_{st}$
, each of order
![]() $\frac{n}{st}$
. For all
$\frac{n}{st}$
. For all
![]() $i\in [s]$
let
$i\in [s]$
let
![]() $A_{i1}\cup \cdots \cup A_{it}$
be a clique, and for all
$A_{i1}\cup \cdots \cup A_{it}$
be a clique, and for all
![]() $j\in [t]$
let
$j\in [t]$
let
![]() $A_{1j}\cup \cdots \cup A_{sj}$
be a clique.
$A_{1j}\cup \cdots \cup A_{sj}$
be a clique.
The natural 2-colouring of
![]() $G_n(s,t)$
is defined by colouring all of the edges inside the ‘rows’
$G_n(s,t)$
is defined by colouring all of the edges inside the ‘rows’
![]() $A_{i1}\cup \cdots \cup A_{it}$
red and all of the edges inside the ‘columns’
$A_{i1}\cup \cdots \cup A_{it}$
red and all of the edges inside the ‘columns’
![]() $A_{1j}\cup \cdots \cup A_{sj}$
blue (the edges inside the sets
$A_{1j}\cup \cdots \cup A_{sj}$
blue (the edges inside the sets
![]() $A_{ij}$
can be coloured with either colour).
$A_{ij}$
can be coloured with either colour).
We have
![]() $\alpha _2(G_n(s,t))=\min \{\frac{\lceil s/2\rceil \lfloor t/2\rfloor }{st}n, \frac{\lfloor s/2\rfloor \lceil t/2\rceil }{st}n\}$
and the largest monochromatic component in the natural colouring of
$\alpha _2(G_n(s,t))=\min \{\frac{\lceil s/2\rceil \lfloor t/2\rfloor }{st}n, \frac{\lfloor s/2\rfloor \lceil t/2\rceil }{st}n\}$
and the largest monochromatic component in the natural colouring of
![]() $G_n(s,t)$
has order
$G_n(s,t)$
has order
![]() $\frac{n}{s}$
.
$\frac{n}{s}$
.
Proof. Set
![]() $G\;:\!=\;G_n(s,t)$
and take the natural 2-colouring of
$G\;:\!=\;G_n(s,t)$
and take the natural 2-colouring of
![]() $G$
. The fact that the largest monochromatic component has order
$G$
. The fact that the largest monochromatic component has order
![]() $\frac{n}{s}$
is evident by the way the graph and its colouring is defined since
$\frac{n}{s}$
is evident by the way the graph and its colouring is defined since
![]() $s\leq t$
. To see that
$s\leq t$
. To see that
![]() $\alpha _2(G)=\frac{\lceil s/2\rceil \lfloor t/2\rfloor }{st}n$
, let
$\alpha _2(G)=\frac{\lceil s/2\rceil \lfloor t/2\rfloor }{st}n$
, let
![]() $X, Y\subseteq V(G)$
be maximal disjoint sets witnessing the value of
$X, Y\subseteq V(G)$
be maximal disjoint sets witnessing the value of
![]() $\alpha _2(G)$
; that is,
$\alpha _2(G)$
; that is,
![]() $\min \{|X|, |Y|\}=\alpha _2(G)$
and
$\min \{|X|, |Y|\}=\alpha _2(G)$
and
![]() $e(X,Y)=0$
. By the maximality of
$e(X,Y)=0$
. By the maximality of
![]() $X,Y$
and the structure of
$X,Y$
and the structure of
![]() $G$
, we have that if
$G$
, we have that if
![]() $X\cap A_{ij}\neq \emptyset$
then
$X\cap A_{ij}\neq \emptyset$
then
![]() $X\cap A_{ij}=A_{ij}$
and likewise
$X\cap A_{ij}=A_{ij}$
and likewise
![]() $Y\cap A_{ij}\neq \emptyset$
implies
$Y\cap A_{ij}\neq \emptyset$
implies
![]() $Y\cap A_{ij}=A_{ij}$
. Let
$Y\cap A_{ij}=A_{ij}$
. Let
![]() $I=\{i\in [s]\;:\; X\cap A_{ij}\neq \emptyset$
for some
$I=\{i\in [s]\;:\; X\cap A_{ij}\neq \emptyset$
for some
![]() $j\in [t]\}$
and
$j\in [t]\}$
and
![]() $J=\{j\in [t]\;:\; X\cap A_{ij}\neq \emptyset$
for some
$J=\{j\in [t]\;:\; X\cap A_{ij}\neq \emptyset$
for some
![]() $i\in [s]\}$
. This implies that if
$i\in [s]\}$
. This implies that if
![]() $Y\cap A_{ij}\neq \emptyset$
, then
$Y\cap A_{ij}\neq \emptyset$
, then
![]() $i\in [s]\setminus I$
and
$i\in [s]\setminus I$
and
![]() $j\in [t]\setminus J$
. So we have
$j\in [t]\setminus J$
. So we have
![]() $|X|=\frac{|I||J|n}{st}$
and
$|X|=\frac{|I||J|n}{st}$
and
![]() $|Y|=\frac{(s-|I|)(t-|J|)n}{st}$
and thus
$|Y|=\frac{(s-|I|)(t-|J|)n}{st}$
and thus
![]() $\alpha _2(G)=\min \{|X|, |Y|\}$
is maximised when
$\alpha _2(G)=\min \{|X|, |Y|\}$
is maximised when
![]() $|I|=\lceil s/2\rceil$
and
$|I|=\lceil s/2\rceil$
and
![]() $|J|=\lfloor t/2\rfloor$
(equivalently,
$|J|=\lfloor t/2\rfloor$
(equivalently,
![]() $|I|=\lfloor s/2\rfloor$
and
$|I|=\lfloor s/2\rfloor$
and
![]() $|J|=\lceil t/2\rceil$
).
$|J|=\lceil t/2\rceil$
).
For random graphs
![]() $G(n,p)$
, it was shown in [Reference Bal and DeBiasio2] and [Reference Dudek and Prałat8] that for
$G(n,p)$
, it was shown in [Reference Bal and DeBiasio2] and [Reference Dudek and Prałat8] that for
![]() $p=\frac{\omega (1)}{n}$
, we have w.h.p.,
$p=\frac{\omega (1)}{n}$
, we have w.h.p.,
![]() ${\mathrm{mc}}_r(G(n,p))\geq \left (\frac{1}{r-1}-o(1)\right )n$
and thus (whenever an affine plane of order
${\mathrm{mc}}_r(G(n,p))\geq \left (\frac{1}{r-1}-o(1)\right )n$
and thus (whenever an affine plane of order
![]() $r-1$
exists) we have
$r-1$
exists) we have
![]() ${\mathrm{mc}}_r(G(n,p)) = (1-o(1)){\mathrm{mc}}_r(K_n)$
. Analogously, for random hypergraphs it was shown in [Reference Bennett, DeBiasio, Dudek and English5] that for
${\mathrm{mc}}_r(G(n,p)) = (1-o(1)){\mathrm{mc}}_r(K_n)$
. Analogously, for random hypergraphs it was shown in [Reference Bennett, DeBiasio, Dudek and English5] that for
![]() $r\geq 4$
and
$r\geq 4$
and
![]() $p= \frac{\omega (1)}{n^{r-2}}$
, we have w.h.p.,
$p= \frac{\omega (1)}{n^{r-2}}$
, we have w.h.p.,
![]() ${\mathrm{mc}}_r(H^{r-1}(n,p)) \ge (\frac{r-1}{r} - o(1))n$
and thus
${\mathrm{mc}}_r(H^{r-1}(n,p)) \ge (\frac{r-1}{r} - o(1))n$
and thus
![]() ${\mathrm{mc}}_r(H^{r-1}(n,p)) = (1-o(1)){\mathrm{mc}}_r(K_n^{r-1})$
.
${\mathrm{mc}}_r(H^{r-1}(n,p)) = (1-o(1)){\mathrm{mc}}_r(K_n^{r-1})$
.
The following observation shows that for sufficiently small
![]() $p$
(but above the thresholds mentioned above), we have
$p$
(but above the thresholds mentioned above), we have
![]() ${\mathrm{mc}}_r(G(n,p))$
is bounded away from
${\mathrm{mc}}_r(G(n,p))$
is bounded away from
![]() ${\mathrm{mc}}_r(K_n)$
by a constant and
${\mathrm{mc}}_r(K_n)$
by a constant and
![]() ${\mathrm{mc}}_r(H^{r-1}(n,p))$
is bounded away from
${\mathrm{mc}}_r(H^{r-1}(n,p))$
is bounded away from
![]() ${\mathrm{mc}}_r(K_n^{r-1})$
by a constant.
${\mathrm{mc}}_r(K_n^{r-1})$
by a constant.
Observation 3.6.
Let
![]() $r$
and
$r$
and
![]() $C$
be integers with
$C$
be integers with
![]() $r\geq 2$
and
$r\geq 2$
and
![]() $C\geq 1$
.
$C\geq 1$
.
-
(i) If an affine plane of order
 $r-1$
exists, then for
$r-1$
exists, then for
 $\frac{\omega (1)}{n}=p\lt \frac{1}{2Cr(r-1)^2}$
we have w.h.p.,
$\frac{\omega (1)}{n}=p\lt \frac{1}{2Cr(r-1)^2}$
we have w.h.p.,
 \begin{equation*}\left (\frac {1}{r-1}-o(1)\right )n={\mathrm {mc}}_r(G(n,p))\leq \frac {n}{r-1}-C.\end{equation*}
\begin{equation*}\left (\frac {1}{r-1}-o(1)\right )n={\mathrm {mc}}_r(G(n,p))\leq \frac {n}{r-1}-C.\end{equation*}
-
(ii) If
 $r\geq 4$
, then for
$r\geq 4$
, then for
 $\frac{\omega (1)}{n^{r-2}}=p=\frac{o(\sqrt{n})}{n^{r-2}}$
we have w.h.p.,
$\frac{\omega (1)}{n^{r-2}}=p=\frac{o(\sqrt{n})}{n^{r-2}}$
we have w.h.p.,
 \begin{equation*}\left (\frac {r-1}{r}-o(1)\right )n={\mathrm {mc}}_r(H^{r-1}(n,p)) \le \frac {r-1}{r}n - C(r-1).\end{equation*}
\begin{equation*}\left (\frac {r-1}{r}-o(1)\right )n={\mathrm {mc}}_r(H^{r-1}(n,p)) \le \frac {r-1}{r}n - C(r-1).\end{equation*}
Proof. (i) Note that
![]() $p$
is small enough so that with high probability,
$p$
is small enough so that with high probability,
![]() $G(n,p)$
has an independent set
$G(n,p)$
has an independent set
![]() $X$
with
$X$
with
![]() $Cr$
vertices such that
$Cr$
vertices such that
![]() $|\bigcup _{v\in X}N(v)|\leq \frac{n-Cr}{(r-1)^2}$
. Partition
$|\bigcup _{v\in X}N(v)|\leq \frac{n-Cr}{(r-1)^2}$
. Partition
![]() $X$
into
$X$
into
![]() $r$
sets
$r$
sets
![]() $\{X_1, \ldots, X_r\}$
each of order
$\{X_1, \ldots, X_r\}$
each of order
![]() $C$
and partition the vertices of
$C$
and partition the vertices of
![]() $V(G)-X$
into sets of size
$V(G)-X$
into sets of size
![]() $\frac{n-Cr}{(r-1)^2}$
, with one of those sets containing
$\frac{n-Cr}{(r-1)^2}$
, with one of those sets containing
![]() $\bigcup _{v\in X}N(v)$
, and colour the edges of
$\bigcup _{v\in X}N(v)$
, and colour the edges of
![]() $G-X$
according to the affine plane colouring. Now colour all edges incident with
$G-X$
according to the affine plane colouring. Now colour all edges incident with
![]() $X_i$
with colour
$X_i$
with colour
![]() $i$
for all
$i$
for all
![]() $i\in [r]$
. So every component of colour
$i\in [r]$
. So every component of colour
![]() $i$
has order at most
$i$
has order at most
![]() $\frac{n-Cr}{r-1}+C\leq \frac{n}{r-1}-C$
.
$\frac{n-Cr}{r-1}+C\leq \frac{n}{r-1}-C$
.
(ii) Note that
![]() $p$
is small enough so that with high probability there exists an independent set
$p$
is small enough so that with high probability there exists an independent set
![]() $X$
of order
$X$
of order
![]() $Cr$
. Partition
$Cr$
. Partition
![]() $X$
into
$X$
into
![]() $r$
sets
$r$
sets
![]() $\{X_1, \ldots, X_r\}$
each of order
$\{X_1, \ldots, X_r\}$
each of order
![]() $C$
and let
$C$
and let
![]() $E_i=\{e\; :\; e\cap X_i\neq \emptyset \}$
for all
$E_i=\{e\; :\; e\cap X_i\neq \emptyset \}$
for all
![]() $i\in [r]$
. Additionally,
$i\in [r]$
. Additionally,
![]() $p$
is small enough so that with high probability for all
$p$
is small enough so that with high probability for all
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $|\bigcup _{e\in E_i}e|\leq \frac{n}{r}$
, and for all distinct
$|\bigcup _{e\in E_i}e|\leq \frac{n}{r}$
, and for all distinct
![]() $i,j\in [r]$
, all
$i,j\in [r]$
, all
![]() $e_i\in E_i$
, and all
$e_i\in E_i$
, and all
![]() $e_j\in E_j$
, we have
$e_j\in E_j$
, we have
![]() $e_i\cap e_j=\emptyset$
.
$e_i\cap e_j=\emptyset$
.
Let
![]() $\{A_1, \ldots, A_r\}$
be a partition of
$\{A_1, \ldots, A_r\}$
be a partition of
![]() $V(G)$
into sets which are as equally sized as possible having the property that for all
$V(G)$
into sets which are as equally sized as possible having the property that for all
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $\bigcup _{e\in E_i}e\subseteq A_i$
. Now for all
$\bigcup _{e\in E_i}e\subseteq A_i$
. Now for all
![]() $i\in [r]$
colour the edges in
$i\in [r]$
colour the edges in
![]() $E_i$
with colour
$E_i$
with colour
![]() $i$
. For all
$i$
. For all
![]() $e\in E(G)\setminus \cup _{i\in [r]}E_i$
, note that since
$e\in E(G)\setminus \cup _{i\in [r]}E_i$
, note that since
![]() $|e|=r-1$
, there exists
$|e|=r-1$
, there exists
![]() $i\in [r]$
such that
$i\in [r]$
such that
![]() $e\cap A_i=\emptyset$
and thus we assign any such colour
$e\cap A_i=\emptyset$
and thus we assign any such colour
![]() $i$
to the edge
$i$
to the edge
![]() $e$
. So we have that for all
$e$
. So we have that for all
![]() $i\in [r]$
, there is a component of colour
$i\in [r]$
, there is a component of colour
![]() $i$
containing
$i$
containing
![]() $X_i$
and having order at most
$X_i$
and having order at most
![]() $n/r$
and there is a component colour
$n/r$
and there is a component colour
![]() $i$
which avoids
$i$
which avoids
![]() $X$
and
$X$
and
![]() $A_i$
and thus has order at most
$A_i$
and thus has order at most
![]() $\frac{r-1}{r}n-(r-1)C$
.
$\frac{r-1}{r}n-(r-1)C$
.
On the other hand, when
![]() $p$
is sufficiently close to 1, the minimum degree of
$p$
is sufficiently close to 1, the minimum degree of
![]() $G(n,p)$
is close to
$G(n,p)$
is close to
![]() $n$
and the results of [Reference Füredi and Luo10] apply to give
$n$
and the results of [Reference Füredi and Luo10] apply to give
![]() ${\mathrm{mc}}_r(G(n,p)) ={\mathrm{mc}}_r(K_n)$
. Likewise when
${\mathrm{mc}}_r(G(n,p)) ={\mathrm{mc}}_r(K_n)$
. Likewise when
![]() $p$
is sufficiently close to 1, the minimum co-degree of
$p$
is sufficiently close to 1, the minimum co-degree of
![]() $H^{r-1}(n,p)$
is close to
$H^{r-1}(n,p)$
is close to
![]() $n$
and the results of [Reference Bal and DeBiasio3] apply to give
$n$
and the results of [Reference Bal and DeBiasio3] apply to give
![]() ${\mathrm{mc}}_r(H^{r-1}(n,p)) ={\mathrm{mc}}_r(K_n^{r-1})$
. This observation together with Observation 3.6 leads us to the following problem.
${\mathrm{mc}}_r(H^{r-1}(n,p)) ={\mathrm{mc}}_r(K_n^{r-1})$
. This observation together with Observation 3.6 leads us to the following problem.
Problem 3.7.
Determine the smallest
![]() $p$
such that
$p$
such that
![]() ${\mathrm{mc}}_r(G(n,p)) ={\mathrm{mc}}_r(K_n)$
, and for all
${\mathrm{mc}}_r(G(n,p)) ={\mathrm{mc}}_r(K_n)$
, and for all
![]() $r\geq 4$
, determine the smallest
$r\geq 4$
, determine the smallest
![]() $p$
such that
$p$
such that
![]() ${\mathrm{mc}}_r(H^{r-1}(n,p)) ={\mathrm{mc}}_r(K_n^{r-1})$
.
${\mathrm{mc}}_r(H^{r-1}(n,p)) ={\mathrm{mc}}_r(K_n^{r-1})$
.
4. Main results in the dual language
All of the results of this section are of the type ‘For all
![]() $k, r$
there exists
$k, r$
there exists
![]() $c_{k,r}, d_{k,r}$
such that if
$c_{k,r}, d_{k,r}$
such that if
![]() $G$
is a
$G$
is a
![]() $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
![]() $n$
vertices with
$n$
vertices with
![]() $\alpha _k(G)\lt c_{k,r} n$
, then
$\alpha _k(G)\lt c_{k,r} n$
, then
![]() ${\mathrm{mc}}_r(G)\geq{\mathrm{mc}}_r(K_n^k)-d_{k,r}\alpha _k(G)$
’; however we prove these statements in the equivalent dual form ‘For all
${\mathrm{mc}}_r(G)\geq{\mathrm{mc}}_r(K_n^k)-d_{k,r}\alpha _k(G)$
’; however we prove these statements in the equivalent dual form ‘For all
![]() $k, r$
there exists
$k, r$
there exists
![]() $c_{k,r}, d_{k,r}\gt 0$
such that if
$c_{k,r}, d_{k,r}\gt 0$
such that if
![]() $H$
is an
$H$
is an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multihypergraph with
$r$
-uniform multihypergraph with
![]() $n$
edges and
$n$
edges and
![]() $\nu _k(H)\lt c_{k,r}$
, then
$\nu _k(H)\lt c_{k,r}$
, then
![]() $\Delta (H)\geq{\mathrm{mc}}_r(K_n^k)-d_{k,r}\nu _k(G)$
’.
$\Delta (H)\geq{\mathrm{mc}}_r(K_n^k)-d_{k,r}\nu _k(G)$
’.
Theorem 4.1 (Dual of Theorem 1.3(i)(a)). Let
![]() $H$
be a bipartite multigraph with
$H$
be a bipartite multigraph with
![]() $n$
edges. If
$n$
edges. If
![]() $\nu _2(H)\lt n/6$
, then
$\nu _2(H)\lt n/6$
, then
![]() $\Delta (H)\geq n-2\nu _2(H)$
.
$\Delta (H)\geq n-2\nu _2(H)$
.
Theorem 4.2 (Dual of Theorem 1.4(i)). Let
![]() $H$
be an
$H$
be an
![]() $3$
-partite
$3$
-partite
![]() $3$
-uniform multi-hypergraph with
$3$
-uniform multi-hypergraph with
![]() $n$
edges. If
$n$
edges. If
![]() $\nu _{2}(H)\leq \frac{n}{3^9}$
, then
$\nu _{2}(H)\leq \frac{n}{3^9}$
, then
![]() $\Delta (H)\geq \frac{n}{2}-2\nu _2(H)$
.
$\Delta (H)\geq \frac{n}{2}-2\nu _2(H)$
.
Theorem 4.3 (Dual of Theorem 1.5(i)). Let
![]() $r\geq 3$
and let
$r\geq 3$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform hypergraph with
$r$
-uniform hypergraph with
![]() $n$
edges. If
$n$
edges. If
![]() $\nu _r(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
$\nu _r(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
![]() $\Delta (H)\geq n-(r-1)\nu _r(H)$
.
$\Delta (H)\geq n-(r-1)\nu _r(H)$
.
Theorem 4.4 (Dual of Theorem 1.6(i)). Let
![]() $r\geq 3$
and let
$r\geq 3$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform hypergraph with
$r$
-uniform hypergraph with
![]() $n$
edges. If
$n$
edges. If
![]() $\nu _{r-1}(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
$\nu _{r-1}(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
![]() $\Delta (H)\geq \frac{(r-1)n}{r}-\binom{r}{2}\nu _{r-1}(H)$
.
$\Delta (H)\geq \frac{(r-1)n}{r}-\binom{r}{2}\nu _{r-1}(H)$
.
4.1. General lemmas
In this section we collect a number of general lemmas. We begin with an elementary lemma that will be used throughout the proofs in this section. This lemma basically says that if we have a collection of edge sets in an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform hypergraph, then for any part
$r$
-uniform hypergraph, then for any part
![]() $V_i$
of the partition, either there is a vertex in
$V_i$
of the partition, either there is a vertex in
![]() $V_i$
which is incident with a large number of edges from each set, or else there is a large subset of each edge set which does not cross-intersect in
$V_i$
which is incident with a large number of edges from each set, or else there is a large subset of each edge set which does not cross-intersect in
![]() $V_i$
.
$V_i$
.
Lemma 4.5.
Let
![]() $\nu, \ell, a_1, \ldots, a_\ell$
be positive integers. Let
$\nu, \ell, a_1, \ldots, a_\ell$
be positive integers. Let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with parts
$r$
-uniform multi-hypergraph with parts
![]() $V_1,\ldots, V_r$
and let
$V_1,\ldots, V_r$
and let
![]() $F_1, \ldots, F_\ell \subseteq E(H)$
such that
$F_1, \ldots, F_\ell \subseteq E(H)$
such that
![]() $|F_1|\geq 3a_1\nu +1$
and
$|F_1|\geq 3a_1\nu +1$
and
![]() $|F_j|\geq 2a_j\nu +1$
for all
$|F_j|\geq 2a_j\nu +1$
for all
![]() $j\in [2,\ell ]$
. For all
$j\in [2,\ell ]$
. For all
![]() $i\in [r]$
, either
$i\in [r]$
, either
-
(B1) there exists
 $u\in V_i$
such that for all
$u\in V_i$
such that for all
 $j\in [\ell ]$
,
$j\in [\ell ]$
,
 $u$
is incident with at least
$u$
is incident with at least
 $|F_j|-a_j\nu$
edges of
$|F_j|-a_j\nu$
edges of
 $F_j$
, or
$F_j$
, or
-
(B2) there exists a subset
 $F^{\prime}_1\subseteq F_1$
with
$F^{\prime}_1\subseteq F_1$
with
 $|F^{\prime}_1|\geq a_1\nu +1$
and a subset
$|F^{\prime}_1|\geq a_1\nu +1$
and a subset
 $F^{\prime}_j\subseteq F_j$
for some
$F^{\prime}_j\subseteq F_j$
for some
 $j\in [2,\ell ]$
with
$j\in [2,\ell ]$
with
 $|F^{\prime}_j|\geq a_j\nu +1$
such that
$|F^{\prime}_j|\geq a_j\nu +1$
such that
 $F^{\prime}_1,F_2 \ldots, F_{j-1}, F^{\prime}_j, F_{j+1}, \ldots, F_{\ell }$
is not cross-intersecting in
$F^{\prime}_1,F_2 \ldots, F_{j-1}, F^{\prime}_j, F_{j+1}, \ldots, F_{\ell }$
is not cross-intersecting in
 $V_i$
.
$V_i$
.
Proof. Let
![]() $i\in [r]$
and suppose (B1) doesn’t hold. If there exists
$i\in [r]$
and suppose (B1) doesn’t hold. If there exists
![]() $u\in V_i$
such that
$u\in V_i$
such that
![]() $u$
is incident with at least
$u$
is incident with at least
![]() $|F_1|-a_1\nu$
edges from
$|F_1|-a_1\nu$
edges from
![]() $F_1$
, then by the assumption, there exists
$F_1$
, then by the assumption, there exists
![]() $j\in [2,\ell ]$
such that
$j\in [2,\ell ]$
such that
![]() $u$
is incident with at most
$u$
is incident with at most
![]() $|F_j|-a_j\nu -1$
edges of
$|F_j|-a_j\nu -1$
edges of
![]() $F_j$
and thus at least
$F_j$
and thus at least
![]() $a_j\nu +1$
edges of
$a_j\nu +1$
edges of
![]() $F_j$
intersect
$F_j$
intersect
![]() $V_{i}-u$
and thus (B2) is satisfied.
$V_{i}-u$
and thus (B2) is satisfied.
So suppose that every
![]() $u\in V_i$
is incident with at most
$u\in V_i$
is incident with at most
![]() $|F_1|-a_1\nu -1$
edges of
$|F_1|-a_1\nu -1$
edges of
![]() $F_1$
. Let
$F_1$
. Let
![]() $V_i^1\subseteq V_i$
be a minimal set of vertices incident with at least
$V_i^1\subseteq V_i$
be a minimal set of vertices incident with at least
![]() $a_1\nu +1$
edges of
$a_1\nu +1$
edges of
![]() $F_1$
. By minimality, and the fact that every
$F_1$
. By minimality, and the fact that every
![]() $u\in V_i$
is incident with at most
$u\in V_i$
is incident with at most
![]() $|F_1|-a_1\nu -1$
edges of
$|F_1|-a_1\nu -1$
edges of
![]() $F_1$
, we have that both
$F_1$
, we have that both
![]() $V_i^1$
and
$V_i^1$
and
![]() $V_i^2\;:\!=\;V_i\setminus V_i^1$
are incident with at least
$V_i^2\;:\!=\;V_i\setminus V_i^1$
are incident with at least
![]() $a_1\nu +1$
edges of
$a_1\nu +1$
edges of
![]() $F_1$
. Now either
$F_1$
. Now either
![]() $V_i^1$
or
$V_i^1$
or
![]() $V_i^2$
is incident with at least
$V_i^2$
is incident with at least
![]() $\lfloor |F_2|/2\rfloor \geq a_2\nu +1$
edges of
$\lfloor |F_2|/2\rfloor \geq a_2\nu +1$
edges of
![]() $F_2$
, and either way (B2) is satisfied.
$F_2$
, and either way (B2) is satisfied.
A simpler version of the above lemma which suffices whenever we don’t care about the exact bounds is as follows.
Lemma 4.6.
Let
![]() $\nu, \ell, a_1, \ldots, a_{\ell }$
be positive integers. Let
$\nu, \ell, a_1, \ldots, a_{\ell }$
be positive integers. Let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with parts
$r$
-uniform multi-hypergraph with parts
![]() $V_1,\ldots, V_r$
, and let
$V_1,\ldots, V_r$
, and let
![]() $F_1, \ldots, F_\ell \subseteq E(H)$
such that
$F_1, \ldots, F_\ell \subseteq E(H)$
such that
![]() $|F_j|\geq 3a_j\nu +1$
for all
$|F_j|\geq 3a_j\nu +1$
for all
![]() $j\in [\ell ]$
. For all
$j\in [\ell ]$
. For all
![]() $i\in [r]$
, either
$i\in [r]$
, either
-
(B1′)there exists
 $u\in V_i$
such that for all
$u\in V_i$
such that for all
 $j\in [\ell ]$
,
$j\in [\ell ]$
,
 $u$
is incident with at least
$u$
is incident with at least
 $|F_j|-a_j\nu$
edges of
$|F_j|-a_j\nu$
edges of
 $F_j$
, or
$F_j$
, or
-
(B2′)for all
 $j\in [\ell ]$
there exists a subset
$j\in [\ell ]$
there exists a subset
 $F^{\prime}_j\subseteq F_j$
with
$F^{\prime}_j\subseteq F_j$
with
 $|F^{\prime}_j|\geq a_j\nu +1$
such that
$|F^{\prime}_j|\geq a_j\nu +1$
such that
 $F^{\prime}_1, \ldots, F^{\prime}_\ell $
is not cross-intersecting in
$F^{\prime}_1, \ldots, F^{\prime}_\ell $
is not cross-intersecting in
 $V_i$
.
$V_i$
.
The following observation explicitly gives a relationship between
![]() $\nu _s$
and
$\nu _s$
and
![]() $\nu _t$
for
$\nu _t$
for
![]() $s\leq t$
.
$s\leq t$
.
Observation 4.7.
Let
![]() $2\leq s\lt t\leq r$
and let
$2\leq s\lt t\leq r$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph on
$r$
-uniform multi-hypergraph on
![]() $n$
edges. If
$n$
edges. If
![]() $\nu _t(H)\leq \frac{n}{t}-1$
, then
$\nu _t(H)\leq \frac{n}{t}-1$
, then
![]() $\nu _s(H)\leq \nu _t(H)$
.
$\nu _s(H)\leq \nu _t(H)$
.
Proof. Suppose
![]() $\nu _t(H)\leq \frac{n}{t}-1$
and suppose for contradiction that
$\nu _t(H)\leq \frac{n}{t}-1$
and suppose for contradiction that
![]() $\nu _s(H)\gt \nu _t(H)$
. So there exists disjoint sets
$\nu _s(H)\gt \nu _t(H)$
. So there exists disjoint sets
![]() $E_1, \ldots, E_s$
with
$E_1, \ldots, E_s$
with
![]() $|E_i|= \nu _t(H)+1$
for all
$|E_i|= \nu _t(H)+1$
for all
![]() $i\in [s]$
such that
$i\in [s]$
such that
![]() $E_1, \ldots, E_s$
is not cross-intersecting. Since
$E_1, \ldots, E_s$
is not cross-intersecting. Since
![]() $\nu _t(H)\leq \frac{n}{t}-1$
, we have
$\nu _t(H)\leq \frac{n}{t}-1$
, we have
![]() $|E_i|\leq \frac{n}{t}$
for all
$|E_i|\leq \frac{n}{t}$
for all
![]() $i\in [s]$
and thus
$i\in [s]$
and thus
![]() $|E(H)\setminus (E_1\cup \cdots \cup E_s)|\geq n-s\frac{n}{t}= (t-s)\frac{n}{t}$
and thus there is a partition of
$|E(H)\setminus (E_1\cup \cdots \cup E_s)|\geq n-s\frac{n}{t}= (t-s)\frac{n}{t}$
and thus there is a partition of
![]() $E(H)\setminus (E_1\cup \cdots \cup E_s)$
into
$E(H)\setminus (E_1\cup \cdots \cup E_s)$
into
![]() $t-s$
sets
$t-s$
sets
![]() $E_{s+1}, \ldots, E_t$
each of order greater than
$E_{s+1}, \ldots, E_t$
each of order greater than
![]() $\nu _t(H)$
such that
$\nu _t(H)$
such that
![]() $E_1, \ldots, E_s, E_{s+1}, \ldots, E_t$
is not cross-intersecting.
$E_1, \ldots, E_s, E_{s+1}, \ldots, E_t$
is not cross-intersecting.
We now show that if
![]() $H$
is an
$H$
is an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph on
$r$
-uniform multi-hypergraph on
![]() $n$
edges with
$n$
edges with
![]() $\nu _s(H)$
small enough in terms of
$\nu _s(H)$
small enough in terms of
![]() $n$
and
$n$
and
![]() $r$
, then there must be a vertex of fairly large degree.
$r$
, then there must be a vertex of fairly large degree.
Lemma 4.8.
Let
![]() $\Delta, r, s$
be positive integers with
$\Delta, r, s$
be positive integers with
![]() $2\leq s\leq r$
. Let
$2\leq s\leq r$
. Let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with
$r$
-uniform multi-hypergraph with
![]() $n$
edges and set
$n$
edges and set
![]() $\nu \;:\!=\;\nu _s(H)$
. If
$\nu \;:\!=\;\nu _s(H)$
. If
![]() $\nu \leq \frac{n}{3^r\Delta }$
, then
$\nu \leq \frac{n}{3^r\Delta }$
, then
![]() $\Delta (H)\geq \Delta \nu +1$
.
$\Delta (H)\geq \Delta \nu +1$
.
Proof. Suppose
![]() $\nu \leq \frac{n}{3^r\Delta }$
and suppose for contradiction that
$\nu \leq \frac{n}{3^r\Delta }$
and suppose for contradiction that
![]() $\Delta (H)\leq \Delta \nu$
. Note that by Observation 4.7 we have
$\Delta (H)\leq \Delta \nu$
. Note that by Observation 4.7 we have
![]() $\nu _2(H)\leq \nu \leq \frac{n}{3^r\Delta }$
.
$\nu _2(H)\leq \nu \leq \frac{n}{3^r\Delta }$
.
Let
![]() $V_1, \ldots, V_r$
be the parts of
$V_1, \ldots, V_r$
be the parts of
![]() $H$
. Let
$H$
. Let
![]() $V^{\prime}_1\subseteq V_1$
be a minimum set of vertices incident with at least
$V^{\prime}_1\subseteq V_1$
be a minimum set of vertices incident with at least
![]() $3^{r-1}\Delta \nu +1$
edges. By minimality, we have
$3^{r-1}\Delta \nu +1$
edges. By minimality, we have
and consequently, since
![]() $\nu \leq \frac{n}{3^r\Delta }$
, we have
$\nu \leq \frac{n}{3^r\Delta }$
, we have
Let
![]() $F_1^1$
and
$F_1^1$
and
![]() $F_2^1$
be the sets of edges incident with
$F_2^1$
be the sets of edges incident with
![]() $V^{\prime}_1$
and
$V^{\prime}_1$
and
![]() $V_1\setminus V^{\prime}_1$
respectively. Now we apply Lemma 4.6 (with
$V_1\setminus V^{\prime}_1$
respectively. Now we apply Lemma 4.6 (with
![]() $a_1=a_2=3^{r-2}\Delta$
and
$a_1=a_2=3^{r-2}\Delta$
and
![]() $i=2$
), and since we are assuming
$i=2$
), and since we are assuming
![]() $\Delta (H)\leq \Delta \nu$
, (B2
′) must happen. Now we have sets
$\Delta (H)\leq \Delta \nu$
, (B2
′) must happen. Now we have sets
![]() $F_1^2\subseteq F_1^1$
and
$F_1^2\subseteq F_1^1$
and
![]() $F_2^2\subseteq F_2^1$
such that
$F_2^2\subseteq F_2^1$
such that
![]() $|F_1^2|, |F_2^2|\geq 3^{r-2}\Delta \nu +1$
and
$|F_1^2|, |F_2^2|\geq 3^{r-2}\Delta \nu +1$
and
![]() $F_1^2$
and
$F_1^2$
and
![]() $F_2^2$
are not cross-intersecting in
$F_2^2$
are not cross-intersecting in
![]() $V_1\cup V_2$
. Now we repeatedly apply Lemma 4.6 until we have sets
$V_1\cup V_2$
. Now we repeatedly apply Lemma 4.6 until we have sets
![]() $F_1^{r-1}$
and
$F_1^{r-1}$
and
![]() $F_{2}^{r-1}$
with
$F_{2}^{r-1}$
with
![]() $|F_{1}^{r-1}|, |F_{2}^{r-1}|\geq 3\Delta \nu +1$
and
$|F_{1}^{r-1}|, |F_{2}^{r-1}|\geq 3\Delta \nu +1$
and
![]() $F_{1}^{r-1}$
and
$F_{1}^{r-1}$
and
![]() $F_{2}^{r-1}$
are not cross-intersecting in
$F_{2}^{r-1}$
are not cross-intersecting in
![]() $V_1\cup \cdots \cup V_{r-1}$
. In the final step (where we apply Lemma 4.6 with
$V_1\cup \cdots \cup V_{r-1}$
. In the final step (where we apply Lemma 4.6 with
![]() $a_1=a_2=\Delta$
and
$a_1=a_2=\Delta$
and
![]() $i=r$
), either (B2
′) happens and we have a contradiction to
$i=r$
), either (B2
′) happens and we have a contradiction to
![]() $\nu _2(H)\leq \nu$
, or (B1
′) happens and we have
$\nu _2(H)\leq \nu$
, or (B1
′) happens and we have
![]() $\Delta (H) \geq \Delta \nu +1$
, contradicting the assumption.
$\Delta (H) \geq \Delta \nu +1$
, contradicting the assumption.
For the last result in this subsection we show that if there is a vertex of fairly large degree, then either we have an edge of multiplicity at least
![]() $\nu +1$
or there is a vertex of even larger degree.
$\nu +1$
or there is a vertex of even larger degree.
Lemma 4.9.
Let
![]() $r$
be an integer with
$r$
be an integer with
![]() $r\geq 3$
and let
$r\geq 3$
and let
![]() $s\in \{2,r-1,r\}$
. Let
$s\in \{2,r-1,r\}$
. Let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with
$r$
-uniform multi-hypergraph with
![]() $n$
edges and set
$n$
edges and set
![]() $\nu \;:\!=\;\nu _s(H)$
. If
$\nu \;:\!=\;\nu _s(H)$
. If
![]() $\nu \leq \frac{n}{2^r}$
and
$\nu \leq \frac{n}{2^r}$
and
![]() $\Delta (H)\geq 3^{\binom{r+1}{2}}\nu +1$
, then either
$\Delta (H)\geq 3^{\binom{r+1}{2}}\nu +1$
, then either
![]() $H$
has an edge of multiplicity at least
$H$
has an edge of multiplicity at least
![]() $\nu +1$
or
$\nu +1$
or
-
(i) if
 $s=2$
, then
$s=2$
, then
 $\Delta (H)\geq \frac{n-2\nu }{r-1}$
.
$\Delta (H)\geq \frac{n-2\nu }{r-1}$
. -
(ii) if
 $s=r$
, then
$s=r$
, then
 $\Delta (H)\geq n-2\nu$
.
$\Delta (H)\geq n-2\nu$
. -
(iii) if
 $s=r-1\geq 3$
, then
$s=r-1\geq 3$
, then
 $\Delta (H)\geq \frac{(r-1)n}{r}-2(r-1)\nu$
.
$\Delta (H)\geq \frac{(r-1)n}{r}-2(r-1)\nu$
.
Proof. Let
![]() $V_1, \ldots, V_r$
be the parts of
$V_1, \ldots, V_r$
be the parts of
![]() $H$
. For a set
$H$
. For a set
![]() $U\subseteq V(H)$
, let
$U\subseteq V(H)$
, let
![]() $d(U)$
denote the number of edges, counting multiplicity, which contain
$d(U)$
denote the number of edges, counting multiplicity, which contain
![]() $U$
(i.e.
$U$
(i.e.
![]() $d(U)$
is the degree of
$d(U)$
is the degree of
![]() $U$
). Note that since
$U$
). Note that since
![]() $H$
is
$H$
is
![]() $r$
-partite,
$r$
-partite,
![]() $d(U)\gt 0$
implies that
$d(U)\gt 0$
implies that
![]() $U$
contains at most one vertex from each part
$U$
contains at most one vertex from each part
![]() $V_i$
. Let
$V_i$
. Let
![]() $U\subseteq V(H)$
be maximum such that
$U\subseteq V(H)$
be maximum such that
![]() $d(U)\geq 3^{\binom{r+2-|U|}{2}} \nu +1$
and note that
$d(U)\geq 3^{\binom{r+2-|U|}{2}} \nu +1$
and note that
![]() $U\neq \emptyset$
by the degree condition. Without loss of generality, suppose
$U\neq \emptyset$
by the degree condition. Without loss of generality, suppose
![]() $U=\{u_1, \ldots, u_\ell \}$
with
$U=\{u_1, \ldots, u_\ell \}$
with
![]() $u_i\in V_i$
for all
$u_i\in V_i$
for all
![]() $i\in [\ell ]$
and let
$i\in [\ell ]$
and let
![]() $E$
be the set of edges containing
$E$
be the set of edges containing
![]() $U$
. If
$U$
. If
![]() $\ell =r$
, we have an edge of multiplicity at least
$\ell =r$
, we have an edge of multiplicity at least
![]() $3\nu +1\geq \nu +1$
and we are done; so suppose
$3\nu +1\geq \nu +1$
and we are done; so suppose
![]() $1\leq \ell \leq r-1$
.
$1\leq \ell \leq r-1$
.
Case (i) (
![]() $s=2$
). Let
$s=2$
). Let
![]() $F=\{f\in E(H)\;:\; f\cap U=\emptyset \}$
. If
$F=\{f\in E(H)\;:\; f\cap U=\emptyset \}$
. If
![]() $|F|\leq \frac{(r-1-\ell )n+2\ell \nu }{r-1}$
, then for some
$|F|\leq \frac{(r-1-\ell )n+2\ell \nu }{r-1}$
, then for some
![]() $i\in [\ell ]$
,
$i\in [\ell ]$
,
and we are done; so suppose
![]() $|F|\gt \frac{(r-1-\ell )n+2\ell \nu }{r-1}\geq 2^{r-\ell }\nu$
(where the last inequality holds since
$|F|\gt \frac{(r-1-\ell )n+2\ell \nu }{r-1}\geq 2^{r-\ell }\nu$
(where the last inequality holds since
![]() $\nu \leq \frac{n}{2^r}$
) and thus we have
$\nu \leq \frac{n}{2^r}$
) and thus we have
![]() $|F|\geq 2^{r-\ell }\nu +1$
.
$|F|\geq 2^{r-\ell }\nu +1$
.
Applying Lemma 4.5 at most
![]() $r-\ell$
times with
$r-\ell$
times with
![]() $E, F$
and using the fact that
$E, F$
and using the fact that
![]() $\nu _2(H)\leq \nu$
, it must be the case that (B1) holds within
$\nu _2(H)\leq \nu$
, it must be the case that (B1) holds within
![]() $r-\ell$
steps and we obtain a vertex which is incident with at least
$r-\ell$
steps and we obtain a vertex which is incident with at least
![]() $\frac{3^{\binom{r+2-\ell }{2}-1}}{3^{r-\ell }}\nu +1=3^{\binom{r+2-(\ell +1)}{2}}\nu +1$
edges of
$\frac{3^{\binom{r+2-\ell }{2}-1}}{3^{r-\ell }}\nu +1=3^{\binom{r+2-(\ell +1)}{2}}\nu +1$
edges of
![]() $E$
contradicting the maximality of
$E$
contradicting the maximality of
![]() $U$
.
$U$
.
Case (ii) and (iii) (
![]() $r-1\leq s\leq r$
).
$r-1\leq s\leq r$
).
Since
![]() $|E|=d(U)\geq 3^{\binom{r+2-\ell }{2}}\geq 2(3^{\binom{r+2-\ell }{2}-1}\nu +1)$
, we can choose disjoint subsets
$|E|=d(U)\geq 3^{\binom{r+2-\ell }{2}}\geq 2(3^{\binom{r+2-\ell }{2}-1}\nu +1)$
, we can choose disjoint subsets
![]() $E_1$
and
$E_1$
and
![]() $E_2$
of
$E_2$
of
![]() $E$
, each with at least
$E$
, each with at least
![]() $3^{\binom{r+2-\ell }{2}-1} \nu +1$
edges. Applying Lemma 4.6 at most
$3^{\binom{r+2-\ell }{2}-1} \nu +1$
edges. Applying Lemma 4.6 at most
![]() $r-\ell$
times with
$r-\ell$
times with
![]() $E_1,E_2$
, we will either find a vertex which is contained in at least
$E_1,E_2$
, we will either find a vertex which is contained in at least
![]() $\frac{3^{\binom{r+2-\ell }{2}-1}}{3^{r-\ell }}\nu +1=3^{\binom{r+2-(\ell +1)}{2}}\nu +1$
edges from both
$\frac{3^{\binom{r+2-\ell }{2}-1}}{3^{r-\ell }}\nu +1=3^{\binom{r+2-(\ell +1)}{2}}\nu +1$
edges from both
![]() $E_1$
and
$E_1$
and
![]() $E_2$
, which would violate the maximality of
$E_2$
, which would violate the maximality of
![]() $U$
, or else we will get sets
$U$
, or else we will get sets
![]() $E^{\prime}_1\subseteq E_1$
and
$E^{\prime}_1\subseteq E_1$
and
![]() $E^{\prime}_2\subseteq E_2$
with
$E^{\prime}_2\subseteq E_2$
with
(where the last inequality holds since
![]() $\ell \leq r-1$
).
$\ell \leq r-1$
).
Case (ii) (
![]() $s=r$
). We have the desired degree condition unless for all
$s=r$
). We have the desired degree condition unless for all
![]() $i\in [\ell ]$
, the set
$i\in [\ell ]$
, the set
![]() $F_i$
of edges which avoids
$F_i$
of edges which avoids
![]() $u_i$
has order at least
$u_i$
has order at least
![]() $2\nu +1$
. If
$2\nu +1$
. If
![]() $\ell \leq r-2$
, then
$\ell \leq r-2$
, then
![]() $E^{\prime}_1, E^{\prime}_2, F_1, \ldots, F_\ell$
is a collection of
$E^{\prime}_1, E^{\prime}_2, F_1, \ldots, F_\ell$
is a collection of
![]() $\ell +2\leq r$
sets each of order at least
$\ell +2\leq r$
sets each of order at least
![]() $\nu +1$
which are not cross intersecting, violating the bound on
$\nu +1$
which are not cross intersecting, violating the bound on
![]() $\nu _r(H)$
.
$\nu _r(H)$
.
So suppose
![]() $\ell =r-1$
. Applying Lemma 4.5 with
$\ell =r-1$
. Applying Lemma 4.5 with
![]() $E, F_1, \ldots, F_\ell$
and using the fact that
$E, F_1, \ldots, F_\ell$
and using the fact that
![]() $\ell +1\leq r$
and
$\ell +1\leq r$
and
![]() $\nu _r(H)\leq \nu$
, it must be the case that (B1) holds and we obtain a vertex which is incident with at least
$\nu _r(H)\leq \nu$
, it must be the case that (B1) holds and we obtain a vertex which is incident with at least
![]() $3\nu +1$
; that is, an edge of multiplicity at least
$3\nu +1$
; that is, an edge of multiplicity at least
![]() $\nu +1$
.
$\nu +1$
.
Case (iii) (
![]() $s=r-1\geq 3$
). We have the desired degree condition unless for all
$s=r-1\geq 3$
). We have the desired degree condition unless for all
![]() $i\in [\ell ]$
, the set
$i\in [\ell ]$
, the set
![]() $F_i$
of edges which avoids
$F_i$
of edges which avoids
![]() $u_i$
has order at least
$u_i$
has order at least
![]() $\frac{n}{r}+2(r-1)\nu +1$
. If
$\frac{n}{r}+2(r-1)\nu +1$
. If
![]() $\ell \leq r-3$
, then
$\ell \leq r-3$
, then
![]() $E^{\prime}_1, E^{\prime}_2, F_1, \ldots, F_\ell$
is a family of
$E^{\prime}_1, E^{\prime}_2, F_1, \ldots, F_\ell$
is a family of
![]() $\ell +2\leq r-1$
sets of at least
$\ell +2\leq r-1$
sets of at least
![]() $\nu +1$
edges each which are not cross intersecting and thus
$\nu +1$
edges each which are not cross intersecting and thus
![]() $\nu _{r-1}(H)\geq \nu _{\ell +2}(H)\geq \nu +1$
, contradicting the assumption. If
$\nu _{r-1}(H)\geq \nu _{\ell +2}(H)\geq \nu +1$
, contradicting the assumption. If
![]() $\ell = r-2$
, then applying Lemma 4.5 at most twice with
$\ell = r-2$
, then applying Lemma 4.5 at most twice with
![]() $E, F_1, \ldots, F_\ell$
and using the fact that
$E, F_1, \ldots, F_\ell$
and using the fact that
![]() $\ell +1\leq r-1$
and
$\ell +1\leq r-1$
and
![]() $\nu _{r-1}(H)\leq \nu$
, it must be the case that (B1) holds within two steps and we obtain a vertex which is incident with at least
$\nu _{r-1}(H)\leq \nu$
, it must be the case that (B1) holds within two steps and we obtain a vertex which is incident with at least
![]() $\frac{3^{\binom{4}{2}-1}}{3^{2}}\nu +1=3^3\nu +1$
edges of
$\frac{3^{\binom{4}{2}-1}}{3^{2}}\nu +1=3^3\nu +1$
edges of
![]() $E$
contradicting the maximality of
$E$
contradicting the maximality of
![]() $U$
.
$U$
.
So finally suppose
![]() $\ell =r-1$
. If there exists distinct
$\ell =r-1$
. If there exists distinct
![]() $i,j\in [r-1]$
such that
$i,j\in [r-1]$
such that
![]() $|F_i\cap F_j|\geq 2\nu +1$
, without loss of generality say
$|F_i\cap F_j|\geq 2\nu +1$
, without loss of generality say
![]() $|F_{r-2}\cap F_{r-1}|\geq 2\nu +1$
, then we apply Lemma 4.5 with
$|F_{r-2}\cap F_{r-1}|\geq 2\nu +1$
, then we apply Lemma 4.5 with
![]() $E, F_1, \ldots, F_{r-3}, F_{r-2}\cap F_{r-1}$
and since (B2) can’t happen, we have (B1) which gives us an edge of multiplicity at least
$E, F_1, \ldots, F_{r-3}, F_{r-2}\cap F_{r-1}$
and since (B2) can’t happen, we have (B1) which gives us an edge of multiplicity at least
![]() $\nu +1$
. So suppose
$\nu +1$
. So suppose
![]() $|F_i\cap F_j|\leq 2\nu$
for all distinct
$|F_i\cap F_j|\leq 2\nu$
for all distinct
![]() $i,j\in [r-1]$
. For all
$i,j\in [r-1]$
. For all
![]() $i\in [r-1]$
, let
$i\in [r-1]$
, let
![]() $F_i^*=F_i\setminus (\bigcup _{j\in [r-1]\setminus \{i\}}F_j)$
and note that by the previous sentence and the bound on
$F_i^*=F_i\setminus (\bigcup _{j\in [r-1]\setminus \{i\}}F_j)$
and note that by the previous sentence and the bound on
![]() $|F_i|$
, we have
$|F_i|$
, we have
![]() $|F_i^*|\geq |F_i|-2(r-2)\nu \geq \frac{n}{r}+2\nu +1$
. Note that
$|F_i^*|\geq |F_i|-2(r-2)\nu \geq \frac{n}{r}+2\nu +1$
. Note that
![]() $F_1^*, \ldots, F_{r-1}^*$
must be cross-intersecting and by the way the sets are defined, the cross-intersection must happen in
$F_1^*, \ldots, F_{r-1}^*$
must be cross-intersecting and by the way the sets are defined, the cross-intersection must happen in
![]() $V_r$
. Now applying Lemma 4.5 with
$V_r$
. Now applying Lemma 4.5 with
![]() $F_1^*, \ldots, F_{r-1}^*$
, we get a vertex in
$F_1^*, \ldots, F_{r-1}^*$
, we get a vertex in
![]() $V_r$
which is adjacent with at least
$V_r$
which is adjacent with at least
![]() $|F_i^*|-\nu \geq \frac{n}{r}$
edges from each of
$|F_i^*|-\nu \geq \frac{n}{r}$
edges from each of
![]() $F_1^*, \ldots, F_{r-1}^*$
giving us a vertex of degree at least
$F_1^*, \ldots, F_{r-1}^*$
giving us a vertex of degree at least
![]() $\frac{r-1}{r}n\geq \frac{r-1}{r}n-2(r-1)\nu$
as desired.
$\frac{r-1}{r}n\geq \frac{r-1}{r}n-2(r-1)\nu$
as desired.
4.2. Theorem 4.1 and Theorem 4.2
Lemma 4.10.
Let
![]() $r\geq 2$
and let
$r\geq 2$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite multi-hypergraph with
$r$
-partite multi-hypergraph with
![]() $n$
edges and set
$n$
edges and set
![]() $\nu \;:\!=\;\nu _{2}(H)$
. If
$\nu \;:\!=\;\nu _{2}(H)$
. If
![]() $H$
has an edge
$H$
has an edge
![]() $e=\{u_1, \ldots, u_r\}$
of multiplicity at least
$e=\{u_1, \ldots, u_r\}$
of multiplicity at least
![]() $\nu +1$
, then
$\nu +1$
, then
-
(i) there are at least
 $n-\nu$
edges incident with
$n-\nu$
edges incident with
 $e$
,
$e$
, -
(ii) for all
 $e'\subseteq e$
with
$e'\subseteq e$
with
 $1\leq |e'|\leq r-1$
, either the number of edges incident with every vertex in
$1\leq |e'|\leq r-1$
, either the number of edges incident with every vertex in
 $e'$
and no vertex in
$e'$
and no vertex in
 $e\setminus e'$
is at most
$e\setminus e'$
is at most
 $\nu$
, or the number of edges incident with every vertex in
$\nu$
, or the number of edges incident with every vertex in
 $e\setminus e'$
and no vertex in
$e\setminus e'$
and no vertex in
 $e'$
is at most
$e'$
is at most
 $\nu$
, and
$\nu$
, and
-
(iii) either
 $\Delta (H)\geq \frac{n}{r-1}-2\nu$
, or for all
$\Delta (H)\geq \frac{n}{r-1}-2\nu$
, or for all
 $e'\subseteq e$
with
$e'\subseteq e$
with
 $1\leq |e'|\leq r-1$
, there are at least
$1\leq |e'|\leq r-1$
, there are at least
 $\frac{(r-1-|e'|)n}{r-1}+(2|e'|-1)\nu +1$
edges incident with
$\frac{(r-1-|e'|)n}{r-1}+(2|e'|-1)\nu +1$
edges incident with
 $e\setminus e'$
but not
$e\setminus e'$
but not
 $e'$
.
$e'$
.
Proof. Note that (i) and (ii) just follow from the condition on
![]() $\nu _2(H)$
. To see (iii), let
$\nu _2(H)$
. To see (iii), let
![]() $e'\subseteq e$
with
$e'\subseteq e$
with
![]() $1\leq |e'|\;=\!:\;t\leq r-1$
. If the number of edges incident with
$1\leq |e'|\;=\!:\;t\leq r-1$
. If the number of edges incident with
![]() $e'$
is at least
$e'$
is at least
![]() $\frac{tn}{r-1}-2t\nu$
, then some
$\frac{tn}{r-1}-2t\nu$
, then some
![]() $u\in e'$
satisfies
$u\in e'$
satisfies
![]() $d(u)\geq \frac{n}{r-1}-2\nu$
and we are done. So suppose that
$d(u)\geq \frac{n}{r-1}-2\nu$
and we are done. So suppose that
![]() $e'$
is incident with fewer than
$e'$
is incident with fewer than
![]() $\frac{tn}{r-1}-2t\nu$
edges, which means there are at least
$\frac{tn}{r-1}-2t\nu$
edges, which means there are at least
edges which are incident with
![]() $e\setminus e'$
but not
$e\setminus e'$
but not
![]() $e'$
.
$e'$
.
Now we prove that if
![]() $H$
is a bipartite multigraph with
$H$
is a bipartite multigraph with
![]() $n$
edges and
$n$
edges and
![]() $\nu _2(H)\lt n/6$
, then
$\nu _2(H)\lt n/6$
, then
![]() $\Delta (H)\geq n-2\nu _2(H)$
.
$\Delta (H)\geq n-2\nu _2(H)$
.
Proof of Theorem
4.1. Let
![]() $V_1, V_2$
be the parts of
$V_1, V_2$
be the parts of
![]() $H$
and set
$H$
and set
![]() $\nu \;:\!=\;\nu _2(H)\lt n/6$
.
$\nu \;:\!=\;\nu _2(H)\lt n/6$
.
Case 1 (There exists an edge
![]() $u_1u_2$
of multiplicity at least
$u_1u_2$
of multiplicity at least
![]() $\nu +1$
). By Lemma 4.10(i) and (ii), there are at least
$\nu +1$
). By Lemma 4.10(i) and (ii), there are at least
![]() $n-\nu$
edges incident with
$n-\nu$
edges incident with
![]() $\{u_1,u_2\}$
and without loss of generality, there are at most
$\{u_1,u_2\}$
and without loss of generality, there are at most
![]() $\nu$
edges which are incident with
$\nu$
edges which are incident with
![]() $u_2$
but not
$u_2$
but not
![]() $u_1$
. Thus there are at least
$u_1$
. Thus there are at least
![]() $n-2\nu$
edges incident with
$n-2\nu$
edges incident with
![]() $u_1$
; that is,
$u_1$
; that is,
![]() $\Delta (H)\geq n-2\nu$
.
$\Delta (H)\geq n-2\nu$
.
Case 2 (Every edge has multiplicity at most
![]() $\nu$
). Suppose first that there exists
$\nu$
). Suppose first that there exists
![]() $u_1\in V_1, u_2\in V_2$
so that
$u_1\in V_1, u_2\in V_2$
so that
![]() $d(u_1), d(u_2)\geq 2\nu +1$
. Since
$d(u_1), d(u_2)\geq 2\nu +1$
. Since
![]() $u_1u_2$
has multiplicity at most
$u_1u_2$
has multiplicity at most
![]() $\nu$
, there are at least
$\nu$
, there are at least
![]() $\nu +1$
edges incident with
$\nu +1$
edges incident with
![]() $u_1$
but not
$u_1$
but not
![]() $u_2$
and at least
$u_2$
and at least
![]() $\nu +1$
edges incident with
$\nu +1$
edges incident with
![]() $u_2$
but not
$u_2$
but not
![]() $u_1$
, a violation of the fact that
$u_1$
, a violation of the fact that
![]() $\nu _2(H)\leq \nu$
. So suppose without loss of generality that
$\nu _2(H)\leq \nu$
. So suppose without loss of generality that
Now let
![]() $V^{\prime}_2\subseteq V_2$
be minimal such that
$V^{\prime}_2\subseteq V_2$
be minimal such that
![]() $e(V^{\prime}_2, V_1)\geq 2\nu +1$
. By (2) and minimality, we have
$e(V^{\prime}_2, V_1)\geq 2\nu +1$
. By (2) and minimality, we have
![]() $2\nu +1\leq e(V^{\prime}_2, V_1)\leq 4\nu$
. Since
$2\nu +1\leq e(V^{\prime}_2, V_1)\leq 4\nu$
. Since
![]() $6\nu \lt n$
, we also have
$6\nu \lt n$
, we also have
![]() $e(V_2\setminus V^{\prime}_2, V_1) = n - e(V^{\prime}_2, V_1)\geq 2\nu +1$
. Furthermore, by pigeonhole and the fact that
$e(V_2\setminus V^{\prime}_2, V_1) = n - e(V^{\prime}_2, V_1)\geq 2\nu +1$
. Furthermore, by pigeonhole and the fact that
![]() $6\nu \lt n$
, we have either
$6\nu \lt n$
, we have either
![]() $e(V^{\prime}_2, V_1)\geq 3\nu +1$
or
$e(V^{\prime}_2, V_1)\geq 3\nu +1$
or
![]() $e(V_2\setminus V^{\prime}_2, V_1)\geq 3\nu +1$
. So by applying Lemma 4.5 (with
$e(V_2\setminus V^{\prime}_2, V_1)\geq 3\nu +1$
. So by applying Lemma 4.5 (with
![]() $a_1=a_2=1$
,
$a_1=a_2=1$
,
![]() $i=1$
,
$i=1$
,
![]() $F_1=E(V^{\prime}_2, V_1)$
, and
$F_1=E(V^{\prime}_2, V_1)$
, and
![]() $F_2=E(V_2\setminus V^{\prime}_2, V_1)$
), we either have (B2) (that is, there exists
$F_2=E(V_2\setminus V^{\prime}_2, V_1)$
), we either have (B2) (that is, there exists
![]() $F^{\prime}_1\subseteq F_1$
with
$F^{\prime}_1\subseteq F_1$
with
![]() $|F^{\prime}_1|\geq \nu +1$
and
$|F^{\prime}_1|\geq \nu +1$
and
![]() $F^{\prime}_2\subseteq F_2$
with
$F^{\prime}_2\subseteq F_2$
with
![]() $|F^{\prime}_2|\geq \nu +1$
such that
$|F^{\prime}_2|\geq \nu +1$
such that
![]() $F^{\prime}_1$
and
$F^{\prime}_1$
and
![]() $F^{\prime}_2$
are not cross intersecting in
$F^{\prime}_2$
are not cross intersecting in
![]() $V_1$
) which violates the fact that
$V_1$
) which violates the fact that
![]() $\nu _2(H)\leq \nu$
, or (B1) which implies that there exists a vertex in
$\nu _2(H)\leq \nu$
, or (B1) which implies that there exists a vertex in
![]() $V_1$
which is incident with at least
$V_1$
which is incident with at least
![]() $|F_1|+|F_2|-2\nu =n-2\nu$
edges; that is,
$|F_1|+|F_2|-2\nu =n-2\nu$
edges; that is,
![]() $\Delta (H)\geq n-2\nu$
.
$\Delta (H)\geq n-2\nu$
.
Proposition 4.11.
Let
![]() $H$
be an
$H$
be an
![]() $3$
-partite
$3$
-partite
![]() $3$
-uniform multi-hypergraph with
$3$
-uniform multi-hypergraph with
![]() $n$
edges and set
$n$
edges and set
![]() $\nu \;:\!=\;\nu _{2}(H)$
. If
$\nu \;:\!=\;\nu _{2}(H)$
. If
![]() $H$
has an edge of multiplicity at least
$H$
has an edge of multiplicity at least
![]() $\nu +1$
, then
$\nu +1$
, then
![]() $\Delta (H)\geq \frac{n}{2}-2\nu$
.
$\Delta (H)\geq \frac{n}{2}-2\nu$
.
Proof. Let
![]() $e=\{u_1,u_2, u_3\}$
be an edge of multiplicity at least
$e=\{u_1,u_2, u_3\}$
be an edge of multiplicity at least
![]() $\nu +1$
. For all distinct
$\nu +1$
. For all distinct
![]() $i,j,k\in [3]$
, let
$i,j,k\in [3]$
, let
![]() $E_i$
be the set of edges incident with
$E_i$
be the set of edges incident with
![]() $u_i$
and let
$u_i$
and let
![]() $E^{\prime}_i=E_i\setminus (E_j\cup E_k)$
. By Lemma 4.10.(iii) we have
$E^{\prime}_i=E_i\setminus (E_j\cup E_k)$
. By Lemma 4.10.(iii) we have
![]() $|(E_1\cup E_2)\setminus E_3|\geq \frac{n}{2}+\nu +1$
and for all
$|(E_1\cup E_2)\setminus E_3|\geq \frac{n}{2}+\nu +1$
and for all
![]() $i\in [3]$
,
$i\in [3]$
,
![]() $|E^{\prime}_i|\geq 3\nu +1$
. So by Lemma 4.10.(ii),
$|E^{\prime}_i|\geq 3\nu +1$
. So by Lemma 4.10.(ii),
![]() $|(E_1\cap E_2)\setminus E_3|\leq \nu$
. Thus
$|(E_1\cap E_2)\setminus E_3|\leq \nu$
. Thus
![]() $|E^{\prime}_1|+|E^{\prime}_2|\geq \frac{n}{2}+1$
. Now applying Lemma 4.6 with
$|E^{\prime}_1|+|E^{\prime}_2|\geq \frac{n}{2}+1$
. Now applying Lemma 4.6 with
![]() $E^{\prime}_1$
and
$E^{\prime}_1$
and
![]() $E^{\prime}_2$
, we can’t have (B2
′), thus (B1
′) holds and we have a vertex in
$E^{\prime}_2$
, we can’t have (B2
′), thus (B1
′) holds and we have a vertex in
![]() $V_3$
which is incident with more than
$V_3$
which is incident with more than
![]() $\frac{n}{2}-2\nu$
edges.
$\frac{n}{2}-2\nu$
edges.
Now we prove that if
![]() $H$
is a
$H$
is a
![]() $3$
-partite
$3$
-partite
![]() $3$
-uniform multi-hypergraph with
$3$
-uniform multi-hypergraph with
![]() $n$
edges and
$n$
edges and
![]() $\nu _{2}(H)\leq \frac{n}{3^9}=\frac{n}{19683}$
, then
$\nu _{2}(H)\leq \frac{n}{3^9}=\frac{n}{19683}$
, then
![]() $\Delta (H)\geq \frac{n}{2}-2\nu _2(H)$
.
$\Delta (H)\geq \frac{n}{2}-2\nu _2(H)$
.
Proof of Theorem
4.2. Set
![]() $\nu \;:\!=\;\nu _2(H)$
. By Lemma 4.8 (with
$\nu \;:\!=\;\nu _2(H)$
. By Lemma 4.8 (with
![]() $\Delta =729=3^6$
), we have
$\Delta =729=3^6$
), we have
![]() $\Delta (H)\geq 729 \nu +1=3^{\binom{3+1}{2}}\nu +1$
. Now by Lemma 4.9, we are done or we have an edge of multiplicity at least
$\Delta (H)\geq 729 \nu +1=3^{\binom{3+1}{2}}\nu +1$
. Now by Lemma 4.9, we are done or we have an edge of multiplicity at least
![]() $\nu +1$
in which case we are done by Proposition 4.11.
$\nu +1$
in which case we are done by Proposition 4.11.
In this subsection we solved Problem 1.2 in the case
![]() $k=2$
and
$k=2$
and
![]() $2\leq r\leq 3$
. Because of Lemma 4.8 and Lemma 4.9, in order to solve Problem 1.2 in the case
$2\leq r\leq 3$
. Because of Lemma 4.8 and Lemma 4.9, in order to solve Problem 1.2 in the case
![]() $k=2$
and
$k=2$
and
![]() $r\geq 4$
it suffices to prove the following generalisation of Proposition 4.11.
$r\geq 4$
it suffices to prove the following generalisation of Proposition 4.11.
Conjecture 4.12.
Let
![]() $r\geq 4$
and let
$r\geq 4$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with
$r$
-uniform multi-hypergraph with
![]() $n$
edges and set
$n$
edges and set
![]() $\nu \;:\!=\;\nu _{2}(H)$
. There exists
$\nu \;:\!=\;\nu _{2}(H)$
. There exists
![]() $d_r\gt 0$
such that if
$d_r\gt 0$
such that if
![]() $H$
has an edge of multiplicity at least
$H$
has an edge of multiplicity at least
![]() $\nu +1$
, then
$\nu +1$
, then
![]() $\Delta (H)\geq \frac{n}{r-1}-d_r\nu$
.
$\Delta (H)\geq \frac{n}{r-1}-d_r\nu$
.
The following is essentially a much weaker version of the previous conjecture.
Proposition 4.13.
Let
![]() $r\geq 4$
and let
$r\geq 4$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform multi-hypergraph with
$r$
-uniform multi-hypergraph with
![]() $n$
edges. If
$n$
edges. If
![]() $\nu _{2}(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
$\nu _{2}(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
![]() $\Delta (H)\geq \frac{n-\nu _2(H)}{r}$
.
$\Delta (H)\geq \frac{n-\nu _2(H)}{r}$
.
Proof. Set
![]() $\nu \;:\!=\;\nu _{2}(H)$
. By Lemma 4.8 we have
$\nu \;:\!=\;\nu _{2}(H)$
. By Lemma 4.8 we have
![]() $\Delta (H)\geq 3^{\binom{r+1}{2}}\nu +1$
. Now by Lemma 4.9, we are done or we have an edge
$\Delta (H)\geq 3^{\binom{r+1}{2}}\nu +1$
. Now by Lemma 4.9, we are done or we have an edge
![]() $e$
of multiplicity at least
$e$
of multiplicity at least
![]() $\nu +1$
. Thus by Lemma 4.10.(i), we have
$\nu +1$
. Thus by Lemma 4.10.(i), we have
![]() $n-\nu$
edges incident with
$n-\nu$
edges incident with
![]() $e$
so, by averaging, one of these vertices has degree at least
$e$
so, by averaging, one of these vertices has degree at least
![]() $\frac{n-\nu }{r}$
.
$\frac{n-\nu }{r}$
.
4.3. Theorem 4.3
Proposition 4.14.
Let
![]() $r\geq 3$
and let
$r\geq 3$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform hypergraph with
$r$
-uniform hypergraph with
![]() $n$
edges and set
$n$
edges and set
![]() $\nu \;:\!=\;\nu _r(H)$
. If
$\nu \;:\!=\;\nu _r(H)$
. If
![]() $H$
has an edge of multiplicity at least
$H$
has an edge of multiplicity at least
![]() $\nu +1$
, then
$\nu +1$
, then
![]() $\Delta (H)\geq n-(r-1)\nu$
.
$\Delta (H)\geq n-(r-1)\nu$
.
Proof. Assume there exists an edge
![]() $e=\{u_1, \ldots, u_r\}$
of multiplicity at least
$e=\{u_1, \ldots, u_r\}$
of multiplicity at least
![]() $\nu +1$
. For all
$\nu +1$
. For all
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $F_i$
be the set of edges which avoid
$F_i$
be the set of edges which avoid
![]() $u_i$
. If
$u_i$
. If
![]() $|F_i|\leq (r-1)\nu$
for some
$|F_i|\leq (r-1)\nu$
for some
![]() $i\in [r]$
, then
$i\in [r]$
, then
![]() $d(u_i)\geq n-(r-1)\nu$
and we are done; so suppose
$d(u_i)\geq n-(r-1)\nu$
and we are done; so suppose
![]() $|F_i|\geq (r-1)\nu +1$
for all
$|F_i|\geq (r-1)\nu +1$
for all
![]() $i\in [r]$
.
$i\in [r]$
.
Claim 4.15.
For all distinct
![]() $i,j\in [r]$
,
$i,j\in [r]$
,
![]() $|F_i\cap F_j|\leq \nu$
.
$|F_i\cap F_j|\leq \nu$
.
Proof. Suppose for contradiction that
![]() $|F_i\cap F_j|\geq \nu +1$
for some distinct
$|F_i\cap F_j|\geq \nu +1$
for some distinct
![]() $i,j\in [r]$
and without loss of generality suppose
$i,j\in [r]$
and without loss of generality suppose
![]() $\{i,j\}=[2]$
. Now
$\{i,j\}=[2]$
. Now
![]() $e, F_1\cap F_2, F_3, \ldots, F_r$
is a collection of
$e, F_1\cap F_2, F_3, \ldots, F_r$
is a collection of
![]() $r$
sets violating
$r$
sets violating
![]() $\nu _{r}(H)\leq \nu$
.
$\nu _{r}(H)\leq \nu$
.
Now for all
![]() $i\in [r-1]$
, let
$i\in [r-1]$
, let
![]() $F^{\prime}_i=F_i\setminus \bigcup _{j\in [r]\setminus \{i,i+1\}}F_j$
and let
$F^{\prime}_i=F_i\setminus \bigcup _{j\in [r]\setminus \{i,i+1\}}F_j$
and let
![]() $F^{\prime}_r=F_r\setminus \bigcup _{j\in [r]\setminus \{r,1\}}F_j$
. Note that by Claim 4.15 we have that for all
$F^{\prime}_r=F_r\setminus \bigcup _{j\in [r]\setminus \{r,1\}}F_j$
. Note that by Claim 4.15 we have that for all
![]() $i\in [r]$
,
$i\in [r]$
,
![]() $|F^{\prime}_i|\geq (r-1)\nu +1-(r-2)\nu =\nu +1$
. Furthermore, by construction, we have
$|F^{\prime}_i|\geq (r-1)\nu +1-(r-2)\nu =\nu +1$
. Furthermore, by construction, we have
![]() $F^{\prime}_i\cap F^{\prime}_j=\emptyset$
for all distinct
$F^{\prime}_i\cap F^{\prime}_j=\emptyset$
for all distinct
![]() $i,j\in [r]$
. So we have
$i,j\in [r]$
. So we have
![]() $r$
disjoint sets
$r$
disjoint sets
![]() $F^{\prime}_1, \ldots, F_r'$
each of order at least
$F^{\prime}_1, \ldots, F_r'$
each of order at least
![]() $\nu +1$
which are not cross intersecting, violating the assumption. Indeed, let
$\nu +1$
which are not cross intersecting, violating the assumption. Indeed, let
![]() $e_i\in F^{\prime}_i$
for all
$e_i\in F^{\prime}_i$
for all
![]() $i\in [r]$
and suppose for contradiction that
$i\in [r]$
and suppose for contradiction that
![]() $\bigcap _{i\in [r]}e_i\neq \emptyset$
. Let
$\bigcap _{i\in [r]}e_i\neq \emptyset$
. Let
![]() $u\in \bigcap _{i\in [r]}e_i$
and suppose without loss of generality that
$u\in \bigcap _{i\in [r]}e_i$
and suppose without loss of generality that
![]() $u\in V_1$
. We cannot have
$u\in V_1$
. We cannot have
![]() $u=u_1$
since
$u=u_1$
since
![]() $e_1\in F^{\prime}_1\subseteq F_1$
misses the vertex
$e_1\in F^{\prime}_1\subseteq F_1$
misses the vertex
![]() $u_1$
, but also we cannot have
$u_1$
, but also we cannot have
![]() $u\neq u_1$
since
$u\neq u_1$
since
![]() $e_2\in F^{\prime}_2$
and
$e_2\in F^{\prime}_2$
and
![]() $F^{\prime}_2\cap F_1=\emptyset$
and thus
$F^{\prime}_2\cap F_1=\emptyset$
and thus
![]() $e_2$
touches
$e_2$
touches
![]() $u_1$
.
$u_1$
.
Now we prove that if
![]() $r\geq 3$
and
$r\geq 3$
and
![]() $H$
is an
$H$
is an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform hypergraph with
$r$
-uniform hypergraph with
![]() $n$
edges and
$n$
edges and
![]() $\nu _r(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
$\nu _r(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
![]() $\Delta (H)\geq n-(r-1)\nu _r(H)$
.
$\Delta (H)\geq n-(r-1)\nu _r(H)$
.
4.4. Theorem 4.4
Proposition 4.16.
Let
![]() $r\geq 4$
and let
$r\geq 4$
and let
![]() $H$
be an
$H$
be an
![]() $r$
-partite multi-hypergraph with
$r$
-partite multi-hypergraph with
![]() $n$
edges and set
$n$
edges and set
![]() $\nu \;:\!=\;\nu _{r-1}(H)$
. If
$\nu \;:\!=\;\nu _{r-1}(H)$
. If
![]() $H$
has an edge of multiplicity at least
$H$
has an edge of multiplicity at least
![]() $\nu +1$
, then
$\nu +1$
, then
![]() $\Delta (H)\geq \frac{r-1}{r}n-\binom{r}{2}\nu$
.
$\Delta (H)\geq \frac{r-1}{r}n-\binom{r}{2}\nu$
.
Proof. Assume there exists an edge
![]() $e=\{u_1, \ldots, u_r\}$
of multiplicity at least
$e=\{u_1, \ldots, u_r\}$
of multiplicity at least
![]() $\nu +1$
. For all
$\nu +1$
. For all
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $F_i$
be the set of edges which avoid
$F_i$
be the set of edges which avoid
![]() $u_i$
. If
$u_i$
. If
![]() $|F_i|\leq \frac{n}{r}+\binom{r}{2}\nu$
for some
$|F_i|\leq \frac{n}{r}+\binom{r}{2}\nu$
for some
![]() $i\in [r]$
, then
$i\in [r]$
, then
![]() $\Delta (H)\geq \frac{r-1}{r}n-\binom{r}{2}\nu$
and we are done; so suppose
$\Delta (H)\geq \frac{r-1}{r}n-\binom{r}{2}\nu$
and we are done; so suppose
![]() $|F_i|\gt \frac{n}{r}+\binom{r}{2}\nu \ge (r-1)\nu +1$
for all
$|F_i|\gt \frac{n}{r}+\binom{r}{2}\nu \ge (r-1)\nu +1$
for all
![]() $i\in [r]$
. Let
$i\in [r]$
. Let
![]() $F=F_1\cup \cdots \cup F_r$
.
$F=F_1\cup \cdots \cup F_r$
.
Claim 4.17.
For all distinct
![]() $h,i,j\in [r]$
,
$h,i,j\in [r]$
,
![]() $|F_h\cap F_i\cap F_j|\leq \nu$
.
$|F_h\cap F_i\cap F_j|\leq \nu$
.
Proof. Suppose for contradiction that
![]() $|F_h\cap F_i\cap F_j|\geq \nu +1$
for some distinct
$|F_h\cap F_i\cap F_j|\geq \nu +1$
for some distinct
![]() $h,i,j\in [r]$
and without loss of generality suppose
$h,i,j\in [r]$
and without loss of generality suppose
![]() $\{h,i,j\}=[3]$
. Now
$\{h,i,j\}=[3]$
. Now
![]() $e, F_1\cap F_2\cap F_3, F_4, \ldots, F_r$
is a collection of
$e, F_1\cap F_2\cap F_3, F_4, \ldots, F_r$
is a collection of
![]() $r-1$
sets violating
$r-1$
sets violating
![]() $\nu _{r-1}(H)\leq \nu$
.
$\nu _{r-1}(H)\leq \nu$
.
Claim 4.18.
For all distinct
![]() $h,i,j,k\in [r]$
,
$h,i,j,k\in [r]$
,
![]() $|F_h\cap F_i|\leq \nu$
or
$|F_h\cap F_i|\leq \nu$
or
![]() $|F_j\cap F_k|\leq \nu$
.
$|F_j\cap F_k|\leq \nu$
.
Proof. Suppose for contradiction that
![]() $|F_h\cap F_i|\geq \nu +1$
and
$|F_h\cap F_i|\geq \nu +1$
and
![]() $|F_j\cap F_k|\geq \nu +1$
for some distinct
$|F_j\cap F_k|\geq \nu +1$
for some distinct
![]() $h,i,j,k\in [r]$
and without loss of generality suppose
$h,i,j,k\in [r]$
and without loss of generality suppose
![]() $\{h,i,j,k\}=[4]$
. Now
$\{h,i,j,k\}=[4]$
. Now
![]() $e, F_1\cap F_2, F_3\cap F_4, F_5, \ldots, F_r$
is a collection of
$e, F_1\cap F_2, F_3\cap F_4, F_5, \ldots, F_r$
is a collection of
![]() $r-1$
sets violating
$r-1$
sets violating
![]() $\nu _{r-1}(H)\leq \nu$
.
$\nu _{r-1}(H)\leq \nu$
.
For all
![]() $S\subseteq [r]$
, let
$S\subseteq [r]$
, let
![]() $\left (\cap _{i\in S}F_i\right )^*=\left (\cap _{i\in S}F_i\right )\setminus \left (\cup _{j\in [r]\setminus S}F_j\right )$
. In other words
$\left (\cap _{i\in S}F_i\right )^*=\left (\cap _{i\in S}F_i\right )\setminus \left (\cup _{j\in [r]\setminus S}F_j\right )$
. In other words
![]() $\left (\cap _{i\in S}F_i\right )^*$
is the collection of elements which are in all of the sets
$\left (\cap _{i\in S}F_i\right )^*$
is the collection of elements which are in all of the sets
![]() $F_i$
,
$F_i$
,
![]() $i\in S$
, but none of the other sets
$i\in S$
, but none of the other sets
![]() $F_j$
,
$F_j$
,
![]() $j\in [r]\setminus S$
.
$j\in [r]\setminus S$
.
Claim 4.19.
For all distinct
![]() $h,i,j\in [r]$
,
$h,i,j\in [r]$
,
![]() $|(F_h\cap F_i)^*|\leq \nu$
or
$|(F_h\cap F_i)^*|\leq \nu$
or
![]() $|F_j^*|\leq \nu$
.
$|F_j^*|\leq \nu$
.
Proof. Suppose for contradiction that
![]() $|(F_h\cap F_i)^*|\geq \nu +1$
and
$|(F_h\cap F_i)^*|\geq \nu +1$
and
![]() $|F_j^*|\geq \nu +1$
for some distinct
$|F_j^*|\geq \nu +1$
for some distinct
![]() $h,i,j\in [r]$
and without loss of generality suppose
$h,i,j\in [r]$
and without loss of generality suppose
![]() $\{h,i,j\}=[3]$
. Now the sets
$\{h,i,j\}=[3]$
. Now the sets
![]() $(F_1\cap F_2)^*, F_3^*, F_4, \ldots, F_r$
is a collection of
$(F_1\cap F_2)^*, F_3^*, F_4, \ldots, F_r$
is a collection of
![]() $r-1$
sets violating
$r-1$
sets violating
![]() $\nu _{r-1}(H)\leq \nu$
.
$\nu _{r-1}(H)\leq \nu$
.
Since
![]() $|F_i|\gt \frac{n}{r}+\binom{r}{2}\nu$
for all
$|F_i|\gt \frac{n}{r}+\binom{r}{2}\nu$
for all
![]() $i\in [r]$
, inclusion-exclusion implies that
$i\in [r]$
, inclusion-exclusion implies that
![]() $|F_i\cap F_j|\geq (r-1)\nu +1$
for some distinct
$|F_i\cap F_j|\geq (r-1)\nu +1$
for some distinct
![]() $i,j\in [r]$
; without loss of generality, say
$i,j\in [r]$
; without loss of generality, say
![]() $i=r-1$
and
$i=r-1$
and
![]() $j=r$
. Furthermore, by Claim 4.17 we must have that
$j=r$
. Furthermore, by Claim 4.17 we must have that
![]() $|(F_{r-1}\cap F_{r})^*|\geq \nu +1$
. Thus by Claim 4.18, we have that for all distinct
$|(F_{r-1}\cap F_{r})^*|\geq \nu +1$
. Thus by Claim 4.18, we have that for all distinct
![]() $i,j\in [r-2]$
,
$i,j\in [r-2]$
,
![]() $|F_i\cap F_j|\leq \nu$
, and by Claim 4.19 we have that for all
$|F_i\cap F_j|\leq \nu$
, and by Claim 4.19 we have that for all
![]() $i\in [r-2]$
,
$i\in [r-2]$
,
![]() $|F_i^*|\leq \nu$
.
$|F_i^*|\leq \nu$
.
So for all
![]() $i\in [r-2]$
, we have
$i\in [r-2]$
, we have
![]() $|F_i\setminus (F\setminus F_i)|\leq \nu$
,
$|F_i\setminus (F\setminus F_i)|\leq \nu$
,
![]() $|F_i\cap F_{r-1}\cap F_r|\leq \nu$
, and for all
$|F_i\cap F_{r-1}\cap F_r|\leq \nu$
, and for all
![]() $j\in [r-2]\setminus \{i\}$
,
$j\in [r-2]\setminus \{i\}$
,
![]() $|F_i\cap F_j|\leq \nu$
, thus
$|F_i\cap F_j|\leq \nu$
, thus
Let
![]() $i\in [r-2]$
. Without loss of generality, suppose
$i\in [r-2]$
. Without loss of generality, suppose
![]() $|F_i\cap F_r|\geq \frac{1}{2}(|F_i\cap F_{r-1}|+|F_i\cap F_r|)\geq \frac{n}{2r}+\nu \gt \nu$
. Thus by Claim 4.18 we have that for all
$|F_i\cap F_r|\geq \frac{1}{2}(|F_i\cap F_{r-1}|+|F_i\cap F_r|)\geq \frac{n}{2r}+\nu \gt \nu$
. Thus by Claim 4.18 we have that for all
![]() $j\in [r-2]\setminus \{i\}$
,
$j\in [r-2]\setminus \{i\}$
,
![]() $|F_j\cap F_{r-1}|\leq \nu$
which in turn implies that for all
$|F_j\cap F_{r-1}|\leq \nu$
which in turn implies that for all
![]() $i\in [r-2]$
,
$i\in [r-2]$
,
![]() $|(F_i\cap F_r)^*|\geq |F_i|-r\nu \gt \frac{n}{r}+\nu$
. By Claim 4.19 this implies that
$|(F_i\cap F_r)^*|\geq |F_i|-r\nu \gt \frac{n}{r}+\nu$
. By Claim 4.19 this implies that
![]() $|F_{r-1}^*|\leq \nu$
. Thus
$|F_{r-1}^*|\leq \nu$
. Thus
![]() $|(F_{r-1}\cap F_{r})\setminus (F_1\cup \cdots \cup F_{r-2})|\geq |F_{r-1}|-\nu -(r-2)\nu \geq \frac{n}{r}+\nu$
. Now we have a collection of
$|(F_{r-1}\cap F_{r})\setminus (F_1\cup \cdots \cup F_{r-2})|\geq |F_{r-1}|-\nu -(r-2)\nu \geq \frac{n}{r}+\nu$
. Now we have a collection of
![]() $r-1$
sets,
$r-1$
sets,
![]() $(F_1\cap F_r)^*, \ldots, (F_{r-2}\cap F_r)^*, (F_{r-1}\cap F_{r})^*$
all with more than
$(F_1\cap F_r)^*, \ldots, (F_{r-2}\cap F_r)^*, (F_{r-1}\cap F_{r})^*$
all with more than
![]() $\frac{n}{r}+\nu$
elements. Now applying Lemma 4.6 (with
$\frac{n}{r}+\nu$
elements. Now applying Lemma 4.6 (with
![]() $a_1=\cdots =a_{r-1}=1$
) to the collection of
$a_1=\cdots =a_{r-1}=1$
) to the collection of
![]() $r-1$
sets, we cannot have (B2
′) by the bound on
$r-1$
sets, we cannot have (B2
′) by the bound on
![]() $\nu _{r-1}(H)$
, so we must have (B1
′) which gives us a vertex in
$\nu _{r-1}(H)$
, so we must have (B1
′) which gives us a vertex in
![]() $V_r\setminus \{u_r\}$
with degree at least
$V_r\setminus \{u_r\}$
with degree at least
![]() $(r-1)((\frac{n}{r}+\nu )-\nu )=\frac{r-1}{r}n$
.
$(r-1)((\frac{n}{r}+\nu )-\nu )=\frac{r-1}{r}n$
.
Now we prove that if
![]() $r\geq 3$
and
$r\geq 3$
and
![]() $H$
is an
$H$
is an
![]() $r$
-partite
$r$
-partite
![]() $r$
-uniform hypergraph with
$r$
-uniform hypergraph with
![]() $n$
edges and
$n$
edges and
![]() $\nu _{r-1}(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
$\nu _{r-1}(H)\leq \frac{n}{3^{\binom{r+1}{2}+r}}$
, then
![]() $\Delta (H)\geq \frac{(r-1)n}{r}-\binom{r}{2}\nu _{r-1}(H)$
.
$\Delta (H)\geq \frac{(r-1)n}{r}-\binom{r}{2}\nu _{r-1}(H)$
.
5. Conclusion
We were able to solve Problem 1.2 in all cases corresponding to Theorem 1.1 except when
![]() $k=2$
and
$k=2$
and
![]() $r\geq 4$
. However because of Lemma 4.8 and Lemma 4.9, in order to solve the case
$r\geq 4$
. However because of Lemma 4.8 and Lemma 4.9, in order to solve the case
![]() $k=2$
and
$k=2$
and
![]() $r\geq 4$
it suffices to prove Conjecture 4.12. It would be very interesting to prove Conjecture 4.12 even in the case
$r\geq 4$
it suffices to prove Conjecture 4.12. It would be very interesting to prove Conjecture 4.12 even in the case
![]() $k=4$
.
$k=4$
.
Another possible direction for further study involves replacing large monochromatic components with long monochromatic paths. Letzter [Reference Letzter16] showed that in every 2-colouring of
![]() $G(n,p)$
with
$G(n,p)$
with
![]() $p=\frac{\omega (1)}{n}$
, there is w.h.p., a monochromatic cycle (path) of order at least
$p=\frac{\omega (1)}{n}$
, there is w.h.p., a monochromatic cycle (path) of order at least
![]() $(2/3-o(1))n$
. Bennett, DeBiasio, Dudek, and English [Reference Bennett, DeBiasio, Dudek and English5] generalised this result showing that if
$(2/3-o(1))n$
. Bennett, DeBiasio, Dudek, and English [Reference Bennett, DeBiasio, Dudek and English5] generalised this result showing that if
![]() $p=\frac{\omega (1)}{n^{k-1}}$
, then a.a.s. there is a monochromatic loose-cycle (loose-path) of order at least
$p=\frac{\omega (1)}{n^{k-1}}$
, then a.a.s. there is a monochromatic loose-cycle (loose-path) of order at least
![]() $(\frac{2k-2}{2k-1}-o(1))n$
in every 2-colouring of
$(\frac{2k-2}{2k-1}-o(1))n$
in every 2-colouring of
![]() $H^k(n,p)$
. Both of those results use sparse regularity and implicitly only use the fact
$H^k(n,p)$
. Both of those results use sparse regularity and implicitly only use the fact
![]() $\alpha _k(H)=o(n)$
, so we can retroactively rephrase their result as follows.
$\alpha _k(H)=o(n)$
, so we can retroactively rephrase their result as follows.
Theorem 5.1 (Bennett, DeBiasio, Dudek, and English [Reference Bennett, DeBiasio, Dudek and English5]). If
![]() $H$
is a
$H$
is a
![]() $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
![]() $n$
vertices with
$n$
vertices with
![]() $\alpha _k(H)=o(n)$
, then in every
$\alpha _k(H)=o(n)$
, then in every
![]() $2$
-colouring of the edges of
$2$
-colouring of the edges of
![]() $H$
, there exists a monochromatic loose-cycle (loose-path) of order at least
$H$
, there exists a monochromatic loose-cycle (loose-path) of order at least
![]() $(\frac{2k-2}{2k-1}-o(1))n$
.
$(\frac{2k-2}{2k-1}-o(1))n$
.
The idea is that it would be nice to extend the above theorem to hold when
![]() $\alpha _k(G)$
can be considerably larger (especially in the case
$\alpha _k(G)$
can be considerably larger (especially in the case
![]() $k=2$
).
$k=2$
).
There are two results in the literature which implicitly broach this subject. Balogh, Barát, Gerbner, Gyárfás, Sárközy [Reference Balogh, Barát, Gerbner, Gyárfás and Sárközy4] proved that in every 2-colouring of the edges of a graph
![]() $G$
on
$G$
on
![]() $n$
vertices there exist two vertex disjoint monochromatic paths covering at least
$n$
vertices there exist two vertex disjoint monochromatic paths covering at least
![]() $n-1000(50\alpha _2(G))^{\alpha _2(G)}$
vertices. Letzter [Reference Letzter16] implicitly proved that in every 2-colouring of every graph
$n-1000(50\alpha _2(G))^{\alpha _2(G)}$
vertices. Letzter [Reference Letzter16] implicitly proved that in every 2-colouring of every graph
![]() $G$
on
$G$
on
![]() $n$
vertices there is a monochromatic path of order at least
$n$
vertices there is a monochromatic path of order at least
![]() $\frac{n}{2}-2\alpha _2(G)$
.
$\frac{n}{2}-2\alpha _2(G)$
.
So a particular case of the general problem we are interested in is the following.
Problem 5.2.
Given
![]() $n$
sufficiently large, determine the largest value of
$n$
sufficiently large, determine the largest value of
![]() $\alpha$
such that if
$\alpha$
such that if
![]() $G$
is a graph on
$G$
is a graph on
![]() $n$
vertices with
$n$
vertices with
![]() $\alpha _2(G)\leq \alpha$
, then in every 2-colouring of
$\alpha _2(G)\leq \alpha$
, then in every 2-colouring of
![]() $G$
there is a monochromatic path of order greater than
$G$
there is a monochromatic path of order greater than
![]() $n/2$
.
$n/2$
.
Finally, we mention that the best upper bounds on the size-Ramsey number of a path come from random
![]() $d$
-regular graphs
$d$
-regular graphs
![]() $G(n,d)$
(see [Reference Dudek and Prałat7]). An upper bound on
$G(n,d)$
(see [Reference Dudek and Prałat7]). An upper bound on
![]() ${\mathrm{mc}}_2(G(n,d))$
would give an upper bound on the longest monochromatic path. However, determining an upper bound on the largest monochromatic component in an arbitrary 2-colouring of
${\mathrm{mc}}_2(G(n,d))$
would give an upper bound on the longest monochromatic path. However, determining an upper bound on the largest monochromatic component in an arbitrary 2-colouring of
![]() $G(n,d)$
for small
$G(n,d)$
for small
![]() $d$
falls outside the purview of this paper (partly since
$d$
falls outside the purview of this paper (partly since
![]() $\alpha _2$
can be large in this case). So we raise the following problem.
$\alpha _2$
can be large in this case). So we raise the following problem.
Problem 5.3.
Determine bounds on
![]() ${\mathrm{mc}}_2(G(n,d))$
for
${\mathrm{mc}}_2(G(n,d))$
for
![]() $d\geq 5$
. More generally, determine bounds on
$d\geq 5$
. More generally, determine bounds on
![]() ${\mathrm{mc}}_r(G(n,d))$
for
${\mathrm{mc}}_r(G(n,d))$
for
![]() $d\geq 2r+1$
.
$d\geq 2r+1$
.
Note that a result of Anastos and Bal [Reference Anastos and Bal1] implies that
![]() ${\mathrm{mc}}_r(G(n,d))=o(n)$
when
${\mathrm{mc}}_r(G(n,d))=o(n)$
when
![]() $d\leq 2r$
.
$d\leq 2r$
.
Acknowledgements
We would like to thank the anonymous referees, whose numerous comments helped improve the paper. In particular we thank one of the referees for the proof of Observation 3.6(ii).