For 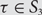$$\tau \in {S_3}$$, let 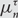$$\mu _n^\tau $$ denote the uniformly random probability measure on the set of $$\tau $$-avoiding permutations in 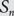$${S_n}$$. Let 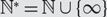$${\mathbb {N}^*} = {\mathbb {N}} \cup \{ \infty \} $$ with an appropriate metric and denote by 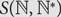$$S({\mathbb{N}},{\mathbb{N}^*})$$ the compact metric space consisting of functions 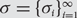$$\sigma {\rm{ = }}\{ {\sigma _i}\} _{i = 1}^\infty {\rm{ }}$$ from 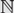$$\mathbb {N}$$ to 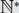$${\mathbb {N}^ * }$$ which are injections when restricted to 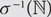$${\sigma ^{ - 1}}(\mathbb {N})$$; that is, if 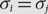$${\sigma _i}{\rm{ = }}{\sigma _j}$$, 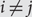$$i \ne j$$, then $${\sigma _i} = \infty $$. Extending permutations 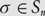$$\sigma \in {S_n}$$ by defining $${\sigma _j} = j$$, for 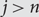$$j \gt n$$, we have 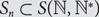$${S_n} \subset S({\mathbb{N}},{{\mathbb{N}}^*})$$. For each $$\tau \in {S_3}$$, we study the limiting behaviour of the measures 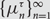$$\{ \mu _n^\tau \} _{n = 1}^\infty $$ on 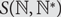$$S({\mathbb{N}},{\mathbb{N}^*})$$. We obtain partial results for the permutation 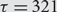$$\tau = 321$$ and complete results for the other five permutations 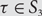$$\tau \in {S_3}$$.