Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T13:29:36.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Independent sets of a given size and structure in the hypercube

Part of: Equilibrium statistical mechanics Limit theorems Graph theory

Published online by Cambridge University Press:  06 January 2022

Matthew Jenssen ,
Will Perkins Open the ORCID record for Will Perkins [Opens in a new window]  and
Aditya Potukuchi
Matthew Jenssen
Affiliation:
School of Mathematics, University of Birmingham, Birmingham, UK
Will Perkins*
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL 60607, USA
Aditya Potukuchi
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL 60607, USA
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the asymptotics of the number of independent sets of size 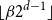$\lfloor \beta 2^{d-1} \rfloor$ in the discrete hypercube 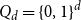$Q_d = \{0,1\}^d$ for any fixed 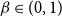$\beta \in (0,1)$ as 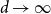$d \to \infty$ , extending a result of Galvin for 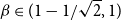$\beta \in (1-1/\sqrt{2},1)$ . Moreover, we prove a multivariate local central limit theorem for structural features of independent sets in 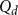$Q_d$ drawn according to the hard-core model at any fixed fugacity 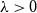$\lambda>0$ . In proving these results we develop several general tools for performing combinatorial enumeration using polymer models and the cluster expansion from statistical physics along with local central limit theorems.

Keywords

independent setshypercubecluster expansionlocal central limit theoremasymptotic enumerationpolymer models

MSC classification

Primary: 05C30: Enumeration in graph theory 05C69: Dominating sets, independent sets, cliques
Secondary: 82B20: Lattice systems (Ising, dimer, Potts, etc.) and systems on graphs 60F05: Central limit and other weak theorems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 4 , July 2022 , pp. 702 - 720
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, R. and Tavaré, S. (1994) Independent process approximations for random combinatorial structures. Adv. Math. 104(1) 90–154.10.1006/aima.1994.1022CrossRefGoogle Scholar
Balogh, J., Garcia, R. I. and Li, L. (2021) Independent sets in the middle two layers of Boolean lattice. J. Comb. Theory Ser. A 178 105341.CrossRefGoogle Scholar
Barvinok, A. and Hartigan, J. (2010) Maximum entropy gaussian approximations for the number of integer points and volumes of polytopes. Adv. Appl. Math. 45(2) 252–289.10.1016/j.aam.2010.01.004CrossRefGoogle Scholar
Barvinok, A. and Hartigan, J. (2012) An asymptotic formula for the number of non-negative integer matrices with prescribed row and column sums. Trans. Am. Math. Soc. 364(8) 4323–4368.10.1090/S0002-9947-2012-05585-1CrossRefGoogle Scholar
Barvinok, A. and Hartigan, J. A. (2013) The number of graphs and a random graph with a given degree sequence. Random Struct. Algorithms 42(3) 301–348.CrossRefGoogle Scholar
Campanino, M., Capocaccia, D. and Tirozzi, B. (1979) The local central limit theorem for a Gibbs random field. Commun. Math. Phys. 70(2) 125–132.10.1007/BF01982350CrossRefGoogle Scholar
DeSalvo, S. and Menz, G. (2016) A robust quantitative local central limit theorem with applications to enumerative combinatorics and random combinatorial structures. arXiv preprint arXiv:1610.07664.Google Scholar
Dobrushin, R. and Tirozzi, B. (1977) The central limit theorem and the problem of equivalence of ensembles. Commun. Math. Phys. 54(2) 173–192.10.1007/BF01614136CrossRefGoogle Scholar
Fristedt, B. (1993) The structure of random partitions of large integers. Trans. Am. Math. Soc. 337(2) 703–735.10.1090/S0002-9947-1993-1094553-1CrossRefGoogle Scholar
Galvin, D. (2011) A threshold phenomenon for random independent sets in the discrete hypercube. Comb. Prob. Comput. 20(1) 27–51.10.1017/S0963548310000155CrossRefGoogle Scholar
Galvin, D. (2012) The independent set sequence of regular bipartite graphs. Discrete Math. 312(19) 2881–2892.10.1016/j.disc.2012.06.011CrossRefGoogle Scholar
Isaev, M. and McKay, B. D. (2018) Complex martingales and asymptotic enumeration. Random Struct. Algorithms 52(4) 617–661.10.1002/rsa.20754CrossRefGoogle Scholar
Jenssen, M. and Keevash, P. (2020) Homomorphisms from the torus. arXiv preprint arXiv:2009.08315.Google Scholar
Jenssen, M., Keevash, P. and Perkins, W. (2020) Algorithms for #BIS-hard problems on expander graphs. SIAM J. Comput. 49(4) 681–710.10.1137/19M1286669CrossRefGoogle Scholar
Jenssen, M. and Perkins, W. (2020) Independent sets in the hypercube revisited. J. London Math. Soc. 102(2) 645–669.CrossRefGoogle Scholar
Korshunov, A. and Sapozhenko, A. (1983) The number of binary codes with distance 2. Problemy Kibernet 40 111–130.Google Scholar
McKinley, G., Michelen, M. and Perkins, W. (2020) Maximum entropy and integer partitions. arXiv preprint arXiv:2012.14498.Google Scholar
Melczer, S., Panova, G. and Pemantle, R. (2020) Counting partitions inside a rectangle. SIAM J. Discrete Math. 34(4) 2388–2410.10.1137/20M1315828CrossRefGoogle Scholar
Romik, D. (2005) Partitions of n into $t\sqrt{n}$ parts. Eur. J. Comb. 26(1) 1–17.CrossRefGoogle Scholar
Sapozhenko, A. (1987) On the number of connected subsets with given cardinality of the boundary in bipartite graphs. Metody Diskret Analiz 45 42–70.Google Scholar