Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T21:41:12.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved Bounds for the Ramsey Number of Tight Cycles Versus Cliques

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  08 March 2016

DHRUV MUBAYI
DHRUV MUBAYI*
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois, Chicago, IL 60607, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The 3-uniform tight cycle Cs3 has vertex set 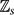${\mathbb Z}_s$ and edge set {{i, i + 1, i + 2}: i ∈ 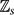${\mathbb Z}_s$}. We prove that for every s ≢ 0 (mod 3) with s ⩾ 16 or s ∈ {8, 11, 14} there is a cs > 0 such that the 3-uniform hypergraph Ramsey number r(Cs3, Kn3) satisfies

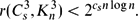$$\begin{equation*} r(C_s^3, K_n^3)< 2^{c_s n \log n}.\ \end{equation*}$$
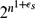This answers in a strong form a question of the author and Rödl, who asked for an upper bound of the form $2^{n^{1+\epsilon_s}}$ for each fixed s ⩾ 4, where εs → 0 as s → ∞ and n is sufficiently large. The result is nearly tight as the lower bound is known to be exponential in n.

MSC classification

Primary: 05C65: Hypergraphs
Secondary: 05D10: Ramsey theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 5 , September 2016 , pp. 791 - 796
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ajtai, M., Komlós, J. and Szemerédi, E. (1980) A note on Ramsey numbers. J. Combin. Theory Ser. A 29 354–360.CrossRefGoogle Scholar
[2] Bohman, T. and Keevash, P. (2010) The early evolution of the H-free process. Invent. Math. 181 291–336.Google Scholar
[3] Bohman, T. and Keevash, P. (2013) Dynamic concentration of the triangle-free process. The Seventh European Conference on Combinatorics, Graph Theory and Applications, (Norm, P.. ed.), vol. 16, CRM Series, pp. 489–495.CrossRefGoogle Scholar
[4] Caro, Y., Li, Y., Rousseau, C. and Zhang, Y. (2000) Asymptotic bounds for some bipartite graph: Complete graph Ramsey numbers. Discrete Math. 220 51–56.Google Scholar
[5] Conlon, D., Fox, J. and Sudakov, B. (2010) Hypergraph Ramsey numbers. J. Amer. Math. Soc. 23 247–266.CrossRefGoogle Scholar
[6] Erdős, P. (1984) Extremal problems in number theory, combinatorics and geometry. In Proc. International Congress of Mathematicians, PWN, Warsaw, pp. 51–70.Google Scholar
[7] Erdős, P. and Hajnal, A. (1972) On Ramsey like theorems, problems and results. In Combinatorics: Proc. Conference Combinatorial Mathematics, IMA, Southend-on-Sea, pp. 123–140.Google Scholar
[8] Fiz Pontiveros, G., Griffiths, S. and Morris, R. The triangle-free process and R(3,k). arXiv:1302.6279 Google Scholar
[9] Kim, J. H. (1995) The Ramsey number R(3,t) has order of magnitude t 2/log t. Random Struct. Alg. 7 173–207.Google Scholar
[10] Kostochka, A., Mubayi, D. and Verstraëte, J. (2014) On independent sets in hypergraphs. Random Struct. Alg. 44 224–239.CrossRefGoogle Scholar
[11] Mubayi, D. and Rödl, V. (2016) Hypergraph Ramsey numbers: Tight cycles versus cliques. Bull. Lond. Math. Soc. 48 127–134.Google Scholar
[12] Spencer, J. (1972) Turán theorem for k-graphs. Discrete Math. 2 183–186.Google Scholar
[13] Sudakov, B. (2005) A new lower bound for a Ramsey-type problem. Combinatorica 25 487–498.CrossRefGoogle Scholar