Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T04:01:18.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Identifying and Locating–Dominating Codes in (Random) Geometric Networks

Published online by Cambridge University Press:  11 August 2009

T. MÜLLER  and
J.-S. SERENI
T. MÜLLER
Affiliation:
School of Mathematics, Tel Aviv University, Ramat Aviv 69978, Israel (e-mail: [email protected])
J.-S. SERENI
Affiliation:
CNRS (LIAFA, Université Denis Diderot), Paris, France and Department of Applied Mathematics (KAM), Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

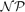We model a problem about networks built from wireless devices using identifying and locating–dominating codes in unit disk graphs. It is known that minimizing the size of an identifying code is -complete even for bipartite graphs. First, we improve this result by showing that the problem remains 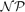-complete for bipartite planar unit disk graphs. Then, we address the question of the existence of an identifying code for random unit disk graphs. We derive the probability that there exists an identifying code as a function of the radius of the disks, and we find that for all interesting ranges of r this probability is bounded away from one. The results obtained are in sharp contrast to those concerning random graphs in the Erdős–Rényi model. Another well-studied class of codes is that of locating–dominating codes, which are less demanding than identifying codes. A locating–dominating code always exists, but minimizing its size is still 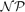-complete in general. We extend this result to our setting by showing that this question remains 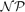-complete for arbitrary planar unit disk graphs. Finally, we study the minimum size of such a code in random unit disk graphs, and we prove that with probability tending to one, it is of size (n/r)2/3+o(1) if r ≤ 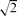/2−ϵ is chosen such that nr2 → ∞, and of size n1+o(1) if nr2 ≪ lnn.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 6 , November 2009 , pp. 925 - 952
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Agarwal, A. and Spencer, J. (2006) Undecidable statements and the zero-one law in random geometric graphs to appear in Discrete Comp. Geometry.Google Scholar
[2]Breu, H. and Kirkpatrick, D. G. (1998) Unit disk graph recognition is NP-hard. Comput. Geom. 9 3–24.CrossRefGoogle Scholar
[3]Chakrabarty, K., Karpovsky, M. G. and Levitin, L. B. (1998) Fault isolation and diagnosis in multiprocessor systems with point-to-point connections. In Fault-Tolerant Parallel and Distributed Systems (Avresky, D. R. and Kaeli, D. R., eds), Kluwer, pp. 285–301.CrossRefGoogle Scholar
[4]Charon, I., Hudry, O. and Lobstein, A. (2003) Minimizing the size of an identifying or locating–dominating code in a graph is NP-hard. Theoret. Comput. Sci. 290 2109–2120.CrossRefGoogle Scholar
[5]Clark, B. N., Colbourn, C. J. and Johnson, D. S. (1990) Unit disk graphs. Discrete Math. 86 165–177.CrossRefGoogle Scholar
[6]Colbourn, C. J., Slater, P. J. and Stewart, L. K. (1987) Locating dominating sets in series parallel networks. Congr. Numer. 56 135–162.Google Scholar
[7]Fößmeier, U., Kant, G. and Kaufmann, M. (1996) 2-visibility drawings of plane graphs. In Proc. Graph Drawing '96, Vol. 1190 of Lecture Notes in Computer Science, Springer, Berlin, pp. 155–168.Google Scholar
[8]Frieze, A., Martin, R., Moncel, J., Ruszinko, M. and Smyth, C. (2007) Codes identifying sets of vertices in random networks. Discrete Math. 307 1094–1107.CrossRefGoogle Scholar
[9]Honkala, I., Karpovsky, M. G. and Levitin, L. B. (2006) On robust and dynamic identifying codes. IEEE Trans. Inform. Theory 52 599–612.CrossRefGoogle Scholar
[10]Janson, S. (1998) New versions of Suen's correlation inequality. In Proc. 8th International Conference ‘Random Structures and Algorithms’ (Poznan 1997), Vol. 13, pp. 467–483.3.0.CO;2-W>CrossRefGoogle Scholar
[11]Karpovsky, M. G., Chakrabarty, K. and Levitin, L. B. (1998) On a new class of codes for identifying vertices in graphs. IEEE Trans. Inform. Theory 44 599–611.CrossRefGoogle Scholar
[12]Lichtenstein, D. (1982) Planar formulae and their uses. SIAM J. Comput. 11 329–343.CrossRefGoogle Scholar
[13]Mainwaring, A., Culler, D., Polastre, J., Szewczyk, R. and Anderson, J. (2002) Wireless sensor networks for habitat monitoring. In Proc. 1st ACM International Workshop on Wireless Sensor Networks and Applications, pp. 88–97.CrossRefGoogle Scholar
[14]Papakostas, A. and Tollis, I. G. (1998) Orthogonal drawings of high degree graphs with small area and few bends. In Proc. 5th Workshop on Algorithms and Data Structures, Vol. 1272 of Lecture Notes in Computer Science, Springer, Berlin, pp. 354–367.Google Scholar
[15]Penrose, M. D. (2003) Random Geometric Graphs, Oxford University Press, Oxford.CrossRefGoogle Scholar
[16]Ray, S., Starobinski, D., Trachtenberg, A. and Ungrangsi, R. (2004) Robust location detection with sensor networks. IEEE Journal on Selected Areas in Communications (Special Issue on Fundamental Performance Limits of Wireless Sensor Networks) 22 1016–1025.Google Scholar
[17]Suen, W.-C. S. (1990) A correlation inequality and a Poisson limit theorem for nonoverlapping balanced subgraphs of a random graph. Random Struct. Alg. 1 231–242.CrossRefGoogle Scholar