Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-01T20:57:57.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypergraph independence polynomials with a zero close to the origin

Part of: Equilibrium statistical mechanics Graph theory

Published online by Cambridge University Press:  22 January 2025

Shengtong Zhang Open the ORCID record for Shengtong Zhang [Opens in a new window]
Shengtong Zhang*
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA, USA
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For each uniformity 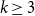$k \geq 3$, we construct 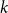$k$ uniform linear hypergraphs 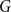$G$ with arbitrarily large maximum degree 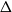$\Delta$ whose independence polynomial 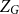$Z_G$ has a zero 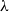$\lambda$ with 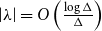$\left \vert \lambda \right \vert = O\left (\frac {\log \Delta }{\Delta }\right )$. This disproves a recent conjecture of Galvin, McKinley, Perkins, Sarantis, and Tetali.

Keywords

Independence polynomialhypergraphzero-free region

MSC classification

Primary: 05C31: Graph polynomials
Secondary: 05C69: Dominating sets, independent sets, cliques 82B20: Lattice systems (Ising, dimer, Potts, etc.) and systems on graphs
Type
Paper
Information
Combinatorics, Probability and Computing , First View , pp. 1 - 5
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Davies, E. and Perkins, W. (2023) Approximately counting independent sets of a given size in bounded-degree graphs. SIAM J. Comput 52 618–640.CrossRefGoogle Scholar
Galvin, D. McKinley, G. Perkins, W. Sarantis, M. and Tetali, P. (2024) On the zeroes of hypergraph independence polynomials. Combin. Probab. Comput 33 65–84.CrossRefGoogle Scholar
Heilmann, O. J. and Lieb, E. H. (1972) Theory of monomer-dimer systems. Comm. Math. Phys 25 190–232.CrossRefGoogle Scholar
Jain, V., Perkins, W., Sah, A. and Sawhney, M. (2022) Approximate counting and sampling via local central limit theorems. In STOC ’22—Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing, ACM, New York, pp. 1473–1486. ©2022CrossRefGoogle Scholar
Mousset, F. Noever, A. Panagiotou, K. and Samotij, W. (2020) On the probability of nonexistence in binomial subsets. Ann. Probab 48 493–525.CrossRefGoogle Scholar
Peters, H. and Regts, G. (2019) On a conjecture of Sokal concerning roots of the independence polynomial. Michigan Math. J 68 33–55.CrossRefGoogle Scholar
Scott, A. D. and Sokal, A. D. (2005) The repulsive lattice gas, the independent-set polynomial, and the Lovász local lemma. J. Stat. Phys 118 1151–1261.CrossRefGoogle Scholar
Shearer, J. B. (1985) On a problem of Spencer. Combinatorica 5 241–245.CrossRefGoogle Scholar
Sly, A. (2010) Computational transition at the uniqueness threshold. In 2010 IEEE 51st Annual Symposium on Foundations of Computer Science—FOCS 2010, IEEE Computer Soc, Los Alamitos, CA, pp. 287–296.CrossRefGoogle Scholar
Weitz, D. (2006) Counting independent sets up to the tree threshold. In STOC’06: Proceedings of the 38th Annual ACM Symposium on Theory of Computing, ACM, New York, pp. 140–149.CrossRefGoogle Scholar