Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Edwards, Keith
1996.
The Harmonious Chromatic Number of Bounded Degree Trees.
Combinatorics, Probability and Computing,
Vol. 5,
Issue. 1,
p.
15.
Edwards, Keith
1999.
The harmonious chromatic number of complete r-ary trees.
Discrete Mathematics,
Vol. 203,
Issue. 1-3,
p.
83.
Muntaner-Batle, Francisco Antonio
Vernold Vivin, J.
and
Venkatachalam, M.
2014.
Harmonious Coloring on Corona Product of Complete Graphs.
National Academy Science Letters,
Vol. 37,
Issue. 5,
p.
461.
Drgas-Burchardt, Ewa
and
Gibek, Katarzyna
2017.
Harmonious colourings of graphs.
Discrete Applied Mathematics,
Vol. 217,
Issue. ,
p.
175.
Franklin Thamil Selvi, M. S.
and
Amutha, A.
2021.
RETRACTED ARTICLE: A study on harmonious chromatic number of total graph of central graph of generalized Petersen graph.
Journal of Ambient Intelligence and Humanized Computing,
Vol. 12,
Issue. 3,
p.
3815.
Franklin Thamil Selvi, M. S
and
Amutha, A.
2021.
Optimization of Harmonious Coloring Problem in Mesh Derived Architecture.
Journal of Physics: Conference Series,
Vol. 1770,
Issue. 1,
p.
012082.


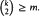 ≥
≥ 