Hostname: page-component-5cf477f64f-h6p2m Total loading time: 0 Render date: 2025-04-01T20:54:13.892Z Has data issue: false hasContentIssue false
  • English
  • Français

Hamiltonicity of sparse pseudorandom graphs

Part of: Graph theory

Published online by Cambridge University Press:  25 March 2025

Asaf Ferber ,
Jie Han ,
Dingjia Mao Open the ORCID record for Dingjia Mao [Opens in a new window]  and
Roman Vershynin
Asaf Ferber
Affiliation:
Department of Mathematics, University of California, Irvine, CA, USA
Jie Han
Affiliation:
School of Mathematics and Statistics and Center for Applied Mathematics, Beijing Institute of Technology, Beijing, China
Dingjia Mao*
Affiliation:
Department of Mathematics, University of California, Irvine, CA, USA
Roman Vershynin
Affiliation:
Department of Mathematics, University of California, Irvine, CA, USA
*
Corresponding author: Dingjia Mao; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

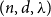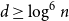We show that every $(n,d,\lambda )$-graph contains a Hamilton cycle for sufficiently large $n$, assuming that $d\geq \log ^{6}n$ and 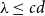$\lambda \leq cd$, where 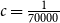$c=\frac {1}{70000}$. This significantly improves a recent result of Glock, Correia, and Sudakov, who obtained a similar result for $d$ that grows polynomially with $n$. The proof is based on a new result regarding the second largest eigenvalue of the adjacency matrix of a subgraph induced by a random subset of vertices, combined with a recent result on connecting designated pairs of vertices by vertex-disjoint paths in 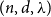$(n,d,\lambda )$-graphs. We believe that the former result is of independent interest and will have further applications.

Keywords

Hamilton cycleexpander graph

MSC classification

Secondary: 05C45: Eulerian and Hamiltonian graphs 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , First View , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, P., Böttcher, J., Hàn, H., Kohayakawa, Y. and Person, Y. (2014) Powers of Hamilton cycles in Pseudorandom graphs.In LATIN 2014: Theoretical Informatics: 11th Latin American Symposium, Springer, Montevideo, Uruguay, pp. 355–366, Proceedings 11, March 31–April 4.CrossRefGoogle Scholar
Alon, N., Krivelevich, M. and Sudakov, B. (2007) Embedding nearly-spanning bounded degree trees. Combinatorica 27(6) 629–644.CrossRefGoogle Scholar
Alon, N. and Spencer, J. H. (2016) The probabilistic method. John Wiley & Sons.Google Scholar
Balogh, J., Csaba, B., Pei, M. and Samotij, W. (2010) Large bounded degree trees in expanding graphs. Electron. J. Comb. 17(1) R6–R6.CrossRefGoogle Scholar
Bollobás, B. (1984) The evolution of sparse graphs. In Graph theory and combinatorics (Cambridge, 1983), pp. 35–57Google Scholar
Brouwer, A. E. and Haemers, W. H. (2011) Spectra of graphs. Springer Science & Business Media.Google Scholar
Chung, F. and Horn, P. (2007) The spectral gap of a random subgraph of a graph. Internet Math. 4(2–3) 225–244.Google Scholar
Conlon, D., Fox, J. and Zhao, Y. (2014) Extremal results in sparse Pseudorandom graphs. Adv. Math 256 206–290.CrossRefGoogle Scholar
Dirac, G. A. (1952) Some theorems on abstract graphs. Proc. Lond. Math. Soc. 3(1) 69–81.CrossRefGoogle Scholar
Draganić, N., Montgomery, R., Correia, D. M., Pokrovskiy, A. and Sudakov, B. (2024) Hamiltonicity of expanders: optimal bounds and applications, arXiv: 2402.06603.Google Scholar
Friedman, J. and Pippenger, N. (1987) Expanding graphs contain all small trees. Combinatorica 7(1) 71–76.CrossRefGoogle Scholar
Frieze, A. (2019) Hamilton cycles in random graphs: a bibliography, arXiv preprint arXiv: 1901.07139.Google Scholar
Frieze, A. and Karoński, M. (2016) Introduction to random graphs. Cambridge University Press.Google Scholar
Glock, S., Correia, D. M. and Sudakov, B. (2024) Hamilton cycles in Pseudorandom graphs. Adv. Math 458 109984.CrossRefGoogle Scholar
Hàn, H., Han, J. and Morris, P. (2022) Factors and loose Hamilton cycles in sparse pseudo-random hypergraphs. Random Struct. Algor. 61(1) 101–125.Google Scholar
Han, J., Kohayakawa, Y., Morris, P. and Person, Y. (2021) Finding any given 2-factor in sparse pseudorandom graphs efficiently. J. Graph Theor. 96(1) 87–108.CrossRefGoogle Scholar
Han, J. and Yang, D. (2022) Spanning trees in sparse expanders, arXiv preprint arXiv: 2211.04758.Google Scholar
Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58(301) 13–30.CrossRefGoogle Scholar
Hoory, S., Linial, N. and Wigderson, A. (2006) Expander graphs and their applications. Bull. Am. Math. Soc. 43(04) 439–561.Google Scholar
Hyde, J., Morrison, N., Müyesser, A. and Pavez-Signé, M. (2023) Spanning trees in pseudorandom graphs via sorting networks, arXiv preprint arXiv: 2311.03185.Google Scholar
Karp, R. M. (1972) Reducibility among combinatorial problems, Complexity of computer computations. Springer, pp. 85–103.Google Scholar
Kohayakawa, Y., Rödl, V., Schacht, M., Sissokho, P. and Skokan, J. (2007) Turán’s theorem for Pseudo-random graphs. J. Comb. Theory Ser. A 114(4) 631–657.CrossRefGoogle Scholar
Komlós, J. and Szemerédi, E. (1983) Limit distribution for the existence of Hamiltonian cycles in a random graph. Discrete Math. 43(1) 55–63.Google Scholar
Korshunov, A. D. (1976) Solution of a problem of Erdős and Renyi on Hamiltonian cycles in nonoriented graphs, Doklady Akademii Nauk, Vol. 228, Russian Academy of Sciences, pp. 529–532.Google Scholar
Krivelevich, M. and Sudakov, B. (2003) Sparse Pseudo-random graphs are Hamiltonian. J. Graph. Theor. 42(1) 17–33.Google Scholar
Krivelevich, M. and Sudakov, B. (2006) Pseudo-random graphs, More sets, graphs and numbers: A Salute to Vera Sos and András Hajnal. Springer, pp. 199–262.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2012) A survey on Hamilton cycles in directed graphs. Eur. J. Combin. 33(5) 750–766.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2014) Hamilton cycles in graphs and hypergraphs: an extremal perspective. In Proceedings of the International Congress of Mathematicians 2014, Seoul, Korea, vol. 4, KyungMoon Sa, Seoul, pp. 381–406.Google Scholar
Lee, C. and Sudakov, B. (2012) Dirac’s theorem for random graphs. Random Struct. Algor. 41(3) 293–305.CrossRefGoogle Scholar
Montgomery, R. (2019) Hamiltonicity in random graphs is born resilient. J. Comb. Theory Ser. B 139 316–341.Google Scholar
Nenadov, R. (2019) Triangle-factors in Pseudorandom graphs. Bull. Lond. Math. Soc. 51(3) 421–430.CrossRefGoogle Scholar
Nenadov, R., Steger, A. and Trujić, M. (2019) Resilience of perfect matchings and Hamiltonicity in random graph processes. Random Struct. Algor. 54(4) 797–819.Google Scholar
Pavez-Signé, M. (2023) Spanning trees in the square of pseudorandom graphs, arXiv: 2307.00322.Google Scholar
Pósa, L. (1976) Hamiltonian circuits in random graphs. Discrete Math. 14(4) 359–364.CrossRefGoogle Scholar
Rudelson, M. and Vershynin, R. (2007) Sampling from large matrices: an approach through geometric functional analysis. J. ACM (JACM) 54(4) 21–es.CrossRefGoogle Scholar
Sudakov, B. and Vu, V. H. (2008) Local resilience of graphs. Random Struct. Algor. 33(4) 409–433.CrossRefGoogle Scholar
Thomason, A. (1987) Pseudo-random graphs, North-Holland Mathematics Studies, Vol. 144, Elsevier, pp. 307–331.Google Scholar
Thomason, A. (1987) Random graphs, strongly regular graphs and Pseudorandom graphs. Surv. Comb. 123(173–195) 1.Google Scholar
Thompson, R. C. (1972) Principal submatrices ix: interlacing inequalities for singular values of submatrices. Linear Algebra Appl. 5(1) 1–12.CrossRefGoogle Scholar
Tropp, J. (2008) The random paving property for uniformly bounded matrices. Stud. Math. 185(1) 67–82.CrossRefGoogle Scholar
Tropp, J. A. (2008) Norms of random submatrices and sparse approximation. C R Math. 346(23–24) 1271–1274.CrossRefGoogle Scholar
West, D. B. et al. (2001) West, etal, Introduction to graph theory, Vol. 2, Prentice hall Upper Saddle River.Google Scholar