Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T23:42:50.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Greedy Random Walk

Published online by Cambridge University Press:  20 November 2013

TAL ORENSHTEIN  and
IGOR SHINKAR
TAL ORENSHTEIN
Affiliation:
Department of Mathematics, Weizmann Institute of Science, Rehovot, Israel (e-mail: [email protected] and [email protected])
IGOR SHINKAR
Affiliation:
Department of Mathematics, Weizmann Institute of Science, Rehovot, Israel (e-mail: [email protected] and [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a discrete time self-interacting random process on graphs, which we call greedy random walk. The walker is located initially at some vertex. As time evolves, each vertex maintains the set of adjacent edges touching it that have not yet been crossed by the walker. At each step, the walker, being at some vertex, picks an adjacent edge among the edges that have not traversed thus far according to some (deterministic or randomized) rule. If all the adjacent edges have already been traversed, then an adjacent edge is chosen uniformly at random. After picking an edge the walker jumps along it to the neighbouring vertex. We show that the expected edge cover time of the greedy random walk is linear in the number of edges for certain natural families of graphs. Examples of such graphs include the complete graph, even degree expanders of logarithmic girth, and the hypercube graph. We also show that GRW is transient in 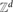$\mathbb{Z}^d$ for all d ≥ 3.

Keywords

Primary 05C85Secondary 60K35
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 2 , March 2014 , pp. 269 - 289
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aldous, D. J. (1989) Lower bounds for covering times for reversible Markov chains and random walks on graphs. J. Theoret. Probab. 2 91–100.CrossRefGoogle Scholar
[2]Aldous, D. J. (1991) Random walk covering of some special trees. J. Math. Anal. Appl. 157 271–283.CrossRefGoogle Scholar
[3]Aleliunas, R., Karp, R. M., Lipton, R. J., Lovasz, L. and Charles, R. (1979) Random walks, universal traversal sequences, and the complexity of maze problems. In Proc. 20th Annual Symposium on Foundations of Computer Science, pp. 218–223.CrossRefGoogle Scholar
[4]Alon, N., Benjamini, I., Lubetzky, E. and Sodin, S. (2007) Non-backtracking random walks mix faster. Commun. Contemp. Math. 9 585–603.CrossRefGoogle Scholar
[5]Avin, C. and Krishnamachari, B. (2008) The power of choice in random walks: An empirical study. Comput. Networks 52 44–60.CrossRefGoogle Scholar
[6]Benjamini, I., Gurel-Gurevich, O. and Morris, B. (2013) Linear cover time is exponentially unlikely. Probab. Theory Rel. Fields 155 451–461.CrossRefGoogle Scholar
[7]Benjamini, I. and Wilson, D. B. (2003) Excited random walk. Elect. Comm. Probab. 8 86–92.Google Scholar
[8]Berenbrink, P., Cooper, C., Elsässer, R., Radzik, T. and Sauerwald, T. (2010) Speeding up random walks with neighborhood exploration. In Proc. 21st Annual ACM–SIAM Symposium on Discrete Algorithms, pp. 1422–1435.CrossRefGoogle Scholar
[9]Berenbrink, P., Cooper, C. and Friedetzky, T. (2012) Random walks which prefer unvisited edges, and exploring high girth even degree expanders in linear time. In Proc. 31st Annual ACM SIGACT–SIGOPS Symposium on Principles of Distributed Computing.CrossRefGoogle Scholar
[10]Bollobás, B. (2001) Random Graphs, Cambridge University Press.CrossRefGoogle Scholar
[11]Broder, A. Z. and Karlin, A. R. (1989) Bounds on the cover time. J. Theoret. Probab. 2 101–120.CrossRefGoogle Scholar
[12]Bunimovich, L. A. and Troubetzkoy, S. E. (1992) Recurrence properties of Lorentz lattice gas cellular automata. J. Statist. Phys. 67 289–302.CrossRefGoogle Scholar
[13]Feige, U. (1995) A tight lower bound on the cover time for random walks on graphs. Random Struct. Alg. 6 433–438.CrossRefGoogle Scholar
[14]Friedrich, T. and Sauerwald, T. (2010) The cover time of deterministic random walks. In Proc. 16th Annual International Conference on Computing and Combinatorics: COCOON'10, Springer, pp. 130–139.CrossRefGoogle Scholar
[15]Hoory, S., Linial, N. and Wigderson, A. (2006) Expander graphs and their applications. Bull. Amer. Math. Soc. 43 439–561.CrossRefGoogle Scholar
[16]Madras, N. and Wu, C. C. (2005) Self-avoiding walks on hyperbolic graphs. Combin. Probab. Comput. 14 523–548.CrossRefGoogle Scholar
[17]Pemantle, R. (2007) A survey of random processes with reinforcement. Probability Surveys 4 1–79.CrossRefGoogle Scholar
[18]Ruijgrok, T. and Cohen, E. (1988) Deterministic lattice gas models. Phys. Lett. A 133 415–418.CrossRefGoogle Scholar
[19]Yaari, Y. (2011) MSc thesis, Weizmann Institute of Science, Israel.Google Scholar
[20]Zuckerman, D. (1990) A technique for lower bounding the cover time. In Proc. 22nd annual ACM Symposium on Theory of Computing: STOC '90, ACM, pp. 254–259.CrossRefGoogle Scholar