Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T21:08:48.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Forward Clusters for Degenerate Random Environments

Part of: Special processes

Published online by Cambridge University Press:  24 May 2016

MARK HOLMES  and
THOMAS S. SALISBURY
MARK HOLMES
Affiliation:
Department of Statistics, University of Auckland, 38 Princes Street, Auckland, 1010, New Zealand (e-mail: [email protected])
THOMAS S. SALISBURY
Affiliation:
Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, ON M3J 1P3, Canada (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider connectivity properties and asymptotic slopes for certain random directed graphs on ℤ2 in which the set of points 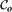$\mathcal{C}_o$ that the origin connects to is always infinite. We obtain conditions under which the complement of 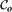$\mathcal{C}_o$ has no infinite connected component. Applying these results to one of the most interesting such models leads to an improved lower bound for the critical occupation probability for oriented site percolation on the triangular lattice in two dimensions.

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 5 , September 2016 , pp. 744 - 765
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Balister, P., Bollobás, B. and Stacey, A. (1994) Improved upper bounds for the critical probability of oriented percolation in two dimensions. Random Struct. Alg. 5 573–589.Google Scholar
[2] Berger, N. and Deuschel, J.-D. (2012) Quenched invariance principle for random walk in balanced random environment. Probab. Theory Rel. Fields 152 207–230.Google Scholar
[3] De'Bell, K. and Essam, J. W. (1983) Estimates of the site percolation probability exponents for some directed lattices. J. Phys. A 16 3145–3147.CrossRefGoogle Scholar
[4] Durrett, R. (1984) Oriented percolation in two dimensions. Ann. Probab. 12 999–1040.CrossRefGoogle Scholar
[5] Grimmett, G. and Hiemer, P. (2002) Directed percolation and random walk. In In and Out of Equilibrium: Mambucaba 2000, Vol. 51 of Progress in Probability, Birkhäuser, pp. 273–297.CrossRefGoogle Scholar
[6] Holmes, M. and Salisbury, T. S. (2014) Degenerate random environments. Random Struct. Alg. 45 111–137.CrossRefGoogle Scholar
[7] Holmes, M. and Salisbury, T. S. (2014) Random walks in degenerate random environments. Canadian J. Math. 66 1050–1077.Google Scholar
[8] Holmes, M. and Salisbury, T. S. (2016) Ballisticity and invariance principle for random walk in non-elliptic random environment. Preprint.CrossRefGoogle Scholar
[9] Holmes, M. and Salisbury, T. S. (2016) Notes on oriented percolation. arXiv:1603.07806 Google Scholar
[10] Hughes, B. D. (1995/1996) Random Walks and Random Environments, Vols 1, 2, Oxford University Press.CrossRefGoogle Scholar
[11] Jensen, I. and Guttmann, A. J. (1996) Series expansions of the percolation probability on the directed triangular lattice. J. Phys. A 29 497–517.Google Scholar